Quantum interference effects in biphenyl dithiol for gas detection

Abstract

Based on density functional theory and non-equilibrium Green's function method, we investigate the transport properties of four different gases (NO, NO₂, NH₃, and CO) adsorbed on biphenyl dithiol molecules coupled to gold leads. Since the transmission function is strongly affected by quantum interference, namely antiresonance and Fano resonances, significant changes in conductance caused by the adsorption of molecular gases are archived. Our findings suggest that biphenyl dithiol exhibits strong sensitivity for NO and NO₂ which results from their interference features being close to the Fermi energy of the gold leads and dominate the transport of the system. Moreover, the quantum interference effects also result in enhanced and suppressed conductance, which enable us to significantly improve the selectivity. In particular, a distinction between NO, NO₂ and NH₃ gases based on the biphenyl dithiol appears possible.

---

1 Introduction

Charge transport in metal–molecule–metal junctions is of fundamental interest since such junctions represent a significant step toward the understanding of quantum transport theories^1,2 and pave the way towards possible applications³ in nanoelectronics. Many phenomena in single molecules connected to nano-gap electrodes: e.g. giant magnetoresistance,⁴ conductance switching,^5–8 negative differential resistance,^9–11 have been observed. Additionally, theorists have predicted that it should be possible to observe quantum interference in single molecules,^12–14 which is a characteristic of coherent transport. As previously discussed,^15–20 quantum interference can control electrical transport, leading to the possibility of modulating the conductance through molecular conformation, charge distribution and frontier molecular orbitals, and gives us opportunities for more advanced molecular electronic components.

Experimentally, it has been demonstrated that quantum interference in molecular junctions could be measured at room temperature.^16–20 On the other hand, there are only few reports where interference-based devices have been proposed; for example, H–H tautomerization molecular switch studied by us,²¹ quantum interference effect transistors²² as well as quantum interferences in DNA sequencing.^23,24 So far, to the best of our knowledge, no studies have demonstrated applications as gas sensor devices based on quantum interference. Over the last few years, several nanoscale gas sensors have been developed utilizing nanostructured materials; for instance, carbon nanotubes,^25,26 graphene,^27,28 silicene²⁹ and other layered nanomaterials.^30,31 Moreover, it has been suggested that organic materials, such as metal porphyrin^32,33 or phthalocyanine,³⁴ can be used to detect various gases with high sensitivity and selectivity due to a direct modification of their molecular orbital states as well as their unique properties of molecular recognition.

Several theoretical and experimental studies have been previously reported concerning single-molecule biphenyl dithiol (BPDT) junctions for the possibility of future applications in nanoelectronics such as molecular switches based on conformational change^35–38 and thermoelectricity in molecular junctions.^39,40 Particularly in the latter case,⁴⁰ it was experimentally demonstrated that the electrical conductance of molecular junctions can be controlled by a gate electrode. A few theoretical studies^37,38,41,42 based on a combination of the non-equilibrium Green's function (NEGF) technique and density functional theory (DFT) were carried out to investigate the electronic structure and transport properties of BPDT. However, to our knowledge, there is no study on a quantum interference sensor device based on BPDT. At least one DFT-based study⁴³ has demonstrated quantum interference effects in Au–S–BPDT–S–Au junctions, resulting from different molecular bridge sites between the BPDT and electrodes.

The purpose of our study was to investigate the quantum interference effects of BPDT with gas adsorption to assess the usefulness of this setup for the purpose of gas sensing. We study the transport properties of BPDT coupled to two Au(111) surfaces using a combination of NEGF techniques^44–46 and DFT.⁴⁷ Four gas molecules; i.e., NO, NO₂, NH₃, and CO, which are all of main interest for industrial, environmental and medical purposes, were adsorbed onto BPDT. The results indicate changes in conductance due to interference features in the electronic transmission. The possibility to discriminate four different gas molecules (NO, NO₂, NH₃, and CO) has been discussed in terms of sensitivity and selectivity.

2 Methodology

The molecular structure of BPDT, whose S atoms were terminated with H atoms, was first optimized. The obtained bond lengths and molecular configuration are similar to previous DFT studies.^41,42,48 To construct the BPDT molecular device, the molecule was placed between semi-infinite Au(111)-(3 × 3) electrodes (see Fig. 1a). Such a system was divided into three regions: left and right electrodes and a central region. The central region contains a portion of the electrode to screen out any perturbation of the metal coming from BPDT. The molecular adsorption of a thiol was determined by placing BPDT above different adsorption sites: on top, bridge, fcc and hcp, on Au(111) surface. The BPDT is adsorbed at a hollow site at which the average distance between the S atom and the two nearest neighbor Au atoms is 2.53 Å. The device configuration with two electrodes was then optimized again, allowing all atoms in the scattering region to relax.

Fig. 1 (a) A schematic setup of a two-probe system with a single molecule BPDT coupled to Au(111) leads, where the most stable configurations for the four gas species NO, NH₃, NO₂, and CO adsorbed on the BPDT are presented, and (b) their transmission functions (top) and PDOS of the scattering region (bottom) as a function of energy E.

All optimizations were performed using DFT,^49,50 as implemented in the SIESTA package.⁴⁷ We employed a van der Waals correction^51,52 taking into account the weak dispersive interactions to the generalized gradient approximation of Perdew, Burke, and Ernzerhof (PBE–GGA).⁵³

A description of van der Waals (vdW) interactions was included in our calculations using the non-local van der Waals density functional (vdW-DF) of Dion et al.⁵⁴ In this approach, the exchange–correlation energy is written as E_xc = E^GGA_x + E^LDA_c + E^nl_c, where the exchange energy E^GGA_x uses the GGA functional, and E^LDA_c is the local density approximation (LDA) to correlation energy. The nonlocal correlation-energy part, E^nl_c, is defined to include the longest-ranged or most nonlocal energy term which is zero for systems with constant density.

A double-ζ plus polarization (DZP) basis and norm-conserving pseudopotentials⁵⁵ were employed. The k-point was set to 5 × 5 × 3 for the Brillouin zone integration. The mesh cutoff value was 350 Ry for the real-space grid. The binding energy between the BPDT and the gas molecules was calculated as (E_BPDT + E_gas) − E_total, where E_total is the total energy of the system (BPDT + gas), and E_BPDT and E_gas are the energy of the BPDT and gas, respectively.

The transport properties were investigated by the quantum transport code TranSIESTA, with the NEGF method. Since TranSIESTA uses the SIESTA code as its DFT platform, the basis sets and real-space grid employed are the same as those used for the geometrical relaxation part. Within the NEGF approach, the transmission indicating the probability for electrons with incident energy E to be transferred from the left to the right electrode, is calculated from T(E) = Tr[Γ_R(E)G^R(E)Γ_L(E)G^A(E)], where Γ_L,(R)(E) is the broadening matrix of the left (right) electrode, and G^R,(A)(E) is the retarded (advanced) Green's function.⁴⁵ We simply evaluated the conductance, G = G₀T(E_F),⁵⁶ where is the quantum conductance, e is the charge of the electron, and h is Planck's constant. Throughout this paper, it should be noted that we will focus on zero-bias transmission, in which the pronounced interference features appear and are the most straightforward to understand.

3 Results

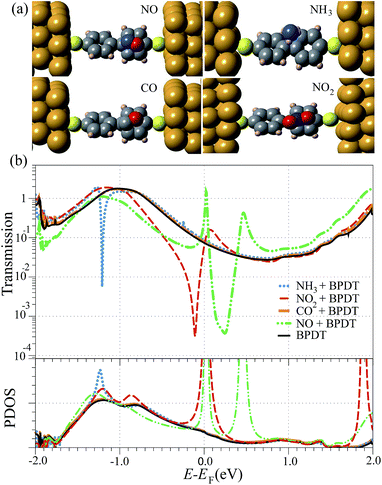
Fig. 1a shows the most favorable adsorption configurations of the NO₂, NO, NH₃ and CO molecules on the BPDT. Different molecular orientations of the gases were initially placed at different positions on the BPDT molecule (see more details in the ESI†). The C and N atoms of CO and NO adsorbed on the ring-connecting C atom of the BPDT molecule with a binding distance of 3.02 Å and 2.52 Å, respectively, while five non-connecting C atoms become less stable adsorption sites. Note that the binding distance is defined as the shortest atom-to-atom distance between the BPDT and the gas molecules. Similarly, NO₂ prefers binding to the ring-connecting C atom with a binding distance of 2.50 Å. In the case of NH₃, its three hydrogen atoms pointing toward the BPDT were found to be the most favorable configuration with a binding distance of 3.11 Å. The NH₃ has also a tendency to lie above the ring-connecting C atom, however, the binding energies of NH₃ adsorbed on each site of the BPDT are slightly different due to a weak interaction between them. The binding energies of NO₂, NO, NH₃ and CO adsorbed on the BPDT were found to be 0.17, 0.14, 0.09, and 0.07 eV, respectively. The binding energies of NH₃ and CO adsorbed on the BPDT are rather weak, whereas for the NO and NO₂ the interaction is stronger. This is due to the fact that the presence of one unpaired electron makes the latter molecules chemically reactive toward BPDT. Mulliken population analysis indicates that the BPDT acts as an electron donor, and the charge transfer from BPDT to NO₂, NO, NH₃ and CO is found to be 0.097|e|, 0.02|e|, 0.015|e| and 0.01|e|, respectively. The adsorption energies and charge transfer suggest that gas molecules are physisorbed on BPDT.

Fig. 1b presents the transmission T(E) of the NO, NO₂, CO and NH₃ molecules adsorbed on the BPDT devices (top panel) and the Projected Density of States (PDOS) for atoms in the central region (bottom panel). The black solid line corresponds to the reference transmittance without the presence of gas molecules. Let us first discuss the T(E) of BPDT without gas adsorption. The HOMO level of BPDT, which gives rise to a broad resonance peak below the Fermi energy (E − E_F ∼ −1 eV), plays the dominant role in the electron transport of BPDT, whereas the LUMO energy level is further away from the Fermi energy. Comparing the transport properties of BPDT–Au junction with previously reported results^37,38,41,42 using the NEGF-DFT approach, the main features of PDOS and T(E) are very similar. A variation in the transmission peak height could be due to the difference between exchange–correlation functionals, energy cutoff and number of k-points. When compared the T(E) and the PDOS peaks, we obtained a good agreement. The broad PDOS peak below the Fermi energy indicates the strong interaction between the HOMO of BPDT and the electrodes. The HOMO mainly arises from a π-type molecular orbital, which compares well with several previous studies.^41,42,57

Except in the case of CO, the transmission was strongly affected (see Fig. 1b) when the gas molecules were adsorbed on BPDT. A sharp rise in the PDOS suggests that the coupling between the electronic states of the gas and the electrodes is weak. As a result, the discrete energy states of NO, NO₂ and NH₃ couple to the continuum electronic states of BPDT, leading to pronounced interference effects in the window around E_F.

The signature of quantum interference, appearing in the transmission, needs to be addressed in details. In the case of NH₃, the sharp dip in T(E) appears at ∼−1.21 eV below the Fermi energy indicating antiresonance. To clarify the origin of the observed quantum interference, we investigated the local currents of NH₃ adsorbed on the BPDT around the interference feature; i.e., −1.22 eV and −1.20 eV. These are shown in Fig. 2a, left panel; the arrows point the direction of net current flow from the left to the right electrode. For NH₃, we could observe the multi-path quantum interference, which exhibits the suppression at one of the current paths. The antiresonance can be characterized by the reversal of ring currents.⁵⁸ For BPDT without gas adsorption, a previous study⁴³ has demonstrated that large transmission near the Fermi energy results from constructive contributions from HOMO and LUMO. As seen in Fig. 2a (right), two paths of the local currents around the ring at a specific energy; i.e. E − E_F = −1.00 eV, constructively interact, which are consistent with those previous results.⁴³

Fig. 2 (a) Local currents in BDPT–Au junctions with and without the adsorption of NH₃ gas at a selection of energies indicated by the shaded and numbered regions. (b) The transmitting eigenchannel wavefunctions from the left to the right electrode. The colors indicate the two different signs of the real-valued wavefunction.

The transmitting eigenchannel wavefunctions from the left to the right electrode⁴⁶ were investigated to provide a clear physical picture to help us understand the interference features characterizing the transmission, as presented in Fig. 2b. For NH₃ adsorbed on BPDT, it is evident that the behavior on either side of the orbital wave function differs; the sign of the orbital wave functions is reversed above the dip (area 2 shaded in orange), whereas for BPDT without gas this reversal in sign of the wave function wasn't observed (area 3 shaded in gray). The interference feature in this case, therefore, arises from destructive quantum interference, in which the wave functions propagate through different spatial quantum paths in the π-system of BPDT backbone.

Another type of quantum interference in the transmission: i.e., Fano resonance, was observed around the Fermi energy for the NO and NO₂, as shown in Fig. 1b. The origin of Fano resonance arises from the constructive and destructive interference of a narrow discrete resonance with a broad spectral line or continuum.^15,59,60 In our study, PDOS peaks indicate the strong coupling of BPDT–electrode and weak coupling for gas molecules since the PDOS peak widths of the former case are broader. As a result, the Fano resonance arises from coupling between the discrete energy states of the NO and NO₂ and the continuum of states supplied by the BPDT–electrode (see ESI, Fig. S2†). A dip and a peak in the transmission spectra around the Fermi energy are in agreement with the Fano resonance characteristics.

For NO, the Fano resonance gives rise to the transmission peak close to the Fermi energy whose scattering state with π character (the area 5 shaded in red) is localized along the backbone of the BPDT. The eigenchannel wavefunctions shown were the ones below and above the Fermi level (area 4 and 6 shaded in yellow and pink), showing the exponential decay of the π electron state. Particularly, we noticed that the sign of the orbital wave functions of BPDT is reversed above the transmission peak (area 4 shaded in pink). Similarly, the Fano resonance induced by NO₂ causes the dip and the peak in the transmission close to the Fermi level, and the phase reversal of the eigenchannels was also observed just above transmission dip (area 8 shaded in green).

Next, we turn our attention to the capability of BPDT as a gas sensor to distinguish four different gas molecules (NO, NO₂, NH₃ and CO). The performance of this sensor device would be discussed in terms of sensitivity and selectivity to various gases. Electron transmission changes around the Fermi level results in a variation in conductance. The sensitivity can be defined as , where G(T) and G₀(T₀) are the zero bias conductance (transmission) for a gas sensor with and without gas adsorption, respectively. Furthermore, it may be possible to improve the selectivity; the quantum interference effects can be tuned by applying a gate voltage to the system,⁶¹ leading to a change in the position and the dip and peak features. The conductance for a small gate voltage can be defined as , where the μ = E_F − eV_g is the chemical potential.

The sensitivity as a function of the gate voltage was determined, as shown in Fig. 3. Note that positive and negative sensitivities in Fig. 3 indicate the predicted enhanced and suppressed conductance, respectively. At V_g = 0 V, the interference feature of NO and NO₂ is very close to the Fermi energy and dominates the transport of the system, whereas those of NH₃ are far from the Fermi energy. Nevertheless, the sensitivity histograms exhibit a distinction between NO, NO₂ and NH₃ appears possible with a zero-bias voltage applied. The positive of NH₃ and negative values of NO₂ indicate the predicted enhanced and suppressed conductance, respectively. The absolute values of sensitivities were found to follow an ascending order; i.e., CO ≪ NH₃ ∼ NO₂ ≪ NO. The very large sensitivity of NO adsorbed on BPDT enables us to distinguish it from others, while the NH₃ and NO₂ adsorbed on BPDT shows a reversal in conductance allowing for the electrical distinction between them. At V_g = −1.2, −0.1 and 0.2 V, the BPDT shows the sensitivity towards NO with decreasing conductance, as opposed to large increasing conductance at V_g = 0 V. For NO₂, the conductance at V_g = 0.2 and −0.1 V is shown to be increased and decreased, respectively. For NH₃, the decrease in conductance was observed only at V_g = −1.2. Hence, applying the gate voltages to this setup should help to distinguish between different gas molecules.

Fig. 3 For different gate voltages, we plot the calculated sensitivities for NO, NO₂, NH₃ gas adsorbed on the BPDT. Positive and negative sensitivities indicate the predicted enhanced and suppressed conductance.

4 Conclusions

In summary, we investigated the quantum interference effects in the tunneling conductance of BPDT-molecules adsorption, connected to gold leads. We employed first-principles methods based on DFT formalism to determine the favorable adsorption configurations, binding energies and charge transfer of gas molecules (NO, NO₂, NH₃, and CO) on BPDT. Our results indicate that NH₃ adsorbed on BPDT exhibits destructive quantum interference giving rise an antiresonance in the transmission, while Fano resonance features in the transmission were observed for NO and NO₂. Based on our results, a BPDT device is capable of detecting different gas species with high sensitivity and selectivity. The findings reported by us here can be considered important enough to experimentalists who might be encouraged by our positive results to consider our proposed design and take on the challenging task of fabricating this setup to put our predictions to the test of gas sensing through direct measurements.

Acknowledgements

J. P. acknowledges the Higher Education Research Promotion and National Research University Project of Thailand, Office of the Higher Education Commission, the Thailand Research Fund (MRG5980185), and the National Nanotechnology Center (NANOTEC), NSTDA, Ministry of Science and Technology, Thailand, through its program of Centers of Excellence Network. A. R. R. would like to acknowledge Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP).

References

1. A. Nitzan and M. A. Ratner, Science, 2003, 300, 1384–1389.
2. S. Datta, Electron Transport in Mesoscopic Systems, Cambridge University Press, Cambridge, 1995.
3. N. J. Tao, Nat. Nanotechnol., 2006, 1, 173–181.
4. S. Schmaus, A. Bagrets, Y. Nahas, T. K. Yamada, A. Bork, M. Bowen, E. Beaurepaire, F. Evers and W. Wulfhekel, Nat. Nanotechnol., 2011, 6, 185–189.
5. S. J. van der Molen and P. Liljeroth, J. Phys.: Condens. Matter, 2010, 22, 133001.
6. J. Prasongkit, A. Grigoriev and R. Ahuja, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155434.
7. B. Standley, W. Bao, H. Zhang, J. Bruck, C. N. Lau and M. Bockrath, Nano Lett., 2008, 8, 3345–3349.
8. Q. Fu, J. Yang and Y. Luo, Appl. Phys. Lett., 2009, 95, 182103.
9. M.-Q. Long, K.-Q. Chen, L. Wang, W. Qing, B. S. Zou and Z. Shuai, Appl. Phys. Lett., 2008, 92, 243303.
10. H. S. Majumdar, J. K. Baral, R. Österbacka, O. Ikkala and H. Stubb, Org. Electron., 2005, 6, 188–192.
11. Y. Karzazi, J. Cornil and J. L. Bredas, J. Am. Chem. Soc., 2001, 123, 10076–10084.
12. P. Sautet and C. Joachim, Chem. Phys. Lett., 1988, 153, 511–516.
13. D. Walter, D. Neuhauser and R. Baer, Chem. Phys., 2004, 299, 139–145.
14. D. Q. Andrews, G. C. Solomon, R. P. V. Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130, 17309–17319.
15. C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888.
16. C. M. Guédon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. van der Molen, Nat. Nanotechnol., 2012, 7, 305–309.
17. H. Vazquez, R. Skouta, S. Schneebeli, M. Kamenetska, R. Breslow, L. Venkataraman and M. S. Hybertsen, Nat. Nanotechnol., 2012, 7, 663–667.
18. S. Ballmann, R. Härtle, P. B. Coto, M. Elbing, M. Mayor, M. R. Bryce, M. Thoss and H. B. Weber, Phys. Rev. Lett., 2012, 109, 056801.
19. V. Kaliginedi, P. Moreno-Garca, H. Valkenier, W. Hong, V. M. Garca-Surez, P. Buiter, J. L. H. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 5262–5275.
20. S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399–410.
21. J. Prasongkit, A. Grigoriev, R. Ahuja and G. Wendin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165437.
22. C. A. Stafford, D. M. Cardamone and S. Mazumdar, Nanotechnology, 2007, 18, 424014–424017.
23. H. Jeong, H. S. Kim, S. H. Lee, D. Lee and Y. H. Kim, Appl. Phys. Lett., 2013, 103, 023701.
24. S. K. Min, W. Y. Kim, Y. Cho and K. S. Kim, Nat. Nanotechnol., 2011, 6, 1–4.
25. R. G. Amorim, A. Fazzio, A. J. R. da Silva and A. R. Rocha, Nanoscale, 2013, 5, 2798–2803.
26. J. Li, Y. Lu, Q. Ye, M. Cinke, J. Han and M. Meyyappan, Nano Lett., 2003, 3, 929–933.
27. J. D. Fowler, M. J. Allen, V. C. Tung, Y. Yang, R. B. Kaner and B. H. Weiller, ACS Nano, 2009, 3, 301–306.
28. F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655.
29. J. Prasongkit, R. G. Amorim, S. Chakraborty, R. Ahuja, R. H. Scheicher and V. Amornkitbamrung, J. Phys. Chem. C, 2015, 119, 16934–16940.
30. L. Kou, T. Frauenheim and C. Chen, J. Phys. Chem. Lett., 2014, 5, 2675–2681.
31. B. Cho, M. G. Hahm, M. Choi, J. Yoon, A. R. Kim, Y.-J. Lee, S.-G. Park, J.-D. Kwon, C. S. Kim, M. Song, Y. Jeong, K.-S. Nam, S. Lee, T. J. Yoo, C. G. Kang, B. H. Lee, H. C. Ko, P. M. Ajayan and D.-H. Kim, Sci. Rep., 2015, 5, 8052.
32. H. Kondo, J. Nara and T. Ohno, J. Phys. Chem. C, 2011, 115, 6886–6892.
33. N. Wang, H. Liu, J. Zhao, Y. Cui, Z. Xu, Y. Ye, M. Kiguchi and K. Murakoshi, J. Phys. Chem. C, 2009, 113, 7416–7423.
34. F. I. Bohrer, C. N. Colesniuc, J. Park, M. E. Ruidiaz, I. K. Schuller, A. C. Kummel and W. C. Trogler, J. Am. Chem. Soc., 2009, 131, 478–485.
35. A. Mishchenko, D. Vonlanthen, V. Meded, M. Bürkle, C. Li, I. V. Pobelov, A. Bagrets, J. K. Viljas, F. Pauly, F. Evers, M. Mayor and T. Wandlowski, Nano Lett., 2010, 10, 156–163.
36. M. E. Z. Michoff, M. E. Castillo and E. P. M. Leiva, J. Phys. Chem. C, 2013, 117, 25724–25732.
37. M. Bürkle, J. K. Viljas, D. Vonlanthen and A. Mishchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 075417.
38. F. Pauly, J. K. Viljas, J. C. Cuevas and G. Schön, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155312–155319.
39. N. Sergueev, S. Shin, M. Kaviany and B. Dunietz, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195415–195512.
40. Y. Kim, Nat. Nanotechnol., 2014, 9, 881–885.
41. H. Kondo, J. Nara, H. Kino and T. Ohno, J. Chem. Phys., 2008, 128, 064701–064708.
42. H. Kondo, J. Nara, H. Kino and T. Ohno, J. Phys.: Condens. Matter, 2009, 21, 064220.
43. N. Gorczak, N. Renaud, S. Tarkuç, A. J. Houtepen, R. Eelkema, L. D. A. Siebbeles and F. C. Grozema, Chem. Sci., 2015, 6, 4196–4206.
44. M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401.
45. Y. Xue, S. Datta and M. A. Ratner, Chem. Phys., 2002, 281, 151–170.
46. M. Paulsson and M. Brandbyge, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115117.
47. M. Soler, E. Artacho, J. D. Gale, A. Garc, J. Junquera, P. Ordej and S. Daniel, J. Phys.: Condens. Matter, 2002, 2745, 2745–2779.
48. M. Mamatkulov, L. Stauffer, C. Minot and P. Sonnet, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 035321–035327.
49. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 155, 864–870.
50. W. Kohn and L. Sham, Phys. Rev., 1965, 385, 1133–1138.
51. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
52. G. Román-Pérez and J. Soler, Phys. Rev. Lett., 2009, 103, 096102.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
54. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
55. N. Troullier, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006.
56. D. S. Fisher and P. A. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6851–6854.
57. R. Cohen, K. Stokbro, J. M. L. Martin and M. A. Ratner, J. Phys. Chem. C, 2007, 111, 14893–14902.
58. G. C. Solomon, C. Herrmann, T. Hansen, V. Mujica and M. A. Ratner, Nat. Chem., 2010, 2, 223–228.
59. A. E. Miroshnichenko, S. Flach and Y. S. Kivshar, Rev. Mod. Phys., 2010, 82, 2257–2298.
60. B. Luk’yanchuk, N. I. Zheludev, S. A. Maier, N. J. Halas, P. Nordlander, H. Giessen and C. T. Chong, Nat. Mater., 2010, 9, 707–715.
61. G. C. Solomon, D. Q. Andrews, R. H. Goldsmith, T. Hansen, M. R. Wasielewski, R. P. Van Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130, 17301–17308.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra06578c

---