Evaluation of the performance of kinetic inhibitors for clathrate hydrate using unidirectional growth apparatus

Abstract

We study the formation of tetrahydrofuran (THF) clathrate hydrate from polyvinylpyrrolidone (PVP) aqueous solution as a function of growth rate V and adsorbed PVP concentration c using the unidirectional growth technique. This study aims to propose a simple method for evaluating the performance of kinetic hydrate inhibitors (KHIs) for the clathrate hydrate–aqueous solution system. The degree of super cooling ΔT calculated from the growth-induced interface shift under steady-state conditions was used for evaluating the KHIs performance. ΔT at c = 0 wt%, denoted ΔT₀, gradually increased with increasing V. This result suggests that the growth of THF hydrate in solution is limited by the inherent kinetics of the process on the crystal surface. Thus, when evaluating KHIs for an inhibiting effect, the effect of increasing ΔT₀ must be offset by using the formula ΔT − ΔT₀. The dependence of ΔT − ΔT₀ on c at lower growth rates is qualitatively consistent with the theory of Raymond and Devries. However, the trend in the results at a higher growth rate does not agree with the theory. This discrepancy suggests that the crystal grain boundaries trap PVP and complicate the apparent distribution coefficient in the higher growth rate region. Using this method, a single experimental run can be completed within 3.5 h of the compulsory nucleation by setting V = 5 μm s⁻¹. We believe this method is useful for screening various KHIs and clarifying the inhibition mechanism of KHIs.

---

Introduction

Gas hydrates are crystalline compounds that incorporate guest gas molecules within hydrogen-bonded water cages.¹ Large amounts of naturally occurring methane hydrates (MHs) are found under the ocean floor and permafrost regions.

MHs are interesting future energy resources. In March 2013, the world's first production test to extract gas from natural marine gas hydrate-bearing sediments was conducted in the eastern Nankai Trough. The gas-hydrate research program led by the Research Consortium for Methane Hydrate Resources in Japan is known as MH21. This field trial succeeded in gas production using the “depressurization method”.²

In 1934, Hammerschmidt discovered blockages in pipelines because of gas hydrate formation.³ The formation of natural gas hydrate in pipelines and production equipment is a potential problem. To prevent gas hydrate formation in pipelines, thermodynamic or kinetic hydrate inhibitors (KHIs) have been developed. Thermodynamic inhibitors shift the phase equilibrium condition for gas hydrates to higher pressure and lower temperature. Thermodynamic inhibitors such as methanol or ethylene glycol are typically required in vast quantities in the range 20–50 wt% to be added to water.⁴ KHIs are generally low molecular weight polymers such as polyvinylpyrrolidone (PVP) or polyvinylcaprolactam dissolved in water.⁴ KHIs act primarily to delay gas hydrate nucleation and inhibit gas hydrate growth rate. KHIs only need to be added at concentrations in the range 0.01–5 wt%.⁵ Thus, KHIs have advantages such as low cost of transportation to gas production pipelines.

Various indices exist for representing the performance of KHIs in inhibiting hydrate formation. The super cooling degree is one such index. Some studies define the super cooling degree to be the difference between the hydrate equilibrium temperature and the operating temperature at a given pressure.^1,4,5 For evaluating KHI performance, Lederhos et al. formed gas hydrate by agitating guest gas and water added various KHIs in a high pressure vessel. They compared KHIs performance by measuring gas consumption amount with time due to hydrate formation using the apparatus.⁶ Anderson et al. developed a crystal growth inhibition (CGI) method.^7,8 They also formed a gas hydrate by agitating guest gas and water with added KHIs in a high pressure vessel. The CGI method comprises a number of hydrate growth-dissociation cycles with repeated cooling and heating of the system at a constant rate. They classified the characteristic crystal growth-dissociation inhibition regions that resulted from the KHI's effect on the pressure temperature diagram according to the relative growth-dissociation rate change.

KHIs inhibit the nucleation and growth rate of clathrate hydrate crystals. The proposed nucleation or growth inhibition mechanisms of KHIs are still much debated till this day.^9–11 However, the definitive inhibition mechanism is not yet entirely understood.

KHIs are generally water soluble chemical polymers, although some KHIs based on proteins are known, called antifreeze glycoproteins (AFGP) and antifreeze proteins (AFP). Many studies have been conducted to clarify the antifreeze effect on ice crystal growth.^10–12 These studies show that ice crystals do not grow when the super cooling degree is lower than a critical value while melting temperatures do not change; this is called thermal hysteresis.¹²

Furukawa et al. studied the inhibition effect of AFGPs on ice crystals.¹² They observed patterns in the growth of the ice-water interface from an aqueous AFGP solution using the unidirectional growth technique.¹³ They measured the dependence of interfacial kinetic super cooling ΔT on the growth rate in a solution with the same AFGP concentration by in situ crystal morphology observation.

The unidirectional growth technique has the advantage of enabling easy observation of the interfacial phenomenon of crystal growth. However, this technique has not been applied to the system of clathrate hydrates formed from aqueous KHI solutions. In this study, we study the formation of tetrahydrofuran (THF) clathrate hydrate from KHI (PVP) aqueous solution using the unidirectional growth technique. This study aims to propose a simple method for evaluation of the performance of KHIs for the clathrate hydrate–aqueous solution system. This study focuses on the growth inhibition effect of KHIs, not on the inhibition of crystal nucleation.

Experimental

A stoichiometric THF–water solution (THF–17H₂O) was used in this study. Dehydrate stabilizer-free THF (99.5 wt% purity, Kanto Chemical Co., Japan) and ultrapure water (18.2 MΩ cm resistivity) were used. PVP (K-90, average molecular weight = 1 200 000, Junsei Chemical Co., Ltd. Japan) used as the KHI was added to the THF–water solution.

Fig. 1 shows schematics of (a) the sample cell and (b) the unidirectional growth apparatus. The sample cell comprises two glass plates (26 × 76 × 1 mm) and rubber spacers that were inserted between them. Chemical resistant rubber sheet (Kalrez compound 6375, 0.5 mm thick, DuPont) and tubing (polytetrafluoroethylene (PTFE), AS ONE Co., Japan) were used as spacer and capillary, respectively. Thermocouples (TYPE K, 01-K, Ninomiya Electric Wire Co., Ltd, Japan) were inserted between the rubber spacer and the glass plate. The calibrated thermocouples have an accuracy of 0.2 °C. The capillaries were connected to both sides of the cell. The outsides of the spacers were bonded using an epoxy bonding agent. The wire of the thermocouples was sealed by the rubber spacers. Two thermocouple wires were fixed in the sample cell. These wires are denoted by no. 1 and 2. The measurement position of the thermocouples was approximately 5 mm (no. 1) and 15 mm (no. 2) from the right edge of the inner cell, as shown in Fig. 1a.

Fig. 1 Schematics of (a) sample cell and (b) unidirectional growth apparatus.

The unidirectional growth apparatus comprises a cold block (lower than the equilibrium temperature T_eq) and a hot block (higher than T_eq). The blocks were composed of copper. The temperature of the blocks was maintained by thermoelectric modules, which comprised Peltier devices (9500/127/085B, Ferro Tec Co., Japan) and a Peltier controller (TDC-1020A, Cell System Co., Ltd., Japan).

The sample cell was placed on the cold and hot blocks. An almost constant temperature gradient G was applied across the sample cell and was measured using the thermocouples that were connected to a data logger (ZR-RX45, Omron Co., Japan). Hydrate crystals were compulsory nucleated by cooling the colder side of the capillary using a cold spray. Then, to form a flat interface, an initial growth interface of an extra 0.3 mm was formed. Next, the extra hydrates were melted by moving the sample cell slightly to the hot block side. The cell was maintained under stationary conditions for 2 h.

The sample cell was moved at a constant velocity, V, toward the colder block using a pulse motor. The total distance moved by the cell to finish a single experiment was 25 mm.

The hydrate interfaces were observed using an optical zoom lens (VZM 600I, Edmund optics) and a CCD camera (EO-1312M, Edmund optics). The CCD camera was connected to a personal computer running the Windows operating system (Windows 8). The observed images were recorded as digital image files on the personal computer.

The concentration of PVP c and movement velocity V were the variables in this study.

Results

Fig. 2 shows sequential images of the hydrate growth interface with added PVP concentration c = 0.5 wt% and V = 3 μm s⁻¹. The growth times are (a) t = 0 min, (b) t = 5 min, and (c) t = 20 min. The entire interfacial pattern at t = 0 was almost along the isothermal line corresponding to T_eq = 4.4 °C. The local interface shape is not perfectly flat and has many small concave–convex patterns. From t = 0 to t = 20 min, the growth interface gradually shifted toward the cold block side under the applied temperature gradient. After t = 20 min, the interface position became constant (i.e., steady-state conditions). The double-headed arrow in Fig. 2c shows the distance the interface shifted from the initial condition, i.e., Δx_i(t).

Fig. 2 Sequential images of the growth interface of THF hydrate with added PVP concentration c = 0.5 wt% and V = 3 μm s⁻¹. The growth times are (a) t = 0 min, (b) t = 5 min, and (c) t = 20 min.

Fig. 3a shows the relation between Δx_i(t) and distance moved by the sample cell x_cell(t) for V = 0.5, 1, 5 μm s⁻¹ at c = 1.0 wt%. Δx_i is the apparent position change of the interface as observed by optical lens as mentioned above. x_cell is the distance moved by the sample cell, with the origin at the position of the cell at t = 0. The values for Δx_i were obtained by averaging 10 measured values at different positions along the interface at the same time. The dotted line shows the hypothetical case of Δx_i = x_cell. Following this line means that the position of the growth interface relative to the cell does not change (i.e., the hydrate does not grow after t = 0). The actual results show that as x_cell increased, Δx_i increased from 0 to 5 mm for each value of V. After x_cell = 5 mm, each Δx_i was almost constant. In this steady-state condition, Δx_i increased as V increased. Fig. 3b shows the dependence of the super cooling degree of the growth interface ΔT_i on x_cell. ΔT_i was calculated using the simple formula ΔT_i = G_aveΔx_i. The linear temperature gradient G_ave is determined by G_ave = (G₁ + G₂)/2. G₁ and G₂ are the temperature gradients recorded by thermocouples 1 and 2, respectively. In these experiments, G was almost equal to 1.0 °C mm⁻¹ for all experimental runs. In the steady-state condition, ΔT_i increased as V increased. The filled points show the difference between T_eq (=4.4 °C) and the temperatures T₁ and T₂ measured by thermocouples 1 and 2, respectively. These results show that the estimated and measured ΔT_i values almost agree.

Fig. 3 Dependence of (a) Δx_i and (b) ΔT_i on the distance moved by the sample cell, x_cell(t), for V = 0.5, 1, and 5 μm s⁻¹ at c = 1.0 wt%.

Fig. 4a shows the dependence of Δx_i on x_cell for c = 0.5, 1.0, 2.0 wt% at V = 1 μm s⁻¹. These results show that the dependencies of Δx_i and x_cell on c are similar to their dependence on V. Thus, Δx_i also increased with increasing c, with Δx_i and x_cell increasing from 0 to 5 mm. After x_cell = 5 mm, each Δx_i was also almost constant. Fig. 4b shows the relation between ΔT_i and x_cell. In the steady-state condition, ΔT_i increased as c increased. In the following section, we explain the results obtained under steady-state conditions.

Fig. 4 Dependence of (a) Δx_i and (b) ΔT_i on x_cell for c = 0.5, 1.0, and 2.0 wt% at V = 1 μm s⁻¹.

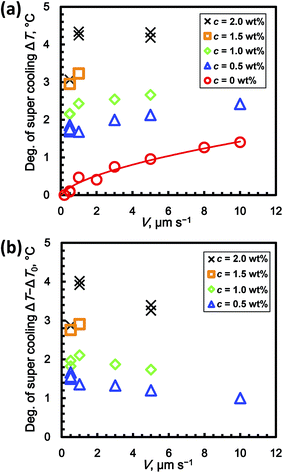
Fig. 5a shows the relationship between ΔT and V for c = 0 to 2 wt% in the steady-state condition. Although there are some exceptions in the graph, ΔT basically increased with increasing c. At c = 0 wt% (stoichiometric THF–17H₂O solution without added PVP), ΔT gradually increased with increasing V. The super cooling degree at c = 0 wt% is denoted ΔT₀(V). To evaluate the inhibiting effect of the KHIs on ΔT, it is necessary to offset ΔT₀. The reason for this is discussed in the next section. The values of ΔT₀ are fitted by a power-law function of V

ΔT₀ = 0.38V^0.59. (1)

Fig. 5 Dependence of (a) the degree of super cooling, ΔT, and (b) ΔT − ΔT₀ on V for c = 0 to 2 wt%.

Fig. 5b shows the relation between ΔT − ΔT₀ and V, where ΔT₀ is estimated using eqn (1). For c = 1, 1.5, and 2 wt%, ΔT − ΔT₀ increased from 0.5 to 1.0 μm s⁻¹. From 1.0 to 10 μm s⁻¹, ΔT − ΔT₀ decreased. At c = 0.5 wt%, ΔT − ΔT₀ decreased from 0.5 to 10.0 μm s⁻¹.

Fig. 6a shows the relation between ΔT and c for V = 0.5 to 10 μm s⁻¹ in the steady-state condition. For all V, ΔT increased with increasing c. In addition, ΔT basically increased with V and with increasing c from 0 to 2 wt%. The values of ΔT are fitted by power-law functions of c, namely ΔT = 2.2c^0.44 + 0.10 at V = 0.5 μm s⁻¹, ΔT = 2.0c^0.92 + 0.50 at V = 1.0 μm s⁻¹, and ΔT = 1.8c^0.84 + 0.98 at V = 5.0 μm s⁻¹.

Fig. 6 Dependence of (a) the degree of super cooling, ΔT, and (b) ΔT − ΔT₀ on c for V = 0.5 to 10 μm s⁻¹.

Fig. 6b shows the relation between ΔT − ΔT₀ and V for c = 0 to 2 wt% in the steady state condition. For all V, ΔT − ΔT₀ increased with increasing c. At c = 0.5 wt%, ΔT − ΔT₀ for V = 0.5 μm s⁻¹ has its highest value. Above c = 1 wt%, ΔT − ΔT₀ for V = 0.5 μm s⁻¹ has lower values. In contrast, ΔT − ΔT₀ for V = 1.0 μm s⁻¹ has the highest value at c = 2.0 wt%. ΔT − ΔT₀ for V = 5.0 μm s⁻¹ has relatively lower values, which are lower than the value for V = 1.0 μm s⁻¹ at c = 2.0 wt%. The values of ΔT − ΔT₀ can be fitted by power-law functions of c, namely ΔT − ΔT₀ = 2.1c^0.47 at V = 0.5 μm s⁻¹, ΔT − ΔT₀ = 2.2c^0.85 at V = 1.0 μm s⁻¹, and ΔT − ΔT₀ = 1.9c^0.81 at V = 5.0 μm s⁻¹.

Discussion

Fig. 5a shows ΔT at c = 0 wt% (i.e. ΔT₀) increased with increasing V. This result indicates that the growth rate of THF hydrate from solution is limited by the inherent kinetics of the THF hydrate formation process. Thus, the inherent kinetic effect should be eliminated when evaluating the kinetic inhibition effect using the formula ΔT − ΔT₀. Since the molar concentrations of PVP in the solution for all experimental runs are negligibly small, they should not cause super cooling.

Next, we discuss the decrease in ΔT − ΔT₀ with increasing V, as shown in Fig. 5b. Zepeda et al. showed the morphological instability of the growing ice crystal interface in solutions to which AFGP had been added.¹⁴ Their results showed that zigzag patterns are formed at the growing interface, which rejected AFGP. In contrast, the results also showed that AFGP is incorporated into the gaps between the growing ice interface boundaries. The dependence of ΔT − ΔT₀ on V in our results is also quantitatively explained by crystal grain boundary formation. If V is higher, the number of crystal grain boundaries in the growing interface might increase, while the solution containing the kinetic inhibitor might be entrapped in the crystal grain boundaries. Thus, if V is higher, the amount of entrapped kinetic inhibitor increases.

Fig. 6b shows that ΔT − ΔT₀ ∝ c^0.5 at V = 0.5 μm s⁻¹. The exponent N (=0.5) agrees with the one in the mechanism proposed by Raymond and Devries.¹⁰ Their hypothesis for the mechanism is that AFGP inhibits crystal growth via the Kelvin effect, which results from AFGP adsorbing to the ice surface. However, when V ≥ 1 μm s⁻¹, the exponent N is not 0.5, which is in disagreement with this mechanism. This discrepancy might result from the fact that the theory of Raymond and Devries does not consider the effect of crystal grain boundaries entrapping KHIs, as mentioned above. Thus, when V is lower, both trends agree because the amount of entrapped PVP in crystal grain boundaries is low. When V is higher, the trends do not agree because the number of crystal grain boundaries increases, thereby complicating interpretation of the apparent distribution coefficient. To clarify the mechanism, in situ observation of the distribution field and crystal grain boundaries using a higher resolution optical system and interferometry is needed. The unidirectional growth technique has the advantage that various observation techniques can easily be combined.^15,16

The local concentration of PVP in aqueous phase should increase by the rejection of PVP at growth interface. To maintain the concentration as the initial value throughout the experiment, it is necessary that the length of the sample cell be sufficiently larger than the diffusion length of PVP. Nagashima et al.¹⁶ observed the diffusion length of a solute in the front region of a unidirectional growing THF hydrate formed from stoichiometric THF–water solution with the addition of 3 wt% sodium chloride using interferometric observations. Their results demonstrated the relation between the diffusion length of the solute, l_s, and the growth velocity, V. At V = 1 μm s⁻¹, l_s is approximately 1 mm. We believe the inner length of the sample cell (=70 mm) is sufficiently larger than the diffusion length of PVP.

This study does not focus on crystal nucleation inhibition. However, Anderson et al. and Luna-Ortiz suggested that the KHI induced induction times are currently the primary factor in determining the suitability for field use.^7,8 They also investigated the relation between the induction time, t_i, and CGI region boundaries. The relation between t_i and the super cooling degree ΔT for the KHI aqueous gas hydrate system was observed. The result showed that t_i exponentially reduces from infinite to very long to very short as ΔT increases. The drastically changing boundaries of t_i agree with the characteristic CGI region boundaries. Therefore, they proposed that the CGI data could be used to assess the t_i patterns without direct t_i measurement. If the t_i of the THF hydrate is very long or infinite at the super cooling degree of the system lower than ΔT or ΔT − ΔT₀ determined from the present method as shown in Fig. 5 or 6, our method could also be used to efficiently assess the nucleation inhibition performance in the same way as the CGI method. To verify this method, measuring the relation between t_i and ΔT of the THF hydrate formed from the KHI aqueous solution is necessary.

Conclusions

We evaluated the PVP inhibiting effect on THF hydrate growth as a function of growth rate V and added PVP concentration, c, by using the unidirectional growth technique. The aim of this experiment was to propose a simple method for evaluation of KHI performance.

The results showed that the growth interface gradually shifted towards the cold block side under an applied temperature gradient with increasing time. After a certain time, the interface position was constant (i.e. a steady-state condition was reached). Here, the degree of super cooling ΔT calculated from the growth interface shift under steady-state conditions was used for evaluating the performance of KHIs.

The results also showed that ΔT increased with increasing V at any given concentration c. In addition, at c = 0 wt%, ΔT gradually increased with increasing V. This suggests that the growth of THF hydrate in solution is limited by the inherent kinetics of the process on the crystal surface. Thus, when evaluating KHIs for their inhibiting effects, it is necessary to offset ΔT at a given concentration by ΔT at c = 0 wt%, denoted ΔT₀. When V ≥ 1 μm s⁻¹, ΔT − ΔT₀ decreased with increasing V. This result suggests that crystal grain boundaries entrap the PVP solution.

The dependence of ΔT − ΔT₀ on c at V = 0.5 μm s⁻¹ agrees with the trend predicted by the theory of Raymond and Devries. However, when V ≥ 1 μm s⁻¹, the results do not agree with the theory. This suggests that the crystal grain boundaries complicate the interpretation of the apparent distribution coefficient in the higher growth rate region.

The following are the most important steps in the proposed evaluation method using the unidirectional growth technique. The first step is using a stoichiometric THF–water solution (THF–17H₂O) for preventing diffusion limitation of guest molecules. The second step is measuring the growth interface shift under steady-state conditions and converting the shift to ΔT. The third step offsetting ΔT using the formula ΔT − ΔT₀. Note that it is necessary to select a unified value of V for eliminating complexity from the growth kinetics when evaluating the performance of KHIs. If V = 5 μm s⁻¹ is selected, a single experimental run can be completed within 3.5 h of compulsory nucleation. We believe that this method is useful for screening various KHIs and clarifying the inhibition mechanism of KHIs.

Acknowledgements

This study was financially supported by the MH21 Research Consortium for Methane Hydrate Resources in Japan and the National Methane Hydrate Exploitation Program by the Ministry of Economy, Trade, and Industry. The authors would like to thank K. Nagashima for his assistance with this study.

Notes and references

1. E. D. Sloan and C. A. Koh, Clathrate Hydrates of Natural Gases, CRC Press, Boca Raton, Fla, 3rd edn, 2007.
2. K. Yamamoto, Mar. Pet. Geol., 2015, 66, 296–309.
3. E. G. Hammerschmidt, Ind. Eng. Chem., 1934, 26, 851–855.
4. M. A. Kelland, Energy Fuels, 2006, 20, 825–847.
5. A. Perrin, O. M. Musa and J. W. Steed, Chem. Soc. Rev., 2013, 42, 1996–2015.
6. J. P. Lederhos, J. P. Long, A. Sum, R. L. Christiansen and E. D. Sloan, Chem. Eng. Sci., 1996, 51, 1221–1229.
7. R. Anderson, H. Mozaffar and B. Tohidi, Proceedings of the 7th International Conference on Gas Hydrates, Edinburgh, Scotland, UK, 2011.
8. E. Luna-Ortiz, M. Healey, R. Anderson and E. Sørhaug, Energy Fuels, 2014, 28, 2902–2913.
9. M. Ohtake, Y. Yamamoto, T. Kawamura, A. Wakisaka, W. F. de Souza and A. M. de Freitas, J. Phys. Chem. B, 2005, 109, 16879–16885.
10. J. A. Raymond and A. L. DeVries, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 2589–2593.
11. C. A. Knight, Nature, 2000, 406, 249–251.
12. Y. Furukawa, N. Inohara and E. Yokoyama, J. Cryst. Growth, 2005, 275, 167–174.
13. K. Nagashima and Y. Furukawa, J. Cryst. Growth, 1997, 171, 577–585.
14. S. Zepeda, Y. Uda and Y. Furukawa, J. Jpn. Assoc. Cryst. Growth, 2008, 35, 151–160.
15. K. Watanabe, J. Cryst. Growth, 2000, 213, 135–140.
16. K. Nagashima, Y. Yamamoto, M. Takahashi and T. Komai, Fluid Phase Equilib., 2003, 214, 11–24.

---