On the adhesion of hierarchical electrospun fibrous structures and prediction of their pull-off strength
Abstract
In this study, we used electrospinning combined with template wetting method to fabricate hierarchical poly(methyl methacrylate) (PMMA) fibrous structures. The adhesion performance of these samples was investigated using a nanoindenter. A flat circular diamond indenter of 10 μm diameter was brought in contact with the sample and then retracted back. The force required to detach the indenter from the sample was determined to be the pull-off force. The effect of indentation depth on the pull-off force was also investigated. Following this, an empirical relationship 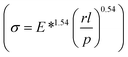 to predict the pull-off strength (σ) was established for a given fibril radius (r), fibril height (l), preload (p), and effective Young's modulus (E*). The pull-off force values recorded for hierarchical PMMA fibrous structure were also used to validate the empirical relationship. The empirical relationship demonstrated good correlation between the recorded pull-off strength and system parameters. We believe that this empirical relationship will be helpful in designing high strength synthetic dry-adhesives as the relationship can be used to predict the pull-off strength a priori.
to predict the pull-off strength (σ) was established for a given fibril radius (r), fibril height (l), preload (p), and effective Young's modulus (E*). The pull-off force values recorded for hierarchical PMMA fibrous structure were also used to validate the empirical relationship. The empirical relationship demonstrated good correlation between the recorded pull-off strength and system parameters. We believe that this empirical relationship will be helpful in designing high strength synthetic dry-adhesives as the relationship can be used to predict the pull-off strength a priori.


 Please wait while we load your content...
Please wait while we load your content...