Phonon optics, thermal expansion tensor, thermodynamic and chemical bonding properties of Al4SiC4 and Al4Si2C5: a first-principles study
Y. F. Li*a,
B. Xiaob,
L. Suna,
Y. M. Gaoa and
Y. H. Chengc
aState Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710049, China. E-mail: liyefei@mail.xjtu.edu.cn; Fax: +86 29 82668606; Tel: +86 29 82668606
bDepartment of Earth Sciences, University College London, London, WC1E 6BT, England, UK
cState Key Laboratory of Electric Insulation and Power Equipment, Xi'an Jiaotong University, Xi'an 710049, China
First published on 26th April 2016
Abstract
The phonon spectra, chemical bonding, thermal and thermodynamic properties of Al4SiC4 and Al4Si2C5 are calculated by first-principles using density functional theory. Raman and infrared (IR) active phonon modes and their eigenvectors are analyzed. Phonon mode-Grünseisen parameter and macroscopic Grünseisen constants are evaluated from phonon spectra. Employing quasiharmonic approximation (QHA), the thermal expansion tensor is obtained. The calculated volumetric thermal expansion coefficient (TEC) of Al4SiC4 is high than that of Al4Si2C5; and the linear TEC in the [001] direction is slightly higher than that of the [100] direction for both compounds. The computed average linear TECs for Al4SiC4 and Al4Si2C5 are 9.96 × 10−6 K−1 and 8.9 × 10−6 K−1 in a range from room temperature to 1500 K, respectively. Other thermal properties such as specific heats (CV, and CP), entropy (S), isothermal and isobaric bulk moduli (KT and KS) are also discussed. Using Slack's model, it is found that thermal conductivities are 59.9 W m−1 K−1 and 78.3 W m−1 K−1 at room temperature for Al4SiC4 and Al4Si2C5, respectively. The response of chemical bonds to hydrostatic pressure is discussed using Milliken population analysis. We also plot the charge density and its reduced density gradient to reveal the covalent bonds in the structure.
1. Introduction
Aluminum-containing ternary ceramics (Al4SiC4 and Al4Si2C5) are regarded as low cost potential materials for high-temperature structural devices, heat-exchange materials, and weight sensitive applications.1–5 The oxidation behavior of Al4SiC4 was investigated by Yamamoto et al.,4 who pointed out that the remarkable oxidation occurred in temperature range of 1123 K to 1423 K. Few years ago, thermodynamic behaviors of the same material were investigated through thermal conductivity5,6 and electrical resistivity7 measurements. Wen and Huang5 provided the linear thermal expansion coefficient (TEC) of Al4SiC4 of 6.2 × 10−6 K−1 in the temperature range from 473 K to 1723 K; they also gave the bending strength of 297.5 MPa and vickers hardness of 10.6 GPa. Inoue et al.6 claimed the thermal conductivity and linear TEC of highly densitied Al4SiC4 ceramic from room temperature to 1473 K were 80 W m−1 K−1 and 7.16 × 10−6 K−1, respectively. Inoue and Yamaguchi7 studied the temperature dependence of electrical resistivity of bulk Al4SiC4 material, and they concluded that the electrical resistivity exhibited as an insulator. Al4Si2C5 is another stable phase below 2310 K and mechanical properties of Al4Si2C5 are comparable to these of the dense Al4SiC4 bulk phase.8 The crystallographic parameters of Al4Si2C5 were provided in detail by Inoue et al.1 Linnarsson et al.9 found that Al4Si2C5 could form from a supersaturated solution of Al-doped 4H–SiC at 1700–2000 °C. Meanwhile, the chemical bonding, optical and elastic properties of Al4SiC4 and Al4Si2C5 have been reported.10,11 The band gaps of 1.05 eV and 1.02 eV were claimed for Al4SiC4 and Al4Si2C5 by Hussain et al.10 Liao et al.11 investigated the atomic displacements under deformation and the theoretical strengths of Al4SiC4, they suggested that structural failure occurs in tensile deformation firstly.Although the ternary aluminum silicon carbides are of great importance. To our knowledge, there is less information available about the phonon optics, Grüneisen parameters, heat capacity, entropy, temperature dependence thermal expansion and thermal conductivity, especially for Al4Si2C5. In present work, we will perform systematic studies on the phonon properties, thermodynamic parameters and chemical bonding behaviors.
2. Calculation methods and models
2.1. Density functional theory calculations
The ternary carbides discussed here have hexagonal structure (P63mc for Al4SiC4, R-3m for Al4Si2C5),1 and the conventional crystal structures (2 f.u. of Al4SiC4, and 3 f.u. of Al4Si2C5) were employed here; the detailed structural information of which can be found in ref. 10 and 11 The all first-principles calculations were performed using the plane wave basis and Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional of generalized gradient approximation (GGA) as implemented in CASTEP code.12–14 The Broyden–Fletcher–Goldfarb–Shannon (BFGS) algorithm was applied to relax both lattice parameters and atomic fractional coordinates. The kinetic energy cut-off value of 700 eV was used for plane wave expansion in reciprocal space. The ultra-soft pseudopotentials (USPPs) were employed to describe the Coulomb interactions between the valence electrons and pseudo-ion core. The valence electrons of USPPs were: Al: 3s23p1, Si: 3s23p2, C: 2s22p2, respectively. The sampling k-point mesh in the first irreducible Brillouin zone was generated by Monkhorst–Pack method,15 using a 6 × 6 × 1 grid for each structure. The convergence criterion for electronic self-consistency was 10−8 eV per atom for total energy, and the forces per atom were reduced to 10−4 eV Å−1.2.2. Thermodynamic properties and thermal expansion tensor
Furthermore, in order to calculate the thermal expansions, the Helmholtz free energy at the elevated temperature was calculated, which is given by F(V, T) = Egs(V) + Fvib(V, T) + Fele(V, T).16 The Egs represents ground state total energy. The vibration free energy (Fvib) is calculated by phonon spectra in standard quasiharmonic approximation (QHA).
 | (1) |
Within an appropriately normalized phonon density of states (PHDOS)  . In eqn (1), N the total number of atoms in the unit cell, and ω is the angular frequency.
. In eqn (1), N the total number of atoms in the unit cell, and ω is the angular frequency.
In this work, the phonon spectra were calculated in CASTEP code by finite element displacement method by setting a cutoff radius of 3 Å, which resulted in 2 × 2 × 1 supercell structure; and the LO–TO splitting was ignored. Fele is the thermal electronic contribution to Helmholtz free energy, which is obtained by Mermin statistics Fele = Eele − TSele.
Minimizing the Helmholtz free energy F(V, T) with respect to cell volume V as a function of temperature gives the equilibrium volumes at different temperatures. This can be easily realized by fitting well known Birch–Murnaghan equation of state.17 Finally, the volumetric TEC λ(T) can be determined by  , where V0 and V1 represent the equilibrium volumes at temperatures T0 and T1, respectively.
, where V0 and V1 represent the equilibrium volumes at temperatures T0 and T1, respectively.
The Grüneisen parameters of a crystal structure indicate its anharmonic effects in the phonon spectrum due to the change of cell volume.18 In this paper, the phonon-mode Grüneisen constant (γ(ωi)) and macroscopic Grüneisen parameter (γ) were calculated. The former one describing the phonon frequency shift with respect to volume can be calculated by:
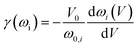 | (2) |
 | (3) |
The determination of the mode Grüneisen parameters was achieved by computing the phonon spectra at two additional unit cell volumes, which were deformed from equilibrium volume by expanding or compressing by 1%, and re-optimizing the atomic positions.
In this work, we also predict the dependence of thermal conductivity on temperature by employing the Slack's expression:19,20
 | (4) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) [in g mol−1] is the average mass per atom in the cell, δ [m] is the cube root of the average volume per atom, n is the number of atoms in the primitive unit cell, γ(T) represents the macroscopic Grüneisen parameters, computed by eqn (3). Julian21 determined the value for the physical constant A [W mol g−1 m−2 K−3] with A = 2.43 × 104/(1 − 0.514/γ + 0.228/γ2). ΘD [K] is the Debye temperature which can be calculated from the elastic constants.
[in g mol−1] is the average mass per atom in the cell, δ [m] is the cube root of the average volume per atom, n is the number of atoms in the primitive unit cell, γ(T) represents the macroscopic Grüneisen parameters, computed by eqn (3). Julian21 determined the value for the physical constant A [W mol g−1 m−2 K−3] with A = 2.43 × 104/(1 − 0.514/γ + 0.228/γ2). ΘD [K] is the Debye temperature which can be calculated from the elastic constants.
Besides the phonon spectra, all other properties were calculated using our own home-made post-processing programs.
3. Results and discussions
3.1. Phonon properties and Grüneisen parameters
The phonon dispersion curves give a criterion for the crystal stability. If all phonon frequencies are positive, the crystal is dynamically stable, while the imaginary frequencies (soft modes) indicates the system is unstable with respect to certain atomic displacement patterns. The phonon spectra of both aluminum silicon carbides at equilibrium states are shown in Fig. 1a and 2a. No imaginary frequencies can be found in the whole Brillouin zone for both phases implying their stability nature. We also checked that they remain stable under certain lattice deformation (±10%). In addition, due to the fact that carbon atom has a smaller mass than aluminum and silicon atoms, the vibration frequency of carbon atoms is higher than that of other atoms. As a consequence, the PHDOS of both ternary carbides can be viewed as two parts (Fig. 1b and 2b). One refers to the part lower than 13 THz where the main contribution comes from the Al sub-lattice while the other part higher than 13 THz is dominated by the dynamics of carbon atoms. Both parts have contributions from silicon atoms. From the phonon spectra, a pseudo-gap is seen around 20 THz for two structures. Above this pseudo-gap, lattice vibrations are dominated by C atoms.In the Al4SiC4 structure, there are 18 atoms (2 f.u.). Therefore, totally 54 phonon branches exist in the phonon spectrum, including 3 acoustic modes and 51 optical modes. Factoring all 54 phonon modes at Γ-point based on their irreducible representations of point group C6v, we have Γ3 = E1 + A1 for three acoustic phonons and Γ51 = 8A1 + 9B2 + 8E1 + 9E2 for remaining optical ones. The crystal structure of Al4Si2C5 contains 33 atoms (3 f.u.), giving rise to a total number of 99 phonon branches. Group theory dissociates three acoustic phonon modes into Γ3 = Eu + A2u. Similarly, we obtain Γ96 = 5Eu + 5A2u + 5Eg + 5A1g + 11G + 11E, where G and E refer to four-fold and two-fold degeneracies. All phonon modes at Γ point given by G and E representations are neither infrared (IR) active nor Raman active in Al4Si2C5 structure. Using the character table of point group D3d, one can show that G = Eg + Eu and E = A1g + A2u. Therefore, G and E are obtained by a linear combination of IR and Raman active irreducible representations. In Table 1, we summarize the frequencies and irreducible representations of IR and Raman active phonon modes for Al4SiC4 and Al4Si2C5 structures.
| Symmetry | Al4SiC4 | Symmetry | Al4Si2C5 | ||||
|---|---|---|---|---|---|---|---|
| IR | Raman | [u v w] | IR | Raman | [u v w] | ||
| E2 | 78.0 | [x y 0] | Eu | 118.3 | [x y 0] | ||
| E2 | 96.0 | [x 0 0]/[0 y 0] | Eg | 161.1 | [x y 0] | ||
| E1 | 139.7 | [x 0 0]/[0 y 0] | Eu | 218.7 | [x y 0] | ||
| E1 | 188.6 | 188.6 | [x y 0] | A2u | 247.3 | [0 0 z] | |
| E2 | 203.9 | [x y 0] | A1g | 258.5 | [0 0 z] | ||
| E2 | 262.6 | [x y 0] | Eg | 270.4 | [x y 0] | ||
| E1 | 268.1 | 268.1 | [x y 0] | Eg | 279.0 | [x y 0] | |
| E1 | 278.2 | 278.2 | [x y 0] | A1g | 369.4 | [0 0 z] | |
| E2 | 280.5 | [x y 0] | A2u | 431.9 | [0 0 z] | ||
| A1 | 290.1 | 290.1 | [0 0 z] | Eu | 476.1 | [x y 0] | |
| A1 | 303.4 | 303.4 | [0 0 z] | A1g | 543.5 | [0 0 z] | |
| A1 | 397.9 | 397.9 | [0 0 z] | A2u | 561.6 | [0 0 z] | |
| E1 | 443.0 | 443.0 | [x y 0] | Eu | 614.6 | [x y 0] | |
| E2 | 443.6 | 443.6 | [x y 0] | Eg | 616.0 | [x y 0] | |
| A1 | 517.8 | 517.8 | [0 0 z] | A2u | 740.9 | [0 0 z] | |
| A1 | 578.4 | 578.4 | [0 0 z] | Eg | 800.4 | [x y 0] | |
| E1 | 596.4 | 596.4 | [x y 0] | Eu | 807.1 | [x y 0] | |
| E2 | 596.8 | [x y 0] | A1g | 810.6 | [0 0 z] | ||
| A1 | 720.1 | 720.1 | [0 0 z] | A2u | 815.3 | [0 0 z] | |
| E1 | 755.7 | 755.7 | [x y 0] | A1g | 880.3 | [0 0 z] | |
| E2 | 755.7 | 755.7 | [x y 0] | ||||
| E1 | 777.6 | 777.6 | [x y 0] | ||||
| E2 | 777.7 | 777.7 | [x y 0] | ||||
| A1 | 807.7 | 807.7 | [0 0 z] | ||||
| A1 | 862.0 | 862.0 | [0 0 z] | ||||
The general forms of eigenvector of all optical active phonon modes are also given in Table 1. Phonon eigenvector is related to atomic displacement in a particular phonon mode by the following expression.
uj(ri,t) = ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) j,0 j,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[i(kr − ωt)] exp[i(kr − ωt)]
| (5) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) j,0. Assuming t = 0, then we may rewrite eqn (5) as
j,0. Assuming t = 0, then we may rewrite eqn (5) as
uj(ri,t) = ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) j,0 j,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[ikr] exp[ikr]
| (6) |
Eqn (6) implies that the atomic displacement is a complex number at an arbitrary k point except the Γ-point. In our discussion, we only consider all phonon modes at Γ-point. Therefore, the phonon eigenvector also indicates the magnitude and direction of atomic displacement directly.
In both Al4SiC4 and Al4Si2C5 phases, there are only two types of eigenvector, i.e., [x y 0] and [0 0 z]. Those phonon modes with displacements involving only x–y basal plane are represented by [x y 0] type eigenvector. Meanwhile, other phonon modes moving merely in [001] direction are described by [0 0 z] type eigenvectors. Some representative phonon eigenvectors are illustrated in Fig. 3 and 4 using VESTA software.22 As can be seen from both figures, the in-phase displacement patterns on x–y crystallographic plane correspond to the lower part of phonon spectrum. The out-of-phase motions of Si, Al and C atoms on the same plane have relatively large frequencies, partially because Si–C or Al–C bonds are stretched indirectly. Obviously, vibrations in [001] direction are anticipated to give large phonon frequencies. In Al4SiC4 and Al4Si2C5 phases, some Al–C and Si–C bonds are aligned in c-direction. Therefore, displacing atoms in [001] direction either in-phase or out-of-phase would be the most effective way to change the bond length aligned in this direction. As a result, those phonon modes have the largest frequencies in two structures. For example, in Al4SiC4 structure, A1 mode (IR + R, 862.03 cm−1): the out-of-phase compression of Si–C bond in [001] direction; A1 (IR + R, 807.70 cm−1): out-of-phase compression of Al–C bond in [001] direction; A1 (IR + R, 720.13 cm−1): out-of-phase stretching of Si–C bonds in [001] direction. Similarly, for Al4Si2C5 structure, A1g (R, 880.28 cm−1): out-of-phase stretching of Si–C bonds in [001] direction; A1g (R, 814.64 cm−1): out-of-phase compression of Al–C bonds in [001] direction; A2u (IR, 247.28 cm−1): in-phase stretching of Al–C and Si–C bonds in [001] direction.
The acoustic branches of the both ternary carbides can be employed to estimate the elastic constants by Christoffel equation.23
| |Γij − ρv2δij| = 0 | (7) |
 | (8) |
The directional cosines are n1 = sin(θ)cos(φ), n2 = sin(θ)sin(φ), and n3 = cos(φ). Solving eqn (8) for hexagonal crystal structure in Γ–A, Γ–M and Γ–K directions, the solutions are related to elastic constants by the following expressions.
In Γ–A direction ([001]),
 | (9) |
In Γ–M direction ([010]),
 | (10) |
In Γ–K direction [110],
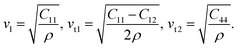 | (11) |
| Compounds | Sound velocities | Elastic constants | |||||||
|---|---|---|---|---|---|---|---|---|---|
| [001] vl | [100] vt | [010] vl | [100] vt1 | [001] vt2 | C11 | C12 | C33 | C44 | |
| a Cal. data by stress-strain method.b Cal. data obtained by Liao et al.11 | |||||||||
| Al4SiC4 | 11.2 | 6.1 | 11.0 | 7.2 | 5.9 | 363, (369.5a, 386b) | 52.1, (117a, 118b) | 376.3, (383.5a, 409b) | 111.6, (110.2a, 122b) |
| Al4Si2C5 | 7.3 | 6.1 | 11.1 | 7.4 | 5.9 | 373.3, (371.7a) | 41.5, (112.1a) | 161.5, (396a) | 112.7, (100.5a) |
Both compounds show slightly anisotropy in sound wave velocity. The sound velocities ranging from 5.9–11.2 km s−1 and 5.9–11.1 km s−1 can be observed for Al4SiC4 and Al4Si2C5, respectively. Meanwhile, the calculated elastic constants of Al4SiC4 are C11 = 363 GPa, C12 = 52.1 GPa, C33 = 376.3 GPa, C44 = 111.6 GPa; and the values of Al4Si2C5 are C11 = 373.3 GPa, C12 = 41.5 GPa, C33 = 161.5 GPa, C44 = 112.7 GPa. Compared with the results obtained by stress-strain method,24,25 the values of C11 and C44 are in good agreement between two methods (in Table 2). The biaxial elastic modulus C12 is significantly smaller than that predicted by strain–stress method. In the case of Al4Si2C5, the uniaxial modulus C33 is also underestimated, compared to strain–stress value. Since we employ PBE to calculate phonon spectrum, it is likely that acoustic phonon dispersions in [001] direction are become softer than they would be.
Based on the phonon spectra of the equilibrium and deformed cells (±1%), the mode Grüneisen parameters are obtained, and the results are displayed in Fig. 1c and 2c. For Al4SiC4, the mode Grüneisen parameters are positive throughout the Brillouin zone for almost all phonon branches except for few of them exhibit negative values. On the other hand, Al4Si2C5 phase has a large number of phonon modes with negative γ(ω) values, and all of them are seen in both acoustic and optical branches in low frequency part. The observed negative γ(ω) at low frequency part of Al4Si2C5 may be relevant to its thermal expansion behavior, i.e., at very low temperature, the thermal expansion coefficients of Al4Si2C5 may decrease with the increasing of temperature. The origin of negative mode-Grüneisen parameter is illustrated in Fig. 5, using a phonon eigenvector of Al4SiC4 as an example. This particular phonon mode at Γ-point gives a negative mode-Grüneisen parameter of −0.28. As can be seen from Fig. 5, the eigenvector is obviously [x y 0] type, and which corresponds to the in-plane movement of all atoms. The eigenvectors of all Si and C atoms are in-phase on basal plane. Out-of-phase motions are seen for Al and C atoms in CAl4 and CSi3Al tetrahedral. The most intriguing result due to those atomic displacements is the creation of stacking fault between Si and Al layers. As a result, it is likely to increase the electrostatic repulsion between two positively charged atomic layers due to the lack of proper screening, i.e., Al–Al and Al–Si. Such repulsive interaction is weakened by increasing the cell volume. Therefore, the force constant and phonon frequency are actually larger in a stretched cell than those of a compressed cell. For Al4SiC4 and Al4Si2C5, negative mode-Grüneisen parameter is not observed in high-frequency optical phonons. Most lower-laying optical phonons are very likely to create stacking fault on basal plane in the crystal structure. Therefore, we may conclude that the increasing of electrostatic energy between two mismatched atomic layers due to the stacking fault results in the negative mode-Grüneisen constant in both structures.
The macroscopic Grüneisen parameters are calculated by eqn (3) and the results are shown in Fig. 6. Basically, at low temperature, the macroscopic Grüneisen parameter is determined by acoustic phonons and low-frequency optical band modes; and at high temperature, the macroscopic Grüneisen parameters are dominated mostly by optical phonons. The macroscopic Grüneisen parameters along a or b axis (γ[100]) increase continuously with the temperature (Fig. 6a and c) for Al4SiC4 and Al4Si2C5. However, the γ[001] versus T curves show different behaviors in both ternary carbides. Here, γ[001] of Al4SiC4 increases with the temperature, and the opposite trend is obtained for Al4Si2C5. This is reasonable because the optical mode-Grüneisen parameters of Al4SiC4 have larger values along H–K and M–L paths ([001] crystal directions) than those of Al4Si2C5. Meanwhile, the Grüneisen parameter of both phases along c axis is higher than that along a or b axis. The observed anisotropy in Grüneisen parameter reflects the difference in chemical bonding of [001] direction and x–y basal plane. As a result, we would expect the linear thermal expansion coefficient of [001] direction will be higher than that along [100] or [010] direction.
 | ||
| Fig. 6 The macroscopic Grüneisen parameters for Al4SiC4 (a and b) and Al4Si2C5 (c and d) in principal directions. | ||
3.2. Thermodynamic properties
The obtained Helmholtz free energy curves for temperatures ranging from 0 K to 1600 K are shown in Fig. 7. We can clearly see that the free energy decreases with the temperature, and the equilibrium volume increases with the temperature. Based on this facts, the volumetric and linear thermal expansion coefficients are shown in Fig. 8. For hexagonal structure, the linear TECs can be calculated from volumetric TECs and macroscopic Grüneisen parameters:18| λ(T) = 2αa(T) + αc(T) | (12) |
 | (13) |
 | ||
| Fig. 7 Dependence of the Helmholtz free energy F (V, T) on the cell volume at different temperature from 0 to 1600 K for Al4SiC4 (a) and Al4Si2C5 (b). The calculated equilibrium volumes of Al4SiC4 and Al4Si2C5 at 0 K are 204.45 Å3 and 369.09 Å3, respectively. These values are slightly higher than experimental data (201.6 Å3 for Al4SiC4 and 367.1 Å3 for Al4Si2C5) obtained by Inoue et al.1 Because the PBE functional was used for calculation. | ||
 | ||
| Fig. 8 Thermal expansion coefficients (TECs) of Al4SiC4 (a) and Al4Si2C5 (b) as a function of temperature. | ||
Using eqn (11) and (12), the linear TEC tensor can be determined from volumetric TEC.18 The calculated tensor components are used here to illustrate the anisotropy in TEC of hexagonal Al4SiC4 and Al4Si2C5. In Fig. 9, the two-dimensional planar projections are shown for two structures. In the calculations, we use temperature-averaged linear TECs computed between 300 K and 1500 K. For Al4SiC4, we find 9.75 × 10−6 K−1 in [100] direction and 11.1 × 10−6 K−1 in [001] direction, and the values for Al4Si2C5 in those directions are 8.79 × 10−6 K−1 and 9.69 × 10−6 K−1. For both structures, the linear TECs in two principal crystallographic directions are not significantly different to each other. The anisotropy in linear TEC tensor is expected, as shown in Fig. 9. However, Al4SiC4 and Al4Si2C5 are not considered as the typical layered structures where physical properties are very different in the directions parallel and perpendicular to layers in latter case. From our current results, the chemical bonds intra- and inter-layer are not quite unlike in two structures.
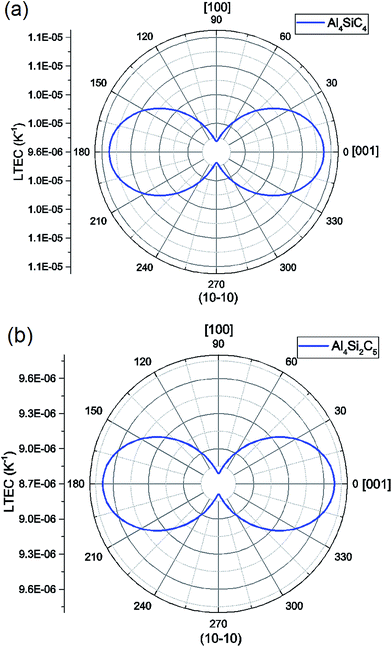 | ||
| Fig. 9 Anisotropy in thermal expansion tensor is illustrated by 2-D projection. (a) Al4SiC4; (b) Al4Si2C5. | ||
Isothermal bulk modulus as a function of temperature is shown in Fig. 10. Al4Si2C5 has larger bulk modulus than Al4SiC4 implying the small incompressibility of Al4Si2C5. We may conclude that incorporating more Si and C atoms in the Al–Si–C ternary compounds would increase the mechanical modulus, because the formation of more Si–C bonds in the crystal structure of Al4Si2C5. The bulk moduli of both phases decrease with increasing of temperature. At 1600 K, the bulk modulus of Al4SiC4 is decreased by ∼33.8 GPa of the value at 0 K, and which is little smaller than that of Al4Si2C5 by ∼34.9 GPa. Then, isobaric bulk modulus as a function of temperature can be computed using expression below:
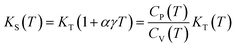 | (14) |
 | ||
| Fig. 10 Isothermal bulk modulus (a) and isobaric bulk modulus (b) of aluminum silicon carbides as a function of temperature. | ||
Base on the thermal expansion results, we calculated the specific heat at constant pressure (CP) with CP = CV + λ2V(T)TKT.23 Here, λ is the volumetric TEC, KT is the isothermal bulk modulus at different temperature. Meanwhile, the specific heat CV and entropy S as a function of temperature were evaluated by standard expressions in ref. 30 and 31.
The specific heats (CV and CP) results are illustrated in Fig. 11. The obtained CP values of Al4SiC4 and Al4Si2C5 at room temperature are 16.5 and 18.8 J mol−1 K−1·atom, respectively. Constant pressure specific heat increases with temperature due to volumetric thermal expansion. Above room temperature, an increasing of the value linearly with temperature implies that anharmonic effects are relatively weak in crystal structure. Thus, QHA is an accurate approximation for computing thermal properties. Below room temperature, the difference between CP and CV is very small because the thermal expansion is nearly negligible. CP and CV behave differently at high temperature, CV tends to approaching the classical Dulong–Petit asymptotic limit of 24.93 J mol−1 K−1; while CP keeps growing at high temperature due to the work done by the volumetric expansion.
 | ||
| Fig. 11 The specific heats at constant pressure or volume of Al4SiC4 (a) and Al4Si2C5 (b) as a function of temperature. The horizontal line represents classic Dulong–Petit law. | ||
In Fig. 12 the dependence of the entropy on the temperature of both phases are shown. The calculated values for Al4SiC4 and Al4Si2C5 at 300 K are 12.2 and 11.7 J mol−1 K−1·atom and increase continuously with the temperature. Al4Si2C5 has a slightly higher value than Al4SiC4 due to more vibrational modes in former structure.
The thermal conductivity, which characterizes the heat transportation capability of crystal structures, are very important for high-temperature structural materials. The dependence of thermal conductivity on temperature is plotted in Fig. 13. As expected from Slack model, thermal conductivity decreases with the increasing of temperature by the law 1/T. The average thermal conductivities in the temperature range of 300–1500 K are 29.9 and 23.4 W m−1·K−1 for Al4SiC4 and Al4Si2C5, respectively. The unit cell of Al4Si2C5 has more atoms than formal structure, resulting in a lower thermal conductivity due to more optical phonons in the structure.32 For comparison, we want to list some available experimental data for Al4SiC4. Wills and Goodrich26 gave the experimental thermal conductivity of 8 W m−1 K−1 without clearly indicating the temperature. Inoue et al.6 claimed a constant thermal conductivity of 80 W m−1 K−1 in the temperature range from 300 K to 1473 K. Actually, our calculated average thermal conductivity of Al4SiC4 is situated between them. Unfortunately, to our knowledge, the experimental thermal conductivity for Al4Si2C5 is not available at the moment.
3.3. Chemical bonding
In this part, we would like to discuss the chemical bonding properties of the aluminum silicon carbides under hydrostatic pressure. Fig. 14 shows the normalized bond lengths as a function of pressure. Generally speaking, all bond lengths decrease with the increasing of pressure. The chemical bonds, which are easy to change under pressure, are situated on the lower part of graphs, showing a stronger dependence on pressure. Specifically, Al–C bonds are softer than Si–C bonds under compression. In both Al4SiC4 and Al4Si2C5 structures, Si–C bonds aligned in [001] direction are stiff and exhibit small compressibility among all chemical bonds. Although, several different bond lengths are observed for either Si–C or Al–C bonds, the general trend is the same in two structures.Using the volume at different pressures, we could calculate the isothermal bulk modulus by fitting volume versus pressure data, using a proper equation of state (EOS). The bulk moduli of Al4SiC4 and Al4Si2C5 are 173.6 and 178.2 GPa, and which are slightly higher than the data shown in Fig. 10. The uniaxial modulus can be defined by Bx = −x0(dP(x)/dx) where x refers to lattice parameters (a or c). The calculated uniaxial moduli of the two ternary carbides show anisotropy. For Al4SiC4 the Ba and Bc are 541.4 and 478.7 GPa, while for Al4Si2C5, the values are 558.7 and 489.8 GPa, respectively. These uniaxial moduli along principal axes are expected to be at least comparable to elastic constants in the same direction. The calculated values are actually larger than the corresponding elastic constants. The observed discrepancies in the two data sets can be traced back to the calculation of elastic constants under finite strain (hydrostatic pressure), as shown in eqn (15).
 | (15) |
The value of Ba is larger than that of Bc implying the anisotropy in compressibility. In addition, the difference between Ba and Bc is mainly attributed to layered like crystal structure in MAX phases.
The insightful chemical bonding information are provided by population analysis results shown in Table 3. It is clearly indicated that C carries the negative charges in both ternary carbides. The positive charges are carried by Al and Si atoms. We suggest two possible electron transfer mechanisms. The first one refers to s–p orbital hybridization of the same atom (C, Al and Si). The other one is induced by the ionic bonding among C and Al (or Si). In the former case, the electrons are transferred from (C, Al, Si)-s states to (C, Al, Si)-p states of same atom, and those hybridized atomic orbitals overlap with each other in upper valence band region between atoms. In the latter case, the electrons are transferred from Al atom to C atom, implying an ionic bonding character between them. However, the bonding mechanism between Si and C is anticipated to be mainly covalent. The calculated bond overlap populations and bond lengths of Si–C pair confirm this conjecture. Besides, for both ternary carbides, the Al–C (and Si–C) bond deviate from c axis behave the largest overlap populations and relatively short bond length, compared to those of Al–C bonds aligned along c axis. For Al–C bond along c axis type II, a quite small electron-overlap population value (0.08 electrons) is found, and which implies Al–C bond along [001] direction is close to perfect ionic bond. The quite large bond length also supports this conclusion. From the calculated linear bulk moduli in [100] and [001] directions, we may conclude that the overall bond strength at basal plane (x–y) is slightly stronger than that of z direction in two hexagonal structures.
| Polymorph | Species (ion) | s | p | Total electrons | Charges |
|---|---|---|---|---|---|
| Al4SiC4 | C(1–8) | 1.49 | 3.92 | 5.41 | −1.41 |
| Al(1–8) | 0.66 | 1.2 | 1.86 | 1.14 | |
| Si(1–2) | 1.04 | 1.84 | 2.88 | 1.12 | |
| Al4Si2C5 | C(1–15) | 1.48 | 3.91 | 5.39 | −1.39 |
| Al(1–12) | 0.67 | 1.17 | 1.84 | 1.16 | |
| Si(1–6) | 1.03 | 1.84 | 2.87 | 1.13 |
| Polymorph | Bond | n | L |
|---|---|---|---|
| Al4SiC4 | Al–C bond along c axis type I | 0.45 | 1.91 |
| Al–C bond along c axis type II | 0.08 | 2.18 | |
| Al–C bond along c axis type III | 0.44 | 1.96 | |
| Al–C bond deviate from c axis | Avg. 1.68, (1.37–2.00) | Avg. 2.03, (1.92–2.14) | |
| Si–C bond along c axis | 0.49 | 1.86 | |
| Si–C bond deviate from c axis | 2.25 | 1.98 | |
| Al4Si2C5 | Al–C bond along c axis type I | 0.45 | 1.95 |
| Al–C bond along c axis type II | 0.08 | 2.21 | |
| Al–C bond deviate from c axis | Avg. 1.65, (1.36–1.94) | Avg. 2.02, (1.91–2.13) | |
| Si–C bond along c axis | 0.5 | 1.86 | |
| Si–C bond deviate from c axis | 2.25 | 1.97 |
Finally, we would like to analyze the charge density of Al4SiC4 structure at the equilibrium volume. Similar plots for Al4Si2C5 are omitted here, because they show little difference to Al4SiC4 case. In Fig. 15, the total electron density is shown on (100) crystallographic plane. The accumulation of charge density around different atoms is consistent with their electronegativity values. The average electron density at the position of C atom is significantly higher than those of Al and Si. This observation is supported by the electron population results given in Table 3. Obviously, electron density of Al–C bond is strongly polarized, and the ionic bond between them is further confirmed. Meanwhile, Si–C bond shows covalent character, as implied by large charge density shared between two atoms. The local uniformity of electron density in the system is depicted in Fig. 15, using reduced density gradient (s). We use the eqn (15) to calculate s from total electron density on a crystallographic plane.
 | (16) |
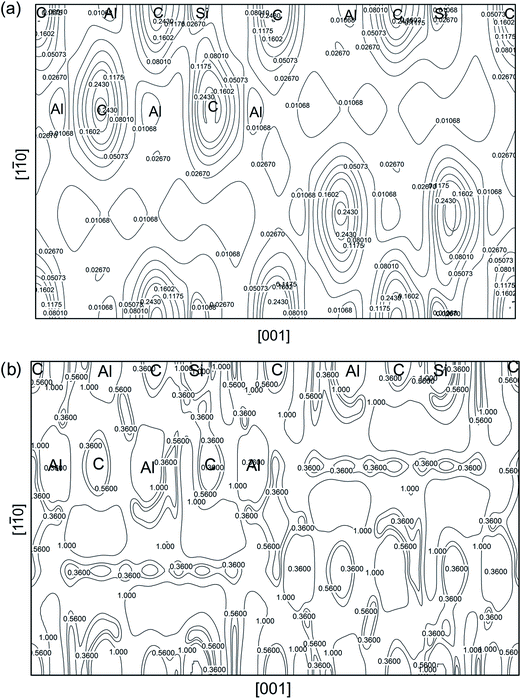 | ||
| Fig. 15 Charge density properties of Al4SiC4. (a) Electron density distribution at (100) plane; (b) reduced density gradient (s) at the same plane. The unit for electron density is e Å−3. | ||
4. Conclusions
Using first-principles calculations based on DFT, the phonon spectra and Grüneisen parameters were calculated. No imaginary phonon frequencies can be found in the whole Brillouin zone for Al4SiC4 and Al4Si2C5 implying their stability nature. IR and Raman active phonon modes and their eigenvectors were analyzed. The Grüneisen parameters of both phases along c axis are higher than that along a or b axis. Therefore, the linear TECs of both ternary carbides along [001] direction are higher that along [100] or [010] direction. The average linear TECs for Al4SiC4 and Al4Si2C5 in the temperature range from 300 K to 1500 K are 9.96 × 10−6 and 8.9 × 10−6 K−1, respectively. The calculated components of TEC tensor are used to illustrate its anisotropy in Al4SiC4 and Al4Si2C5. The results indicate both compounds are not considered as the typical layered structures where physical properties are very different in the directions parallel and perpendicular to layers. The CP of Al4SiC4 and Al4Si2C5 at room temperature are 16.5 and 18.8 J mol−1 K−1·atom and increase monotonically with temperature up to 1600 K. The average thermal conductivities in the temperature between 300 K and 1500 K are 29.9 and 23.4 W m−1 K−1 for Al4SiC4 and Al4Si2C5, respectively. The uni-axial modulus Ba and Bc of Al4SiC4 are 541.4 and 478.7 GPa, while for Al4Si2C5, the values are 558.7 and 489.8 GPa, respectively. Chemical bonding properties were investigated under different hydrostatic pressures by Milliken population analysis. The electron density and its reduced density gradient distributions on (110) crystallographic plane were shown to illustrate the characteristics of Al–C and Si–C bonds in the structures. It was found that Si–C bonds are mainly covalent, in contrast to the ionic dominated Al–C bonds.Acknowledgements
This work was supported by the Natural Science Foundation of China (51501139), the Science and Technology Project of Guangdong Province in China (Special Foundation for Additive Manufacturing Technologies: No. 2015B010122003, and Special Foundation for Practical Science and Technology Research and Development Project: No. 2015B090926009), the Postdoctoral Science Foundation funded project of China (No. 2014M552434).References
- Z. Inoue, Y. Inomata, H. Tanaka and H. Kawabata, J. Mater. Sci., 1980, 15, 575–580 CrossRef CAS.
- O. Gaballa, B. Cook and A. Russell, Ceram. Int., 2011, 37, 3117–3121 CrossRef CAS.
- K. Inoue and A. Yamaguchi, J. Am. Ceram. Soc., 2003, 86, 1028–1030 CrossRef CAS.
- O. Yamamoto, M. Ohtani and T. Sasamoto, J. Mater. Res., 2002, 17, 774–778 CrossRef CAS.
- G. W. Wen and X. X. Huang, J. Eur. Ceram. Soc., 2006, 26, 1281–1286 CrossRef CAS.
- K. Inoue, S. Mori and A. Yamaguchi, J. Ceram. Soc. Jpn., 2003, 111, 348–351 CrossRef CAS.
- K. Inoue and A. Yamaguchi, J. Ceram. Soc. Jpn., 2003, 111, 267–270 CrossRef CAS.
- C. Yu, H. Zhu, W. Yuan, C. Deng and S. Zhou, Adv. Mater. Res., 2014, 881–883, 854–857 CrossRef.
- M. K. Linnarsson, M. S. Janson, U. Zimmermann, B. G. Svensson, P. O. A. Persson, L. Hultman, J. Wong-Leung, S. Karlsson, A. Schoner, H. Bleichner and E. Olsson, Appl. Phys. Lett., 2001, 79, 2016–2018 CrossRef CAS.
- A. Hussain, S. Aryal, P. Rulis, M. A. Choudhry and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 195102 CrossRef.
- T. Liao, J. Wang and Y. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 174112 CrossRef.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- A. E. Mattsson, P. A. Schultz, M. P. Desjarlais, T. R. Mattsson and K. Leung, Modell. Simul. Mater. Sci. Eng., 2005, 13, R1 CrossRef CAS.
- L. Z. Cao, J. Shen and N. X. Chen, J. Alloys Compd., 2002, 336, 18–28 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- G. Kern, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8551 CrossRef CAS.
- F. Birch, Phys. Rev., 1947, 71, 809 CrossRef CAS.
- Y. C. Ding and B. Xiao, RSC Adv., 2015, 5, 18391–18400 RSC.
- G. A. Slack, Solid State Phys., 1979, 34, 1–71 CAS.
- B. Peng, H. Zhang, H. Shao, Y. Xu, X. Zhang and H. Zhu, RSC Adv., 2016, 6, 5767 RSC.
- C. L. Julian, Phys. Rev., 1965, 137, A128 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- G. Grimval, Thermophysical Properties of Materials, North Holland, 1999 Search PubMed.
- J. J. Zhao, J. M. Winey and Y. M. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 094105 CrossRef.
- J. Feng, B. Xiao, R. Zhou and W. Pan, Acta Mater., 2013, 61, 7364 CrossRef CAS.
- R. Wills and S. Goodrich, in The Oxidation of Aluminum Silicon Carbide: Proceedings of 29th International Conference on Advanced Ceramics and Composites, ed. D. Zhu and K. Plucknett, The American Ceramic Society, Florida, Ohio, USA, 23-28 January 2005, pp. 181–188 Search PubMed.
- M. W. Barsoum and T. EI-Raghy, J. Am. Ceram. Soc., 1996, 79, 1953–1956 CrossRef CAS.
- N. V. Tzenov and M. W. Barsoum, J. Am. Ceram. Soc., 2000, 83, 825–832 CrossRef CAS.
- N. J. Lane, S. C. Vogel, E. N. Caspi and M. W. Barsoum, J. Appl. Phys., 2013, 113, 183519 CrossRef.
- P. Hermet, A. Lignie, G. Fraysse, P. Armand and P. Papet, Phys. Chem. Chem. Phys., 2013, 15, 15943–15948 RSC.
- S. Baroni, S. Gironcoli, A. D. Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843–15852 RSC.
- B. Xiao, J. Sun, A. Ruzsinszky, J. Feng, R. Haunschild, G. E. Scuseria and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 184103 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |








