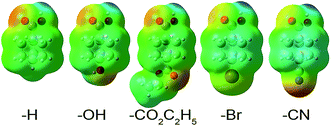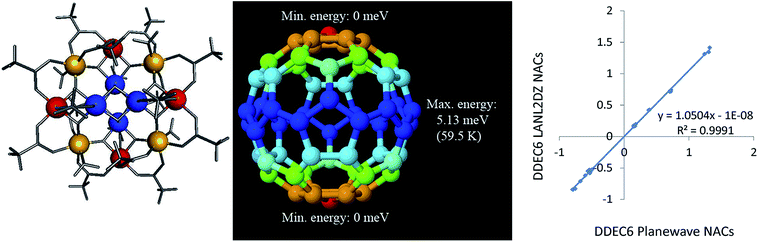Introducing DDEC6 atomic population analysis: part 2. Computed results for a wide range of periodic and nonperiodic materials†
Nidia Gabaldon Limas and
Thomas A. Manz*
Department of Chemical & Materials Engineering, New Mexico State University, Las Cruces, New Mexico 88003-8001, USA. E-mail: tmanz@nmsu.edu
First published on 25th April 2016
Abstract
Net atomic charges (NACs) are widely used throughout the chemical sciences to concisely summarize key information about charge transfer between atoms in materials. The vast majority of NAC definitions proposed to date are unsuitable for describing the wide range of material types encountered across the chemical sciences. In this article, we show the DDEC6 method reproduces important chemical, theoretical, and experimental properties across an extremely broad range of material types including small and large molecules, organometallics, nanoclusters, porous solids, nonporous solids, and solid surfaces. Some important comparisons we make are: (a) correlations between various NAC models and spectroscopically measured core-electron binding energy shifts for Ti-, Fe-, and Mo-containing solids, (b) comparisons between DDEC6 and experimentally extracted NACs for formamide and natrolite, (c) comparisons of accuracy of different NAC methods for reproducing the electrostatic potential surrounding a material across one and multiple system conformations, (d) comparisons between calculated and chemically expected electron transfer trends for atoms in numerous dense solids, solid surfaces, and molecules, (e) an assessment of NAC transferability between three crystal phases of the diisopropylammonium bromide organic ferroelectric, and (f) comparisons between DDEC6 and polarized neutron diffraction atomic spin moments for the Mn12-acetate single-molecule magnet. We find the DDEC6 NACs are ideally suited for constructing flexible force-fields and give reasonable agreement with force-fields commonly used to simulate biomolecules and water. We find the DDEC6 method is more accurate than the DDEC3 method for analyzing a broad range of materials. This broad applicability to periodic and non-periodic materials irrespective of the basis set type makes the DDEC6 method suited for use as a default atomic population analysis method in quantum chemistry programs.
1. Introduction
The concept of atoms in materials is one of the most universal concepts in the chemical sciences. For example, a water molecule is comprised of two hydrogen atoms and one oxygen atom. Materials contain a cloud of electrons surrounding atomic nuclei. Conceptually partitioning a material into constituent atoms is equivalent to assigning fractions of the electron cloud to each atomic nucleus. The net atomic charge (NAC) assigned to each atom in the material is defined by| qA = zA − NA | (1) |
There is some flexibility when assigning quantitative properties to the individual atoms in materials. Different definitions for assigning electrons to each atom in a material lead to different NAC values. For example, a method that assigns 8.7 (0.65) electrons to each oxygen (hydrogen) atom in water yields NACs of −0.7 (+0.35) for each oxygen (hydrogen) atom, while a method that assigns 8.8 (0.60) electrons to each oxygen (hydrogen) atom in water yields NACs of −0.8 (+0.4) for each oxygen (hydrogen) atom.
Currently, there is a pressing need to develop an atomic population analysis method suitable for use as a default method in quantum chemistry programs. Because quantum chemistry programs are used to study a broad range of material types, such a method should have extremely broad applicability. Because different quantum chemistry programs use different basis set types (e.g., plane-waves, Gaussian basis functions, Slater-type orbitals, numerical basis sets, etc.), it is preferable for the method to have no explicit basis set dependence. This will ensure the method converges towards a well-defined mathematical limit as the basis set is improved towards completeness. In contrast, the Mulliken1 and Davidson–Löwdin2 population analysis methods currently used as default methods in some quantum chemistry programs do not have any mathematical limits as the basis set is systematically improved towards completeness.3 Several charge partitioning methods with well-defined basis set limits have been developed, but these have other limitations as described in our prior article.4 To address these limitations, we introduced a new atomic population analysis method, called DDEC6, that is suitable for use as a default method in quantum chemistry programs.4
The theory and computational methods for the DDEC6 method were described in our prior article.4 The purpose of the present article is to test the performance of the DDEC6 method across a wider range of material types. A diverse materials set was carefully selected to evaluate the accuracy of our new charge partitioning method. To test whether the DDEC6 method consistently performs better than the DDEC3 method, we include many systems for which the DDEC3 method was originally tested.5 In addition, we study many new materials carefully selected for their ability to make falsifiable tests of a charge assignment method's ability to describe electron transfer. One of the most frequent concerns about charge assignment methods is that it is difficult to compare them directly to experimental data. Therefore, we included many materials having strong experimental data. These comparisons to experimental data allow our Results and discussion to be viewed not only as applications of the DDEC6 method but also as performance tests.
A few remarks are appropriate pertaining to the charge assignment methods against which the new DDEC6 charge partitioning is compared. Because there are so many different charge assignment methods, it was impractical to compare all charge assignment methods for each material studied here. Therefore, we adopted the policy to compare against an appropriate subset of charge assignment methods for each material. Since DDEC6 is the successor to DDEC3, we compared DDEC6 to DDEC3 in most cases. In most cases, we included the charge assignment methods one would expect to perform the best for each kind of material. For example, electrostatic potential fitting (ESP6,7 or REPEAT8) NACs were included in most comparisons based on the electrostatic potential root-mean-squared error (RMSE) and relative root-mean-squared error (RRMSE). For dense solids, Bader's quantum chemical topology9,10 was included, because it is currently the most widely used charge partitioning method for dense solids. We avoided Mulliken and Davidson–Löwdin charges, because these are extremely sensitive to the basis set choice.3 We included comparisons to the Hirshfeld11 (HD) method in many cases, because it is easy to do even though the HD method usually underestimates NAC magnitudes.5,12–14 We restricted comparisons to Iterative Hirshfeld13 (IH) and related methods to previously published results, because the several different variations of these methods and their various reference ion densities is beyond the scope of this article.13,15–20 (In our prior article, we presented data for three systems proving for the first time that the IH optimization landscape is sometimes non-convex and converges to non-unique solutions.4) Because several of the systems studied here were suggested in an article by Wang et al.21 focusing on applications of CM5, we compared DDEC6 to CM5 results in those cases and a few others. For a few molecular systems, we also compared results to Natural Population Analysis3 (NPA) and Iterated Stockholder Atoms22 (ISA) charges. None of the dense materials included comparisons to the ISA charges, because these are known to perform poorly for dense solids.23 We do not include comparisons to Atomic Polar Tensor24 (APT) or Born effective25 charges, because DDEC6 charges quantify a system's static electron distribution while APT and Born effective charges quantify the system's response to a perturbation.4,24,25 As discussed in our prior article, APT and Born effective charges are not designed to assign core electrons to the host atom.4
2. Computational details
We performed periodic quantum chemistry calculations using VASP26,27 software. Our VASP calculations used the projector augmented wave (PAW) method28,29 to perform all-electron frozen-core calculations including scalar relativistic effects with a plane-wave basis set cutoff energy of 400 eV. For all systems, the number of k-points times the unit cell volume exceeded 4000 Å3. This is enough k-points to converge relevant properties including geometries and atoms-in-materials (AIM) properties (NACs, ASMs, etc.). Except where otherwise specified, geometry optimizations relaxed both the unit cell vectors and ionic positions. The solid surface calculations (see Section S3 of the ESI†) used the Density Functional Theory (DFT) optimized bulk lattice vectors and relaxed the ionic positions. Where noted, experimental crystal structures or other geometries from the published literature were used. A Prec = accurate (∼0.14 bohr) electron density grid spacing was used. Bader NACs were computed using the program of Henkelman and coworkers.30We performed non-periodic quantum chemistry calculations using GAUSSIAN 09 (ref. 31) software. ESP NACs were computed in GAUSSIAN 09 using the Merz–Singh–Kollman scheme.6,7
Computational details for the DDEC6 charge partitioning and for the electrostatic potential RMSE are described in our previous article.4 Our parallelized code for computing DDEC6 NACs, ASMs, and bond orders is currently available in the CHARGEMOL program distributed via http://ddec.sourceforge.net.32
3. Results and discussion
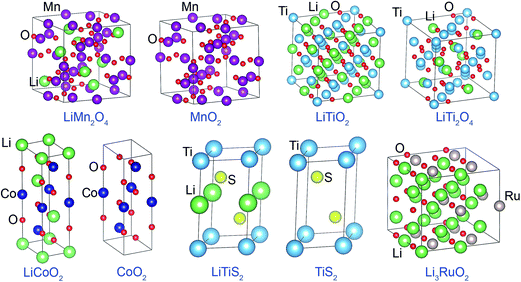
3.1 Representing electron transfer between atoms
| Crystal | HD | CM5 | DDEC3 | DDEC6 | Bader | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Li | TM | Anion | Li | TM | Anion | Li | TM | Anion | Li | TM | Anion | Li | TM | Anion | |
| a NACs from ref. 21 using M06L optimized geometries and electron distributions.b LiMn2O4 has a spinel structure that undergoes a charge-ordering transition as shown in experiments;35–37 the PBE functional shows charge disproportionation between the Mn sites (i.e., a charge-ordered phase) while the M06L functional gives equal NACs on all Mn sites21 (i.e., a high-temperature phase without charge ordering). | |||||||||||||||
| LiCoO2 | 0.11 | 0.34 | −0.23 | 0.49 | 0.73 | −0.61 | 1.03 (1.00a) | 1.47 (1.45a) | −1.25 (−1.23a) | 0.87 | 1.07 | −0.97 | 0.88 | 1.22 | −1.05 |
| CoO2 | — | 0.35 | −0.18 | — | 0.80 | −0.40 | — | 1.14 (1.23a) | −0.57 (−0.62a) | — | 1.12 | −0.56 | — | 1.39 | −0.69 |
| LiTiS2 | 0.07 | 0.40 | −0.23 | 0.27 | 0.79 | −0.53 | 0.98 (0.97a) | 1.67 (1.48a) | −1.33 (−1.23a) | 0.86 | 1.38 | −1.12 | 0.89 | 1.48 | −1.18 |
| TiS2 | — | 0.43 | −0.21 | — | 0.86 | −0.43 | — | 1.06 (1.06a) | −0.53 (−0.53a) | — | 1.32 | −0.66 | — | 1.61 | −0.80 |
| LiTiO2 | 0.11 | 0.56 | −0.34 | 0.46 | 1.16 | −0.81 | 1.05 (1.00a) | 2.17 (2.10a) | −1.61 (−1.55a) | 0.89 | 1.65 | −1.27 | 0.89 | 1.57 | −1.23 |
| LiTi2O4 | 0.16 | 0.64 | −0.36 | 0.48 | 1.31 | −0.78 | 1.03 (1.00a) | 2.33 (2.32a) | −1.42 (−1.41a) | 0.90 | 1.94 | −1.19 | 0.91 | 1.84 | −1.15 |
| LiMn2O4b | 0.17 | 0.34 | −0.21 | 0.53 | 0.84 | −0.55 | 0.99 (1.00a) | 1.56 (1.95a) | −1.03 (−1.23a) | 0.86 | 1.23 | −0.83 | 0.89 | 1.59 | −1.02 |
| MnO2 | — | 0.36 | −0.18 | — | 0.88 | −0.44 | — | 1.24 (1.47a) | −0.62 (−0.73a) | — | 1.25 | −0.63 | — | 1.69 | −0.85 |
| Li3RuO2 | 0.11 | 0.31 | −0.32 | 0.33 | 0.58 | −0.79 | 0.83 | −0.18 | −1.15 | 0.72 | −0.08 | −1.04 | 0.82 | 0.12 | −1.30 |
| Material | H chargea | Pd chargea | X chargea | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bader | DDEC3 | DDEC6 | HD | CM5 | Bader | DDEC3 | DDEC6 | HD | CM5 | Bader | DDEC3 | DDEC6 | HD | CM5 | |
| a Bader and DDEC3 NACs are from ref. 5. | |||||||||||||||
| H in Pd | −0.04 | −0.25 | −0.05 | −0.13 | −0.12 | 0.001 | 0.008 | 0.001 | 0.004 | 0.004 | n.a. | n.a. | n.a. | n.a. | n.a. |
| Pd3V | n.a. | n.a. | n.a. | n.a. | n.a. | −0.35 | −0.10 | −0.15 | 0.02 | 0.02 | 1.04 | 0.31 | 0.44 | −0.06 | −0.06 |
| H in Pd3V | −0.22 | −0.32 | −0.14 | −0.15 | −0.13 | −0.34 | −0.09 | −0.14 | 0.03 | 0.02 | 1.04 | 0.32 | 0.44 | −0.06 | −0.06 |
| H in Pd3In | −0.05 | −0.18 | −0.05 | −0.11 | −0.09 | −0.21 | −0.08 | −0.07 | 0.06 | 0.16 | 0.64 | 0.27 | 0.22 | −0.16 | −0.47 |
| H in Pd3Hf | −0.05 | 0.02 | −0.01 | −0.10 | −0.09 | −0.53 | −0.31 | −0.23 | 0.08 | 0.08 | 1.58 | 0.92 | 0.69 | −0.22 | −0.22 |
Why did the HD and CM5 methods yield negative NACs for the V, In, and Hf atoms? It is well-known that isolated neutral atoms usually become more contracted upon going from left to right within the same subshell of a periodic table row due to the increasing nuclear charge that contracts the subshell. (Deviations from this trend can occur where electron configurations deviate from the Aufbau principle, such as Pd through Cd.) Moreover, atoms usually become slightly more diffuse or remain about the same size down a periodic table column. Accordingly, an isolated neutral Hf atom is more diffuse than an isolated neutral Pd atom. The Pauling scale electronegativity will usually follow the opposite trend, with the Pauling scale electronegativity increasing left to right within the same subshell of a periodic table row and decreasing down a periodic table column except where electron configurations deviate from the Aufbau principle. Because the neutral Hf reference atom is more diffuse than the neutral Pd reference atom, during HD partitioning the Hf atoms steal electrons from the more electronegative Pd atoms. Thus, in this case, the HD method predicts the wrong charge transfer direction. The CM5 method adds a correction to the HD NACs, but this correction is zero between two transition metal atoms.12 Consequently, the HD and CM5 NACs are identical for Pd3V. In the other materials, there is a non-zero CM5 correction between the main-group elements H and In and the other elements, which causes the CM5 NACs to slightly differ from the HD NACs.
To avoid this problem, the DDEC3 and DDEC6 methods include a constraint that forces wA(rA) for tails of buried atoms to decay at least as fast as exp(−1.75rA/bohr).5 Second, the DDEC6 method sets the reference ion charge for each atom in the material to a weighted average of a stockholder type charge partitioning and a smoothed localized charge partitioning.4 This ensures the reference ion charge resembles the charge in the local vicinity of the atom in order to prevent atoms from becoming too diffuse or too contracted. This makes DDEC6 NACs more accurately describe the true charge transfer direction.
| Method | Systema | ||||||
|---|---|---|---|---|---|---|---|
| MgO | (MgO)2 | (MgO)3 | (MgO)4 | (MgO)5 | (MgO)6 | Bulk MgO | |
| a NACs and dipole moments for the HD, CM5, and DDEC3 methods for the (MgO)n molecules are from ref. 21.b ESP NAC cannot be reported for bulk MgO, because there are no surface atoms. | |||||||
| NAC of central Mg | |||||||
| HD | 0.59 | 0.69 | 0.56 | 0.42 | 0.28 | 0.15 | 0.33 |
| CM5 | 0.79 | 0.97 | 0.93 | 0.88 | 0.82 | 0.77 | 0.77 |
| DDEC6 | 0.99 | 1.45 | 1.57 | 1.60 | 1.61 | 1.61 | 1.47 |
| Bader | 1.18 | 1.54 | 1.65 | 1.62 | 1.57 | 1.48 | 1.70 |
| DDEC3 | 1.00 | 1.55 | 1.72 | 1.76 | 1.79 | 1.84 | 2.01 |
| ESP | 0.89 | 1.16 | 1.04 | 0.96 | 0.58 | −1.72 | b |
| Method | Moleculea | |||||||
|---|---|---|---|---|---|---|---|---|
| MgO | (MgO)2 | (MgO)3 | (MgO)4 | (MgO)5 | (MgO)6 | MAE | ||
| Dipole moment in a.u. | ||||||||
| Full density | 2.71 | 2.32 | 1.39 | 1.70 | 0.48 | 1.97 | 0.00 | |
| HD | 1.87 | 1.97 | 1.28 | 2.08 | 0.88 | 1.98 | 0.35 | |
| ESP | 2.82 | 2.74 | 1.87 | 2.13 | 1.12 | 2.43 | 0.42 | |
| CM5 | 2.51 | 2.54 | 1.91 | 2.47 | 1.51 | 2.61 | 0.56 | |
| DDEC6 | M | 3.14 | 3.18 | 2.37 | 2.49 | 1.68 | 2.91 | 0.87 |
| D | 2.71 | 2.32 | 1.39 | 1.70 | 0.48 | 1.97 | 0.00 | |
| DDEC3 | 3.17 | 3.31 | 2.48 | 2.57 | 1.79 | 3.08 | 0.97 | |
| Bader | 3.71 | 3.39 | 2.46 | 3.09 | 1.63 | 3.77 | 1.25 | |
| Method | Moleculea | |||||||
|---|---|---|---|---|---|---|---|---|
| MgO | (MgO)2 | (MgO)3 | (MgO)4 | (MgO)5 | (MgO)6 | Average RMSE | ||
| RMSE in kcal mol−1 (RRMSE) | ||||||||
| ESP | 2.81 (0.10) | 5.40 (0.23) | 4.59 (0.24) | 5.16 (0.27) | 4.96 (0.27) | 3.79 (0.21) | 4.45 | |
| CM5 | 3.98 (0.15) | 6.50 (0.28) | 4.77 (0.25) | 5.90 (0.31) | 6.12 (0.33) | 5.28 (0.29) | 5.43 | |
| HD | 9.27 (0.35) | 10.05 (0.43) | 6.06 (0.32) | 5.99 (0.31) | 4.90 (0.26) | 4.01 (0.22) | 6.71 | |
| DDEC6 | M | 4.25 (0.16) | 7.24 (0.31) | 6.75 (0.35) | 7.70 (0.40) | 7.77 (0.42) | 6.58 (0.36) | 6.71 |
| M + SCP | 4.63 (0.17) | 7.40 (0.32) | 6.98 (0.36) | 7.82 (0.41) | 7.98 (0.43) | 6.78 (0.37) | 6.93 | |
| D | 1.31 (0.05) | 2.60 (0.11) | 2.87 (0.15) | 2.86 (0.15) | 3.09 (0.17) | 3.03 (0.16) | 2.63 | |
| D + SCP | 0.86 (0.03) | 1.55 (0.07) | 1.67 (0.09) | 1.61 (0.08) | 1.74 (0.09) | 1.70 (0.09) | 1.52 | |
| DDEC3 | 4.44 (0.17) | 8.48 (0.36) | 7.52 (0.39) | 8.48 (0.44) | 8.42 (0.45) | 7.08 (0.39) | 7.40 | |
| Bader | 9.10 (0.34) | 9.26 (0.40) | 10.81 (0.56) | 12.87 (0.67) | 14.20 (0.76) | 14.11 (0.77) | 11.73 | |
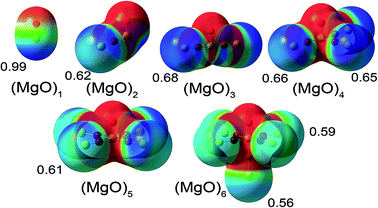
Based on the much lower Pauling scale electronegativity of Mg (1.31) than O (3.44), a substantial transfer of electrons from Mg to O is expected. A simple chemical argument suggests that as the central Mg atom is surrounded by more oxygen anions, electrostatic stabilization of the central Mg cation by the oxygen anions should increase, thereby stabilizing more electron transfer from the central Mg atom to the adjacent oxygen atoms. This simple chemical argument predicts an increase in the central Mg atom NAC as the number of adjacent O atoms increases. Examining Table 3, only the DDEC3 method consistently followed this trend. The trend for terminal Mg NACs can be inferred from the electrostatic potential values. As shown in Fig. 2, the electrostatic potential and DDEC6 NACs are most positive near the terminal Mg atoms following the trend MgO > (MgO)3 > (MgO)4 > (MgO)2 > (MgO)5 > (MgO)6.
As shown in Table 3, the Mg NAC in bulk MgO followed the trend DDEC3 (2.01) > Bader (1.70) > DDEC6 (1.47) > CM5 (0.77) > HD (0.33). The DDEC3 NAC of 2.01 for bulk MgO is similar to some recent high-resolution diffraction experiments and their interpretations in terms of fully ionized Mg2+ and O2− ions.40,41 However, the situation is not as straightforward as it first appears, because (i) charge partitioning in the experimentally measured electron distribution depends on model definitions used to assign NACs and (ii) the low-order structure factors in simple cubic crystals (e.g., MgO and NaCl) have low sensitivity to the amount of charge transfer.21,40–42 Zuo et al. used a convergent beam electron diffraction technique to improve the resolution of the low-order structure factors and concluded the crystal's electron distribution is consistent with fully ionized Mg2+ and O2− ions,40 but this does not rule out other interpretations.
These tests on (MgO)n and bulk MgO illustrate some possible compromises between matching the chemical state trends on the one hand and the electrostatic potential trends on the other hand. Dipole mean absolute error (MAE) followed the trend HD (0.35) < ESP (0.42) < CM5 (0.56) < DDEC6 (0.87) < DDEC3 (0.97) < Bader (1.25). Electrostatic potential RMSE (kcal mol−1) followed the trend ESP (4.45) < CM5 (5.43) < HD, DDEC6 (6.71) < DDEC3 (7.40) < Bader (11.73). Although the ESP method gave low dipole MAE and electrostatic potential RMSE, we do not recommend the ESP method for assigning NACs, because the ESP NACs of the central Mg atom fluctuated erratically from 1.16 for (MgO)2 to −1.72 for (MgO)6. Because the Bader point charges had the highest dipole moment MAE and the highest average electrostatic potential RMSE, we do not recommend Bader NACs for use in force-field point charge models for classical atomistic simulations. Choosing between the remaining four point charge methods (i.e., HD, CM5, DDEC3, and DDEC6) is complicated by the fact that dipole MAE and electrostatic potential RMSE followed a different trend than the central Mg atom NAC. On the basis of the central Mg atom NAC increasing monotonically from MgO molecule to (MgO)6 molecule to bulk MgO, the DDEC3 method would be preferable, but the DDEC3 method gave the largest dipole MAE and average electrostatic potential RMSE among these four charge assignment methods. The HD and CM5 methods had comparatively low dipole MAE and average electrostatic potential RMSE, but yielded low values of 0.33 (HD) and 0.77 (CM5) for the Mg NAC in bulk MgO. Results for the DDEC6 method were intermediate for central Mg NAC, dipole MAE, and average electrostatic potential RMSE.
Finally, Table 3 investigates effects of atomic dipoles and spherical charge penetration. Including atomic dipoles for any AIM method (e.g., HD, DDEC6, Bader, DDEC3), eliminates the dipole prediction error to within a grid integration tolerance (e.g., ∼0.01). Because the dipole moment of a spherical charge distribution is zero, the spherical charge penetration term has no effect on the computed dipoles. Including DDEC6 atomic dipoles decreased the average RMSE from 6.71 to 2.63 kcal mol−1. Although the spherical charge penetration term slightly increased the average RMSE at the DDEC6 (M + SCP) level, it dramatically reduced the average RMSE to 1.52 kcal mol−1 at the DDEC6 (D + SCP) level. Notably, the DDEC6 (D + SCP) average RMSE was ∼3 times lower than any of the point charge models.
3.2 Comparison to spectroscopic results for various materials
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and the shape functions for the charged atoms are represented as expanded or contracted versions of the neutral atoms.5 Here, we revisit two examples for which DDEC3 and experimentally extracted NACs were compared in ref. 5: the formamide and natrolite structures shown Fig. 3. We refer the reader to the earlier publications for a discussion of the experimental details and analysis.5,46–48 The same geometries and electron distributions are used in this work as in ref. 5.
) and the shape functions for the charged atoms are represented as expanded or contracted versions of the neutral atoms.5 Here, we revisit two examples for which DDEC3 and experimentally extracted NACs were compared in ref. 5: the formamide and natrolite structures shown Fig. 3. We refer the reader to the earlier publications for a discussion of the experimental details and analysis.5,46–48 The same geometries and electron distributions are used in this work as in ref. 5.
 | ||
| Fig. 3 Formamide and natrolite structures. The lines in natrolite indicate the unit cell boundaries. Figure reproduced with permission from ref. 5. © American Chemical Society 2012. | ||
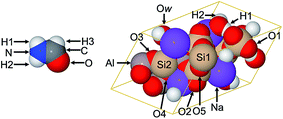
As shown in Table 4, both the DDEC3 and DDEC6 NACs follow a trend similar to the experimentally extracted NACs for natrolite, except the DDEC3 NACs on all atoms except Na are significantly higher in magnitude than the experimentally extracted ones. For all atoms, the DDEC6 NACs are slightly lower in magnitude than the DDEC3 NACs, leading to an overall better agreement between the DDEC6 and experimentally extracted NACs. Only for the Na atom, which was fixed to a value of 1.00 in the experimental analysis,48 is the experimentally extracted NAC closer to the DDEC3 value than the DDEC6 value.
| High res. XRDa | DDEC3b | DDEC6 | |
|---|---|---|---|
| a High resolution XRD data from ref. 48.b DDEC3 NACs from ref. 5. | |||
| Si1 | 1.84 ± 0.12 | 2.172 | 1.772 |
| Si2 | 1.65 ± 0.10 | 2.207 | 1.760 |
| Al | 1.51 ± 0.11 | 2.067 | 1.762 |
| O1 | −0.90 ± 0.05 | −1.227 | −1.036 |
| O2 | −1.21 ± 0.05 | −1.318 | −1.103 |
| O3 | −1.03 ± 0.05 | −1.337 | −1.094 |
| O4 | −1.07 ± 0.05 | −1.320 | −1.110 |
| O5 | −0.87 ± 0.05 | −1.113 | −0.913 |
| Na | 1.00 | 1.000 | 0.896 |
| Ow | −0.59 ± 0.03 | −0.926 | −0.862 |
| H1 | 0.24 ± 0.03 | 0.446 | 0.408 |
| H2 | 0.36 ± 0.03 | 0.435 | 0.405 |
Table 5 summarizes experimentally extracted and computed NACs for formamide. Theoretical charges were computed using the B3LYP49,50 functional with aug-cc-pvtz51 basis set. The high-resolution X-ray diffraction (XRD) results were extracted using fully optimized radial factors for all atoms.46 Maximum absolute differences from the experimentally extracted NACs are 0.07 (NPA), 0.11 (DDEC3), 0.12 (DDEC6), 0.13 (IH), 0.17 (ESP), 0.22 (ISA), 0.64 (HD), and 0.96 (Bader). The DDEC6, ESP, DDEC3, and ISA point charge dipoles were within ±5% of the full wavefunction value of 1.55. Errors for the other point charge dipoles were −6% (IH), +23% (NPA), and +66% (Bader). Of course, when atomic dipoles are included, all of the AIM methods (Bader, DDEC3, DDEC6, HD, IH, and ISA) yield the exact dipole moment to the integration grid precision. The errors of the point charge models for reproducing the electrostatic potential followed the trend ESP < DDEC6 < DDEC3 < ISA < IH < NPA < HD < Bader. When atomic dipoles were included, the RMSE for the DDEC6 method decreased from 0.74 to 0.49 kcal mol−1. When the spherical charge penetration term was included, the RMSE values for the DDEC6 method were unchanged (within a computational tolerance of 0.01 kcal mol−1) at 0.74 (M + SCP) and 0.49 (D + SCP), indicating a negligible impact of spherical charge penetration over the RMSE grid points. In summary, the DDEC6 NACs did a good job of simultaneously reproducing the electrostatic potential, the molecular dipole moment, and the experimentally extracted NACs.
| High res. XRDa | Baderb | DDEC3b | DDEC6 M (D)d | ESPb | HDb | IHb | ISAb | NPAb | |
|---|---|---|---|---|---|---|---|---|---|
| a From ref. 46.b Bader, DDEC3, ESP, HD, IH, ISA, and NPA NACs are from ref. 5.c Dipole moment of the B3LYP/aug-cc-pvtz wavefunction was 1.55.d M denotes point charge (monopole) model; D denotes the inclusion of atomic dipoles. | |||||||||
| O | −0.55 ± 0.04 | −1.149 | −0.557 | −0.506 | −0.562 | −0.304 | −0.537 | −0.593 | −0.605 |
| N | −0.78 ± 0.07 | −1.183 | −0.788 | −0.662 | −0.923 | −0.136 | −0.862 | −0.911 | −0.808 |
| C | 0.51 ± 0.08 | 1.469 | 0.624 | 0.519 | 0.680 | 0.139 | 0.644 | 0.726 | 0.534 |
| H1 | 0.39 ± 0.03 | 0.411 | 0.352 | 0.329 | 0.389 | 0.128 | 0.360 | 0.389 | 0.394 |
| H2 | 0.40 ± 0.03 | 0.426 | 0.369 | 0.313 | 0.429 | 0.133 | 0.377 | 0.407 | 0.388 |
| H3 | 0.03 ± 0.03 | 0.026 | 0.000 | 0.007 | −0.012 | 0.040 | 0.018 | −0.019 | 0.096 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Dipole momentc | 2.57 | 1.59 | 1.53 (1.55) | 1.57 | 1.13 | 1.46 | 1.62 | 1.91 | |
| RMSE | 9.85 | 0.85 | 0.74 (0.49) | 0.58 | 3.32 | 1.43 | 0.99 | 3.13 | |
| RRMSE | 0.89 | 0.08 | 0.07 (0.04) | 0.05 | 0.30 | 0.13 | 0.09 | 0.28 | |
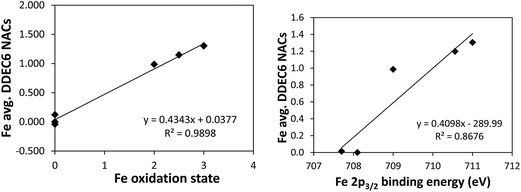
Here, we are most interested in correlations between core electron binding energy shifts and NACs that occur for some crystalline materials.58–62 We now consider a series of Ti, Mo, and Fe compounds as examples. Table 6 summarizes linear correlations between core electron binding energies and NACs. The HD, DDEC6, and Bader methods gave reasonable performance (i.e., R-squared ≥ 0.704) for all three elements, while the DDEC3 and CM5 methods performed poorly (i.e., R-squared ≤ 0.360) for the Ti compounds. Overall, the strength of the correlation between NACs and core electron binding energies followed the trend HD > DDEC6 > Bader > DDEC3 > CM5. Table S1† summarizes details for the Ti-containing solids. NACs were computed using the PBE electron distributions for the experimental geometries defined by the Inorganic Crystal Structure Database (ICSD) codes in Table S1,† except for SrTiO3 which was geometry optimized. The poor correlation of the DDEC3 method for the Ti-containing solids was primarily due to high NACs for TiO, TiN, and TiB2 and a lower NAC for TiCl4 than for TiO.
| Ti compounds | Mo compounds | Fe compounds | |
|---|---|---|---|
| HD | 0.795 | 0.987 | 0.819 |
| DDEC6 | 0.704 | 0.978 | 0.868 |
| Bader | 0.727 | 0.911 | 0.817 |
| DDEC3 | 0.360 | 0.977 | 0.905 |
| CM5 | 0.345 | 0.898 | 0.747 |
Table S2† summarizes results for the Mo-containing solids. NACs were computed using the PBE electron distributions for the experimental geometries defined by the ICSD codes in Table S2.† For structures listing two ISCD codes, both crystal structures were included in the correlation to the experimental K-edge energy. Li et al. measured these K-edge energies using XANES.62 The K-edge energy is correlated to the binding energy of the K-shell (i.e., 1s) core electrons.55,63 Our analysis and correlation for these Mo-containing solids is identical to that of Li et al.62 using DDEC3 and Bader NACs, except we have extended it to DDEC6, CM5, and HD NACs.
Fig. 4 shows linear regression plots between the average Fe DDEC6 NACs and the oxidation state (left panel) and the 2p3/2 core electron binding energy (right panel). NACs were computed using the PBE electron distributions based on the following geometries: Fe (NAC is zero due to symmetry), Fe2SiO4 (PBE-optimized geometry of anti-ferromagnetic spinel phase5), Fe2O3 (PBE-optimized geometry of anti-ferromagnetic phase5), Fe3O4 (PBE-optimized geometry of anti-ferrimagnetic phase5), and Fe3Si (experimental crystal structure64). Our analysis for Fe-containing solids is similar to that of Manz and Sholl5 using DDEC3 NACs, except we have extended it to DDEC6, CM5, HD, and Bader NACs.
3.3 Reproducing the electrostatic potential in one system conformation
Because the assigned atomic electron distributions {ρA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A)} exactly sum to the total electron distribution ρ(
A)} exactly sum to the total electron distribution ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) at each position in space, all AIM methods yield a formally exact representation of the electrostatic potential in the form of a polyatomic multipole expansion with charge-penetration terms.23,65,66 For conciseness, it is desirable to have this polyatomic multipole expansion converge rapidly with most of the electrostatic potential described by the leading-order terms. Many force-fields used in classical molecular dynamics and Monte Carlo simulations use point-charge models to estimate the electrostatic interaction energies between chemical species.67–69 These types of force-fields can be parameterized using NACs and optionally atomic multipoles computed via quantum chemistry calculations. To be suitable for this purpose, we desire the DDEC6 NACs to approximately reproduce the electrostatic potential surrounding a material.
) at each position in space, all AIM methods yield a formally exact representation of the electrostatic potential in the form of a polyatomic multipole expansion with charge-penetration terms.23,65,66 For conciseness, it is desirable to have this polyatomic multipole expansion converge rapidly with most of the electrostatic potential described by the leading-order terms. Many force-fields used in classical molecular dynamics and Monte Carlo simulations use point-charge models to estimate the electrostatic interaction energies between chemical species.67–69 These types of force-fields can be parameterized using NACs and optionally atomic multipoles computed via quantum chemistry calculations. To be suitable for this purpose, we desire the DDEC6 NACs to approximately reproduce the electrostatic potential surrounding a material.
In this section, we compare the accuracy of the DDEC3 and DDEC6 NACs for reproducing the electrostatic potential surrounding a single geometric conformation. Table 7 lists 13 materials including small molecules and ion, a large biomolecule, several metal–organic frameworks, a nanosheet, and a nanotube. This represents several kinds of materials often encountered in classical molecular dynamics or Monte Carlo simulations.67,68,70,71 For each material, the same electrostatic potential grid point files were used to compute the DDEC3 and DDEC6 RMSE values. The DDEC6 NACs reproduced the electrostatic potential better than the DDEC3 NACs in 8 of these systems. This shows the DDEC6 NACs are a slight improvement compared to the DDEC3 NACs for reproducing the electrostatic potential surrounding a material. Including DDEC6 atomic dipoles improved the RSME by > 0.4 kcal mol−1 for the BN nanotube, lp-MIL-53(Al), IRMOF-1 (XRD and DFT geometries), Zn-nicotinate, and H2PO4−. This shows that overall including atomic dipoles produces a modest improvement in the RMSE accuracy. Adding spherical charge penetration at the monopole or dipole levels (i.e., M + SCP and D + SCP) had no significant effect for these materials.
| Material | Geom | XC | Basis set | RMSE (kcal mol−1) | RRMSE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| DDEC3a | DDEC6 | DDEC3a | DDEC6 | ||||||||
| M | D | M (M + SCP) | D (D + SCP) | M | D | M (M + SCP) | D (D + SCP) | ||||
| a DDEC3 data (except BN sheet, formamide, Zn-nicotinate, water, H2PO4− and DNA) is from ref. 5.b From ref. 23.c From ref. 5.d From ref. 72.e From ref. 73.f From ref. 74. | |||||||||||
| B4N4 | DFTb | PW91 | 6-311+G* | 0.26 | 0.33 | 0.17 (0.19) | 0.35 (0.35) | 0.08 | 0.10 | 0.05 (0.05) | 0.10 (0.10) |
| BN tube | DFTb | PW91 | Planewave | 8.81 | 2.40 | 5.91 (5.94) | 1.11 (1.09) | 2.13 | 0.58 | 1.43 (1.44) | 0.27 (0.26) |
| BN sheet | DFT | PBE | Planewave | 0.07 | 0.07 | 0.07 (0.07) | 0.07 (0.07) | 0.64 | 0.64 | 0.64 (0.61) | 0.64 (0.61) |
| Formamide | DFTc | B3LYP | Aug-cc-pvtz | 0.85 | 0.40 | 0.74 (0.74) | 0.49 (0.49) | 0.08 | 0.04 | 0.07 (0.07) | 0.04 (0.04) |
| lp-MIL-53(Al) | XRDd | PW91 | Planewave | 1.57 | 0.59 | 1.46 (1.47) | 0.60 (0.58) | 0.80 | 0.30 | 0.74 (0.75) | 0.30 (0.30) |
| IRMOF-1 | XRDe | PW91 | Planewave | 0.83 | 0.44 | 0.86 (0.86) | 0.26 (0.24) | 0.39 | 0.20 | 0.40 (0.40) | 0.12 (0.11) |
| IRMOF-1 | DFTf | PW91 | Planewave | 0.65 | 0.58 | 0.82 (0.81) | 0.28 (0.27) | 0.27 | 0.24 | 0.33 (0.33) | 0.12 (0.11) |
| ZIF-8 | DFTf | PW91 | Planewave | 0.88 | 0.72 | 0.85 (0.81) | 0.79 (0.76) | 0.57 | 0.47 | 0.56 (0.53) | 0.52 (0.50) |
| ZIF-90 | DFTf | PW91 | Planewave | 0.81 | 0.84 | 1.03 (0.97) | 0.93 (0.88) | 0.12 | 0.12 | 0.15 (0.14) | 0.14 (0.13) |
| Zn-nicotinate | DFT | PBE | Planewave | 0.82 | 0.44 | 0.90 (0.89) | 0.41 (0.40) | 0.46 | 0.25 | 0.51 (0.51) | 0.23 (0.23) |
| Water | DFT | B3LYP | 6-311++G** | 1.31 | 0.80 | 1.16 (1.16) | 0.88 (0.88) | 0.14 | 0.08 | 0.12 (0.12) | 0.09 (0.09) |
| H2PO4− | DFT | M06L | Aug-cc-pvtz | 2.16 | 0.41 | 1.65 (1.65) | 0.49 (0.49) | 0.17 | 0.03 | 0.13 (0.13) | 0.04 (0.04) |
| DNA | DFT | PBE | Planewave | 13.91 | 13.79 | 12.67 (12.68) | 12.77 (12.77) | 0.59 | 0.58 | 0.54 (0.54) | 0.54 (0.54) |
Water is the most abundant solvent in biology and chemical processing. Because water is vital to life on earth, it plays a key role in nearly all health applications. Water also plays a key role in environmental, weather, and climate change processes. Consequently, water is the most important molecule for molecular modeling in general. Because many classical atomistic molecular dynamics and Monte Carlo simulations will use DDEC6 NACs for non-water molecules combined with a well-established commonly used water model for the water solvent, it is desirable for the DDEC6 NACs for the water molecule to be approximately consistent with those of commonly used water models. Lee et al. computed NACs for large unit cells of simulated bulk water (∼2500 atoms with PBE functional and large psinc basis sets) and showed the DDEC/cc2 (qH = 0.3915, qO = −0.783) and DDEC3 (qH = 0.402, qO = −0.804) results are similar to common 3-site water models.79,80 Table 8 lists commonly used 3-site water models that have been optimized to reproduce various properties of bulk water in classical atomistic simulations.75–78 For comparison, DDEC6 results for the isolated water molecule with B3LYP/6-311++G** optimized geometry and electron distribution are qH = 0.3953, qO = −0.7906. A recent study by Farmahini et al. computed DDEC3 NACs to study changes in the hydrophobicity/hydrophilicity of nanoporous silicon carbide-derived carbon upon fluorine doping.81 These results show the DDEC methods are well-suited for studying water molecules.
The B-DNA decamer (CCATTAATGG)2 structure was obtained from a neutron diffraction experiment performed by Arai et al. (PDB ID 1WQZ).84 The 25H2O molecules in the crystal structure are from the solvent and are hydrogen-bonded to the B-DNA as shown in Fig. 5. We added a Na+ ion next to each phosphate group, following previous studies to simulate the B-DNA being in a real solution.85 Using the PBE functional, we optimized the positions of the Na+ ions in VASP while keeping the experimental B-DNA structure fixed. The left panel of Fig. 5 shows the optimized B-DNA decamer including the Na+ ions and hydrogen-bonded water molecules. Because the DDEC6 NACs can be used as input for classical molecular dynamics or Monte Carlo simulations of biomolecules, it is instructive to compare the DDEC6 NACs to those of common biomolecular force-fields.79,80 The right panel of Fig. 5 compares the DDEC6 NACs to the CHARMM27 and AMBER4.1 forcefield NACs for DNA. There is some scatter in the data, but the overall correlation between DDEC6 and force-field NACs is good with R-squared correlation coefficients of 0.93 (CHARMM27) and 0.91 (AMBER4.1). The phosphorus NAC was 1.5 (ref. 82) for CHARMM compared to 1.166 (ref. 83) for AMBER, with the DDEC6 value of 1.38 in-between. Moreover, our DDEC6 NACs for this B-DNA decamer are similar to our previous DDEC3 results.86 Finally, we note that recent articles by Lee et al. studied applications of DDEC NACs to atomistic simulations of large biomolecules including a comparison of force-fields based on AMBER and DDEC NACs for several large proteins.79,80
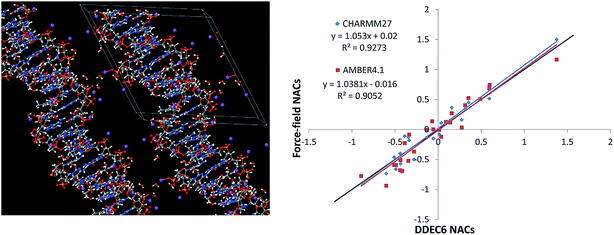 | ||
| Fig. 5 Left: B-DNA decamer (CCATTAATGG)2, the lines mark the unit cell boundaries. Right: Correlation between DDEC6, CHARMM, and AMBER force-field NACs for all atoms excluding the bound water molecules and added Na+ atoms. The black line has a slope of 1 and intercept of 0. CHARMM27 NACs from Foloppe and Mackerell.82 AMBER4.1 NACs from Cornell et al.83 | ||
3.4 Reproducing the electrostatic potential across multiple system conformations for constructing flexible force-fields
We now show these desirable properties are further improved by the DDEC6 NACs. The B3LYP/6-311++G** optimized geometries and electron distributions from ref. 5 are used. Table 9 summarizes the fragment charges for each of these charge assignment methods, where the weighted sum as defined by Manz and Sholl5 is:
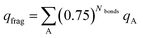 | (2) |
| X | Substituent net chargeb | Weighted sum of eqn (2)b | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| σ′a | HD | DDEC6 | DDEC3 | ISA | IH | NPA | ESP | HD | DDEC6 | DDEC3 | ISA | IH | NPA | ESP | |
| a From ref. 87.b DDEC3, ESP, HD, IH, ISA, and NPA NACs are from ref. 5. | |||||||||||||||
| H | 0.000 | 0.03 | 0.05 | 0.04 | −0.01 | 0.07 | 0.21 | −0.02 | −0.01 | −0.04 | −0.03 | 0.02 | −0.06 | −0.20 | −0.01 |
| OH | 0.283 | −0.08 | −0.22 | −0.25 | −0.31 | −0.25 | −0.29 | −0.33 | −0.05 | −0.12 | −0.12 | −0.09 | −0.15 | −0.34 | −0.10 |
| CO2C2H5 | 0.297 | −0.03 | −0.02 | −0.02 | −0.07 | 0.06 | 0.02 | −0.04 | −0.04 | −0.10 | −0.08 | −0.04 | −0.09 | −0.29 | −0.02 |
| Br | 0.454 | −0.1 | −0.23 | −0.25 | −0.29 | −0.11 | −0.02 | −0.19 | −0.07 | −0.17 | −0.16 | −0.15 | −0.13 | −0.30 | −0.18 |
| CN | 0.579 | −0.16 | −0.17 | −0.16 | −0.25 | −0.12 | −0.02 | −0.31 | −0.11 | −0.16 | −0.14 | −0.10 | −0.16 | −0.32 | −0.10 |
| R2 corr. coef. | 0.92 | 0.54 | 0.44 | 0.51 | 0.26 | 0.17 | 0.44 | 0.93 | 0.90 | 0.81 | 0.71 | 0.69 | 0.59 | 0.47 | |
We now consider accuracy of these charge assignment methods for reproducing the electrostatic potential across various system conformations. As shown in Table 10, the conformational transferability of the charge assignment methods from best to worst ordered HD > NPA > DDEC6 > IH > DDEC3 > ISA > ESP. Reasonable conformational transferability of IH charges and poor conformational transferability of ISA charges have also been shown in prior work.5,88,89 Table 11 compares the electrostatic potential RMSE and RRMSE values averaged across all molecular conformations for each of the point charge models using (a) NACs optimized individually for each conformation, (b) conformation averaged NACs, and (c) the low energy conformation NACs. DDEC6 values at the M + SCP (individually optimized for each conformation and using the low energy conformation), D (individually optimized for each conformation), and D + SCP (individually optimized for each conformation) levels are also shown for comparison. As expected, the ESP NACs reproduced the electrostatic potential most accurately among all point charge models optimized individually for each conformation. Although the DDEC6 NACs gave significantly higher RMSE and RRMSE values than the ESP NACs, the DDEC6 RMSE and RRMSE values including atomic dipoles (e.g., D and D + SCP) were approximately the same as those for ESP NACs optimized individually for each conformation. When using the conformation averaged NACs, ESP NACs still yielded the best overall results with the DDEC3 and DDEC6 NACs not far behind. When using NACs from the low energy conformation, the DDEC6 method provided the best overall results.
| Substituent | Mean unsigned deviation of NACsa | ||||
|---|---|---|---|---|---|
| H | Br | CN | OH | Ester | |
| a Mean unsigned deviations of NACs for the DDEC3, ESP, HD, IH, ISA, and NPA methods are from ref. 5. | |||||
| Conformations | 4 | 4 | 4 | 8 | 16 |
| HD | 0.002 | 0.002 | 0.002 | 0.003 | 0.002 |
| NPA | 0.004 | 0.004 | 0.004 | 0.006 | 0.006 |
| DDEC6 | 0.005 | 0.005 | 0.005 | 0.007 | 0.006 |
| IH | 0.006 | 0.006 | 0.006 | 0.007 | 0.007 |
| DDEC3 | 0.007 | 0.007 | 0.007 | 0.010 | 0.008 |
| ISA | 0.015 | 0.015 | 0.016 | 0.025 | 0.016 |
| ESP | 0.038 | 0.057 | 0.051 | 0.045 | 0.041 |
| Substituent | Avg. RMSEa (kcal mol−1) | Avg. RRMSEa | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H | Br | CN | OH | Ester | H | Br | CN | OH | Ester | ||
| a RMSE and RRMSE for the DDEC3, ESP, HD, IH, ISA, and NPA methods are from ref. 5. | |||||||||||
| NACs optimized separately for each conformation | |||||||||||
| DDEC3 | 0.81 | 1.15 | 0.87 | 0.89 | 0.77 | 0.13 | 0.18 | 0.10 | 0.13 | 0.10 | |
| DDEC6 | M | 0.90 | 1.17 | 1.04 | 1.16 | 1.02 | 0.14 | 0.18 | 0.12 | 0.16 | 0.13 |
| M + SCP | 0.89 | 1.16 | 1.03 | 1.15 | 1.01 | 0.14 | 0.18 | 0.11 | 0.16 | 0.13 | |
| D | 0.33 | 0.87 | 0.37 | 0.47 | 0.38 | 0.05 | 0.13 | 0.04 | 0.07 | 0.05 | |
| D + SCP | 0.32 | 0.88 | 0.37 | 0.48 | 0.38 | 0.05 | 0.13 | 0.04 | 0.07 | 0.05 | |
| ESP | 0.49 | 0.93 | 0.38 | 0.48 | 0.42 | 0.07 | 0.14 | 0.04 | 0.07 | 0.04 | |
| HD | 2.85 | 3.26 | 3.67 | 3.73 | 3.27 | 0.41 | 0.48 | 0.40 | 0.51 | 0.41 | |
| IH | 1.12 | 2.49 | 1.60 | 1.35 | 1.05 | 0.18 | 0.38 | 0.18 | 0.20 | 0.14 | |
| ISA | 0.73 | 1.45 | 0.74 | 0.71 | 0.70 | 0.11 | 0.22 | 0.08 | 0.10 | 0.09 | |
| NPA | 1.71 | 3.23 | 2.56 | 1.94 | 2.98 | 0.25 | 0.49 | 0.29 | 0.27 | 0.31 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| Conformation averaged NACs | |||||||||||
| DDEC3 | 1.27 | 1.48 | 1.29 | 1.40 | 1.25 | 0.18 | 0.22 | 0.14 | 0.19 | 0.16 | |
| DDEC6 | 1.21 | 1.41 | 1.31 | 1.38 | 1.27 | 0.18 | 0.21 | 0.14 | 0.19 | 0.16 | |
| ESP | 1.10 | 1.36 | 1.00 | 1.37 | 1.38 | 0.15 | 0.20 | 0.11 | 0.19 | 0.14 | |
| HD | 2.88 | 3.31 | 3.70 | 3.71 | 3.31 | 0.41 | 0.50 | 0.41 | 0.50 | 0.42 | |
| IH | 1.48 | 2.65 | 1.84 | 1.75 | 1.39 | 0.23 | 0.41 | 0.21 | 0.25 | 0.18 | |
| ISA | 1.33 | 1.81 | 1.31 | 1.57 | 1.43 | 0.18 | 0.26 | 0.14 | 0.21 | 0.18 | |
| NPA | 2.12 | 3.47 | 2.86 | 2.42 | 3.71 | 0.30 | 0.52 | 0.32 | 0.33 | 0.38 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| All conformations use NACs from low energy conformation | |||||||||||
| DDEC3 | 1.39 | 1.61 | 1.38 | 1.73 | 1.44 | 0.19 | 0.23 | 0.15 | 0.24 | 0.18 | |
| DDEC6 | M | 1.31 | 1.49 | 1.35 | 1.63 | 1.34 | 0.18 | 0.22 | 0.15 | 0.22 | 0.17 |
| M + SCP | 1.30 | 1.49 | 1.44 | 1.62 | 1.33 | 0.18 | 0.22 | 0.15 | 0.22 | 0.17 | |
| ESP | 1.49 | 1.73 | 1.26 | 2.12 | 1.91 | 0.19 | 0.24 | 0.13 | 0.28 | 0.20 | |
| HD | 2.97 | 3.24 | 3.68 | 3.74 | 3.31 | 0.42 | 0.48 | 0.41 | 0.51 | 0.42 | |
| IH | 1.55 | 2.61 | 1.85 | 1.98 | 1.48 | 0.23 | 0.40 | 0.21 | 0.28 | 0.19 | |
| ISA | 1.46 | 1.97 | 1.41 | 1.98 | 1.74 | 0.19 | 0.29 | 0.15 | 0.27 | 0.21 | |
| NPA | 2.23 | 3.50 | 2.93 | 2.57 | 4.05 | 0.31 | 0.52 | 0.32 | 0.35 | 0.42 | |
Finally, we considered the 25 conformations of the –OH substituted carboxylic acid generated by the ab initio molecular dynamics (AIMD) calculations of Manz and Sholl at 300 K (Nosé thermostat).5 Following AIMD calculations in VASP using the PW91 functional with D2 dispersion corrections, Manz and Sholl computed the electron distributions and electrostatic potentials in GAUSSIAN 09 using the B3LYP/6-311++G** level of theory for each geometry.5 We use these same geometries, electron distributions, and electrostatic potentials here. Our purpose here is to see how the DDEC6 NACs perform compared to the previously reported results5 for the DDEC3, ESP, HD, IH, ISA, and NPA methods. As shown in Table 12, the DDEC6 NACs had lower electrostatic potential RMSE and RRMSE values across these AIMD conformations than any of the other six charge assignment methods when using either the low energy NACs or the conformation averaged NACs from Table 11. In summary, all of these tests for substituted carboxylic acids show the DDEC6 NACs have desirable properties for constructing flexible force-fields for classical atomistic simulations of materials: (a) reproduce chemical trends, (b) good conformational transferability, and (b) reasonable accuracy for reproducing the electrostatic potential across various system conformations.
| DDEC3a | DDEC6 | ESPa | HDa | IHa | ISAa | NPAa | |
|---|---|---|---|---|---|---|---|
| a From ref. 5. | |||||||
| Using the low energy conformation NACs of Table 11 | |||||||
| RMSE | 2.51 | 2.17 | 3.23 | 4.38 | 2.55 | 3.04 | 3.65 |
| RRMSE | 0.27 | 0.23 | 0.35 | 0.47 | 0.27 | 0.33 | 0.39 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Using the conformation averaged NACs of Table 11 | |||||||
| RMSE | 2.08 | 1.88 | 2.11 | 4.31 | 2.11 | 2.44 | 3.39 |
| RRMSE | 0.23 | 0.20 | 0.23 | 0.47 | 0.23 | 0.26 | 0.37 |
Table 13 summarizes computed NACs for each of the geometries studied by Wang et al.21 plus the global low energy conformation using the M06L/def2-TZVP level of theory. The global low energy conformation is a linear molecule corresponding to a 180° angle. The Dipole charge cannot be computed for this low energy conformation, because its molecular dipole is zero irrespective of the NAC. For all of the charge assignment methods except the Bader method, the NAC increased monotonically as the angle increased. (For the Bader method, the increase was almost monotonic.) In order of smallest to largest Li NACs, the charge assignment methods were HD < CM5 < Dipole charge < NPA, ESP, DDEC6, Bader < DDEC3.
| Angle | Li net atomic chargea | (Geom opt) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | |
| a Except for the linear molecule NACs for the HD, CM5, DDEC3, ESP, NPA, and Dipole charge methods are from ref. 21.b Cannot be determined because the dipole moment is zero and the molecule is linear and symmetric. | ||||||||||
| Bader | 0.83 | 0.85 | 0.85 | 0.86 | 0.86 | 0.86 | 0.86 | 0.87 | 0.86 | 0.87 |
| CM5 | 0.55 | 0.56 | 0.57 | 0.58 | 0.59 | 0.60 | 0.60 | 0.61 | 0.61 | 0.62 |
| DDEC3 | 0.83 | 0.88 | 0.92 | 0.94 | 0.96 | 0.97 | 0.98 | 0.98 | 0.98 | 0.98 |
| DDEC6 | 0.77 | 0.80 | 0.83 | 0.85 | 0.87 | 0.88 | 0.89 | 0.90 | 0.90 | 0.90 |
| Dipole charge | 0.59 | 0.59 | 0.60 | 0.60 | 0.60 | 0.61 | 0.62 | 0.64 | 0.65 | b |
| ESP | 0.61 | 0.63 | 0.65 | 0.67 | 0.70 | 0.74 | 0.79 | 0.83 | 0.86 | 0.87 |
| HD | 0.39 | 0.40 | 0.40 | 0.41 | 0.41 | 0.42 | 0.42 | 0.43 | 0.43 | 0.44 |
| NPA | 0.78 | 0.79 | 0.80 | 0.81 | 0.83 | 0.84 | 0.85 | 0.85 | 0.86 | 0.86 |
To further understand these trends, Table 14 summarizes the electrostatic potential RMSE and RRMSE, dipole moment MAE, and the mean unsigned deviation (MUD) from the conformation averaged NAC. From best to worst conformational transferability, the charge assignment methods ordered Bader > Dipole charge, HD > CM5, NPA > DDEC6, DDEC3 > ESP. From best to worst accuracy in reproducing the dipole moment, the methods ordered Dipole charge > CM5 > ESP > HD > NPA > DDEC6 > Bader > DDEC3. For the RMSE and RRMSE, HD performed the worst of all the charge assignment methods, and DDEC3 performed the second worst. Among the different point charge models, the ESP NACs provided the lowest RMSE and RRMSE when the NACs were optimized separately for each molecular conformation.
| Conformation averaged NACs | NACs optimized separately for each conformation | NACs from the lowest energy conformation | Dipole moment MAE | NAC conformational transferability (MUD) | |||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | RRMSE | RMSE | RRMSE | RMSE | RRMSE | ||||
| a Not computed.b Not computed, because the variation in the molecular conformation affects the orientation of the atomic dipoles.c Dipole charges cannot be determined, because the dipole moment of the lowest energy (i.e., linear) conformation is zero irrespective of the NAC values.d Since no Dipole charges were available for the linear molecule, these represent values for the nine non-linear conformations. | |||||||||
| Bader | 6.46 | 0.25 | 6.30 | 0.25 | 7.18 | 0.28 | 0.63 | 0.01 | |
| CM5 | 6.92 | 0.29 | 6.90 | 0.29 | 6.31 | 0.26 | 0.07 | 0.03 | |
| DDEC3 | 8.01 | 0.31 | 7.55 | 0.30 | 9.09 | 0.36 | 0.80 | 0.05 | |
| DDEC6 | M | 6.48 | 0.26 | 5.76 | 0.23 | 7.17 | 0.28 | 0.59 | 0.05 |
| M + SCP | a | a | 5.85 | 0.23 | 7.19 | 0.28 | 0.59 | 0.05 | |
| D | b | b | 1.43 | 0.06 | b | b | 0.00 | 0.05 | |
| D + SCP | b | b | 1.20 | 0.05 | b | b | 0.00 | 0.05 | |
| Dipole charged | 6.68 | 0.29 | 6.62 | 0.28 | c | c | 0.00 | 0.02 | |
| ESP | 5.55 | 0.23 | 4.40 | 0.18 | 7.27 | 0.28 | 0.19 | 0.11 | |
| HD | 11.40 | 0.48 | 11.49 | 0.48 | 10.72 | 0.44 | 0.50 | 0.02 | |
| NPA | 6.10 | 0.24 | 5.56 | 0.22 | 7.03 | 0.28 | 0.53 | 0.03 | |
Across all of the accuracy measures listed in Table 14, the following overall trends were observed: (a) the NPA, DDEC6, CM5, and Bader NACs performed better than the DDEC3 NACs, (b) the NPA NACs performed better than the DDEC6 NACs, (c) across the subset of accuracy measures where the Dipole charges were defined, they performed as good as or better than the CM5 and DDEC3 NACs, and (d) all other comparisons between NAC methods yielded mixed results, with better performance for at least one accuracy measure and worse performance for at least one accuracy measure.
For comparison, Table 14 also lists DDEC6 results including spherical charge penetration and atomic dipoles. Adding spherical charge penetration to the point charges had negligible effect on the results. However, adding spherical charge penetration to the DDEC6 point charges plus atomic dipoles decreased the conformation specific RMSE to 1.20 kcal mol−1, which was dramatically better than any of the point charge only models.
What conclusions can be drawn from these results? We can definitely say the HD NACs were too small in magnitude and the DDEC3 NACs were too large in magnitude for this material.21 We can also say the Dipole charge is a limited concept, because it cannot be computed for some molecular conformations. Overall, this example illustrates some of the compromises involved in designing a general-purpose charge assignment method: (a) the molecular dipole moment can be reproduced exactly using a point charge plus atomic dipole model, but this makes the model more complicated than a point charge only model. (b) Fitting the electrostatic potential directly to a point charge model for each conformation leads to comparatively low RMSE values, but this degrades the conformational transferability as demonstrated by the ESP results. (c) The electrostatic potential can be more accurately reproduced by a (truncated) multipole model with charge penetration terms (e.g., D + SCP), but this results in more complicated force-field terms.
3.5 Exact for isolated atomic ion limit
The isolated atomic ion limit corresponds to spatially separated and negligibly overlapping atomic ions, such as occurs when each atomic ion is ∼10 Å or more from all other atoms. It is the only situation for which an exact {wA(rA)} is uniquely defined. Specifically, in the isolated atomic ion limit, the atomic weighting factors should equal the spherical average of each isolated density: wA(rA) = ρavgA(rA).Consider the specific example of a periodic cubic array with Na and F ions at alternating vertices. By symmetry, the atomic dipole, quadrupole, and octupole moments are zero. Since atomic hexadecapole moments are the leading non-zero atomic multipoles, the atomic electron distributions are approximately (but not exactly) spherically symmetric. Thus, in this idealized example, the total electron density can be approximated as the sum of individual spherical ion densities:
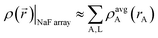 | (3) |
We consider two limiting cases: (a) a periodic array having a 20 Å distance between nearest Na atoms and (b) the PBE-optimized low energy crystal structure having 2.27 Å between nearest Na atoms.
There are two possible strategies for the IH method: (i) use reference ions for the isolated ions without charge compensation (as done when the IH method was introduced13) or (ii) use reference ions that mimic the ion shapes in condensed crystals by including charge compensation effects (as done in later modifications of the IH method17,18,20,42,90). If choice (i) is made, the reference ion shapes will match the ions in example (a). If choice (ii) is made, the reference ion shapes will match the ions in example (b). Due to charge compensation and electrostatic screening effects, anions in the condensed phase are more contracted than their isolated gas-phase counterparts. Therefore, the IH method must choose which of these two limits to reproduce. Moreover, to yield wA(rA) = ρavgA(rA) the IH reference ions would also need to be computed using a similar exchange-correlation theory and basis set as used to study the material of interest.
The DDEC6 method accurately reproduces both limits, because the reference ion densities are conditioned to the material of interest. In the isolated atomic ion limit (structure (a)), wDDEC6A(rA) = ρcondA(rA) = ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) refA(rA,qrefA)〈ρ(
refA(rA,qrefA)〈ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )/
)/![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ref(
ref(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )〉rA= ρavgA(rA) and additional conditioning steps do not alter wDDEC6A(rA). Because the DDEC6 method derives {wDDEC6A(rA)} from partitions of ρ(
)〉rA= ρavgA(rA) and additional conditioning steps do not alter wDDEC6A(rA). Because the DDEC6 method derives {wDDEC6A(rA)} from partitions of ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) (i.e., a conditioning process), the DDEC6 method returns wA(rA) = ρavgA(rA) in the isolated atomic ion limit even when the DDEC6 reference ions are computed using a different exchange-correlation theory, different basis sets, and different local chemical environment than used in the system of interest! In the optimized crystal geometry (structure (b)), the symmetry makes the atomic dipole, quadrupole, and octupole moments zero. Consequently, ρA(
) (i.e., a conditioning process), the DDEC6 method returns wA(rA) = ρavgA(rA) in the isolated atomic ion limit even when the DDEC6 reference ions are computed using a different exchange-correlation theory, different basis sets, and different local chemical environment than used in the system of interest! In the optimized crystal geometry (structure (b)), the symmetry makes the atomic dipole, quadrupole, and octupole moments zero. Consequently, ρA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A) ≈ ρavgA(rA) which implies 〈(ρ(
A) ≈ ρavgA(rA) which implies 〈(ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )/W(
)/W(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ))2〉rA− 〈ρ(
))2〉rA− 〈ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )/W(
)/W(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )〉rA2 ≈ 0. Since {wDDEC6A(rA)} are computed via conditioning steps that make 〈ρ(
)〉rA2 ≈ 0. Since {wDDEC6A(rA)} are computed via conditioning steps that make 〈ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )/W(
)/W(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )〉rA ≈ 1, this means the conditioning process combined with the crystal symmetry makes ρ(
)〉rA ≈ 1, this means the conditioning process combined with the crystal symmetry makes ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )/W(
)/W(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ≈ 1. This gives ρA(
) ≈ 1. This gives ρA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) A) ≈ wDDEC6A(rA) ≈ ρavgA(rA). Thus, the DDEC6 method accurately recovers the nearly exact limit for both structures (a) and (b).
A) ≈ wDDEC6A(rA) ≈ ρavgA(rA). Thus, the DDEC6 method accurately recovers the nearly exact limit for both structures (a) and (b).
Now consider the NACs for structures (a) and (b). Since the atoms are fully separated in structure (a), the computed Bader, DDEC6, HD, and ISA NACs were the same within an integration tolerance. In this fully separated atomic ion limit, the results depend only on the exchange-correlation theory used to generate the electron distribution. For structure (a), the atomic charge magnitudes were 1.00 (Hartree–Fock method), 0.56 (HSE06 (ref. 91) functional), and 0.58 (PBE functional). Now consider the PBE-optimized low-energy crystal structure having 2.27 Å between nearest Na atoms. Analysis of experimental data shows the NaF crystal is mostly ionic.92 The computed HD (0.28) and ISA (0.48) atomic charge magnitudes are too small chemically. The Bader (0.86) and DDEC6 (0.85) atomic charge magnitudes are more reasonable. Thus, even when considering these simple NaF structures, some key advantages of DDEC6 over the HD and ISA methods are apparent.
Although the DDEC6 and HD methods returned the same NACs in the isolated atomic ion limit, there is a crucial distinction between these two approaches. Consider a situation intermediate between the isolated atomic ion limit and strongly overlapping atoms. For example, an array of atomic ions in which the adjacent atoms are ∼6 Å apart. In this situation, the adjacent atoms have small but non-zero overlaps. As explained above, wDDEC6A(rA) approaches ρavgA(rA) in the isolated atomic ion limit, while wHDA(rA) does not (for charged atoms). Thus, the DDEC6 atomic weighting factors approach the correct limit as the atoms are mostly separated while the HD atomic weighting factors do not.
3.6 Diisopropylammonium bromide ferroelectric crystal
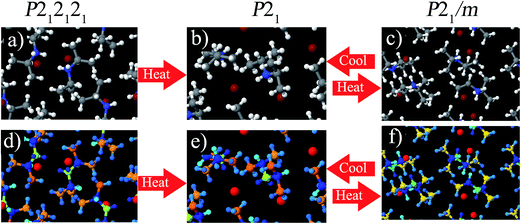
Diisopropylammonium bromide (DIPAB) is a remarkable organic ferroelectric compound in numerous aspects.93,94 It has a high spontaneous polarization (measured by electric field cycling), a high dielectric constant, and a low coercive field.93,94 These characteristics are desirable for many potential applications.93,94In this section, we study several DIPAB crystal phases. The crystal structures were obtained using X-ray diffraction: P21 (293 K), P212121 (293 K), and P21/m (438 K).94 Phase P21 is ferroelectric.94,95 Phase P212121 transitions to P21 when heated, and phase P21 transitions to P21/m when heated more.94,95 P21/m transitions to P21 when cooled but not to P212121 if cooled further.94,95 The P21 ferroelectric phase is stable at temperatures from 90 to 425 K.95
A ferroelectric phase has a net dipole moment per unit cell. The polarization density is the average dipole moment per unit volume. Fu et al. performed measurements and calculations of the polarization density of DIPAB phase P21.94 Using a Sawyer–Tower circuit at 25 Hz, they measured a polarization density of approximately 11 μC cm−2.94 Using a pyroelectric technique, they measured a spontaneous polarization density of approximately 23 μC cm−2.94 Using DFT calculations, they computed a polarization density of 24 μC cm−2; however, insufficient computational details were provided.94 The computed polarization density depends upon the particular ferroelectric motion. Fu et al. did not specify the particular ferroelectric motion associated with their polarization density measurements and calculations.94 Jiang et al. measured DIPAB ferroelectric hysteresis scaling behavior as a function of applied electric field and cycling frequency.96 They measured saturation polarization densities of around 5 to 11 μC cm−2.96 Alsaad et al. used the Berry phase method to compute a DIPAB polarization of 23 μC cm−2, but they did not compute the continuous deformation pathway (i.e., ferroelectric motion) associated with this polarization value.97
We performed DFT calculations using the PBE exchange-correlation functional on these three phases using VASP. For P21 and P212121, the lattice constants and angles where held at the experimental values and the positions of all atoms were fully relaxed. For P21/m, the experimental X-ray structure shows disordered atoms,94 so we created a super-cell including both components of the disordered structure and relaxed the atomic positions. Fig. 7 shows the structures of these three phases. As shown in the lower half of Fig. 7, the DDEC6 NACs had good transferability between these three phases.
Table 15 summarizes computed NACs for these three DIPAB phases. NACs for atoms with similar connectivity were averaged. The MUD was computed as the mean unsigned deviation between the NAC of an individual atom and its connectivity-averaged NAC. As shown in Table 15, the MUD was small for the DDEC6, HD, and CM5 methods and larger for the Bader method. The DDEC6 NACs for the three phases were similar. Only the ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) (H)3(C) NACs exhibited a maximum difference > 0.1e among the three phases. Because the results for all three phases were similar, Table 15 only shows the HD, CM5, and Bader results for the ferroelectric P21 phase. (The individual NACs for all three phases are given in the ESI.†) As expected, the HD NACs are lower in magnitude than NACs computed using the other methods. All methods except HD gave a negative NAC for N. All methods gave a positive NAC for the H atoms bound to N. All methods except Bader gave a positive NAC for the H atoms bound to C. All methods gave a positive
(H)3(C) NACs exhibited a maximum difference > 0.1e among the three phases. Because the results for all three phases were similar, Table 15 only shows the HD, CM5, and Bader results for the ferroelectric P21 phase. (The individual NACs for all three phases are given in the ESI.†) As expected, the HD NACs are lower in magnitude than NACs computed using the other methods. All methods except HD gave a negative NAC for N. All methods gave a positive NAC for the H atoms bound to N. All methods except Bader gave a positive NAC for the H atoms bound to C. All methods gave a positive ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) (H)(C)2(N) NAC. All methods except Bader gave a negative
(H)(C)2(N) NAC. All methods except Bader gave a negative ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) (H)3(C) NAC. All methods gave a negative Br NAC. The Bader and CM5 methods gave a more negative NAC for N than for Br, while the DDEC6 method gave a more negative NAC for Br than for N.
(H)3(C) NAC. All methods gave a negative Br NAC. The Bader and CM5 methods gave a more negative NAC for N than for Br, while the DDEC6 method gave a more negative NAC for Br than for N.
| Atom | Phase→ | P21 | P21 | P21 | P21 | P212121 | P21/m |
|---|---|---|---|---|---|---|---|
| Connectivity | DDEC6 | HD | CM5 | Bader | DDEC6 | DDEC6 | |
| N | N(H)2(C)2 | −0.326 | 0.034 | −0.628 | −1.146 | −0.324 | −0.261 |
| H | H2N | 0.291 | 0.099 | 0.359 | 0.517 | 0.290 | 0.254 |
| H | HC | 0.048 | 0.034 | 0.123 | −0.011 | 0.049 | 0.058 |
| H | H3C | 0.160 | 0.037 | 0.111 | −0.103 | 0.160 | 0.126 |
| C | ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) (H)(C)2(N) (H)(C)2(N) |
0.266 | 0.062 | 0.009 | 0.334 | 0.268 | 0.227 |
| C | ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) (H)3(C) (H)3(C) |
−0.533 | −0.118 | −0.322 | 0.373 | −0.535 | −0.429 |
| Br | Br | −0.668 | −0.394 | −0.402 | −0.790 | −0.674 | −0.617 |
| MUD | 0.005 | 0.003 | 0.003 | 0.026 | 0.004 | 0.004 | |
3.7 Collinear and non-collinear magnetic materials
For both the collinear and non-collinear magnetic systems described below, DDEC6 ASMs were computed with the method of Manz and Sholl98 using the DDEC6 atomic electron distributions and the recommended value χspin = 0.5. Electron and spin density grids with a uniform spacing of ~0.14 bohr were used. Spherical averages were computed over 100 uniformly spaced radial shells up to a cutoff radius of 5 Å.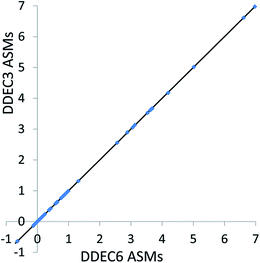 | ||
| Fig. 8 Comparison of DDEC3 and DDEC6 atomic spin moments for systems with collinear magnetism. The black line has a slope of 1 and an intercept of 0. | ||
As an additional example, we consider the Mn12-acetate (formula unit Mn12C32H56O48) single molecule magnet illustrated in Fig. 9 (left panel). Mn12-acetate is one of the most widely studied of all single molecule magnets since its synthesis and discovery by Lis.100–102 We performed calculations in GAUSSIAN 09 using the PBE functional with LANL2DZ103 basis sets and in VASP using the PBE/planewave method. Experiments support a conceptual model with an S = 10 and SZ = 10 ground state.104 Accordingly, we set SZ = 10 as a constraint on the GAUSSIAN 09 and VASP electron and spin distributions we computed. In VASP, we optimized the atomic positions and used the experimental lattice parameters of Farrell et al.105 (Cambridge Structural Database ID BESXAA). In GAUSSIAN 09, we used an isolated molecule and optimized the atomic positions. As shown in Table 16, the DDEC6 ASMs computed using the PBE functional with both LANL2DZ and planewave basis sets were in good agreement with Robinson et al.'s106 polarized neutron diffraction experiments and Pederson and Khanna's107 PBE computations. The DDEC6 results are similar to the NACs and ASMs we previously obtained for Mn12-acetate using DDEC3.86 ASMs on all atoms except Mn atoms were almost negligible in magnitude (i.e., ≤0.033 (planewave) and ≤0.077 (LANL2DZ)), which agrees with the experimental finding that “there is no evidence for net [magnetic] moments on the oxygen atoms”.106 The magnetic anisotropy barrier of a single molecule magnet is the energy required to flip the magnetic moment orientation relative to the molecular structure.101 We computed this barrier by performing 62 single-point spin–orbit coupling calculations in VASP, where the electron and spin distributions were kept constant while the magnetic direction was rotated (by varying the SAXIS parameter in VASP). A 1 × 1 × 2 Monkhorst–Pack k-point mesh was used with Fermi smearing (smearing width = 0.05 eV). To ensure the computed gradient field (and hence exchange-correlation energy density) does not break the crystal symmetry, a spherical cutoff was applied to the reciprocal vectors, {![[G with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0047_20d1.gif) }, such that only reciprocal vectors with |
}, such that only reciprocal vectors with |![[G with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0047_20d1.gif) | < Gcut are included where Gcut defines a sphere enclosed within the parallelepiped defined by the reciprocal space FFT grid.26 The one-center PAW charge densities were stored up to an angular momentum
| < Gcut are included where Gcut defines a sphere enclosed within the parallelepiped defined by the reciprocal space FFT grid.26 The one-center PAW charge densities were stored up to an angular momentum ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 6. As shown in Fig. 9 (middle panel), the spin–orbit coupling potential energy surface had global energy minima at the poles and a global energy maximum at the equator with no other local energy minima or maxima. This yielded a magnetic anisotropy barrier of 5.13 meV (59.5 K), which is in good agreement with Fort et al.'s108 experimental value of 60–62 K and Pederson and Khanna's computed value of 55.6–55.8 K.107 As shown in Fig. 9 (right panel), DDEC6 NACs computed with the LANL2DZ basis set are nearly identical to those computed using the planewave basis set. This shows the DDEC6 NACs are not overly sensitive to the basis set choice.
= 6. As shown in Fig. 9 (middle panel), the spin–orbit coupling potential energy surface had global energy minima at the poles and a global energy maximum at the equator with no other local energy minima or maxima. This yielded a magnetic anisotropy barrier of 5.13 meV (59.5 K), which is in good agreement with Fort et al.'s108 experimental value of 60–62 K and Pederson and Khanna's computed value of 55.6–55.8 K.107 As shown in Fig. 9 (right panel), DDEC6 NACs computed with the LANL2DZ basis set are nearly identical to those computed using the planewave basis set. This shows the DDEC6 NACs are not overly sensitive to the basis set choice.
| Atom type | DDEC6 PBE planewave | DDEC6 PBE LANL2DZ | Experiments | Pederson Khanna PBEb |
|---|---|---|---|---|
| a Polarized neutron diffraction experiments of Robinson et al.106b Pederson and Khanna using integration of the spin density over spheres of 2.5 bohr radius to compute the ASMs.107c Fort et al.108 | ||||
| Atomic spin moment | ||||
| Mn type 1 | −2.80 | −2.56 | −2.34 ± 0.13a | −2.6 |
| Mn type 2 | 3.82 | 3.63 | 3.79 ± 0.12a | 3.6 |
| Mn type 3 | 3.81 | 3.57 | 3.69 ± 0.14a | 3.6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Magnetic anisotropy barrier (Kelvin) | ||||
| 59.5 | 60–62c | 55.6–55.8 | ||
![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) A} for this material using the same electron and spin magnetization density files as ref. 98. As shown in the center panel, the DDEC6 NACs followed a similar trend and magnitude as the DDEC3 NACs reported in ref. 5. The atomic spin magnitudes are the magnitudes of the atomic spin magnetization vectors: MA = |
A} for this material using the same electron and spin magnetization density files as ref. 98. As shown in the center panel, the DDEC6 NACs followed a similar trend and magnitude as the DDEC3 NACs reported in ref. 5. The atomic spin magnitudes are the magnitudes of the atomic spin magnetization vectors: MA = |![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) A|. As shown in the right panel, the DDEC6 atomic spin magnitudes were virtually identical to the DDEC3 values. The total wall time from CHARGEMOL program start (before input file reading) to end (after output printing finished) was 16.3 minutes for this calculation run on a single processor core in Intel Xeon E5-2680v3 at the Comet supercomputing cluster. This works out to 8.7 seconds per atom. This calculation utilized a volume of 2.9 × 10−3 bohr3 per grid point. These results demonstrate that DDEC6 is well-suited for quantifying NACs and atomic spins in non-collinear magnets.
A|. As shown in the right panel, the DDEC6 atomic spin magnitudes were virtually identical to the DDEC3 values. The total wall time from CHARGEMOL program start (before input file reading) to end (after output printing finished) was 16.3 minutes for this calculation run on a single processor core in Intel Xeon E5-2680v3 at the Comet supercomputing cluster. This works out to 8.7 seconds per atom. This calculation utilized a volume of 2.9 × 10−3 bohr3 per grid point. These results demonstrate that DDEC6 is well-suited for quantifying NACs and atomic spins in non-collinear magnets.
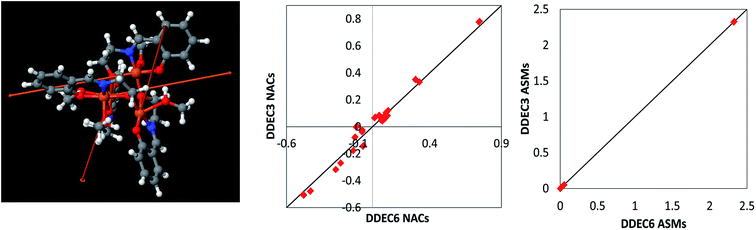 | ||
| Fig. 10 Left: Fe4O12N4C40H52 noncollinear single molecule magnet structure reproduced with permission from ref. 98 (© American Chemical Society 2011). The arrows show the magnitude and direction of the atomic spin magnetization vectors on each atom. The atomic spin magnitudes are small on all atoms except the four iron atoms. Center: Comparison of DDEC3 and DDEC6 net atomic charges. Right: Comparison of DDEC3 and DDEC6 atomic spin magnitudes. The black lines have a slope of 1 and an intercept of 0. | ||
3.8 Summary of systems studied
Table 17 summarizes the types of systems analyzed using the DDEC6 method. The 231 systems studied include those in this article and the previous article4 introducing the DDEC6 method. In this context, the same material investigated with different levels of theory counts as different systems. Four different system classifications are summarized in Table 17: (a) according to magnetic property, (b) according to material type, (c) according to exchange-correlation theory, and (d) according to basis set type.| Number of systems | |
|---|---|
| According to magnetic property | |
| Non-magnetic | 185 |
| Collinear magnetism | 44 |
| Noncollinear magnetism | 2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| According to material type | |
| Small molecules (<100 atoms) | 118 |
| Nonporous solids | 69 |
| Porous solids | 29 |
| Large molecules (≥100 atoms) | 6 |
| Surface slabs or sheets | 4 |
| Stretched NaF periodic arrays | 3 |
| 1-D periodic systems | 2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| According to exchange-correlation theory | |
| PBE | 112 |
| B3LYP | 71 |
| PW91 | 19 |
| M06L | 17 |
| CCSD | 3 |
| CAS-SCF | 2 |
| SAC-CI | 2 |
| CISD | 1 |
| DFT + dispersion | 1 |
| DFT+U | 1 |
| HF | 1 |
| HSE06 | 1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| According to basis set type | |
| Planewave | 123 |
| Gaussian function | 108 |
| Number of distinct chemical elements studied = 44 | |
Even though the Mn12-acetate single molecule magnet exhibits collinear magnetism, we had to compute its fully noncollinear magnetization densities in order to compute the spin–orbit coupling potential energy surface (Fig. 9) and magnetic anisotropy barrier. Therefore, the two noncollinear magnetism systems included the noncollinear single molecule magnet of Section 3.7.2 as well as the PBE/planewave noncollinear magnetism calculation of the Mn12-acetate single molecule magnet. The PBE/LANL2DZ analysis of the Mn12-acetate single molecule magnet was a collinear magnetism calculation.
We showed the DDEC6 method gives good performance across a broad range of material types: (a) small molecules, (b) nonporous solids, (c) porous solids, (d) large molecules, (e) surface slabs or sheets, (f) near the isolated atomic ion limit (e.g., stretched NaF periodic arrays), and (g) 1-D periodic systems. The 1-D periodic systems included the B-DNA decamer and the BN nanotube. Some materials are described in the ESI.† Fig. S1 in Section S2 of the ESI† compares DDEC6 to DDEC3 NACs for 14 different materials comprised almost entirely of surface atoms. The differences between DDEC6 and DDEC3 NAC values was minor for these materials, but some statistically significant differences occur. Fig. S2 in Section S3 of the ESI† compares DDEC6 to DDEC3 NACs for three solid surface slabs: (a) Mo2C(110) surface with K adatom, (b) NaF(001) surface, and (c) SrTiO3(100) surface. Atomic dipoles and quadrupoles for the SrTiO3(100) surface and bulk crystal are listed in Table S3.† These results were included in the ESI,† because the differences between DDEC3 and DDEC6 results was minor. For SrTiO3 and NaF, a comparison between DDEC3, DDEC6, Bader, and IH NACs for the bulk crystals is shown in Tables S4 and S5,† respectively.
Yang and Manz have previously reported DDEC6 NACs, ASMs, and bond orders for 96 organometallic complexes containing >100 atoms.109 Including these would have significantly raised the total for large molecules.
The exchange-correlation theories we considered included coupled-cluster methods (e.g., CCSD110 and SAC-CI111,112), configuration interaction methods (e.g., CAS-SCF113 and CISD114), GGA functionals (e.g., PBE34 and PW91 (ref. 115)), a meta-GGA functional (e.g., M06L33), a hybrid functional (e.g., B3LYP49,50), a range-separated hybrid functional (e.g., HSE06 (ref. 91)), a DFT+U method (e.g., PBE+Ueff116), a dispersion-corrected functional (e.g., PBE + D3 (ref. 117)), and the Hartree–Fock (HF) method. We do not recommend the HF method, because it neglects the correlation energy. Any of the correlated methods, whether wavefunction or DFT-based, can be utilized as long as it provides acceptable accuracy for the system's energy, electron distribution, and spin magnetization distribution. Electron and spin distributions for some of these levels of theory were first computed in earlier papers on the DDEC methods and were re-used here; the reader is referred to those earlier papers for calculation details.5,23 For example, Fig. S1 of the ESI† comparing DDEC6 to DDEC3 NACs includes CCSD, SAC-CI, and CAS-SCF results for different ozone spin states, and the reader is referred to earlier DDEC papers5,23 for the quantum chemistry calculation details of these systems. The PBE + D3 dispersion-corrected functional calculation was for the Li3 cluster calculation.4 The CISD calculation was for the H2 triplet with constrained bond length.4 The PBE+Ueff calculation was for the Fe3O4 (magnetite) bulk crystal appearing as a datapoint in Fig. 8. The HSE06 and HF results were for the stretched NaF periodic array discussed in Section 3.5 above.
Because the DDEC6 results are a functional of the electron and spin magnetization distributions, the results have no explicit basis set dependence. As shown Table 17, our DDEC6 calculations were almost evenly divided between planewave and Gaussian function basis sets.
The materials we studied in this article and the previous article4 introducing the DDEC6 method included 44 different chemical elements. However, the number of distinct chemical elements analyzed to date using the DDEC6 method (in works beyond these two articles) extends well beyond this number. The important message is that the DDEC6 method works well across a broad range of chemical elements.
4. Conclusions
We tested the performance of the DDEC6 method across a diverse set of periodic and non-periodic materials with numerous comparisons to experimental data. Our computational tests showed the DDEC6 method has substantially better overall performance than the DDEC3 method. Therefore, we recommend the DDEC6 method be used instead of the DDEC3 method. The DDEC6 method's excellent performance across a wide range of important properties and material types makes it suited for use as a default method in quantum chemistry programs. Our computational tests showed the DDEC6 NACs are well-suited both for describing chemical electron transfer trends between atoms in materials and for constructing flexible force-fields for classical atomistic simulations of complex materials.We first studied electron transfer trends in several solids and clusters. As pointed out by Wang et al.,21 the DDEC3 method predicts the incorrect electron transfer sign for the transition metal atom for the delithiation of solid LiCoO2 to CoO2. The DDEC6 method fixes this problem. We also showed the DDEC6 method yields reasonable electron transfer trends for the LiTiS2, TiS2, LiTiO2, LiTi2O4, LiMn2O4, MnO2, and Li3RuO2 solids. For several Pd-containing alloys, we compared the electron transfer direction predicted by element electronegativities to computed NACs: the Bader, DDEC3, and DDEC6 NACs followed the Pauling scale electronegativity trends while the HD and CM5 NACs did not. For (MgO)n (n = 1 to 6) clusters, we found the DDEC6 method exhibits overall better performance than DDEC3 for reproducing the electrostatic potential and dipole moments.
We then compared NACs to spectroscopic results for various materials. For natrolite, the DDEC6 NACs were smaller in magnitude than the DDEC3 NACs. For this material, the DDEC6 NACs were closer than DDEC3 NACs to the NACs extracted from high-resolution diffraction data using kappa refinement (with the exception of the Na atom which was not refined). DDEC3 and DDEC6 were both in excellent agreement with formamide NACs extracted from high-resolution diffraction data using spherical atom refinement. For a series of Ti-containing compounds, core-electron binding energy shifts were approximately linearly correlated to the DDEC6, HD, and Bader NACs but not to the DDEC3 and CM5 NACs. All five charge assignment methods gave reasonably good correlations between core electron binding shifts and computed NACs for the Mo-containing and Fe-containing compounds.
For 13 materials studied at the low energy conformation, the DDEC6 NACs reproduced the electrostatic potential slightly better than the DDEC3 NACs in 8 of the 13 materials. This shows the DDEC6 NACs are suited for constructing force-fields for materials containing small molecules, porous solids, water, and large biomolecules. A detailed study across various conformations of Li2O and five carboxylic acids showed the DDEC6 NACs have excellent conformational transferability and are ideally suited for constructing flexible force-fields to approximately reproduce the electrostatic potential across various system conformations.
We then studied a series of materials containing surface atoms. For a series of systems comprised almost entirely of surface atoms (see ESI Section S2†), the DDEC6 and DDEC3 NACs exhibited similar trends with some statistically significant differences in NAC values. Additional tests for three solid surfaces (K adatom on a Mo2C (110) surface, NaF(001) slab, and SrTiO3(100) slab) showed the DDEC6 method maintains a consistent treatment of surface and buried atoms (see ESI Section S3†). As explained in Section 3.5 above, the DDEC6 method is asymptotically exact in the isolated atomic ion limit.
As an example of a material with interesting phase change behavior, we studied three DIPAB crystal phases. One of these three phases is ferroelectric. Prior experimental studies have noted the exceptionally good performance of DIPAB for an organic ferroelectric.93,94 We showed the DDEC6 NACs for this material are chemically reasonable and have good transferability among the three DIPAB crystal phases.
Finally, we examined materials with collinear and non-collinear magnetism and found the DDEC6 atomic spin moments (ASMs) are essentially identical to the DDEC3 ASMs. For the Mn12-acetate single molecule magnet, the computed DDEC6 ASMs were in excellent agreement with previous experiments106 and computations.107 We computed the spin–orbit coupling potential energy surface for this material and found the resulting magnetic anisotropy barrier (5.13 meV) to be in excellent agreement with previous experiments108 and computations.107 The NACs and ASMs are computed efficiently. For example, it took only 16.3 minutes to compute them on a single processor core when analyzing a Fe4O12N4C40H52 single molecule magnet with non-collinear magnetism containing 112 atoms.
Acknowledgements
Supercomputing resources were provided by the Extreme Science and Engineering Discovery Environment (XSEDE). XSEDE is funded by NSF grant ACI-1053575. XSEDE project grant TG-CTS100027 provided allocations on the Trestles and Comet clusters at the San Diego Supercomputing Center (SDSC) and the Stampede cluster at the Texas Advanced Computing Center (TACC).References
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- G. Bruhn, E. R. Davidson, I. Mayer and A. E. Clark, Int. J. Quantum Chem., 2006, 106, 2065–2072 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- T. A. Manz and N. Gabaldon Limas, Introducing DDEC6 Atomic Population Analysis: Part 1. Charge Partitioning Theory and Methodology, RSC Adv., 2016, 6 10.1039/c6ra04656h.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2012, 8, 2844–2867 CrossRef CAS PubMed.
- B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439 CrossRef CAS.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- C. Campana, B. Mussard and T. K. Woo, J. Chem. Theory Comput., 2009, 5, 2866–2878 CrossRef CAS PubMed.
- R. F. W. Bader, Acc. Chem. Res., 1975, 8, 34–40 CrossRef CAS.
- R. F. W. Bader, P. J. MacDougal and C. D. H. Lau, J. Am. Chem. Soc., 1984, 106, 1594–1605 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 527–541 CrossRef CAS PubMed.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbo-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed.
- E. R. Davidson and S. Chakravorty, Theor. Chim. Acta, 1992, 83, 319–330 CrossRef CAS.
- D. Geldof, A. Krishtal, F. Blockhuys and C. Van Alsenoy, J. Chem. Theory Comput., 2011, 7, 1328–1335 CrossRef CAS PubMed.
- T. Verstraelen, P. W. Ayers, V. Van Speybroeck and M. Waroquier, J. Chem. Theory Comput., 2013, 9, 2221–2225 CrossRef CAS PubMed.
- D. E. P. Vanpoucke, P. Bultinck and I. Van Driessche, J. Comput. Chem., 2013, 34, 405–417 CrossRef CAS PubMed.
- T. Bucko, S. Lebegue, J. Hafner and J. G. Angyan, J. Chem. Theory Comput., 2013, 9, 4293–4299 CrossRef CAS PubMed.
- K. Finzel, A. M. Pendas and E. Francisco, J. Chem. Phys., 2015, 143, 084115 CrossRef PubMed.
- T. Bucko, S. Lebegue, J. G. Angyan and J. Hafner, J. Chem. Phys., 2014, 141, 034114 CrossRef PubMed.
- B. Wang, S. H. L. Li and D. G. Truhlar, J. Chem. Theory Comput., 2014, 10, 5640–5650 CrossRef CAS PubMed.
- T. C. Lillestolen and R. J. Wheatley, Chem. Commun., 2008, 5909–5911 RSC.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2010, 6, 2455–2468 CrossRef CAS PubMed.
- J. Cioslowski, J. Am. Chem. Soc., 1989, 111, 8333–8336 CrossRef CAS.
- P. Ghosez, J. P. Michenaud and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 6224–6240 CrossRef CAS.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- T. A. Manz and N. Gabaldon Limas, Chargemol program for performing DDEC analysis, version 3.4, accessed December 2015, http://ddec.sourceforge.net Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Yamada and M. Tanaka, Mater. Res. Bull., 1995, 30, 715–721 CrossRef CAS.
- J. Rodriguez-Carvajal, G. Rousse, C. Masquelier and M. Hervieu, Phys. Rev. Lett., 1998, 81, 4660–4663 CrossRef CAS.
- A. Paolone, P. Roy, G. Rousse, C. Masquelier and J. Rodriguez-Carvajal, Solid State Commun., 1999, 111, 453–458 CrossRef CAS.
- Electronegativity, in CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, Florida, 88th edn, 2007–2008, p. 9.81 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. M. Zuo, M. OKeeffe, P. Rez and J. C. H. Spence, Phys. Rev. Lett., 1997, 78, 4777–4780 CrossRef CAS.
- J. M. Zuo, Rep. Prog. Phys., 2004, 67, 2053–2103 CrossRef CAS.
- D. E. P. Vanpoucke, I. Van Driessche and P. Bultinck, J. Comput. Chem., 2013, 34, 422–427 CrossRef CAS PubMed.
- N. K. Hansen and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 909–921 CrossRef.
- Y. A. Abramov, A. V. Volkov and P. Coppens, Chem. Phys. Lett., 1999, 311, 81–86 CrossRef CAS.
- P. Coppens, T. N. Guru-Row, P. Leung, E. D. Stevens, P. J. Becker and Y. W. Yang, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1979, 35, 63–72 CrossRef.
- E. D. Stevens, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 544–551 CrossRef.
- E. D. Stevens, J. Rys and P. Coppens, J. Am. Chem. Soc., 1978, 100, 2324–2328 CrossRef CAS.
- N. E. Ghermani, C. Lecomte and Y. Dusausoy, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 5231–5239 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- U. Gelius, P. F. Heden, J. Hedman, B. J. Lindberg, R. Manne, R. Nordberg, C. Nordling and K. Siegbahn, Phys. Scr., 1970, 2, 70–80 CrossRef CAS.
- U. Gelius, Phys. Scr., 1974, 9, 133–147 CrossRef CAS.
- W. L. Jolly and W. B. Perry, J. Am. Chem. Soc., 1973, 95, 5442–5450 CrossRef CAS.
- Handbook of X-Ray and Ultraviolet Photoelectron Spectroscopy, ed. D. Briggs, Heyden, London, 1977, pp. 53–77 Search PubMed.
- Photoemission in Solids I. General Principles, ed. M. Cardona and L. Ley, Springer-Verlag, Berlin, 1978, pp. 60–75, 165–195 Search PubMed.
- J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy, ULVAC-PHI Inc., Chigasaki, Japan, 1995. pp. 1–261 Search PubMed.
- J. C. Carver, G. K. Schweitzer and T. A. Carlson, J. Chem. Phys., 1972, 57, 973–982 CrossRef CAS.
- J. Wong, F. W. Lytle, R. P. Messmer and D. H. Maylotte, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 5596–5610 CrossRef CAS.
- S. P. Cramer, T. K. Eccles, F. W. Kutzler, K. O. Hodgson and L. E. Mortenson, J. Am. Chem. Soc., 1976, 98, 1287–1288 CrossRef CAS PubMed.
- M. J. Guittet, J. P. Crocombette and M. Gautier-Soyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 125117 CrossRef.
- L. W. Li, M. R. Morrill, H. Shou, D. G. Barton, D. Ferrari, R. J. Davis, P. K. Agrawal, C. W. Jones and D. S. Sholl, J. Phys. Chem. C, 2013, 117, 2769–2773 CAS.
- X-Ray Absorption: Principles, Applications, Techniques of EXAFS, SEXAFS and XANES, ed. D. C. Koningsberger and R. Prins, John Wiley & Sons, New York, 1988, pp. 1–673 Search PubMed.
- Y. Zuxiang, Rock Miner. Anal., 1984, 3, 231–238 Search PubMed.
- S. Cardamone, T. J. Hughes and P. L. A. Popelier, Phys. Chem. Chem. Phys., 2014, 16, 10367–10387 RSC.
- D. M. Elking, L. Perera and L. G. Pedersen, Comput. Phys. Commun., 2012, 183, 390–397 CrossRef CAS PubMed.
- Q. Yang, D. Liu, C. Zhong and J.-R. Li, Chem. Rev., 2013, 113, 8261–8323 CrossRef CAS PubMed.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- D. Golze, J. Hutter and M. Iannuzzi, Phys. Chem. Chem. Phys., 2015, 17, 14307–14316 RSC.
- T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Ferey, Chem.–Eur. J., 2004, 10, 1373–1382 CrossRef CAS PubMed.
- H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279 CrossRef CAS.
- T. Watanabe, T. A. Manz and D. S. Sholl, J. Phys. Chem. C, 2011, 115, 4824–4836 CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. von Gunsteren and J. Hermans, Intermolecular Forces, Reidel, Dordrecht, Holland, 1981, p. 331 Search PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- W. L. Jorgensen, J. Am. Chem. Soc., 1981, 103, 335–340 CrossRef CAS.
- L. P. Lee, D. J. Cole, C.-K. Skylaris, W. L. Jorgensen and M. C. Payne, J. Chem. Theory Comput., 2013, 9, 2981–2991 CrossRef CAS PubMed.
- L. P. Lee, N. Gabaldon Limas, D. J. Cole, M. C. Payne, C.-K. Skylaris and T. A. Manz, J. Chem. Theory Comput., 2014, 10, 5377–5390 CrossRef CAS PubMed.
- A. H. Farmahini, D. S. Sholl and S. K. Bhatia, J. Am. Chem. Soc., 2015, 137, 5969–5979 CrossRef CAS PubMed.
- N. Foloppe and A. D. MacKerell, J. Comput. Chem., 2000, 21, 86–104 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- S. Arai, T. Chatake, T. Ohhara, K. Kurihara, I. Tanaka, N. Suzuki, Z. Fujimoto, H. Mizuno and N. Niimura, Nucleic Acids Res., 2005, 33, 3017–3024 CrossRef CAS PubMed.
- T. Tsukamoto, Y. Ishikawa, M. J. Vilkas, T. Natsume, K. Dedachi and N. Kurita, Chem. Phys. Lett., 2006, 429, 563–569 CrossRef CAS.
- N. Gabaldon Limas, MS Thesis, New Mexico State University, 2014.
- J. D. Roberts and W. T. Moreland, J. Am. Chem. Soc., 1953, 75, 2167–2173 CrossRef CAS.
- T. Verstraelen, E. Pauwels, F. De Proft, V. Van Speybroeck, P. Geerlings and M. Waroquier, J. Chem. Theory Comput., 2012, 8, 661–676 CrossRef CAS PubMed.
- T. Verstraelen, P. W. Ayers, V. Van Speybroeck and M. Waroquier, Chem. Phys. Lett., 2012, 545, 138–143 CrossRef CAS.
- T. A. Manz, J. Comput. Chem., 2013, 34, 418–421 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- Z. W. Su and P. Coppens, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 27–32 CrossRef.
- D. A. Bonnell, Science, 2013, 339, 401–402 CrossRef CAS PubMed.
- D. W. Fu, H. L. Cai, Y. M. Liu, Q. Ye, W. Zhang, Y. Zhang, X. Y. Chen, G. Giovannetti, M. Capone, J. Y. Li and R. G. Xiong, Science, 2013, 339, 425–428 CrossRef CAS PubMed.
- A. Piecha, A. Gagor, R. Jakubas and P. Szklarz, CrystEngComm, 2013, 15, 940–944 RSC.
- C. L. Jiang, H. C. Lin, C. H. Luo, Y. Y. Zhang, J. Yang, H. Peng and C. G. Duan, J. Cryst. Growth, 2016, 438, 25–30 CrossRef CAS.
- A. Alsaad, I. A. Qattan, A. A. Ahmad, N. Al-Aqtash and R. F. Sabirianov, IOP Conf. Ser.: Mater. Sci. Eng., 2015, 92, 012017 CrossRef.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2011, 7, 4146–4164 CrossRef CAS PubMed.
- E. Ruiz, J. Cirera and S. Alvarez, Coord. Chem. Rev., 2005, 249, 2649–2660 CrossRef CAS.
- T. Lis, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2042–2046 CrossRef.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS PubMed.
- K. M. Mertes, Y. Suzuki, M. P. Sarachik, Y. Myasoedov, H. Shtrikman, E. Zeldov, E. M. Rumberger, D. N. Hendrickson and G. Christou, Solid State Commun., 2003, 127, 131–139 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, J. Am. Chem. Soc., 1991, 113, 5873–5874 CrossRef CAS.
- A. R. Farrell, J. A. Coome, M. R. Probert, A. E. Goeta, J. A. K. Howard, M. H. Lemee-Cailleau, S. Parsons and M. Murrie, CrystEngComm, 2013, 15, 3423–3429 RSC.
- R. A. Robinson, P. J. Brown, D. N. Argyriou, D. N. Hendrickson and S. M. J. Aubin, J. Phys.: Condens. Matter, 2000, 12, 2805–2810 CrossRef CAS.
- M. R. Pederson and S. N. Khanna, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 9566–9572 CrossRef CAS.
- A. Fort, A. Rettori, J. Villain, D. Gatteschi and R. Sessoli, Phys. Rev. Lett., 1998, 80, 612–615 CrossRef CAS.
- B. Yang and T. A. Manz, Theor. Chem. Acc., 2016, 135, 21 CrossRef.
- G. E. Scuseria, C. L. Janssen and H. F. Schaefer, J. Chem. Phys., 1988, 89, 7382–7387 CrossRef CAS.
- H. Nakatsuji and K. Hirao, J. Chem. Phys., 1978, 68, 2053–2065 CrossRef CAS.
- H. Nakatsuji, Chem. Phys. Lett., 1979, 67, 334–342 CrossRef CAS.
- N. Yamamoto, T. Vreven, M. A. Robb, M. J. Frisch and H. B. Schlegel, Chem. Phys. Lett., 1996, 250, 373–378 CrossRef CAS.
- J. A. Pople, R. Seeger and R. Krishnan, Int. J. Quantum Chem., 1977, 12, 149–163 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables listing spectroscopically measured core electron energies and Bader, CM5, DDEC3, DDEC6, HD NACs for Ti- and Mo-containing solids; plot comparing DDEC6 to DDEC3 NACs for 14 systems comprised almost entirely of surface atoms; DDEC6 and DDEC3 NACs for Mo2C(110) surface with K adatom and NaF(001) surface; DDEC6 and DDEC3 NACs, atomic dipoles, and atomic quadrupoles for SrTiO3(100) surface and bulk crystal; DDEC6, DDEC3, Bader, and IH NACs for NaF and SrTiO3 bulk crystals; xyz files (which can be read using any text editor or the free Jmol visualization program downloadable from jmol.sourceforge.net) containing geometries, NACs, atomic dipoles and quadrupoles, fitted tail decay exponents, and ASMs. See DOI: 10.1039/c6ra05507a |
| This journal is © The Royal Society of Chemistry 2016 |