Experimental and computational evidence on conformational fluctuations as a source of catalytic defects in genetic diseases

Abstract

Theoretical and experimental evidence has shown that protein function, regulation and degradation are intrinsically linked to the dynamic and fluctuating nature of protein ensembles. However, the effect of missense mutations on catalytic performance are often interpreted from conformational analyses derived from X-ray crystallography, molecular dynamics and modeling, while effects on conformational fluctuations at the active site as the source of catalytic defects are rarely investigated. Here, we explore the role of conformational fluctuations in the catalytic efficiency of WT and three missense mutations in the UDP-galactose 4′-epimerase (GALE) protein causing type III galactosemia. Using comprehensive molecular dynamics simulations and small angle X-ray scattering we correlate low NAD⁺ binding affinity in some mutants with an increased population of non-competent conformations for NAD⁺ binding. Proteolysis studies combined with thermodynamic calculations reveal that mutations affecting GALE catalytic performance favor larger conformational fluctuations at the N-terminal domain and NAD⁺ binding site, shifting the equilibrium towards non-binding competent states in the native ensemble. Therefore, we provide a novel ensemble-based thermodynamic mechanism to explain catalytic defects caused by missense mutations that links large and transient conformational fluctuations and loss of catalytic efficiency and substrate/coenzyme affinity. In the context of this mechanism, we propose that allosteric ligands aimed at modulating these transient conformational fluctuations might correct catalytic defects in inherited metabolic diseases, representing a different approach to current small ligand therapies which target the low stability, but not catalytic defects, of mutations.

---

1. Introduction

Conformational fluctuations are essential to understanding protein function, regulation and degradation.^1–4 Fluctuations may be either local or involve large changes (unfolding) of protein structure.^1,5–8 Importantly, the role of dynamic alterations in the pathogenic mechanisms of loss-of-function genetic diseases, such as catalytic defects and protein misfolding, are poorly understood. Catalytic defects are often identified experimentally by enzyme kinetic analyses and structurally explained by the combination of X-ray diffraction crystal structures, molecular dynamics simulations and modeling procedures, often providing a static view of the local structural changes at the active sites to explain catalytic defects. Protein destabilization and misfolding are customarily identified by in vitro experiments such as thermal denaturation/inactivation and proteolysis,^9–14 and again, the destabilizing effect can be rationalized using structural information, as well as energy and sequence-based algorithms.^15–19 Novel therapies aimed at overcoming destabilizing effects of mutations using small ligands (natural and pharmacological chaperones) are being described.^20–24

Despite the emergent importance of native state dynamics on protein functionality, its role in mutation-associated catalytic defects in inherited metabolic diseases has been largely unexplored. Here, we investigate the relationship between dynamic alterations and catalytic defects in three catalytic mutations of UDP-galactose 4′-epimerase (GALE, EC 5.1.3.2) causing type III galactosemia. GALE catalyzes the interconversion between UDP-galactose and UDP-glucose using NAD⁺ as cofactor.²⁵ Two common GALE disease-causing mutations (p.N34S and p.G90E) decrease NAD⁺ binding affinity, selectively decrease protein unfolding cooperativity and facilitate proteolytic cleavage at the loop formed by residues 34–45 near the NAD⁺ binding site.¹² The impaired catalytic performance in these two mutants may arise from structural fluctuations of the NAD⁺ binding site that energetically penalize coenzyme binding. The p.V94M mutant greatly reduces GALE catalytic efficiency,^25,26 possibly due to binding of the substrate in a non-competent fashion for catalysis,²⁷ without largely affecting protein stability and flexibility.¹² We have combined molecular dynamic (MD) simulations and small angle X-ray scattering (SAXS) to ascertain the effects of these mutations on the native conformation and dynamics. Furthermore, we have experimentally characterized the overall conformation and relative population of partially unfolded states under native conditions using partial proteolysis in combination with thermodynamic analyses. Our results allow to propose a thermodynamic mechanism that explains how mutational defects on NAD⁺ binding occur due to an increment of the population of non-competent binding states and changes in their structure, and as result, allosteric ligands that bind to and stabilize the N-terminal domain of GALE might be used to overcome functional defects in type III galactosemia. We propose that these results may generally apply to inherited metabolic diseases in which point mutations, distant from the enzyme active site, influence binding or catalysis by similar mechanisms.

2. Materials and methods

2.1. Molecular dynamics simulations

We performed molecular dynamics (MD) simulations of wild-type and mutant GALE both in monomeric and dimeric state, and in presence and absence of the NAD⁺ cofactor. In total we performed 16 independent MD simulations of eight monomeric and eight dimeric systems. For each assembly state we investigated apo and NAD⁺-bound states of the wild-type (WT) enzyme as well as the three mutants p.N34S, p.G90E, and p.V94M. All simulations were based on a crystal structure of GALE in complex with NAD⁺ (PDB:1EK5 ²⁸) that was prepared for simulations using MOE's protonate3D and mutate function.²⁹

MD simulations were performed using the GPU code of pmemd in Amber12.³⁰ Amino acids were parameterized using the Amber force field 99SB with ILDN corrections,³¹ whilst the NAD⁺ co-factors were described according to parameters from Walker and Pavelites.^32,33 We employed an extensive equilibration protocol³⁴ before performing unrestrained sampling simulations for 100 ns in NpT ensemble at 300 K and 1 bar. We stored 1000 equal-spaced snapshots to trajectory for later analysis. Shorter sampling periods (i.e. 10 ps) yielded essentially the same results (data not shown).

We checked the simulations for energetic and structural stability and found maximum Cα RMSD values to be below 3.5 Å over all 692 protein residues. Resulting conformational ensembles were analyzed using ptraj and cpptraj from AmberTools.³⁵ We extracted residue-wise B-factors derived from root mean squared fluctuations of Cα atoms following a global alignment. Additionally, we calculated thermodynamic entropies from the distributions of protein backbone torsion angles and summarized the three individual degrees of freedom to residue-wise and total entropies.³⁶ To study the behavior of the 34–45 loop, we performed an alignment to the whole respective protein subunits and recorded occurring loop movements. Subsequently, we clustered the loop structures according to their Cα RMSD into two states using a hierarchical agglomerative clustering approach. Respective cluster centroids were extracted as representative structures and compared in terms of structure and cluster occupancy. Values for dimeric systems are reported as average over both individual sub-units. Structures were visualized using Pymol.³⁷

2.2. Protein expression, purification and preparation

GALE enzymes were expressed and purified as described¹² and stored in HEPES (4-(2-hydroxyethyl)piperazine-1-ethanesulfonic acid)–KOH 50 mM, 1 mM TCEP (Tris(2-carboxyethyl)phosphine hydrochloride), pH 7.4. Thermolysin from Bacillus thermoproteolyticus Rokko was purchased from Sigma-Aldrich, exchanged to (HEPES)–KOH 50 mM, CaCl₂ 100 mM, 1 mM TCEP, pH 7.4. Proteins were flash frozen in liquid nitrogen and stored at −80 °C. Protein concentration was measured spectrophotometrically based on protein primary sequences.¹²

2.3. Small-angle X-ray scattering (SAXS)

Small-angle X-ray scattering (SAXS) measurements of wild-type and p.G90E GALE mutant in solution were performed at Diamond Light Source beamline B21 (Oxforshire, UK), using a BioSAXS robot for sample loading from solutions of both proteins at different concentrations in 50 mM HEPES–KOH pH 7.4 and 1 mM TCEP at 277  K. During the experiment the samples were exposed for 300 s in 10 s acquisition blocks using a sample to detector distance of 3.9 m and X-ray wavelength of 1 Å. The data were analyzed, buffer-subtracted, scaled, and merged using the Scatter software package (http://www.bioisis.net). This software was also used to check possible radiation damage of the samples by visual inspection of the Guinier region as a function of exposure time during data collection. R_G and D_max values were calculated with PRIMUS and GNOM, and shape estimation was carried out with DAMMIF/DAMMIN. Real-space scattering profiles of atomic models were calculated using CRYSOL and the final ab initio models were superimposed with the high-resolution structure using the program SUPCOMB. The program OLIGOMER was used to calculate the ratio of the species present in the solutions. All the SAXS programs are included in the ATSAS programs package.³⁸

2.4. Urea induced denaturation

Urea stock solutions were daily prepared in HEPES–KOH 50 mM, 1 mM TCEP, pH 7.4 at a 9 M concentration based on refractive index measurements. GALE enzymes (5 μM in protein monomer) were incubated in HEPES–KOH 50 mM, 1 mM TCEP, pH 7.4, in the presence of urea (0–4 M) for 16 h at 25 °C. Far-UV CD spectra were acquired in a Jasco J-710 spectropolarimeter using 1 mm path-length cuvettes at a 100 nm min⁻¹ scan rate and 4 scans were registered and averaged.

2.5. Proteolysis kinetics and thermodynamic analysis

GALE enzymes (20 μM in protein monomer) were incubated for at least 6 h at 25 °C in HEPES–KOH 50 mM, 1 mM TCEP, pH 7.4, in the presence of urea (0–0.6 M), and in the absence or presence of NAD⁺ 80 μM. Proteolysis was initiated by adding thermolysin to a final concentration of 0.1–0.6 μM. Aliquots were withdrawn at different times, and proteolysis was quenched by adding EDTA (ethylenediaminetetraacetic acid) pH 8 (to a 20 mM final concentration) and mixed with an equal volume of Laemmli's buffer. Control experiments without thermolysin were prepared in the same way and used to normalize the proteolysis kinetics. Proteolysis reactions were evaluated using 12% acrylamide SDS-PAGE (sodium dodecyl sulfate-polyacrylamide gel electrophoresis) and the bands corresponding to full length GALE were scanned and analyzed using the ImageJ software (http://rsbweb.nih.gov/ij/).

The apparent rate constants for proteolysis (k_p) were determined using a single exponental function. For the estimation of equilibrium m values, k_p was corrected for the inhibitory effect of urea on thermolysin degradation using the values previously reported.³⁹ The corrected rate constants (k′_p) were used to determine the equilibrium m values between the native and cleavable state (X) by determining their urea concentration dependence using the following equation:

where R is the ideal gas constant (1.987 cal mol⁻¹ K⁻¹) and T is the absolute temperature (298.15 K). The theoretical equilibrium m value for the global unfolding of GALE monomers was determined using the correlations from.⁴⁰

To estimate the effect of mutations on the thermodynamic stability of the native vs. the cleavable state, we have assumed that mutations do not affect the intrinsic proteolytic step (X → F), and thus, changes in the overall proteolysis rate after normalization using protease concentration (k_WT and k_mut) reflect changes in the equilibrium constant between N and X (N ↔ X;⁴¹), and therefore in their free energy changes (ΔΔG), following eqn (2):

ΔΔG_mut–WT = −RT ln(k_mut/k_WT) (2)

3. Results

3.1. Molecular dynamics (MD) simulations identify changes in conformational states in the native ensemble due to catalytic GALE mutations

GALE disease-associated variants affect catalytic properties and binding of NAD⁺ increasing proteolysis susceptibility.^{12,25,26,42–44} Indeed, based on proteolysis sensitivity measurements and the crystal structure of GALE,¹² we have proposed that certain catalytic mutations (e.g. p.N34S and p.G90E) could affect the local flexibility of the loop 34–45, which encloses the NAD⁺ binding site. Knowing that p.G90E and p.V94M present only 0.1% and 3% respectively of the wild-type catalytic activity, and p.N34S shows 4-fold lower affinity for NAD⁺ which is abolished in p.G90E, we hypothesize that the catalytic defects and NAD⁺ binding effects could be associated with conformational changes arising from dynamic alterations in the native state ensemble.

MD simulations were used to characterize the conformational microstates present in native GALE ensembles at atomic resolution. GALE monomeric enzymes are rather unstable over 100 ns simulation time, and therefore, subsequent analyses were carried out using the functional GALE dimer only. We have focused our analyses on the 34–45 loop where major conformational transitions are found (reaching RMSD values up to 8 Å in apo GALE systems; see Fig. S1† for a 2D RMSD plot). By contrast, NAD⁺-bound GALE complexes show drastically reduced loop mobility (Fig. S1†), supporting its stabilizing effect towards proteolysis.¹² The aggregate simulation time of 1.6 μs of the dimer (i.e. 3.2 μs sampling time for individual loops) make us confident on the observed trends for loop dynamics, despite individual simulation (100 ns) is at the lower limit for investigating changes in loop movements.⁴⁵ In this regard, enhanced sampling methods⁴⁶ could be helpful to provide further insight into the loop trends described here.

We performed a cluster analysis to investigate plausible loop conformations during molecular dynamics simulations (Fig. 1A–D). MD trajectories were clustered into two states: the major one representing a ground state (close to that of the crystal structure) and the minor excited (i.e. high-energy) state. The relative populations of the major and minor states depend on the cut-off values used in the clustering procedure, even though the qualitative trends described here for the effect of mutations and NAD⁺ binding are robust.

Fig. 1 Molecular dynamics simulations reveal conformational heterogeneity in GALE. (A–D) Characterization of two alternative conformations of the loop 34–45 from a two-state clustering of MD trajectories. The major conformations (ground states) of the 34–45 loop (shown as cartoon and lines) are colored in black and minor conformations (excited states) in white. The NAD⁺ cofactor is shown in stick representation where present and the thermolysin cleavage site in the loop is indicated as a white sphere. Cluster analyses correspond to WT GALE without (A) and with NAD⁺ (B) and p.G90E without (C) and with NAD⁺ (D). (E) Population of excited states in the absence and presence of NAD⁺ from representative cluster analyses. (F) Changes in local dynamics (B-factors) around the thermolysin cleavage site (loop 34–45) in the absence (left panel) or the presence of NAD⁺ (right panel).

In the absence of NAD⁺, the minor conformation is more populated in the p.N34S and p.G90E mutants (Fig. 1E), defective in NAD⁺ binding, while generally the thermolysin cleavage site Ala38–Phe39 is more solvent exposed in these high-energy states (Fig. 1A and C). In the presence of NAD⁺, a much lower population of the high-energy states is found, except for p.V94M (Fig. 1E), an in all cases the conformation of the ground and excited states is more similar (Fig. 1B and D). These analyses support that two conformational states exist in equilibrium in the absence of NAD⁺, with the more populated displaying higher affinity for NAD⁺ due to higher structural complementarity that likely prevents from thermolysin cleavage (Fig. 1A–D). Therefore, the lower affinity for NAD⁺ in p.N34S and the inability of p.G90E to bind it, can be partly explained by a shift in the conformational equilibrium towards non-binding competent states, remodeling the protein energy landscape in such a way that cofactor binding is thermodynamically penalized.^4,47

According to this proposed mechanism, p.N34S and p.G90E could be more susceptible to proteolytic attack at the 34–45 loop since they increase the population of cleavable (excited) non-binding competent states, while NAD⁺ binding reduces the population of cleavable states explaining its protective effect.¹² Alternatively, accelerated proteolysis and low binding affinity could also be explained by enhancement of local dynamics at the NAD⁺ binding site that impedes its correct spatial complementarity towards the cofactor. To distinguish between these two mechanisms, we have analyzed local dynamics at the residue level by MD simulations (Fig. 1F). Interestingly, we find that the flexibility around the cleavage site (loop 34–45) does not correlate with the experimentally determined proteolysis susceptibility (Fig. 1F and ref. 12), implying that proteolysis susceptibility is not directly linked to local dynamics in this case. Additionally, p.N34S and p.G90E facilitate thermally induced partial unfolding¹² which supports a population-shift mechanism. Addition of NAD⁺ decreases the local dynamics around the cleavage site, which likely reflects the shift towards binding competent states (Fig. 1E).

3.2. Conformation of WT and p.G90E in solution studied by small-angle X-ray scattering (SAXS)

To investigate experimentally the effect of a catalytic mutation on GALE conformational ensemble, we have determined the low-resolution conformation of WT and p.G90E by SAXS. The overall parameters for SAXS modeling are summarized in Table S1.† Scattering profiles of both proteins show differences in the radius of gyration calculated both in real and reciprocal space, as well as in their corresponding D_max values, and Kratky plots suggested an increase in the flexibility in the p.G90E mutant (Fig. 2A–D). Envelope reconstruction clearly results in a more elongated shape of the p.G90E mutant than the WT protein (Fig. 2E and F). The ab initio shape reconstructions superimposed well with the available crystallographic data (PDB entry 1EK6), but exhibited a molecular envelope larger than that observed in the crystal structure, especially in the p.G90E mutant.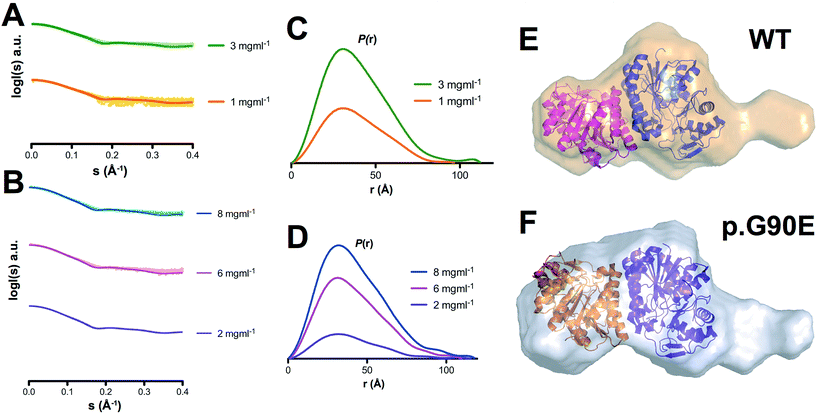

Fig. 2 Structural models of GALE WT and p.G90E in solution by SAXS. (A and B) Experimental scattering curves (dots) and calculated (lines) SAXS data for GALE WT (A) and p.G90E (B) at different protein concentrations. (C and D) P(r) functions for GALE WT (C) and p.G90E (D). The tail reveals the more elongated dimer shape of the p.G90E mutant. (E and F) Ab initio shape reconstructions of GALE WT and p.G90E were superimposed on the crystal structure (PDB entry 1EK6).

In combination with our results using MD simulations (Fig. 1), these SAXS analyses support the existence of conformational fluctuations (i.e. high-energy states) in GALE in solution, which are enhanced by the p.G90E mutation.

3.3. Thermodynamic characterization of high-energy states under native conditions by proteolysis

We have used proteolysis to evaluate the effect of GALE mutations on the energetics of the native state ensemble, particularly on high-energy excited (cleavable) states, such as those detected by MD simulations and difficult to characterize experimentally. Proteolysis of GALE under native conditions is well-described by the following mechanism: N ⇔ X ⇒ F, where X is the cleavable state in equilibrium with the native state (N), and undergoes proteolytic cleavage to produce a proteolyzed state F. The step N ↔ X is governed by a equilibrium constant K, while the step X → F is determined by an intrinsic proteolysis rate constant k. To provide insight into the conformation of X, we have measured proteolysis kinetics in the presence of low urea concentrations. Urea and protease concentrations were kept very low to minimize deviations from native conditions (Fig. S2†) and to ensure that the proteolysis step X → F is rate-limiting, and thus, the overall proteolysis rate constant k_p ≈ Kk.^8,41,48 Experimental k_p values (Fig. 3A–D) were determined from first-order kinetic decays (Fig. S3†). Based on this mechanism, and upon correction of k_p values due to modest inhibition caused by urea,³⁹ changes in proteolysis kinetics were used to determine equilibrium m values using eqn (1) (Fig. 3E–H). These equilibrium m values (Fig. 3I) are proportional to the magnitude of the conformational change between native and cleavable states (Fig. 3J; i.e. degree of unfolding), and thus provide structural information on the cleavable state X.

Fig. 3 Urea dependence of proteolysis rate constants and thermodynamic analysis. (A–D) proteolysis rate constants (k_p) at different urea concentrations in the absence or presence of NAD⁺; (E–H) corrected proteolysis rate constants (k′_p) by urea inhibition of thermolysin as reported by ref. 39. The slopes of these plots are used to determined equilibrium m values. (I and J) Equilibrium m values (I) for the native-to-cleavable state (X) equilibrium determined by proteolysis and the corresponding fraction of accessible surface area (ASA) unfolded in the X state (J). (K) Effect of mutations on the change in free energy (ΔΔG_(mut–WT)) between native and cleavable states. Error bars are fitting errors or those propagated from them.

The sensitivity to thermolysin degradation correlates well with the effect of urea on proteolysis kinetics (Fig. 3I–K): the higher the sensitivity to proteolysis of a GALE variant, the higher the effect of urea. For WT and p.V94M, we found fairly similar equilibrium m values, on average a 0.55 kcal mol⁻¹ M⁻¹, which implies that ∼15% of the native structure (∼50 residues) is unfolded in the cleavable state X (Fig. 3J). In the case of p.N34S and p.G90E, the equilibrium m value is around 1.4 kcal mol⁻¹ M⁻¹, and thus, about ∼40% of the native structure (∼130 residues) is unfolded in the cleavable state for these two mutants. Therefore, p.N34S and p.G90E populate a more extensively unfolded cleavable state under native conditions, and since proteolysis occur at Ala38–Phe39,¹² likely involves the N-terminal domain that contains the NAD⁺ binding site. Moreover, a direct comparison of proteolysis rate constants normalized by protease concentration provides a measure of the thermodynamic destabilization induced by p.N34S and p.G90E on the N ↔ X equilibrium (eqn (2)), which amounts to 1.5–2 kcal mol⁻¹, while the effect of p.V94M is marginal (Fig. 3K). These results show that p.N34S and p.G90E shift the N ↔ X towards the cleavable state by a factor of 22.5 ± 4.5 and 14.1 ± 3.1. Overall, in the context of the population-shift mechanism, the lower affinity for NAD⁺ in p.N34S and p.G90E is explained by the stabilization of non-competent binding states and changes in their structure under native conditions.

Addition of NAD⁺ has a stabilizing effect towards proteolysis (Fig. 3 and S3†), although this effect is variant-dependent. In p.G90E, only a 20% decrease in the proteolysis rate constant is found, while this effect is of 40% in WT, 60% in p.N34S and 130% in p.V94M. The stabilization agrees well with their corresponding affinities for NAD⁺.¹² Importantly, the stabilization exerted by NAD⁺ does not cause large changes in the equilibrium m values (Fig. 3I), indicating that NAD⁺ binding does not alter the structure of the cleavable state but instead simply shifts the conformational equilibrium towards more protease-resistant NAD⁺ binding competent states.

4. Discussion

Inherited metabolic diseases are often caused by missense mutations impairing enzyme activity, regulatory properties and/or intracellular stability.^{21,24,49–53} Two of the most common pathogenic mechanisms either involve native state destabilization or catalytic alterations, which are customarily considered as separate mechanisms. Here we explore the possibility of a relationship between these two mechanisms, by describing how two mutations in GALE associated to type III galactosemia affect the affinity for NAD⁺, and therefore their catalytic performance, promoting unfolding of the N-terminal domain and NAD⁺ binding site. We identify alterations in the conformational ensemble of p.N34S and p.G90E consistent with a shift in the conformational equilibrium towards partially unfolded non-competent states for NAD⁺ binding as shown by a combination of proteolysis and SAXS experiments and MD simulations. Therefore, we provide experimental and computational evidence to support an ensemble-based mechanism to explain catalytic mutations, in which structural and chemical perturbations caused by the mutations shift the equilibrium towards inactive conformations in the native state ensemble.

It must be noted that conformational fluctuations at the NAD⁺ binding site occur even in GALE variants with WT-like binding affinity (Fig. 1 and 3). Non-binding competent excited states can be used by nature to provide the appropriate binding affinity for enzyme function at physiologically relevant ligand concentrations, allowing conformational excursions to states with different degrees of unfolding.^6,47 In this context, p.N34S and p.G90E are deleterious because they shift the conformational equilibrium towards more unstructured partially unfolded conformations in the native state ensemble thus energetically penalizing NAD⁺ binding (Fig. 4A and B). These excited states seem to be populated to significant levels, as seen by the ability of our MD simulations to detect them even at the low microsecond sampling time scale (Fig. 1), although variants with low binding affinity for NAD⁺ clearly promote the population of excited states. This population-shift is reflected in our SAXS analyses as an expansion in the average ensemble in solution (Fig. 2), thus overall supporting this conformational-selection mechanism for the binding of NAD⁺ to GALE. In addition, proteolysis experiment revealed an increase in population of these excited states in p.N34S and p.G90E as well as a change in their overall structure, showing a higher degree of unfolding (Fig. 3). Importantly, since the population of these excited states is inversely proportional to NAD⁺ binding affinity, it is plausible that allosteric effectors would be able to bind to WT-like excited states destabilized by catalytic mutations such as p.N34S and p.G90E, thus partially restoring the binding affinity for NAD⁺ (Fig. 4C).

Fig. 4 Pictorial representation of the effect of catalytic mutations on the structure of excited states and NAD⁺ binding affinity and its potential correction by allosteric effectors. Panels (A) and (B) show the equilibrium between native GALE WT (A) and p.G90E (B) and the excited, cleavable states as inferred from native proteolysis experiments. In panel (C), the potential effect of an allosteric ligand binding to an unstructured region of the excited state of a catalytic mutant leading to correction of its NAD⁺ binding affinity by a coupled binding-folding process. For sake of simplicity, only the GALE monomer is displayed (based on PDB:1EK5).

So far, we have identified a thermodynamic signature for mutations affecting NAD⁺ binding to GALE. Consistently, this signature is not found in p.V94M, a mutant strongly reducing catalytic efficiency with mild effects on the apparent affinities for the substrate and cofactor.^12,25 Previous MD simulations have suggested little effect of p.V94M on the interaction with substrate and cofactor.²⁷ However, p.V94M seems to severely affect the ability of GALE active site to bring together the NAD⁺ cofactor, the substrate and the catalytic Tyr157, leading to non-optimal ternary complex for catalysis.²⁵ In the case of p.N34S and p.G90E, their low binding affinity for NAD⁺ (Fig. 4 and ref. 12) is caused by a shift in the conformational equilibrium of the apo-state towards NAD⁺ non-binding competent states, and in addition, p.G90E could develop unfavorable electrostatic interactions that may also contribute to its apparent inability to bind the cofactor and its dramatically low activity.^12,25

5. Conclusions

In conclusion, we describe a computational and experimental approach that directly links mutational effects on native state fluctuations to catalytic and coenzyme binding defects in an inherited metabolic disease. We propose that our strategy, in the context of an ensemble-based mechanism, would be helpful to understand better mutational effects on catalysis and regulation (such as allostery and cooperativity), which are frequently altered in inborn errors of metabolism such as phenylketonuria,^10,50,54 classical homocystinuria,^13,55 inherited galactosemias^25,56 and primary hyperoxaluria type I.⁴⁹ Interestingly, several previous works allow to propose some correlation between altered proteolytic susceptibility and allosteric response in inborn errors of metabolism,^10,13,57 but not for catalytic alterations. Therefore, we advance the general hypothesis that disease-associated point mutations often adversely disturb native-state dynamics. More generally, we expect that future work with mutations associated to other metabolic diseases will test whether our ensemble-based mechanism provides a unifying framework to reconcile analysis from enzyme kinetic and ligand binding studies, X-ray crystal structures, extensive molecular dynamic simulations and experimental ensemble studies using techniques such as SAXS and proteolysis. From a therapeutic viewpoint, we propose a strategy aimed at identifying molecules which can (partially) reverse the changes in active-site conformational fluctuations upon binding to cryptic allosteric sites (Fig. 4), alternative to current approaches that focus on compounds which promote proper folding of affected proteins.

Acknowledgements

This work was supported by grants from MINECO (BIO2015-66426-R, CSD2009-00088) and Junta de Andalucía (P11-CTS-07187). A. L. P. was supported by a Ramón y Cajal research contract from MINECO/University of Granada (RYC-2009-04147). We thank the Diamond beam line B21 for access to synchrotron radiation and to Robert Rambo and Katsuaki Inoue for assistance during SAXS experiments.

References

1. J. S. Fraser, M. W. Clarkson, S. C. Degnan, R. Erion, D. Kern and T. Alber, Nature, 2009, 462, 669–673.
2. S. R. Tzeng and C. G. Kalodimos, Nature, 2009, 462, 368–372.
3. D. Berko, S. Tabachnick-Cherny, D. Shental-Bechor, P. Cascio, S. Mioletti, Y. Levy, A. Admon, T. Ziv, B. Tirosh, A. L. Goldberg and A. Navon, Mol. Cell, 2012, 48, 601–611.
4. H. N. Motlagh, J. O. Wrabl, J. Li and V. J. Hilser, Nature, 2014, 508, 331–339.
5. A. Sekhar and L. E. Kay, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12867–12874.
6. T. P. Schrank, D. W. Bolen and V. J. Hilser, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16984–16989.
7. N. Cremades, J. Sancho and E. Freire, Trends Biochem. Sci., 2006, 31, 494–496.
8. E. Medina-Carmona, R. J. Palomino-Morales, J. E. Fuchs, E. Padín-Gonzalez, N. Mesa-Torres, E. Salido, D. J. Timson and A. L. Pey, Sci. Rep., 2016, 6, 20331.
9. B. J. Henriques, P. Bross and C. M. Gomes, Biochim. Biophys. Acta, 2010, 1802, 1070–1077.
10. S. W. Gersting, K. F. Kemter, M. Staudigl, D. D. Messing, M. K. Danecka, F. B. Lagler, C. P. Sommerhoff, A. A. Roscher and A. C. Muntau, Am. J. Hum. Genet., 2008, 83, 5–17.
11. A. L. Pey, M. Maggi and G. Valentini, J. Inherited Metab. Dis., 2014, 37, 909–916.
12. A. L. Pey, E. Padin-Gonzalez, N. Mesa-Torres and D. J. Timson, Arch. Biochem. Biophys., 2014, 562, 103–114.
13. M. I. Mendes, A. S. Santos, D. E. Smith, P. R. Lino, H. G. Colaco, I. T. de Almeida, J. B. Vicente, G. S. Salomons, I. Rivera, H. J. Blom and P. Leandro, Hum. Mutat., 2014, 35, 1195–1202.
14. A. L. Pey, T. Majtan, J. M. Sanchez-Ruiz and J. P. Kraus, Biochem. J., 2013, 449, 109–121.
15. A. L. Pey, F. Stricher, L. Serrano and A. Martinez, Am. J. Hum. Genet., 2007, 81, 1006–1024.
16. A. C. Tsolis, N. C. Papandreou, V. A. Iconomidou and S. J. Hamodrakas, PLoS One, 2013, 8, e54175.
17. M. Vihinen, Hum. Mutat., 2013, 34, 275–282.
18. M. Vihinen, Hum. Mutat., 2014, 35, 912–914.
19. Y. Yang, B. Chen, G. Tan, M. Vihinen and B. Shen, Amino Acids, 2013, 44, 847–855.
20. A. L. Pey, M. Ying, N. Cremades, A. Velazquez-Campoy, T. Scherer, B. Thony, J. Sancho and A. Martinez, J. Clin. Invest., 2008, 118, 2858–2867.
21. A. L. Pey, Amino Acids, 2013, 45, 1331–1341.
22. J. V. Rodrigues, B. J. Henriques, T. G. Lucas and C. M. Gomes, Curr. Top. Med. Chem., 2012, 12, 2546–2559.
23. A. Jorge-Finnigan, S. Brasil, J. Underhaug, P. Ruiz-Sala, B. Merinero, R. Banerjee, L. R. Desviat, M. Ugarte, A. Martinez and B. Perez, Hum. Mol. Genet., 2013, 22, 3680–3689.
24. A. C. Muntau, J. Leandro, M. Staudigl, F. Mayer and S. W. Gersting, J. Inherited Metab. Dis., 2014, 37, 505–523.
25. D. J. Timson, FEBS J., 2005, 272, 6170–6177.
26. T. M. Wohlers and J. L. Fridovich-Keil, J. Inherited Metab. Dis., 2000, 23, 713–729.
27. D. J. Timson and S. Lindert, Gene, 2013, 526, 318–324.
28. J. B. Thoden, T. M. Wohlers, J. L. Fridovich-Keil and H. M. Holden, Biochemistry, 2000, 39, 5691–5701.
29. P. Labute, Proteins, 2009, 75, 187–205.
30. R. Salomon-Ferrer, A. W. Götz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888.
31. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins, 2010, 78, 1950–1958.
32. R. D. Walker, M. M. de Souza, I. P. Mercer, I. R. Gould and D. R. Klug, J. Phys. Chem. B, 2002, 106, 11658–11665.
33. J. J. Pavelites, J. Gao, P. A. Bash and A. D. Mackerell Jr, J. Comput. Chem., 1997, 18, 221–239.
34. J. E. Fuchs, R. G. Huber, S. von Grafenstein, H. G. Wallnoefer, G. M. Spitzer, D. Fuchs and K. R. Liedl, PLoS One, 2012, 7, e53005.
35. D. R. Roe and T. E. Cheatham III, J. Chem. Theory Comput., 2013, 9, 3084–3095.
36. R. G. Huber, C. Eibl and J. E. Fuchs, Protein Sci., 2015, 24, 174–181.
37. Schrodinger LLC, 2010.
38. M. V. Petoukhov, D. Franke, A. V. Shkumatov, G. Tria, A. G. Kikhney, M. Gajda, C. Gorba, H. D. Mertens, P. V. Konarev and D. I. Svergun, J. Appl. Crystallogr., 2012, 45, 342–350.
39. C. Park and S. Marqusee, J. Mol. Biol., 2004, 343, 1467–1476.
40. J. K. Myers, C. N. Pace and J. M. Scholtz, Protein Sci., 1995, 4, 2138–2148.
41. A. L. Pey, Biochim. Biophys. Acta, 2013, 1834, 2502–2511.
42. T. J. McCorvie, Y. Liu, A. Frazer, T. J. Gleason, J. L. Fridovich-Keil and D. J. Timson, Biochim. Biophys. Acta, 2012, 1822, 1516–1526.
43. B. B. Quimby, A. Alano, S. Almashanu, A. M. DeSandro, T. M. Cowan and J. L. Fridovich-Keil, Am. J. Hum. Genet., 1997, 61, 590–598.
44. J. Wasilenko, M. E. Lucas, J. B. Thoden, H. M. Holden and J. L. Fridovich-Keil, Mol. Genet. Metab., 2005, 84, 32–38.
45. J. E. Fuchs, B. J. Waldner, R. G. Huber, S. von Grafenstein, C. Kramer and K. R. Liedl, J. Chem. Theory Comput., 2015, 11, 851–860.
46. Y. Miao, V. A. Feher and J. A. McCammon, J. Chem. Theory Comput., 2015, 11, 3584–3595.
47. S. Vega, O. Abian and A. Velazquez-Campoy, Biochim. Biophys. Acta, 2016, 1860, 868–878.
48. G. Tur-Arlandis, D. Rodriguez-Larrea, B. Ibarra-Molero and J. M. Sanchez-Ruiz, Biophys. J., 2010, 98, L12–L14.
49. E. Oppici, R. Montioli and B. Cellini, Biochim. Biophys. Acta, 2015, 1854, 1212–1219.
50. H. Erlandsen, A. L. Pey, A. Gamez, B. Perez, L. R. Desviat, C. Aguado, R. Koch, S. Surendran, S. Tyring, R. Matalon, C. R. Scriver, M. Ugarte, A. Martinez and R. C. Stevens, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16903–16908.
51. N. Gregersen, P. Bross, S. Vang and J. H. Christensen, Annu. Rev. Genomics Hum. Genet., 2006, 7, 103–124.
52. C. M. Gomes, Curr. Top. Med. Chem., 2012, 12, 2460–2469.
53. J. Ereno-Orbea, T. Majtan, I. Oyenarte, J. P. Kraus and L. A. Martinez-Cruz, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E3845–E3852.
54. E. Bjorgo, P. M. Knappskog, A. Martinez, R. C. Stevens and T. Flatmark, Eur. J. Biochem., 1998, 257, 1–10.
55. T. Majtan, L. Liu, J. F. Carpenter and J. P. Kraus, J. Biol. Chem., 2010, 285, 15866–15873.
56. A. I. Coelho, M. Trabuco, R. Ramos, M. J. Silva, I. Tavares de Almeida, P. Leandro, I. Rivera and J. B. Vicente, Mol. Genet. Genomic Med., 2014, 2, 484–496.
57. A. Hnizda, T. Majtan, L. Liu, A. L. Pey, J. F. Carpenter, M. Kodicek, V. Kozich and J. P. Kraus, Biochemistry, 2012, 51, 4755–4763.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra05499d

---