Enhancement of battery performance of LiMn2O4: correlations between electrochemical and magnetic properties†
S. Demirela,
E. Oza,
S. Altina,
A. Bayria,
E. Altinb and
S. Avci*c
aInonu University, Physics Department, 44280, Malatya, Turkey
bInonu University, Scientific and Technological Research Center, 44280 Malatya, Turkey
cIstanbul Medeniyet University, Faculty of Engineering and Natural Sciences, 34700 Istanbul, Turkey. E-mail: sevda.avci@medeniyet.edu.tr
First published on 26th April 2016
Abstract
We report the results of a systematic investigation of structural, electrical transport, magnetic, and electrochemical properties of LiBxMn2−xO4 (where x = 0.0–1), synthesized via a one-step solid state reaction technique. We find that the parent compound (x = 0) has the non-stoichiometric Li1.05Mn2O4 phase and the B ions successfully incorporate the structure for x ≤ 0.5. The resistivity anomaly of the parent compound below 100 K is attributed to the antiferromagnetic correlations. The linear part of the χ−1–T data are used to calculate the effective magnetic moments and to determine the total number of Mn3+ and Mn4+ ions. Magnetization measurements show that Jahn–Teller active Mn3+ ions have high spin configuration. Average valance of Mn ions increases with increasing boron content. Electrochemical studies show improved capacity retention for x = 0.125 for 100 charge–discharge cycles. This improvement is attributed to subtle modifications in the structural and magnetic properties upon substitution.
Introduction
Li-based batteries have gained importance in the last two decades due to their high capacity and high energy density. Among the cathode materials, spinel LiMn2O4 have many advantages such as environmental safety, low cost, high stability and less toxicity.1–3 However, spinel LiMn2O4 cathode suffers from a significant capacity loss after repeated cycling. The main reasons for the capacity loss are reported as Jahn–Teller distortion of [MnO6] octahedron, dissolution of Mn ions in electrolyte, the structural degradation during lithiation and delithiation and high self-discharging during the storage.4–6 Mainly two methods have been employed to overcome these problems. One of them is the surface coating to minimize the contact between the electrolytes and the active materials.7,8 The second method is the modification of the intrinsic properties via partial substitution of Mn.9–11 So far, many substitutions (S, F, Br, Si, B, Mg, Al, Bi, Cu, Ni, Ru, Ga, Ag, etc.12–24) have been studied to increase the cycle life of LiMn2O4 cathode. The main idea behind this approach is to suppress the Jahn–Teller distortion via increasing the valance state of Mn ions and to stabilize the spinel structure during cycling.25 In an octahedral environment, 3d electrons occupy five orbitals, eg douplet, which lie along the x, y, z axis, and t2g triplet which lie in between the axis, forming MnO6 octahedron. The six ligands of the octahedron interact more with the eg orbitals than with t2g orbitals. Thus, the degeneracy of the five orbitals is lost and an energy difference between eg and t2g orbitals is formed. If the two eg orbitals have different number of electrons, further degeneracy loss is observed causing geometric distortions also known as Jahn–Teller effect.26The crystal structure of LiMn2O4 have a spinel-type cubic structure with Fd3m space group above a Verwey transition at ∼285 K.27,28 Li ions are located in the 8a tetrahedral sites. The Mn ions, 50% Mn3+ and 50% Mn4+, are distributed randomly over the octahedral sites (16d) with an average valance state of 3.5.29 The Mn4+ and Jahn–Teller active Mn3+ ions have t32ge0g and t32ge1g configurations, respectively.30,31 A single electron in eg orbital of Mn3+ is expected to cause a strong Jahn–Teller distortion.32 Such distortion is preferred in order to reduce both the orbital degeneracy and overall electron–electron repulsion energy. The eg electrons in LiMn2O4 can be localized causing a semiconducting type conductivity.33–36 A structural transition from cubic to tetragonal with I41/amd space group is driven by a partial charge ordering between Mn3+ and Mn4+ among the distinct Mn sites. The transition is attributed to cooperative Jahn–Teller effect of Mn3+ ions.37,38 On the other hand, LiMn2O4 has interesting magnetic properties related closely with the battery performance. It is a geometrically frustrated antiferromagnet, since the magnetic sublattice consists of a network of vertex sharing tetrahedra.
The electrical conduction mechanism of LiMn2O4 is another important phenomena in terms of the battery performance and understanding the nature of LiMn2O4.39 There are two types of conductivity mechanism in LiMn2O4 as the ionic conductivity of Li ions and the non-adiabatic small polaron of eg electrons of Mn3+ ions.40 Iguchi et al. suggested that the ionic conductivity due to Li ions is not probable primary mechanism and the conductivity can be mainly due to nonadiabatic small polarons.41
Effects of substitution on cell performance of LiMn2O4 can be studied in many aspects such as the mass, size, valance state or magnetic properties of the substituted elements. There are many reasons to use boron as a substitution element. Despite the conflicting reports,42 substitution of Mn by elements heavier than the atomic weight of manganese is expected to decrease the specific capacity of doped LiMn2O4.43 In addition, Mn3+ ions are Jahn–Teller active and it is essential to decrease the number of Mn3+ ions and hence to increase the structural stability. Thus, substitution Mn3+ ions with a non-magnetic element with 3+ valance state is expected to increase the structural stability by suppressing the Jahn–Teller distortion.44 Substitution by ions with smaller ionic radius than the ionic radius of Mn is expected to decrease the cell parameters and make the structure more stable. However, there are many conflicting reports on this issue. For example substitution of Mn3+ (ionic radius: 0.58 Å, atomic mass: 54.93 amu) ions by 1% Y3+ (0.9 Å, 88.9 amu) shrinks the cell by ∼2%.43 On the other hand, substitution by Al3+ (0.53 Å, 26.98 amu) slightly expands the cell.41 Non-magnetic B3+ with smaller ionic radius and smaller mass than Mn3+ is a good choice for substitution. Besides, there is limited number of studies regarding the effects of B substitution in LiMn2O4 on its electrochemical performance. These studies can be classified in two categories; Lithium Boron Oxide (LBO) coated on the LiMn2O4 and direct doping of B in Mn sites of LiMn2O4.12–25,45 S. H. Choi et al. investigated the (LBO) glass modified LiMn2O4 cathode materials and they found that LBO coated LiMn2O4 has a better capacity retention (86% with 100 cycles) than that of the pure LiMn2O4 (65% with 100 cycles), however, coating LiMn2O4 with 5 wt% LBO decreases the initial capacity from 143 to 123 mA h g−1.46 H. W. Chan et al. also investigated the LBO coating effect on LiMn2O4 and found a capacity enhancement for the 0.4 wt% LBO coated LiMn2O4 cathode materials.16 H. Şahan et al. reported that LBO coated LiMn2O4 have better cyclability after 30 cycles than that of the uncoated LiMn2O4.45 R. Thirunakaran et al. synthesized LiBxMn2−xO4 (where x = 0–0.4) and reported improved electrochemical performance for x = 0.1 sample.47 In another study, J. H. Lee et al. investigated the effects of different doping elements as Li, B, Al, Co and Ni and they found that LiB0.05Mn1.95O4 has the worst battery performance compared to other compounds examined in Lee et al.'s study.48
In this work, we examined the effects of B doping on the structural, magnetic and electrochemical properties of LiMn2O4. We found that the cell parameters and the cell volume increases with increasing B content. Electrochemical measurements show that 6.25% B substitution (x = 0.125 sample) improves the capacity retention significantly for 100 cycles. We revisited the magnetic and electrical transport properties of LiMn2O4 and studied the correlations between the electrochemical properties and structural, electrical, and magnetic properties of LiMn2−xBxO4.
Experimental
Nominal compositions of LiBxMn2−xO4 (where x = 0.0–1) were prepared by conventional solid state reaction technique. Appropriate amounts of reagent grade Li2O, Mn2O3, and B2O3 were mixed in agate mortar for 1 h in glove box. We used 8% Li rich composition due to high temperature fast evaporation of Li as indicated in ref. 49 The mixture was heated in an α-Al2O3 crucible at 750 °C for 24 h under air and cooled down to room temperature.Crystal structure investigation was carried out by X-ray diffraction (XRD). Automated Rigaku RadB Dmax X-ray diffractometer with Cu-kα (λCukα = 1.5405 Å) radiation was used for the XRD analysis with a scan rate of 2° min−1.
Temperature dependences of resistivity (ρ–T) of the samples were measured by closed cycle Leybold LT-10 cryostat system combined SRS AC bridge system with 17.7 Hz frequency using four probe technique. The magnetic properties of the samples were measured simultaneously from 300 K to 2 K by Quantum Design-Physical Properties Measurement System (PPMS) with VSM attachment.
To fabricate the coin cell batteries, LiBxMn2−xO4 active materials, acetylene black and polyvinylidene fluoride (80%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10%
10%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10%) were mixed into slurries in N-methyl-2-pyrrolidone into an agate mortar. They were then cast on aluminum foils with a micrometer adjustable film applicator blade and then dried at 110 °C for 10 hours to obtain several electrode laminates. After these transactions, the laminates were put into the vacuum at ∼25 °C for 24 h. Discs (diameter 1/4 14 mm) of the laminates were punched and transferred to an argon filled glove box (MBraun UNILab Pro Modular Glove Box). A typical loading of the active material was approximately 5.0–6.0 mg. Afterwards, CR-2032 type coin-cells with pure Li metal as the counter electrode were assembled in the glove box with the LiPF6 electrolyte. The cells were cycled by 8 channel battery analyzer system MTI-(BST8-MA) in the voltage window from 3.0 to 4.2 V at 1C current rate. Also the cyclic voltammograms (CV) of the cells were measured with MTI-BST8-STAT-EIS-LD Single Channel Potentiostat/Galvanostat workstation from 3.5 to 4.5 V at a scan rate of 0.2 mV s−1. All measurements of the cells were conducted at room temperature.
10%) were mixed into slurries in N-methyl-2-pyrrolidone into an agate mortar. They were then cast on aluminum foils with a micrometer adjustable film applicator blade and then dried at 110 °C for 10 hours to obtain several electrode laminates. After these transactions, the laminates were put into the vacuum at ∼25 °C for 24 h. Discs (diameter 1/4 14 mm) of the laminates were punched and transferred to an argon filled glove box (MBraun UNILab Pro Modular Glove Box). A typical loading of the active material was approximately 5.0–6.0 mg. Afterwards, CR-2032 type coin-cells with pure Li metal as the counter electrode were assembled in the glove box with the LiPF6 electrolyte. The cells were cycled by 8 channel battery analyzer system MTI-(BST8-MA) in the voltage window from 3.0 to 4.2 V at 1C current rate. Also the cyclic voltammograms (CV) of the cells were measured with MTI-BST8-STAT-EIS-LD Single Channel Potentiostat/Galvanostat workstation from 3.5 to 4.5 V at a scan rate of 0.2 mV s−1. All measurements of the cells were conducted at room temperature.
Results and discussion
Structural properties
The XRD data (Fig. 1) show no impurity phases in the LiMn2O4 and the peak positions match well with the standard PDF card (35-0782) of LiMn2O4. The lattice parameter of LiMn2O4 is calculated as a = 8.2186 (89) Å by using Rietvelt-Refinement technique. M. Kopec et al. investigated the effects of Li concentration on the structural properties of LiMn2O4 and they found that Li content can change the lattice parameters significantly.50 Our unsubstituted sample's lattice constants are closer to the lattice constants of Li1.05Mn2O4,50 considering the 8% extra Li addition during the synthesis. XRD pattern of the LiMn2−xBxO4 x = 0.0–0.5 samples are almost identical with x = 0 sample without major impurity peaks indicating that boron is doped into the lattice of LiMn2O4 successfully. Impurity phase (Mn3(BO3)2) is visible for x > 0.5 samples. The lattice parameters obtained via Rietveld refinement are listed in the Table 1.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry
m symmetry
| x | a (Å) = b (Å) = c (Å) | RMn–Mn (Å) | V (Å3) |
|---|---|---|---|
| 0 | 8.21861 ± 0.00895 | 2.905 ± 0.005 | 555.1305 |
| 0.125 | 8.22520 ± 0.00265 | 2.907 ± 0.002 | 556.4669 |
| 0.25 | 8.22859 ± 0.00632 | 2.909 ± 0.004 | 557.1553 |
| 0.50 | 8.23268 ± 0.01243 | 2.910 ± 0.006 | 557.9865 |
| 0.75 | 8.24501 ± 0.00988 | 2.915 ± 0.005 | 560.4973 |
| 1.00 | 8.24838 ± 0.00454 | 2.916 ± 0.003 | 561.1849 |
There are controversial reports regarding the effects of B substitution on lattice volume of the LiMn2O4. A. Veluchamy et al.51 and S. H. Choi et al.43 determined a decrease in lattice volume with B substitution.
On the other hand, J. H. Lee et al.,48 R. Thirunakaran et al.47 and Ebin et al.53 reported that B substitution increases the cell parameters and expands the cell volume of LiMn2O4. Ebin et al. claim that some of the B3+ ions occupy the 8a tetrahedral sites instead of the 16d octahedral sites causing an expansion in the unit cell volume. In our data, the cell parameters increase with increasing B content, consistent with Ebin et al.'s results. In spite of this increase in the cell parameters, we observed that B substitution does not significantly affect the morphology of the samples (see ESI†).
Magnetic properties
LiMn2O4 has attracted attention from the scientists due to not only its battery performance but also its rich magnetic properties. Network of vertex sharing tetrahedra causes geometric frustration of magnetism in LiMn2O4. In these kind of materials, the magnetic ground state has a large number of degeneracy since the moments at the vertexes of a tetrahedron cannot have a definite spin structure. In the case of cubic spinels, however, magnetic exchange interactions between neighboring atoms have the ability to break the degeneracy of the ground state manifold. Depending on the balance between the exchange pathways, the system can have a unique magnetic ground state.28 Previous literature holds conflicting reports about the magnetic properties of LiMn2O4 at low temperatures. Massarotti et al.54 reported existence of long-range magnetic order below 65 K while Oohara et al.55 reported only short-range correlations down to 8 K via neutron diffraction studies. In our LiMn2O4, although we did not observe any anomalies in our magnetic measurements showing antiferromagnetic correlations, we observed a resistivity anomaly below 100 K which is discussed in the following section.The magnetic properties of LiMn2O4 are very sensitive to Li content in the structure. Excess Li ions replace with the Mn ions in the lattice and can cause changes in the electronic and magnetic properties.50,52,56,57 Y. Shimakawa et al. reported that the cell parameters (from 8.24 Å to 8.21 Å for Li content of 1 to 1.1), Curie–Weiss constant (from 2.44 to 2.12 for per Mn) and the Mn3+/Mn4+ ratio (average Mn valance from +3.5 to 3.78) decrease with excess Li.58,59 Neutron scattering measurements60 show that excess Li suppresses the Jahn–Teller distortion down to 4 K increasing the stability of the cubic spinel structure. Boron substitution is another reason for decrease in Mn3+/Mn4+ ratio since the Mn3+ ions are substituted with B3+ ions. In this case, eg electrons of the Mn3+ ions are the main reasons for the Jahn–Teller distortion. Any decrease in the number of Mn3+ ions is expected to suppress such structural instability.
The χ–T (magnetic susceptibility vs. temperature) curves of LiBxMn2−xO4 for x = 0, 0.25, 0.5, 0.75 and 1 under 50 kOe (Fig. 2) show that the room temperature χ values decreases with increasing B content. Both excess Li and B substitution in our samples may suppress Jahn–Teller distortion and increase the structural stability with decreasing number of Mn3+ ions.61,62
On the other hand, below 50 K, magnetic susceptibility of x = 1 sample is higher than that of x = 0.75 sample. This is attributed to the increased amount of impurity phases as the boron content increases. XRD data in Fig. 1 shows that intensity of the Mn2(BO3)2 impurity for x = 1 sample is higher than that of x = 0.75 sample. Thus, increase in the magnetic susceptibility of x = 1 sample below 50 K can be related with Mn2(BO3)2 impurity phase.
In order to quantitatively understand the change of the susceptibility due to B substitution in LiMn2O4, one can concentrate on the Curie–Weiss form of the susceptibility as;
 | (1) |
Therefore, only the linear part of the χ−1–T curves are taken into account for Curie–Weiss fittings as (Fig. 3);
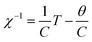 | (2) |
 | ||
| Fig. 3 χ−1–T data for LiBxMn2−xO4 where x = 0, 0.25, 0.5, 0.75 and 1. The solid blue lines indicate the Curie–Weiss fitting. | ||
The fitting parameters are listed in Table 2. The C and θ values for LiMn2O4 are determined as 4.518 emu K mol−1 and −253 K, respectively, in good agreement with the literature.64–66 The negative θ value shows that the antiferromagnetic interactions are dominant in LiMn2O4.
| x | C | χ | μeff from χ–T | μeff from eqn (4)a | z in eqn (4) | Mean valence of Mn ions | Chemical formula of compounds extracted from eqn (4) |
|---|---|---|---|---|---|---|---|
| a Using equal number Mn3+ and Mn4+ for HS of Mn3+ and HS of Mn4+. | |||||||
| 0 | 4.518 | −253 | 6.03665 | 6.16541 | 0.41081 | 3.589 | Li1.05Mn3+0.8Mn4+1.15O4 |
| 0.25 | 4.424 | −277 | 5.97358 | 5.75664 | 0.66572 | 3.334 | Li1.05Mn3+1.13Mn4+0.57B3+0.25O4 |
| 0.5 | 3.698 | −247 | 5.46173 | 5.31653 | 0.61948 | 3.379 | Li1.05Mn3+0.9Mn4+0.55 B3+0.5O4 |
| 0.75 | 3.182 | −273 | 5.06631 | 4.83654 | 0.70991 | 3.292 | Li1.05Mn3+0.85Mn4+0.35B3+0.75O4 |
| 1.00 | 2.486 | −251 | 4.64451 | 4.30334 | 0.85574 | 3.147 | Li1.05Mn3+0.81Mn4+0.14 B3+1.0O4 |
Our Curie Weiss parameters for LiMn2O4 are consistent with the Curie Weiss parameters of Li1.05Mn1.95O4 reported in the literature.61–63 In the paramagnetic region of χ–T data, the Curie constant can be written as;
 | (3) |
| μeff2 = (2 − y)[zμeff2(Mn3+) + (1 − z)μeff2(Mn4+)] | (4) |
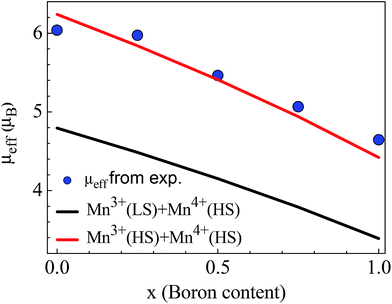 | ||
| Fig. 4 Boron content dependence of μeff. The green and black lines indicate the theoretical μeff values determined by eqn (4) for Mn3+(HS), Mn4+(HS) and Mn3+(LS), Mn4+(HS), respectively. The solid circles represent the experimental μeff values extracted from χ−1–T data using Curie–Weiss law. | ||
Using eqn (4), we theoretically calculated the μeff value depending on the number of Mn3+ and Mn4+ ions with different spin states, shown in Fig. 4. The theoretical values for HS state of Mn3+ ions match well with the experimental values indicating that the HS state is more probable than the LS state for Mn3+ ions.
Schimel et al. reported via inelastic neutron scattering measurements that Mn3+ ions are in low spin state in Li [Mn1.94Li0.04]O3.94.68 However, they also admitted that small compositional differences may affect the spin state of Mn and occurrence of Jahn–Teller distortions due to their dynamic nature.68
We calculated the theoretical effective magnetic moment of the pure LiMn2O4 as μeff = 6.16 μB for the whole sample assuming that the number of Mn3+ and Mn4+ are equal. We also extracted the experimental effective magnetic moment from the χ–T curve as = 6.04 μB for the whole sample which is slightly lower than the theoretical one. Experimental μeff values decrease with increasing boron content as seen in Fig. 4 and Table 2. Average valence state and the mole fractions of Mn ions are also listed in Table 2. Average valance state of Mn ions decrease with increasing boron content, consistent with the results obtained by J. H. Lee et al.48 We have determined the Mn3+/Mn4+ ratio in Li1.05Mn1.95O4 as 0.76 (=∼0.8/∼1.15). From the Curie–Weiss fitting of susceptibility, μeff is found as 3.015 μB/Mn ion which is a slightly smaller value than the one obtained from eqn (4).
All these small differences between the theoretical and experimental values can be due to the replacement of the Mn3+ ions with excess Li and B and/or the spin–orbit coupling. It is well known that Mn3+ for a d4 configuration of transition metals, the high spin state is f32ge1g in an octahedral environment. In the absence of the octahedral field, the configuration of the four d- electrons of the Mn3+ ion in the incomplete 3d shell is 5D ground term. A weak crystal field causes this term to split into two states that 5D term splits into the orbital doublet 5Eg as the ground sub-term and excited orbital triplet 5T2g.69 The Jahn–Teller distortion of Mn3+ in a weak field has 5Eg, the ground state which has an imbalance in the filling electrons in orbitals. As a result, a significant distortion from the octahedral symmetry takes place.
Normally, the 5Eg ground state is paramagnetic from four unpaired electrons with μspin-only = 4.9 μB. However, the spin-only magnetic moment is not always observed. Although the ground state has no orbital contribution, the excited electronic states with same spin multiplicity can be mixed with the ground state. This may be the case for high spin state of Mn3+ ions and the effective magnetic moment will deviate from the spin-only formula value causing small discrepancies between theoretical and experimental results.70
Electrical transport properties
LiMn2O4 has almost equal number of Mn3+ and Mn4+ ions and they order below 285 K with a Verwey transition.28 The crystal field splits the d-electrons of Mn ions as t2g and eg configurations. The eg levels of Mn3+ and Mn4+ in the lattice have one and zero electrons, respectively. The eg electrons in Mn3+ does not go to the neighboring Mn4+ sites causing insulating type conductivity.71 The resistivity value of our LiMn2O4 at room temperature is determined as 5 kohm cm which is consistent with the above explanation. Room temperature resistivity values of LiMn2−xBxO4 increases with increasing B content as shown in Fig. 5. Here, B3+ ions replace the Mn3+ ions and atomic energy levels of B and Mn are significantly different from each other causing such increase in room temperature resistivity values. The conduction mechanism of LiMn2O4 depends on the hoping electrons between Mn ions with different valance states.72,73 The overlapping of the wave functions due to the Mn–Mn distances can affect the conduction mechanism of the samples as explained in ref. 74. The distance of Mn–Mn atoms is given74 as where a is the lattice constant of LiMn2O4. While the distance is lower than 2.743 Å, the sample shows metallic conductivity, otherwise it exhibits non-conducting behavior.75 The calculated values of Mn–Mn distances, listed in Table 3, increase with increasing B content which is consistent with the resistivity data. Yuan et al. reported a separation of ZFC (zero field cooling) and FC (field cooling) curves at 65 K in the magnetization data since spin–spin correlations are effective above 65 K and the structural transition was observed at around 100 K.33 M. Kopec et al. reported the Neel temperature of LiMn2O4 as 65 K which is related to the onset of a completed charge ordering.50 Neutron diffraction studies on LiMn2O4 show short range correlations above 100 K.28 All these antiferromagnetic correlations are expected to appear as a resistivity anomaly below 100 K.50 Fig. 6 shows the temperature dependent resistivity data for pure LiMn2O4. The sample has semiconducting type conductivity down to 97.8 K and then the resistivity gives a small deep at 66.5 K before starting to increase with decreasing temperature.
where a is the lattice constant of LiMn2O4. While the distance is lower than 2.743 Å, the sample shows metallic conductivity, otherwise it exhibits non-conducting behavior.75 The calculated values of Mn–Mn distances, listed in Table 3, increase with increasing B content which is consistent with the resistivity data. Yuan et al. reported a separation of ZFC (zero field cooling) and FC (field cooling) curves at 65 K in the magnetization data since spin–spin correlations are effective above 65 K and the structural transition was observed at around 100 K.33 M. Kopec et al. reported the Neel temperature of LiMn2O4 as 65 K which is related to the onset of a completed charge ordering.50 Neutron diffraction studies on LiMn2O4 show short range correlations above 100 K.28 All these antiferromagnetic correlations are expected to appear as a resistivity anomaly below 100 K.50 Fig. 6 shows the temperature dependent resistivity data for pure LiMn2O4. The sample has semiconducting type conductivity down to 97.8 K and then the resistivity gives a small deep at 66.5 K before starting to increase with decreasing temperature.
| x (content) | Anodic peaks | Cathodic peaks | ΔE1 (V) | ΔE2 (V) | ||
|---|---|---|---|---|---|---|
| P1 (V) | P2 (V) | P1 (V) | P2 (V) | |||
| 0 | 4.11 | 4.24 | 3.88 | 4.00 | 0.23 | 0.24 |
| 0.125 | 4.06 | 4.19 | 3.90 | 4.07 | 0.16 | 0.12 |
| 0.25 | 4.12 | 4.28 | 3.84 | 4.01 | 0.28 | 0.27 |
| 0.375 | 4.06 | 4.19 | 3.90 | 4.05 | 0.16 | 0.14 |
| 0.5 | 4.06 | 4.22 | 3.91 | 4.05 | 0.15 | 0.17 |
The differential change of magnetization with temperature has two critical points as shown in the Fig. 6. The first deviation point from linearity in the dM/dT is related to start of the antiferromagnetic correlations and the second point is 65.2 K which corresponds to the resistivity minimum on ρ–T curve. It is possible that this resistivity anomaly region corresponds to the transition from short-range correlations to long range antiferromagnetic ordering.76,77 These results will be confirmed by ongoing neutron scattering studies.
Electrochemical properties
The electrochemical properties of the B doped LiMn2O4 are investigated systematically. The cycling voltammograms, in the potential region of 3.5–4.5 V at the sweep rate of 0.2 mV s−1, of the electrodes fabricated by different boron content are given in Fig. 7. There are two redox current peaks at 4.11/3.88 and 4.24/4.01 V for LiMn2O4 electrode. The two peak structure in voltammogram is attributed to the intercalation reaction of lithium ions occupying 8a sites in the LiMn2O4.36,78–80 The first peak in the voltammogram corresponds to the removal of Li-ions from the tetrahedral sites where Li–Li interactions are dominant and the second peak corresponds to the removal of lithium ions again from the tetrahedral sites but where Li–Li interactions are insignificant.4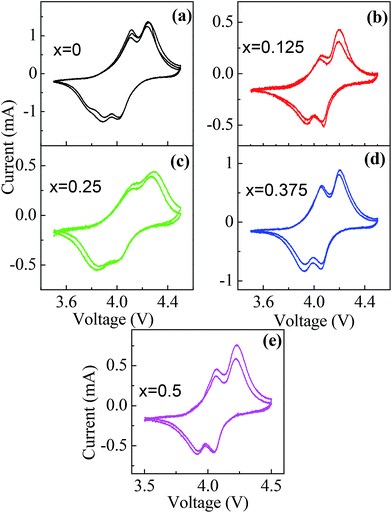 | ||
| Fig. 7 Cyclic voltammograms of (a) x = 0, (b) x = 0.125, (c) x = 0.250, (d) x = 0.375 and (e) x = 0.5 samples for first 3 cycles. | ||
The reactions during the charge and discharge of electrodes can be expressed as LiMn2O4 ↔ Li0.5Mn2O4 ↔ λ-MnO2.81 It is expected that the potential differences between anodic and cathodic current should be as low as possible due to the reversible process of electrodes.
The obtained differences in the voltammogram are within these limits. The peak positions of the LiMn2−xBxO4 cathodes for various B contents (Table 3) are almost identical. As mentioned above, substitution of Jahn–Teller active Mn3+ ions with B3+ ions suppresses the Jahn–Teller distortion and makes the structure more stable during charge–discharge cycles. Almost identical peak positions of cathodes with various B contents (Fig. 7) confirm this structural stability upon B substitution.
Fig. 8 shows the charge–discharge curves of the batteries with LiMn2−xBxO4 cathodes for various B content up to 100 cycles. The battery cells are activated until 4.2 V and then they are cycled between 3.0 and 4.2 V. There are two plateaus during the charge (at 4 V and 4.14 V) and discharge (at 4.1 V and 3.8 V) processes. The first plateau is due to the extraction of Li ions from half of tetrahedral site with Li–Li interaction and the second is due to the extraction of the other part of Li ions in the charging curve. The discharge process is the inverse of the charging process as explained in ref. 82. The numbers of Mn4+ and Mn3+ ions are important parameters for high cell capacity. If the number of Mn4+ ions is more than that of the Mn3+, lattice parameters may become smaller due to ionic radii of Mn ions. As a result of smaller lattice parameters Mn–O bonds get stronger while Li–O interactions weaken.83 Thus, the number of Li ions contributing the charge and discharge process increase.49,82 On the other hand, Mn3+ ions are Jahn–Teller active and they can cause the lattice parameters to expand and the capacity to fade. Yamada et al. reported that the Jahn–Teller instability due to Mn3+ ions can be reduced by 2–3% substitution of Mn ions by other elements.80 In this study, the highest number of Mn3+ ions are obtained in x = 0.25 sample (Table 2) which gives the lowest initial cell capacity.
 | ||
| Fig. 8 Charge–discharge profiles of (a) x = 0, (b) x = 0.125, (c) x = 0.250, (d) x = 0.375 and (e) x = 0.5 samples. | ||
The cycling performance of the cells fabricated with LiMn2−xBxO4 cathodes up to 100 cycles are shown in Fig. 9. Although B substitution decreases the maximal capacity of the cells with increasing boron content, LiMn1.875B0.125O4 (6.25% substitution) shows higher cycling performance after 60 cycles than that of the pure LiMn2O4 (Table 4).
| x (content) | 1 cycle (mA h g−1) | 25 cycle (mA h g−1) | 50 cycle (mA h g−1) | 75 cycle (mA h g−1) | 100 cycle (mA h g−1) |
|---|---|---|---|---|---|
| 0 | 122.23558 | 103.96484 | 96.33511 | 82.30601 | 77.36307 |
| 0.125 | 122.22481 | 103.4814 | 95.48102 | 91.42203 | 87.36305 |
| 0.25 | 94.56857 | 85.57071 | 79.99714 | 79.96071 | 78.32143 |
| 0.375 | 105.4476 | 73.7613 | 75.7044 | 66.7233 | 68.3451 |
| 0.5 | 98.4555 | 40.88696 | 31.92052 | 30.84455 | 30.48589 |
Electrochemical performance of LiMn2O4 spinel is highly affected by Jahn–Teller distortion.79 Although Mn3+ ions are in HS configuration which induces this distortion, replacing these Jahn–Teller active ions with non-magnetic B3+ ions helps suppressing the Jahn–Teller effect and enhances the electrochemical performance. Especially x = 0.125 sample has a higher capacity retention (71% for 100 cycle) than the x = 0 sample (63% for 100 cycle) showing that 6.25% B substitution makes LiMn2O4 structurally more stable. We attribute this result to a fine balance of the interatomic distances and the Mn3+/Mn4+ ratio upon substitution. As explained in the above sections B3+ ions with small ionic radius (27 pm) replace with the Mn3+ ions and some of them may go into the 8a tetrahedral Li sites. Average valance of Mn ions change with increasing B content.
Thus, B3+ substitution affects the magnetic and structural properties and especially 6.25% substitution is a promising cathode for Li-ion batteries. Initial capacities of x = 0.15, 0.375 and 0.5 samples are significantly lower than that of the x = 0 and 0.125 samples. Moreover, there are no detectable impurity phases in the XRD data (Fig. 1) of these samples. This result supports that some of the B3+ ions are placed in the 8a Li sites and decrease the number of electrochemically active Li+ ions and the initial capacities. Further investigations are ongoing to determine the structural, magnetic and electrochemical properties of x < 0.125 samples with finer intervals of x.
Conclusions
The structural, magnetic and electrical properties of LiMn2−xBxO4, 0 ≤ x ≤ 1 are studied in detail. The structural studies show that there are no impurity phases in x ≥ 0.5 samples. Unit cell parameters increase with increasing boron content, indicating that some of the boron ions are located in 8a tetrahedral sites instead of 16d octahedral sites. The observed anomaly in the temperature dependent resistivity data is attributed to the transition from short range correlations to long range antiferromagnetic ordering. The μeff values of the samples are determined from the linear part of the χ−1–T curves. The amount of Mn3+ ions, which are in the HS state and Jahn–Teller active mode, decreases with increasing B content. Such decrease is expected to suppresses the Jahn–Teller distortion and make the structure more stable during electrochemical cycling. Electrochemical measurements give promising results for x = 0.125 sample in terms of the capacity retention which is important for the improvement of the Li-ion battery technology. Significantly low initial cell capacities of the samples with high B content (x = 0.25, 0.375 and 0.5) confirms that some of the B3+ ions are placed in the Li sites.Acknowledgements
This study was supported by TUBITAK (The Scientific and Technical Research Council of Turkey) under grant no. TUBITAK 112M487 and IUBAP (Inonu University Scientific Research council)-2014/02.References
- C. Wei, J. Shen, J. Zhang, H. Zhang and C. Zhu, RSC Adv., 2014, 4, 44525 RSC.
- B.-S. Liu, Z.-B. Wang, Y. Zhang, F.-D. Yu, Y. Xue, K. Ke and F.-F. Li, J. Alloys Compd., 2015, 622, 902 CrossRef CAS.
- D.-L. Fang, J.-C. Li, X. Liu, P.-F. Huang, T.-R. Xu, M.-C. Qian and C.-H. Zheng, J. Alloys Compd., 2015, 640, 82 CrossRef CAS.
- G. Xu, Z. Liu, C. Zhang, G. Cui and L. Chen, J. Mater. Chem. A, 2015, 3, 4092 CAS.
- H. Huang, C. A. Vincent and P. G. Bruce, J. Electrochem. Soc., 1999, 146, 481 CrossRef CAS.
- M. M. Thackeray, Y. Shao-Horn, A. J. Kahaian, K. D. Kepler, E. Skinner, J. T. Vaughey and S. A. Hackney, Electrochem. Solid-State Lett., 1998, 1, 7 CrossRef CAS.
- J. M. Zheng, J. Li, Z. R. Zhang, X. J. Guo and Y. Yang, Solid State Ionics, 2008, 179, 794 CrossRef.
- X. Liu, J. Wang, J. Zhang and S. Yang, Mater. Sci. Eng., A, 2006, 430, 248 CrossRef.
- J. Cabana, L. Monconduit, D. Larcher and M. R. Palacín, Adv. Mater., 2010, 22, E170 CrossRef CAS PubMed.
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359 CrossRef CAS PubMed.
- M. G. Kim and J. Cho, Adv. Funct. Mater., 2009, 19, 1497 CrossRef CAS.
- Q. Liu, S. Wang, H. Tan, Z. Yang and J. Zeng, Energies, 2013, 6, 1718 CrossRef CAS.
- D. Zhan, Y. Liang, P. Cui and Z. Xiao, RSC Adv., 2015, 5, 6372 RSC.
- C.-G. Han, C. Zhu, G. Saito and T. Akiyama, RSC Adv., 2015, 5, 73315 RSC.
- A. Iturrondobeitia, A. Goñi, L. Lezama, C. Kim, M. Doeff, J. Cabana and T. Rojo, J. Mater. Chem. A, 2013, 1, 10857–10862 CAS.
- H. W. Chan, J. G. Duh and S. R. Sheen, Surf. Coat. Technol., 2004, 188, 116 CrossRef.
- P. Singh, A. Sil, M. Nath and S. Ray, Ceram.-Silik., 2010, 54, 38 CAS.
- F. A. Amaral, N. Bocchi, R. F. Brocenschi, S. R. Biaggio and R. C. Rocha-Filho, J. Power Sources, 2010, 195, 3293 CrossRef CAS.
- D. Q. Liu, X. Q. Liu and Z. Z. He, Mater. Chem. Phys., 2007, 105, 362 CrossRef CAS.
- Z. D. Peng, Q. L. Jiang, K. Du, W. G. Wang, G. R. Hu and Y. X. Liu, J. Alloys Compd., 2010, 493, 640 CrossRef CAS.
- Y. Ein Eli, R. C. Urian, W. Wen and S. Mukerjee, Electrochim. Acta, 2005, 50, 1931 CrossRef CAS.
- Y. Xu, G. Chen, E. Fu, M. Zhou, M. Dunwell, L. Fei, S. Deng, P. Andersen, Y. Wang, Q. Jiad and H. Luo, RSC Adv., 2013, 3, 18441 RSC.
- H. L. Wang, T. A. Tan, P. Yang, M. O. Lai and L. Lui, J. Phys. Chem., 2011, 115, 6102 CrossRef CAS PubMed.
- D. Q. Liu, Z. Z. He and X. Q. Liu, J. Alloys Compd., 2007, 440, 69 CrossRef CAS.
- H. Zhang, Y. Xu and D. Liu, RSC Adv., 2015, 5, 11091 RSC.
- H. A. Jahn and E. Teller, Proc. R. Soc. London, Ser. A, 1937, 161, 220 CrossRef CAS.
- D. G. Fauteux, A. Massucco, J. Shi and C. Lampe-Önnerud, J. Appl. Electrochem., 1997, 27, 543 CrossRef CAS.
- A. S. Wills, N. P. Raju and J. E. Greedan, Chem. Mater., 1999, 11, 1510 CrossRef CAS.
- M. Bianchini, F. Fauth, E. Suard, J.-B. Leriche, C. Masquelier and L. Croguennec, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 688 CAS.
- P. Umek, A. Gloter, M. Pregelj, R. Dominko, M. Jagodič and Z. Jagličić, J. Phys. Chem. C, 2009, 113, 14798 CAS.
- S. K. Ranjan and M. S. Sundar, Solid State Sci., 2003, 5, 549 CrossRef CAS.
- J. A. Alonso, M. J. Martinez-Lope and M. T. Casais, Inorg. Chem., 2000, 39, 917 CrossRef CAS PubMed.
- Y. F. Yuan, H. M. Wu, S. Y. Guo, J. B. Wu, J. L. Yang, X. L. Wang and J. P. Tu, Appl. Surf. Sci., 2008, 255, 2225 CrossRef CAS.
- D. H. Jang, Y. J. Shin and S. M. Oh, J. Electrochem. Soc., 1996, 143, 2204 CrossRef CAS.
- Y. Xia, N. Kumada and M. Yoshio, J. Power Sources, 2000, 90, 135 CrossRef CAS.
- L. Guohua, H. Ikuta, T. Uchida and M. Wakihara, J. Electrochem. Soc., 1996, 143, 178 CrossRef.
- C. Y. Ouyang, S. Q. Shi and M. S. Lei, J. Alloys Compd., 2009, 474, 370 CrossRef CAS.
- D. Capsoni, M. Bini, G. Chiodelli, V. Massarotti, C. B. Azzoni, M. C. Mozzati and A. Comin, Phys. Chem. Chem. Phys., 2001, 3, 2162 RSC.
- J. Marzec, K. Świerczek, J. Przewoźnik, J. Molenda, D. R. Simon, E. M. Kelder and J. Schoonman, Solid State Ionics, 2002, 146, 225 CrossRef CAS.
- K. Hoang, J. Mater. Chem. A, 2014, 2, 18271 CAS.
- E. Iguchi, Y. Tokuda, H. Nakatsugawa and F. Munakata, J. Appl. Phys., 2002, 91, 2149 CrossRef CAS.
- M. V. Reddy, S. S. Manoharan, J. John, B. Singh, G. V. Subba Rao and B. V. R. Chowdari, J. Electrochem. Soc., 2009, 156, A652 CrossRef CAS.
- D. K. Lee, S. C. Han, D. Ahn, S. P. Singh, K.-S. Sohn and M. Pyo, ACS Appl. Mater. Interfaces, 2012, 4, 6842 CAS.
- D. Capsoni, M. Bini, G. Chiodelli, P. Mustarelli, V. Massarotti, C. B. Azzoni, M. C. Mozzati and L. Linati, J. Phys. Chem. B, 2002, 106, 7432 CrossRef CAS.
- H. Şahan, H. Göktepe, Ş. Patat and A. Ülgen, Solid State Ionics, 2008, 178, 1837 CrossRef.
- S. H. Choi, J. H. Kim, Y. N. Ko and Y. C. Kang, Int. J. Electrochem. Sci., 2013, 8, 1146 CAS.
- R. Thirunakaran, K.-T. Kim, Y.-M. Kang and J.-Y. Lee, Ionics, 2004, 10, 188 CrossRef CAS.
- J. H. Lee, J. K. Hong, D. H. Jang, Y.-K. Sun and S. M. Oh, J. Power Sources, 2000, 89, 7 CrossRef CAS.
- Z. Chang, Z. Chen, F. Wu, H. Tang, X. Z. Yuan and H. Wang, Electrochem. Solid-State Lett., 2008, 11, A229 CrossRef CAS.
- M. Kopec, J. R. Dygas, F. Krok, A. Mauger, F. Gendron and C. M. Julien, J. Phys. Chem. Solids, 2008, 69, 955 CrossRef CAS.
- A. Veluchamy, H. Ikuta and M. Wakihara, Solid State Ionics, 2001, 143, 161 CrossRef CAS.
- C. Masquelier, M. Tabuchi, K. Ado, R. Kanno, Y. Kobayashi, Y. Maki, O. Nakamura and J. B. Goodenough, J. Solid State Chem., 1996, 123, 255 CrossRef CAS.
- B. Ebin, G. Lindbergh and S. Gürmen, J. Alloys Compd., 2015, 620, 399 CrossRef CAS.
- V. Massarotti, D. Capsoni, M. Bini, P. Scardi, M. Leoni, V. Baron and H. Berg, J. Appl. Crystallogr., 1999, 32, 1186 CrossRef CAS.
- Y. Oohara, J. Sugiyama and M. Kontani, J. Phys. Soc. Jpn., 1999, 68, 242 CrossRef CAS.
- K. Yamaura, Q. Huang, L. Zhang, K. Takada, Y. Baba, T. Nagai, Y. Matsui, K. Kosuda and E. Takayama-Muromachi, J. Am. Chem. Soc., 2006, 128, 9448 CrossRef CAS PubMed.
- C. M. Julien, A. Ait-Salah, A. Mauger and F. Gendron, Ionics, 2006, 12, 21 CrossRef CAS.
- Y. Shimakawa, T. Numata and J. Tabuchi, J. Solid State Chem., 1997, 131, 138 CrossRef CAS.
- J. M. Tarascon, E. Wang, F. K. Shokoohi, W. R. McKinnon and S. Colson, J. Electrochem. Soc., 1991, 138, 2859 CrossRef CAS.
- H. G. Schimmel, W. Montfrooij, G. J. Kearley, V. W. J. Verhoeven and I. M. de Schepper, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 214409 CrossRef.
- J. Sugiyama, T. Atsumi, A. Koiwai, T. Sasaki, T. Hioki, S. Noda and N. Kamegashira, J. Phys.: Condens. Matter, 1999, 9, 1729 CrossRef.
- R. Englman and B. Halperin, Phys. Rev. B: Solid State, 1970, 2, 75 CrossRef.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
- Y.-I. Jang, F. C. Chou, B. Huang, D. R. Sadoway and Y.-M. Chiang, J. Phys. Chem. Solids, 2003, 64, 2525 CrossRef CAS.
- M. Tabuchi, C. Masquelier, H. Kobayashi, R. Kanno, Y. Kobayashi, T. Akai, Y. Maki, H. Kageyama and O. Nakamura, J. Power Sources, 1997, 68, 623 CrossRef CAS.
- K. Mukai and J. Sugiyama, Chem. Lett., 2009, 38, 944 CrossRef CAS.
- T. Eriksson, A. M. Andersson, A. G. Bishop, C. Gejke, T. Gustafsson and J. O. Thomas, J. Electrochem. Soc., 2002, 149, A69 CrossRef CAS.
- D. Wu, G. L. Liu, C. Jing, Y. Z. Wu, D. Loison, G. S. Dong, X. F. Jin and D.-S. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 214403 CrossRef.
- R. J. Radwanski and Z. Ropka, J. Magn. Magn. Mater., 2004, 272, e259 CrossRef.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Magnets, Oxford University press, Newyork, 2006 Search PubMed.
- M. Park, X. Zhang, M. Chung, G. B. Less and A. M. Sastry, J. Power Sources, 2010, 195, 7904 CrossRef CAS.
- J. M. Amarilla, K. Petrov, F. Pico, G. Avdeev, J. M. Rojo and R. M. Rojas, J. Power Sources, 2009, 191, 591 CrossRef CAS.
- K. Tateishi, D. du Boulay and N. T. Ishizawa, Appl. Phys. Lett., 2004, 84, 529 CrossRef CAS.
- J. Guan and M. Liu, Solid State Ionics, 1998, 110, 21 CrossRef CAS.
- J. Blasco, J. García, J. M. de Teresa, M. R. Ibarra, P. A. Algarabel and C. Marquina, J. Phys.: Condens. Matter, 1996, 8, 7427 CrossRef CAS.
- J. Cho, J. Mater. Chem., 2008, 18, 2257 RSC.
- R. Basu and R. Seshadri, J. Mater. Chem., 2000, 10, 507 RSC.
- S. Chitra, P. Kalyani, T. Mohan, R. Gangadharan, B. Yebka, S. Castro-Garcia, M. Massot, C. Julien and M. Eddrief, J. Electroceram., 1999, 3, 433 CrossRef CAS.
- Y. Xia, Y. Zhou and M. Yoshio, J. Electrochem. Soc., 1997, 144, 2593 CrossRef CAS.
- J. Yamada, Solid State Chem., 1996, 122, 160 CrossRef.
- B. Ammundsen, G. R. Burns, M. S. Islam, H. Kanoh and J. Rozière, J. Phys. Chem. B, 1999, 103, 5175 CrossRef CAS.
- S. Chen, C. Mi, L. Su, B. Gao, Q. Fu, X. Zhang, M. Zhao, L. Yao and T.-Y. Zhang, J. Appl. Electrochem., 2009, 39, 1943 CrossRef CAS.
- B. Ying, W. Chuan, W. Feng and W. Guo-qing, Nonferrous Met., 2006, 16, 402 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra05032h |
| This journal is © The Royal Society of Chemistry 2016 |





