Mg2Sn: a potential mid-temperature thermoelectric material
Abstract
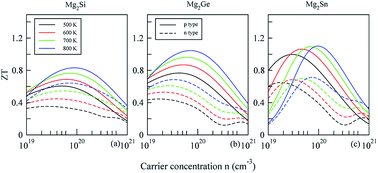
The electronic structure and the thermoelectric properties of Mg2X (X = Si, Ge, and Sn) were studied using the density functional theory and the semi-classical Boltzmann transport theory. The three compounds of Mg2X (X = Si, Ge, and Sn) were found to be indirect band-gap semiconductors with gap magnitudes of 0.66, 0.63, and 0.29 eV, respectively. By studying the carrier concentration dependence of the transport properties, we find that the p-type Mg2X exhibit superior thermoelectric performance originating from a large density-of-states effective mass due to the large valley degeneracy of valence bands. In particular, a maximum ZT value of 1.1 for p-type Mg2Sn can be achieved at 800 K with a carrier concentration of 9.8 × 1019 cm−3, which is higher than that of Mg2Si (0.8) and Mg2Ge (1.0). The high ZT of Mg2Sn is mainly attributed to its low lattice thermal conductivity that is a consequence of the low velocity of the optical modes caused by the large mass density. These findings suggest that Mg2Sn is a promising mid-temperature thermoelectric material.

 Please wait while we load your content...
Please wait while we load your content...