Molecular dynamics simulation of the structural, elastic, and thermal properties of pyrochlores
Liyuan Donga,
Yuhong Li*a,
Ram Devanathanb and
Fei Gao*c
aSchool of Nuclear Science and Technology, Lanzhou University, Lanzhou, Gansu 730000, China. E-mail: liyuhong@lzu.edu.cn
bEnergy and Environment Directorate, Pacific Northwest National Laboratory, Richland, WA 99352, USA
cDepartment of Nuclear Engineering & Radiological Sciences, University of Michigan, Ann Arbor, MI 48109, USA. E-mail: gaofeium@umich.edu
First published on 20th April 2016
Abstract
We present a comprehensive simulation study of the effect of composition on the structural, elastic and thermal properties of 25 different compounds from the pyrochlore family. We joined a repulsive potential to an existing interatomic potential to enable molecular dynamics simulations of conditions away from equilibrium. We systematically varied the chemistry of the pyrochlore by substituting different cations in the A and B sites of the A2B2O7 formula unit. The A cations varied from Lu3+ to La3+, and the B cations from Ti4+ to Ce4+. The lattice parameter increased steadily with increasing the radius of A or B cations, but the bulk modulus showed a decreasing trend with increasing cation radius. However, the specific heat capacity and thermal expansion coefficient remained almost unchanged with increasing the radii of A and B cations. It is of interest to note that Ce on the B site significantly reduces the specific heat capacity and thermal expansion coefficient, which could have implications for annealing of radiation damage in cerate pyrochlores. The present results are consistent with the experimental measurements, which suggests that these potentials are appropriate for studying the problem of interest, namely simulation of dynamical processes, radiation damage, and defect migration in pyrochlores.
1. Introduction
Pyrochlore, with a general formula of A2B2O7 (A3+ = Lu3+, Yb3+, Er3+, Y3+, Gd3+, Eu3+, Sm3+, Nd3+, Ce3+, La3+; B4+ = Ti4+, Ru4+, Mo4+, Sn4+, Zr4+, Pb4+, Ce4+), has been proposed as a durable waste form for the immobilization of high-level nuclear waste.1–4 These oxygen-deficient fluorite structural derivative compounds exhibit fast ion transport, radiation tolerance, and structural stability, which makes this family of compounds well-suited for accommodating plutonium (239Pu) from nuclear weapons.1–4 The high thermal expansion coefficient and low thermal conductivity of pyrochlores makes them suitable as thermal barrier coatings.5,6 In view of these attractive properties, it is essential to understand the effect of cation chemistry on the structural, mechanical and physical properties of pyrochlores, such as bulk modulus, specific heat capacity, and thermal expansion coefficient.In the current study, we employed classical molecular dynamics (MD) simulations to determine important thermal and physical properties in a series of rare-earth pyrochlores. MD simulation has been widely used to characterize the structural, mechanical and physical properties of metals, ceramics and glasses.7–12 It can be applied to not only predict experimental observations, but also to guide the design of the experimental process.
Previously, several experimental and theoretical studies have explored the fundamental atomic level mechanisms that make pyrochlore a promising wasteform for nuclear waste immobilization. In particular, Sickafus et al.1,13 suggested that A and B ionic radii can affect the order–disorder (O–D) transformation, amorphization resistance and radiation tolerance. They showed that the formation energy of an antisite defect is accompanied by a high energy cost in compounds containing large A cations and comparatively smaller B cations, while the compounds with similar radii exhibit the greatest susceptibility to lattice destabilization (and possible amorphization). Minervini et al.12 revealed that the choice of A site and B site cation can affect the disorder and defect formation energy in pyrochlores, and disorder increases with increasing B cation radius and with decreasing A cation radius. Wang et al.14 observed that the radiation resistance improves with increasing Zr content in a series of compounds with composition Gd2(Ti1−xZrx)2O7. Wilde15 and Catlow16 investigated the dependence of conductivity on the A and B cations. Devanathan et al.11 showed that cation choice can affect the radiation tolerance of pyrochlores, and the ease of cation disorder increases and the volume swelling of the damage core decreases with increasing Zr content. Fan et al.17 showed that the thermal expansion coefficients depend on cation radii. They suggested that the B-site doping is more effective than A-site doping for developing a new thermal barrier material with a higher thermal expansion coefficient.
Although previous studies have shed light on the structural and physical properties of pyrochlores, systematic studies of the variation of structural, mechanical, thermal and physical properties with composition in a series of rare-earth pyrochlores are needed. The key knowledge gap is the effect of cation radius on properties, such as lattice parameter, cohesive energies, bulk modulus, thermal expansion coefficient, and specific heat capacity. This paper address this need by using classical MD simulation to calculate the lattice parameter, cohesive energy, bulk modulus, specific heat capacity at constant volume and constant pressure, and thermal expansion coefficient, and to determine the effects of the cation radius on these properties.
2. Simulation details
2.1 Crystal structure
The pyrochlore crystal structure is based on the fluorite structure. The ideal fluorite structure is cubic (space group is 225, Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with the general formula of AO2 (A4+ = Zr4+, Ce4+, Hf4+, Th4+, U4+, Pu4+). It has two independent crystal positions: the A site at the 4a (0, 0, 0) position is occupied by a cation with a formal charge of +4e, while the B site at the 4b (0.5, 0.5, 0.5) position is occupied by an anion with a formal charge of −2e. Here, e is the magnitude of the electron charge. Fig. 1a shows the ideal fluorite structure. Similar to the fluorite structure, pyrochlore also has the cubic crystal structure (space group 227, Fd
m) with the general formula of AO2 (A4+ = Zr4+, Ce4+, Hf4+, Th4+, U4+, Pu4+). It has two independent crystal positions: the A site at the 4a (0, 0, 0) position is occupied by a cation with a formal charge of +4e, while the B site at the 4b (0.5, 0.5, 0.5) position is occupied by an anion with a formal charge of −2e. Here, e is the magnitude of the electron charge. Fig. 1a shows the ideal fluorite structure. Similar to the fluorite structure, pyrochlore also has the cubic crystal structure (space group 227, Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), with half of these cations replaced by cations with charge of +3e. Oxygen structural vacancies have to be introduced to achieve charge balance. The general formula of a pyrochlore is A2B2O7 (A3+ = Lu3+, Yb3+, Er3+, Y3+, Gd3+, Eu3+, Sm3+, Nd3+, Ce3+, La3+; B4+ = Ti4+, Ru4+, Mo4+, Sn4+, Zr4+, Pb4+, Ce4+ for the present study). Atoms occupy 4 special positions: A3+ cation at 16d (0.5, 0.5, 0.5), B4+ cation at 16c (0, 0, 0), O2− at 48f (x, 0.125, 0.125) and 8b (0.375, 0.375, 0.375). 8a is the oxygen vacancy site. Each unit cell contains 88 ions, including 16A cations, 16B cations and 56 oxygen anions. The perfect pyrochlore structure can be seen in Fig. 1b.
m), with half of these cations replaced by cations with charge of +3e. Oxygen structural vacancies have to be introduced to achieve charge balance. The general formula of a pyrochlore is A2B2O7 (A3+ = Lu3+, Yb3+, Er3+, Y3+, Gd3+, Eu3+, Sm3+, Nd3+, Ce3+, La3+; B4+ = Ti4+, Ru4+, Mo4+, Sn4+, Zr4+, Pb4+, Ce4+ for the present study). Atoms occupy 4 special positions: A3+ cation at 16d (0.5, 0.5, 0.5), B4+ cation at 16c (0, 0, 0), O2− at 48f (x, 0.125, 0.125) and 8b (0.375, 0.375, 0.375). 8a is the oxygen vacancy site. Each unit cell contains 88 ions, including 16A cations, 16B cations and 56 oxygen anions. The perfect pyrochlore structure can be seen in Fig. 1b.
 | ||
| Fig. 1 Crystal structure: of (a) fluorite and (b) pyrochlore, where yellow, blue and red spheres represent the A, B and O, respectively in the AO2 or A2B2O7 formula unit. | ||
2.2 Interatomic potentials
Previous MD simulations of pyrochlore have mainly used short-range Buckingham and long-range Coulomb potentials.18–20 In the present study, we used similar potential functions with the potential parameters given by Minervini et al.12,21 (see the details below). In order to avoid unrealistic attraction between close ion pairs due to the dominance of the dispersion term at very short distances, we used a spline function to connect the Buckingham pair potential to the Ziegler–Biersack–Littmark (ZBL) repulsive potential.22 The spline function has an exponential form as shown below. This modification of the short range potential enables the use of these potentials to study radiation damage and other high-energy dynamic processes. The pair potential form used in this work is given by:
 | (1) |
| Φ(x) = 0.1818e−3.2x + 0.5099e−0.9423x + 0.2802e−0.4029x + 0.02817e−0.2016x, | (2) |
 | (3) |
The parameters A, ρ, and C of the Buckingham potential have been fitted by Minervini et al.12,21 These potentials are transferable over a wide composition range and thus enable the study of the effect of pyrochlore chemistry on properties of interest. Table 1 lists all the parameters for these interatomic potentials.
| A (eV) | ρ (Å) | C (eV Å6) | P1 (eV) | P2 (eV Å−1) | P3 (eV Å−2) | P4 (eV Å−3) | r1 (Å) | r2 (Å) | |
|---|---|---|---|---|---|---|---|---|---|
| Lu3+–O2− | 1618.80 | 0.33849 | 19.27 | 10.0119 | −7.15593 | 1.91572 | −0.214047 | 0.8 | 1.5 |
| Yb3+–O2− | 1649.80 | 0.3386 | 16.57 | 10.4029 | −8.38232 | 3.08766 | −0.555607 | 0.6 | 1.5 |
| Er3+–O2− | 1739.91 | 0.3389 | 17.55 | 10.7888 | −9.62575 | 4.30523 | −0.912113 | 0.8 | 1.5 |
| Y3+–O2− | 1766.40 | 0.33849 | 19.43 | 12.6212 | −17.2211 | 12.5197 | −3.58205 | 0.75 | 1.25 |
| Gd3+–O2− | 1885.75 | 0.3399 | 20.34 | 11.5878 | −12.2057 | 6.80753 | −1.64416 | 0.8 | 1.4 |
| Eu3+–O2− | 1925.71 | 0.3403 | 20.59 | 11.7605 | −12.7613 | 7.33435 | −1.79137 | 0.8 | 1.5 |
| Sm3+–O2− | 1944.44 | 0.3414 | 21.49 | 10.7741 | −10.1831 | 5.23363 | −1.23787 | 0.6 | 1.5 |
| Nd3+–O2− | 1995.20 | 0.3430 | 22.59 | 10.8570 | −10.6026 | 5.73341 | −1.39560 | 0.6 | 1.5 |
| La3+–O2− | 2088.79 | 0.3460 | 23.25 | 10.8324 | −10.8029 | 6.13654 | −1.54184 | 0.5 | 1.5 |
| Ce3+–O2− | 1731.62 | 0.364 | 14.43 | 10.8546 | −10.8314 | 6.14749 | −1.52581 | 0.6 | 1.5 |
| Ti4+–O2− | 2131.04 | 0.3038 | 0.0 | 10.6245 | −14.8008 | 14.7894 | −6.28961 | 0.3 | 0.85 |
| Ru4+–O2− | 1215.78 | 0.3441 | 0.0 | 10.1949 | −9.03509 | 4.04960 | −0.891829 | 0.8 | 1.5 |
| Mo4+–O2− | 1223.97 | 0.3470 | 0.0 | 10.9623 | −11.3557 | 6.13531 | −1.47438 | 0.8 | 1.5 |
| Sn4+–O2− | 1414.32 | 0.3479 | 13.66 | 10.3575 | −9.24810 | 4.22309 | −0.921421 | 0.6 | 1.5 |
| Zr4+–O2− | 1502.11 | 0.3477 | 5.1 | 11.7658 | −14.6926 | 10.1837 | −2.88129 | 0.7 | 1.3 |
| Pb4+–O2− | 1640.34 | 0.3507 | 19.5 | 10.5929 | −8.61311 | 3.26215 | −5.82430 | 0.6 | 1.5 |
| Ce4+–O2− | 1809.68 | 0.3547 | 20.40 | 10.9148 | −10.9211 | 6.09939 | −1.49782 | 0.6 | 1.5 |
| O2−–O2− | 9547.96 | 0.2192 | 32.00 | 9.35520 | −10.7135 | 6.23226 | −1.68139 | 0.8 | 2.1 |
2.3 MD simulation method
We used the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) code23 to perform classical MD simulation of a series of pyrochlores with different A and B cations. We used periodic boundary conditions with a simulation cell composed of 8 (2 × 2 × 2) unit cells containing 704 atoms for all simulations associated with structural and physical properties. The cutoff radius for Coulomb and Buckingham potentials was 10 Å. We used energy minimization to determine the lattice parameter and cohesive energy for each pyrochlore. At first, we relaxed all the atoms in the system at 0 K through energy minimization using the conjugate gradient (CG) algorithm. The stopping tolerances for energy and force were 1 × 10−4 eV and 1 × 10−6 eV per angstrom, respectively. The maximum iterations for minimization were 10, and the maximum number of force/energy evaluations was 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. We used the Ewald k-space method24 for the long-range columbic interaction, with an accuracy of 1.0 × 10−5. The lattice parameter varied from 9 Å to 13 Å, with an increment of Δa0 = ±0.1 Å.
000. We used the Ewald k-space method24 for the long-range columbic interaction, with an accuracy of 1.0 × 10−5. The lattice parameter varied from 9 Å to 13 Å, with an increment of Δa0 = ±0.1 Å.
The bulk modulus (B0) is one of important elastic properties of material, and represents the resistance to compressibility. We followed common practice25 to determine the bulk modulus for a cubic structure as:
 | (4) |
 | (5) |
Specific heat capacity is one of the important thermal properties for the material,26 which can be determined by
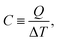 | (6) |
Therefore, the specific heat capacity at constant volume (CV) is given by:
 | (7) |
 | (8) |
We used Ewald summation,24 with a cutoff radius of 10 Å and tolerance of 1.0 × 10−8, to calculate the specific heat capacity. We calculated the isobaric specific heat capacities CP with the NPT ensemble and volumetric specific heat capacities CV with the NVT ensemble. We initially thermalized the system at 200 K for 1 ps, and then heated it to 2000 K with a time step of 0.5 fs for 120000 time steps (60 ps) to obtain the E–T scatter graph from the MD simulation. The E–T curve was fit using first-order polynomial fitting (also called linear fit) with the least squares method, which gave the slope of the E–T line (dE/dT). Thus, the isobaric specific heat capacity CP and volumetric specific heat capacity CV can be determined by eqn (7) and (8), respectively.
The thermal expansion coefficient (TEC) is another important thermal property of the material. In recent years, pyrochlore has been proposed as a next generation candidate material for thermal barrier coatings due to its high thermal expansion coefficient (TEC) and low thermal conductivity.6 It is necessary to better understand the thermal expansion of various pyrochlores. The thermal expansion coefficient27 describes the volumetric and lattice parameter expansion with increasing temperature. Linear TEC and volumetric TEC are given by
 | (9) |
 | (10) |
| αV = 3αL, | (11) |
We carried out the calculation of TEC by the following two steps. Initially, we thermalized the system at 200 K with the NVT ensemble for 1 ps (run 2000 time steps), and then used the NPT ensemble to heat the system to 2000 K with an increment of 100 K. We equilibrated the system for 3 ps at each temperature, and the total simulation time was about 60 ps. From the V–T curve obtained by the simulations, the V–T function and its slope (dV/dT) can be determined through the linear fitting with the least-square method. Thus, volumetric thermal expansion coefficient can be calculated by eqn (10) and eqn (11), respectively. Similarly, the a–T curve can be obtained by using the equation of  , and the linear thermal expansion coefficient can be calculated by eqn (9).
, and the linear thermal expansion coefficient can be calculated by eqn (9).
3. Results and discussion
3.1 Equilibrium lattice parameter and cohesive energy
The total energy of a system can be determined as a function of lattice parameter using molecular static calculations, and the results for Gd2Zr2O7 are shown in Fig. 2. Red stars represent the E–a points calculated from MD simulation, and blue line stands for the fitting line using a polynomial function with the least-squares fitting method. The total energy of the system changes significantly with increasing lattice parameter and has a minimum value. The MATLAB program28 was used to determine the value of minimum energy by solving the first derivative equation dE/da = 0. The minimum value represents the cohesive energy of the system, and the corresponding lattice parameter is the equilibrium lattice parameter. We applied this method to other pyrochlores, and the results are summarized in Fig. 3 showing the lattice parameter as a function of cation radii. The cation size refers to Shannon radii29 and corresponds to 8-coordinate B cation and 6-coordinate A cation. The change of lattice parameter with increasing A cation size in the A2Zr2O7 and A2Ti2O7 (A3+ = Lu3+, Yb3+, Er3+, Y3+, Gd3+, Eu3+, Sm3+, Nd3+, Ce3+, La3+) is shown in Fig. 3a. It is of interest to note that the lattice parameter increases almost linearly with increasing A cation size, and the lattice parameter of zirconate pyrochlore is much larger than that of the titanate pyrochlore, which may be due to the larger ion size of the Zr4+ as compared to that of the Ti4+. Brixner30 measured the lattice parameters of titanate pyrochlores using X-ray diffraction (XRD), while Minervini et al.12 used atomistic computer simulations to predict the lattice parameters for both titanate and zirconate pyrochlores. These results are superimposed in Fig. 3a for comparison, and our results are in excellent agreement with the previous studies. The lattice parameter of Ce2Zr2O7 is slightly overestimated as compared with the experimental measurement of Surble et al.,31 but the difference is only about 1.7%. The reason may be due to the Buckingham potential parameters21,32 for Ce3+–O2− interaction, which is good for calculating the surface energy and ionic conductivity, but not for lattice parameter. | ||
| Fig. 3 Variation of lattice parameter with (a) A cation radius and (b) the B cation radius. (Experimenta after Surble31 and Subramanian,33 predictionb after Minervini,12 experimentc after Brixner,30 experimentd after Subramanian,33 experimente after Subramanian.33) | ||
The variation of lattice parameter with the different B cations in the Sm2B2O7 and Gd2B2O7 (B4+ = Ti4+, Ru4+, Mo4+, Sn4+, Zr4+, Pb4+, Ce4+) is shown in Fig. 3b. The lattice parameter increases almost linearly with the size of B cations, but the slope is much larger than that for A cations, which suggests that the influence of B cations on lattice parameter is more significant than that of A cations. The trend of increasing lattice parameter is almost the same for Gd2B2O7 and Sm2B2O7. The difference between Gd2B2O7 and Sm2B2O7 is quite small for the same B cation, which is because the radii of Gd3+ and Sm3+ are very close to each other. Again, our results are in excellent agreement with the experimental measurements and Minervini et al.'s calculations.12,33
3.2 Bulk modulus
We used the E–a graph in Fig. 2 to determine the bulk modulus, and the MATLAB program28 to obtain the second derivative of the system energy, d2E/da2, at the equilibrium lattice parameter, and then calculated the bulk modulus by eqn (4). Alternatively, the bulk modulus can be computed by fitting the Birch–Murnaghan (B–M) equation of state in eqn (5).34,35 Fig. 4 is a plot of the bulk modulus as a function of cation radius in a series of pyrochlores. Fig. 4a shows the variation of the bulk modulus with increasing radius of A cations for the A2Zr2O7 and A2Ti2O7 (A3+ = Lu3+, Yb3+, Er3+, Y3+, Gd3+, Eu3+, Sm3+, Nd3+, Ce3+, La3+) pyrochlores. The bulk modulus of titanate pyrochlores is generally larger than that of zirconate pyrochlores for the same A cation. The bulk modulus slightly decreases with increasing A cationic radius, with small fluctuations. Comparison of the results obtained by the polynomial function and B–M equation fitting suggests that the B–M equation fitting yields lower values than the polynomial function fitting, and is closer to the experimental results. The B–M equation may provide more accurate results than polynomial function. It is well known the B–M equation is based on Eulerian strain, and thus can be applied to determine the compressibility and elastic properties of cubic crystals, but the polynomial fit is a simpler approximation.34,35 In addition, previous studies have demonstrated that using the B–M equation is an excellent approach to fit the experimental data, and most experimentalists have used the B–M equation to determine their bulk modulus.36–39 | ||
| Fig. 4 Bulk modulus varies with cation radii: (a) A cations in A2Ti2O7 and A2Zr2O7 pyrochlores, and (b) B cations in Gd2B2O7 and Sm2B2O7 pyrochlores. | ||
Fig. 4b shows the variation of the bulk modulus with different radii of B cations in the Sm2B2O7 and Gd2B2O7 (B4+ = Ti4+, Ru4+, Mo4+, Sn4+, Zr4+, Pb4+, Ce4+). In contrast to the case of A cations, the bulk modulus decreases more rapidly with increasing B cation radius. The influence of B cations on the bulk modulus is more significant than that of A cations. This is in good agreement with ab initio calculations,40 which suggested that the effect of B cation is more important than that of A cation. Thus, the B cation can be selected, based on its radius, to achieve the desired bulk modulus in pyrochlores.
A detailed comparison between our results and DFT predictions40–44 as well as available experimental data45–48 is listed in Table 2. It can be seen that our calculated results are generally in good agreement with experimental measurements (noted Exp. 2),48 but are slightly overestimated compared to some DFT predictions41 and the results of Exp. 1 (ref. 45–47). This deviation from experimental data may be due to the fact that the experimental sample inevitably has defects, such as voids, cracks, line defects and grain boundaries.45,49 Also, it should be noted the values presented in Table 2 were obtained at T = 0 K, and temperature effects generally reduce the values of elastic constants.40 The experimental values were measured at room temperature.
| Material | B0 (GPa) | B–M fit (GPa) | DFT (GPa) | Exp. 1 (GPa) | Exp. 2 (GPa) |
|---|---|---|---|---|---|
| Y2Zr2O7 | 222.7759 | 215.79 | 225 (ref. 40) | 225 (ref. 45) | |
| Gd2Zr2O7 | 214.0659 | 202.38 | 165 (ref. 41) | 186 (ref. 45) | 205 (ref. 48) |
| Eu2Zr2O7 | 218.9443 | 201.405 | 149 (ref. 41) | ||
| Sm2Zr2O7 | 217.6662 | 200.176 | 197 (ref. 41) | 231 (ref. 48) | |
| Nd2Zr2O7 | 215.5551 | 198.06 | 127 (ref. 41) | 167 (ref. 46) | 219 (ref. 48) |
| Ce2Zr2O7 | 200.0141 | 189.125 | 214 (ref. 45) | ||
| La2Zr2O7 | 211.4111 | 194.33 | 200 (ref. 40) | 171 (ref. 47) | |
| Lu2Ti2O7 | 295.936 | 297.31 | 191.9 (ref. 43) | ||
| Er2Ti2O7 | 291.818 | 286.524 | 191 (ref. 43) | ||
| Y2Ti2O7 | 297.3775 | 279.401 | 229 (ref. 40) | ||
| Gd2Ti2O7 | 286.6858 | 281.45 | 186.9 (ref. 43) | ||
| Sm2Ti2O7 | 283.3667 | 268.8 | 185 (ref. 44) | ||
| La2Ti2O7 | 273.1637 | 254.203 | 211 (ref. 40) |
3.3 Specific heat capacity at constant volume or pressure
The derivative of the total energy with respect to temperature, at constant pressure, gives the isobaric specific heat capacity CP. Data from a sample of Gd2Zr2O7 is shown in Fig. 5, from which it can be seen that the total energy increases linearly with increasing temperature. We used linear fitting with the least-squares method to obtain the E–T function, and then calculated its slope (dE/dT). The isobaric specific heat capacity, CP, can be calculated by eqn (8). Similarly, the volumetric specific heat capacity, CV, can be obtained by eqn (7).Fig. 6 shows the specific heat capacity at constant volume (CV) and pressure (CP) in a series of pyrochlores as a function of cation radius. Fig. 6a indicates CV and CP variation with increasing A cation size in A2Zr2O7 and A2Ti2O7 (A3+ = Lu3+, Er3+, Y3+, Gd3+, Eu3+, Sm3+, Ce3+, La3+) pyrochlores. The specific heat capacity for these pyrochlores remains almost constant, which implies that the atomic size of A cations affects specific heat capacity only slightly, except for Er2Ti2O7. The exact reason for this unusual behavior of Er2Ti2O7 is unclear, but this may be, again, associated with the atomistic potentials used in the current simulations. However, we have observed that the total energy in Er2Ti2O7 does not increase linearly, which may cause the unusual behavior observed, and it is also likely that Er in A site of titanate pyrochlores may affect some of the thermal properties, which needs to be further confirmed by using different interatomic potentials.
 | ||
| Fig. 6 Variation of specific heat capacity with the cation radii of (a) A cation in A2Zr2O7 and A2Ti2O7, and (b) B cation in Gd2B2O7 and Sm2B2O7. | ||
Fig. 6b shows the variation of CP and CV with the different radii of B cations in Sm2B2O7 and Gd2B2O7 (B4+ = Ti4+, Ru4+, Mo4+, Sn4+, Zr4+, Pb4+, Ce4+). Similar to the case of A cations, both CV and CP are slightly affected by the B cationic radii, except for Ce. However, the result suggests that Ce has a significant effect on the specific heat capacity in pyrochlores, which may alter their thermal properties, which could influence defect production by radiation damage and subsequent defect annealing.
To the best of our knowledge, no experimental data are available for comparison in most pyrochlores studied in this work. Table 3 summarizes the specific heat capacity in several pyrochlores, along with available experiment data50–52 for comparison. Bolech et al.51 determined the specific heat capacity of La2Zr2O7 and Ce2Zr2O7 in the temperatures from 298.15–1000 K and Sedmidubsky et al.50 measured the specific heat capacity of Nd2Zr2O7 and La2Zr2O7 in the temperatures from 298–1550 K. Based on these data, it is clearly that our simulation results are in excellent agreement with the experimental values of the specific heat capacity in these pyrochlores.
| Materials | CV (J K−1 mol−1) | CP (J K−1 mol−1) | Exp. CP (J K−1 mol−1) |
|---|---|---|---|
| La2Zr2O7 | 273.8859 | 278.8043 | 223.05–290.2 (ref. 50 and 51) |
| Nd2Zr2O7 | 273.5623 | 279.8894 | 235.32–323.08 (ref. 50) |
| Ce2Zr2O7 | 272.8640 | 278.7681 | 233.74–316.00 (ref. 51) |
| Gd2Zr2O7 | 273.1741 | 279.6561 | 277–279 (ref. 52) |
3.4 Thermal expansion coefficient
The volume change as a function of temperature can be determined using the MD method with constant pressure condition, and an example of the volume expansion in Y2Zr2O7 is shown in Fig. 7. The volume increases with the increasing temperature. Although there exist some fluctuations in the volume, the data can be well described by a linear relationship. We used linear fitting with the least-squares method to compute the derivative with respect to temperature (dV/dT), and then determined the thermal expansion coefficients (TECs) by eqn (9) and (10).Thermal expansion coefficients are shown on Fig. 8a for A2Zr2O7 and A2Ti2O7 pyrochlores (A3+ = Lu3+, Er3+, Y3+, Gd3+, Eu3+, Sm3+, Nd3+, Ce3+, La3+). The TECs remain almost the same with increasing A cation radius, and the effect of the choice of A cations on the thermal expansion coefficients is small. The thermal expansion coefficients of zirconate pyrochlores are generally larger than those of titanate pyrochlores for the same A cation. Fig. 8b shows the variation of the TECs with different B cation radii in the Sm2B2O7 and Gd2B2O7 (B4+ = Ti4+, Ru4+, Mo4+, Sn4+, Zr4+, Pb4+, Ce4+) pyrochlores. The TECs of this series of pyrochlores are almost unchanged except for titanate and cerate pyrochlores that show much lower TECs as compared with other pyrochlores. Overall, the choice of B cation has little effect on the TEC.
 | ||
| Fig. 8 Variation of thermal expansion coefficient with the cation radii of (a) A cation in A2Zr2O7 and A2Ti2O7, and (b) B cation in Gd2B2O7 and Sm2B2O7. | ||
Table 4 summarizes the calculated TECs in A2Zr2O7 pyrochlores, along with the available experiment results53–57 and other calculations by Fan et al.17 for comparison. Our calculated values are smaller than the experiment results, but comparable to Fan's results. As discussed by Fan, the reasons for the difference may be due to the existing defects in the real crystals, such as voids and cracks, which may weaken the bond and lead to higher TECs. However, the trends of TECs are the same as the experimental results. Note that our results are slightly lower than Fan's results, which may be due to the different potentials used in our calculations.
| Name | αL (×10−6 K−1) | Exp. (×10−6 K−1) | Other calc. (×10−6 K−1) |
|---|---|---|---|
| Lu2Zr2O7 | 6.0306 | 8.57 (ref. 17) | |
| Er2Zr2O7 | 6.1555 | 8.00 (ref. 17) | |
| Y2Zr2O7 | 6.20 | ||
| Gd2Zr2O7 | 6.1168 | 11.6 (ref. 53) | 7.91 (ref. 17) |
| Eu2Zr2O7 | 6.0005 | 7.81 (ref. 17) | |
| Sm2Zr2O7 | 5.9146 | 10.8 (ref. 54) | 7.77 (ref. 17) |
| Nd2Zr2O7 | 5.7985 | 9.50 (ref. 55) | 7.80 (ref. 17) |
| Ce2Zr2O7 | 5.6034 | 8.42 (ref. 56) | |
| La2Zr2O7 | 5.769 | 9.1 (ref. 57) | 7.82 (ref. 17) |
4. Conclusions
We examined the effect of chemistry on the physical properties of a large number of pyrochlores by modifying pair potentials for the A2B2O7 pyrochlore system to connect the Buckingham potential to short-range ZBL potentials. This modification yields a simple model to simulate thermal and mechanical properties in a series of pyrochlores. We determined the lattice parameter, bulk modulus, specific heat capacity and thermal expansion coefficient in a number of pyrochlores as a function of A and B cation radii by means of molecular dynamic simulations. This study fills key gaps in current understanding of these systematic relations. Our findings are as follows:(i) Lattice parameter increases dramatically with increasing A and B cation radii, but the influence of B cations on the lattice parameter is much larger than that of A cations.
(ii) Bulk modulus slightly decreases with increasing A cation radii, but rapidly decreases with increasing B cation radii. Similarly, the influence of B cations on bulk modulus is much larger than that of A cations.
(iii) Volumetric and isobaric specific heat capacities remain almost the same with increasing A and B cation radii. However, Ce in the B site significantly decreases both the volumetric and isobaric specific heat capacities.
(iv) The influence of A and B cation radii on thermal expansion coefficient is small, but, Ce in the B site also leads to an apparent decrease in the thermal expansion coefficient.
(v) It is of interest to note that Ce on the B site can influence most properties of A2B2O7 pyrochlores, including specific heat capacities and thermal expansion. Therefore, immobilized Ce or other actinides in pyrochlore ceramics may lead to the dramatic changes of these properties, which could affect their resistance to radiation damage.
Compared with the experimental results and DFT calculations, the current results, including structural, physical and thermal properties, show consistent trends, which indicate that these interatomic potentials can be further employed to simulate defect production in a large family of pyrochlores.
Acknowledgements
LY Dong wants to thank China Scholarship Council for supporting her study at the Pacific Northwest National Laboratory and University of Michigan. This work was partially supported by the National Natural Science Foundation of China (No. 11475076 and 11175076). F. Gao is supported by the award NRC-HQ-13-G-38-0007 from the US Nuclear Regulatory Commission. The statements, findings, conclusions, and recommendations are those of the authors and do not necessarily reflect the view of the US Nuclear Regulatory Commission.References
- K. E. Sickafus, L. Minervini, R. W. Grimes, J. A. Valdez, M. Ishimaru, F. Li, K. J. McClellan and T. Hartmann, Science, 2000, 289, 748 CrossRef CAS PubMed.
- R. C. Ewing, W. J. Weber and L. H. Brixner, J. Appl. Phys., 2004, 95, 5949 CrossRef CAS.
- R. C. Ewing, W. J. Weber and F. W. Clinard, J. Mater. Res., 1995, 10, 63 CrossRef.
- W. J. Weber, W. R. Ewing, C. R. A. Catlow, T. Diaz de la Rubia, L. W. Hobbs, C. Kinoshita, H. j. Matzke, A. T. Motta, M. Nastasi, E. K. H. Salje, E. R. Vance and S. J. Zinkle, J. Mater. Res., 1998, 13, 1434 CrossRef CAS.
- X. Q. Cao, R. Vassen and D. Stoever, J. Eur. Ceram. Soc., 2004, 24, 1 CrossRef CAS.
- C. G. Levi, Curr. Opin. Solid State Mater. Sci., 2004, 8, 77 CrossRef CAS.
- M. Matsui and A. Masaki, Mol. Simul., 1991, 6, 239 CrossRef.
- C. A. J. Fisher and H. Matsubara, Comput. Mater. Sci., 1999, 14, 177 CrossRef CAS.
- P. K. Schelling, Comput. Mater. Sci., 2010, 48, 336 CrossRef CAS.
- P. Chakraborty, A. Moitra and T. S. Dasgupta, J. Nucl. Mater., 2015, 466, 172 CrossRef CAS.
- R. Devanathan, F. Gao and C. J. Sundgren, RSC Adv., 2013, 3, 2901 RSC.
- L. Minervini and R. W. Grimes, J. Am. Ceram. Soc., 2000, 83, 1873 CrossRef CAS.
- K. E. Sickafus, R. W. Grimes, J. A. Valdez, A. Cleave, M. Tang, M. Ishimaru, S. M. Corish, C. R. Stanek and B. P. Uberuaga, Nat. Mater., 2007, 6, 217 CrossRef CAS PubMed.
- S. X. Wang, B. D. Begg, L. M. Wang, R. C. Ewing, W. J. Weber and K. V. Kutty, J. Mater. Res., 1999, 14, 4470 CrossRef CAS.
- P. J. Wilde and C. R. A. Catlow, Solid State Ionics, 1998, 112, 173 CrossRef CAS.
- P. J. Wilde and C. R. A. Catlow, Solid State Ionics, 1998, 112, 185 CrossRef CAS.
- Q. B. Fan, F. Zhang, F. C. Wang and L. Wang, Comput. Mater. Sci., 2009, 46, 716 CrossRef CAS.
- S. Saha, D. V. S. Muthu, C. Pascanut, N. Dragoe, R. Suryanarayanan, G. Dhalenne and A. Revcolevschi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 064109 CrossRef.
- L. Minervini, R. W. Grimes, Y. Tabira, R. L. Withers and K. E. Sickafus, Philos. Mag. A, 2002, 82, 123–135 CAS.
- A. Chartier, C. Meis and J. P. Crocombette, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 174102 CrossRef.
- G. Balducci, J. Kašpar, P. Fornasiero and M. Graziani, J. Phys. Chem. B, 1998, 102, 557 CrossRef CAS.
- J. F. Ziegler, J. P. Biersack and U. Littmark, The stopping and range of ions in solids, Pergamon, New York, 1985 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577 CrossRef CAS.
- C. Kittel, Hyperphysics, ISBN 0-471-41526-X, 2005, p. 52 Search PubMed.
- D. Halliday and R. Resnick, Fundamentals of Physics, Wiley, 2013, p. 524 Search PubMed.
- P. A. Tipler and G. Mosca, Physics for Scientists and Engineers, Worth Publishers, New York, NY, 6th edn, ISBN 1-4292-0132-0, 2008, vol. 1, p. 666 Search PubMed.
- MATLAB and Statistics Toolbox Release, The MathWorks, Inc., Natick, Massachusetts, United States, 2015b Search PubMed.
- R. D. Shanon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751 CrossRef.
- L. H. Brixner, Preparation and properties of the Ln2Ti2O7-type rare earth titanate, Inorg. Chem., 1964, 3.7, 1065 CrossRef.
- S. Surble, S. Heathman, P. E. Raison, D. Bouexiere, K. Popa and R. Caciuffo, Phys. Chem. Miner., 2010, 37, 761 CrossRef CAS.
- T. Sayle, S. C. Parker and C. R. A. Catlow, Surf. Sci., 1994, 316, 329 CrossRef CAS.
- M. A. Subramanian, G. Aravamudan and G. V. S. Rao, Prog. Solid State Chem., 1983, 15, 55 CrossRef CAS.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244 CrossRef CAS.
- F. Birch, Phys. Rev., 1947, 71, 809 CrossRef CAS.
- O. T. Lord, A. R. Thomson, E. T. Wann, I. G. Wood, D. P. Dobson and L. Vocadlo, J. Appl. Crystallogr., 2015, 48, 1914 CAS.
- S. Desgreniers, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 14102 CrossRef CAS.
- L. Gerward, J. S. Olsen, L. Petit, G. Vaitheeswaran, V. Kanchana and A. Svane, J. Alloys Compd., 2005, 400, 56 CrossRef CAS.
- J. S. Olsen, L. Gerward, V. Kanchana and G. Vaitheeswaran, J. Alloys Compd., 2004, 381, 37 CrossRef CAS.
- J. M. Pruneda and E. Artacho, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085107 CrossRef.
- J. Feng, B. Xiao, C. L. Wan, Z. X. Qu, Z. C. Huang, J. C. Chen, R. Zhou and W. Pan, Acta Mater., 2014, 72, 263 CrossRef CAS.
- W. R. Panero, L. Stixrude and R. C. Ewing, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 054110 CrossRef.
- C. G. Liu, L. J. Chen, D. Y. Yang, J. Wen, L. Y. Dong and Y. H. Li, Comput. Mater. Sci., 2016, 114, 233 CrossRef CAS.
- B. Winkler, A. Friedrich, W. Morgenroth, E. Haussuhl, V. Milman, C. R. Stanek and K. J. McClellan, Chin. Sci. Bull., 2014, 59, 5278 CrossRef CAS.
- D. Errandonea, R. S. Kumar, S. N. Achary, O. Gomis and F. J. Manjón, J. Appl. Phys., 2012, 111, 053519 CrossRef.
- P. Shukla, T. Watanabe, J. C. Nino, J. S. Tulenko and S. R. Phillpot, J. Nucl. Mater., 2008, 380, 1 CrossRef CAS.
- C. L. Wan, W. Pan, Q. Xu, Y. X. Qin, J. D. Wang, Z. X. Qu and M. H. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 144109 CrossRef.
- M. P. van Dijk, K. J. de Vries and A. J. Burggraaf, Solid State Ionics, 1983, 9 & 10, 913 Search PubMed.
- F. X. Zhang, M. Lang and R. C. Ewing, Appl. Phys. Lett., 2015, 106, 191902 CrossRef.
- D. Sedmidubsky, O. Benes and R. J. M. Konings, J. Chem. Thermodyn., 2005, 37, 1098 CrossRef CAS.
- M. Bolech, E. H. P. Cordfunke, A. C. G. van Genderen, R. R. van der Lann, F. J. J. G. Janssen and J. C. van Miltenburg, J. Phys. Chem. Solids, 1997, 58, 433 CrossRef CAS.
- Z. Liu, J. Ouyang and Y. Zhou, Bull. Mater. Sci., 2009, 32, 603 CrossRef CAS.
- Y. S. Touloukian, R. K. Kirby, R. E. Taylor and T. Y. R. Lee, Thermal Expansion-Non Metallic Solids, IFI/Plenum, New York, 1977, vol. 13 Search PubMed.
- G. L. Catchen and T. M. Rearick, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 9890 CrossRef CAS.
- H. Lehmann, D. Pitzer and G. Prach, et al., J. Am. Ceram. Soc., 2003, 86, 1338–1344 CrossRef CAS.
- P. E. Raison, C. C. Pavel, R. Jardin, E. Suard, R. G. Haire and K. Popa, Phys. Chem. Miner., 2010, 37, 555 CrossRef CAS.
- R. Vassen, X. Q. Cao, F. Tietz, D. Basu and D. Stover, J. Am. Ceram. Soc., 2000, 83, 2023 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |



