New microsecond intramolecular reactions of human telomeric DNA in solution

Abstract

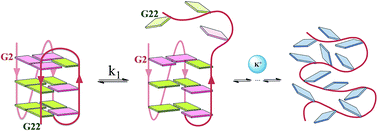
Careful T-jump relaxation kinetic experiments in the microsecond timescale conducted in dilute solutions of human telomeric DNA at pH = 7.5 and 25 °C, have evinced for the first time two different equilibria. The sets of data recorded concur with two G-quadruplex ↔ G-triplex equilibria coexisting in the presence of both Na⁺ and K⁺-buffer ions.

---

Nucleic acids with four-stranded architectures, also known as G-quadruplexes, are endowed with technological applications and potentially impact biological regulation mechanisms and define a new area of research.^1–3 The possibility of building different conformations from the same sequence is a complex issue that confers G-quadruplexes with very interesting physical chemistry features. On the other hand, the obtaining of reliable kinetic data constitutes quite an adequate tool to determine reaction mechanisms between conformations in equilibrium. However, despite the number of articles published on G-quadruplex structures and related properties, equilibrium studies on fast intramolecular rearrangement remain virtually unexplored, whereas kinetic studies on irreversible folding–unfolding in solution abound in the literature.^4–10 The steps involved in such processes display a variety of rates. The fastest folding of G-quadruplexes involving four-stranded structures evolve between 40 and 80 ms in K⁺ buffer,⁶ and between 20 and 60 ms in Na⁺ buffer, depending on the particular sequence.¹⁰ In this work, we report on faster reactions between different structures in equilibrium in these buffers, once the G-quadruplexes are formed at 25 °C and pH = 7.5.

Telomeres, the ends of eukaryotic chromosomes, play an important role in cellular senescence and are central to the chromosome stability.¹¹ The human telomere presents single stranded overhanging at the 3′ end, which consist of repeats of the TTAGGG sequence that can fold into intramolecular G-quadruplexes. Thus, the representative d(AGGG(TTAGGG)₃) sequence of the human telomeric DNA, also known as ‘Tel22’, has been used to conduct this study. The T-jump relaxation technique is ideally suited to observe reactions in equilibrium capable of evolving in milliseconds to microseconds, provided that the reaction enthalpy differs from zero. To the best of our knowledge, this type of study has not been reported hitherto.

The type of G-quadruplex folding is determined by the type of ions in the medium, K⁺ or Na⁺,^5,12,13 whereas the DNA concentration,¹⁴ the cosolvent used,¹⁵ or even the sequence inversion in G-rich DNA from 5′ → 3′ to 3′ → 5′,¹³ exert a substantial effect on the number of structures formed.

The circular dichroism (CD) spectra of Tel22 recorded in aqueous solution containing either 0.15 M NaCl or 0.15 M KCl (Fig. 1A) support G-quadruplex structures. In 0.15 M NaCl medium, the observed CD bands, positive at ∼295 nm and negative at ∼260 nm, reveal the presence of the basket-type G-quadruplex structure. Likewise, in 0.15 M KCl medium, the strong positive peak at ∼290 nm, with a weak shoulder at ∼250 nm, and the weak negative band at ∼235 nm, primarily denote mixed parallel/antiparallel hybrid-type G-quadruplex structure.¹⁶ Nevertheless, also is true that, despite these findings, different G-quadruplex polymorphic forms in solution should not be excluded, because the CD technique is useful to differentiate single conformations but not to distinguish between different polymorphisms of same conformation.¹⁷

Fig. 1 CD spectra of Tel22 G-quadruplexes formed in the presence of 0.15 M NaCl () and 0.15 M KCl (). C_P = 5 μM, pH = 7.5 (10 mM Tris–HCl, 1 mM EDTA) and T = 25 °C (A). G-Quartet structure stabilized by Hoogsteen H-bonding and a monovalent ion resided in the central channel (B).

Fig. 2 shows two examples of T-jump kinetic curves recorded at 25 °C and pH = 7.5 in 0.15 M NaCl and 0.15 M KCl solutions for two different Tel22 concentrations. The kinetic traces obtained in the presence of Na⁺ (Fig. 2A) and K⁺ (Fig. 2B) are very similar. The data treatment of equilibrium reactions monitored by T-jump relaxation measurements is compatible with exponential functions only, regardless of the number and concentration of reactants and products involved. Thus, the kinetic constants were obtained by fitting the biexponential kinetic eqn (1) to the relaxation curves:

where k₁ and k₂ are the kinetic constants (s⁻¹) that govern the two fast reactions.

Fig. 2 T-Jump millivolts (mV)–time (t) relaxation curves recorded for Tel22 G-quadruplex (P) at C_P concentration, (a) C_P = 5 μM and (b) C_P = 15 μM in the presence of (A) 0.15 M NaCl and (B) 0.15 M KCl. λ = 260 nm, pH = 7.5 (10 mM Tris–HCl, 1 mM EDTA), T = 25 °C, ΔT = 2.5 °C, rise time = 5 μs. Continuous red lines were obtained from biexponential fitting of eqn (1) to the data pairs.

The values obtained for k₁ and k₂ are independent of the Tel22 concentration (Fig. 3), revealing unimolecular mechanism in both Na⁺ and K⁺ buffering ions. Moreover, the average values for k₁ and k₂ were close to each other (Table 1), suggesting the occurrence of two concurrent reactions.

Fig. 3 k₁ (s⁻¹) () and k₂ (s⁻¹) () versus Tel22 concentration (C_P) plots in the presence of (A) 0.15 M NaCl and (B) 0.15 M KCl. pH = 7.5 (10 mM Tris–HCl, 1 mM EDTA) and T = 25 °C.

Table 1 Average rate constants, k₁ (s⁻¹) and k₂ (s⁻¹) and thermodynamic constant, K_F = [F1M]/[F2M] (M = Na⁺ or K⁺), obtained for the Tel22 G-quadruplex in 0.15 M NaCl and 0.15 M KCl, pH = 7.5 (10 mM Tris–HCl, 1 mM EDTA) and T = 25 °C

	10^−4 k1 (s^−1)	10^−4 k2 (s^−1)	KF
Tel22 (NaCl)	5.2 ± 0.1	4.92 ± 0.04	0.39 ± 0.02
Tel22 (KCl)	5.8 ± 0.2	5.4 ± 0.4	0.23 ± 0.02

---

At the same time, the difference in intensity and sign of the reaction amplitudes A₁ and A₂ (Fig. 2), reveal different spectroscopic or thermodynamic features and confirm that the two reactions involve different Tel22 structural forms in Na⁺ and K⁺ buffers. On the basis of these observations, the scheme proposed includes two folded G-quadruplex forms in both Na⁺ and K⁺ ions, hereinafter referred to as FiM in equilibrium with triplex forms (see below), denoted as Fi′M (i = 1, 2 and M = Na⁺ or K⁺) (Fig. 4).

Fig. 4 Representation of Tel22 G-quadruplex with two major folded conformations F1M and F2M (M representing K⁺ and Na⁺ ions), in equilibrium with the G-triplex structures F1′M and F2′M, respectively. Loops are coloured red; anti and syn guanines are coloured green and pink, respectively. The F1M ↔ F2M equilibria between G-quadruplexes occur through the random coil. Other long-live intermediates should not be ruled out.

In K⁺ solutions, the main conformation of human telomeric DNA is a G-quadruplex hybrid-type fold with (3 + 1) G-tetrad core containing three tetrads, one double-chain-reversal loop and two edgewise loops. Two structures containing this core with the same type and number of loops but differing by their loop arrangement have been identified. This feature reveals the existence of different hybrid G-quadruplex forms for Tel22 under physiological conditions (F1K and F2K, Fig. 4, left).¹⁸ In Na⁺ diluted solutions, the antiparallel basket-type structure was found for the Tel22 sequence (F1Na, Fig. 4, right).¹⁹ Although the basket form has been acknowledged openly as the only folded conformation, recent studies have provided convincing evidence for the polymorphism of telomeric sequences in Na⁺, with possible interconversion between various structural forms.²⁰ Noer et al., using single molecule FRET microscopy, have identified at least four different G-quadruplex states in Na⁺, an unfolded state and three G-quadruplex related states that can convert into each other.²¹ These states are dynamically populated with times around 10 s. It seems clear that these states do not correspond with those we have observed, because the difference in reaction rates is too large.

In this work, we provide kinetic evidence for at least four species (F1Na, F2Na, F1′Na and F2′Na) in equilibrium in solution of Na⁺, in a similar way as in the presence of K⁺ ions. Considering that the F1M ↔ F2M interconversion is rather slow,^7,22 we propose that k₁ and k₂ correspond to the much faster reactions , , and (microsecond time scale). Being monomolecular reactions in nature, k₁ and k₂ are the overall {forward (k_fi) + backward (k_di)} kinetic constants and therefore the equilibrium constants, K = k_fi/k_di, of the FiM ↔ Fi′M reactions cannot be determined.

Thus, the point is how to explain the similar rates of the FiM ↔ Fi′M equilibrium for different G-quadruplex structures in different buffer ions.

Hydrophobic interactions determine the fast reaction rates FiM ↔ Fi′M

To determine the type of interaction that governs the FiM ↔ Fi′M conversion, we can compare the main features of our reactions (microsecond time scale and buffer ion) with the processes involved in the formation of G-quartets (H-bonding and specific ionic interactions M⁺⋯O, see Fig. 1B) and of G-quadruplex structures (stacking of successive planes of four guanine residues arranged as a square planar G-quartet).

Regarding G-quartets, the rates of H-bonding formation and dissociation fall into picoseconds.²³ An important issue is that hydrogen bonds are weak enough so as to continuously dissociate and reform at room temperature. Some of the most significant biological processes, such as DNA replication and protein folding, are feasible due to the reversible nature of hydrogen-bond formation.²⁴ According to Eigen, coordination of Na⁺ and K⁺ ions to the O atoms, similar to G-quartets interactions, occurs in nanoseconds.^25,26 This outcome has enabled us to exclude H-bonding and M⁺⋯O interactions as the effects observed by T-jump.

As for G-quadruplexes, channel, loop and phosphates are main regions where the ion binding may occur. Ida and Wu have reported that the residence time of Na⁺ ions inside the channel of the antiparallel bimolecular G-quadruplex (G₄T₄G₄) is 20 ms, whereas the residence time of Na⁺ ions in the loop is 220 μs, the latter value being comparable with our results.²⁷ However, the slower mobility of K⁺ ions relative to Na⁺ ions²⁸ together with the difference in the loops of the Na⁺ and K⁺ conformations and the topologically more complex Na⁺-stabilized fold⁵ should yield different k₁ and k₂ constants in Na⁺ and K⁺ media, contrary to our observations. Actually, the kinetics and thermodynamics of formation of quadruplexes have been found cation-dependent.^5,12 Lastly, the electrostatic binding cation/DNA phosphate, which leads to a mobile cloud, yields rate constants close to diffusion-controlled.²⁹ In conclusion, according to literature data, none of the interactions that govern the formation of G-quartets or the release of ions from G-quadruplex described so far, evolve in the microsecond timescale and are independent of the type of ion, as occurs in our case.

Although the type of ion, Na⁺ or K⁺, affects the conformational equilibria of G-quadruplex (F1M ↔ F2M) and facilitates the FiM ↔ Fi′M equilibria due to the decrease in electrostatic repulsion, the monocation species is not involved in the rate-determining step and has no influence on the reaction rates. According to Record³⁰ and Kool,³¹ the observation that the k₁ and k₂ constants are the same order in Na⁺ and K⁺ solutions confirms that the hydrophobic effects are larger than other stabilizing stacking effects, such as electrostatic and dispersion effects. Therefore, we can conclude that hydrophobic stacking interactions are key to these reactions.

G-Triplex structures in equilibrium with G-quadruplexes

A particular type of reaction governed by hydrophobic interactions occurs in the microsecond time scale and can be studied by T-jump, namely, on-slot ↔ off-slot equilibrium reactions of intercalation (on) and dissociation (off) of an aromatic ligand between the DNA base-pairs.^32–34 These features have enabled us to establish parallelism between the observed mechanism of Tel22 in solution and the intercalation reaction. According to Fig. 4, three guanines linked to the terminal strand in the G-quadruplexes are prone to dissociate (off) and link (on) to the G-quartet by fast on-G ↔ off-G equilibria determined by stacking interactions between each guanine and the adjacent G-leaflets. These interactions are responsible for the k₁ and k₂ constants in the presence of K⁺ and Na⁺ ions. This type of reaction is common to all conformations and could justify the non-dependence of the reaction rate on both the conformation, structural form and type of buffer cation.

Hydrophobic stacking interactions can also be present in another type of intermediates, such as quadruplex dimers or hairpins. For dimerization, such reaction would be bimolecular, 2Fi ↔ (Fi)₂, and the rate constants k₁ and k₂ would depend on the oligonucleotide concentration, in contrast to our results.

Hairpin-like structures have been suggested as intermediates in folding processes from single-stranded guanine (G)-rich DNA.^18,29 Chang et al. have identified two Watson–Crick base-pairing topologies of hairpin structure as well as the Hoogsteen H-bonding patterns of the WT22 G4 structure induced by addition of K⁺ ions.²² The kinetics associated with the potassium ion-induced hairpin-to-G4 transition are very slow, and fall into the 4800 s time scale, the unfolding of the hairpin structure being the rate-determining step for formation of WT22 G4. Therefore, folding and unfolding of single-stranded guanine (G)-rich DNA to form hairpin structures in microseconds should be discarded.

On the other side, also Sponer et al. have simulated the theoretical interconversion between hairpins involved in folding of human telomeric sequence quadruplexes with sub-μs scale rearrangement between them.³⁵ We have excluded the reactions observed in this work to occur between hairpins in equilibrium, mainly because interconversion between hairpins implies rearrangement of H-bonding, whose lifetime is of some picoseconds.²³ Moreover, to be able to record appreciable T-jump kinetic traces, the absorbances of the reactant and the reaction product must differ appreciably at the particular wavelength used; we believe that the absorbance of the simulated hairpins will be very similar and therefore the amplitude of the kinetic traces would be negligible or even vanish.

Therefore, equilibria of G-quadruplex ↔ G-triplex type, such as those proposed in Fig. 4, could be consistent with the type of interaction and the experimental observations.

As reported in the Introduction section, the FiM G-quadruplex structures in K⁺ and Na⁺ buffers are supported by literature data.^17,18 Additionally, recent computational studies support the triplex structures proposed for Fi′M. Molecular dynamics calculations by Sugiyama et al. have suggested that, in potassium media, folded human telomeric F1K and F2K structures are formed through intermediate species.³⁶ Random coils may form to a first stage hairpins and triplexes, and afterwards the latter can form type-1 and type-2 G-quadruplex structures (similar to F1K and F2K). All of the intermediates would be in equilibrium in a way such that F1K and F2K can interconvert to each other only through the random coil form, which entails slow interconversion. The G-triplex structures suggested by these authors are similar to F1′K and F2′K (Fig. 4, left). That is, F1′K and F2′K could be intermediate species in the F1K ↔ F2K equilibria.

Moreover, Sponer et al., based on molecular dynamics simulations, have reported that several triplexes (such as F1′K) remain stable in the microsecond time scale.³⁷ Our experimental observations concur with this time scale and with the existence of short-lived intermediate G-triplex species, not only in the presence of K⁺ ions, but also in the presence of Na⁺ ions. This way, F1′Na and F2′Na would be intermediate G-triplexes also in the equilibrium F1Na ↔ F2Na (Fig. 4, right). Fig. 4 outlines schematically a parallel behaviour as a function of the type of salt employed with the different structural forms.

In addition to k₁ and k₂, the equilibrium constant between the folded conformations, K_F = [F2M]/[F1M], can also be assessed. Fig. 2 shows that, even though the amplitudes A₁ and A₂ vary with the Tel22 concentration, the A₂/A₁ ratio remains constant and is reproducible for each buffer and Tel22 concentration. Since the k₁ and k₂ constants are close to each other, the A₂/A₁ ratio provides at 25 °C the K_F values 0.23 and 0.39, respectively, for the equilibrium constants, F1K ↔ F2K in 0.15 M KCl and F1Na ↔ F2Na in 0.15 M NaCl (Table 1). Very close K_F values have been reported for interconversion between two stable folding conformations with similar sequence and under close conditions.⁴ Burrows et al. have demonstrated that in KCl solution the hybrid-1 dominates over hybrid-2 for the human telomeric sequence 5′-TAGGG(TTAGGG)₃TT-3′, being K_F = 0.45 at 37 °C, pH 7.9 in 50 mM KCl.³⁸ Likewise, these authors have suggested the formation of triplex structures.

Conclusions

The T-jump technique has allowed us to characterise kinetically and thermodynamically the processes that occur in dilute aqueous solutions of human telomeric DNA containing both Na⁺ and K⁺ ions in near physiological conditions. We have shown that this is a very complex system, in which at least four different forms, two G-quadruplexes and two G-triplexes, coexist in equilibrium in both Na⁺ and K⁺ buffers. The reaction is governed by hydrophobic guanine–guanine interactions, regardless of the type of buffering ion and Tel22 conformation.

Experimental

Sample preparation. Dried d[AGGG(TTAGGG)₃] DNA oligonucleotide, labeled “Tel22”, was purchased from Thermo Fisher Scientific Inc. Stock solutions were prepared with nuclease-free water in buffers containing 10 mM Tris–HCl, 1 mM EDTA at pH = 7.5 and 0.15 M of either NaCl or KCl. The formation of the G-quadruplex was carried out by heating oligonucleotide solutions up to 90 °C for 6 min and slowly cooling down to room temperature. The solutions were then incubated overnight at 4 °C. The concentration of the single stranded oligonucleotide was determined by measuring at 90 °C the absorbance at 260 nm using the absorptivity value 228 500 M⁻¹ cm⁻¹. To ensure the formation of the G-quadruplex from the d(AGGG(TTAGGG)₃) sequence and that the equilibrium between all of the possible species in solution was reached, the study of these processes was conducted after overnight incubation of the Tel22 sequence.

CD spectra were recorded on a MOS-450 spectrophotometer (Bio-Logic SAS, Claix, France) over the 220–340 nm range at 25 °C, using 1 cm path-length cells with black quartz sides to mask the light beam. The buffer baseline was collected and subtracted from the sample spectra.

Fast kinetic measurements were performed with a Dialog T-jump instrument built according to the Rigler et al. prototype, in 1.0 cm path-length cells, working in the absorbance mode.³⁹ The system is perturbed in microseconds with a sudden 20 kV discharge. The cell was thermostatted at 22.5 °C and, following the discharge, a sudden 2.5 °C increase in temperature occurs in 2.5 μs for [NaCl] = 0.15 M in a standard cell, R = 100 ohm. The relaxation occurs at the final temperature 25 °C, for which the kinetic parameters are calculated. The changes were monitored in the microsecond timescale at 260 nm, where Tel22 displays maximum absorption.

The kinetic curves, collected with an Agilent 54622A oscilloscope (Santa Clara, CA, USA), were transferred to a PC and were evaluated with the Table Curve program of the Jandel Scientific package (AISN software, Richmond, CA, USA). To corroborate the k₁ and k₂ values obtained, the mV versus time data pairs were also analysed using two fitting programs: Origin and Bio-Kinet 32 software (Bio-Logic Science Instruments). In all three cases, the k₁ and k₂ values were obtained by iteration until convergence was attained. The k₁ and k₂ values obtained were reproducible regardless of the program used. In view of the high reproducibility for all of the concentrations and programs, we came to the conclusion that the difference obtained between the k₁ and k₂ values, though not very large, suffices to be fitted by a biexponential function and the values obtained are reliable. Moreover, the time constants were averaged out from 6–10 repeated kinetic experiments.

Acknowledgements

This work was supported by Obra Social “la Caixa” (project OSLC-2012-007) and MINECO, Spain (CTQ2014-58812-C2-2-R, FEDER Funds). C. P.-A. is grateful for the FPU grant from Ministry of Education, Culture and Sports, Madrid, Spain (FPU13/00180).

Notes and references

1. P. Murat and S. Balasubramanian, Curr. Opin. Genet. Dev., 2014, 25, 22–29.
2. S. Dhakal, Y. Cui, D. Koirala, C. Ghimire, S. Kushwaha, Z. Yu, P. M. Yangyuoru and H. Mao, Nucleic Acids Res., 2013, 41, 3915–3923.
3. G. Biffi, D. Tannahill, J. McCafferty and S. Balasubramanian, Nat. Chem., 2013, 5, 182–186.
4. L. Ying, J. J. Green, H. Li, D. Klenerman and S. Balasubramanian, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14629–14634.
5. A. N. Lane, J. B. Chaires, R. D. Gray and J. O. Trent, Nucleic Acids Res., 2008, 36, 5482–5515.
6. A. Y. Q. Zhang and S. Balasubramanian, J. Am. Chem. Soc., 2012, 134, 19297–19308.
7. R. D. Gray, J. O. Trent and J. B. Chaires, J. Mol. Biol., 2014, 426, 1629–1650.
8. N. M. Brown, P. A. Rachwal, T. Brown and K. R. Fox, Org. Biomol. Chem., 2005, 3, 4153–4157.
9. I. Bessi, H. R. A. Jonker, C. Richter and H. Schwalbe, Angew. Chem., Int. Ed., 2015, 54, 8444–8448.
10. R. D. Gray and J. B. Chaires, Nucleic Acids Res., 2008, 36, 4191–4203.
11. R. J. O'Sullivan and J. Karlseder, Nat. Rev. Mol. Cell Biol., 2010, 11, 171–181.
12. E. Largy, A. Marchand, S. Amrane, V. Gabelica and J.-L. Mergny, J. Am. Chem. Soc., 2016, 138, 2780–2792.
13. M. Marusic and J. Plavec, Angew. Chem., Int. Ed., 2015, 54, 11716–11719.
14. J. Palacky, M. Vorlickova, I. Kejnovska and P. Mojzes, Nucleic Acids Res., 2013, 41, 1005–1016.
15. R. Buscaglia, M. C. Miller, W. L. Dean, R. D. Gray, A. N. Lane, J. O. Trent and J. B. Chaires, Nucleic Acids Res., 2013, 41, 7934–7946.
16. A. Ambrus, D. Chen, J. Dai, T. Bialis, R. A. Jones and D. Yang, Nucleic Acids Res., 2006, 34, 2723–2735.
17. A. I. Karsisiotis, N. M. A. Hessari, E. Novellino, G. P. Spada, A. Randazzo and D. S. M. Webba, Angew. Chem., Int. Ed., 2011, 50, 10645–10648.
18. A. T. Phan, K. N. Luu and D. J. Patel, Nucleic Acids Res., 2006, 34, 5715–5719.
19. Y. Wang and D. J. Patel, Structure, 1993, 1, 263–282.
20. K. W. Lim, V. C. M. Ng, N. Martin-Pintado, B. Heddi and A. T. Phan, Nucleic Acids Res., 2013, 41, 10556–10562.
21. S. L. Noer, S. Preus, D. Gudnason, M. Aznauryan, V. Birkedal and J.-L. Mergny, Nucleic Acids Res., 2016, 44, 464–471.
22. M. H.-J. Kuo, Z.-F. Wang, T.-Y. Tseng, M.-H. Li, S.-T. D. Hsu, J.-J. Lin and T.-C. Chang, J. Am. Chem. Soc., 2015, 137, 210–218.
23. J. Zheng and M. D. Fayer, J. Am. Chem. Soc., 2007, 129, 4328–4335.
24. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond: In Structural Chemistry and Biology, Oxford University Press, 1999.
25. M. Eigen and K. Tamm, Z. Elektrochem. Angew. Phys. Chem., 1962, 66, 107–121.
26. M. Eigen, Pure Appl. Chem., 1963, 6, 97–115.
27. R. Ida and G. Wu, J. Am. Chem. Soc., 2008, 130, 3590–3602.
28. J. Toehl and W. Eimer, J. Mol. Model., 1996, 2, 327–329.
29. H. Diebler, F. Secco and M. Venturini, Biophys. Chem., 1987, 26, 193–205.
30. M. T. Record Jr, C. F. Anderson and T. M. Lohman, Q. Rev. Biophys., 1978, 11, 103–178.
31. K. M. Guckian, B. A. Schweitzer, R. X. F. Ren, C. J. Sheils, D. C. Tahmassebi and E. T. Kool, J. Am. Chem. Soc., 2000, 122, 2213–2222.
32. F. J. Meyer-Almes and D. Porschke, Biochemistry, 1993, 32, 4246–4253.
33. N. Busto, B. Garcia, J. M. Leal, F. Secco and M. Venturini, Org. Biomol. Chem., 2012, 10, 2594–2602.
34. J. Valladolid, C. Hortigueela, N. Busto, G. Espino, A. M. Rodriguez, J. M. Leal, F. A. Jalon, B. R. Manzano, A. Carbayo and B. Garcia, Dalton Trans., 2014, 43, 2629–2645.
35. P. Stadlbauer, P. Kuhrova, P. Banas, M. Otyepka, J. Koca, G. Bussi, L. Trantirek and J. Sponer, Nucleic Acids Res., 2015, 43, 9626–9644.
36. T. Mashimo, H. Yagi, Y. Sannohe, A. Rajendran and H. Sugiyama, J. Am. Chem. Soc., 2010, 132, 14910–14918.
37. P. Stadlbauer, L. Trantirek, T. E. Cheatham III, J. Koca and J. Sponer, Biochimie, 2014, 105, 22–35.
38. N. An, A. M. Fleming and C. J. Burrows, J. Am. Chem. Soc., 2013, 135, 8562–8570.
39. R. Rigler, C. R. Rabl and T. M. Jovin, Rev. Sci. Instrum., 1974, 45, 580–588.

---