Novel polyester diol obtained from PET waste and its application in the synthesis of polyurethane and carbon nanotube-based composites: swelling behavior and characteristic properties
Ramin Shamsi and
Gity Mir Mohamad Sadeghi*
Polymer Engineering and Color Technology Department, Amirkabir University of Technology, Tehran, P.O. Box 15875/4413, Iran. E-mail: gsadeghi@aut.ac.ir
First published on 31st March 2016
Abstract
Waste recycling is considered a major concern for industry due to the environmental regulations imposed on industry to protect the environment. In this regard, chemical methods are not only helpful in the decomposition of wastes but also in upgrading them into worthwhile commercial materials. In this investigation, soft-drink bottles composed of polyethylene terephthalate (PET) were depolymerized via glycolysis using 2-methyl-1,3-propanediol (MPD) to obtain oligomeric dioles (diol). Nevertheless, there has been no report on the use of MPD in PET degradation. Diol can be reacted with adipic acid to lengthen the chains to obtain a polyester diol. This polyester diol has the potential for further reactions to produce various products. Here, the diol and polyester diol were characterized using FT-IR, 1H-NMR spectroscopy, and viscosity-Brookfield tests. Moreover, the molecular weight and concentration of the hydroxyl groups were determined. In the second step, novel value-added polyurethanes (cross-linked and non-cross-linked) and carbon nanotube-based polyurethane composites with different molar ratios of diisocyanate to diol (NCO/OH) were prepared using hexamethylene diisocyanate (HDI), polyester diol, and carbon nanotubes. Fourier transform infrared spectra, the thermal transitions, and degradation of the synthesized polyurethanes and nanocomposites were investigated. The swelling characteristics of the cross-linked polyurethanes were fully studied in a wide variety of non-polar to polar solvents. The diffusion profile in different solvents and the absorption kinetics were evaluated as well. The transportation of the solvents showed a Fickian sorption mechanism, while the absorption kinetics followed a pseudo-second-order model. The influence of the NCO/OH molar ratio on the swelling behavior was also investigated. The polyurethane samples, obtained from PET waste, could be used in various applications, such as industrial parts, membranes and O-rings.
1. Introduction
Poly(ethylene terephthalate) (PET) is a semi-crystalline thermoplastic polymer, which is used in the preparation of a variety of products, such as soft-drink bottles, textile fibers, photographic films, etc. Polyester makes up about 18% of the global polymer production and is the fourth-most-produced polymer, preceded by polyethylene (PE), polypropylene (PP), and polyvinyl chloride (PVC), respectively.1During 2004–2011, the world's PET annual production increased from nearly 11.3 million tons to around 18.6 million tons, registering an average annual growth of over 7%. In 2012, it surpassed the 19.8 million tons mark. Furthermore, the PET market is predicted to experience positive growth in the upcoming years, driven by a combination of factors, such as the rapidly increasing global population, the rising demand from end users, improving life standards worldwide, and the upcoming launches of a variety of PET projects. In 2015, the global PET production was expected to exceed 24.39 million tons.2 This wide production and usage of these polymeric materials has led to waste disposal management difficulties. Large numbers of postconsumer PET products, especially bottles and containers, do not create a direct hazard to the environment, but are raising concerns due to their substantial volume fraction in the solid-waste streams and their poor biodegradability and photodegradability.1
Therefore, the necessity of finding a simple economic method for recycling PET waste is a key concern for sustainable recycling.3 The recycling of PET not only serves as a partial solution to the solid-waste problem, but it can also be regarded as a source of raw material to some industries and thus can also make a contribution to the conservation of raw petrochemical products and energy, which is of high significance due to the high cost of energy.4
The chemical recycling of PET includes chemolysis of the polyester with an excess of reactants, such as ammonia (ammonolysis),5 amines (aminolysis),6–11 water (hydrolysis),12–16 alcohol (alcoholysis),17,18 and glycols (glycolysis).19–35
The main chemical recycling technique applied to PET wastes is glycolysis, which can result in value-added products. Glycolysis may be described as a depolymerization process by ester interchange between PET ester groups and a diol. The use of diols for the glycolysis of PET can involve one of the following types: ethylene glycol (EG),19–22,25,33,34 polyethylene glycol,35 diethylene glycol (DEG),23–26 triethylene glycol.25–27 Propylene glycol,25,28,29 dipropylene glycol,3 butanediol,27,31 neopentyl glycol,32 or glycerol.30 Generally, the obtained oligomers are reacted with a diacid, different from the terephthalic acid contained in the PET, in order to lengthen the chains and synthesize the polyester diols.36,37
On the other hand, many attempts have been made to reduce the cost of polyurethane products by using inexpensive polyols. Polyester diol made from the glycolyzation of poly(ethylene terphthalate) (PET) wastes with different alcohols can be considered as one of the most important classes of low-cost polyols suitable for the production of different kinds of polyurethane products.
Although polyurethanes have been widely used in diverse industrial applications, limited literature exists concerning polyurethane synthesis from PET waste. In one example though, Lee et al. synthesized polyurethane elastomers containing 4,4-methylene bis (phenyl isocyanate) (MDI) or toluene 2,4-diisocyanate (TDI) and a polyester diol. The polyester diol was synthesized by the reaction of adipic acid with a PET glycolysate, obtained by depolymerization using EG. The kinetics of the glycolysis reactions by EG, polycondensation with adipic acid, and finally, polymerization with a diisocyanate were investigated. The thermal and mechanical properties of the obtained polyurethanes were determined as well.38,39
Similarly, Colomines et al. synthesized a series of oligoesters via the transesterification of dimethyl isophthalate with neopentyl glycol or tetraethylene glycol and the esterification of adipic acid with neopentyl glycol or tetraethylene glycol under diol/diester or diol/diacid molar ratios sufficient to limit the increase of the molecular weight. These oligoesters were used to depolymerize PET in a continuous reactive extrusion process. The hydroxyl index of the PET glycolysates was determined, and then, various polyurethanes were obtained by the reaction of PET glycolysates and MDI. The swelling properties and the molecular distribution of the synthesized polyurethanes were also determined and the polyurethanes were further characterized by DSC, TGA, and DMA.40
In our previous work, adhesive polyurethanes were synthesized based on the product obtained from the aminolysis of PET waste (BHETA), 1,4-butanediol, ether-type polyol, and various molar ratios of hexamethylene diisocyanate (HDI). To appraise the effect of BHETA, the properties of the polyurethanes were compared in the presence and absence of BHETA. Fourier transform infrared spectra (FT-IR), thermal transitions, degradation, swelling ratio, and the chemical resistance of the synthesized polyurethanes were also investigated. Moreover, the polyurethanes were used as adhesives on various substrates. A comparison of the maximum bond strength of the synthesized polyurethane to that of commercial adhesives showed a 2.2-fold increase.6
In an earlier work, we synthesized novel biodegradable polyurethanes using BHETA. At first, polyols with different molecular weights were synthesized through a ring opening polymerization of caprolactone by BHETA, and then urethane linkages were formed using HDI without a chain extender. The chemical, thermal, mechanical and dynamic mechanical properties, biodegradability, morphology, and UV resistance of the synthesized polyurethanes were also evaluated.7
It is noteworthy that extensive studies have so far been conducted on the synthesis of polyurethanes and the corresponding nanocomposites based on commercial and custom polyols,41–43 but these studies have not focused much on the synthesis of these materials (except polyurethane foams) from polyols based on PET waste. This subject thus requires special attention considering the problem of PET waste and also the high price of polyurethanes.
In the current research, PET waste was glycolized by using 2-methyl-1,3-propanediol (MPD), which, to the best of the authors' knowledge, has not been reported in the literature yet. Then, polyurethane and polyurethane nanocomposite syntheses were conducted in three stages. First, the glycolysis of PET was performed using 2-methyl-1,3-propanediol (MPD) for producing diol. In the second stage, the obtained diol was reacted with adipic acid to lengthen the chains and synthesize the polyester diol. And finally, polyurethanes (cross-linked and non-cross-linked) and carbon nanotube-based polyurethane composites with different molar ratios of diisocyanate to diol were prepared using hexamethylene diisocyanate (HDI), polyester diol, and carbon nanotubes. Chemical structures of the produced samples were characterized by FT-IR and H-NMR. Since these polyurethane samples have the potential to be used in various applications, such as industrial parts, membranes, and O-rings, their thermal and swelling behaviors were studied in detail. The transport behavior of a wide variety of non-polar and polar solvents through cross-linked polyurethanes were also investigated. The swelling equilibrium, diffusion profile, mechanism of diffusion, and absorption kinetics are also explained in the current paper.
The work presented in this article is innovative in several ways, namely:
(1) The first to use MPD in the glycolysis of PET waste.
(2) The first to carry out the synthesis of carbon-nanotubes-based polyurethane composites based on PET waste.
(3) The first to carry out a precise analysis of the swelling behaviors on cross-linked polyurethanes derived from PET waste.
2. Materials and methods
2.1. Materials
Postconsumer waste PET bottles were procured from the local market. After removing the caps and labels, the bottles were cut into approximately 1 cm × 1 cm pieces followed by washing with soap and methanol for the removal of adhesive materials. 2-Methyl-1,3-propanediol (MPD) was obtained from Aldrich. Adipic acid (AA); zinc acetate, dibutyltin dilaurate (DBTDL), hexamethylene diisocyanate (HDI), dimethyl formamide (DMF), dimethyl sulfoxide (DMSO), toluene, hexane, tetra hydrofurane (THF), chloroform, dichloromethane (DCM), dimethyl acetamide (DMAc), ethanol, and methanol were supplied from Merck. Multi-wall carbon nanotubes (diameter: 8–15 μm, length: 50 μm, hydroxyl content: 3.7 wt%, purity: >95 wt%) were purchased from the American Elements Co., USA. All the reagents were used as received.2.2. Depolymerization of PET to prepare diol
MPD was used for the glycolysis of PET waste materials using the molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 (PET
6 (PET![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MPD) in the presence of zinc acetate as the catalyst (0.5% by weight of PET). The glycolysis was carried out at 200–210 °C under reflux for 6 h in a nitrogen atmosphere. At the end of the reaction, the mixture was allowed to cool to room temperature, and after discarding the unreacted PET, the glycolyzed product (diol) was obtained.
MPD) in the presence of zinc acetate as the catalyst (0.5% by weight of PET). The glycolysis was carried out at 200–210 °C under reflux for 6 h in a nitrogen atmosphere. At the end of the reaction, the mixture was allowed to cool to room temperature, and after discarding the unreacted PET, the glycolyzed product (diol) was obtained.
2.3. Synthesis of polyester diol
Polyester diol was prepared by reacting the glycolysized PET oligomers (diol) with adipic acid at a fixed hydroxyl to carboxyl ratio of about 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in a two-necked 250 ml round-bottomed flask equipped with a Dean–Stark trap, a magnetic stirrer, and a condenser. The mixture was heated at 160 °C for 3 h while collecting water in the Dean–Stark trap. When the visible water collection ended, the mixture temperature was maintained at 180–190 °C for another 2 h. After cooling, the product became a light brown viscous liquid.
1 in a two-necked 250 ml round-bottomed flask equipped with a Dean–Stark trap, a magnetic stirrer, and a condenser. The mixture was heated at 160 °C for 3 h while collecting water in the Dean–Stark trap. When the visible water collection ended, the mixture temperature was maintained at 180–190 °C for another 2 h. After cooling, the product became a light brown viscous liquid.
2.4. Characterization of diol and polyester diol
FT-IR spectra of the diol and polyester diol were recorded in the absorption mode with the BOMEM SRG 1100G instrument. 1H-NMR spectra were recorded on the BRUKER NMR spectrometer (250 MHz). The spectra were recorded using chloroform as the solvent for the diol and polyester diol. The chemical shifts in the discussion herein are reported in parts per million. The hydroxyl and acid values were determined based on the standard method presented by Colomines et al.44 Viscosity values of diol and the polyester diol were determined with a Brookfield viscometer (Mod RVT-E) in a rotating spindle of 10 rpm.2.5. Synthesis of the polyurethanes
For the synthesis of the polyurethanes (PU-1, PU-1.7, PU-2), polyester diol (10 g, 9.38 × 10−3 mol) and DBTDL (0.1 g, 1.6 × 10−4 mol) were first dissolved in 70 ml DMF in a round-bottom flask equipped with a condenser, stirrer, thermometer, and nitrogen gas-inlet tube. Once the temperature was elevated to 50 °C, a certain amount of HDI (in accordance with Table 1) was added drop-wise to the reactor. Then, the temperature was raised from 50 °C to 100 °C, and after reacting for 2 h, the mixture was poured slowly into a clean Teflon mold, and the polyurethane samples were post-cured for 1 h at 50 °C and then 12 h at 80 °C.| Sample | NCO/OH (molar ratio) | CNT (wt%) | Physical state |
|---|---|---|---|
| PU-1 | 1 | — | Thermoplastic |
| PU-1.7 | 1.7 | — | Thermoset |
| PU-2 | 2 | — | Thermoset |
| PUCNT-1 | 1 | 0.5 | Powder |
| PUCNT-1.7 | 1.7 | 0.5 | Thermoplastic |
| PUCNT-2 | 2 | 0.5 | Thermoplastic |
2.6. Synthesis of the polyurethane nanocomposites
CNTs (0.5 wt% of polyester diol) were dispersed in a mixture of polyester diol (10 g), DMF (70 ml), and DBTDL (0.1 g) to obtain a suspension system via an ultrasonicator at room temperature. Afterwards, the suspension was heated to 50 °C in a round-bottom flask equipped with a condenser, stirrer, thermometer, and nitrogen gas-inlet tube, and then, HDI was added with different molar ratios in accordance with Table 1. Afterwards, the temperature was raised from 50 °C to 100 °C, followed by reacting for 2 h. Finally, the mixture was poured slowly into a clean Teflon mold, and the PU/CNT composites were post-cured for 1 h at 50 °C and then 12 h at 80 °C.2.7. Characterization of the polyurethanes and polyurethane nanocomposites
TGA was carried out at a heating rate of 10 °C min−1 under a nitrogen atmosphere from 25 °C to 600 °C using the METTLER TOLEDO instrument.
3. Results and discussion
The main objective of this work is to study the depolymerization of PET with MPD and to utilize the produced glycolized oligoester (diol) as a potential raw material for the synthesis of polyester diol. To this end, the as-synthesized polyester diol was used to produce the polyurethanes and nanocomposites.3.1. Depolymerization of PET waste
The glycolysis of PET with MPD was conducted according to the reaction shown in Scheme 1. The glycolysis includes the transesterification of PET and also the destruction of its polymer chain resulting in a reduction of its molecular weight. Using glycols in the depolymerization of PET, the obtained oligoesters possess two hydroxyl end groups, i.e., oligoester diols (diol) are formed. According to the structure shown in scheme 1, in order to identify the diol structure, it is necessary to determine the amount of ‘m’. In the diol structure, if ‘m’ is replaced with 0 and 1, the following molecular weights are obtained: 310 and 502, respectively. By comparing these values with those obtained by 1HNMR and the hydroxyl value index (Table 2), it can be concluded that the above structure is confirmed with 0 < m < 1.| Sample | Hydroxyl number (in mg KOH per g sample) | Acid number (in mg KOH per g sample) | Mn (obtained from hydroxyl number test) (g mol−1) | Mn (obtained from H-NMR method) (g mol−1) | Brookfield viscosity (cp) |
|---|---|---|---|---|---|
| Diol | 260.58 | 1 | 429 | 405 | 328 |
| Polyester diol | 83 | 9.13 | 1218 | 1067 | 6350 |
Fig. 1 gives 1H NMR spectra for diol, where the first resonance peak (0.84–1.07 ppm) corresponds to –CH3 groups attached to the backbone of the chain (e), while the 1.86–1.95 ppm bands are assigned to the hydrogen attached to the third-type carbon (d). Bands that appear at 3.5–3.69 ppm correspond to –CH2– adjacent to the terminal hydroxyl groups (b), while the 3.837 ppm peak corresponds to –CH2– (c), the 4.336–4.36 ppm peaks correspond to –OH groups (a), and the appearance of an 8.1 ppm peak indicates the aromatic ring protons (f).6,7,45,46
H-NMR data were also used to determine the molecular weight according to the method used in ref. 7 and 46. The following equation, eqn (1), was used to estimate the average molecular weight for diol, Mn(diol), via the H-NMR technique:
| Mn(diol) = 11.92S(diol) + 114.62 | (1) |
By using the above equation, the number average molecular weight was calculated to be 405 g mol−1 for diol. It is noteworthy that the molecular weights were also estimated via the hydroxyl and acid number indices. The following empirical formula, eqn (2), can be used to determine the number molecular weight (Mn):47
 | (2) |
It can be concluded that both the NMR and OH-value methods lead to similar estimations of the molecular weight for the synthesized diol. Moreover, the Brookfield viscosity was also determined as 328 cp for diol (Table 2).
3.2. Synthesis of polyester diol
Polyester diol was synthesized through a step polymerization of diol with adipic acid (Scheme 2). Fig. 2 shows the H-NMR spectrum for the as-synthesized polyester diol, which further confirms the proposed chemical structure for the synthesized polyester diol. As shown in Fig. 2, the peaks at 1.64 ppm (h) and 2.33 ppm (g) are assigned to adipic acid protons, and other resonance peaks are related to protons in the diol structure of the polyester diol. The number average molecular weight of the polyester diol (Mn(polyester diol)) was determined by H-NMR using eqn (3):| Mn(polyester diol) = 18.676S(polyester diol) + 48.024SAA + 143.388 | (3) |
As a result, the average molecular weight of the polyester diol was calculated to be 1067 g mol−1. Also, based on eqn (2) and with HN = 83 and AN = 9.13, Mn can be calculated as 1218 for polyester diol.
Here, both the NMR and OH-value indices methods again give similar estimations of the molecular weight of the synthesized polyester diol. The Brookfield viscosity was determined as 6350 cp for polyester diol. As is seen, as the molecular weight increases, viscosity also increased, i.e., from 328 cp for diol to 6350 cp for the polyester diol (Table 2).
FT-IR spectrum of the used MPD in this work can also be observed in Fig. 3. As is evident, a very strong and broad peak at 3450 cm−1 is seen, which can be attributed to the O–H stretching of hydroxyl groups in the chemical structure of MPD. Moreover, peaks at 2860 and 2930 cm−1 are due to the symmetric and asymmetric C–H stretching, respectively. Fig. 3 also displays the FT-IR spectra for the synthesized diol and polyester diol. The major difference between the spectra of MPD and diol is the appearance of a strong peak at 1720 cm−1, which can be ascribed to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the as-formed ester carbonyl group. This result could prove that PET waste was properly reacted with MPD, and as a result, ester groups were formed.
O stretching of the as-formed ester carbonyl group. This result could prove that PET waste was properly reacted with MPD, and as a result, ester groups were formed.
Table 3 shows the normalized peak absorbance ratios for two important regions, including the hydroxyl stretching peak at 3450 cm−1 and the carboxyl stretching peak at 1720 cm−1. As can be seen, the A3450/A2920 ratio has the highest value for MPD and the lowest value for polyester diol, indicating a decrease in the hydroxyl group concentration as polyester diol is synthesized. As mentioned earlier, MPD first reacts with PET waste, leading to the formation of diol, which has a low molecular weight, and then, it further reacts with adipic acid to increase its molecular weight. Therefore, the reduced absorbance ratio in the hydroxyl stretching region further proves that the molecular weight was increased and the polyester diol was formed. On the other hand, the A1720/A2920 ratio for the carboxyl stretching is zero for MPD due to the absence of carbonyl groups in its structure; however, this ratio is increased to 1.789 and 1.793 for diol and polyester diol, respectively. Such an increment suggests that the reaction of MPD with PET waste was carried out in a proper direction, that is, via the formation of the carbonyl ester group. The higher carbonyl ratio of polyester diol is also reasonable since the number of carbonyl groups per chain increases as the reaction of diol with adipic acid proceeds. Therefore, our main aim, which was formation of an ester-based polyol with a proper molecular weight, was achieved. This ester-based polyol was utilized to synthesize all the polyurethane samples from PET waste in the current study.
| Absorbance ratio | MPD | Diol | Polyester diol |
|---|---|---|---|
| A3450/A2920 | 2.115 | 1.559 | 0.688 |
| A1720/A2920 | — | 1.789 | 1.793 |
3.3. Synthesis of polyurethanes and polyurethane nanocomposites
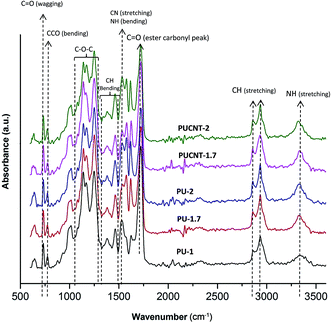
The as-synthesized polyester diol was used to produce the polyurethanes and nanocomposites in various molar ratios of hexamethylene diisocyanate to diol (or NCO/OH) in accordance with Table 1. The polyurethanes are named PU-1, PU-1.7 and PU-2, and the polyurethane nanocomposites are introduced as PUCNT-1, PUCNT-1.7, and PUCNT-2. For further simplification, PU and PUCNT represent the polyurethane samples and their corresponding nanocomposites, respectively, and the numbers indicate a serial order of synthesis with NCO/OH ratios equal to: 1, 1.7 and 2. The physical state for PU-1 is thermoplastic, while PU-1.7 and PU-2 exhibit a thermoset character (cross-linked). These behaviors were quite predictable because once the NCO/OH molar ratio is higher than unity, the polyurethanes become cross-linked through the reaction of free isocyanate groups with urethane groups, leading to tri-functional allophanate.48 A comparison between the polyurethanes and their corresponding nanocomposites reveals that there is a characteristic difference in the physical state (Table 1). Unlike polyurethanes, the formation of cross-links was impeded in the case of nanocomposites once the NCO/OH molar ratio was increased above unity. This unexpected phenomenon is most probably due to the steric hindrance effect of CNTs. However, once the NCO/OH molar ratio was equal to unity, the presence of CNTs impeded the formation of polymer chains causing a powder-like structure to be formed. In this work, the swelling characteristics of the cross-linked samples (PU-1.7 and PU-2) along with chemical structures and thermal properties of PU-1, PU-1.7, PU-2, PUCNT-1.7, and PUCNT-2 were determined and interpreted. The mechanical, dynamic mechanical and morphological properties of these samples will be presented in our future publication.All the spectra were characterized by the NH stretching vibrations observed in the 3200–3500 cm−1 wavenumber region. The symmetric and asymmetric stretching modes of CH2 groups were observed at 2860 and 2930 cm−1, respectively. C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching was the most distinctive absorption band in IR due to its high intensity around 1730 cm−1. Generally, aromatics display a characteristic C
O stretching was the most distinctive absorption band in IR due to its high intensity around 1730 cm−1. Generally, aromatics display a characteristic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching at about 1620 cm−1. Thus, the strong band observed at 1534 cm−1 may be attributed to the coupling of CN stretching and NH bending. The bands observed between 1400 and 1460 cm−1 were attributed to CH2 scissoring vibrations. The moderate band found at 1380 cm−1 was assigned to the wagging vibrations of methylene groups, whereas the band at 1340 cm−1 belonged to the CH2 twisting. The bands at 1080 and 1250 cm−1 were assigned to the C–O–C vibrations of ester functional groups, which were correlated with the soft-segment orientation behavior. Moreover, the bands appearing at 1140 and 1170 cm−1 were attributed to the C–O–C vibrations of ester functional groups within the hard-segment phase. There were also several bands observed in the 820–1013 cm−1 and 645 cm−1 wavenumber regions, which were assigned to the bending vibrations of the methylene group. A C
C stretching at about 1620 cm−1. Thus, the strong band observed at 1534 cm−1 may be attributed to the coupling of CN stretching and NH bending. The bands observed between 1400 and 1460 cm−1 were attributed to CH2 scissoring vibrations. The moderate band found at 1380 cm−1 was assigned to the wagging vibrations of methylene groups, whereas the band at 1340 cm−1 belonged to the CH2 twisting. The bands at 1080 and 1250 cm−1 were assigned to the C–O–C vibrations of ester functional groups, which were correlated with the soft-segment orientation behavior. Moreover, the bands appearing at 1140 and 1170 cm−1 were attributed to the C–O–C vibrations of ester functional groups within the hard-segment phase. There were also several bands observed in the 820–1013 cm−1 and 645 cm−1 wavenumber regions, which were assigned to the bending vibrations of the methylene group. A C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O wagging vibration was also observed at 730 cm−1.49–54
O wagging vibration was also observed at 730 cm−1.49–54
3.3.2.1. Swelling equilibrium studies. The equilibrium swelling characteristics, molecular weight between cross-links (Mc (g mol−1)), cross-link densities (νe (mol cm−3)) and degree of cross-linking (ν (mol g−1)) of the thermoset samples (PU-1.7 and PU-2) were all determined using the Flory Rehner equation.55 Mc is defined as the average molecular weight of chains between two cross-link sites, and the degree of cross-linking (ν) determines the extent of cross-links per unit weight of polymer. Low amounts of ν imply the formation of fewer cross-links per unit weight of polymer, whereas high amounts of ν might refer to the formation of a higher cross-link content.56
 | (4) |
 | (5) |
 | (6) |
 | (7) |
| q = 1 + Q | (8) |
 | (9) |
 | (10) |
The solubility parameters of the PU-1.7 and PU-2 samples were attained by plotting the swelling coefficients (Qsc) of the samples against solubility parameters of the ten solvents used.
The Qsc values for each network in various solvents were calculated using eqn (11):
 | (11) |
The swelling coefficient values, together with their corresponding Gaussian fits obtained for the PU-1.7 and PU-2 samples, are shown in Fig. 5. The maximum on each curve was assigned as the polymer solubility parameter. Hence, the values of δp were computed as 10.068 and 10.085 (cal cm−3)0.5 for PU-1.7 and PU-2, respectively, since each cross-linked polyurethane represents the maximum swelling coefficient value in chloroform (δs = 9.3), then in DMAc (δs = 10.8) and DCM (δs = 9.7) as compared with the other solvents.
 | ||
| Fig. 5 Gaussian fit of the swelling coefficients versus solubility parameters for the PU-1.7 and PU-2 samples. | ||
Further calculations led to an estimation of χ, Mc, νe, and ν. Hexane, toluene, THF, chloroform, DCM, DMAc, DMF, DMSO, ethanol, and methanol were the solvents chosen for the PU-1.7 and PU-2 samples in these calculations. The results for each cross-link are shown in Table 4.
| Solvent | δa (cal cm−3)0.5 | χ | Mc (g mol−1) | ν × 10−3 (mol g−1) | νe × 10−3 (mol cm−3) | ||||
|---|---|---|---|---|---|---|---|---|---|
| PU-1.7 | PU-2 | PU-1.7 | PU-2 | PU-1.7 | PU-2 | PU-1.7 | PU-2 | ||
| a Data taken from ref. 59. | |||||||||
| Hexane | 7.3 | 2.0420 | 2.063 | 173.3 | 256.6 | 2.884 | 1.948 | 7.013 | 4.84 |
| Toluene | 8.9 | 0.5847 | 0.5919 | 360.5 | 509.8 | 1.387 | 0.981 | 3.372 | 2.436 |
| THF | 9.1 | 0.468 | 0.472 | 566.8 | 701.1 | 0.882 | 0.713 | 2.145 | 1.771 |
| Chloroform | 9.3 | 0.4198 | 0.4233 | 2261 | 2795 | 0.221 | 0.179 | 0.538 | 0.444 |
| DCM | 9.7 | 0.3546 | 0.356 | 676.3 | 802.9 | 0.739 | 0.623 | 1.798 | 1.547 |
| DMAc | 10.8 | 0.424 | 0.420 | 1526 | 1842 | 0.327 | 0.271 | 0.796 | 0.674 |
| DMF | 12.1 | 0.8987 | 0.8895 | 1501 | 1602 | 0.333 | 0.312 | 0.81 | 0.775 |
| Ethanol | 12.92 | 1.130 | 1.1210 | 987.7 | 628.8 | 0.506 | 0.795 | 1.231 | 1.975 |
| DMSO | 12.93 | 1.3217 | 1.3100 | 298.5 | 306.8 | 1.675 | 1.629 | 4.073 | 4.048 |
| Methanol | 14.5 | 1.6815 | 1.6712 | 83.5 | 86.3 | 5.986 | 5.793 | 14.558 | 14.39 |
It is noteworthy to point out that the thermosetting polyurethanes can be synthesized by NCO/OH molar ratios higher than unity. Generally, the cross-link density could be increased by increasing the NCO/OH ratio. The polyurethanes might be cross-linked by the reaction of free isocyanate groups with urethane groups or via moisture leading to the formation of tri-functional allophanate and urea structures, respectively.48
Quite unexpectedly, the PU-1.7 sample (with NCO/OH = 1.7) shows a higher cross-link density than the PU-2 sample (with NCO/OH = 2) in the course of swelling for all of the solvents (Table 6). This abnormal behavior can be explained by the higher chain length of the PU-1.7 compared to PU-2, leading to a better phase separation during the post-curing process.
In fact, the polyurethane phase separation strongly depends on the formation of hydrogen bonds between the urethane linkages, the soft-segment molecular weight, soft-segment type, the manufacturing process and the reaction conditions.60 Here, the formation of hydrogen bonds between the urethane linkages and also the molecular weight of the chains can be regarded as the dominant factors since the others remained unchanged in all the samples. Generally, the reaction between polyester diol and diisocyanate for the synthesis of polyurethane is regarded as a step polymerization, and thus, a decrease in molecular weight of the polyurethane chains can be obtained upon increasing the NCO/OH molar ratio. As the polyurethane molecular weight is diminished, the phase mixing increases. Furthermore, the molecular weight of the chains is a governing factor since the higher molecular weights easily form rich phases on account of an entropic contribution.60
Herein, it should be noted that in order to complete the cross-linking reactions, the pre-polymers were post-cured in the mold at an elevated temperature of 80 °C. The higher chains' molecular weight in the case of PU-1.7 caused a higher level of inter-hydrogen bonding and phase separation; and thus, more adjacent chains, which led to more chemical cross-linking reactions rather than for PU-2 during the post-curing process.
Comparing Mc, νe, and ν data obtained by the swelling studies in different solvents, it was found that an irregular trend was followed because they were simultaneously subjected to multiple parameters, such as polymer density, the volume fraction of the polymer in the swollen mass, solvent density, the molar volume of solvent and also the polymer–solvent interaction parameter (χ).
3.3.2.2. Diffusion profile. Data from the swelling studies are presented as plots of the mole percent uptake of the solvent (Qt) against t0.5/h, where t is the time and h is the thickness of the sample. Qt at each time period was obtained by the following equation:
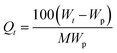 | (12) |
Sorption plots for the PU-1.7 and PU-2 samples in a total of ten solvents are shown in Fig. 6. For all the samples, the Qt values increased rapidly during the initial sorption stage, followed by further enhancement at a relatively slower sorption rate, before finally reaching an equilibrium value. However, variations were found in the equilibrium sorption values as well as in the diagram slope (the rate of solvent uptake) prior to attaining the equilibrium in different solvents.
 | ||
| Fig. 6 Mole percent uptake of the solvent (Qt) against t0.5/h in different solvents for: (a) PU-1.7 and (b) PU-2. | ||
Both the equilibrium sorption value (Qe) and the rate of solvent uptake follow the same trend in the cross-linked polyurethanes (PU-1.7 and PU-2), such that they were high for chloroform and DMAc but low for toluene and hexane. The Qe data are shown in Table 6. Many parameters related to the solvents, such as polarity, molar volume, molecular weight, density, and the solubility parameter, may affect the equilibrium extent of swelling and solvent transmission through the polymer chains. These parameters are discussed in detail in the following.
According to Fig. 7, it is reasonable that Qe and the rate of solvent uptake are higher for PU-2 than for PU-1.7 in all of the solvents. This behavior can be attributed to the lower cross-link density of PU-2 compared to PU-1.7. Hence, the reduction in cross-linking density resulted in higher solvent uptake values.
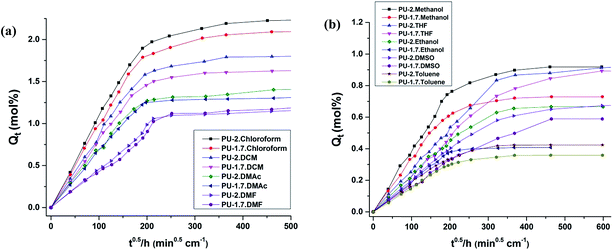 | ||
| Fig. 7 Comparison of the percentage mass uptake between PU-1.7 and PU-2: (a) in chloroform, DCM, DMAc and DMF solvents and (b) in methanol, THF, ethanol, DMSO and toluene solvents. | ||
3.3.2.3. Mechanism of diffusion. In order to find out the mechanism of diffusion, the swelling data of the cross-linked samples were fitted into the following empirical equations:
 | (13) |
 | (14) |
n < 0.5, Pseudo-Fickian.
0.5 < n <1, anomalous.
n = 1, Case II.
n > 1, Super Case II.
Non-Fickian diffusion processes are mainly observed in glassy polymers, i.e., when the temperature is below Tg. At a specific temperature below Tg, the polymer chains are not sufficiently mobile to allow immediate diffusion of the solvent into the polymer core. Two kinds of non-Fickian diffusions have been defined: Case II diffusion and anomalous diffusion. The main difference between these two diffusion categories concerns the solvent diffusion rate. In Case II diffusion, the solvent diffusion rate is faster than the polymer relaxation process (Rdiff ≫ Rrelax), whereas in the case of anomalous diffusion, the solvent diffusion rate and the polymer relaxation are about the same order of magnitude (Rdiff ∼ Rrelax).61
From Table 5, the values of ‘n’ varied between 0.4 and 0.6 in the investigated solvents for both the PU-1.7 and PU-2 samples suggesting that the transport mechanism is very close to the Fickian mode, and the rate of polymer relaxation tends to be greater than the diffusion rate of the solvent.
| Solvent | PU-1.7 | PU-2 | ||
|---|---|---|---|---|
| n | k | n | k | |
| Hexane | 0.437 | 0.0683 | 0.335 | 0.1 |
| Toluene | 0.504 | 0.2948 | 0.451 | 0.326 |
| THF | 0.535 | 0.1552 | 0.508 | 0.169 |
| Chloroform | 0.437 | 0.3238 | 0.245 | 0.469 |
| DCM | 0.448 | 0.3145 | 0.555 | 0.252 |
| DMAc | 0.4682 | 0.3139 | 0.476 | 0.282 |
| DMF | 0.5855 | 0.2387 | 0.614 | 0.204 |
| Ethanol | 0.508 | 0.3061 | 0.584 | 0.199 |
| DMSO | 0.535 | 0.1646 | 0.542 | 0.172 |
| Methanol | 0.423 | 0.3382 | 0.523 | 0.266 |
Based on the discussion mentioned above, one can conclude that the Deborah number (De) is much less than unity (De ≪ 1) for our samples. The Deborah number is defined as the ratio of the relaxation time to the diffusion time:
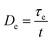 | (15) |
The Deborah number is an effective scaling parameter for describing the markedly different behaviors frequently observed in diffusion processes. If the Deborah number is much less than unity, relaxation is fast, and the penetrants are diffusing and conformational changes in the polymer structure take place very quickly. Therefore, the diffusion mechanism would be Fickian.63
3.3.2.4. Absorption kinetics. Several kinetics models can be used to describe the kinetics of absorption. In this study, in order to examine the controlling mechanism of the absorption process, a pseudo-first-order model and a pseudo-second-order kinetics model were used to analyze the experimental data.
The pseudo-first-order kinetics model can be formulated as eqn (16):64–66
ln(Qe(1) − Qt) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qe(1) − k1t Qe(1) − k1t
| (16) |
The pseudo-second-order model can be expressed as eqn (17):65,66
 | (17) |
The validity of these two models can be further confirmed by analyzing the linearized plots, and a comparison between the equilibrium sorption values were obtained from the experimental swelling uptake (Qe) with Qe(1) and Qe(2).
Fig. 8 and 9 show the curve-fitting plots of these models for the PU-1.7 and PU-2 samples in different solvents. The obtained kinetics parameters are summarized in Table 6. For PU-1.7 and PU-2, in all of the solvents (except hexane), the calculated correlation coefficients (R2) are closer to unity (R2 > 0.99) for the pseudo-second-order kinetics model compared with those from the pseudo-first-order kinetics model. In addition, the theoretical equilibrium sorption value calculated from the pseudo-second-order kinetics model (Qe(2)) agreed well with the experimental equilibrium amount of the samples (Qe), whereas there was a remarkable difference between these values for the pseudo-first-order kinetics model (Qe(1)) (Table 6).
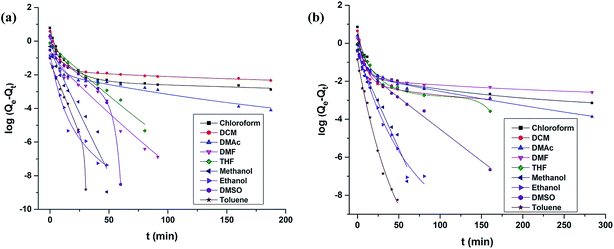 | ||
| Fig. 8 Comparison of the curve-fitting plots of the first-order model in different solvents for (a) PU-1.7 and (b) PU-2. | ||
 | ||
| Fig. 9 Comparison of the curve-fitting plots of the second-order model in different solvents for (a) PU-1.7 and (b) PU-2. | ||
| Solvent | PU-1.7 | PU-2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Qe | Pseudo-first-order model | Pseudo-second-order model | Qe | Pseudo-first-order model | Pseudo-second-order model | |||||||||
| Qe(1) | K1 | R2 | Qe(2) | K2 | R2 | Qe(1) | K1 | R2 | Qe(2) | K2 | R2 | |||
| a Qe: the experimental equilibrium amount of the samples. Qe(1): the theoretical equilibrium sorption value calculated from the pseudo-first-order kinetics model. Qe(2): the theoretical equilibrium sorption value calculated from the pseudo-second-order kinetics model. | ||||||||||||||
| Hexane | 0.023 | 0.021 | 0.013 | 0.9808 | 0.028 | 0.75 | 0.9034 | 0.026 | 0.035 | 0.046 | 0.8316 | 0.031 | 0.651 | 0.9189 |
| Toluene | 0.358 | 0.424 | 0.226 | 0.9248 | 0.374 | 0.012 | 0.9991 | 0.424 | 0.269 | 0.156 | 0.9728 | 0.443 | 0.972 | 0.9989 |
| THF | 0.892 | 0.782 | 0.059 | 0.9874 | 0.946 | 0.133 | 0.9976 | 0.969 | 0.436 | 0.021 | 0.7512 | 0.984 | 0.152 | 0.9998 |
| Chloroform | 2.183 | 0.412 | 0.014 | 0.499 | 2.189 | 0.180 | 0.9999 | 2.347 | 0.419 | 0.01 | 0.5081 | 2.35 | 0.150 | 0.9999 |
| DCM | 1.775 | 0.381 | 0.01 | 0.4052 | 1.774 | 0.145 | 0.9997 | 1.901 | 0.389 | 0.018 | 0.4691 | 1.909 | 0.218 | 0.9999 |
| DMAc | 1.385 | 0.284 | 0.017 | 0.6812 | 1.391 | 0.315 | 0.9999 | 1.501 | 0.358 | 0.011 | 0.6647 | 1.505 | 0.207 | 0.9999 |
| DMF | 1.231 | 0.559 | 0.071 | 0.9452 | 1.254 | 0.295 | 0.9996 | 1.291 | 0.314 | 0.007 | 0.3711 | 1.288 | 0.181 | 0.9995 |
| Ethanol | 0.408 | 0.161 | 0.132 | 0.8886 | 0.432 | 1.135 | 0.9988 | 0.666 | 0.431 | 0.090 | 0.9475 | 0.713 | 0.308 | 0.9972 |
| DMSO | 0.588 | 0.871 | 0.098 | 0.7548 | 0.645 | 0.433 | 0.9921 | 0.694 | 0.428 | 0.037 | 0.977 | 0.714 | 0.211 | 0.9996 |
| Methanol | 0.729 | 0.585 | 0.147 | 0.9263 | 0.756 | 0.588 | 0.9994 | 0.918 | 0.606 | 0.102 | 0.9617 | 0.959 | 0.368 | 0.9991 |
Therefore, these results indicate that the solvent absorption (except for hexane absorption) in PU-1.7 and PU-2 could be described very well by the pseudo-second-order kinetics model.
3.3.2.5. Transport behavior. The transport of small molecules through polymers generally occurs through a solution diffusion mechanism, i.e., the solvent molecules are initially absorbed by the polymer followed by diffusion through the polymer membrane. The net diffusion through polymer depends on the difference in the amount of probe molecules between the two successive layers.67
In order to further study the penetrants' transport behavior, it is necessary that the diffusion coefficient (D), the sorption coefficient (S), and the permeation coefficient (P) of different solvents in the PU-1.7 and PU-2 samples are determined and then interpreted.
For Fickian transport, the rate of approach to equilibrium swelling can be characterized by a diffusion coefficient (D). D, which is a thermodynamic parameter in short times, was calculated using the following relation:67–69
 | (18) |
When plotting the Qt against t0.5, a straight line is initially obtained in the majority of cases. Thus, D can be calculated from a rearrangement of eqn (18) as (19):68,69
 | (19) |
Due to the substantial swelling in a short period, a swelling correction is essential to obtain the correct diffusion coefficient, known as the intrinsic diffusion coefficient (D*). This can be determined using the following equation:69
 | (20) |
| Solvent | PU-1.7 | PU-2 | ||||
|---|---|---|---|---|---|---|
| D* × 104 (cm2 s−1) | S | P × 104 (cm2 s−1) | D* × 104 (cm2 s−1) | S | P × 104 (cm2 s−1) | |
| Hexane | 190.15 | 0.02 | 3.803 | 192.15 | 0.023 | 4.419 |
| Toluene | 285.45 | 0.33 | 94.19 | 354.63 | 0.39 | 138.3 |
| THF | 1241.73 | 0.64 | 794.7 | 1417.93 | 0.699 | 991.1 |
| Chloroform | 5381.89 | 2.606 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 025.2 025.2 |
6374.93 | 2.802 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862 862 |
| DCM | 2895.33 | 1.508 | 4366.15 | 3262.76 | 1.614 | 5266 |
| DMAc | 3402.62 | 1.207 | 4106.96 | 3938.72 | 1.307 | 5147.9 |
| DMF | 1910.25 | 0.899 | 1717.31 | 2170.29 | 0.943 | 2046.6 |
| Ethanol | 823.48 | 0.460 | 378.8 | 934.46 | 0.542 | 506.47 |
| DMSO | 690.57 | 0.188 | 129.82 | 833 | 0.273 | 227.41 |
| Methanol | 778.67 | 0.233 | 181.43 | 878.47 | 0.294 | 258.27 |
A comparison of the intrinsic diffusion coefficient (D*) between the PU-1.7 and PU-2 samples in the different solvents shows a higher penetrant diffusion in PU-2 rather than in PU-1.7.
It is known that the transport phenomena are strongly related to the cross-link density of the polymers. The diffusivity decreased linearly with an increase in the cross-link density.70 Comparing the intrinsic diffusion coefficients confirms the higher cross-link density for PU-1.7 over PU-2.
Moreover, based on Table 7, it can be observed that the intrinsic diffusion coefficient parameters of the solvents are in the following order: chloroform, DMAc, DCM > DMF > THF > DMSO > methanol > ethanol > toluene > hexane. The effective parameters for the solvents diffusivity are the penetrant size, polarity, and also the molecular interaction between the penetrants and polymer chains. A decrease in diffusivity with an increase in the size of the solvent has been reported by many researchers.71,72 Better molecular interaction between the penetrants and polyurethane chains could be obtained if the polymer–solvent interaction parameter (χ) and also the ability for the formation of hydrogen bonds between the polymer and solvent are decreased.
The diffusivity in the samples by chloroform, DMAc, and DCM solvents is superlative since their solubility parameters are closer to those of the polyurethane samples (the minimum of χ). The lower χ for the THF and DMSO penetrants as compared with the methanol, ethanol, toluene, and hexane penetrants leads to a better diffusivity. Comparing the diffusivity of ethanol with methanol reveals that the particle size is more important than χ. The lowest diffusivity was obtained for toluene and hexane penetrants because they are non-polar as opposed to the polar polyurethane chains. Moreover, the lower dielectric constant (ε) for hexane (ε = 2) compared to toluene (ε = 2.38) minimized the diffusivity of the hexane molecules through the polyurethane chains.
It is quite surprising that despite having a larger molecular size and greater χ value as compared with THF, DMF showed more diffusivity in both the PU-1.7 and PU-2 samples. The ability to form hydrogen bonds between the DMF molecules and the urethane groups could be responsible for such behavior.
In summary, the D* or diffusivity depends more on the molecular interactions between the penetrants and the polymer rather than the penetrant molecular size. This behavior is in conformity with the obtained results by Gopakumar and Nair.69
In order to acquire a better understanding of this, the strength of interaction between the polyurethane networks and solvents, the sorption coefficient, (S), which is a thermodynamic parameter, and the permeation coefficient (P), which is a thermo-kinetic parameter, were also studied.
The sorption coefficient was calculated by using eqn (21):
 | (21) |
According to Table 7, it can be observed that the chloroform-polymer system exhibits the maximum S value while the hexane–polymer system shows the minimum S value. The higher interaction of the chloroform molecules with the polyurethane segments (the low χ) is responsible for this observed behavior. The minimum value for hexane is due to its non-polar character.
The permeability coefficient, P, is defined as the volume of the penetrant passing per unit time through the unit area of the polymer with a unit thickness and with a unit pressure difference across the system. The permeability depends on the solubility coefficient, S, as well as the diffusion coefficient. eqn (22) expresses the permeability in terms of solubility (S) and diffusivity (D).73
| P = DS | (22) |
In Table 7, P values for the PU-1.7 and PU-2 samples in different solvents are given. The permeability coefficients show similar trends to the intrinsic diffusion coefficient.
In conclusion, if the obtained D*, P, and S in all the solvents are compared, S would exhibit higher values than those of D* and P. Consequently, it is conceivable to deduce that sorption predominates over diffusion in the permeation process of this understudied system.
 | ||
| Fig. 10 Different DSC traces for the PU samples and corresponding nanocomposites: (a) first heating scan, (b) cooling scan, and (c) second heating scan. | ||
Comparing the observed melting behaviors in the case of PU-1.7 with PUCNT-1.7, it can be seen that instead of a high temperature endotherm, a melting peak appears around 30 °C for the nanocomposite sample due to an insignificant formation of crystals in the soft segment. The reduced level of phase separation regarding PU-1.7, due to the steric hindrance effect of the CNT particles, may be the major reason for disappearance of the high temperature endotherm. On the other hand, since this sample is thermoplastic, the mobility of the soft-segment chains are increased compared with the thermoset PU-1.7, leading to the formation of crystals within the soft-segment phase, which then melt at rather low temperatures. Another comparison can be made for the PU-2 and PUCNT-2 samples regarding the appearance of a very weak melting endotherm at around 210 °C. This difference can be attributed to the thermoplastic character of PUCNT-2, and thus the higher mobility of the PU chains.
| Sample | PU-1 | PU-1.7 | PU-2 | PUCNT-1.7 | PUCNT-2 |
|---|---|---|---|---|---|
| T5 | 271.5 | 287.5 | 283 | 282.5 | 285.5 |
| T10 | 298 | 301 | 300 | 298 | 299 |
| T30 | 324 | 327 | 325.5 | 325 | 326 |
| T50 | 341.5 | 347 | 345 | 345.5 | 346.5 |
| T60 | 362 | 367.5 | 362 | 365.5 | 371 |
| T70 | 407 | 408.5 | 394 | 404 | 417 |
| T80 | 448.5 | 445 | 439 | 443 | 447 |
| T90 | 473.5 | 466.5 | 463 | 471 | 466.5 |
| Char residue (wt%) | 6.6 | 5.4 | 4.9 | 7.3 | 5.5 |
According to the DTGA curves, it is evident that all the polyurethane samples, regardless of the NCO/OH ratio and CNT inclusion, undergo two major degradation stages. It is known that the first stage of degradation occurs as a result of urethane bond decomposition,75 resulting in a dissociation to isocyanate and alcohol, primary amines, a terminal olefinic group on the polyester chain, and secondary amines and CO2.76 According to Table 8, increasing the NCO/OH ratio in the case of PU-1.7 and PU-2 increased the thermal stability of the hard segment (T10–T60) as compared to PU-1. For example, T50 which is the sample's temperature at 50% weight loss, is increased from 341 °C to 347 °C upon increasing the NCO/OH ratio from unity to 1.7. This increment in thermal stability may be due to the formation of cross-links, which lead to a thermoset character. However, a further increment of the NCO/OH ratio from 1.7 to 2 caused a reduction in the thermal stability. This unexpected result could be attributed to the higher cross-link density of PU-1.7 compared to PU-2, which was found to be based on the swelling results. It is known that the thermal stability of polyurethanes strongly depends on the number of urethane groups per unit volume.77 Therefore, the unexpected reduction of thermal stability for PU-2 could be attributed to the formation of a higher level of urethane bonds, making the polymer more susceptible to decomposition in this temperature range.
Interestingly, the thermal stability of the soft segment (T70–T90) conforms to the following trend: PU-1 > PU-1.7 > PU-2. It was previously demonstrated that the synthesized polyester diol has aromatic rings in its chain structure since it was originally obtained from PET waste. Therefore, due to the fact that the soft-segment content is higher in the case of PU-1 as compared to in the other two samples with higher NCO/OH ratios, the thermal stability is enhanced within the mentioned temperature range. This explanation could also be the reason for the formation of the higher content of char for PU-1. Another reason could be the fact that the as-formed char in the case of PU-1 is more uniform. As mentioned earlier, this sample exhibits a thermoplastic behavior, and thus, melts at high temperatures as opposed to the thermoset samples (PU-1.7 and PU-2). Accordingly, the as-formed char layer could migrate onto the sample surface, leading to formation of a higher level of char residue with more uniformity. Such uniformity could not be achieved in the case of those thermoset samples, and thus, a lower level of char residue is formed for the thermoset samples.
Another interesting observation is that the thermal stability of PUCNT-2 is higher than that of PUCNT-1.7 over the whole temperature range. The higher NCO/OH ratio causes stronger interactions between the PU chains and CNTs, as previously observed by FT-IR. However, the char residue was higher for PUCNT-1.7, which could be again attributed to the higher content of soft segments with aromatic rings due to the lower NCO/OH ratio.
Once the NCO/OH ratio is fixed at 1.7, the effect of the introduction of CNTs on the thermal stability could be evaluated with the corresponding nanocomposite sample containing 0.5 wt% of CNTs. Quite unexpectedly, it can be seen that thermal stability is slightly diminished upon the introduction of CNTs. For instance, T70 is decreased from 408.5 °C to 403.5 °C through the addition of CNTs. Such unexpected results could be attributed to the change of character from thermoset into thermoplastic upon the inclusion of carbon nanotubes. In fact, the formation of cross-links was impeded due to the steric hindrance effect of the CNTs, which might be the reason for the reduced thermal stability.
Quite unexpectedly, the observed trend is reversed in the case of PU-2 and PUCNT-2, since the nanocomposite sample exhibited a higher thermal stability within a wide temperature range. In fact, the presence of CNTs in this system is associated with opposing effects. On the one hand, CNTs tend to improve the thermal stability of PU due to the formation of a carbonaceous char and the so-called tortuous path mechanism. On the other hand, the steric hindrance effect of CNTs on the formation of cross-links leads to a reduction of thermal stability due to the lower level of cross-linking density. However, once the NCO/OH ratio is further increased from 1.7 to 2, the hindrance effect becomes weaker due to the very high amount of diisocyanate in the system, and thus, the other effect, namely the formation of a carbonaceous char layer, dominates, leading to the better thermal stability of PUCNT-2 compared to PU-2.
4. Conclusions
This paper focuses on the experimental production of novel value-added materials from PET waste. PET waste can be depolymerized by glycolysizing it with MPD. Polyester diol can then be obtained by reacting the glycolysized products with adipic acid. Characterization analyses were performed, namely NMR, FT-IR, OH-value index, and viscosity-Brookfield, and confirmed the trans-esterification reaction of PET and the destruction of its polymer chain to prepare diol, as well as the step polymerization of diol with adipic acid for synthesizing polyester diol. The novel value-added polyurethanes and polyurethane nanocomposites were then synthesized by reaction of this polyester diol with hexamethylene diisocyanate. The prepared samples were characterized by FT-IR, swelling tests, DSC, and TGA. The experimental results can be summarized as follow:(1) A comparison of the polyurethanes with the nanocomposites showed a characteristic difference in their physical state. Unlike with the polyurethanes, the formation of cross-links was impeded in the case of nanocomposites once the NCO/OH molar ratio was higher than unity.
(2) The PU-1.7 sample exhibited a higher cross-link density compared to PU-2 during swelling.
(3) Comparisons of the Mc, νe, and ν data obtained by the swelling studies in different solvents showed that they follow an irregular trend. However, both the equilibrium sorption value (Qe) and the rate of solvent uptake followed the same trend in the cross-linked polyurethanes (PU-1.7 and PU-2). It was also found that Qe and the rate of solvent uptake were higher for PU-2 than PU-1.7.
(4) The transport of solvents followed the Fickian sorption mechanism, and the Deborah number was less than unity.
(5) The solvent absorption followed a pseudo-second-order kinetics.
(6) A comparison of D*, S, and P between the PU-1.7 and PU-2 samples in the different solvents showed higher a penetrant diffusion in PU-2 than in PU-1.7.
(7) It was found that the magnitude of the intrinsic diffusion coefficient parameter of the solvents through the polyurethane samples were in the following order: chloroform, DMAc, DCM > DMF > THF > DMSO > methanol > ethanol > toluene > hexane.
The DSC and TGA analyses revealed various interesting results for both the NCO/OH molar ratio and CNT particles as follow:
(1) From the first heating scan in the DSC analyses, in the case of PU-1 and PUCNT-1.7, several melting endotherms could be observed. For the other samples, these endotherms either disappeared or became very insignificant. The detected endotherms in the first heating scan could be attributed to the melting of the crystals formed during the casting of the as-synthesized polymers.
(2) At cooling scan in DSC, there isn't seen any crystalline area in thermograms for all samples.
(3) In the second heating scan, PU-1 showed no melting endotherms. However, PU-1.7 exhibited a rather insignificant melting endotherm at temperatures near 200 °C. Nevertheless, compared to PU-2, a higher level of phase separation was detected for PU-1.7, resulting in the formation of stronger hard-segment domains, which might have led to crystallization of the hard segments. When comparing the observed melting behavior in the case of PU-1.7 with PUCNT-1.7, it can be seen that, instead of a high temperature endotherm, a melting peak appears around 30 °C for the nanocomposite sample, with this peak belonging to an insignificant formation of crystals in the soft segment. The reduced level of phase separation regarding PU-1.7, due to the steric hindrance effect of the CNT particles, could be the reason for the disappearance of the high temperature endotherm. Another difference for the PU-2 and PUCNT-2 samples, is the appearance of a very weak melting endotherm at around 210 °C. This difference can be attributed to the thermoplastic character of PUCNT-2, and thus the higher mobility of the PU chains.
(4) The TGA analyses showed that for all the polyurethanes and nanocomposites, the decomposition started at approximately 230 °C and ended at around 500 °C. All the polyurethane samples, regardless of the NCO/OH ratio or CNT inclusion, underwent two major degradation stages related to hard and soft-segment degradation. Increasing the NCO/OH ratio in the case of PU-1.7 and PU-2 increased the thermal stability of the hard segment (T10–T60) as compared to PU-1, while a further increment of the NCO/OH ratio from 1.7 to 2 caused a reduction in the thermal stability. The thermal stability of the soft segment (T70–T90) conformed to the following trend: PU-1 > PU-1.7 > PU-2. Another interesting observation was that thermal stability of PUCNT-2 was higher than that of PUCNT-1.7 over the whole temperature range. Quite unexpectedly, the observed trend was reversed in the case of PU-2 and PUCNT-2, since the nanocomposite sample exhibited higher thermal stability over a wide temperature range. In fact, the presence of CNTs in this system is associated with opposing effects. On the one hand, the inclusion of CNTs tends to improve the thermal stability of PU due to formation of a carbonaceous char and the so-called tortuous path mechanism. On the other hand, the steric hindrance effect of CNTs on the formation of cross-links leads to a reduction in the thermal stability due to the lower level of cross-linking density. However, once the NCO/OH ratio is further increased from 1.7 to 2, the hindrance effect becomes weaker due to the very high amount of diisocyanate in the system, and thus, the other effect, which is the formation of a carbonaceous char layer, dominates, leading to the better thermal stability of PUCNT-2 compared with PU-2.
Finally, good agreement was found between the experimental data obtained for the polyurethanes and carbon nanotube-based composites prepared from PET waste.
References
- J. Scheirs, Polymer recycling: science, technology and applications, Wiley, 1998 Search PubMed.
- http://www.mcgroup.co.uk/news/20140117/global-pet-supply-exceed-2439-mln-tonnes-2015.html CrossRef CAS; D. Paszun and T. Spychaj, Chemical Recycling of Poly(ethylene terephthalate), Ind. Eng. Chem. Res., 1997, 36(4), 1373–1383 CrossRef CAS.
- D. Abu Bakar, I. Ahmad and A. Ramli, Malays. J. Biochem. Mol. Biol., 2006, 8, 22–26 Search PubMed.
- A. B. Raheem and L. Uyigue, Arch. Appl. Sci. Res., 2010, 2(4), 240–254 CAS.
- K. P. Blackmon, D. W. Fox and S. J. Shafer, US Pat., 4973746, 1990.
- R. Shamsi, M. Abdouss, G. Mir Mohamad Sadeghi and F. AfsharTaromi, Polym. Int., 2009, 58, 22–30, DOI:10.1002/pi.2488.
- G. Mir Mohamad Sadeghi, R. Shamsi and M. Sayaf, J. Polym. Environ., 2011, 19, 522–534, DOI:10.1007/s10924-011-0283-7.
- S. Elsaeed and R. Farag, J. Appl. Polym. Sci., 2009, 112, 3327–3336, DOI:10.1002/app.29527.
- Y. Parab, N. Pingale and S. Shukla, J. Appl. Polym. Sci., 2012, 125, 1103–1107, DOI:10.1002/app.34855.
- M. Tawfik, N. Ahmed and S. Eskander, J. Appl. Polym. Sci., 2011, 120, 2842–2855, DOI:10.1002/app.33350.
- T. Spychaj, E. Fabrycy, S. Spychaj and M. Kacperski, J. Mater. Cycles Waste Manage., 2001, 3, 24–31 CAS.
- A. Kumar and T. Rajeswara Rao, J. Appl. Polym. Sci., 2003, 87, 1781–1783 CrossRef CAS.
- C. Kao, W. Cheng and B. Wan, J. Appl. Polym. Sci., 1998, 70, 1939–1945 CrossRef CAS.
- R. Campanelli, D. Cooper and M. Kama, J. Appl. Polym. Sci., 1994, 53, 985–991 CrossRef.
- G. Grause, T. Handa, T. Kameda, T. Mizoguchi and T. Yoshioka, Chem. Eng. J., 2011, 166, 523–528, DOI:10.1016/j.cej.2010.11.010.
- R. López-Fonseca, J. R. González-Velasco and J. I. Gutiérrez-Ortiz, Chem. Eng. J., 2009, 146, 287–294, DOI:10.1016/j.cej.2008.09.039.
- H. Kurokawa, M. Ohshima, K. Sugiyama and H. Miura, Polym. Degrad. Stab., 2003, 79, 529–533, DOI:10.1016/s0141-3910(02)00370-1.
- Q. Liu, R. Li and T. Fang, Chem. Eng. J., 2015, 270, 535–541, DOI:10.1016/j.cej.2015.02.039.
- C. Chen, J. Appl. Polym. Sci., 2003, 87, 2004–2010, DOI:10.1002/app.11694.
- M. Ghaemy and K. Mossaddegh, Polym. Degrad. Stab., 2005, 90, 570–576, DOI:10.1016/j.polymdegradstab.2005.03.011.
- I. Vitkauskienė and R. Makuška, Chemija, 2008, 19, 29–34 Search PubMed.
- A. Sabnis, V. Bhave, M. Kathalewar, S. Mare and P. Raut, Arch. Appl. Sci. Res., 2012, 4(1), 85–93 CAS.
- C. Aiemsa-art, P. Phanwiroj and P. Potiyaraj, Energy Procedia, 2011, 9, 428–434, DOI:10.1016/j.egypro.2011.09.047.
- G. Colomines, A. Lee, J. Robin and B. Boutevin, Macromol. Chem. Phys., 2006, 207, 1461–1473, DOI:10.1002/macp.200600189.
- Y. Öztürka and G. Güçlüa, Polym.-Plast. Technol. Eng., 2005, 43, 1539–1552, DOI:10.1081/ppt-200030272.
- M. Abdelaal, T. Sobahi and M. Makki, Construct. Build. Mater., 2011, 25, 3267–3271, DOI:10.1016/j.conbuildmat.2011.03.013.
- S. Mansour and N. Ikladious, Polym. Test., 2002, 21, 497–505 CrossRef CAS.
- D. Suh, O. Park and K. Yoon, Polymer, 2000, 41, 461–466, DOI:10.1016/s0032-3861(99)00168-8.
- O. Saravari, B. Vessabutr and V. Pimpan, J. Appl. Polym. Sci., 2004, 92, 3040–3045 CrossRef CAS.
- F. F. Pardal and G. Tersac, Polym. Degrad. Stab., 2006, 91, 2567–2578, DOI:10.1016/j.polymdegradstab.2006.05.016.
- M. Patel, J. Patel, D. Mishra and V. Sinha, J. Polym. Environ., 2007, 15, 97–105, DOI:10.1007/s10924-007-0050-y.
- M. Kathalewar, N. Dhopatkar, B. Pacharane, A. Sabnis, P. Raut and V. Bhave, Prog. Org. Coat., 2013, 76, 147–156 CrossRef CAS.
- R. López-Fonseca, I. Duque-Ingunza, B. de Rivas, L. Flores-Giraldo and J. I. Gutiérrez-Ortiz, Chem. Eng. J., 2011, 168, 312–320, DOI:10.1016/j.cej.2011.01.031.
- M. E. Viana, A. Riul, G. M. Carvalho, A. F. Rubira and E. C. Muniz, Chem. Eng. J., 2011, 173, 210–219, DOI:10.1016/j.cej.2011.07.031.
- S. Cakić, I. Ristić, M. M. Cincović, N. Nikolić, O. Ili, D. Stojiljković and J. B. Simendić, Prog. Org. Coat., 2012, 74, 115–124, DOI:10.1016/j.porgcoat.2011.11.024.
- M. Billiau-Loreau, G. Durand and G. Tersac, Polymer, 2002, 43, 21–28 CrossRef CAS.
- R. Vaidya and V. Nadkarni, J. Appl. Polym. Sci., 1988, 35, 775–785 CrossRef.
- S. Lee, Y. Sze and C. Lin, J. Appl. Polym. Sci., 1994, 52, 869–873 CrossRef CAS.
- S. Lee, Y. Sze and C. Lin, J. Appl. Polym. Sci., 1995, 55, 1271–1273 CrossRef CAS.
- G. Colomines, F. Rivas, M. Lacoste and J. Robin, Macromol. Mater. Eng., 2005, 290, 710–720, DOI:10.1002/mame.200400391.
- P. Pokharel and D. S. Lee, Chem. Eng. J., 2014, 253, 356–365, DOI:10.1016/j.cej.2014.05.046.
- H. Souguir, F. Salaün, P. Douillet, I. Vroman and S. Chatterjee, Chem. Eng. J., 2013, 221, 133–145 CrossRef CAS.
- S. Das, A. K. Banthia and B. Adhikari, Chem. Eng. J., 2008, 138, 215–223 CrossRef CAS.
- G. Colomines, J. Robin and G. Tersac, Polymer, 2005, 46, 3230–3247, DOI:10.1016/j.polymer.2005.02.047.
- D. Pavia, G. Lampman and G. Kriz, Introduction to Spectroscopy, Brooks Cole, 3rd edn, 2000, ISBN 0030319617, 9780030319617 Search PubMed.
- G. Mir Mohammad Sadeghi, J. Morshedian and M. Barikani, Polym. Test., 2003, 22, 165–168 CrossRef.
- M. Mohammadnia, P. Salaryan, Z. KhaliliAzimi and F. TatarogluSeyidov, IJCBS, 2012, 2, 36–41 Search PubMed.
- D. Crawford and J. Escarsega, Thermochim. Acta, 2000, 357–358, 161–168 CrossRef CAS.
- L. Bistričić, M. Leskovac, G. Baranović and S. Lučić Blagojević, J. Appl. Polym. Sci., 2008, 108, 791–803, DOI:10.1002/app.27754.
- D. K. Chattopadhyay, B. Sreedhar and K. V. S. N. Raju, Polymer, 2006, 47, 3814–3825, DOI:10.1016/j.polymer.2006.03.092.
- H. L. Sui, X. Y. Liu, F. C. Zhong, X. Y. Li and X. Ju, Polym. Degrad. Stab., 2013, 98, 255–260 CrossRef CAS.
- M. Velencoso, M. Ramos, R. Klein, A. De Lucas and J. Rodriguez, Polym. Degrad. Stab., 2014, 101, 40–51 CrossRef CAS.
- G. Biemond, J. Feijen and R. Gaymans, Macromol. Mater. Eng., 2009, 294, 492–501, DOI:10.1002/mame.200900093.
- U. Šebenik and M. Krajnc, Int. J. Adhes. Adhes., 2007, 27, 527–535, DOI:10.1016/j.ijadhadh.2006.10.001.
- L. H. Sperling, Introduction to physical polymer science, Wiley, New York, Chichester, 2nd edn, 1992 Search PubMed.
- S. Das, P. Pandey, S. Mohanty and S. Nayak, Mater. Express, 2015, 5, 377–389, DOI:10.1166/mex.2015.1254.
- S. Li, R. Vatanparast and H. Lemmetyinen, Polymer, 2000, 41, 5571–5576 CrossRef CAS.
- D. W. Van Krevelen, Properties of polymers: their correlation with chemical structure; their numerical estimation and prediction from additive group contributions, Elsevier Science, Amsterdam, 3rd edn, 1990 Search PubMed.
- Polymer Handbook, ed. J. Brandrup, E. H. Immergut and E. A. Grulke, John Wiley, New York, 4th edn, 1999, vol. 7, pp. 675–711 Search PubMed.
- C. Prisacariu, Polyurethane Elastomers: From Morphology to Mechanical Aspects, Springer-Verlag/Wien, 2011, DOI:10.1007/978-3-7091-0514-6, ISBN 978-3-7091-0513-9.
- L. Masaro and X. Zhu, Prog. Polym. Sci., 1999, 24, 731–775 CrossRef CAS.
- L. H. Sperling, Introduction to Physical Polymer Science, Wiley Interscience, 4th edn, 2006, 13987-0-471-70606-9 Search PubMed.
- J. Vrentas, C. Jarzebski and J. Duda, A Deborah number for diffusion in polymer-solvent systems, AIChE J., 1975, 21, 894–901 CrossRef CAS , ISSN 0001–1541 No. 5.
- S. Lagergren, K. Sven. Vetenskapsakad. Handl., 1898, 24(4), 1–39 Search PubMed.
- Y. S. Ho and G. McKay, Process Saf. Environ. Prot., 1998, 76(4), 332–340 CrossRef CAS.
- C. Zhou, Q. Wu, T. Lei and I. Negulescu, Chem. Eng. J., 2014, 251, 17–24 CrossRef CAS.
- S. B. Harogoppad and T. M. Aminabhavi, Macromolecules, 1991, 24, 2598–2605, DOI:10.1021/ma00009a070.
- H. Kumar and H. Siddaramaiah, Polymer, 2005, 46, 7140–7155 CrossRef CAS.
- S. Gopakumar and M. Gopinathan Nair, Polymer, 2005, 46, 10419–10430 CrossRef CAS.
- S. George and S. Thomas, Prog. Polym. Sci., 2001, 26, 985–1017 CrossRef CAS.
- S. Prager, E. Bagley and F. Long, J. Am. Chem. Soc., 1953, 75, 1255–1256 CrossRef CAS.
- G. Hung, Microchem. J., 1974, 19, 130–152 CrossRef CAS.
- J. MarkoÅ, Mass Transfer in Chemical Engineering Processes, In. Tech, 2011, ISBN 978-953-307-619-5 Search PubMed.
- D. Chattopadhyay and D. Webster, Prog. Polym. Sci., 2009, 34, 1068–1133 CrossRef CAS.
- Z. Petrović, Z. Zavargo, J. Flyn and W. Macknight, J. Appl. Polym. Sci., 1994, 51, 1087–1095 CrossRef.
- S. Levchik and E. Weil, Polym. Int., 2004, 53, 1585–1610 CrossRef CAS.
- M. Corcuera, L. Rueda, B. Fernandez d’Arlas, A. Arbelaiz, C. Marieta, I. Mondragon and A. Eceiza, Polym. Degrad. Stab., 2010, 95, 2175–2184, DOI:10.1016/j.polymdegradstab.2010.03.001.
| This journal is © The Royal Society of Chemistry 2016 |