Colloidal nanocrystal superlattices as phononic crystals: plane wave expansion modeling of phonon band structure†
Seid M. Sadat and
Robert Y. Wang*
School for Engineering of Matter, Transport & Energy, Arizona State University, Tempe, Arizona 85287, USA. E-mail: rywang@asu.edu
First published on 29th April 2016
Abstract
Colloidal nanocrystals consist of an inorganic crystalline core with organic ligands bound to the surface and naturally self-assemble into periodic arrays known as superlattices. This periodic structure makes superlattices promising for phononic crystal applications. To explore this potential, we use plane wave expansion methods to model the phonon band structure. We find that the nanoscale periodicity of these superlattices yield phononic band gaps with very high center frequencies on the order of 102 GHz. We also find that the large acoustic contrast between the hard nanocrystal cores and the soft ligand matrix lead to very large phononic band gap widths on the order of 101 GHz. We systematically vary nanocrystal core diameter, d, nanocrystal core elastic modulus, ENC core, interparticle distance (i.e. ligand length), L, and ligand elastic modulus, Eligand, and report on the corresponding effects on the phonon band structure. Our modeling shows that the band gap center frequency increases as d and L are decreased, or as ENC core and Eligand are increased. The band gap width behaves non-monotonically with d, L, ENC core, and Eligand, and intercoupling of these variables can eliminate the band gap. Lastly, we observe multiple phononic band gaps in many superlattices and find a correlation between an increase in the number of band gaps and increases in d and ENC core. We find that increases in the property mismatch between phononic crystal components (i.e. d/L and ENC core/Eligand) flattens the phonon branches and are a key driver in increasing the number of phononic band gaps. Our predicted phononic band gap center frequencies and widths far exceed those in current experimental demonstrations of 3-dimensional phononic crystals. This suggests that colloidal nanocrystal superlattices are promising candidates for use in high frequency phononic crystal applications.
1. Introduction
Phonons are vibrational waves that transport sound and heat.1 The phononic band diagram (also known as the dispersion relationship) relates the frequency of a given phonon to its corresponding wave vector and is analogous to electronic and photonic band diagrams. By exercising control over the phonon band structure, it is possible to manipulate the transport of sound and heat. One common method of engineering band structure is to create phononic crystals, which are artificially made materials with periodic variations in acoustic impedance (e.g. alternating hard and soft materials). This periodicity results in a phononic band gap that forbids the propagation of phonons in a particular frequency range.2–5 The phononic crystal is the vibrational wave analogue to the well-known photonic crystal, which uses periodic variations in refractive index to create a photonic band gap.6,7 Two key characteristics of a phononic band gap are its center frequency and its width. The band gap fundamentally arises from wave interference, which requires that the periodicity be comparable to the phonon wavelength; hence shorter periodicities lead to phononic band gaps with higher center frequencies. The width of the phononic band gap depends on the acoustic impedance ratio of the phononic crystal's components; the further this ratio deviates from unity, the wider the band gap.2 Hence a phononic crystal made of alternating hard and soft materials will have a wider band gap than one made of two alternating hard materials. Depending on the number of dimensions in which periodicity occurs, phononic crystals are described as 1-, 2-, or 3-dimensional (i.e. periodic planes, cylinders, and spheres, respectively). Phononic crystals are a promising class of materials for sound and heat manipulation and have been used to create phonon waveguides, cavities, filters, sensors, switches and rectifiers.8–14Phononic crystals are commonly constructed through the assembly of macroscopic building blocks or top-down fabrication methods such as lithography.15–17 These fabrication approaches have yielded phononic band gaps with center frequencies in the ∼1 kHz to 10 GHz frequency range. Extending this center frequency range above 10 GHz is desirable because such structures can potentially manipulate heat conduction14,18,19 and/or enable novel optomechanical devices.20–23 Creating phononic band gaps in this frequency range generally requires nanostructured materials with periodicities of ≤10 nm. While 1-dimensional phononic crystals made via sequential thin film deposition have achieved band gaps in this frequency range,24,25 creating 3-dimensional periodicities on this length scale is much more difficult. Phononic band gaps with center frequencies above 10 GHz have yet to be experimentally observed in 3-dimensional phononic crystals.26,27
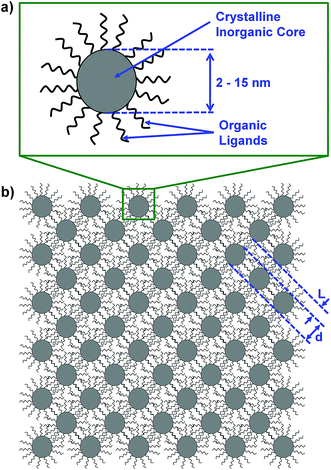
In this work, we suggest that colloidal nanocrystals form a natural basis for the bottom-up assembly of 3-dimensional phononic crystals with record high frequency band gaps. Colloidal nanocrystals consist of an inorganic crystalline core with organic ligands (e.g. oleic acid, alkanethiols, etc.) bound to the surface (Fig. 1a). Elegant precision and control over colloidal nanocrystal size, shape, and composition is now commonplace and is summarized in a number of reviews.28–31 Colloidal nanocrystal-based materials have received attention for a wide range of applications spanning photovoltaics,32,33 light-emitting diodes,34,35 thermoelectrics,36–38 thermal storage,39–41 and electronics.42,43 In contrast, the use of colloidal nanocrystals for phononic crystals has received very limited attention.44,45 The diameter of a colloidal nanocrystal core is typically controlled to be between ∼2 and 15 nm, which overlaps nicely with the necessary length-scales needed to achieve phononic band gaps in the 101 to 102 GHz frequency range. In addition, van der Waals interactions between the nanocrystal ligand molecules facilitate the self-assembly of colloidal nanocrystals into periodic three-dimensional arrays.46,47 Analogous to the atomic lattice of a crystal, the colloidal nanocrystal community refers to these assemblies as “nanocrystal superlattices.” These superlattices are a natural choice for phononic crystals because their periodic nanocrystal cores and ligand matrix can function as the two components of a phononic crystal (Fig. 1b). In addition to having high band gap center frequencies due to small-scale periodicity, colloidal nanocrystal superlattices should also have wide band gaps due to the acoustic contrast between the hard inorganic nanocrystal cores and the soft ligand matrix.
In this work, we use plane wave expansion (PWE) techniques to model the phonon band structure of colloidal nanocrystal superlattices and explore their potential as phononic crystals. Our modeling demonstrates that superlattices can have phononic band gaps with center frequencies on the order of ∼102 GHz and band gap widths on the order of ∼101 GHz. We also systematically vary nanocrystal core diameter, d, nanocrystal core elastic modulus, ENC core, interparticle distance (i.e., ligand length), L, and ligand elastic modulus, Eligand, and report on the corresponding effects on the phonon band structure. Our modeling shows that the band gap center frequency increases as d and L are decreased, or as ENC core and Eligand are increased. The band gap width behaves non-monotonically with d, L, ENC core, and Eligand, and intercoupling of these variables can eliminate the band gap. Lastly, we observe multiple phononic band gaps in many superlattices and find a correlation between an increase in the number of band gaps and increases in d and ENC core. We find that increases in the property mismatch between phononic crystal components (i.e., d/L and ENC core/Eligand) flattens the phonon branches and is a key driver in increasing the number of phononic band gaps.
2. Methodology
Calculating the phonon band structure requires solving for the phononic crystal's normal modes of vibration and determining their corresponding characteristic frequencies. This is often accomplished using finite difference time domain methods,48–50 finite element methods,45,51,52 plane wave expansion (PWE) methods,53–55 and combined molecular dynamics–lattice dynamics approaches.44,56,57 We utilize the PWE method to determine the phonon band structure in this paper. The PWE method's chief strength is that in-house codes that are computationally inexpensive and adaptable to parallel computation can be written with relative ease. This enables users to achieve maximum control over their computational goals. While many commercial finite element method packages are available, computational flexibility is lost when using these packages. Although molecular dynamics and finite difference time domain methods are also powerful approaches, they suffer from being computationally expensive.In the PWE method, the elastic wave equation is converted into an eigenvalue/eigenvector problem by utilizing the periodicity of the lattice and Bloch's theorem.58 Since the eigenvectors and eigenvalues correspond to the phonon wave vectors, k, and angular frequencies, ω, the PWE method directly yields the phonon band diagram. Our implementation of the PWE method follows the procedure described by Economou and Sigalas.53,59 We begin with the elastic wave equation in three dimensions for a locally isotropic medium:
 | (1) |
 | (2a) |
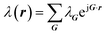 | (2b) |
 | (2c) |
 | (3) |
| u = ej(k·r − ωt) | (4) |
Eqn (1)–(4) can be combined to yield the following eigenvalue problem:53
 | (5) |
 | (6a) |
 | (6b) |
To apply the PWE method to colloidal nanocrystal superlattices we consider the nanocrystal cores and nanocrystal ligands as the two components of a phononic crystal (i.e. a periodic arrangement of inorganic spheres embedded in ligand matrix). We focus our modeling effort on face-centered-cubic lattices because this is the arrangement that colloidal nanocrystal superlattices most commonly adopt.61 Fig. 2 illustrates the conventional unit cell, primitive unit cell, and first Brillouin zone of a face-centered cubic lattice with nanocrystal diameter, d, interparticle distance, L, and lattice constant, a.
Of the many varieties of colloidal nanocrystal superlattices, the most complete set of experimentally measured mechanical properties correspond to superlattices consisting of PbS nanocrystals with oleic acid ligands.60–62 Consequently we initiate our phonon band diagram discussion on this particular superlattice (Fig. 3), and use input values of interparticle distance, L = 1.5 nm, nanocrystal core elastic modulus, ENC core = 54 GPa, ligand matrix elastic modulus, Eligand = 2.6 GPa, nanocrystal core density, ρNC core = 7600 kg m−3, ligand matrix density, ρligand = 895 kg m−3, nanocrystal core Poisson's ratio, νNC core = 1/3, and ligand matrix Poisson's ratio, νligand = 1/3. Unless otherwise stated, these parameters are used in all of this paper's calculations.
Since the PWE method assumes that the phonon medium can be treated as a continuum, there is a maximum frequency and minimum length scale for which it is valid. Past studies have shown that continuum methods can reasonably predict phonon band structures up to a frequency of ∼1 THz.64,65 To stay well below this threshold, we limit our model to frequencies ≤500 GHz. Furthermore, the shortest phonon wavelength considered in our calculations is 37.9 Å (this corresponds to the W point in the Brillouin zone for a nanocrystal core diameter of 2 nm and interparticle distance of 1 nm). This phonon wavelength is an order of magnitude larger than typical interatomic distances and represents a reasonable threshold for applying continuum approximations. Our use of the elastic wave equation implicitly assumes that the mechanical response of the material is within the linear regime, which means that our model only considers small vibrational wave amplitudes. The PWE method also uses periodic boundary conditions, which is equivalent to having perfect superlattice order. The primary effect of superlattice disorder would be to introduce phonon scattering sites and/or localized phonons (i.e. phonons that are not plane waves) that are not captured in the band diagram. In addition to the physical approximations of our methodology, numerical accuracy of our code is also important. To confirm our accuracy, we have checked it for computational convergence and benchmarked it against other PWE results in the literature (see Fig. S2†). Additional details on the computational methodology used in this work are available in the ESI.†
3. Results and discussion
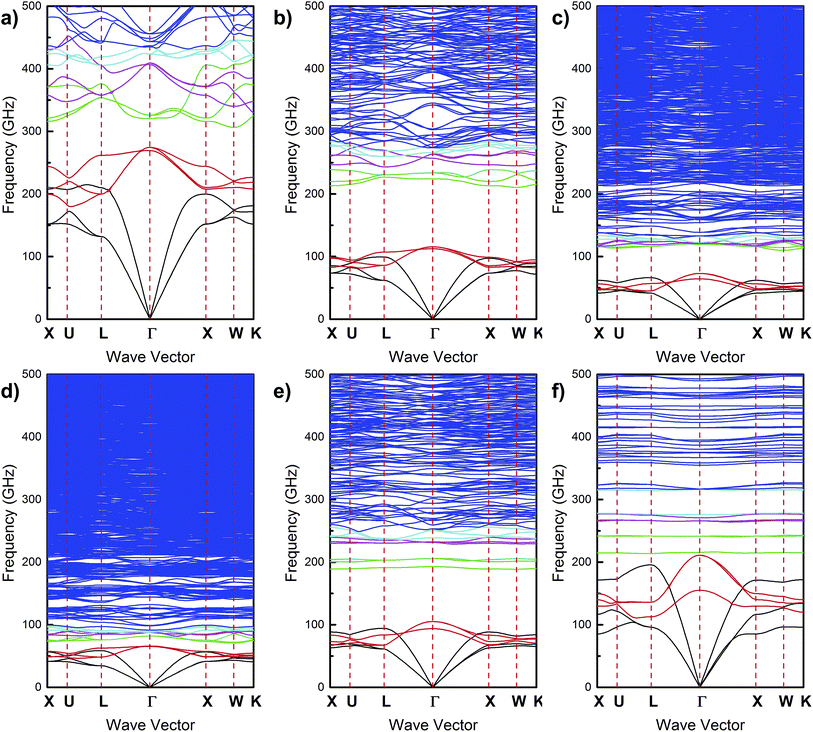
Fig. 3 shows the phonon band diagram for a superlattice consisting of PbS nanocrystals with oleic acid ligands and illustrates that these materials can have wide phononic band gaps with center frequencies in the 100 GHz-range. Phononic crystals with 3-dimensional periodicity commonly have band gaps that exist only along particular crystallographic directions. A band gap that exists in every direction is less common and is referred to as an “absolute” or “complete” band gap.66 Fig. 3 shows that the PbS nanocrystal – oleic acid ligand superlattice exhibits this less common feature. The phonon branches that intersect the Γ point at the origin are known as “acoustic” branches whereas those that intersect the Γ point at non-zero frequency are known as “optical” branches. These branches appear in groups of three due to the three mechanical degrees of freedom. In typical atomic crystals (e.g. bulk GaP, AlAs, GaSb, etc.), the band gap commonly resides in between the acoustic phonon branches and the first set of optical branches. In contrast, the phononic band gap in the nanocrystal superlattice falls in between the first and second set of optical branches. Accompanying this band gap characteristic is a strong frequency overlap between the first set of optical phonon branches and the acoustic branches. This frequency overlap creates a large phase space for phonon–phonon scattering processes that satisfy scattering selection rules (i.e., conservations of energy and crystal momentum). This large phase space in turn creates opportunities for fast energy transfer between acoustic and optical phonons. Furthermore, since optical phonons interact with light and acoustic phonons do not, this frequency resonance between the optical and acoustic phonons suggests that fast energy transfer between photons and acoustic phonons can occur in nanocrystal superlattices.We next discuss the effect of changing the nanocrystal core diameter, interparticle distance, and colloidal nanocrystal mechanical properties on the phonon band structure. In principle, there are eight phononic crystal variables, d, L, ENC core, Eligand, ρNC core, ρligand, νNC core, and νligand. We vary the nanocrystal core through a typical colloidal nanocrystal diameter range of 2–15 nm. The interparticle distance in a nanocrystal superlattice is controlled by the organic ligands on the nanocrystal core surface. These ligands are typically small organic molecules such as oleic acid and alkanethiols. Consequently we vary the interparticle distance and matrix elastic modulus from 1–3 nm and 1–8 GPa, respectively, which are ranges that are representative of typical organic ligands. Since a very wide variety of nanocrystal core compositions are possible,28–31 we vary the elastic modulus of the nanocrystal core over a large range of 10–1250 GPa. We found that varying Poisson's ratio had only a minor effect on the phononic band gap characteristics, and we therefore leave out discussion of this parameter (Fig. S6 in ESI†). Inspection of eqn (5) and (6) reveal that density only shows up as a denominator for the elastic modulus and Poisson's ratio (i.e. E/ρ and ν/ρ). Since Poisson's ratio has only a minor effect on the band gap characteristics, the effect of varying density can be inferred by rescaling our results for varying elastic modulus. Phononic crystals are often described in terms of their volume fraction of matrix inclusions, which in our case corresponds to the nanocrystal core volume fraction. Since our calculations vary both nanocrystal core diameter and interparticle distance (which is directly related to ligand length, see Fig. 1), our calculations implicitly span a nanocrystal core volume fraction range of 4.7% to 61.0%. Lastly, we note that in some cases we observe multiple phononic band gaps (see below); however, the most prominent band gap is the gap occurring between the first and second set of optical branches. Unless otherwise stated, the following discussion focuses on this band gap.
Fig. 4a shows that decreasing the nanoparticle diameter and/or interparticle distance increases the center frequency of the band gap. This behavior arises because the center frequencies of phononic band gaps correspond to wavelengths that satisfy the Bragg condition (i.e., constructive interference of scattered waves from a periodic medium). Decreasing the nanoparticle diameter and/or interparticle distance decreases the unit cell length, which decreases the Bragg wavelength and increases the center frequency. The impact of changing interparticle distance on the center frequency is most pronounced at smaller nanoparticle diameters. This is because interparticle distance changes lead to large relative changes in unit cell sizes in this diameter regime. For large nanoparticle diameters, the effect of interparticle distance on center frequency is small because the unit cell size is dominated by the nanoparticle diameter. The band gap width can go to zero when combining small nanocrystal diameters with large interparticle distances and so we do not plot center frequencies in these instances (Fig. 4a).
 | ||
| Fig. 4 The effect of nanocrystal core diameter on the center frequency of the phononic band gap for: (a) varying interparticle distance, L; (b) varying elastic modulus of the ligand matrix, Eligand; and (c) varying elastic modulus of the nanocrystal core, ENC core. Unless otherwise specified, L, Eligand, and ENC core are fixed at 1.5 nm, 2.6 GPa, and 54 GPa, respectively. An equivalent version of this figure shown as a function of nanocrystal core volume fraction can be found in Fig. S4 of the ESI.† | ||
As the elastic modulus of the ligand matrix or nanocrystal core is increased, the center frequency of the phononic band gap increases monotonically (Fig. 4b and c). Although the band gap center frequency increases in all cases, the magnitude of this increase is size dependent and depends on whether the modulus of the nanocrystal core or ligand matrix is changing. The ligand modulus has the greatest impact on the band gap center frequency at small nanoparticle diameters (Fig. 4b). This is intuitive because the ligands make up the greatest fraction of the unit cell when the nanoparticle diameters are small. Analogously, the nanocrystal core modulus has the greatest impact at large nanoparticle diameters because this is when the nanocrystal cores make up the largest fraction of the unit cell (Fig. 4c). Notably the band gap disappears at large diameters when the nanocrystal core modulus is very soft or very hard. For example, we do not observe band gaps above 9 and 13 nm diameters for nanocrystal core moduli of 1250 and 10 GPa, respectively.
The acoustic contrast between the soft ligand matrix and hard nanocrystal cores leads to large band gap widths of up to ∼130 GHz for 2 nm diameters and 1 nm interparticle distances (Fig. 5a). Interestingly, we observe a non-monotonic relationship between band gap width and nanoparticle diameter. The band gap width first rises with increasing diameter, reaches a maximum value at a critical diameter, dcrit, and then decreases. One implication of this non-monotonic behavior is that not all colloidal nanocrystal superlattices will have phononic band gaps. For example, our model predicts the absence of a phononic band gap for nanocrystal diameters below 4 nm with an interparticle distance of 3.0 nm.
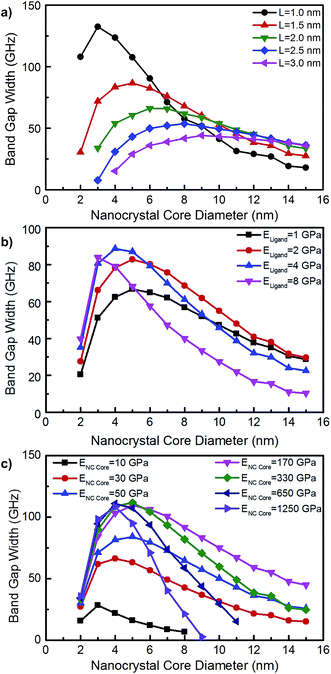 | ||
| Fig. 5 The effect of nanocrystal core diameter on the phononic band gap width for: (a) varying interparticle distance, L; (b) varying elastic modulus of the ligand matrix, Eligand; and (c) varying elastic modulus of the nanocrystal core, ENC core. Unless otherwise specified, L, Eligand, and ENC core are fixed at 1.5 nm, 2.6 GPa, and 54 GPa, respectively. An equivalent version of this figure shown as a function of nanocrystal core volume fraction can be found in Fig. S5 of the ESI.† | ||
The combined effects of d, L, Eligand, and ENC core on phononic band gap width can be visualized in Fig. 5a–c. These figures collectively reveal an intricate and rich behavior between these parameters and phononic band gap width. This behavior is best visualized in Fig. 5c, which shows the relationship between phononic band gap width and nanocrystal core diameter for a large range of ENC core, 10–1250 GPa. In addition to an increasing band gap width below dcrit and a decreasing band gap width above dcrit, a second non-monotonic behavior is observed in Fig. 5c. For nanocrystal core diameters 4 nm and larger, we see that the band gap width first increases with increasing ENC core, reaches a maximum, and then decreases with increasing ENC core. For example, nanocrystal core diameters of 8 nm have an increasing band gap width for 10 GPa < ENC core < 170 GPa and decreasing band gap width for 170 GPa < ENC core < 1250 GPa. This behavior causes the right sides of the curves in Fig. 5c to first sweep diagonally up and then sweep diagonally down as ENC core is changed from 10 to 1250 GPa. A similar, but subtler behavior can be seen in Fig. 5a and b. The subtlety of this behavior for changes in L and Eligand in Fig. 5 arises because these parameters span a more narrow range than ENC core.
The fact that band gap width increases, reaches a maximum, and then decreases as d, L, Eligand, and ENC core are varied suggests that these four parameters impact band gap width in similar manners. This type of behavior has also been observed by Zanjani and Lukes,45 who found that as interparticle distance increased, the phononic band gap width increased, reached a maximum, and then decreased. They explained the origin of this behavior by studying the Bragg frequencies of each phononic crystal component and utilizing a transfer matrix model. Their modeling found that as the Bragg frequency mismatch between the two components increased, the band gap first widened, then reached a maximum at moderate Bragg frequency separation, and then narrowed. Since Bragg frequency is proportional to the square root of elastic modulus and inversely proportional to length, this Bragg frequency explanation can also explain our observed effects of elastic modulus on phononic band gap width. The four parameters varied in Fig. 5, d, L, Eligand, and ENC core, all have similar effects on the band gap width because each parameter has a role in determining the overall Bragg frequency mismatch between the nanocrystal cores and ligand matrix. In effect, the band gap width data in Fig. 5 represents slices of a surface in a 4-dimensional space (i.e. d, L, Eligand, and ENC core).
In many instances, we observe multiple band gaps in the phonon band diagram (Fig. 6 and 7). The band gap between the first and second set of optical branches tends to be the widest and higher frequency band gaps tend to be much more narrow. Our data also shows a correlation between increases in nanocrystal core diameter and the number of band gaps (Fig. 6a and c) and increases in the nanocrystal core elastic modulus and the number of band gaps (Fig. 6b and d). The origins of these correlations can be explained by observing the band diagram characteristics for changes in nanocrystal core diameter (Fig. 7a–c) and nanocrystal core elastic modulus (Fig. 7d–f). It is well known that increasing property mismatches causes flattening of the phonon dispersion branches.67 The effects of increasing nanocrystal core diameter and increasing nanocrystal core elastic modulus are to increase mismatch with the ligand matrix (i.e. d/L and ENC core/Eligand increase). As the phonon branches flatten, this leads to more opportunities to form phononic band gaps and hence we observe a correlation between an increase in the number of band gaps and an increase in nanocrystal core diameter and elastic modulus.
Another notable effect of changing nanocrystal core diameter and elastic modulus on the phonon band diagram is a re-scaling of the frequencies. While this frequency re-scaling leads to meaningful changes in the phonon band structure, its effects on the number of observed band gaps are artificial in nature. When downshifting the frequencies, one effect is the appearance of seemingly more phonon branches. However this apparent effect originates from our maximum frequency limitation of 500 GHz due to the continuum nature of our PWE model. These “new branches” are simply shifting from frequencies above 500 GHz to frequencies below 500 GHz. Another effect of this frequency re-scaling is the potential to flatten bands as the frequencies are downscaled. While one might assume that this frequency re-scaling could be the origin of band flattening described in the above paragraph, it should be noted that band flattening due to frequency re-scaling and band flattening due to property mismatches are independent effects. This is evident when inspecting Fig. 7f, which simultaneously has the flattest optical bands and the least frequency downscaling.
4. Conclusions
The results in this work illustrate that colloidal nanocrystals are excellent candidates for the bottom-up assembly of 3-dimensional phononic crystals. The nanoscale periodicity and acoustic contrast between the hard nanocrystal cores and soft ligand matrix lead to phononic band gaps with center frequencies on the order of ∼102 GHz and band gap widths on the order of ∼101 GHz. In addition, these characteristics can be tuned by changing the nanocrystal core diameter, nanocrystal core elastic modulus, interparticle distance, and ligand modulus. These results suggest that colloidal nanocrystal superlattices are promising candidates for use in high frequency phononic crystal applications that exert control over sound and heat.Acknowledgements
This work was supported by the Young Investigator Research Program of the Air Force Office of Scientific Research through award FA9550-13-1-0163 and by the National Science Foundation through award number CBET-1227979. We would like to thank ASU Research Computing for providing the computational resources Saguaro and Ocotillo clusters for carrying out the current work. We also thank Michael Sigalas for helpful discussions.References
- M. Maldovan, Nature, 2013, 503, 209–217 CrossRef CAS PubMed.
- T. Gorishnyy, M. Maldovan, C. Ullal and E. Thomas, Phys. World, 2005, 18, 24–29 CrossRef CAS.
- M.-H. Lu, L. Feng and Y.-F. Chen, Mater. Today, 2009, 12, 34–42 CrossRef CAS.
- R. Olsson Iii and I. El-Kady, Meas. Sci. Technol., 2009, 20, 012002 CrossRef.
- Y. Pennec, J. O. Vasseur, B. Djafari-Rouhani, L. Dobrzyński and P. A. Deymier, Surf. Sci. Rep., 2010, 65, 229–291 CrossRef CAS.
- M. M. Hossain and M. Gu, Laser Photonics Rev., 2014, 8, 233–249 CrossRef CAS.
- S. John, Phys. Rev. Lett., 1987, 58, 2486–2489 CrossRef CAS PubMed.
- H. Chen and C. T. Chan, J. Phys. D: Appl. Phys., 2010, 43, 113001 CrossRef.
- R. H. O. III and I. El-Kady, Meas. Sci. Technol., 2009, 20, 012002 CrossRef.
- A. Khelif, A. Choujaa, B. Djafari-Rouhani, M. Wilm, S. Ballandras and V. Laude, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 214301 CrossRef.
- J.-H. Sun and T.-T. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 174303 CrossRef.
- S. Yang, J. H. Page, Z. Liu, M. L. Cowan, C. T. Chan and P. Sheng, Phys. Rev. Lett., 2004, 93, 024301 CrossRef PubMed.
- N. Boechler, G. Theocharis and C. Daraio, Nat. Mater., 2011, 10, 665–668 CrossRef CAS PubMed.
- M. Maldovan, Phys. Rev. Lett., 2013, 110, 025902 CrossRef PubMed.
- R. Martinez-Sala, J. Sancho, J. V. Sanchez, V. Gomez, J. Llinares and F. Meseguer, Nature, 1995, 378, 241 CrossRef CAS.
- F. R. Montero de Espinosa, E. Jiménez and M. Torres, Phys. Rev. Lett., 1998, 80, 1208–1211 CrossRef CAS.
- T. Gorishnyy, C. Ullal, M. Maldovan, G. Fytas and E. Thomas, Phys. Rev. Lett., 2005, 94, 115501 CrossRef CAS PubMed.
- S. Alaie, D. F. Goettler, M. Su, Z. C. Leseman, C. M. Reinke and I. El-Kady, Nat. Commun., 2015, 6, 7228 CrossRef CAS PubMed.
- N. Zen, T. A. Puurtinen, T. J. Isotalo, S. Chaudhuri and I. J. Maasilta, Nat. Commun., 2014, 5, 3435 Search PubMed.
- H. Shin, J. A. Cox, R. Jarecki, A. Starbuck, Z. Wang and P. T. Rakich, Nat. Commun., 2015, 6, 6427 CrossRef CAS PubMed.
- J. Gomis-Bresco, D. Navarro-Urrios, M. Oudich, S. El-Jallal, A. Griol, D. Puerto, E. Chavez, Y. Pennec, B. Djafari-Rouhani, F. Alzina, A. Martínez and C. M. S. Torres, Nat. Commun., 2014, 5, 4452 CAS.
- A. Fainstein, N. D. Lanzillotti-Kimura, B. Jusserand and B. Perrin, Phys. Rev. Lett., 2013, 110, 037403 CrossRef CAS PubMed.
- M. Eichenfield, J. Chan, R. M. Camacho, K. J. Vahala and O. Painter, Nature, 2009, 462, 78–82 CrossRef CAS PubMed.
- V. Narayanamurti, H. L. Störmer, M. A. Chin, A. C. Gossard and W. Wiegmann, Phys. Rev. Lett., 1979, 43, 2012–2016 CrossRef CAS.
- O. Koblinger, J. Mebert, E. Dittrich, S. Döttinger, W. Eisenmenger, P. V. Santos and L. Ley, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 9372–9375 CrossRef CAS.
- W. Cheng, J. Wang, U. Jonas, G. Fytas and N. Stefanou, Nat. Mater., 2006, 5, 830–836 CrossRef CAS PubMed.
- E. Alonso-Redondo, M. Schmitt, Z. Urbach, C. M. Hui, R. Sainidou, P. Rembert, K. Matyjaszewski, M. R. Bockstaller and G. Fytas, Nat. Commun., 2015, 6, 8309 CrossRef CAS PubMed.
- C. B. Murray, C. Kagan and M. Bawendi, Annu. Rev. Mater. Sci., 2000, 30, 545–610 CrossRef CAS.
- J. Park, J. Joo, S. G. Kwon, Y. Jang and T. Hyeon, Angew. Chem., Int. Ed., 2007, 46, 4630–4660 CrossRef CAS PubMed.
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2009, 48, 60–103 CrossRef CAS PubMed.
- M. V. Kovalenko, L. Manna, A. Cabot, Z. Hens, D. V. Talapin, C. R. Kagan, V. I. Klimov, A. L. Rogach, P. Reiss, D. J. Milliron, P. Guyot-Sionnnest, G. Konstantatos, W. J. Parak, T. Hyeon, B. A. Korgel, C. B. Murray and W. Heiss, ACS Nano, 2015, 9, 1012–1057 CrossRef CAS PubMed.
- S. A. Mcdonald, G. Konstantatos, S. Zhang, P. W. Cyr, E. J. Klem, L. Levina and E. H. Sargent, Nat. Mater., 2005, 4, 138–142 CrossRef CAS PubMed.
- C.-H. M. Chuang, P. R. Brown, V. Bulović and M. G. Bawendi, Nat. Mater., 2014, 13, 796 CrossRef CAS PubMed.
- X. Dai, Z. Zhang, Y. Jin, Y. Niu, H. Cao, X. Liang, L. Chen, J. Wang and X. Peng, Nature, 2014, 515, 96–99 CrossRef CAS PubMed.
- K.-S. Cho, E. K. Lee, W.-J. Joo, E. Jang, T.-H. Kim, S. J. Lee, S.-J. Kwon, J. Y. Han, B.-K. Kim and B. L. Choi, Nat. Photonics, 2009, 3, 341–345 CrossRef CAS.
- R. Y. Wang, J. P. Feser, J.-S. Lee, D. V. Talapin, R. Segalman and A. Majumdar, Nano Lett., 2008, 8, 2283–2288 CrossRef CAS PubMed.
- F.-J. Fan, B. Yu, Y.-X. Wang, Y.-L. Zhu, X.-J. Liu, S.-H. Yu and Z. Ren, J. Am. Chem. Soc., 2011, 133, 15910–15913 CrossRef CAS PubMed.
- F. J. Fan, Y. X. Wang, X. J. Liu, L. Wu and S. H. Yu, Adv. Mater., 2012, 24, 6158–6163 CrossRef CAS PubMed.
- M. Liu and R. Y. Wang, Sci. Rep., 2015, 5, 16353 CrossRef CAS PubMed.
- M. Liu and R. Y. Wang, Nanoscale, 2013, 5, 7234–7237 RSC.
- M. Liu, Y. Ma, H. Wu and R. Y. Wang, ACS Nano, 2015, 9, 1341–1351 CrossRef CAS PubMed.
- S. J. Oh, Z. Wang, N. E. Berry, J.-H. Choi, T. Zhao, E. A. Gaulding, T. Paik, Y. Lai, C. B. Murray and C. R. Kagan, Nano Lett., 2014, 14, 6210–6216 CrossRef CAS PubMed.
- M. E. Turk, J.-H. Choi, S. J. Oh, A. T. Fafarman, B. T. Diroll, C. B. Murray, C. R. Kagan and J. M. Kikkawa, Nano Lett., 2014, 14, 5948–5952 CrossRef CAS PubMed.
- M. B. Zanjani and J. R. Lukes, J. Appl. Phys., 2014, 115, 143515 CrossRef.
- M. B. Zanjani and J. R. Lukes, J. Phys. Chem. C, 2015, 119, 16889–16896 CAS.
- E. Shevchenko, D. Talapin, A. Kornowski, F. Wiekhorst, J. Kotzler, M. Haase, A. Rogach and H. Weller, Adv. Mater., 2002, 14, 287 CrossRef CAS.
- D. V. Talapin, E. V. Shevchenko, A. Kornowski, N. Gaponik, M. Haase, A. L. Rogach and H. Weller, Adv. Mater., 2001, 13, 1868 CrossRef CAS.
- N. Aravantinos-Zafiris and M. Sigalas, J. Vib. Acoust., 2013, 135, 041003 CrossRef.
- J.-H. Sun and T.-T. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 104304 CrossRef.
- P.-F. Hsieh, T.-T. Wu and J.-H. Sun, IEEE Trans. Sonics Ultrason., 2006, 53, 148–158 CrossRef.
- P. Jiang, X.-P. Wang, T.-N. Chen and J. Zhu, J. Appl. Phys., 2015, 117, 154301 CrossRef.
- B. Graczykowski, M. Sledzinska, F. Alzina, J. Gomis-Bresco, J. S. Reparaz, M. R. Wagner and C. M. Sotomayor Torres, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 075414 CrossRef.
- E. N. Economou and M. Sigalas, J. Acoust. Soc. Am., 1994, 95, 1734–1740 CrossRef.
- M. Kafesaki, M. M. Sigalas and E. N. Economou, Solid State Commun., 1995, 96, 285–289 CrossRef CAS.
- M. S. Kushwaha, P. Halevi, L. Dobrzynski and B. Djafari-Rouhani, Phys. Rev. Lett., 1993, 71, 2022–2025 CrossRef CAS PubMed.
- R. Meyer, arXiv preprint arXiv:1511.00739, 2015.
- J.-W. Jiang, Nanoscale, 2014, 6, 8326–8333 RSC.
- D. Sjöberg, C. Engström, G. Kristensson, D. J. Wall and N. Wellander, Multiscale Model. Simul., 2005, 4, 149–171 Search PubMed.
- H. Ibach, H. Lüth, L. Mihaly and D. Mandrus, Am. J. Phys., 1992, 60, 1053–1054 CrossRef.
- K. Bian, W. Bassett, Z. Wang and T. Hanrath, J. Phys. Chem. Lett., 2014, 5, 3688–3693 CrossRef CAS PubMed.
- P. Podsiadlo, G. Krylova, B. Lee, K. Critchley, D. J. Gosztola, D. V. Talapin, P. D. Ashby and E. V. Shevchenko, J. Am. Chem. Soc., 2010, 132, 8953–8960 CrossRef CAS PubMed.
- P. Podsiadlo, B. Lee, V. B. Prakapenka, G. V. Krylova, R. D. Schaller, A. Demortière and E. V. Shevchenko, Nano Lett., 2011, 11, 579–588 CrossRef CAS PubMed.
- R. G. Budynas, Advanced strength and applied stress analysis, McGraw-Hill Science/Engineering/Math, 1998 Search PubMed.
- D. Cheney, Computational Modeling of Geometry Dependent Phonon Transport in Silicon Nanostructures, Ph.D. thesis, University of Pennsylvania, 2013.
- D. A. Cheney and J. R. Lukes, J. Heat Transfer, 2013, 135, 091101 CrossRef.
- G. Taras, M. Martin, U. Chaitanya and T. Edwin, Phys. World, 2005, 18, 24 Search PubMed.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Brooks Cole, 1976 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed description of the computational methodology, phononic band gap characteristics as a function of nanocrystal core volume fraction and Poisson's ratio. See DOI: 10.1039/c6ra03876j |
| This journal is © The Royal Society of Chemistry 2016 |