How does an amalgamated Ni cathode affect carbon nanotube growth? A density functional theory study

Abstract

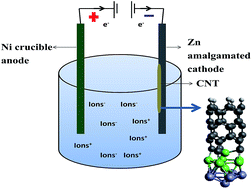
This is a Density Functional Theory (DFT) study on the influence of an alloying mixture of Ni–Zn catalysts on carbon nanotube, CNT, growth. The study is inspired by the one pot synthesis of carbon nanofibers during the electrolysis of Li₂CO₃. Unlike CVD, CNT growth initiates at the liquid/solid, rather than gas/solid interface in the above process. The electrodes are an amalgamated Zn cathode and with a pure Ni crucible as the anode, and both zinc and nickel (or other transition metals) are required for high yield production. The use of transition metals as the catalyst for CNT, CVD growth is well known. However, in this study we show how a mixture of the Zn–Ni alloy can act as the catalyst for the effective CNT growth. Ni and Zn are taken as an example of first row transition metals with a partially empty and completely filled d orbital respectively. The study shows that the π–d bonding between the nanotube and the metal results in strong bond formation at the interface of the nanotube growth. The study remains valid for other such metal alloys with partially and completely filled d orbitals.

---

Introduction

The increase in atmospheric CO₂ has been of great concern due to its effect on global warming. A global effort is underway to find a path to decrease the emission of this greenhouse gas and to mitigate the consequences of climate change.^2,3 An additional focus should also revolve around making a useful product of the CO₂ already present in the atmosphere. This should be done in order to bring down the rate of global warming. While other techniques for CNF formation are energy, equipment, time and cost-extensive, Ren et al.¹ has proposed a “One-Pot Synthesis” of carbon nanofibers (CNFs) from atmospheric CO₂ by electrolysis of molten lithium carbonate (Li₂CO₃) to show an inexpensive way of storing carbon in the form of CNF. The nanofibers are widely used in high strength composites, capacitors, batteries, electrocatalyst etc.^4,5 The study further reported that the production of CNF can be tuned by controlling the electrolysis conditions such as by addition of Ni to act as the nucleation sites, inclusion of Zn during electrolysis and tuning the electron density. Zinc coated (galvanized) steel cathode with the addition of low Ni, Cu, Co or Fe in electrolyte yielded uniform straight CNF. However, with no traces of the aforementioned transition metals there was no growth of CNF. The significance and the motivation of the study are the experimental finding that zinc activates electrochemical synthesis of the CNF (and that the resultant electrochemical synthesis is orders of magnitude less expensive than prior, conventional chemical vapour deposition synthesis). In this paper, we will explore with the help of Density Functional Theory (DFT) how addition of Ni in particular and some transition metals in general, over Zn coated cathode can help in CNF formation.

In general, CNFs are a heterogeneous mixture of different carbon nanotubes. The CNT differ in shape, chirality and length. For this study, we have taken zigzag and armchair single walled carbon nanotubes (SWCNT) as representative for the study of the CNF. This is because the experimental results mainly show various tubular hollow structures similar to SWCNT as its main component. The chiralities of the SWCNT are mentioned in the method section.

The nucleation and growth mechanism of the SWCNT over transition metals have been extensively studied with force field/tight binding technique,^6,7 first principle calculations,^8–14 classical molecular dynamics^15–18 and Monte Carlo simulation.^19,20 For an insight into the topic the readers are directed to the article by Page et al.²¹ and Elliott et al.²² Larsson et al. has studied the SWCNT adhesion strengths on Fe, Co and Ni cluster of 13 and 55 metal atoms.²³ They showed that the adhesion energy of zigzag CNT over the metal cluster is stronger than the armchair nanotubes. In a similar approach Ding et al. showed that the adhesion energy of the SWCNT to the metal cluster must be larger than the energy gained during the formation of a graphene cap at the end of the nanotube.²⁴ This can only be seen for few transition metals like Ni, Fe and Co while Cu, Pd and Au have weaker adhesion energies. Silvearv et al.²⁵ computed the bond strength of 1^st, 2^nd, and 3^rd row transition metals in order to identify potentials catalyst for SWCNT growth. They showed that the adsorption of the nanotube must be within a range in order for successful nanotube growth (known as Goldilocks zone). This is because the metal cluster should support the hollow structure of the tube during growth. A higher energy leads to the formation of metal carbides and a lower energy value does not support the tube growth. The values can be tuned with a mixture of metals or alloys (e.g. Cu/Mo and Pd/W)^8,26 that are otherwise not capable of supporting the growth. This opens up the possibility of mixing various metals below and above the energetically favoured nanotube growth range known as “Goldilocks zone” in order to catalyze the CNT growth. An alloying mixture of metals may also influence the growth of graphene. A mixture of Cu and Ni alloy is sufficient for graphene growth as described by Li et al.¹⁰ Ren et al.¹ has reported in their study that an absence of Ni ion and presence of Ir ion during electrolysis of Li₂CO₃, results in carbon clusters instead of CNF. This might be because the hollow structure of the CNF is not supported during the growth process and is outside the “Goldilocks zone”.

Zn metal is not a good catalyst for nanotube growth due to the filled d orbitals (d¹⁰). These orbitals do not allow efficient π and d orbital overlap with the CNT that might result in the formation of a dative bond. This is also valid for other metals like Cd, Hg, Cu, Ge, Ga etc. On the contrary, metals that have partially filled d orbitals act as good catalyst for CNT growth like Fe, Co and Ni. The study reported in this paper shows the alloy of Zn (above the zone) and Ni (within the zone) acts as the catalyst for the growth of nanotubes. Although the above mentioned article by Silvearv et al.²⁵ has studied a wide range of metals, their numerical values are limited to the use of zigzag nanotubes with a length of 3 Å. Their calculations indicate that the Goldilocks zone (energy range in which the SWCNT can grow) should be within −2.5 to −3.0 eV per atom. Even with larger cluster size the energy range remains unchanged. However, our result shows that there is a size effect on the adhesion energies of the tubes to the metal clusters.

Method

All the calculations are done using first principle Density Functional Theory using quantum espresso package.²⁷ Calculations were performed with generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE)²⁸ exchange-correlation functional using PAW pseudopotentials (http://theossrv1.epfl.ch/Main/Pseudopotentials). The carbon nanotube–metal cluster complexes, the cluster and the nanotube were all modelled in a box of (15 × 15 × 20) Å for the smaller systems and (20 × 20 × 25) Å for the larger systems. All the models were treated as isolated systems in order to avoid any physically inconsistent interactions by the implementation of Martyna–Tuckerman correction to the total energy and the scf potential.²⁹ For the k-point mesh a γ-centre was used. The kinetic energy cut-off for the wave functions was set 42 Ry and for charge density a potential was set at 236 Ry. The Gaussian smearing was turned so that the difference between the free energy and the total energy is less than 1 meV per atom. The energy convergence was set to 1 × 10⁻⁴ a.u. and the force convergence threshold for the ionic minimization was set at 1 × 10⁻³ a.u. Spin nonpolarized calculations were applied as the metals are nonmagnetic under typical growth conditions.²⁴ In our calculations all the atoms are allowed to relax freely and only the nanotubes adsorbed over 55 and 72 metal cluster models have the metal atoms fixed in their position.

An atom by atom growth of SWCNT over the metal and alloy clusters is beyond the scope of this study. At this time it remains beyond the scope of our modelling resources to compute the growth of these nanotubes with full ab initio molecular dynamics. However, there are a few related studies^13,30,31 based on the topic. According to Ren et al.¹ the melting point of the Zn component of the electrode is 420 °C and the Ni electrode starts losing its atoms into the electrolyte above 950 °C. In our current study, we evaluate the effect of temperature using ab initio MD (as implemented in quantum espresso) after the SWCNT has been strongly/poorly adsorbed onto the metal clusters. We compute the dynamics using ab initio calculation for 0.30 ps on a few SWCNT adsorbed onto the metal surface at the reported melting point of the metal clusters. We have used the Verlet algorithm to integrate Newton's equation and used Berendson thermostat in order to keep the temperature constant.

In this study, we have taken 8 Å long (5,0), (5,5) and (9,0) SWCNT. On one end the dangling bonds are hydrogen terminated to simulate a capped end and the other end is attached to the metal centre (Fig. 1). The open end of the CNT has several dangling bonds. The carbon atoms at this end have been fixed in the calculation in order to avoid closure at this end of the tube. In all the calculations the effect of the length of the SWCNT has not been taken into account. Our model systems consist of:

Fig. 1 The figure shows the side view of the optimized geometry of various Ni atoms and clusters adsorbed onto zigzag SWCNT. (a) Shows single Ni atom adsorbed onto (5,0) SWCNT, (b) shows a 13 atom Ni cluster adsorbed onto (5,0) SWCNT, (c) shows 9 Ni atoms adsorbed onto (9,0) SWCNT and (d) 55 Ni atom cluster adsorbed onto (9,0) zigzag CNT. (e) 72 Ni atom cluster adsorbed onto (9,0) zigzag CNT. The details of calculation and the description of the SWCNT and the Ni cluster are mentioned in the method section. Colour code: green: nickel, grey: carbon, white: hydrogen. Similar structure is valid when the Ni metal is replaced with Zn metal.

Zigzag model

(i) (5,0) SWCNT with one metal atom adsorbed at one end (e.g. Fig. 1(a) for Ni atom). (ii) (5,0) SWCNT adsorbed onto a 13 atom metal cluster (Ni/Zn/Ni–Zn) (e.g. Fig. 1(b) for Ni atom). (iii) (9,0) SWCNT with 9 metal atoms adsorbed at one end of the tube (Ni/Zn/Ni–Zn) (e.g. Fig. 1(c) for Ni atom). (iv) (9,0) SWCNT with 55 metal atom cluster adsorbed at the other end of the tube (Ni/Zn/Ni–Zn) (e.g. Fig. 1(d) for Ni atom). (v) (9,0) SWCNT with 72 metal atom cluster (Fig. 1(e) for Ni atom).

Armchair model

(i) (5,5) SWCNT with one metal atom adsorbed at one end. (ii) (5,5) SWCNT with 5 metal atoms adsorbed at one end (Fig. 2). (iii) (5,5) SWCNT adsorbed onto 55 metal atom cluster.

Fig. 2 Shows the optimized arm-chair SWCNT adhesion energies to 5 atom (A) Ni metal (B) Zn metal (C) Ni(2)–Zn(3) alloy. (i) Shows the side view of the SWCNT and (ii) shows the top view of the SWCNT. Colour code: green: nickel, grey: carbon, white: hydrogen, blue–green: zinc.

As a model to study the surface adhesion energies, we have started with one metal adhesion to the nanotube, followed by five and nine metal atoms of Ni, Zn and Ni/Zn mixture. Further we have taken 13 and 55 Ni and Zn icosahedral structures as the surface model. This is because the most stable structural form of Ni and Zn at this scale is icosahedral as described by Gafner et al.³² for Ni and Wu et al.³³ for Zn. Further we have also tested the adhesion energies of a 72 atom Ni(111) and Zn(001) surface model. Any larger size of the metal cluster will be difficult to compute with DFT. In the Ni–Zn alloy cluster, the bottom 2 layers are Zn and the top layers are Ni (Fig. 3). This is a replica of the amalgamated Ni cathode that is used in the experiments by Ren et al.¹ For these energies the metal–carbon adhesion energies per bond were calculated as a measure of M–C bond strength (eqn (1)). All the structures are geometry optimized at 0 K.

ΔE_{(metal–C)bond} = {E_{(SWCNT+metal-cluster)} − (E_SWCNT + E_{metal-cluster})}/{total no. of M–C bonds} (1)

Fig. 3 Shows the side view of the Ni–Zn alloy metal (a) 13 metal atom cluster (b) 55 metal atom cluster that has been used for the calculation. Colour code is same as in Fig. 2.

The energetically favoured nanotube growth “Goldilocks zone” as described by Silvearv et al.²⁵ falls within (+/−0.5) of −2.5 eV per atom for all the transition metals they have studied. However, their data is limited by the size of the model they have used and also the choice of functional, pseudopotential and length of the SWCNT. In our study we have used the principle that a positive ΔE indicates less probability of the formation of the SWCNT and vice versa.

Results and discussion

Table 1 presents the adhesion energy of zigzag SWCNT to 1 atom, 9 atoms, 13 atoms cluster, 55 atoms cluster and 72 atom cluster of Ni, Zn and Ni–Zn alloy. The calculated average distance between the nearest carbon atom in the SWCNT and the metal in the ring/cluster has also been included. In both the cases of a single atom (Ni/Zn) adsorption, as shown in Fig. 1(a), we find that the middle site (i.e. in between 2 dangling bonds of C) is the most stable site for metal adsorption as it passivates two carbon dangling bonds. The same effect has also been determined in previous studies.¹² We find that the single Ni atom adsorbs stronger than the Zn atom to the tube by ∼4 eV. This initial adhesion energy shows that Ni has stronger adsorption to the nanotube than Zn. Although the result broadly indicates that single Zn atom binds to the dangling bond of the nanotube at the end. In the second case there is adhesion of the nanotube to a 13 atom metal cluster, we find that the Ni cluster has stronger adsorption compared to Zn cluster. In fact, the Zn cluster does not adhere to the nanotube as the energy difference (ΔE) is +0.75 eV per atom. Ab initio Molecular Dynamics (MD) study of SWCNT adsorbed onto 13 atoms Ni and Zn cluster respectively (Fig. 4) show that the nanotube remains strongly adsorbed to the Ni cluster at the end of 0.30 picoseconds and in the same duration the nanotube dissociates into individual atoms over a Zn cluster. This is further evidence that the Ni cluster exhibits a stronger adsorption than the Zn cluster.

Table 1 The table shows the adhesion energy (eV per atom) and the metal–carbon distance (Å) for Ni, Zn and Ni–Zn alloy with (5,0) SWCNT and (9,0) SWCNT. Fig. 1 shows the nanotubes adsorbed onto the Ni atoms, rings and clusters. The values in the bracket are the energies from Larsson et al.²³ Although they show similar trend in the adhesion energy their absolute values are different due to the difference in the length of the SWCNT, DFT functional used, cut-off energy and pseudopotential. The paper reported partial closure of the SWCNT at the open end during optimization. This effect was not found during the calculation as reported in this paper

SWCNT	Metal	Adhesion energies (eV per atom) (ΔE)			Metal–SWCNT distance (Å)
		Ni	Zn	Nix–Zny anode	Ni	Zn	Nix–Zny anode
(5,0)	1 atom	−5.64 (−5.48)	−1.56	—	2.14 (1.89)	2.00	—
	13 atom cluster	−1.70 (−2.41)	0.75	−0.68 (x = 8, y = 5 Fig. 2) − 0.80 (x = 10, y = 3)	2.02 (2.16)	1.87	2.00
(9,0)	9 atom cluster	−3.81	0.90	−1.39 (x = 6, y = 3)	1.76	1.90	1.83
	55 atom cluster	−0.40	3.81	−0.80 (x = 37, y = 18 Fig. 2)	1.98	2.05	1.89
	72 atom	−0.11 Ni (111)	3.94 Zn (001)	—	1.98	2.12	—

---

Fig. 4 (A) shows a 0.30 picoseconds MD simulation of (5,0) CNT adsorbed onto a 13 atom Ni cluster. (B) Shows a 0.25 picoseconds MD simulation of (5,0) CNT adsorbed onto a 13 atom Zn cluster.

However, when there is a mixture of Ni–Zn atoms that represents the alloying metal as in the amalgamated cathode, we find that the ΔE increases compared to the Zn adhesion energy but does not exceed the energy of the Ni cluster. Further we find as the number of Ni atoms is increased the adhesion energy also increases (Table 1). This simple model of a Ni–Zn alloy indicates that the adsorption of the metals to the SWCNT can be manipulated by a mixture of metals. The adhesion energies follow the same trend when using a larger nanotube (9,0) and 9 metal atoms adsorbed at one end of the tube. The adsorption is strongest for the Ni atoms, followed by Ni–Zn alloy and then the Zn atom. This model also indicates no adhesion of the Zn to the nanotube. Our second largest model is the (9,0) SWCNT adsorbed onto a 55 metal atom cluster and our largest model is a (9,0) CNT adsorbed onto a 72 atom metal cluster. The trend in the adsorption energy remains the same irrespective of the model. This shows that although the absolute difference between the 5 different models changes, the trend of adhesion energy is always similar. In each case, the adhesion energy of Ni alone may be too strong and inhibit CNT growth; the adhesion energy of Zn alone may be too weak to initiate CNT growth, while the Zn–Ni alloy provides an energetic zone to promote CNT growth.

The armchair model shows the same trend in ΔE as the zigzag model with Ni atom/cluster having the highest adhesion energy, followed by Ni–Zn alloy and then Zn metal in all the three cases that are studied (Table 2). The 5 atom model for Ni metal shows that the Ni atoms tends to form a small ring at the passivated end of the tube with the metal atoms (Fig. 2(A)(ii)). The strong metal–metal bonding energies further bring down the ΔE. A larger metal cluster of 55 atoms shows that there is poor adhesion of the nanotubes to the metal cluster as indicated by ΔE in each of the three cases.

Table 2 The table shows the adhesion energy (eV per atom) and the metal–carbon distance (Å) for Ni, Zn and Ni–Zn alloy with (5,5) SWCNT. The values in the bracket are the energies from the paper of Larsson et al.²³ Although they show similar trend in the energy their absolute values are different due to the length of the SWCNT, DFT functional used, cut-off energy and pseudopotential. The paper reported partial closure of the SWCNT at the open end during optimization. This effect was not found during the calculation as reported in this paper

Metal	Adhesion energies (eV per atom) (ΔE)			Metal–SWCNT distance (Å)
	Ni	Zn	Nix–Zny anode	Ni	Zn	Nix–Zny anode
a The 5 Ni atoms forms a closed structure as shown in Fig. 2(A)(ii). This gives lower adhesion energy due to the metal–metal bonding.
1 atom	−4.59 (−4.11)	−0.79	—	1.87	2.04	—
5 atom Ring	−5.50^a (−2.26)	−1.30	−2.94 (x = 2, y = 3)	1.90	1.98	1.92
55 atom Cluster	−0.43 (−1.51)	4.93	2.46 (x = 37, y = 18 Fig. 2)	2.26	2.11	2.10

---

We find that with an increase in size of the metal cluster the adhesion energies of similar nanotubes to the metal decreases irrespective of the metal or the alloy studied. Also a larger nanotube (9,0) has lesser adhesion energy compared to the smaller tube (5,0) (Table 1). This might be because the hollow structure of the tube cannot be supported by the growing metal atoms. A single metal adhesion to the tube gives an incorrect description of the overall adhesion energy, as the Zn metal shows positive adhesion to the nanotube that is not true. However, it exhibits a similar trend in the ΔE compared to larger models i.e. the adhesion energy of the SWCNT to the metal cluster is Ni > Ni–Zn alloy > Zn. The energy of the Ni atom/cluster adsorption to the nanotube is stronger than Zn atom/cluster in all the cases due to the overlap bonding between the empty d orbital in the Ni (d⁷) and π electron cloud in the SWCNT forming a dative bond between them. This special bond between the metal and the nanotube is absent in the case of Zn as the Zn has filled d¹⁰ orbitals. Hence, the adhesion energy is weak. When there is a mixture of the two metals (Ni–Zn), there is partial overlap of the π bonds from the nanotubes to the empty d orbitals and hence there is adhesion of the tube to the metal alloy. Experimental study shows that using pure Ni cathode can produce CNTs but there is lack of control for the homogeneity (to be published data). The π–d interactions as present in Ni metal, Ni–Zn alloy with the CNT are also present inside organometallic compounds (e.g. metallocene).³⁴ The orbital studies for such compounds can be found in details in the following articles.^35–37

Arm chair nanotubes have extra stabilization compared to the zigzag due to the model presence of triple bonds. Hence, the overall adhesion energies compared to the zigzag model are lower for similar type of arm chair models.²⁰ Also the longer bond distance between the Ni–Ni in the cluster metal might also favour the zigzag nanotube growth formation due to the longest bond length between Ni and C at the interface of the catalyst.

Conclusions

In this paper, density functional theory calculations have been used to study SWCNT–metal/metal–alloy adhesion strengths for (5,0), (9,0) and (5,5) nanotubes bonded to Ni, Zn and Ni–Zn alloy. The different models used in this study gave the correct trend of experimentally observed Ni–Zn promotion of CNT growth, and that adhesion energy i.e. Ni adsorbs stronger than Ni–Zn alloy and this is followed by Zn metal, but the absolute values are different.

We want to emphasize that in addition to the metal alloy nucleation effects demonstrated here, solvation effects will also impact the morphology and growth of the carbon nanotubes, and the magnitude of this effect will be conducted in a separate study. The calculations presented here emphasize the importance of understanding the transition metal nucleation composition on the carbon nanotube growth and align with our previously published experimental results (ref. 1). They show Ni electrode forms NiC, Zn (amalgamated) electrode does not form any nanotube and the Ni coated Zn (amalgamated electrode) shows SWCNT formation. In our theoretical structural growth study presented here, we have taken a similar approach of studying the nanotube growth by changing the metals in the electrode. The data (Tables 1 and 2 in the manuscript) aligns well with the experimental results.

Our density functional calculations shows quintessential metal catalyst for the growth of SWCNT can be replaced by a mixture of metal alloy in order to support the growth of hollow carbon nanotubes. The metal alloys can be the electrodes as in the study of Ren et al.¹ Also it could be added as an additive during the chemical vapour deposition growth of nanotubes. The energies should be within the range of “Goldilocks zone” as described in previous studies. Thinner size of amalgamated cathode and increase in the quantity of Ni ions in the solvents may increase the amount of growth of SWCNT as this increases the number of empty d orbitals for the possible increase in π–d bonding. Stronger adhesion energy of the SWCNT to the metal may result in the formation of graphitic caps on the surface. This is seen during the experiments when only Fe, Co, Cu or Ni electrode were used in the absence of Zn metal.

The arm chair SWCNT is more stable individually. Hence, the adsorption of the SWCNT to the metal centre is weaker compared to the zigzag models. One can improve the growth quality of the SWCNT in the amalgamated cathode by using metals that are below the “Goldilocks zone” as they principally have more vacant d orbitals. This might result in overlap of the filled d orbitals from the Zn and the empty d orbitals from the metals like V, Ti, Cr, Mn, Mo, Ta etc. However, the metals should also have a lower reduction potential than Zn in order to be deposited at the cathode. This should inspire future research in this field. A fundamental difference between SWCNT electrolytic growth and CVD growth is that they first occur at the liquid/solid interface where diffusion effects can be more pronounced, whereas the latter occurs at a gas/solid interface.

Mass transport of the carbon containing reactants is greatly facilitated in the electrolysis compared to the chemical vapour deposition synthesis of nanotubes. The density of tetravalent carbon reactants adjacent to the growth site is several orders of magnitude higher (in the approximate ratio of the density of the molten liquid to the gas density of the CVD reactant) for a liquid carbonate in the electrolysis than in the gas phase of a chemical vapour deposition. We have previously discussed an analogous effect comparing a gas phase carbon dioxide reactant to a solution phase carbonate reactant.¹ In the future we will probe dynamic, rather than static energy models, to understand diffusional effects to optimize CNT growth.

Acknowledgements

We would like to thank Dr Biswajit Santra from Princeton University for useful discussion. This work is partially supported by the national science foundation grant no CHE-1230732.

References

1. J. Ren, F.-F. Li, J. Lau, L. González-Urbina and S. Licht, Nano Lett., 2015, 15, 6142–6148.
2. J. Hansen, M. Sato, R. Ruedy, A. Lacis and V. Oinas, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 9875–9880.
3. P. M. Cox, R. A. Betts, C. D. Jones, S. A. Spall and I. J. Totterdell, Nature, 2000, 408, 184–187.
4. E. Hammel, X. Tang, M. Trampert, T. Schmitt, K. Mauthner, A. Eder and P. Pötschke, Carbon, 2004, 42, 1153–1158.
5. K. P. De Jong and J. W. Geus, Catal. Rev., 2000, 42, 481–510.
6. W. Somers, A. Bogaerts, A. C. T. van Duin and E. C. Neyts, J. Phys. Chem. C, 2012, 116, 20958–20965.
7. H. Amara, J. M. Roussel, C. Bichara, J. P. Gaspard and F. Ducastelle, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 014109.
8. J. P. O'Byrne, Z. Li, J. M. Tobin, J. A. Larsson, P. Larsson, R. Ahuja and J. D. Holmes, J. Phys. Chem. C, 2010, 114, 8115–8119.
9. O. V. Yazyev and A. Pasquarello, Phys. Rev. Lett., 2008, 100, 156102.
10. J. Li, E. Croiset and L. Ricardez-Sandoval, Appl. Surf. Sci., 2014, 317, 923–928.
11. Y. H. Lee, S. G. Kim and D. Tománek, Phys. Rev. Lett., 1997, 78, 2393.
12. J.-C. Charlier, A. De Vita, X. Blase and R. Car, Science, 1997, 275, 647–649.
13. J. Gavillet, A. Loiseau, C. Journet, F. Willaime, F. Ducastelle and J.-C. Charlier, Phys. Rev. Lett., 2001, 87, 275504.
14. A. G.-G. Diego and B. B. Perla, Nanotechnology, 2008, 19, 485604.
15. D. Feng and B. Kim, Nanotechnology, 2006, 17, 543.
16. Y. Shibuta and S. Maruyama, Chem. Phys. Lett., 2003, 382, 381–386.
17. Y. Shibuta and S. Maruyama, Chem. Phys. Lett., 2007, 437, 218–223.
18. S. Irle, G. Zheng, M. Elstner and K. Morokuma, Nano Lett., 2003, 3, 465–470.
19. E. C. Neyts, Y. Shibuta, A. C. T. van Duin and A. Bogaerts, ACS Nano, 2010, 4, 6665–6672.
20. H. Amara, C. Bichara and F. Ducastelle, Phys. Rev. Lett., 2008, 100, 056105.
21. A. J. Page, F. Ding, S. Irle and K. Morokuma, Rep. Prog. Phys., 2015, 78, 036501.
22. J. A. Elliott, Y. Shibuta, H. Amara, C. Bichara and E. C. Neyts, Nanoscale, 2013, 5, 6662–6676.
23. P. Larsson, J. A. Larsson, R. Ahuja, F. Ding, B. I. Yakobson, H. Duan, A. Rosén and K. Bolton, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115419.
24. F. Ding, P. Larsson, J. A. Larsson, R. Ahuja, H. Duan, A. Rosén and K. Bolton, Nano Lett., 2008, 8, 463–468.
25. F. Silvearv, P. Larsson, S. L. T. Jones, R. Ahuja and J. A. Larsson, J. Mater. Chem. C, 2015, 3, 3422–3427.
26. Z. Li, J. A. Larsson, P. Larsson, R. Ahuja, J. M. Tobin, J. O'Byrne, M. A. Morris, G. Attard and J. D. Holmes, J. Phys. Chem. C, 2008, 112, 12201–12206.
27. G. Paolo, B. Stefano, B. Nicola, C. Matteo, C. Roberto, C. Carlo, C. Davide, L. C. Guido, C. Matteo, D. Ismaila, C. Andrea Dal, G. Stefano de, F. Stefano, F. Guido, G. Ralph, G. Uwe, G. Christos, K. Anton, L. Michele, M.-S. Layla, M. Nicola, M. Francesco, M. Riccardo, P. Stefano, P. Alfredo, P. Lorenzo, S. Carlo, S. Sandro, S. Gabriele, P. S. Ari, S. Alexander, U. Paolo and M. W. Renata, J. Phys.: Condens. Matter, 2009, 21, 395502.
28. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413.
29. G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 110, 2810–2821.
30. T. Oguri, K. Shimamura, Y. Shibuta, F. Shimojo and S. Yamaguchi, Chem. Phys. Lett., 2014, 595–596, 185–191.
31. J.-Y. Raty, F. Gygi and G. Galli, Phys. Rev. Lett., 2005, 95, 096103.
32. Y. Y. Gafner, S. L. Gafner and P. Entel, Phys. Solid State, 2004, 46, 1327–1330.
33. K. Wu, S. Lai and W. Lin, Mol. Simul., 2005, 31, 399–403.
34. Metallocenes an introduction to sandwich complexes, ed. N. J. Long, Wiley, 1998.
35. H. Oshio and H. Ichida, J. Phys. Chem., 1995, 99, 3294–3302.
36. T. J. Johnson, K. Folting, W. E. Streib, J. D. Martin, J. C. Huffman, S. A. Jackson, O. Eisenstein and K. G. Caulton, Inorg. Chem., 1995, 34, 488–499.
37. C.-C. Wang, Y. Wang, L.-K. Chou and C.-M. Che, J. Phys. Chem., 1995, 99, 13899–13908.

---