Investigations of the band structures of edge-defect zigzag graphene nanoribbons using density functional theory

Abstract

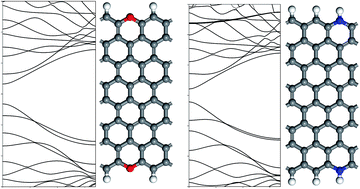
We used density functional theory to investigate the band gap and the electron conductivity of edge-defect zigzag graphene nanoribbons (ZGNR). The band structures of edge-oxidized ZGNRs (ox-ZGNRs) were hardly affected by introducing carboxyl and hydroxyl groups, but were markedly altered near the Fermi level by the ketone and ether groups, resulting in open band gaps of 0.6064 eV and 0.6413 eV, respectively. Unlike carboxyl and hydroxyl groups, the ketone and ether groups caused noticeable changes due to disruption of the sp² hybridization of edge carbon atoms via forming chemical bonds with them. While the band gaps for both-side pyridinic and pyrrolic edge-nitrided ZGNRs (N-ZGNRs) holding aromatic forms are respectively calculated to 0.2882 eV and 0.3057 eV, the non-aromatic graphitic group has a higher band gap of 0.4244 eV. The edge-aromatic ZGNRs including carboxyl or hydroxyl groups in ox-ZGNRs and pyridinic or pyrrolic groups in N-ZGNRs show similar features of band structures and properties as displayed in a pristine ZGNR. On the contrary, the edge-nonaromatic ZGNRs modified with ketone, ether, or graphitic groups have different shapes of the band structures whose band gaps are more open than that of a pristine ZGNR.

---

1. Introduction

Graphene-based nano-electronic devices have attracted considerable research interest because of their potential applications as next-generation electronics,¹ as well as in the fields of optoelectronics² and spintronics.³ In particular, one-dimensional graphene nanoribbons (GNRs) have been intriguing due to their nonzero band gaps⁴ arising from their quantum confinement, edge effect, and high on/off current ratio, in contrast to semi-metallic zero-band-gap graphene.⁵ GNRs have been made by cutting graphene into narrow stripes or by unzipping carbon nanotubes.⁶ But at the same time, oxides adhere to the edges of GNRs, creating edge-oxidized GNRs,⁷ and such inevitable oxidation may diminish the electronic properties and current mobility of those nanoribbons as compared with a perfect pristine GNR.

Depending on the atomic arrangements at their edges, GNRs can be distinguished into two different types, “zigzag” and “armchair”, displaying different electronic properties.⁸ Zigzag GNRs (ZGNRs) in particular form a semiconductor with a flat band near the Fermi level due to its edge-localized state whose band gap decreases as the width of the GNR increases.⁹ In addition, several researchers have focused on modifying the electronic and magnetic properties of ZGNRs by doping heteroatoms in it.¹⁰ Kan et al.^10a examined 8-ZGNR with H, NH₂, NO₂ and CH₃ functional groups to study on the electronic properties and relative stabilities. They found the half-metallic ribbons can be more stable than H-saturated ZGNR by reducing the concentration of big functional groups. Boukhvalov and Katsnelson^10b studied an effect of finite width of 10-ZGNR with the edges functionalized by hydrogen atoms and hydroxyl groups. It is shown that magnetism at graphene edges is fragile with the oxidization. Hod et al.^7a presented theoretical study of the electronic properties and relative stabilities of edge-oxidized 8-ZGNR. The structure of the oxidized ribbons is found to be stabilized than hydrogen-terminated nanoribbons. Li and colleagues^10c investigated the structures of various N-doped ZGNRs and compared their properties with those of pristine ZGNRs. Based on experimental results showing high prevalence of pyridinic and pyrrolic structures in GNRs, the investigators specifically introduced three-nitrogen vacancy (3NV), four-nitrogen vacancy (4ND) defects and graphitic N-substituted onto the edges of ZGNRs and analyzed their electronic and magnetic properties. They found that such introduction of N-doping defects in ZGNRs can be made into half-metals or spin gapless semiconductors which are applicable to gas or bio sensors,¹¹ spin filter devices,¹² etc.

Here, we study the band structures of different edge-defect GNRs using density functional theory (DFT), which are comprised of contingent oxygen or nitrogen compounds at those edges during GNR fabrication in such a gas environment. In general, oxidized groups in graphene oxide (GO) are composed of carboxyl, hydroxyl, ketone, ether groups, etc. to be well dispersed in water and can be converted into nitrided groups via a GO-reduction process using ammonia gas.¹³ In the same way, it is thought that edge-oxidized GNRs can be converted into edge-nitrided GNR via a similar process described in the literature since edge-oxidized GNRs also contained similar oxygen groups. From our investigation of edge-oxidized and edge-nitrided GNRs using DFT, we compare the calculated band structures and electronic properties to provide information such as edge-conversion effects, which should be very useful to develop delicately tuned electronic devices for next generation.

2. Computational details

We optimized the geometry of H-terminated 8-ZGNR using the Vienna ab initio simulation package (VASP)¹⁴ with the projector augmented wave (PAW) method.¹⁵ The generalized gradient approximation (GGA) and Perdew–Burke–Ernzerhof (PBE) functional were employed to describe electron exchange and correlation.¹⁶ The GGA–PBE functional successfully described the carbon-based systems.¹⁷ The cell size was 32.900 × 7.380 × 10.000 Å and the energy cut-off was set at 500 eV. The periodic boundary conditions (PBCs) were applied with the vacuum separation distance set to 15 Å and 10 Å along the x- and z-directions, respectively, to avoid interactions beyond the PBC. The atomic positions were optimized until the change in energy was less than 1 × 10⁻⁶ eV per cell, and the force on each atom was less than 0.01 eV Å⁻¹. Spin-polarization and dipole corrections were also incorporated into the calculations. In the energy and electronic property calculations, k-point samplings for the Brillouin zone were performed using the 2 × 6 × 1 Monkhorst–Pack k-point mesh.¹⁸ We used 8-ZGNRs with hydrogen-saturated edges (both edges were terminated by hydrogen atoms).

3. Results and discussion

3.1 Band structures of edge-oxidized ZGNRs

In this study, we divided ZGNRs into two categories: edge-oxidized ZGNRs and edge-nitrided ZGNRs. Edge-oxidized ZGNRs (ox-ZGNRs) contain carboxyl, hydroxyl, ketone and ether groups at the ZGNR edges. These oxygen-containing functional groups can be made since the oxygen-plasma etching process used in producing the GNR was also applied to the edges of ZGNRs to create oxidized ZGNRs.^13,19 Edge-nitrided ZGNRs (N-ZNGRs) contain pyridinic/pyrrolic-like substructures and graphitic N-substitution at the ZGNR edges.^13,20 Such functional groups were introduced on one or both edges of the ZGNR to check whether or not the electronic properties depend on the symmetry of the spin states of the edges.

Fig. 1 shows models and band structures of ox-ZGNRs with carboxyl and hydroxyl groups. The band structures of the carboxyl and hydroxyl groups show similar tendencies. The magnitudes of the band gaps of ox-ZGNRs are summarized in Table 1. Band gaps of ox-ZGNRs with carboxyl and hydroxyl groups on one ZGNR edge are calculated to be 0.3673 eV and 0.4010 eV, respectively. In band structures, flat bands are observed near Fermi level, which seem to be due to localized edge states of ZGNRs. Milowska et al.²¹ and Kang²² observed similar flat bands in functionalized graphene and CNT systems around Fermi energy due to covalent functionalization. Such flat bands show split depending on spin states of electrons when the functional group is attached on one side of ZGNR. By introducing carboxyl and hydroxyl groups on one edge of each ZGNR, spin polarization around the edges containing carboxyl and hydroxyl groups is occurred, so the total magnetizations of ox-ZGNRs with carboxyl and hydroxyl groups were calculated to be −0.010 μ_B and −0.015 μ_B, respectively (Table S1†). As a result, spin splitting of the bands near the Fermi level is weak. On the other hand, the band gaps of ZGNRs with carboxyl and hydroxyl groups on both edges are 0.4093 eV and 0.4034 eV, respectively. Here, spin splitting of the flat bands near the Fermi level did not occur because spin up and spin down states are made degenerate in all energy bands by the introduction of the carboxyl and hydroxyl groups on both ZGNR edges.

Fig. 1 Band structures of ox-ZGNRs with (a and b) carboxyl groups and (c and d) hydroxyl groups. Spin-up and spin-down bands are indicated by red and blue dashed lines, respectively. (a) and (c) show the structures with these (carboxyl or hydroxyl) functional groups on one edge of the nanoribbon, and (b) and (d) are those with the respective functional groups on both edges. Each circle is proportional to the magnitude of the magnetization density at each atom. Red and blue circles correspond to spin-up and spin-down densities, respectively.

Table 1 Band gaps of ox-ZGNRs with carboxyl, hydroxyl, ketone and ether groups

Structure	Band gap (eV)
	Carboxyl	Hydroxyl	Ketone	Ether
One edge	0.3673	0.4010	0.0897	0.1198
Both edges	0.4093	0.4034	0.6064	0.6413

---

All band structures of ox-ZGNRs containing the carboxyl and hydroxyl groups have very similar features except for the spin splitting near the Fermi level; the spin splitting occurs when the carboxyl and hydroxyl groups are introduced on only one edge of the ZGNR. However, the change of magnetization and the degree of spin splitting are marginal when these functional groups are on only one ZGNR edge. Because the carboxyl and hydroxyl groups do not disrupt the sp² hybridization of the edge carbon atoms, the edge states of the ZGNRs are preserved and the electronic properties of the ZNGRs are not much affected. Lee and colleagues²³ showed that the hydroxyl group makes the edge carbon atom hybridized in an sp² form. As a result, the band structure and the spin polarization are very similar to that of H-terminated ZNGRs. Note that the carboxyl group is similar to the hydroxyl group.

Fig. 2 shows models and band structures of ox-ZGNRs with ketone and ether groups. The band structures derived from these two groups have similar features to each other, but differed from the band structures derived from the carboxyl and hydroxyl groups. The band gaps of the structures with the ketone and ether groups on one edge of the nanoribbon were calculated to be 0.0897 eV and 0.1198 eV, respectively, and serious spin splitting occurred near the Fermi level. In the ketone group, the oxygen forms a double bond with a carbon atom at the edge, and the ether group directly replaces a carbon atom at the edge. Therefore, sp² hybridization is not retained for the edge carbons of ZGNR. In addition, the spin polarization around the edges with the ketone and ether groups is considerably suppressed and the magnetization of the edge carbon atoms is calculated to be about −0.002 to 0.000 μ_B. The total magnetizations of ox-ZGNRs with ketone and ether groups were calculated to be 0.511 μ_B and 0.513 μ_B, respectively, (Table S1†) and these values are greater than those of ox-ZGNRs with carboxyl and hydroxyl groups. As a result, the structures with ketone and ether groups attain not only considerable spin splitting near the Fermi level but also spin splitting throughout the whole band structure. In addition, the flat bands near the Fermi level are shifted up and the lower flat band heavily split into spin-up and spin-down; as a result, a small band gap is created between spin-up and spin-down. A small band gap is also observed between spin-up and spin-down for the ether-containing structure, but here as a result of the flat bands near the Fermi level being shifted down and the upper flat band being heavily split into spin-up and spin-down. However, the results of our calculations differed when ketone and ether groups are introduced on both edges of the nanoribbon. The band gaps of the structures containing the ketone and ether functional groups are 0.6064 eV and 0.6413 eV, respectively, and the spin splitting does not occur. These results are due to these functional groups, when introduced onto both edges, completely suppressing spin polarization of edge carbon atoms, and in fact of all the carbon atoms of ox-ZGNRs. Therefore, the magnetization of ox-ZGNRs with the ketone and ether groups on both edges is found to be zero (Table S1†). It has been known that these functional groups cause significant damage to the ZGNR edges when they were introduced to both edges, rather than just one edge, and such damage apparently results in the destruction of localized edge states of ZGNRs which cause the disappearance of the flat bands near the Fermi level. In addition, the conjugation in ZGNRs is partially disrupted by the ketone and ether groups, and thereby, the electron conductivity is deteriorated and the band gaps become bigger. By affecting the magnitudes of the band gaps, the ketone and ether groups have a more adverse effect than carboxyl and hydroxyl groups on the electron conductivity of ZGNRs.

Fig. 2 Band structure of ox-ZGNRs with (a and b) ketone groups and (c and d) ether groups. Spin-up and down bands are indicated by red and blue dashed lines, respectively. (a) and (c) show the structures with these (ketone or ether) functional groups on one edge of the nanoribbon, and (b) and (d) are those with the respective functional groups on both edges. Each circle is proportional to the magnitude of the magnetization density at each atom. Red and blue circles correspond to spin-up and spin-down densities, respectively.

3.2 Band structures of reduced edge N-ZGNR

As an experimental method, oxidized carbon-based materials like graphene oxide have been converted via a specific annealing process into almost original carbon or nitrogen-doped carbon materials in order to restore those electrical conductivity or to impart particular functions with conductivity, such as molecule adsorption¹³ and enhanced electrical performance.²⁰ On the same point of view, we considered the nitrogen-converted ZGNR from edge-oxidized ZGNR. In our calculations, we introduced N onto the edges of ZGNRs, by using pyridinic and pyrrolic functional groups and by substituting certain single C atoms with N atoms (graphitic), in order to study the effects of such doping on the electronic properties of the ZGNRs. As we did for ZGNRs containing oxygen functional groups, we analyzed the band structures of ZGNRs containing pyridinic, pyrrolic, and graphitic group attached on one edge and both edges of the nanoribbon. These N-ZGNR models are shown in Fig. 3 and 4, and their band gaps are summarized in Table 2.

Table 2 Band gaps of N-ZGNRs with pyridinic, pyrrolic and graphitic group

Structure	Band gap (eV)
	Pyridinic	Pyrrolic	Graphitic
One edge	0.2165	0.2606	0.0000
Both edges	0.2882	0.3057	0.4244

---

The band structures for N-ZNGRs with pyridinic and pyrrolic groups (Fig. 3) on one edge are similar to those of ox-ZGNRs with carboxyl and hydroxyl groups. Their band structures are also similar to those of pristine ZGNRs since pyridinic and pyrrolic groups do not disrupt the sp² hybridization form of the edge carbon atoms. The total magnetizations of N-ZGNRs with pyridinic and pyrrolic groups were −0.026 μ_B and −0.016 μ_B, respectively (Table S2†). As a result, weak spin splitting occurs near the Fermi level, as in ox-ZGNRs with carboxyl and hydroxyl groups. However, unlike the carboxyl and hydroxyl groups, pyridinic group directly replaced edge carbon atoms, and hence affected the edge states more strongly than the carboxyl and hydroxyl groups. As a result, spin splitting near the Fermi level for the pyridinic case is more significant than that for carboxyl and hydroxyl, so the band gap of the structure with pyridinic group on one edge was calculated to be 0.2156 eV, which is smaller than that of the ox-ZGNRs with carboxyl and hydroxyl groups. In the case of the pyrrolic structure, the N-ZGNR edge is widened by introducing the pyrrolic group (Fig. 3c and d). The magnitude of the band gap of the structure with pyrrolic group on one edge is calculated to be 0.2602 eV, which is larger than that of the pyridinic because pyrrolic group damaged N-ZGNRs edges more significantly than the pyridinic group. In the cases of N-ZNGRs with pyridinic and pyrrolic groups on both edges of the nanoribbon, their band gaps are 0.2882 eV and 0.3057 eV, respectively, and the spin splitting does not occur because spin-up and spin-down states are degenerate in all energy bands. Band structures for the pyridinic and pyrrolic cases are similar to those for the carboxyl and hydroxyl groups, but the band gaps for the pyridinic and pyrrolic cases are smaller than those for ox-ZGNRs.

Fig. 3 Band structure of N-ZGNRs with (a and b) pyridinic groups and (c and d) pyrrolic groups. Spin-up and down bands are indicated by red and blue dashed lines, respectively. (a) and (c) show the structures with these (pyridinic or pyrrolic) functional groups on one edge of the nanoribbon, and (b) and (d) are those with the respective functional groups on both edges. Each circle is proportional to the magnitude of the magnetization density at each atom. Red and blue circles correspond to spin-up and spin-down densities, respectively.

For N-ZNGRs with a graphitic N on one edge of the ZGNR (Fig. 4a), the band structures are similar to those from ox-ZGNRs with ketone and ether groups. The ether-containing ox-ZGNR structure is particularly similar to the graphitic N-substituted N-ZGNR structure since in both cases a heteroatoms such as oxygen and nitrogen replace an edge carbon atom. In addition, the spin polarization around the edge of the graphitic N-substituted structure is almost completely suppressed. As a result, the total magnetization for this structure is 0.508 μ_B in our calculations, and considerable spin splitting occurs near the Fermi level. However, unlike the case for the ketone and ether groups, the graphitic N-substituted structure has zero band gap. In the case of substitutions of nitrogen on both edges of the N-ZGNR, the band gap is 0.4244 eV and the spin splitting does not occur because these introduced nitrogen atoms completely suppressed spin polarization of the N-ZGNRs and as a result, the flat bands near the Fermi level disappear as they do for ox-ZGNRs with ketone and ether groups. The band gap of the graphitic N-ZGNR is larger than the band gaps of the pyridinic and pyrrolic N-ZGNRs because graphitic N-substitution disrupted the sp² hybridization of edge carbon atoms. As a result, as for the ketone- and ether-containing ox-ZGNRs, graphitic N-substitution changes the types of bonds throughout the N-ZGNR, which in turn affects the band structure. Therefore, the electron conductivity deteriorates and the band gap becomes wider for the graphitic N-substituted N-ZGNR than for the pyridinic and pyrrolic N-ZGNRs.

Fig. 4 Band structure of N-ZGNRs with graphitic N-substitution. Spin-up and down bands are indicated by red and blue dashed lines, respectively. (a) is structure with graphitic N-substitution on one edge of the nanoribbon, and (b) is that with graphitic N-substitution on both edges. Each circle is proportional to the magnitude of the magnetization density at each atom. Red and blue circles correspond to spin-up and spin-down densities, respectively.

In our calculations, N-ZGNRs displays smaller band gaps than ox-ZGNRs. When the sp² hybridization is preserved throughout the N-ZGNR including at its edge, the small band gap is retained. Correspondingly, the edges are less damaged, and the electron conductivity is maintained. Therefore, it is possible to increase the conductivity and narrow the band gap of an ox-ZGNR by reducing it to an N-ZGNR.

4. Conclusion

We have characterized the band structures of edge-oxidized ZGNRs (ox-ZGNRs) and edge-nitrided ZGRNs (N-ZGNRs) using density functional theory. The introduction of oxygen functional groups such as carboxyl, hydroxyl, ketone and ether groups onto the edges of ZGNRs altered the electronic structures of such edges correspondingly. The sp² hybridization of the edge carbon atoms of ox-ZGNR was disrupted by the ketone and ether groups, while it was not affected by the carboxyl and hydroxyl groups. When oxygen functional groups were introduced on only one ZGNR edge, the band gaps were reduced due to spin splitting. In particular, introducing ketone and ether groups disrupted the sp² hybridization of edge carbon atoms. As a result, the band gaps of the ox-ZGNRs were widened and their electronic conductivity became worse. In the cases of N-ZGNRs, the band structures of the N-ZGNRs with pyridinic and pyrrolic groups showed tendencies similar to those ox-ZGNRs with carboxyl and hydroxyl groups due to the preservation of the sp² hybridization of the edge carbon atoms. The band structure of N-ZGNRs with pyrrolic group was similar to that of pyridinic N-ZGNRs, but the band gap of the former was wider than that of the latter. This difference arose because of the greater extent of alteration in the edge of the nanoribbon in the pyrrolic N-ZGNR in comparison to that of the pyridinic N-ZGNR. The band structure of the graphitic N-substituted N-ZGNR has similar feature with wider band gap in comparison to the pyrrolic and pyridinic N-ZGNRs. Although most of ox-ZGNRs have benefit to enlarge their band gaps, the conductivity of the heavier oxidizing-edge ZGNR might be deteriorated. The conductivity of edge-nitrided ZGNR, however, can be well maintained. Therefore, the band gap could be controlled without deteriorating election conductivity by reducing ox-ZGNRs to N-ZGNRs.

Acknowledgements

This research was supported by Global Frontier Program through the Global Frontier Hybrid Interface Materials (GFHIM) of the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (No. 2013M3A6B1078882 and 2013M3A6B1078874).

References

1. (a) S. Bae, H. Kim, Y. Lee, X. F. Xu, J. S. Park, Y. Zheng, J. Balakrishnan, T. Lei, H. R. Kim, Y. I. Song, Y. J. Kim, K. S. Kim, B. Ozyilmaz, J. H. Ahn, B. H. Hong and S. Iijima, Nat. Nanotechnol., 2010, 5, 574; (b) X. M. Wang, H. Tian, M. A. Mohammad, C. Li, C. Wu, Y. Yang and T. L. Ren, Nat. Commun., 2015, 6, 7767.
2. (a) J. G. Son, M. Son, K. J. Moon, B. H. Lee, J. M. Myoung, M. S. Strano, M. H. Ham and C. A. Ross, Adv. Mater., 2013, 25, 4723; (b) F. H. L. Koppens, T. Mueller, P. Avouris, A. C. Ferrari, M. S. Vitiello and M. Polini, Nat. Nanotechnol., 2014, 9, 780.
3. W. X. Zhang, Sci. Rep., 2014, 4, 6320.
4. (a) K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17954; (b) K. Wakabayashi, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 125428; (c) V. Barone, O. Hod and G. E. Scuseria, Nano Lett., 2006, 6, 2748; (d) X. L. Li, X. R. Wang, L. Zhang, S. W. Lee and H. J. Dai, Science, 2008, 319, 1229.
5. (a) K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim and A. K. Geim, Science, 2007, 315, 1379; (b) K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197; (c) F. Schwierz, Nat. Nanotechnol., 2010, 5, 487.
6. (a) L. Y. Jiao, L. Zhang, X. R. Wang, G. Diankov and H. J. Dai, Nature, 2009, 458, 877; (b) D. V. Kosynkin, A. L. Higginbotham, A. Sinitskii, J. R. Lomeda, A. Dimiev, B. K. Price and J. M. Tour, Nature, 2009, 458, 872; (c) C. Berger, Z. M. Song, X. B. Li, X. S. Wu, N. Brown, C. Naud, D. Mayou, T. B. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. de Heer, Science, 2006, 312, 1191; (d) E. Bekyarova, M. E. Itkis, P. Ramesh, C. Berger, M. Sprinkle, W. A. de Heer and R. C. Haddon, J. Am. Chem. Soc., 2009, 131, 1336.
7. (a) O. Hod, V. Barone, J. E. Peralta and G. E. Scuseria, Nano Lett., 2007, 7, 2295; (b) M. Acik, G. Lee, C. Mattevi, M. Chhowalla, K. Cho and Y. J. Chabal, Nat. Mater., 2010, 9, 840; (c) L. R. Radovic and B. Bockrath, J. Am. Chem. Soc., 2005, 127, 5917.
8. S. Dutta and S. K. Pati, J. Mater. Chem., 2010, 20, 8207.
9. Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
10. (a) E. J. Kan, Z. Y. Li, J. L. Yang and J. G. Hou, J. Am. Chem. Soc., 2008, 130, 4224; (b) D. W. Boukhvalov and M. I. Katsnelson, Nano Lett., 2008, 8, 4373; (c) Y. F. Li, Z. Zhou, P. W. Shen and Z. F. Chen, ACS Nano, 2009, 3, 1952; (d) S. S. Kim, H. S. Kim, H. S. Kim and Y. H. Kim, Carbon, 2015, 81, 339; (e) N. Gorjizadeh, A. A. Farajian, K. Esfarjani and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 155427; (f) E. Cruz-Silva, Z. M. Barnett, B. G. Sumpter and V. Meunier, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155445; (g) F. Cervantes-Sodi, G. Csanyi, S. Piscanec and A. C. Ferrari, Phys. Status Solidi B, 2008, 245, 2068; (h) S. S. Yu, W. T. Zheng, Q. B. Wen and Q. Jiang, Carbon, 2008, 46, 537.
11. F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652.
12. (a) T. B. Martins, R. H. Miwa, A. J. R. da Silva and A. Fazzio, Phys. Rev. Lett., 2007, 98, 196803; (b) T. B. Martins, A. J. R. da Silva, R. H. Miwa and A. Fazzio, Nano Lett., 2008, 8, 2293.
13. J. M. Yun, K. N. Kim, J. Y. Kim, D. O. Shin, W. J. Lee, S. H. Lee, M. Lieberman and S. O. Kim, Angew. Chem., Int. Ed., 2012, 51, 912.
14. (a) G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169; (b) G. Kresse, J. Non-Cryst. Solids, 1995, 193, 222.
15. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
16. (a) J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
17. (a) W. Koh, J. I. Choi, K. Donaher, S. G. Lee and S. S. Jang, ACS Appl. Mater. Interfaces, 2011, 3, 1186; (b) W. Koh, J. I. Choi, E. Jeong, S. G. Lee and S. S. Jang, Curr. Appl. Phys., 2014, 14, 1748; (c) W. Koh, J. I. Choi, S. G. Lee, W. R. Lee and S. S. Jang, Carbon, 2011, 49, 286; (d) W. Koh, J. H. Lee, S. G. Lee, J. I. Choi and S. S. Jang, RSC Adv., 2015, 5, 32819; (e) J. H. Lee, S. G. Kang, H. S. Moon, H. Park, I. T. Kim and S. G. Lee, Appl. Surf. Sci., 2015, 351, 193; (f) H. S. Moon, J. H. Lee, S. Kwon, I. T. Kim and S. G. Lee, Carbon Letters, 2015, 16, 116; (g) H. Park, S. H. Noh, J. H. Lee, W. J. Lee, J. Y. Jaung, S. G. Lee and T. H. Han, Sci. Rep., 2015, 5, 14163; (h) W. Koh, H. S. Moon, S. G. Lee, J. I. Choi and S. S. Jang, ChemPhysChem, 2015, 16, 789; (i) J. H. Lee, S. G. Kang, I. T. Kim, S. Kwon, I. Lee and S. G. Lee, Theor. Chem. Acc., 2016, 135, 50.
18. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
19. (a) B. Sommer, J. Sonntag, A. Ganczarczyk, D. Braam, G. Prinz, A. Lorke and M. Geller, Sci. Rep., 2015, 5, 7781; (b) S. Ryu, J. Maultzsch, M. Y. Han, P. Kim and L. E. Brus, ACS Nano, 2011, 5, 4123.
20. D. C. Wei, Y. Q. Liu, Y. Wang, H. L. Zhang, L. P. Huang and G. Yu, Nano Lett., 2009, 9, 1752.
21. (a) K. Z. Milowska and J. A. Majewski, J. Chem. Phys., 2013, 138, 194704; (b) K. Z. Milowska and J. A. Majewski, Phys. Status Solidi B, 2013, 250, 1474; (c) K. Milowska, M. Birowska and J. A. Majewski, Diamond Relat. Mater., 2012, 23, 167.
22. A. Pramanik and H. S. Kang, J. Phys. Chem. C, 2011, 115, 10971.
23. G. Lee and K. Cho, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165440.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra03458f

---