Lead adsorption from aqueous solutions by a granular adsorbent prepared from phoenix tree leaves
Sha Liang,
Nan Ye,
Yuchen Hu,
Yafei Shi,
Wei Zhang,
Wenbo Yu,
Xu Wu and
Jiakuan Yang*
School of Environmental Science and Engineering, Huazhong University of Science and Technology (HUST), Wuhan, Hubei 430074, PR China. E-mail: jkyang@mail.hust.edu.cn; Fax: +86 27 87792102; Tel: +86 27 87792207
First published on 2nd March 2016
Abstract
In this study, a granular adsorbent was prepared from phoenix tree leaf powder with bentonite as the binder. The granular adsorbent was characterized by TG, BET and SEM analyses. The maximum specific surface area and pore volume were 166.3 m2 g−1 and 0.276 cm3 g−1, respectively, after the granular adsorbent was calcined at 500 °C. Effects of pH, adsorption time and initial metal ion concentration on the adsorption of Pb2+ by 500 °C calcined granular adsorbent were investigated in batch experiments. Higher pH was favorable for the adsorption process and significant release of Na+, K+ and Mg2+ were observed, assuming the predominant Pb2+ adsorption mechanism was ion exchange. The adsorption could attain equilibrium within 24 h with a gradual increase of the solution pH. The kinetics data were analyzed using three adsorption kinetic models: the pseudo-first-order, pseudo-second-order and intraparticle diffusion equations. Results show that intraparticle diffusion or chemical adsorption is the rate-limiting step depending on the adsorption time. The adsorption isotherms best fitted the Langmuir–Freundlich model and the maximum Langmuir adsorption capacity was found to be 71 mg g−1. This novel granular adsorbent has proven to be a potential inexpensive adsorbent for Pb2+ removal from aqueous solutions.
1. Introduction
Pollution of water resources by toxic heavy metals, such as mercury, lead, copper, chromium, nickel, cadmium and zinc, has raised great concern in recent decades. These heavy metals are potentially hazardous to humans and aquatic species. Stringent limits have been imposed on potable water supplies as well as effluent discharge. Elevated heavy metal concentrations can be reduced by chemical precipitation, membrane filtration or ion exchange. However, for concentrations below 100 mg L−1, these methods are less effective, more costly and/or difficult to meet the limits. Using inexpensive biomass as adsorbents to remove heavy metals from wastewater has been considered as an economical and environment friendly alternative recently.1,2Phoenix tree (or Firmiana simplex) is commonly used for landscaping in major streets, parks and campus of schools in China. A lot of phoenix tree leaves fall in deep autumn that imposes a great burden on street sweeping. These fallen leaves are mainly landfilled or incinerated. They take up spaces in landfill; and incineration of leaves may release fume, dusts and other potentially harmful gases. Beneficial reuses of them will minimize their adverse environmental impact from disposal. Similar to other agricultural wastes, fallen phoenix tree leaves are mainly composed of cellulose, hemi-cellulose, lignin and a variety of extractives. All of them contain various functional groups, such as carboxyl and hydroxyl, which make adsorption processes possible. Phoenix tree leaves have been proven to effectively remove methylene blue,3,4 Pb(II),5 Mn(II),6 Cd(II)7 and Zn(II)8 from aqueous solutions.
Adsorbents can be in the form of powder, gel or suspension, which can provide a large surface area and a high capacity for adsorption. However, serious operational problems such as pore clogging, excessive pressure drop and mass loss make then unsuitable for direct use in packed beds. In addition, large sedimentation basins or filtration may be needed to recover/remove these adsorbents.9,10 Thus, powdered adsorbents need to be stabilized, fixed or granulated before they can be used in most practical adsorption applications. Granulation is a process to mix the adsorbent powder with a binder, using manual, vibration-dropping, spray coating or extrusion methods. Commercial granular activated carbon has been reported to remove heavy metal ions and dye from aqueous solutions,11,12 but the cost to prepare the granular activated carbon is high. To use the waste biomass powder to prepare granular adsorbent is seldom reported.
Bentonite is a natural clay with a general chemical formula of Nax(Al,Mg)2SiO10(OH)2·nH2O. China is ranked first in the world with regards to bentonite reserves. It is also the traditional low-cost efficient adsorbent, which has high potential for heavy metal removal from wastewater due to its abundance, chemical and mechanical stability, large specific surface area, high cation exchange capacity, and unique structural properties.13 In some studies, bentonite was used as a porous based support material to enhance the dispersibility of nanoscale zero-valent iron for the removal of hexavalent chromium from wastewater.14
In this study, fallen phoenix tree leaves were used as the raw material for preparation of a novel granular adsorbent with bentonite as the binder. The batch adsorption behaviors of the prepared granular adsorbent for removing Pb2+ from aqueous solutions were investigated.
2. Materials and methods
2.1 Materials
All chemicals used were of analytical grade. The Pb stock solution was prepared from Pb(NO3)2 with deionized water. Solutions containing Pb ions were freshly prepared by diluting the Pb stock solution with deionized water.Fallen phoenix tree leaves were collected from the university campus in last autumn. After air dried, the fallen leaves were crushed by a cutting mill and then the powder was passed a sieve of 60 mesh (effective opening size of 0.25 mm). The results of an elemental analysis of leaf powder were N 0.65%, C 44.46%, H 5.95%, S 0.36% and O 41.56% by wt (oxygen was determined from the difference).
Bentonite was obtained from a local chemical company. The raw bentonite was sieved through a 200 mesh screen prior to use. The results of chemical compositions of the bentonite samples are depicted in Table 1. As shown, the main chemical components of the bentonite are SiO2, Al2O3, Na2O, Fe2O3, MgO, K2O and CaO.
| SiO2 | Al2O3 | Na2O | Fe2O3 | MgO | K2O | CaO | TiO2 | P2O5 | SO3 |
|---|---|---|---|---|---|---|---|---|---|
| a LOI: loss of ignition at 1200 °C. | |||||||||
| 67.022 | 15.038 | 3.285 | 2.152 | 1.898 | 1.447 | 1.369 | 0.329 | 0.080 | 0.057 |
| MnO | Rb2O | SrO | Y2O3 | ZrO2 | BaO | PbO | Cl | As2O3 | LOIa |
|---|---|---|---|---|---|---|---|---|---|
| 0.044 | 0.010 | 0.023 | 0.002 | 0.022 | 0.021 | 0.008 | 0.041 | 0.007 | 7.146 |
2.2 Preparation of granular adsorbent
Equal amounts of phoenix tree leaf powder and bentonite were weighed and mixed first. Deionized water was then slowly added into the mixture until a homogeneous paste was formed. The paste was then manually made into granules with a diameter of 5–6 mm and air dried. The granules were then calcined in a tube furnace under N2 atmosphere at 200 °C, 300 °C, 400 °C, 500 °C and 600 °C for 1 h, respectively. The color of the calcined granular adsorbents turned from brownish yellow to dark black with an increasing calcination temperature. In the test experiments, the air dried raw granular adsorbent will slowly disintegrate in water after several hours while the calcined granular adsorbents can maintain their shape after being soaked in water for 24 h.2.3 Adsorption experiments
Batch adsorption experiments were carried out by shaking 200 mg of the granular adsorbent with 40 mL of Pb2+ solutions of certain concentration in a water bath shaker (150 rpm and 30 °C) for a specific time. After adsorption and filtration, the concentrations of metal ions in the filtrate solution were analyzed by using inductive coupled plasma emission spectrometer (Optima 8300 ICP-OES, PerkinElmer). The amount of metal adsorbed (qe, mg g−1) was determined by using the following equation:
 | (1) |
2.4 Characterizations of adsorbents
The thermal analysis of the raw phoenix tree leaf powder, bentonite and the granular adsorbent were performed in a Pt crucible by thermo gravimetric analysis (TG) using a simultaneous thermal analyzer (TA-Q600, USA) in the range of 10–800 °C and at a ramping rate of 10 °C min−1 under a nitrogen atmosphere with gas flow rate of 100 mL min−1.Specific areas of the prepared granular adsorbents calcined at different temperatures were measured by a static nitrogen adsorption analyzer (JW-BK122W, Beijing JWGB Sci&Tech. Co., Ltd, China).
Morphologies of the raw granular adsorbent, the granular adsorbent calcined at 500 °C and the Pb2+-loaded granular adsorbent were studied with scanning electron microscopy (Sirion 200SEM, FEI, Holland) operated at 10 kV after the samples were coated with gold.
3. Results and discussion
3.1 Characterizations of granular adsorbent
 | ||
| Fig. 1 TG–DTG curves of (a) raw phoenix tree leaf powder, (b) bentonite and (c) raw granular adsorbent. | ||
As shown in Fig. 1(b), the weight loss of bentonite under 800 °C is only about 12%. The TG curve presents two stages of mass loss. The first stage corresponds to the evaporation of surface and interlayer absorbed water (8.53%). The second stage corresponds to the removal of structural water (4.2%).
From Fig. 1(c), the TG–DTG curves of the raw granular adsorbent are similar to that of phoenix tree leaf powder, except that the weight loss in each stage of the TG curve is smaller than the corresponding one in the raw phoenix tree leaf power. In addition, the position and intensity of weight loss rate peaks in the DTG curve held towards earlier and lower (0.25% per °C at 311 °C) by the presence of bentonite.
The weight loss percentages of granular adsorbents calcined at 200 °C, 300 °C, 400 °C, 500 °C and 600 °C under N2 atmosphere for 1 h were 11.5%, 25.5%, 29%, 36% and 35%, respectively. This result is consistent with Fig. 1(c) in which the TG curve becomes flatter after 500 °C. But the weight loss percentage of the granular adsorbent is less than the theoretical value from TG curve, which implies that the pyrolysis was not completed.
| Calcination temperature (°C) | Specific surface area (m2 g−1) | Total adsorption pore volume (cm3 g−1) | Average adsorption pore size (nm) | Micropore volume (cm3 g−1) | Mesopore volume (cm3 g−1) | Most probable pore size (nm) |
|---|---|---|---|---|---|---|
| 200 | 8.5 | 0.029 | 14.73 | 0.0036 | 0.026 | 1.262 |
| 300 | 10.3 | 0.049 | 17.53 | 0.0043 | 0.041 | 1.264 |
| 400 | 14.7 | 0.024 | 7.21 | 0.0066 | 0.019 | 1.244 |
| 500 | 166.3 | 0.276 | 5.36 | 0.0465 | 0.177 | 1.077 |
| 600 | 90.1 | 0.060 | 3.98 | 0.0433 | 0.047 | 0.981 |
The nitrogen adsorption/desorption isotherms and pore size distributions of the granular adsorbents calcined at different temperatures are shown in Fig. 2 and 3, respectively. The N2 adsorption/desorption isotherms (Fig. 2) display similar shapes for the granular adsorbents calcined from 200 to 600 °C, exhibiting the presence of an adsorption hysteresis loop, characteristic of type IV isotherms. Such isotherms are typical of mesoporous solids. On the other hand, the pore size distributions in Fig. 3 denote that the degree of micro-, meso- and macroporosity developments of granular adsorbent calcined at 500 °C are significantly greater than those of the other granular adsorbents.
 | ||
| Fig. 2 Nitrogen adsorption–desorption isotherms of the granular adsorbents calcined at different temperatures. | ||
3.2 Effect of the calcination temperature
Effect of the calcination temperature on the adsorption removal of Pb2+ from the aqueous solutions is given in Fig. 4. As shown, the adsorption efficiency and adsorption capacity increase with the increase of temperature from 200 to 500 °C, then decrease afterwards. The highest adsorption efficiency of 99.39% was obtained at 500 °C, which corresponds to the maximum specific surface area and highest adsorption pore volume.Meanwhile, after adsorption and filtration, the total organic carbon concentrations (TOC) of the filtrate solutions were measured by a TOC analyzer (Multi N/C 2100, Analytic Jena AG, Germany). The TOC concentrations of filtrate solutions after adsorption by granular adsorbents calcined at 200 °C, 300 °C, 400 °C, 500 °C and 600 °C were 241.2, 171.7, 52.8, 24.0 and 4.7 mg L−1, respectively. It can be concluded that the TOC concentrations decrease dramatically with the increase of the calcination temperature. The higher TOC concentrations associated with the low-temperature calcined adsorbents was from the dissolution of pigments and other small molecular weight compounds of the granular adsorbent. This can also be judged from the color of the filtrate, which turns from brownish yellow (200 and 300 °C) to light yellow (400 °C) and to colorless (500 and 600 °C). Therefore, the granular adsorbent calcined at 500 °C were chosen for subsequent experiments.
3.3 Effect of pH
Fig. 5 illustrates the effect of pH on adsorption of Pb2+ by the 500 °C-calcined granular adsorbent. It reveals that the adsorption of lead increases from 15 to 99% with an increase in the solution pH from 1.0 to 5.5. The low adsorption efficiency of Pb2+ at a lower pH is due to strong H+ ion competition for the available ion exchange sites. Also, at a low pH, the surface of the granular adsorbent will be more positively or less negatively charged, because of the amphoteric dissociation of oxides of aluminum, silicon, calcium, iron and magnesium presented in bentonite,16 which does not favor the adsorption of positive-charged lead ions. | ||
| Fig. 5 Effect of pH on the adsorption of Pb2+ by the 500 °C-calcined granular adsorbent. (Initial concentration of Pb2+: 200 mg L−1; solid/liquid: 200 mg/40 mL; 30 °C; 24 h). | ||
Concentrations of other ions including Al3+, Si4+, K+, Na+, Ca2+, Mg2+ and Fe2+ in the filtrate were also measured. As shown in Fig. 5, small amounts of Si4+ and Na+ ions were released into the solution under a stronger acidic environment. At a higher pH, significant releases of light metals including Na+, K+ and Mg2+ were observed. Also, the final equilibrium pH was higher than the initial pH and reached 6.2 while the initial pH was 5.0. Thus, ion exchange is considered to be the predominant Pb2+ adsorption mechanism. The amounts of metals bound (Pb2+ + 1/2H+) to the surface of the granular adsorbent and those released (1/2Na+ + 1/2K+ + Mg2+) under initial pHs of 4, 5 and 5.5 were calculated. The results indicate that the amounts of metals bound (Pb2+ + 1/2H+) was more than that of released (1/2Na+ + 1/2K+ + Mg2+). This implies that other mechanisms such as precipitation and physical adsorption, in addition to ion exchange, could possibly take place.17
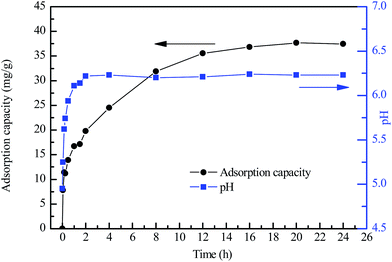
3.4 Effect of adsorption time
Effect of adsorption time on adsorption of Pb2+ by the 500 °C-calcined granular adsorbent and the variations of the solution pH are presented in Fig. 6. As shown, the adsorption efficiency increases with the increase of time until equilibrium reaches at around 20 h. The solution pH increased quickly from 5.0 to around 6.2 in the first two hours, then kept stable afterwards. The reason was that according to the ion exchange mechanism, a certain amount of H+ was replaced by light metal ions like Na+, K+ and Mg2+, which leaded to the increasement of solution pH.Generally, the adsorption process can be divided into four stages: (1) bulk transport; (2) film mass transfer; (3) intraparticle diffusion and (4) adsorption. In a rapid stirred, well mixed batch adsorption, mass transport from the bulk solution to the external surface of the adsorbent is usually fast. In addition, film diffusion plays a significant role at shorter time intervals (within first few minutes) and this cannot be considered as the rate limiting step.18,19 Thus, steps (3) and (4) are the possible rate-limiting steps.
Various models such as pseudo-first- and second-order kinetic equations and intraparticle diffusion equation are used to examine the controlling mechanism of adsorption process.20,21
The pseudo-first-order kinetic model known as the Lagergren equation:
| qt = qe{1 − exp(−k1t)} | (2) |
The pseudo-second-order kinetic model:
 | (3) |
The intraparticle diffusion model:
| qt = kintt1/2 + I | (4) |
The fitting results of the three kinetics models are plotted in Fig. 7(a). The correlation coefficients (R2) of pseudo-first-order, pseudo-second-order and intraparticle diffusion model were 0.862, 0.913 and 0.933, respectively. It appears that intraparticle diffusion model provides the best fitting to the experimental data. However, it can be seen from Fig. 7(a) that at adsorption time less than 4 h, the intraparticle diffusion model fitted the experimental data very well; at adsorption time more than 4 h, pseudo-second-order model fitted the experimental better than intraparticle diffusion model. This suggests the adsorption process may undergo two stages, at first stage of adsorption time less than 4 h, intraparticle diffusion is the rate limiting step; after then, chemical adsorption is the rate limiting step. Fig. 7(b) plots a satisfactory fitting result of the experimental data by two models.
3.5 Adsorption isotherms
Fig. 8 plots the equilibrium adsorption isotherms between the amount of adsorbed lead ions (qe) and the equilibrium lead concentration (Ce) in the solution.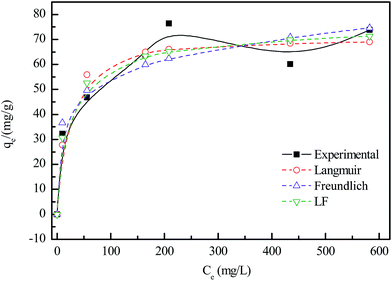 | ||
| Fig. 8 Adsorption isotherms of Pb2+ removal by the 500 °C-calcined granular adsorbent. (Solid/liquid: 200 mg/40 mL; initial pH: 5.0; 30 °C; 24 h). | ||
The isotherms data were fitted by three isotherm models in the present study: Langmuir, Freundlich and Langmuir–Freundlich (LF) and the fitting results were also shown in the form of dotted lines in Fig. 8.20,21
Based on the assumption that all adsorption sites are equivalent and adsorption in active sites is independent of whether the adjacent is occupied, the Langmuir adsorption model can be expressed as:
 | (5) |
The Freundlich model describes non ideal adsorption or adsorption over heterogeneous surfaces and it is not restricted to monolayer formation, which can be expressed as:
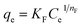 | (6) |
The combined features of the both Langmuir and Freundlich models is given by LF model, which can be expressed as:
 | (7) |
In eqn (7), if 1/nLF becomes 1, then eqn (7) reduces to Langmuir isotherm; at low concentrations, eqn (7) reduces to Freundlich isotherm.
The correlation coefficients (R2) of Langmuir, Freundlich and LF models were 0.786, 0.749 and 0.814, respectively. So the Langmuir–Freundlich (LF) adsorption isotherm model best fits the experimental data. This means that adsorption of Pb2+ on granular adsorbent is occurring by a combined Langmuir–Freundlich model. In other words, adsorption is diffusion controlled at low lead concentrations while monomolecular adsorption with a saturation value takes place at high lead concentrations.
The maximum adsorption capacity of Pb2+ on the granular adsorbent is 71 mg g−1, calculated by Langmuir model. A comparison of adsorption capacity of Pb2+ by some biomass based adsorbents was given in Table 3.
3.6 Swelling behavior of granular adsorbent
According to literature,27 biochar will swell in water to expand internal volume. To study the swelling behavior, around 0.28 g of the dry calcined granular adsorbent was immersed into distilled water for 48 and 72 h, respectively. Then the soaked granular adsorbent was placed on a preweighed filter and all the surface water was removed using suction filtration. The weight of the adsorbent was recorded periodically to obtain the weight loss as a function to time (Fig. 9). The weight losses of the adsorbent due to internal water evaporation after both 48 and 72 h soaking time were the same as 0.28 g, which means internal water occupied about 1 g g−1 adsorbent. The internal pore volume could have occurred by water diffusion into pore walls and expansion of internal pore structure.The SEM images show that after calcination at 500 °C (Fig. 10(b)), surface of the granular adsorbent becomes more porous and rough than the raw granular adsorbent (Fig. 10(a)) due to the removal of volatile material as discussed in Section 3.1.1. After adsorption of Pb2+ (Fig. 10(c)), the granular adsorbent exhibits even more porous and irregular morphology due to the further opening of internal pores by swelling in water.
 | ||
| Fig. 10 The SEM images of granular adsorbents: (a) uncalcined, (b) calcined at 500 °C, and (c) after adsorption of Pb2+. | ||
4. Conclusions
In this study, the granular adsorbent prepared from phoenix tree leaf powder with bentonite as the binder has proven to be a potential inexpensive adsorbent for Pb2+ removal from aqueous solutions. The granular adsorbent was characterized by TG, BET and SEM analyses. The thermogravimetric profile shows three stages of mass loss. The maximum specific surface area and pore volume were 166.3 m2 g−1 and 0.276 cm3 g−1, respectively, when the granular adsorbent was calcined at 500 °C. The adsorption behaviors for Pb2+ by 500 °C-calcined granular adsorbent were investigated in batch studies to study the effects of pH, adsorption and initial metal ion concentration. The results show that the maximum batch adsorption capacity of Pb2+ by the 500 °C-calcined granular adsorbent was 71 mg g−1. For practical application, the column adsorption behaviors of this novel granular adsorbent will be studied in our future work.Acknowledgements
This work was financially supported by the Natural Science Foundation of China for the Youth (51404106), the Youth Innovation Fund from Huazhong University of Science and Technology (2014QN149), project of Innovative and Interdisciplinary Team, Hust (0118261077) and Wuhan Planning Project of Science and Technology, China (2015070404010200). The authors would also like to thank the Analytical and Testing Center of Huazhong University of Science and Technology, for providing the facilities for the experimental measurements.References
- D. Sud, G. Mahajan and M. P. Kaur, Bioresour. Technol., 2008, 99, 6017–6027 CrossRef CAS PubMed.
- B. Volesky, Water Res., 2007, 41, 4017–4029 CrossRef CAS PubMed.
- R. Han, W. Zou, W. Yu, S. Cheng, Y. Wang and J. Shi, J. Hazard. Mater., 2007, 141, 156–162 CrossRef CAS PubMed.
- R. Han, Y. Wang, X. Zhao, Y. Wang, F. Xie, J. Cheng and M. Tang, Desalination, 2009, 245, 284–297 CrossRef CAS.
- Z. Li, X. Tang, Y. Chen, L. Wei and Y. Wang, J. Hazard. Mater., 2009, 169, 386–394 CrossRef CAS PubMed.
- Z. Li, S. Imaizumi, T. Katsumi, T. Inui, X. Tang and Q. Tang, J. Hazard. Mater., 2010, 177, 501–507 CrossRef CAS PubMed.
- Q. Tang, X. Tang, M. Hu, Z. Li, Y. Chen and P. Lou, Removal of Cd(II) from aqueous solution with activated Firmiana simplex leaf: behaviors and affecting factors, J. Hazard. Mater., 2010, 179(1), 95–103 CrossRef CAS PubMed.
- Q. Tang, X. Tang, Z. Li, Y. Wang, M. Hu, X. Zhang and Y. Chen, J. Environ. Eng., 2011, 138, 190–199 CrossRef.
- C. Zhu, Z. Luan, Y. Wang and X. Shan, Sep. Purif. Technol., 2007, 57, 161–169 CrossRef CAS.
- X. Dou, D. Mohan and C. U. Pittman, Water Res., 2013, 47, 2938–2948 CrossRef CAS PubMed.
- J. Goel, K. Kadirvelu, C. Rajagopal and V. K. Garg, J. Hazard. Mater., 2005, 125, 211–220 CrossRef CAS PubMed.
- G. Walker and L. Weatherley, Water Res., 1997, 31, 2093–2101 CrossRef CAS.
- K. G. Bhattacharyya and S. S. Gupta, Adv. Colloid Interface Sci., 2008, 140, 114–131 CrossRef CAS PubMed.
- L.-n. Shi, X. Zhang and Z.-l. Chen, Water Res., 2011, 45, 886–892 CrossRef CAS PubMed.
- N. Farinella, G. Matos and M. Arruda, Bioresour. Technol., 2007, 98, 1940–1946 CrossRef CAS PubMed.
- S. A. Khan and M. A. Khan, Waste Manag., 1995, 15, 271–282 CrossRef CAS.
- D. Mohan, C. U. Pittman Jr, M. Bricka, F. Smith, B. Yancey, J. Mohammad, P. H. Steele, M. F. Alexandre-Franco, V. Gómez-Serrano and H. Gong, J. Colloid Interface Sci., 2007, 310, 57–73 CrossRef CAS PubMed.
- Y. S. Ho, J. C. Y. Ng and G. McKay, Sep. Purif. Technol., 2000, 29, 189–232 CrossRef CAS.
- R. Aravindhan, J. R. Rao and B. U. Nair, J. Hazard. Mater., 2007, 142, 68–76 CrossRef CAS PubMed.
- S. A. Singh, B. Vemparala and G. Madras, J. Environ. Chem. Eng., 2015, 3, 2684–2696 CrossRef CAS.
- S. Liang, X. Y. Guo, N. C. Feng and Q. H. Tian, J. Hazard. Mater., 2010, 174, 756–762 CrossRef CAS PubMed.
- S. Y. Quek, D. A. J. Wase and C. F. Forster, Water SA, 1998, 24, 251–256 CAS.
- M. Iqbal, A. Saeed and S. Iqbal Zafar, J. Hazard. Mater., 2009, 164, 161–171 CrossRef CAS PubMed.
- S. Liang, X. Y. Guo, N. C. Feng and Q. H. Tian, J. Hazard. Mater., 2009, 170, 425–429 CrossRef CAS PubMed.
- B. M. W. P. K. Amarasinghe and R. A. Williams, Chem. Eng. J., 2007, 132, 299–309 CrossRef CAS.
- K. K. Singh, M. Talat and S. H. Hasan, Bioresour. Technol., 2006, 97, 2124–2130 CrossRef CAS PubMed.
- D. Mohan, S. Rajput, V. K. Singh, P. H. Steele and C. U. Pittman Jr, J. Hazard. Mater., 2011, 188, 319–333 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |