Spin-manipulated phonon dynamics during magnetic phase transitions in triangular lattice antiferromagnet CuCr1−xMgxO2 semiconductor films
Xurui Li,
Junyong Wang,
Jinzhong Zhang,
Yawei Li,
Zhigao Hu* and
Junhao Chu
Department of Electronic Engineering, East China Normal University, Shanghai 200241, China. E-mail: zghu@ee.ecnu.edu.cn; Fax: +86-21-54345119; Tel: +86-21-54345150
First published on 4th March 2016
Abstract
Raman scattering and infrared reflectance spectra of CuCr1−xMgxO2 films (x = 0.03, 0.06 and 0.09) in the temperature range of 5–300 K have been studied, combined with first-principles calculations. The abnormal redshift of the Eg Raman mode center with decreasing temperature below 100 K for the lightly doped film (x = 0.03) is ascribed to the Cr 3d–O 2p–Cu 3d interaction. Strong disturbance of the local spin fluctuation at Cr sites in heavily Mg-doped films (x = 0.06 and 0.09) drives the Eg mode center to a normal blueshift with decreasing temperature. With further decreasing temperature, the out-of-plane structure increases the internal spin-charge coupling. It enhances the spin-flip splitting and brings back the abnormal redshift of the Eg Raman mode center. A similar but more obvious trend can be found from temperature-dependent Eu infrared mode center shifts. Two successive magnetic transitions were observed at the corresponding Néel temperatures TN1 around 24.7 K and TN2 around 23.0 K, as manifested by magnetoresistance measurements. The interesting phenomena of phonon dynamics are suggested to be manipulated by the spin structures during the magnetic transitions.
1 Introduction
Geometrically frustrated magnetic systems have been paid much attention in recent years owing to the emergence of their prominent magnetic properties.1,2 A large degeneracy of the ground state of the system can be yielded in frustrated magnetic systems, turning the matter into a fluid-like or wave-like state. This is because the localized magnetic moments or spins interacting through competing exchange interactions cannot be simultaneously satisfied.3 The Heisenberg triangular-lattice antiferromagnet (HTAF) is an excellent model for low-dimensional and frustrated magnetism, although some factors, like additional spin-anisotropy terms, usually make these systems different from the perfect one.4 As one of the most typical frustrated spin systems, delafossite-structured CuCrO2 has attracted considerable attention due to various favorable properties. High transmittance and low resistivity make impurity-doped CuCrO2 a potential candidate for p-type transparent conducting oxide (TCO) semiconductors.5–8 Meanwhile, the magnetoelectric properties of the CuCrO2 system have also attracted a lot of attention, due to the peculiar spin characteristics aroused by the Cr3+ ions. Consequently, how the spin property of the CuCrO2 system evolves under external fields has been a research hotspot, since the equilibrium spin structures are expected to be sensitively dependent on both thermal and magnetic fluctuations.8,9More recently, it has been reported that CuCrO2 undergoes two successive magnetic transitions in the low temperature regions.10 On top of this revelation, a suggestion has been proposed that the triangular lattice antiferromagnet (TLA) structure of CuCrO2 can provide an opportunity for unique magnetoelectric control of spin-chiral ferroelectric domain structures by means of both electric or magnetic fields.11,12 It opens up promising applications for the realization of future devices based on CuCrO2. As advanced techniques that study shifts in energy with information about phonon vibrational modes in a system, Raman scattering and infrared spectra are commonly used to study the intrinsic electromagnetic properties and crystal structures of a system. Nevertheless, few studies have been carried out to expound the influence of spin structure on phonon dynamics for CuCrO2 systems. The intrinsic correlation between optical properties and magnetic transitions for CuCrO2 systems has not been reported up to now. Moreover, it has been suggested that Mg-doped CuCrO2 has some advantages over pure CuCrO2, which has much lower conductivity. Upon doping with 5% Mg, the conductivity can be increased to 220 S cm−1, which is the highest among the delafossite-structured ABO2 systems.5 This property makes them easier to combine with their traditional n-type TCO counterparts. Neutron diffraction measurements have been studied to explore the magnetic properties of Mg-doped CuCrO2. A three-dimensional (3D) long-range character of the magnetic order was proposed to fit the neutron diffraction results instead of the traditional two-dimensional (2D) HTAF model.13 However, the influence on the spin characteristics of CuCrO2 from Mg doping has not been discussed in detail because only CuCr0.98Mg0.02O2 was studied in those measurements. This limits the development of spintronic devices with delafossite-structured CuCrO2 materials.
In this article, the Raman and infrared spectra of CuCr1−xMgxO2 (x = 0.03, 0.06 and 0.09) films have been measured in the temperature region of 5–300 K. The lattice vibration properties have been studied by investigating the experimental observations and first-principles calculations. The magnetoresistance (MR) effect has also been investigated under different magnetic fields to offer more information about the spin structures. By analyzing the optical properties and MR effect, one can discover the intrinsic mechanism of the spin characteristics, which is important for the development of spin transportation for CuCrO2-based devices.
2 Experimental and calculation details
CuCr1−xMgxO2 (x = 0.03, 0.06 and 0.09) films were prepared on (001) sapphire substrates by the sol–gel route, employing a spin-coating process. A detailed fabrication procedure and the film structure parameters can be found in a previous report.14 Temperature-dependent Raman scattering measurements were carried out using a Jobin-Yvon LabRAM HR 800 UV micro-Raman spectrometer. A He–Ne laser with a wavelength of 632.8 nm is taken as the excitation source. The sample was mounted into a continuous flow liquid helium cryostat (Oxford cryostat MicrostatHiResII system) in the temperature range of 5 K to 300 K with a resolution of 0.1 K. To get rid of the trivial temperature dependence, all Raman spectra have been divided by the Bose–Einstein occupation number n(ω) + 1 = 1/[1 − exp(−ħω/kBT) (ħ and kB are the Planck constant and Boltzmann constant, respectively). Note that the derived Raman spectra can be fitted with independent damped harmonic oscillators to uniquely obtain the phonon frequency.Infrared reflectance spectra were recorded using a Bruker Vertex 80V Fourier transform infrared (FT-IR) spectrometer equipped with a specular reflectance setup. The spectra were measured with a Globar lamp (a U-shaped SiC piece), a 6 μm Mylar beamsplitter and a DLaTGS detector in the experimental frequency range with a resolution of 0.5 cm−1. The film was mounted into an Oxford Optistat AC-V12w continuous flow cryostat with the film in He vapor. The experimental temperature region can be varied from 5 K to 300 K. Temperature-dependent resistance measurements were carried out on a home-built system, which is based on an Oxford Spectromag SM4000 magnetic system equipped with a series of precise electrical instruments. Here, the Sub-Femtoamp Remote SourceMeter (Keithley 6430) was used as a powerful tool for high-resistance measurements.
We adopt the density-functional theory (DFT) framework with the generalized gradient approximation (GGA) for the primitive cell of CuCrO2. The Perdew–Burke–Ernzerhof (PBE) functionals are used to address the exchange–correlation interactions.15 To overcome the well-known underestimation of the intra-band Coulomb interactions in metal oxides including 3d electrons, some other methods with additional corrections are often adopted to obtain more accurate results. Density functional theory (DFT) with Hubbard U correction (DFT+U) has been demonstrated to be particularly efficient and effective for treating the self-interaction error in transition metal chemistry.16 Nevertheless, the calculated results from DFT are sufficient for supporting the discussions here. Prior to performing vibration property calculations, the structure was relaxed until the forces on the atoms in the equilibrium position were smaller than 0.01 eV A−1 while keeping lattice parameters fixed and equal to the experimentally determined ones (a = 6.332 Å, α = 24.890 Å, u = 0.103 Å) for the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with atoms Cu, Cr and O occupying 1a(0,0,0) 1b(0.5,0.5,0.5) and 2c(u,u,u). The energy cutoff for the plane wave basis is 400 eV. Charge densities were approximated to 1.0 × 10−6 eV per atom by the self-consistent calculations. The integration within the Brillouin zone was performed over a 11 × 11 × 11 Monkhorst–Pack grid in the reciprocal space. The lattice dynamics were further assessed by the final displacement method with ultrasoft pseudopotential.
m with atoms Cu, Cr and O occupying 1a(0,0,0) 1b(0.5,0.5,0.5) and 2c(u,u,u). The energy cutoff for the plane wave basis is 400 eV. Charge densities were approximated to 1.0 × 10−6 eV per atom by the self-consistent calculations. The integration within the Brillouin zone was performed over a 11 × 11 × 11 Monkhorst–Pack grid in the reciprocal space. The lattice dynamics were further assessed by the final displacement method with ultrasoft pseudopotential.
3 Results and discussion
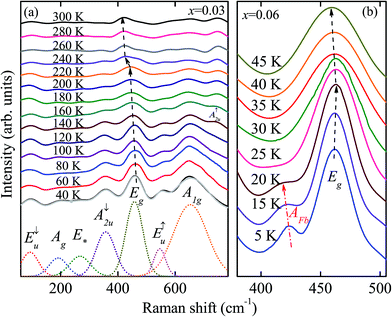
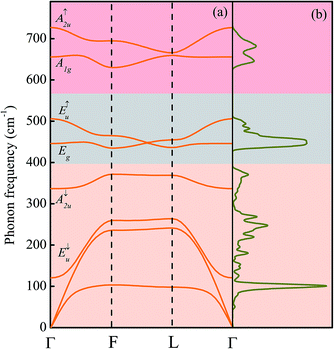
The temperature dependent Raman scattering spectra for CuCr0.97Mg0.03O2 are shown in Fig. 1(a). Several vibration modes can be observed from the Raman spectra. To identify the vibration modes, phonon-dispersion curves yielded by the first-principles calculations are studied, as shown in Fig. 2(a). We have analyzed the symmetry of the phonon patterns at kΓ = (0,0,0), kF = (0.5,0.5,0) and kL = (0,0.5,0), as well as along the ΓL paths. In delafossite compounds (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) such as CuGaO2 and CuCrO2, the primitive unit cell contains four atoms, giving rise to 12 normal modes.17 The Cu and Cr atoms occupy D3d site symmetry, while the O atom occupies C3v site symmetry. Group-theoretical analysis decomposes a general mode for delafossite oxide CuMO2 (M = trivalent cation) at the Brillouin zone center as:
m) such as CuGaO2 and CuCrO2, the primitive unit cell contains four atoms, giving rise to 12 normal modes.17 The Cu and Cr atoms occupy D3d site symmetry, while the O atom occupies C3v site symmetry. Group-theoretical analysis decomposes a general mode for delafossite oxide CuMO2 (M = trivalent cation) at the Brillouin zone center as:| Γ = A1g + Eg + 3A2u + 3Eu. | (1) |
At point Γ, the O atoms move in phase opposition while the Cu and Cr atoms are at rest for the even (g) modes. For the odd (u) modes, the O atoms vibrate in phase while the Cu and Cr atoms move with no restriction. The A modes imply movements of the Cu–O bonds along the hexagonal c-axis, whereas double degenerate E modes describe vibration in the triangular lattice perpendicular to the c-axis, as shown in Fig. 3. Normal vibrations are described in terms of the same irreducible representations as in the Γ point.18 However, the symmetrization of the translation degrees of freedom requires the consideration of two Brillouin zones at the zone edge, and the criterion concerning the O vibration patterns is inverted with respect to the Γ point. From points other than Γ, group theory yields the decompositions as follows:
| L = 4Ag + 2Bg + 2Au + 4Bu, | (2) |
| ΓL = 8A′ + 4A′′. | (3) |
At point L, the O atoms move in phase for the even modes and vibrate in phase opposition for the odd modes, while the metal cations are motionless for the odd modes. The A modes represent vibrations in the σ plane, and B modes represent vibrations along the twofold axis. The only symmetry operation is σ along ΓL. Vibrations take place in the σ plane for the A′ modes, whereas in the A′′ modes they vibrate in the perpendicular direction.19 It can also be observed from Fig. 2(b) that the calculated phonon dispersions along the principal directions in the Brillouin zone of CuCrO2 exhibit three major bands. These bands can be distinguished directly from the observations of density of phonon states (DPS). It is suggested that the O vibration patterns dominate the highest frequency band and the Cu vibration patterns dominate the lowest frequency band, while the transition metal modes make the most contribution to the middle frequency band.20 This indicates that the Cr3+-dominated magnetoelectric properties of CuCrO2 can have greater influence on the behaviour of the E↑u and Eg modes.
Focusing on the patterns at the Brillouin zone center, one of the three Eu odd modes represents an acoustic mode, while the other two modes are infrared-active. The same is the case for the Au modes. Even modes denoted with the “g” subscript are Raman-active. As can be seen from the phonon-dispersion curves, the calculated normal modes arranged in ascending frequencies are E↓u (120 cm−1), A↓2u (336 cm−1), Eg (446 cm−1), E↑u (505 cm−1), A1g (655 cm−1), and A↑2u (726 cm−1). Both Raman and infrared-active modes can be observed from the Raman spectra. The infrared-active modes of the E↓u peak, A↓2u peak and E↑u peak can be found around 100 cm−1, 360 cm−1 and 546 cm−1, respectively. The appearance of the mode at about 193 cm−1 at the lowest temperature is assigned to the Ag mode. Note that the weak mode around 270 cm−1, labeled as E*, is supposed to be from the sapphire substrate.14,21 The modes around 460 cm−1 and 650 cm−1 at 40 K can be assigned to the Eg and A1g modes, respectively. The observed mode centers are quite in accordance with the theoretical ones. Meanwhile, the temperature-dependent evolution of the modes shows a rather complicated behavior. With increasing temperature, most modes become weaker and gradually fade away. However, the A↑2u peak above 740 cm−1 shows a growing trend with increasing temperature. This is because the A↑2u mode considerably polarizes the unit cell and thus creates an important TO/LO splitting. The competition between the splitting modes indicates the anisotropy in the CuCrO2 systems. The splitting effect may also appear in other optical modes, but is relatively small.21 The original A1g mode and some other modes merge into one broadened peak with decreasing temperature. This is ascribed to the enhanced Cr 3d–O 2p–Cu 3d hybridization with decreasing temperature.22 On the other hand, the peak center of the Eg mode shows a generally declining trend below 300 K, as can be seen in Fig. 1(a). The blueshift of the peak center with decreasing temperature is usually attributed to the electron–phonon interaction and lattice thermal expansion. Interestingly, there is a sudden drop at the temperature above a cross point (Tcross) around 220 K, which has not been reported in previous Raman studies on pure CuCrO2. This phenomenon can also be found for CuCr0.94Mg0.06O2 and CuCr0.91Mg0.09O2 at a temperature of around 200 K, as can be seen in Fig. 4(b). This is because there is a transition of the carrier transport mechanism from a thermal activation behavior to a 3D variable range hopping (VRH) one at a specific temperature Tcross for impurity-doped CuCrO2.23,24 The transition behavior has been discovered previously from a complex relationship between the resistance and temperature, whereas the decline of the Eg mode peak center offers more clear evidence for the transition.25 The results also provide further evidence for the 3D HTAF model in the low temperature region mentioned above.
Fig. 1(b) shows the Raman spectra for CuCr0.94Mg0.06O2 in the lower temperature region from 5 K to 45 K. The detailed temperature dependence of the Eg mode center from the best fitting results is shown in Fig. 4(a). The peak center of the Eg mode for the film doped with x = 0.03 gradually diminishes with decreasing temperature to 5 K. This is in accordance with the abnormal band gap redshift trend with decreasing temperature at relatively low temperatures reported previously.26 The anomalous behavior in the low temperature region is related to the strong Cr 3d–O 2p–Cu 3d interaction. The occupied Cr 3d states interact covalently with the neighboring O states and enhance the p–d hybridization. Meanwhile, it was also manifested that the interaction can be weakened by heavy Mg doping due to the stronger disturbance of local spin fluctuation at Cr sites.14,25 This point can be manifested by the normal blueshift of the Eg peak center with decreasing temperature for the heavily doped CuCr1−xMgxO2 (x = 0.06 and 0.09) just below 45 K. However, it is obvious that the peak center of the Eg mode for the heavily doped CuCr1−xMgxO2 again shows a redshift trend with decreasing temperature when the temperature drops below 20 K. It can also be found from Fig. 1(b) that an additional mode just between A↓2u and Eg also appears with decreasing temperature below 20 K. According to previous studies, there are two successive magnetic transitions for CuCrO2 near the temperature around 24 K.10 The turning temperature is well in accordance with the temperature at which an additional mode around 420 cm−1 appears, indicating that they may share the same origin as the magnetic transitions.
The infrared spectra for CuCr1−xMgxO2 have also been studied at different temperatures as a complement to the Raman scattering experiments. The enlarged region of the E↑u mode is shown in Fig. 5(a). The frequency of E↑u here is lower than that observed from the Raman spectra. This is also ascribed to the TO/LO splitting. Further, this splitting is more obvious in the E↑u and A↑2u modes, indicating that the unit cell is more polarized in these modes than in the E↓u and A↓2u modes.27 The peak around 546 cm−1 in the Raman spectra can be assigned to the E↑u (LO) mode while the relatively smaller one from the infrared spectra here is suggested to be the E↑u (TO) mode. The peak center of the E↑u mode firstly shifts to a higher frequency with decreasing temperature, which is mainly caused by the lattice thermal shrinkage. However, when the temperature drops below 20 K, the peak center of the E↑u mode shifts to a lower frequency with decreasing temperature. This trend is similar to the temperature dependence of the Eg mode from the Raman spectra, but with a more obvious feature. The abnormal temperature dependence of the Eg and E↑u modes is ascribed to the influence on the electronic excitations from the crystal field-induced spin flip. It has been manifested that far-infrared spectroscopy offers a unique possibility to directly obtain the energy-level splitting between the low-lying crystal field split states without any further assumptions of the symmetry or the coupling to the neighboring spins.28 The far-infrared spectroscopy for films doped with x = 0.03 and 0.06 show several sharp peaks below 100 cm−1 at 5 K, as can be seen from the inset of Fig. 5(a). These relatively strong vibrations are supposed to be the features of the splitting energies from spin flips, corresponding to the excitation energy labeled by EFlip in Fig. 5(b).29 Nevertheless, the vibration for the CuCr0.91Mg0.09O2 film below 100 cm−1 is very similar to that of sapphire substrates, which is much weaker than that of samples with x = 0.03 and 0.06. This is because heavily doped Mg can disturb the spin fluctuation around Cr3+ and further attenuate the spin flip effect.
 | ||
| Fig. 5 (a) The E↑u mode center from infrared spectroscopy for the CuCr0.94Mg0.06O2 film in the low temperature region. The inset shows the vibration for the far-infrared spectroscopy in the region below 100 cm−1 at 5 K. Note that the vibration state has been normalized with the same scale for each sample. (b) An energy level spacing diagram for the CuCr1−xMgxO2 films was applied to explain the experimental results. The transition shown by the solid arrow-line represents one of the spin-flip energies. The forbidden transition shown by the dash-dot arrow-line corresponds to the absorption peak labeled as AFb in Fig. 1(b). | ||
To explore the intrinsic correlation between these abnormal phenomena and magnetic phase transitions, the magnetoresistance (MR) of CuCr1−xMgxO2 at different temperatures is studied. The shoulder on the temperature-dependent trend of the resistivity under a magnetic field directly induces the magnetic phase transitions, as shown in Fig. 6(a). Negative MR can be observed in the whole variable range-hopping region (not fully shown here) due to enhanced localization around Cr sites.30 What catches our eyes is that the temperature-dependent MR shows a sharp vibration across magnetic transition temperature regions, as shown in the inset of Fig. 6(a). The absolute values of MR for CuCr0.94Mg0.06O2 under different magnetic fields were plotted in Fig. 6(b). The MR shows an obvious peak below a the temperature TN1 around 24.7 K, with an additional valley at a strong magnetic field above 5 Tesla. The MR vibration for CuCr1−xMgxO2 has been found before but hasn’t been discussed in detail so far.23 The frustrated magnetic structure of CuCrO2 is a TLA, with three spins forming 120° angles to neighboring spins.11 The magnetic properties for Heisenberg-type antiferromagnetism with single-ion anisotropy (SIA) can be described on the basis of the following Hamiltonian:
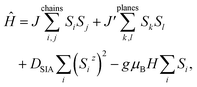 | (4) |
The enhancement of negative MR around the magnetic transition temperature is usually due to a strong spin-charge coupling effect.23 When the temperature decreases below TN1, the structure of CuCr1−xMgxO2 first comes into a collinear antiferromagnetic (CAF) phase (TN2 < T < TN1), whose state can usually be achieved in a triangular lattice including additional hopping processes beyond the nearest neighbours.37 Positive MR can increase in a CAF state due to the influence on spin fluctuations from localized magnetic moments.30 The strong competition between the localization and CAF configuration leads to the sharp vibration of negative MR just below TN1. When the temperature further decreases below TN1, the out-of-plane structure enhances the spin-charge coupling, leading to the strong enhancement of the negative MR. Note that TN1 and TN2 are slightly different from the previously reported results due to Mg doping influences.
Let’s move our attention back to the optical mode behavior. An energy level spacing diagram for the CuCr1−xMgxO2 films was applied to explain the experimental results, as shown in Fig. 5(b). The phonon energy is related to the transition between the ground state and the excited energy level taking the spin flip at low temperatures into account. In the CAF temperature region, the internal spin fluctuation is weak due to the in-plane structure. With decreasing temperature below TN2, the growing spin fluctuation due to the out-of-plane structure increases the splitting energy from the spin flip. The energy gap between the ground state and the excited state decreases. Thus, both the Eg and E↑u mode centers show a red-shift trend with decreasing temperature below TN2. The additional mode just between A↓2u and Eg should also be associated with the spin flip energy, corresponding to the forbidden transition energy labeled as AFb in Fig. 5(b). In order to create a conventionally dipole-forbidden excitation, one needs to overcome the single-ion anisotropy energy. In the temperature region above TN2, the spin flip is quite small, while in the temperature region below TN2, the single-ion anisotropy energy increases. Thus, the additional mode shows a blueshift with decreasing temperature, as can be seen in Fig. 1(b). The negative MR near zero magnetic field below TN2 is very weak [as can be seen from Fig. 6(b)], manifesting that the spin fluctuation is relatively strong. The out-of-plane structure further enhances the spin fluctuation below TN2, which again increases the Cr 3d–O 2p–Cu 3d hybridization. This moves the mode center to lower energy with decreasing temperature for heavily doped films at zero magnetic field.
4 Conclusions
In conclusion, phonon modes from Raman and infrared spectra for Mg-doped CuCrO2 films have been investigated, combined with first-principles calculations. The transition of the carrier transport mechanism from a thermal activation to a 3D variable range hopping one results in a decline in the temperature dependence of the Eg mode peak center. The abnormal redshift of the Eg mode center with decreasing temperature below 40 K for the lightly doped film (x = 0.03) is due to p–d hybridization. The Eu and Eg mode centers for heavily doped films show a normal blueshift just below 40 K owing to stronger disturbance of the local spin fluctuation at Cr sites from Mg doping. The increasing spin-charge coupling caused by the out-of-plane structure below TN2 not only results in the enhancement of negative MR at strong magnetic field, but also brings back the abnormal redshift below TN2 for heavily doped films.Acknowledgements
One of the authors (X. R. Li) is grateful to Dr Meijie Han and Kai Shi for technical support. This work was financially supported by the Major State Basic Research Development Program of China (Grant No. 2013CB922300 and 2011CB922200), Natural and Science Foundation of China (Grant No. 11374097, 61376129 and 61504156), Projects of Science and Technology Commission of Shanghai Municipality (Grant No. 15JC1401600, 14XD1401500, 13JC1402100 and 13JC1404200), and the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning.References
- T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. Tokura, Nature, 2003, 426, 55–58 CrossRef CAS PubMed.
- T. Lottermoser, T. Lonkai, U. Amann, D. Hohlwein, J. Ihringer and M. Fiebig, Nature, 2004, 430, 541–544 CrossRef CAS PubMed.
- L. Balents, Nature, 2010, 464, 199–208 CrossRef CAS PubMed.
- M. Mourigal, W. T. Fuhrman, A. L. Chernyshev and M. E. Zhitomirsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 094407 CrossRef.
- R. Nagarajan, A. D. Draeseke, A. W. Sleight and J. Tate, J. Appl. Phys., 2001, 89, 8022–8025 CrossRef CAS.
- M. J. Han, K. Jiang, J. Z. Zhang, W. L. Yu, Y. W. Li, Z. G. Hu and J. H. Chu, J. Mater. Chem., 2012, 22, 18463–18470 RSC.
- D. O. Scanlon and G. W. Watson, J. Mater. Chem., 2011, 21, 3655–3663 RSC.
- A. Barnabé, Y. Thimont, M. Lalanne, L. Presmanes and P. Tailhades, J. Mater. Chem. C, 2015, 3, 6012–6024 RSC.
- L. Farrell, E. Norton, C. M. Smith, D. Caffrey, I. V. Shvets and K. Fleischer, J. Mater. Chem. C, 2016, 4, 126–134 RSC.
- K. Kimura, H. Nakamura, K. Ohgushi and T. Kimura, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 140401 CrossRef.
- K. Kimura, H. Nakamura, S. Kimura, M. Hagiwara and T. Kimura, Phys. Rev. Lett., 2009, 103, 107201 CrossRef CAS PubMed.
- Y. W. Liu, B. M. Wang, Q. F. Zhan, Z. H. Tang, H. L. Yang, G. Liu, Z. H. Zuo, X. S. Zhang, Y. L. Xie, X. J. Zhu, B. Chen, J. L. Wang and R. W. Li, Sci. Rep., 2014, 4, 6615 CrossRef CAS PubMed.
- M. Poienar, F. Damay, C. Martin, V. Hardy, A. Maignan and G. André, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 014412 CrossRef.
- M. J. Han, Z. H. Duan, J. Z. Zhang, S. Zhang, Y. W. Li, Z. G. Hu and J. H. Chu, J. Appl. Phys., 2013, 114, 163526 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. Guss, M. E. Foster, B. M. Wong, P. Doty, K. Shah, M. R. Squillante, U. Shirwadkar, R. Hawrami, J. Tower and D. Yuan, J. Appl. Phys., 2014, 115, 034908 CrossRef.
- S. L. Li, K. Tsukagoshi, E. Orgiu and P. Samori, Chem. Soc. Rev., 2016, 45, 118–151 RSC.
- S. P. Pavunny, A. Kumar and R. S. Katiyar, J. Appl. Phys., 2010, 107, 013522 CrossRef.
- J. Pellicer-Porres, D. Martínez-García, A. Segura, P. Rodríguez-Hernández, A. Muñoz, J. C. Chervin, N. Garro and D. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 184301 CrossRef.
- B. Klobes, M. Herlitschke, K. Z. Rushchanskii, H.-C. Wille, T. T. A. Lummen, P. H. M. van Loosdrecht, A. A. Nugroho and R. P. Hermann, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 014304 CrossRef.
- J. Pellicer-Porres, A. Segura, E. Martínez, A. M. Saitta, A. Polian, J. C. Chervin and B. Canny, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 064301 CrossRef.
- O. Aktas, K. D. Truong, T. Otani, G. Balakrishnan, M. J. Clouter, T. Kimura and G. Quirion, J. Phys.: Condens. Matter, 2012, 24, 036003 CrossRef CAS PubMed.
- T. Okuda, N. Jufuku, S. Hidaka and N. Terada, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 144403 CrossRef.
- M. Y. Han, J. C. Brant and P. Kim, Phys. Rev. Lett., 2010, 104, 056801 CrossRef PubMed.
- X. R. Li, M. J. Han, P. Chang, Z. G. Hu, Y. W. Li, Z. Q. Zhu and J. H. Chu, Appl. Phys. Lett., 2014, 104, 012103 CrossRef.
- X. R. Li, M. J. Han, X. L. Zhang, C. Shan, Z. G. Hu, Z. Q. Zhu and J. H. Chu, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035308 CrossRef.
- S. Kumar and H. C. Gupta, Comput. Theor. Chem., 2011, 977, 78–85 CrossRef CAS.
- A. J. Sievers and M. Tinkham, Phys. Rev., 1963, 129, 1995–2004 CrossRef CAS.
- S. Haas, E. Heintze, S. Zapf, B. Gorshunov, M. Dressel and L. Bogani, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 174409 CrossRef.
- J. Du, D. Li, Y. B. Li, N. K. Sun, J. Li and Z. D. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 094401 CrossRef.
- M. F. Collins and O. A. Petrenko, Can. J. Phys., 1997, 75, 605–655 CrossRef CAS.
- D. Shin, J. S. Foord, R. G. Egdell and A. Walsh, J. Appl. Phys., 2012, 112, 113718 CrossRef.
- X. C. Liu, U. Gennser, T. Q. Vu and D. Heiman, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 17199–17204 CrossRef CAS.
- A. F. Goncharov, V. V. Struzhkin and S. D. Jacobsen, Science, 2006, 312, 1205–1208 CrossRef CAS PubMed.
- A. Farhan, M. Reissner, A. L. Jasper and W. Steiner, J. Phys.: Conf. Ser., 2010, 217, 012142 CrossRef.
- S. Seki, Y. Onose and Y. Tokura, Phys. Rev. Lett., 2008, 101, 067204 CrossRef CAS PubMed.
- G. Li, P. Höpfner, J. Schäfer, C. Blumenstein, S. Meyer, A. Bostwick, E. Rotenberg, R. Claessen and W. Hanke, Nat. Commun., 2013, 4, 1620 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2016 |