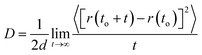DOI:
10.1039/C6RA02844F
(Paper)
RSC Adv., 2016,
6, 43924-43936
Properties of silver nanoclusters and bulk silver, using a new and accurate HFD-like potential, including many-body interactions: the inversion scheme and molecular dynamics simulation
Received
31st January 2016
, Accepted 18th April 2016
First published on 20th April 2016
Abstract
A new pair-potential energy function of silver has been obtained via the inversion of reduced viscosity collision integrals of monatomic silver vapor and fitted to the Hartree–Fock dispersion (HFD)-like potential form. The pair-potential reproduces the transport properties of silver vapor in good agreement with the accurate data over wide ranges of temperatures. In order to use the pair-potential for the solid and nanocluster systems and to take higher-body forces into account, our many-body potential has been used with the two-body HFD-like potential of silver to improve the prediction of the calculated properties. Molecular dynamics (MD) simulation has also been performed to obtain the configurational energy and the equation of state for silver, which agree well with the experiment data compared to the quantum Sutton–Chen potential. We also used the new interaction potential to compute the equation of state, bulk modulus, surface energy, self-diffusion coefficient, and radial distribution function for the silver nanoclusters.
1. Introduction
Nanoparticle systems currently attract considerable interest from both academia and industry because of their interesting and diverse properties, which deviate from those of the bulk systems. Owing to their unique properties, the fabrication of nanostructural materials and devices on the atomic scale has become an emerging interdisciplinary field involving solid-state physics, chemistry, biology, and materials science.1,2 Small clusters of silver atoms are of special interest because they can serve as prototypes for solid surfaces, which have important catalytic properties in bulk and also as nanosilver surfaces.3–5 They are also important in the formation of photographic images.6 Therefore, understanding and predicting the properties of silver nanoclusters are desired for theoretical and practical applications.7
The most important key to the understanding and computation of the structure and properties of solids and nanoclusters is the interaction potential. It is therefore not surprising that there is increasing interest in the study of interaction potentials, which is of significant importance in chemistry, physics, and biology. Two procedures have been used for extracting the intermolecular potential energy function from the experimental data, namely, the fitting and inversion methods. The potentials obtained from the fitting procedure do not appear to be unique, since they depend upon the range of temperature employed and the properties chosen for the test. However, the aim of an inversion method is to obtain the potential by considering the experimental data as a functional form instead of fitting the data to a constrained potential form having a few parameters.8,9
Abbaspour and co-workers determined the accurate HFD-like potential energy functions using the inversion method for different gas and liquid systems.10–13 For the first time, we determined the potential energy function for a metal system using the inversion of the reduced viscosity collision integrals of the vapor. Some transport properties of the silver vapor, such as viscosity, thermal conductivity, and self-diffusion coefficient, have also been calculated using the obtained pair-potential over wide ranges of temperatures.
In order to use the pair-potential for the solid and nanocluster systems and to take higher-body forces into account, our many-body potential14 has been used with the two-body HFD-like potential to improve the prediction of the calculated properties of solid silver. The MD simulation has also been performed to obtain the configurational energy and the equation of state for silver. We also compared our simulation results using the new model with the previous accurate potentials for silver.
Silver nanoclusters are an attractive object for fundamental studies since they provide insight into how properties evolve between the limits of isolated atoms and the bulk material.7 Recently, some theoretical work was carried out to calculate the different properties of silver and silver alloy nanoclusters (such as the melting process) using the MAEAM, EAM, and QSC interaction potentials.2,5,15–17 In order to test our new model for the nanocluster systems, we used the new interaction potential to compute the equation of state and some of the properties of the silver nanoclusters.
2. Collision integrals
The transport properties of a dilute gas (or vapor) can be expressed in terms of a set of collision integrals, Ω(l,s)(T), characterized by the value of l and s; for example, the viscosity and thermal conductivity of a pure gas depend on the collision integral Ω(2,2)(T).12,18 The temperature-dependent collision integral Ω(2,2) for a pure gas is explicitly related to pair-potential energy function, U2B(r), through the classical mechanical triple integral.18 All of the information about the intermolecular potential is therefore contained in the following collision integrals:| |
 | (1) |
| |
 | (2) |
| |
 | (3) |
where E is the relative kinetic energy of a pair of colliding molecules, Q(2)(E) is a transport cross section, b is the impact parameter, χ is the scattering angle, and ro is the classical distance of closest approach in a collision. The inversion scheme produces an isotropic pair potential energy. However, the collision integrals must be averaged over all possible relative orientations occurring in collisions. The average value of Ω(2,2)*, by assuming all relative orientations are equally probable, can be written as follows:| |
 | (4) |
where χ1 and χ2 represent the angles necessary to specify the orientations of two molecules in a binary collision into the plane in which the collision takes place, and φ defines the orientation of the plane in space.18
3. Results and discussion
3.1 Interaction pair-potential
The direct inversion procedure for the determination of pair-potential using reduced viscosity collision integrals is described in detail in the previous papers.9,10 The reduced pair-potential energy function of silver was obtained using the inversion of the reduced viscosity collision integrals of silver vapor5 and is presented in Fig. 1. According to Fig. 1, our calculated pair-potential is in good agreement with the average Ag–Ag interaction potential calculated by Biolsi and Holland.5 They computed the Ag–Ag interaction energies for three low-lying electronic states of Ag2 using the Hulburt–Hirschfelder (HH) potential. The HH potential depends only on the spectroscopic constants and usually gives good agreement with the experimental Rydberg–Klein–Rees (RKR) potential energy curves for atom–atom and atom–ion interactions.5,19–21
 |
| | Fig. 1 Comparison of our pair-potential energy function for silver, calculated using the inversion of reduced viscosity collision integrals of the silver vapor, with the average Hulburt–Hirschfelder (HH) potential.5 | |
The calculated most commonly needed collision integrals and their ratios for silver vapor have also been presented in Table 1. These quantities are needed for computation of the transport properties at any temperature and pressure.
Table 1 Dimensionless collision integrals Ω(l,s)* = Ω(l,s)/πd2 and their related ratios10 for silver vapor
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T* T* |
Ω(1,1)* |
Ω(1,2)* |
Ω(2,2)* |
Ω(1,3)* |
A* |
B* |
C* |
| 0.1000 |
5.4594 |
4.7566 |
5.6014 |
4.2822 |
1.0260 |
1.2188 |
0.8713 |
| 0.1259 |
4.9902 |
4.3338 |
5.1578 |
3.8890 |
1.0336 |
1.2250 |
0.8685 |
| 0.1585 |
4.5510 |
3.9346 |
4.7519 |
3.5108 |
1.0442 |
1.2370 |
0.8646 |
| 0.1995 |
4.1362 |
3.5498 |
4.3789 |
3.1365 |
1.0587 |
1.2580 |
0.8582 |
| 0.2512 |
3.7383 |
3.1713 |
4.0283 |
2.7625 |
1.0776 |
1.2858 |
0.8483 |
| 0.3162 |
3.3513 |
2.7976 |
3.6860 |
2.3960 |
1.0999 |
1.3140 |
0.8348 |
| 0.3981 |
2.9736 |
2.4349 |
3.3405 |
2.0512 |
1.1234 |
1.3351 |
0.8189 |
| 0.5012 |
2.6091 |
2.0948 |
2.9876 |
1.7419 |
1.1451 |
1.3439 |
0.8029 |
| 0.6310 |
2.2657 |
1.7881 |
2.6337 |
1.4765 |
1.1624 |
1.3394 |
0.7892 |
| 0.7943 |
1.9518 |
1.5222 |
2.2931 |
1.2565 |
1.1749 |
1.3243 |
0.7799 |
| 1.0000 |
1.6735 |
1.2982 |
1.9815 |
1.0768 |
1.1840 |
1.3049 |
0.7757 |
| 1.2589 |
1.4332 |
1.1124 |
1.7094 |
0.9288 |
1.1927 |
1.2884 |
0.7761 |
| 1.5849 |
1.2290 |
0.9577 |
1.4792 |
0.8040 |
1.2036 |
1.2794 |
0.7792 |
| 1.9953 |
1.0565 |
0.8273 |
1.2855 |
0.6971 |
1.2168 |
1.2760 |
0.7831 |
| 2.5119 |
0.9107 |
0.7168 |
1.1193 |
0.6068 |
1.2290 |
1.2702 |
0.7871 |
| 3.1623 |
0.7875 |
0.6244 |
0.9727 |
0.5338 |
1.2351 |
1.2533 |
0.7929 |
| 3.9811 |
0.6847 |
0.5497 |
0.8424 |
0.4781 |
1.2303 |
1.2217 |
0.8029 |
| 5.0119 |
0.6006 |
0.4920 |
0.7286 |
0.4382 |
1.2130 |
1.1781 |
0.8192 |
| 6.3096 |
0.5341 |
0.4498 |
0.6328 |
0.4114 |
1.1848 |
1.1295 |
0.8421 |
| 7.9433 |
0.4834 |
0.4204 |
0.5561 |
0.3946 |
1.1505 |
1.0837 |
0.8697 |
| 10.0000 |
0.4463 |
0.4012 |
0.4977 |
0.3848 |
1.1152 |
1.0461 |
0.8990 |
| 12.5890 |
0.4202 |
0.3893 |
0.4553 |
0.3796 |
1.0835 |
1.0189 |
0.9265 |
| 15.8490 |
0.4028 |
0.3826 |
0.4260 |
0.3775 |
1.0577 |
1.0014 |
0.9500 |
| 19.9530 |
0.3917 |
0.3793 |
0.4067 |
0.3770 |
1.0384 |
0.9916 |
0.9684 |
| 25.1190 |
0.3851 |
0.3781 |
0.3947 |
0.3776 |
1.0248 |
0.9872 |
0.9818 |
| 31.6230 |
0.3816 |
0.3781 |
0.3876 |
0.3786 |
1.0157 |
0.9861 |
0.9910 |
| 39.8110 |
0.3800 |
0.3788 |
0.3837 |
0.3797 |
1.0099 |
0.9868 |
0.9968 |
| 50.1190 |
0.3797 |
0.3798 |
0.3820 |
0.3809 |
1.0061 |
0.9882 |
1.0003 |
| 63.0960 |
0.3800 |
0.3809 |
0.3815 |
0.3820 |
1.0039 |
0.9899 |
1.0022 |
| 79.4330 |
0.3807 |
0.3819 |
0.3817 |
0.3830 |
1.0025 |
0.9916 |
1.0031 |
| 100.0000 |
0.3816 |
0.3829 |
0.3822 |
0.3838 |
1.0016 |
0.9931 |
1.0034 |
3.2 Calculation of transport properties of silver vapor
At low densities, the viscosity, η, can be calculated by the following:22| |
 | (5) |
the self-diffusion coefficient, D, is given by| |
 | (6) |
and the translational and internal contributions to the thermal conductivity, λtrans and λinter, can be computed by the following relations:23,24| |
 | (7) |
| |
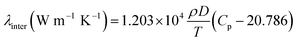 | (8) |
In eqn (5)–(8), T is the temperature (in K), M is the molar mass (in g mol−1), P is the pressure (in bar), Cp is the molar heat capacity at constant pressure (in J mol−1 K−1), and σ2 is in 10−20 Å2.
The viscosity, self-diffusion coefficient, and thermal conductivity of silver atoms at different temperatures at atmospheric pressure have been calculated using eqn (5)–(8) and are compared with the accurate results of Biolsi and Holland,5 as shown in Fig. 2. There is little deviation between our calculated values and the literature values, and it is plausible that the good agreement corresponds to the accuracy of the calculated inversion potential for silver atoms.
 |
| | Fig. 2 Comparison of the calculated transport properties of silver vapor using our potential with the literature values at atmospheric pressure. | |
3.3 Molecular dynamics simulation of silver solid
3.3.1 Interaction potentials. The different thermodynamic, transport, and structural properties of systems of spherical molecules have been intensively and successfully studied over a broad range of temperatures and densities using pair interactions of the HFD-like model.10–14 As such, the HFD-like potential has been used as a two-body potential for silver, which has been obtained via the inversion of the reduced viscosity collision integrals:5| |
 | (9) |
where x = r/σ and U2B(r)* = U2B(r)/ε (σ is the distance at which the intermolecular potential has zero value and ε is the potential well depth). The values of the parameters of the HFD-like potential of silver have been given in Table 2.
Table 2 The coefficients of the HFD-like pair-potential of silver
| Coefficient |
Value |
| ε/K (kJ mol−1) |
49.956 |
| σ (Å) |
2.08 |
| A* |
−315.0 |
| α* |
−6.301 |
| β* |
−12.4588 |
| C*6 |
14.1916 |
| C*8 |
−19.434 |
| C*10 |
4.2432 |
Abbaspour and Akbarzadeh14 introduced the following correction (many-body) term, in conjunction with the two-body HFD-like potential as follows:
where
β is an adjustable parameter and is dependent on the temperature and density. The adjustable parameter
β was obtained by comparison of the prediction of pressure values of silver solid with experimental data at different temperatures and densities, and is presented in
Fig. 3. Therefore, the
β values, which correspond to the difference between the two-body results and the experimental data, not only account for the triple–dipole interaction, but also for other effects (such as the three-body repulsion or many-body terms), which make the calculated values from the pair interaction potential closer to experimental data. According to
Fig. 3, the
β values are greater at higher densities, and this corresponds to greater many-body effects.
 |
| | Fig. 3 The β values for silver solid at different temperatures and densities. The symbols are the calculated values and the corresponding lines are the fitted equation (eqn (13)). | |
Parsafar et al.25 showed that for a wide variety of fluids and solids, the average configurational energy per particle can be given by the following:
| |
 | (11) |
where
ρ = 1/
V is the molar density, and the temperature dependent parameters
Ki depend on the chemical, as well as the physical states of the system. Therefore, according to
eqn (11), the total interaction potential (two-body plus many-body interaction potentials) can be presented as follows:
| |
 | (12) |
where
K6,
K3, and
K12 are temperature dependent parameters. The
U2B is the two-body potential given by
eqn (9) and
UMB is the many-body potential (
eqn (10)). In order to verify the validity of the assumption of
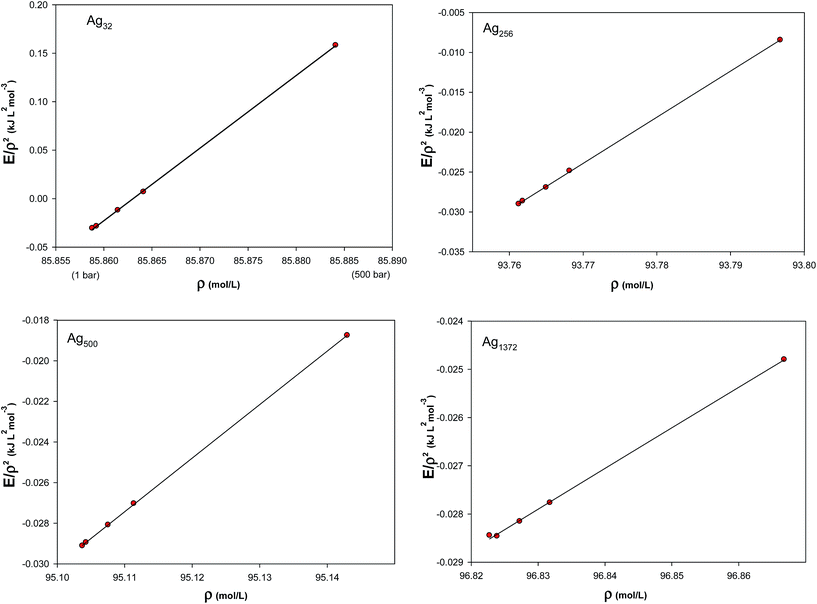
eqn (12) for silver solid, the density dependence of the total configurational energy was studied at different temperatures and densities, shown in
Fig. 4. According to this figure, the quantity
ET/
ρ2 was calculated for the solid silver using the MD simulations. The parameters of the fitted curves (
K6,
K3, and
K12) and the
R2 values of the least-squares method used for the regression are given in
Table 3. In general, the
R2 values show good correlation between the simulation results and the predicted relation for the configurational energy. This verifies the applicability of the many-body expression of
eqn (12) to the solid system.
 |
| | Fig. 4 The density dependence of the total configurational energy of silver solid at different temperatures and densities. | |
Table 3 The parameters of the fit to the total configuration energy equation (eqn (12))
| T (K) |
K6 (kJ L2 mol−3) |
K3 (kJ L mol−2) |
K12 (kJ L4 mol−5) |
R2 |
| 100 |
−0.9768 |
89.1267 |
9.1874 × 10−6 |
0.9961 |
| 200 |
−0.9642 |
87.9007 |
8.8272 × 10−6 |
0.9810 |
| 300 |
−0.0844 |
7.2916 |
8.1311 × 10−7 |
0.8974 |
| 400 |
−0.8501 |
74.7236 |
7.9096 × 10−6 |
0.9755 |
| 500 |
−0.9040 |
80.1429 |
8.4521 × 10−6 |
0.9756 |
| 600 |
−1.0393 |
90.6432 |
1.1289 × 10−5 |
0.9388 |
| 700 |
−1.0124 |
88.0089 |
1.0778 × 10−5 |
0.9921 |
| 800 |
−0.9196 |
79.5303 |
9.3020 × 10−6 |
0.9900 |
| 900 |
−0.8097 |
68.9345 |
7.7095 × 10−6 |
0.9925 |
| 1000 |
−0.8345 |
71.0386 |
8.0276 × 10−6 |
0.9832 |
| 1100 |
−0.8936 |
75.0000 |
9.3330 × 10−6 |
0.9793 |
We can derive the density dependence of β by replacing the UMB in eqn (12) with eqn (10) as follows:
| |
 | (13) |
where
Fig. 3 shows the fitting of equation (
eqn (13)) to the
β values. Therefore, the total (two-body plus many-body) or the effective interaction potential for the solid systems is as follows:
| | |
UT = U2B + UMB = U2B(1 + β)
| (14) |
The significance of this equation is that it allows us to use the two-body potentials to accurately predict the properties of solids without incurring the computational cost of the three-body or quantum calculations.
3.3.2 Simulation details. The MD simulations for fcc silver solid have been performed using MOLDY software26 for a system of a total of 864 atoms in a cubic box, and the conventional periodic boundary condition has been applied. The NVT ensemble has been employed, using a Nose–Hoover thermostat for the atoms interacting via the two-body HFD-like and total potentials (eqn (9) and (14)). The size of the time steps, Δt, the number of time steps, nt, and the cutoff radius, rc, have been chosen as 0.001 ps, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (the equilibration time was 500
000 (the equilibration time was 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps and production runs were 500
000 steps and production runs were 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps), and 3σ, respectively. The long-range correction terms have been evaluated using MOLDY to recover the contribution of the long-range cut-off of the intermolecular potentials on the pressure.
000 steps), and 3σ, respectively. The long-range correction terms have been evaluated using MOLDY to recover the contribution of the long-range cut-off of the intermolecular potentials on the pressure.
3.3.3 Equation of state (EoS) for silver solid. The MD simulation was performed to obtain the pressure of the silver solid using the total potential (eqn (14)). Our results for pressure of the silver solid in the NVT ensemble have been compared with the experimental data27 at 100, 300, 700, and 1000 K and different densities, shown in Fig. 5. We have also compared our pressure values with those calculated by the quantum Sutton–Chen (QSC) potential28,29 in Fig. 5. Our values calculated by the new potential are in better agreement with the experiment than those calculated using the QSC potential. These results verify the importance of our new model.
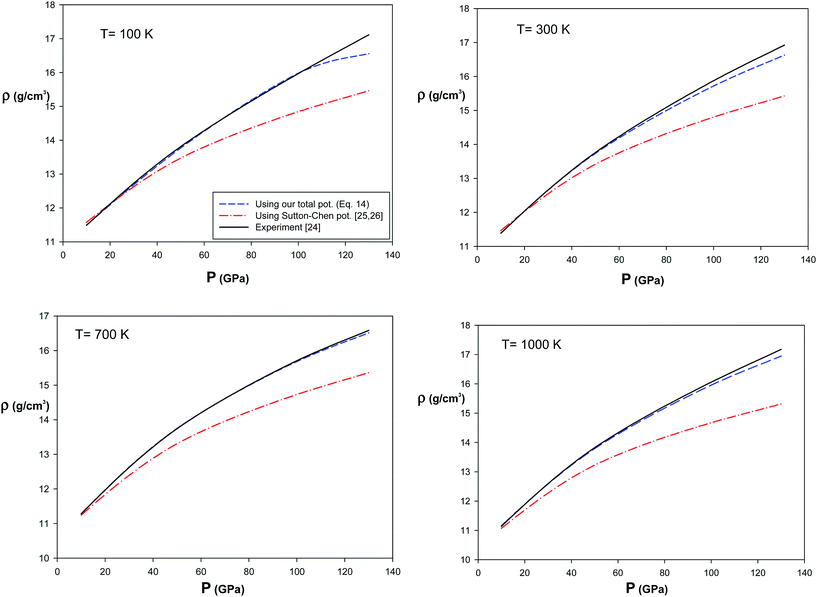 |
| | Fig. 5 Comparison of our results for pressure of silver solid, using our new potential and the QSC potential, with the experimental data27 at different temperatures and densities. | |
Based on the notation used by Parsafar et al.,25,30 the exact thermodynamic EoS for the pressure can be written as follows:
| |
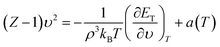 | (15) |
where
Z =
Pυ/
kBT is the compressibility factor and
| |
 | (16) |
is the contribution from the non-ideal thermal pressure. In
eqn (16),
αP and
κT are the isobaric expansion and isothermal compressibility, respectively. Substituting the configurational energy from
eqn (12), the equation of state (
eqn (15)) is rewritten as
| |
 | (17) |
Eqn (17) gives the EoS III (as is named by Parsafar et al.25,30). This EoS can be expressed as:
| |
 | (18) |
where
f =
F6(
T) +
a(
T),
g =
F3(
T), and
h =
F12(
T). The parameters
f,
g, and
h are non-trivial functions of temperature and in general, contain contributions from both the internal and thermal pressures.
30 The values of the
f,
g, and
h parameters at different temperatures are presented in
Table 4. The important result from these equations is that they present us with an alternative way (instead of the trial and error method described for
eqn (10) to derive the
β values and many-body potential. The significance of
eqn (17) and
(18) lies in the fact that they allow us to calculate the
f,
g, and
h parameters using the experimental PVT data (by only a one-time fitting of the equations to the experimental data). Additionally, they allow us to calculate the
K3,
K6, and
K12 coefficients, and to derive the many-body potential (
eqn (13) and
(14)) from the two-body, without incurring the computational cost of the three-body calculations.
Table 4 The parameters of the fit to the EoS (eqn (18))
| T (K) |
f (L2 mol−2) |
g (L mol−1) |
h (L4 mol−4) |
R2 |
| 100 |
0.0001 |
−0.0227 |
−1.2330 × 10−9 |
0.9995 |
| 200 |
0.0001 |
−0.0220 |
−1.1796 × 10−9 |
0.9994 |
| 300 |
0.0001 |
−0.0214 |
−1.0808 × 10−9 |
0.9993 |
| 400 |
0.0001 |
−0.0215 |
−1.1143 × 10−9 |
0.9993 |
| 500 |
0.0001 |
−0.0216 |
−1.1323 × 10−9 |
0.9993 |
| 600 |
0.0001 |
−0.0216 |
−1.1437 × 10−9 |
0.9993 |
| 700 |
0.0001 |
−0.0221 |
−1.2385 × 10−9 |
0.9992 |
| 800 |
0.0001 |
−0.0223 |
−1.2811 × 10−9 |
0.9992 |
| 900 |
0.0001 |
−0.0221 |
−1.2118 × 10−9 |
0.9990 |
| 1000 |
0.0001 |
−0.0222 |
−1.2484 × 10−9 |
0.9990 |
| 1100 |
0.0001 |
−0.0227 |
−1.3864 × 10−9 |
0.9992 |
In order to study the applicability of the EoS (eqn (18)) to silver solid systems, the compressibility factor was calculated and the values of (Z − 1)/ρ2 for the system versus the molar density are shown in Fig. 6. According to this figure, there is a good correlation between the calculated values and the fitted EoS. The parameters of the fitted curves and the R2 values of the least-squares fitting are presented in Table 3. Therefore, the EoS (eqn (18)) gives very accurate predictions for the solid silver.
 |
| | Fig. 6 The values of (Z − 1)/ρ2 for the silver solid, versus the molar density. | |
3.4 Molecular dynamics simulation of silver nanoclusters
3.4.2 Simulation details. The MD simulations were carried out in a NVT ensemble with periodic boundary conditions for the system, including the silver nanocluster, consisting of 32, 108, 256, 500, 864, and 1372 atoms and an ideal gas using DL_POLY 4.03.31 In order to exert external pressure on the nanoclusters (due to the lack of the periodic boundary conditions for the nanocluster systems), we used an ideal gas as the pressure medium. Fig. 8 shows the silver nanocluster with 864 atoms immersed in an ideal gas pressure bath with 500 bar pressure at 300 K. In these simulations, the pressure medium consists of particles that do not interact with each other, but do interact with the Ag atoms in the nanocluster via a soft-sphere potential of the form 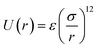 , where r denotes the distance between two particles, σ the interaction range, and ε the interaction strength. We may use argon (or any other ideal gas) as the pressure medium in the simulations.32 Recently, Akbarzadeh et al.32 used a similar procedure to obtain the EoS for Ni nanoclusters.
, where r denotes the distance between two particles, σ the interaction range, and ε the interaction strength. We may use argon (or any other ideal gas) as the pressure medium in the simulations.32 Recently, Akbarzadeh et al.32 used a similar procedure to obtain the EoS for Ni nanoclusters.
 |
| | Fig. 8 A snapshot of the silver nanocluster with 864 atoms (in yellow) immersed in an ideal gas pressure bath (in green) with 500 bar pressure at 300 K. | |
In the slow heating process, the nanocluster is heated from 300 K to 1700 K, with a temperature step of 100 K. These steps are reduced to 50 K near the melting point, then the slow cooling process starts at 1700 K with a temperature step of 300 K and time step of 1 fs. MD simulations are continued until the temperatures reach 300 K. The simulations were carried out for 2 ns of equilibration, followed by a production time of 1 ns for generating time-averaged properties (the equilibration time for the self-diffusion runs was 4 ns).
The temperature was controlled by a Nose–Hoover thermostat. In order to have an isotropic, constant pressure on the cluster, the number of gas particles and the gas volume should be much larger than for the cluster. The equations of motion were integrated using the Verlet leapfrog algorithm,33 with a time step of 0.001 ps. The cutoff length was chosen to be 10 Å in the simulations. The volumes of the clusters were obtained using a volume definition based on a Wigner–Seitz primitive cell.32,34
3.4.3 Equation of state (EoS) for silver nanoclusters. It is well-known that one of the approaches for anticipation of nanocluster behavior and properties is to use the EoS.35 Many investigations have shown that the fcc is a stable form for the silver nanoclusters36–38 (of course, some other forms apart from fcc have been reported39). The previous works also used the fcc structure as the starting structure for simulation of the metal nanoclusters.16,40–44 Therefore, in order to use the most stable structures of the nanoclusters for calculating the EoS, we annealed the nanoclusters from the initial fcc structures to the most stable form at 300 K (as described in the simulation details). We have presented the internal energies for some of the Ag nanoclusters during the heating and cooling processes in Fig. 9. In this figure, the sharp increases in the energy curves can be identified, which indicate the temperature ranges of first order phase transition. According to this figure, a hysteresis (due to the existence of large differences in heating and cooling curves below the melting point temperatures) in the course of the cooling process can be recognized. The presence of such a hysteresis in solid–liquid transitions has been justified theoretically and agrees with similar studies.44,45 The hysteresis manifests itself in state transitions when melting temperature and freezing temperature do not agree. This is due to the fact that after heating and then cooling, the nanoclusters get to a more stable state with lower energy.45
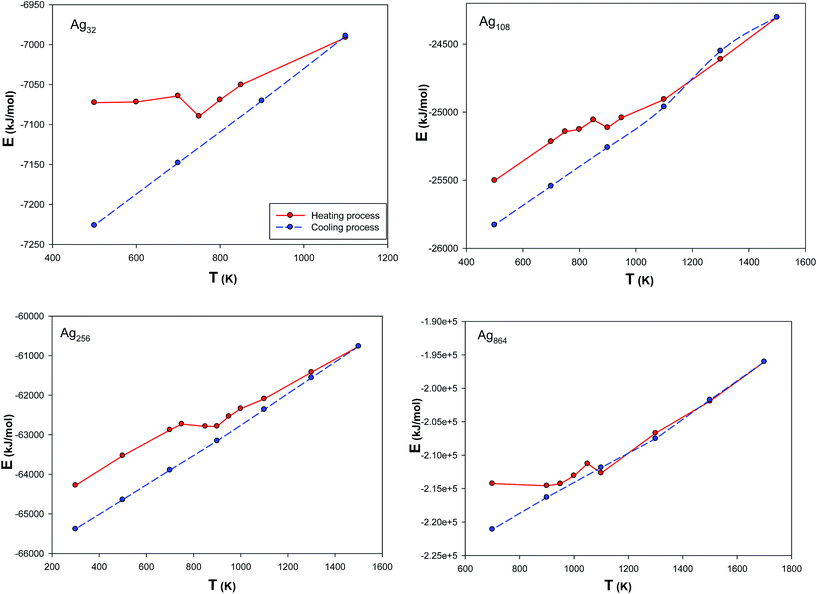 |
| | Fig. 9 The internal energies of the Ag nanoclusters during the heating and cooling processes. | |
We calculated the PVT data of AgN (with N = 32, 108, 256, 500, 864, and 1372) nanoclusters at 300 K using the MD simulations, then we fitted the simulated PVT results to the EoS of Parsafar et al. (eqn (18)). Recently, Akbarzadeh et al.32 and Masoumi and Parsafar35 successfully used this EoS for different nanoclusters and nanocrystals. In this work, we have also extended the EoS parameters of Parsafar et al. in terms of the number of atoms in the nanoclusters (N) as follows:
| |
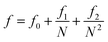 | (19) |
| |
 | (20) |
| |
 | (21) |
where the values of the parameters
fi,
gi, and
hi have been given in
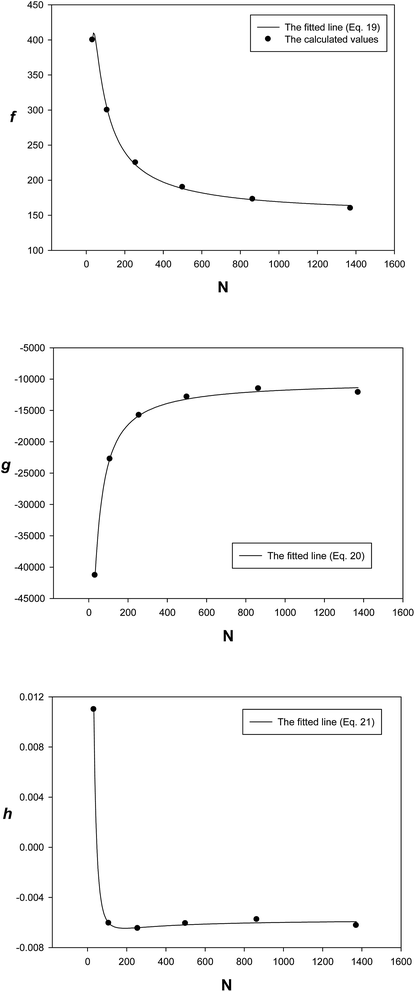
Table 6. The size dependences of the parameters of the extended EoS at 300 K have been shown in
Fig. 10; the points represent the calculated values and the lines represent the fitted equations (
eqn (19) and
(21)), and there is good agreement between the calculated and the fitted lines.
Table 6 The parameters of the EoS for the nanoclusters (eqn (19)–(21))
| Parameter |
Value |
| f0 |
149.6361 |
| f1 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992.7246 992.7246 |
| f2 |
−383![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506.3172 506.3172 |
| g0 |
−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300.6893 300.6893 |
| g1 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473 473![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862.8078 862.8078 |
| g2 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 405 405![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 321.8083 321.8083 |
| h0 |
−0.0057 |
| h1 |
−0.2709 |
| h2 |
25.8118 |
 |
| | Fig. 10 The size dependences of the parameters of the extended EoS at 300 K. | |
The parameters of the EoS have two contributions: one is related to the thermal pressure and the other to the internal pressure, and they have opposite signs32 (Fig. 10). In the case of metals, g corresponds to the attraction and f corresponds to the repulsion interaction of the effective pair potential. It is also shown that the absolute values of the two parameters f and g become smaller for the bigger nanoclusters, due to the smaller fraction of atoms on the surface. The parameter g has a small value whose contribution is insignificant, except at extremely high pressures.32 Such behaviors of the EoS parameters have been observed for the bulk solid (Table 4).
We have also calculated the graphs of (Z − 1)/ρ2 versus ρ for the different sizes of nano clusters at 300 K, presented in Fig. 11. These graphs are almost linear. According to Fig. 11, there is very good agreement between the calculated values (the points) and the EoS (the fitted line).
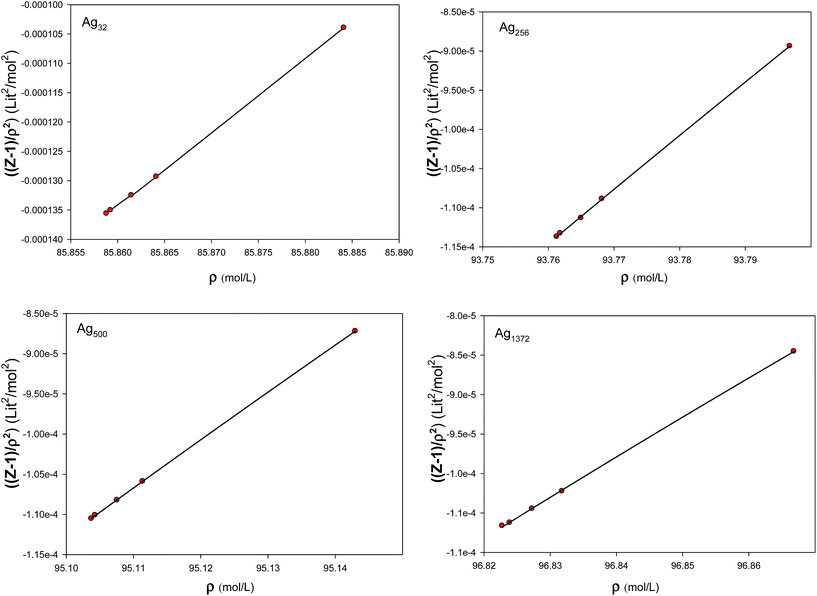 |
| | Fig. 11 The graphs of (Z − 1)/ρ2 versus density for the different sizes of nano clusters at 300 K. | |
3.4.4 Bulk modulus (B). We calculated the bulk modulus at zero pressure (Bo) using the EoS (eqn (18)) for the different nanoclusters at 300 K, using the following equation:| |
Bo = RTρo(3eρo2 + 2fρo + 5gρo4 + ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1)
| (22) |
where ρo is the nanocluster density at zero pressure. According to Fig. 12, the bulk modulus increases as the number of particles decreases. This behavior is due to the fact that as the nanocluster size decreases, proportionally more atoms are on the surface of the nanocluster. Since surface atoms have less binding energy compared to the bulk atoms, with a decrease in the number of particles, the compressibility is expected to decrease. This is called the reverse Hall–Petch effect, which corresponds to the softening of materials for very small nanocluster sizes.46,47 According to Fig. 12, our values at the bulk limit (N → ∞) are in good agreement with the experimental value for the bulk silver (116 GPa).48,49
 |
| | Fig. 12 The bulk modulus at zero pressure (Bo) for the different nanoclusters at 300 K. | |
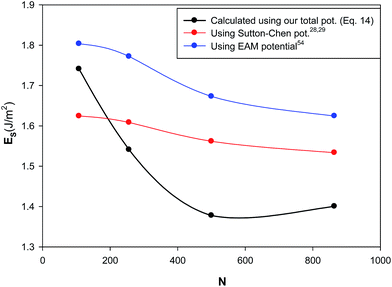
3.4.5 Surface energy (ES). Surface energy is the energy needed to keep the area of the surface in equilibrium, when bringing a molecule to the surface. In thermodynamics, it is defined as the surface free energy per unit surface area (the reversible work per unit area to make a new surface of a substance).50–52 We have calculated the surface energy for the different nanoclusters at 300 K and 1 bar using the following equation,53 presented in Fig. 13:| |
 | (23) |
where Ucluster is the potential energy of the cluster, Ubulk is the potential energy of bulk silver, and Rc is the cluster radius. According to Fig. 13, the surface energy increases as the nanocluster size decreases. This is due to the fact that the smaller nanocluster has the larger surface/volume ratio and so it has higher surface energy than the bigger one. In other words, the smaller cluster has a larger fraction of atoms on its surface. The surface atoms have less binding energy (compared to the bulk atoms), therefore, with decreasing the number of atoms, the magnitude of the potential energy of the nanocluster decreases. Therefore, surface energy decreases with increasing the nanocluster size. We have also compared our results with the surface energy values calculated using the embedded atom model (EAM) of Sheng et al.54 and the quantum Sutton–Chen (QSC) potential28,29 in Fig. 13. According to this figure, our values at the bulk limit (N → ∞) are closer to the experimental value for the bulk silver (which deviates from 0.8 to 1.3 J m−2)53,55,56 than the other potentials. This verifies the importance of our new model.
 |
| | Fig. 13 The surface energies of the different nanoclusters at 300 K and 1 bar. | |
3.4.6 Self-diffusion coefficient (D). The self-diffusion coefficient (D) is proportional to the atomic mean square displacement (MSD) and can be calculated from the following relation:57| |
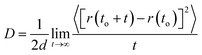 | (24) |
We calculated the self-diffusion coefficients for the different nanoclusters at 300 K and 1 bar from the MSD results (which showed some large oscillations), presented in Fig. 14. As this figure shows, the self-diffusion coefficient decreases as the nanocluster size increases. This is due to the fact that the surface atoms can move more freely than the atoms in the inner part of nanocluster. Therefore, the bigger nanocluster (which has a small fraction of atoms on its surface) has the smaller value of the self-diffusion. Our results are also in agreement with the self-diffusion coefficient of supported Ag nanoclusters obtained using the MD simulations at 300 K (10−12 m2 s−1).16
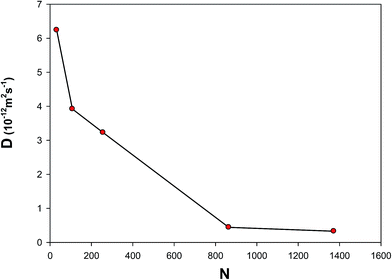 |
| | Fig. 14 The self-diffusion coefficients of the different nanoclusters at 300 K and 1 bar. | |
3.4.7 Radial distribution function (RDF). The radial distribution function (RDF or g(r)), is one of the most important structural quantities characterizing a system. RDF is defined as follows:58| |
 | (25) |
where n is the total number of the atoms in the cluster and rij is the distance between atoms i and j. We have calculated Ag–Ag RDF for the Ag108 and Ag1372 nanoclusters at 300 K and 1 bar, presented in Fig. 15. According to this figure, the Ag–Ag RDF of the bigger cluster is greater than the RDF of the smaller cluster. This is due to the fact that there is a greater probability of finding the particles around a reference silver atom in the bigger cluster than in the smaller one. This result is also due to the fact that the average coordination number is greater for the bigger cluster.
 |
| | Fig. 15 The Ag–Ag RDF for the Ag108 and Ag1372 nanoclusters at 300 K and 1 bar. | |
4. Conclusions
A new pair-potential energy function of silver has been determined via the inversion of reduced viscosity collision integrals of monatomic silver vapor and fitted to obtain the HFD-like potential form (eqn (9)). The pair-potential reproduced the transport properties of silver vapor in good agreement with the accurate data over wide ranges of temperatures. In order to use the pair-potential for the solid and nanocluster systems and to take higher-body forces into account, our many-body potential14 has been used with the two-body HFD-like potential of silver to improve the prediction of the calculated properties. MD simulations have also been performed to obtain the configurational energy and the equation of state for silver, which agree well with the experiment data compared to the QSC potential.
We also used the new interaction potential to compute the equation of state, bulk modulus, surface energy, self-diffusion coefficient, and radial distribution function for the silver nanoclusters, and the following important results have been summarized:
(1) The bulk modulus increases as the number of particles decreases.
(2) The surface energy increases as the nanocluster size decreases. This is due to the larger surface/volume ratio in the smaller cluster than the bigger one.
(3) The self-diffusion coefficient decreases as the nanocluster size increases. This is due to the fact that the surface atoms can move more freely than the atoms in the inner part of nanocluster.
(4) The Ag–Ag RDF of the bigger cluster is greater than the RDF of the smaller cluster. This result is also due to the fact that the average coordination number is greater for the bigger cluster.
References
- H. Gleiter, Acta Mater., 2000, 48, 1 CrossRef CAS.
- W. Hu, Sh. Xiao, H. Deng, W. Luo and L. Deng, Silver Nanoparticles, In-Teh, Olajnica, 2010 Search PubMed.
- R. Romero, A. Mazuelos, I. Palencia and F. Carranza, Hydrometallurgy, 2013, 70, 205 CrossRef.
- Z. Qu, W. Huang, M. Cheng and X. Bao, J. Phys. Chem. B, 2005, 109, 15842 CrossRef CAS PubMed.
- L. Biolsi and P. M. Holland, Int. J. Thermophys., 2007, 28, 835 CrossRef CAS.
- M. R. V. Sayhun, Photogr. Sci. Eng., 1978, 22, 317 Search PubMed.
- Z. Wua, C. Kongb and P. Yu, Adv. Mater. Res., 2011, 268–270, 184 CrossRef.
- G. C. Maitland, M. Rigby, E. B. Smith and W. A. Wakeham, Intermolecular forces, their origin and determination, Clarendon Press, Oxford, 1987 Search PubMed.
- M. Abbaspour and E. K. Goharshadi, Theor. Chem. Acc., 2010, 127, 573 CrossRef CAS.
- M. Abbaspour and E. K. Goharshadi, Chem. Phys., 2006, 330, 313 CrossRef CAS.
- M. Abbaspour, Chem. Phys., 2011, 389, 121 CrossRef CAS.
- M. Abbaspour and S. Naghipour Borj, Fluid Phase Equilib., 2012, 333, 1 CrossRef CAS.
- S. Salemi, M. Abbaspour and M. Ghabdian, J. Supercrit. Fluids, 2014, 89, 119 CrossRef CAS.
- H. Akbarzadeh and M. Abbaspour, RSC Adv., 2015, 5, 11297 RSC.
- H. Kim, S. Lee, H. Kim, J. Ryu and H. Lee, Mater. Trans., 2007, 48, 455 CrossRef CAS.
- H. Akbarzadeh and H. Yaghoubi, J. Colloid Interface Sci., 2014, 418, 178 CrossRef CAS PubMed.
- F. Taherkhani, H. Akbarzadeh, M. Feyzi and H. R. Rafiee, J. Nanopart. Res., 2015, 17, 29 CrossRef.
- S. Chapman and T. G. Cowling, Mathematical Theory of Nonuniform Gases, Cambridge University Press, New York, 1970 Search PubMed.
- A. Lofthus and P. H. Krupenie, J. Phys. Chem. Ref. Data, 1977, 6, 113 CrossRef CAS.
- J. T. Vanderslice, E. A. Mason, W. G. Maisch and E. R. Lippincott, J. Chem. Phys., 1960, 33, 614 CrossRef CAS.
- L. Biolsi and P. M. Holland, in Progress in Astronautics and Aeronautics: Thermophysical Aspects of Re-entry Flows, AIAA, New York, 1986 Search PubMed.
- J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Molecular Theory of Gases and Liquids, Wiley, New York, 1954 Search PubMed.
- E. A. Mason and L. Monchick, J. Chem. Phys., 1962, 36, 1622 CrossRef CAS.
- J. T. Vanderslice, J. T. S. Weissman, E. A. Mason and R. J. Fallon, Phys. Fluids, 1962, 5, 155 CrossRef CAS.
- G. A. Parsafar, H. V. Spohr and G. N. Patey, J. Phys. Chem. B, 2009, 113, 11977 CrossRef CAS PubMed.
- The MOLDY program was coded by K. Refson, and can be downloaded from the internet at http://www.ccp5.ac.uk/moldy/moldy.html.
- W. B. Holzapfel, M. Hartwig and W. Sievers, J. Phys. Chem. Ref. Data, 2001, 30, 515 CrossRef CAS.
- A. P. Sutton, J. Chen, Philos. Mag. Lett., 1990, 61, 139 CrossRef.
- Y. Qi, T. Cagin, Y. Kimura and W. A. Goddard, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3527 CrossRef CAS.
- M. Sadeghi and G. A. Parsafar, J. Phys. Chem. B, 2012, 116, 4943 CrossRef CAS PubMed.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1611 RSC.
- H. Akbarzadeh, H. Abroshan, F. Taherkhani and G. A. Parsafar, Solid State Commun., 2011, 151, 965 CrossRef CAS.
- S. J. Zhao, K. Albe and H. Hahn, Scr. Mater., 2006, 55, 473 CrossRef CAS.
- D. Y. Sun and X. G. Gong, J. Phys.: Condens. Matter, 2002, 14, 487 CrossRef.
- N. Masoumi and G. A. Parsafar, Proceedings of the 4th International Conference on Nanostructures (ICNS4), Kish Island, I.R. Iran, 2012, p. 1701 Search PubMed.
- W. H. Qi, B. Y. Huang, M. P. Wang, F. X. Liu and Z. M. Yin, Comput. Mater. Sci., 2008, 42, 517 CrossRef CAS.
- D. Dorjnamjin, M. Ariunaa and Y. K. Shim, Int. J. Mol. Sci., 2008, 9, 807 CrossRef CAS PubMed.
- S. Agnihotri, S. Mukherji and S. Mukherji, RSC Adv., 2014, 4, 3974 RSC.
- M. A. Gracia-Pinilla, E. Perez-Tijerina, J. A. Garcıa, C. Fernandez-Navarro, A. Tlahuice-Flores, S. Mejia-Rosales, J. M. Montejano-Carrizales and M. Jose- Yacaman, J. Phys. Chem. C, 2008, 112, 13492 CAS.
- S. Jalili, C. Mochani, M. Akhavan and J. Schofield, Mol. Phys., 2012, 110, 267 CrossRef CAS.
- S. Huang, D. S. Mainardi and P. B. Balbuena, Surf. Sci., 2003, 545, 163 CrossRef CAS.
- E. L. Lamas and P. B. Balbuena, J. Phys. Chem. B, 2003, 107, 11682 CrossRef CAS.
- H. Akbarzadeh, H. Yaghoubi, A. N. Shamkhali and F. Taherkhani, J. Phys. Chem. C, 2013, 117, 26287 CAS.
- H. Akbarzadeh, H. Yaghoubi, A. N. Shamkhali and F. Taherkhani, J. Phys. Chem. C, 2014, 118, 9187 CAS.
- H. Akbarzadeh, M. Abbaspour, S. Salemi and M. Abroodi, Phys. Chem. Chem. Phys., 2015, 17, 12747 RSC.
- R. W. Seigel, G. E. Fougere, G. C. Hadjipanayis and R. W. Seigel, Nanophase Materials, Kluwer, Dordrecht, 1994 Search PubMed.
- A. H. Chokshi, A. Rosen, J. Karach and H. Gletter, Scr. Metall., 1989, 23, 1679 CrossRef CAS.
- K. Syassen and W. B. Holzapfel, J. Appl. Phys., 1978, 49, 4427 CrossRef CAS.
- J. Xie, S. P. Chen, S. Gironcoli and S. Baroni, Philos. Mag. B, 1999, 79, 911 CrossRef CAS.
- C. A. Miller and P. Neogi, Interfacial Phenomena: Equilibrium and Dynamic Effects, Marcel Dekker, Inc., New York, 1985 Search PubMed.
- J. Lykema, G. J. Fleer, J. M. Kleijn, F. A. M. Leermakers, W. Norde and T. Van Vliet, Fundamentals of Interface and Colloid Science, Liquid–Fluid Interfaces, Academic Press, 2000, vol. 3 Search PubMed.
- H. Akbarzadeh and F. Taherkhani, Chem. Phys. Lett., 2013, 558, 57 CrossRef CAS.
- L. Wang, Y. Zhang, X. Bian and Y. Chen, Phys. Lett. A, 2003, 310, 197 CrossRef CAS.
- H. W. Sheng, M. J. Kramer, A. Cadien, T. Fujita and M. W. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134118 CrossRef.
- L. Kornblit and A. Ignatiev, Phys. A, 1987, 141, 466 CrossRef.
- S. F. Chernov, Y. V. Fedorov and V. N. Zakharov, Phys. Chem. Solids, 1993, 54, 963 CrossRef CAS.
- S. K. R. S. Sankaranarayanan, V. R. Bhethanabotla and B. Joseph, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 195415 CrossRef.
- D. Cheng and J. Lan, Mol. Simul., 2010, 36, 805 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T*
T*


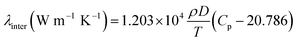







![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (the equilibration time was 500
000 (the equilibration time was 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps and production runs were 500
000 steps and production runs were 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps), and 3σ, respectively. The long-range correction terms have been evaluated using MOLDY to recover the contribution of the long-range cut-off of the intermolecular potentials on the pressure.
000 steps), and 3σ, respectively. The long-range correction terms have been evaluated using MOLDY to recover the contribution of the long-range cut-off of the intermolecular potentials on the pressure.
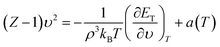



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 381.4368
381.4368![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 523.2663
523.2663![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440.8337
440.8337![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650.8914
650.8914![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700.8281
700.8281![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762.6417
762.6417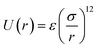 , where r denotes the distance between two particles, σ the interaction range, and ε the interaction strength. We may use argon (or any other ideal gas) as the pressure medium in the simulations.32 Recently, Akbarzadeh et al.32 used a similar procedure to obtain the EoS for Ni nanoclusters.
, where r denotes the distance between two particles, σ the interaction range, and ε the interaction strength. We may use argon (or any other ideal gas) as the pressure medium in the simulations.32 Recently, Akbarzadeh et al.32 used a similar procedure to obtain the EoS for Ni nanoclusters.

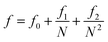


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992.7246
992.7246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506.3172
506.3172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300.6893
300.6893![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473
473![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862.8078
862.8078![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 405
405![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 321.8083
321.8083![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)
1)