Substitution driven structural and magnetic transformation in Ca-doped BiFeO3 nanoparticles†
Abstract
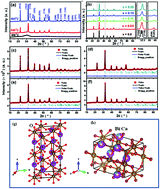
Bi1−xCaxFeO3; (x = 0–0.20) nanoparticles were synthesized by tartaric acid based sol–gel route. X-ray diffraction and electron microscopy studies reveal the phase purity and nanocrystalline nature (45–90 nm) of Bi1−xCaxFeO3 samples. The Ca ion substitution driven structural transition from rhombohedral (space group R3c) to orthorhombic (Pnma) symmetry leads to enhancement in saturation magnetization due to the distorted cycloid spin structure (as also suggested by Mössbauer studies) and uncompensated surface spins which is accorded with electron paramagnetic resonance (EPR) studies as well. The ferromagnetic ordering contribution increases up to x = 0.15 samples with maximum saturation magnetization of 0.09 emu g−1 for x = 0.15 sample. The presence of high content orthorhombic phase for x = 0.20 sample results in the sharp decrease in the ferromagnetic component due to appearance of collinear antiferromagnetic ordering in agreement with EPR results. X-ray photoelectron spectroscopy confirmed the dominancy of Fe3+ oxidation states along with the shifting of the binding energy of Bi 4f orbital indicating the substitution of Ca2+ at Bi-site. Systematic change of Mössbauer parameters of nanoparticulate samples with Ca concentration are obtained by Mössbauer spectroscopy. The results of both one- and two-sextet fittings of the Mössbauer spectra provide evidence for destruction of the spin cycloid in Ca-doped BiFeO3 nanoparticles.

 Please wait while we load your content...
Please wait while we load your content...