Influence of carbon convection field on high quality large single crystal diamonds morphology under high pressure and high temperature

Abstract

The temperature and convection fields of a catalyst with three different heights were simulated in a temperature gradient growth (TGG) system under high pressure and high temperature (HPHT) conditions. Temperature fields were simulated to rule out the influence of temperature on the crystal morphology. The features of the calculated convection field could predict the particular situations of diamond growth systems very well, and could explain the change of diamond morphology accompanying the growth process. According to the calculated results, we predict that the morphology of a diamond crystal changes from cubic crystal to cub-octahedral. A good agreement has been obtained between the calculated results and the observed experimental data. The morphology and structural properties of the synthesized samples are characterized by optical microscopy and a Raman spectrum. The results illustrate that the synthesized diamond crystals have less lattice distortion and with high quality.

---

1. Introduction

Recently, high quality large diamond crystals have been widely used in a series of modern high-tech applications due to their excellent integrated properties,^1–3 including the fields of hard coatings, optical windows, Micro-Electro-Mechanical Systems (MEMS), surface acoustic wave devices (SAW) to electrochemical electrodes and electron emitters. Compared with the CVD method, the temperature gradient growth (TGG) method under HPHT conditions has been an effective way to synthesize high quality large diamond single crystals for several decades.^4–12 Diamond crystals with different morphologies have different applications in the corresponding fields.^13–15 Hence, it is an important research topic to explore the growth mechanism of diamond crystals under HPHT so as to control the morphology and make use of it.¹⁶

Generally, the district for diamond growth is a V-shape region bounded by diamond–graphite equilibrium line and solvent–carbon eutectic melting line in the metal solvent–carbon system.¹⁰ The synthesized diamond usually present the {100} face at lower growth temperatures, while the morphology of diamond is dominantly by {111} face at higher temperatures. Therefore, changing the shape of diamond crystal is mainly by altering the synthetic temperature in traditional methods. Besides, during the crystal growth process, the carbon convection field around the seed diamond also has significant effect on the morphology of the diamond.¹⁷ In order to understand and optimize the growth process of diamond single crystals using the TGG method, it is necessary to investigate the detailed information about the nature of the convection field of particular growth systems. However, it is very difficult to characterize the convection field experimentally, such as the flow tendency and intensity of carbon in the molten catalyst/solvent under HPHT conditions. Until now, there have been very few reports about the effect of carbon convection on the change of the morphology of diamond crystals.

In this paper, we have simulated the temperature field, convection field and growth process of the diamond crystal by the application of finite element method (FEM). The simulation successfully explained the influence of the carbon convection field on diamond morphology in diamond synthesis process. The simulation results indicated that the morphology of diamond crystals could be adjusted by changing the carbon convection field. At the same time, the experimental data obtained from the corresponding synthesis experiments were consistent with the simulation results. The synthesized diamonds were characterized by optical microscope (OM) and Raman spectrum.

2. Simulation and experimental details

2.1 Solid and finite element model

A three-dimensional model was performed on an experimental growth cell. As the growth cell was plane symmetric with symmetric loadings, only 1/4 was modeled for coupled thermal–electrical–fluid analysis taking advantage of plane symmetric thereby reducing model size and lessening the occupation of computer resources. Only the steel ring, WC anvil and the sample assembly were considered for analysis. Fig. 1(a) shows a 1/4 model of diamond growth cell. Enlarged sample assembly is shown in Fig. 1(b). In sample cell assembly, the height of catalyst/solvent H was set as 2.0 mm, 2.4 mm, and 2.8 mm, respectively. 3D Solid69 and 3D Fluid142 were chosen for thermal–electrical–fluid analysis for meshing models.

Fig. 1 Finite element model of a diamond growth cell. (a) 1/4 model (b) enlarged 1/2 sample assembly. (1) Pyrophyllite; (2) steel cap; (3 and 4) the graphite heater; (5, 9 and 10) the insulator; (6) the diamond seed; (7) the catalyst; (8) the carbon source.

As shown in Fig. 1(a), the growth cell was heated when voltage V₁ was applied on the base of the up steel ring and V₂ was set on the base of the low steel ring which contacted a graphite heater and the WC anvils. The bottoms of the six steel rings were kept at a uniform temperature. The velocity constraints on the symmetric surface were symmetry constraints and the other areas of 1/4 catalyst were set as VX = VY = VZ = 0, so that only convection in the catalyst region was allowed. The material parameters and boundary conditions used in the finite element simulation can be found in Tables 1 and 2.^18–20

Table 1 The boundary parameters used in the computations

Boundary parameters	Value
The temperature of circulation water (°C)	45
The temperature of environment (°C)	35
Sample assembly initial temperature (°C)	60
Terminal surface temperature of the steel ring (°C)	50

---

Table 2 Material parameters used in the computations

Material parameters	Value
Density (kg m^−3)
Diamond	3510
Pyrophyllite	2950
Steel	7900
WC	14 700
Nickel	9331–1.046T
Graphite	2200
Insulator	5600
Specific heat (J kg^−1 °C^−1)
Diamond	471
Pyrophyllite	900
Steel	450
WC	200
Nickel	460
Graphite	710
Insulator	450
Electric resistivity (Ω m)
Diamond	1.0 × 10^14
Pyrophyllite	5.0 × 10^9
Steel	9.71 × 10^−8
WC	5.83 × 10^−7
Nickel	1.15 × 10^−8
Graphite	2.46 × 10^−6
Insulator	8.30 × 10^13
Thermal conductivity (W m^−1 K^−1)
Diamond	470
Pyrophyllite	9.04
Steel	79
WC	160
Nickel	20
Graphite	200
Insulator	2.09
Viscosity (Pa s)
Nickel	0.041–3.478 × 10^−5T + 7.941 × 10^−9T^2

---

2.2 Verification test

Experiments on diamond growth were conducted in a China-type large volume cubic high-pressure apparatus (CHPA)(SPD-6 × 1200) with sample chamber of 38 mm edge length at pressure of 5.7 GPa and temperature of 1260 °C in all runs. We chose high-purity graphite (99.9 wt% purity) as the carbon source and NiMnCo alloy (70 : 25 : 5 by wt%) as catalyst/solvent to synthesize diamond. The diamond crystal with {100} face, 0.5 × 0.5 mm² sizes, was used as the seed crystal. The temperature was calibrated using a Pt-30% RH/Pt-6% Rh thermocouple, whose junction was placed near the crystallization sample. Pressure was calibrated at room temperature by the change in resistance of standard substances and at high temperature by the graphite–diamond equilibrium. After synthesis experiments, the collected samples were put into boiling acids of HNO₃ and H₂SO₄ to remove the impurities remaining on the surfaces of the crystals. Then, we obtained the diamond crystals. Optical microscope was used for observe crystal morphologies of the recovered diamond. Raman spectrometer was used to characterize the quality of diamond crystals. In situ high-pressure Raman measurements were obtained using a spectrometer (iHR550, Horiba Jobin Yvon) with a diode lasers at 671 nm (80–3500 cm⁻¹) and 785 nm (60–200 cm⁻¹) as the excitation source. The laser output power on the sample was maintained at 10 mW. All Raman spectra were collected using a backscattering configuration, and the acquisition time for each spectrum was 60 s. The Raman signals were recorded using a liquid nitrogen cooled CCD camera (Symphont II, Horiba Jobin Yvon) with a spectral resolution set at 1 cm⁻¹.

3. Results and discussions

3.1 Simulation results

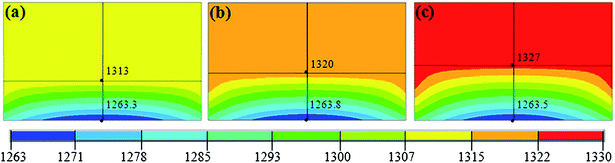
Carbon convection field in HPHT metal solvent is mainly determined by the sample assembly, such as the height of the solvent. To understand the effect of carbon convection on the diamond morphology, the convection distribution of carbon in the growth cell was calculated for catalysts of 2.0 mm, 2.4 mm, and 2.8 mm in height. In this work, we guarantee that the carbon source and the catalyst under the constant total height. Then we add the catalytic height and reduce the carbon source height to gain different carbon convection fields. We applied different voltages in three assemblies to insure the same growth temperature for the seeds, which could rule out the influence of temperature on the crystal morphology.

Temperature has significant effect on diamond morphology. The synthesized diamond usually present the {100} face at lower growth temperatures, while the morphology of diamond is dominantly by {111} face at higher temperatures. Fig. 2 shows the distributions of temperature fields on different heights of catalyst and carbon source. From the simulation results in Fig. 2, we can see that the temperatures of the three seed locations are all 1263 °C, which means that the crystal morphology should be same. Besides, through the color of the cloud of Fig. 2(a)–(c), we can infer that the temperature at the top of the catalyst abutting the carbon source become higher and higher. The solubility of carbon in molten metal also increased with the temperature rising. The carbon concentration modes varied with different growth cells because of the change of solubility gradient in the solvent fluid²¹ and the difference among the increased temperature may have influence on the carbon convection field in molten metallic solvent.

Fig. 2 The distributions of temperature field on different heights of catalyst and carbon source. (a) 2.0 mm catalyst, 4.0 mm carbon source. (b) 2.4 mm catalyst, 3.6 mm carbon source. (c) 2.8 mm catalyst, 3.2 mm carbon source.

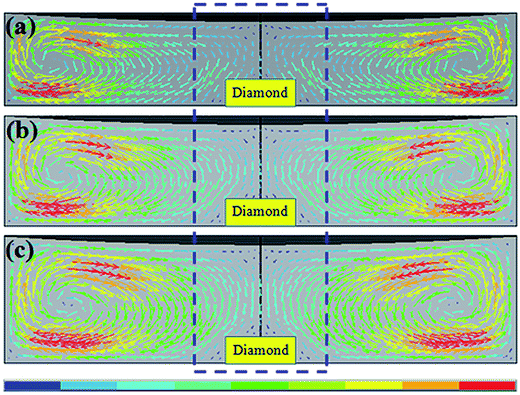
The calculated distributions of the carbon convection are shown in Fig. 3. In the simulated section figure, the arrowheads indicate the flow direction of carbon, the length and the color of the arrows represent the magnitude of carbon flow velocity. Therefore, the relationship between carbon convection distributions and colors (or lengths) of arrowheads are gained. First of all, it is clear that there is a region near the periphery of the solvent where the carbon convection rate is the highest with red arrows. Additionally, it is important to find that the vortex center (black circle with direction) of convection field move closer to the solvent center gradually as the solvent height increases. It is obviously to see that the colors of the arrowheads become deepen and the lengths become larger in the center area of the catalyst/solvent around the seed crystal and the arrow density and length are symmetrically distributed along the vertical direction (inside the blue dotted line).

Fig. 3 Distributions of convection field of the catalyst with three different heights: (a) 2.0 mm (b) 2.4 mm (c) 2.8 mm.

According to the melt–solvent theory, the temperature gradient between the carbon source and diamond seed is the driving force of diamond growth, the carbon element can transport from the carbon source to the crystal surface by temperature gradient. The convection is caused under the action of temperature gradient in the gravitational field. Thus, the convection is also an important factor for diamond growth by HPHT. Convection in crystal growth cell provide carbon transport from carbon source to seed crystal face, so the bigger convection velocity of the carbon, the faster transport of the carbon atoms from source to the seed. From the Fig. 3(a)–(c), we can see that the convection of carbon is deflect and concentrate on the seed crystal, especially in the region near the seed bed and the color and length of arrowheads increase in the centre of the solvent along Y-axis. That is to say, the driving force of diamond crystal growth also increased gradually in the centre of the solvent along Y-axis. Therefore, in the process of diamond growth, the faster carbon transport from source to the seed surface can lead to the quick growth of {100} face. In order to further study the situations of the convection field in the catalyst, we compared the X-axis path and Y-axis path convection velocity. Fig. 4 plots the convection velocity on the X-axis path and Y-axis path. It shows that the convection velocity in X-axis and Y-axis of different heights catalyst both increased (change from 2.0 mm to 2.8 mm). Besides, compared to the X-axis, the convection velocity of Y-axis path grows faster than X-axis. In the diamond crystal growth cell, convection provides a driving force for carbon transport from the carbon source to the crystal surface. Thus, the increased velocity of convection can enhance the carbon transport capacity. As we have mentioned before, the solubility and concentration of carbon in 2.8 mm catalyst are higher than that of in 2.4 mm and 2.0 mm catalyst near the top surface of the catalyst. Thus, there are more carbon can be transported to seed crystal in the growth cell of 2.8 mm catalyst. According to the crystal growth theory, the face growing rapidly disappears firstly and leaves the face which grows slowly.²² As we know, {111} and {100} appear most dominantly on synthetic diamond. So we can predict from the simulated results that convection field of Fig. 3(a) is suitable for growing diamond dominantly with {100} faces, Fig. 3(b) is suitable for {100} and {111} faces morphology diamond and Fig. 3(c) is suitable for diamond with dominated {111} faces and less {100} faces.

Fig. 4 Convection velocity of different heights of catalyst. (a) The convection velocity on the X-axis path. (b) The convection velocity on the Y-axis path.

Since the diamond itself is a good heat conductor, and with the growth of diamond, it will alters the temperature distribution in the cell. To further study the influence of temperature and convection field on crystal growth process, we have simulated the temperature and convection field of the initial stage for 5 h. Fig. 5 shows the temperature field of diamond growth of 5 h. It can be seen that the distribution of temperature field is similar to Fig. 2. The temperature in seed location is the same and the temperature at the top of the catalyst in Fig. 5(c) is highest. Fig. 6 shows the convection field of diamond growth of 5 h. The tendency of convection distribution is consistent with the previous results. Therefore, we believe that the prediction that the convection fields have effect on the crystal morphology is credible.

Fig. 5 The distribution of temperature field in initial stage of diamond growth for 5 h. (a) 2.0 mm (b) 2.4 mm (c) 2.8 mm.

Fig. 6 The distribution of convection field in initial stage of diamond growth for 5 h. (a) 2.0 mm (b) 2.4 mm (c) 2.8 mm.

3.2 Verification experiments

In order to verify our simulation results, we have carried out the synthesis experiments on CHPA, and ensured that the synthesis temperature is 1260 °C. Fig. 7 shows the OM photographs of the synthesized large diamond crystals in Ni-based catalyst with different heights. It can be found that the morphologies of diamonds change obviously. First, the morphology of diamond shows cubic crystals shape with the dominating {100} crystal faces in Fig. 7(a). Then, we see that the diamond has a middle cub-octahedral shape in Fig. 7(b) dominated with {100} and {111} crystal faces and Fig. 7(c) shows the high cub-octahedral shape with dominated {111} faces and less {100} faces. The change of the crystals morphologies indicates that the convection field of carbon has significant effect on diamond morphology. The mechanism of diamond morphology change is understood well by simulating the convection field, and is confirmed by synthesis experiments.

Fig. 7 Synthesized diamond crystals in different heights of Ni-based catalyst under 5.7 GPa and 1260 °C. (a) 2.0 mm (b) 2.4 mm (c) 2.8 mm.

Raman spectroscopy was used to characterize crystal lattice distortion or crystalline quality of diamond crystals. The Raman peak values and the full width at half maximum (FWHM) indicated the relative quality of crystals. Fig. 8 shows Raman spectra recorded from diamond crystals of our sample obtained. The diamond Raman peaks values of those diamond crystals are near 1332 cm⁻¹ and the FWHM of the diamonds are 3.8 cm⁻¹. It is supposed that the observed features of the Raman spectrum of diamond are related to the increasing concentrations of micro-crystallites in boundary, impurities, residual stress, or defects, etc. Therefore, our results illustrate that the change of the convection field only has influence on the crystal morphology and no effect on the crystal quality of diamond.

Fig. 8 Raman spectra of diamond crystals for the samples obtained. (a) 2.0 mm (b) 2.4 mm (c) 2.8 mm.

4. Conclusions

We investigate the effect of carbon convection field on diamond morphology under HPHT conditions using the NiMnCo alloy as catalyst/solvent. The temperature fields of the catalyst with three different heights were simulated to rule out the influence of temperature on the crystal morphology. Three carbon convection fields were simulated and the distributions of the convection field were analyzed by FEM. Based on the calculated results, we predict that the morphology of diamond crystal changes from cubic crystal to cub-octahedral as the convection intensity increasing on the seed crystal surface. The results of simulation for the morphologies of diamond were proved by diamonds synthesis experiments. It indicated that the morphology of diamonds significantly changes due to the change of the carbon convection field.

Acknowledgements

Project supported by National Natural Science Foundation of China (grant no. 51172089, 11504267), Program for New Century Excellent Talents in University, Natural Science Foundation of Guizhou Province Education Department (grant no. KY[2013]183) and Natural Science Foundation of Guizhou Province Science and Technology Agency (No. LH[2015]7232).

Notes and references

1. T. Gaebel, M. Domhan, I. Popa, C. Wittmann, P. Neumann, F. Jelezko, J. R. Rabeau, N. Stavrias, A. D. Greentree, S. Prawer, J. Meijer, J. Twamley, P. R. Hemmer and J. Wrachtrup, Nat. Phys., 2006, 2, 408–413.
2. J. Yan and L. Chang, Nanotechnology, 2006, 17, 5544.
3. S. Wolter, M. McClure, J. Glass and B. Stoner, Appl. Phys. Lett., 1995, 66, 2810–2812.
4. H. Sumiya and S. Satoh, Int. J. Refract. Met. Hard Mater., 1999, 17, 345–350.
5. H. Sumiya and K. Harano, Diamond Relat. Mater., 2012, 24, 44–48.
6. H. Sumiya and S. Satoh, Diamond Relat. Mater., 1996, 5, 1359–1365.
7. R. Burns, J. Hansen, R. Spits, M. Sibanda, C. Welbourn and D. Welch, Diamond Relat. Mater., 1999, 8, 1433–1437.
8. Y. Meng, C. Yan, J. Lai, S. Krasnicki, H. Shu, T. Yu, Q. Liang, H. Mao and R. Hemley, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17620–17625.
9. Y. Li, X. Jia, W. Shi, S. Leng, H. Ma, S. Sun, F. Wang, N. Chen and Y. Li, Int. J. Refract. Met. Hard Mater., 2014, 43, 147–149.
10. X. Liu, X. Jia, X. Guo, Z. Zhang and H. Ma, Cryst. Growth Des., 2010, 10, 2895–2900.
11. S. Sun, X. Jia, B. Yan, F. Wang, N. Chen, Y. Li and H. Ma, CrystEngComm, 2014, 16, 2290.
12. S. Sun, X. Jia, B. Yan, F. Wang, Y. Li, N. Chen and H. A. Ma, Diamond Relat. Mater., 2014, 42, 21–27.
13. L. Zeng, H. Peng, W. Wang, Y. Chen, D. Lei, W. Qi, J. Liang, J. Zhao, X. Kong and H. Zhang, J. Phys. Chem. C, 2008, 112, 6160–6164.
14. M. Hu, H. Ma, W. Liu, Z. Zhang, M. Zhao, Y. Li, W. Guo, J. Qin and X. Jia, J. Cryst. Growth, 2010, 312, 2989–2992.
15. A. S. Barnard, Cryst. Growth Des., 2009, 9, 4860–4863.
16. B. Yan, X. Jia, S. Sun, Z. Zhou, C. Fang, N. Chen, Y. Li, Y. Li and H. Ma, Int. J. Refract. Met. Hard Mater., 2015, 48, 56–60.
17. M. Hu, S. S. Li, H. Ma, T. Su, X. Li, Q. Hu and X. Jia, Chin. Phys. B, 2012, 21, 098101.
18. R. Li, H. Ma, Q. Han, Z. Liang, B. Yin, W. Liu and X. Jia, High Pressure Res., 2007, 27, 249–257.
19. R. Brooks, I. Egry, S. Seetharaman and D. Grant, High Temp.–High Pressures, 2001, 33, 631–637.
20. Z. Li, X. Jia, G. Huang, M. Hu, Y. Li, B. Yan and H. Ma, Chin. Phys. B, 2013, 22, 014701.
21. M. Hu, H. Ma, B. Yan, Y. Li, Z. Li, Z. Zhou and X. Jia, Cryst. Growth Des., 2012, 12, 518–521.
22. L. Ma, H. Ma, H. Xiao, S. Li, Y. Li and X. Jia, Chin. Sci. Bull., 2010, 55, 677–679.

---