DOI:
10.1039/C6RA01358A
(Paper)
RSC Adv., 2016,
6, 31588-31606
VIS and VUV spectroscopy of 12C17O and deperturbation analysis of the A1Π, υ = 1–5 levels
Received
16th January 2016
, Accepted 15th March 2016
First published on 17th March 2016
Abstract
High-accuracy dispersive optical spectroscopy measurements in the visible (VIS) region have been performed on the less-abundant 12C17O isotopologue, observing high-resolution emission bands of the B1Σ+ (υ = 0) → A1Π (υ = 3, 4, and 5) Ångström system. These are combined with high-resolution photoabsorption measurements of the 12C17O B1Σ+ (υ = 0) ← X1Σ+ (υ = 0) and C1Σ+ (υ = 0) ← X1Σ+ (υ = 0) Hopfield–Birge bands recorded with the vacuum-ultraviolet (VUV) Fourier transform spectrometer, installed on the DESIRS beamline at the SOLEIL synchrotron. The frequencies of 429 observed transitions have been determined in the 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100–18
100–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 and 86
400 cm−1 and 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900–92
900–92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 regions with an absolute accuracy of up to 0.003 cm−1 and 0.005 cm−1 for the B–A, and B–X, C–X systems, respectively. These new experimental data were combined with data from the previously analysed C → A and B → A systems. The comprehensive data set, 982 spectral lines belonging to 12 bands, was included in a deperturbation analysis of the A1Π, υ = 1–5 levels of 12C17O, taking into account interactions with levels in the d3Δi, e3Σ−, a′3Σ+, I1Σ− and D1Δ states. The A1Π and perturber states were described in terms of a set of deperturbed molecular constants, spin–orbit and L-uncoupling interaction parameters, equilibrium constants, 309 term values, as well as isotopologue-independent spin–orbit and rotation-electronic perturbation parameters.
100 cm−1 regions with an absolute accuracy of up to 0.003 cm−1 and 0.005 cm−1 for the B–A, and B–X, C–X systems, respectively. These new experimental data were combined with data from the previously analysed C → A and B → A systems. The comprehensive data set, 982 spectral lines belonging to 12 bands, was included in a deperturbation analysis of the A1Π, υ = 1–5 levels of 12C17O, taking into account interactions with levels in the d3Δi, e3Σ−, a′3Σ+, I1Σ− and D1Δ states. The A1Π and perturber states were described in terms of a set of deperturbed molecular constants, spin–orbit and L-uncoupling interaction parameters, equilibrium constants, 309 term values, as well as isotopologue-independent spin–orbit and rotation-electronic perturbation parameters.
1. Introduction
Carbon monoxide (CO) is one of the most thoroughly studied molecules, bearing significance to astronomy and cosmology. After H2, it is the second most abundant molecule in the interstellar medium (ISM), where it is investigated as a tracer of gas properties, structure and kinematics.1,2 In such astrophysical environments CO controls much of the gas-phase chemistry,3 and is a precursor to complex molecules.4 The CO spectrum has been observed in comets, cool dwarfs, quasars, supernova remnants, and interstellar molecular clouds as well as in atmospheres of planets and transiting exoplanets.5,6 Emissions originating from the B1Σ+ (υ = 0), B1Σ+ (υ = 1), and C1Σ+ (υ = 0) vibrational levels were recorded from the Martian and Venusian atmospheres by the Hopkins Ultraviolet Telescope,7 the FUSE satellite,8,9 and the Cassini UVIS instrument.10 Large CO abundances produce detectable signals even for the rare isotopologues, including 12C17O.11–13 Investigations of minor isotopologues are applied to unravel ‘depth effects’ in the interstellar absorptions14 and for precise determination of the [12C]/[13C] and [16O]/[17O]/[18O] ratios in the ISM.13,15 The CO vacuum ultraviolet absorption spectrum is of astrophysical relevance due to the photodissociation of VUV-excited states, e.g. the C1Σ+, B1Σ+ and E1Π states.16 Isotope-dependent photodissociation effects, due to self-shielding in high-column density environments,15,17 lead to isotopic fractionation of CO.13,18
The less-abundant 12C17O isotopologue was detected in the ISM for the first time in 1973 in the Orion Nebula19 and has been studied in the laboratory in a number of investigations.20–25 Hakalla and co-workers have investigated the visible spectrum of 12C17O, comprising the B1Σ+–A1Π Ångström system,26,27 as well as the C1Σ+–A1Π Herzberg system.28 The VUV spectrum of the C1Σ+–X1Σ+ system was investigated by laser excitation22,29 and the B1Σ+–X1Σ+ system by absorption of synchrotron radiation.25
The A1Π state is subject to some of the most extensive and complex perturbations among all the states that are known in the carbon monoxide molecule.30–38 The d3Δi, e3Σ−, a′3Σ+, I1Σ−, and D1Δ electronic states are responsible for all of the existing irregularities. A systematic classification of the perturbations of the A1Π state in the main 12C16O molecule was carried out by Krupenie.39 Simmons et al.40 made a critical analysis of this study as well as completed it. A conclusive analysis and deperturbation calculations were carried out by Field et al.30,32,41 Next, Le Floch et al.31 conducted a comprehensive study of perturbations in the lowest A1Π, υ = 0 vibrational level. In his next works42,43 he analysed perturbations occurring in the A1Π, υ = 0–4 levels, and calculated very precise term values for the A1Π, υ = 0–8 states, respectively. Recently, the A1Π state of the main 12C16O isotopologue has been studied in the A–X transition44–46 by the Amsterdam group by means of highly accurate two-photon Doppler-free excitation using narrow band lasers47 with relative accuracy up to Δλ/λ = 2 × 10−8, as well as by vacuum ultraviolet Fourier-transform spectroscopy (VUV-FTS) at the SOLEIL synchrotron.48–50 An improved deperturbation analysis of A1Π in ordinary CO has recently been performed by Niu et al.44,51 Far fewer deperturbation analyses of the A1Π state have been performed in other isotopologues of CO (12C18O and 13C18O).33,52,53 A considerable contribution to the identification and classification of the A1Π state perturbations has been made by Kępa and Rytel in a number of investigations over the years.54–58
Here, the focus is on a deperturbation analysis of the A1Π (υ = 1, 2, 3, 4, and 5) levels in the 12C17O isotopologue. The deperturbation is based on new observations of the 12C17O B → A (0, 3), (0, 4), (0, 5) bands recorded in visible emission at high resolution and previously published studies of the Ångström26,27 and Herzberg bands.28 The deperturbation analysis prompted some reassignment of lines in the B–A and C–A systems. New, highly accurate measurements of the 12C17O B ← X (0, 0) and C ← X (0, 0) transitions with VUV-FTS were performed and included in the study in order to (i) establish and verify that B (υ = 0) and C (υ = 0) levels are unperturbed, and that our perturbation analysis of A-state is not affected by shifts in the upper states, (ii) include an independent set of improved constants, therewith level energies, of B (υ = 0) and C (υ = 0), as well as (iii) determine level energies of A-state with respect to ground state of CO. The comprehensive fit on B–A, C–A, B–X, and C–X systems allowed us to perform the most accurate deperturbed rotational constants of the states under consideration.
2. Experimental details
2.1. Emission spectra of the B1Σ+ → A1Π system
In this study, a water-cooled, hollow-cathode lamp with two anodes65 and a high-accuracy dispersive optical spectroscopy method were used for a high-resolution spectroscopic investigation of the 12C17O B1Σ+ (υ = 0) → A1Π (υ = 3, 4, and 5) bands in the visible region. The lamp was initially filled with a mixture of helium and acetylene 12C2D2 (Cambridge Isotopes, 12C 99.99%) under the pressure of approximately 6 Torr. An electric current was passed through the mixture for about 200 h, after which a small quantity of 12C carbon became deposited on the electrodes. Subsequently, the lamp was evacuated and oxygen containing the 17O2 isotope (Sigma-Aldrich, 17O2 60%) was admitted at a static gas pressure of 2 Torr. The anodes were operated at 2 × 650 V and 2 × 50 mA dc. During the discharge process the 17O2 molecules decay into atomic oxygen, which then combine with 12C-carbon atoms, ejected from the outer layer of the cathode, thus forming the 12C17O molecules in the gas phase. The temperature of the plasma formed at the centre of the cathode was about 600–700 K. These conditions were found to be optimal for the production of CO molecular spectra under control of isotopic composition. The experimental equipment of the Rzeszów laboratory, where these measurements were conducted, has been described in detail by Hakalla et al.66
Spectroscopic measurements were made by means of a 2 m Ebert plane-grating spectrograph equipped with a 651.5 grooves per mm grating with a total of 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 grooves, blazed at 1.0 μm in 3rd and 4th order, giving reciprocal dispersion and resolving power in the ranges 0.11–0.19 nm mm−1 and 182
600 grooves, blazed at 1.0 μm in 3rd and 4th order, giving reciprocal dispersion and resolving power in the ranges 0.11–0.19 nm mm−1 and 182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–136
400–136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800, respectively. Discharge emission signals were recorded by means of a photomultiplier tube (HAMAMATSU R943-02) mounted on a linear stage (HIWIN KK5002) along the focal curve of the spectrograph. The input and exit slits were 35 μm in width. The intensities of the lines were measured by means of photon counting (HAMAMATSU C3866 photon counting unit and M8784 photon counting board) with a counter gate time of 200–500 ms (no dead time between the gates). The position of the exit slit was measured by means of a He–Ne laser interferometer (LASERTEX) synchronized with the photon counting board. During one exposure of the counter gate, the position was measured 64 times. Simultaneously recorded thorium atomic lines,69 obtained from an auxiliary water-cooled, hollow-cathode tube filled with Th foil were used for absolute CO wavenumber calibration.
800, respectively. Discharge emission signals were recorded by means of a photomultiplier tube (HAMAMATSU R943-02) mounted on a linear stage (HIWIN KK5002) along the focal curve of the spectrograph. The input and exit slits were 35 μm in width. The intensities of the lines were measured by means of photon counting (HAMAMATSU C3866 photon counting unit and M8784 photon counting board) with a counter gate time of 200–500 ms (no dead time between the gates). The position of the exit slit was measured by means of a He–Ne laser interferometer (LASERTEX) synchronized with the photon counting board. During one exposure of the counter gate, the position was measured 64 times. Simultaneously recorded thorium atomic lines,69 obtained from an auxiliary water-cooled, hollow-cathode tube filled with Th foil were used for absolute CO wavenumber calibration.
The peak positions of spectral lines were derived by means of a least-squares procedure assuming a Gaussian line-shape for each spectral contour (30 points per line), with a fitting uncertainty of the peak position for a single unblended line in the range 0.1–0.2 μm, that is 2.5–8 × 10−4 cm−1 in the observed region. To determine the 12C17O B1Σ+ → A1Π wavenumbers, 5th- and 6th-order interpolation polynomials were used for the (0, 3), (0, 4), and (0, 5) bands. The absolute wavenumber calibration at 1σ uncertainty is 0.002 cm−1. The strong and unblended lines exhibit a full-width half-maximum (FWHM) of 0.15 cm−1, maximum signal-to-noise ratio of about 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as well as count rates of up to about 16
1 as well as count rates of up to about 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–60
000–60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 photons per s for the 12C17O B1Σ+ (υ = 0) → A1Π (υ = 3, 4, and 5) bands. The absolute accuracy of the frequency measurements was 0.003 cm−1, corresponding to a relative accuracy of Δλ/λ = 2 × 10−7, for the 15
000 photons per s for the 12C17O B1Σ+ (υ = 0) → A1Π (υ = 3, 4, and 5) bands. The absolute accuracy of the frequency measurements was 0.003 cm−1, corresponding to a relative accuracy of Δλ/λ = 2 × 10−7, for the 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180–18
180–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 spectral region. However, weaker or blended lines have lower accuracy, at worst 0.07 cm−1 or Δλ/λ = 4 × 10−6.
400 cm−1 spectral region. However, weaker or blended lines have lower accuracy, at worst 0.07 cm−1 or Δλ/λ = 4 × 10−6.
Preliminary identification of the B1Σ+ (υ = 0) → A1Π (υ = 3, 4, and 5) bands was carried out by means of the information provided in our recent works on the 12C17O molecule.26,27 For the frequency measurements of the lines investigated, blending effects of the 12C16O Ångström system were taken into account. They occur as a result of using oxygen 17O2 with spectral purity of only 60%. In total, 283 emission lines belonging to the B1Σ+ → A1Π band system in 12C17O were identified and rotationally assigned. The transition frequencies are provided in Table 1. The observed 12C17O B1Σ+ (υ = 0) → A1Π (υ = 3, 4, and 5) spectra, together with extra-lines, assignments, calibrating Th atomic lines, and final simulated spectra are shown in Fig. 1–3. By “extra-lines”, we refer to the spectral emission lines terminating on perturber states and gaining intensity from mixing with the A1Π state. An additional impediment was the appearance of four atomic lines overlapping the region of the 12C17O B → A (0, 5) band with significantly higher intensities and broader FWHMs. They were identified by means of the Atomic Spectra Database (ASD) of NIST59–63 as the C lines at 15186.739 cm−1 and 15197.891 cm−1, as well as the H Balmer-alpha line at 15233.157 cm−1 and deuterium D line at 15237.272 cm−1. As a result, it was not possible to measure the positions of the P(11), P(15), and R(6) B → A (0, 5) lines (marked with empty circles in Fig. 3a).
Table 1 Transition frequencies (in cm−1) of the 12C17O B1Σ+ → A1Π emission bands from the high-accuracy dispersive optical spectroscopy measurementsa
|
J′′ |
B1Σ+ → A1Π (0, 3) |
B1Σ+ → A1Π (0, 4) |
B1Σ+ → A1Π (0, 5) |
| P11ee(J′′) |
Q11ef(J′′) |
R11ee(J′′) |
P11ee(J′′) |
Q11ef(J′′) |
R11ee(J′′) |
P11ee(J′′) |
Q11ef(J′′) |
R11ee(J′′) |
|
The estimated absolute calibration 1σ uncertainty was 0.002 cm−1. Lines marked with ‘w’ were weak and with ‘b’ were blended in the spectra. Absolute accuracy of the line frequency measurements varies between 0.003 and 0.07 cm−1 for the strongest and weakest lines, respectively.
The P(10) line of the B–A(0, 5) band was overlapped by the carbon atomic line at 15197.891 cm−1 of significantly higher intensity and half-width. The identification after NIST ASD.59,60
The P(15) line of the BA(0, 5) band was overlapped by the deuterium atomic line at 15237.272 cm−1 of significantly higher intensity and half-width. The identification after NIST ASD.61,62
The R(6) line of the B–A(0, 5) band was overlapped by the hydrogen atomic line at 15233.157 cm−1 (Hα of the Balmer series) of significantly higher intensity and half-width. The identification after NIST ASD.61,63
The Q(27) line of the B–A(0, 5) band is significantly weakened by multistate, strong perturbations derived from interactions with the d3Δi (υ = 11) and a′3Σ+ (υ = 16) states, by which it was not possible to distinguish this line from the noise.
The additionally assigned lines based on better, than in the previous works26–28 understanding of the spectrum of the 12C17O. The (1, 5) lines originate from above the first predissociation limit of CO located at 90679.1 cm−1.64
|
| 1 |
17873.5415w |
17877.3487 |
17884.9340w |
16511.6992wb |
16515.4938 |
16523.0926wb |
15183.9236w |
15187.7309b |
15195.3164wb |
| 2 |
17871.3560w |
17878.9588 |
17890.3448wb |
16509.6030wb |
16517.1954 |
16528.5907w |
15181.9146wb |
15189.5160 |
15200.9022w |
| 3 |
17869.9711b |
17881.3756 |
17896.5532 |
16508.3534b |
16519.7453 |
16534.9352 |
15180.8067 |
15192.1968 |
15207.3878 |
| 4 |
17869.3988b |
17884.5914 |
17903.5738 |
16507.9558 |
16523.1441b |
16542.1318b |
15180.5825 |
15195.7723 |
15214.7562b |
| 5 |
17869.6231b |
17888.6168 |
17911.3897 |
16508.4044b |
16527.3907 |
16550.1711 |
15181.2601 |
15200.2415 |
15223.0281b |
| 6 |
17870.6627b |
17893.4479b |
17920.0175 |
16509.7149b |
16532.4902 |
16559.0712 |
15182.8347 |
15205.6131 |
d
|
| 7 |
17872.5000 |
17899.0872b |
17929.4448b |
16511.8668b |
16538.4413 |
16568.8116 |
15185.3034 |
15211.8759 |
15242.2470 |
| 8 |
17875.1495 |
17905.5280 |
17939.6817 |
16514.8754 |
16545.2370 |
16579.4055 |
15188.6753 |
15219.0329b |
15253.1997 |
| 9 |
17878.6007 |
17912.7727 |
17950.7216 |
16518.7325 |
16552.8844 |
16590.8456 |
15192.9308 |
15227.0844 |
15265.0420 |
| 10 |
17882.8628 |
17920.8230 |
17962.5630 |
16523.4385 |
16561.3885 |
16603.1382 |
b
|
15236.0352 |
15277.7829 |
| 11 |
17887.9333b |
17929.6776 |
17975.2018 |
16529.0007 |
16570.7363 |
16616.2656 |
15204.1416 |
15245.8790 |
15291.4191 |
| 12 |
17893.8041b |
17939.3388 |
17988.6474 |
16535.4121 |
16580.9368 |
16630.2435 |
15211.1034 |
15256.6216 |
15305.9482b |
| 13 |
17900.4819 |
17949.8052 |
18002.9017 |
16542.6783 |
16591.9832b |
16645.0971 |
15218.9579b |
15268.2593 |
15321.3691 |
| 14 |
17907.9701 |
17961.0768 |
18017.9529 |
16550.7939 |
16603.8795b |
16660.7753 |
15227.7106 |
15280.7983 |
15337.6939 |
| 15 |
17916.2705w |
17973.1496 |
18033.7998 |
16559.7665 |
16616.6342 |
16677.3045 |
c
|
15294.2314 |
15354.9027 |
| 16 |
17925.3745 |
17986.0335 |
18050.4689 |
16569.5907 |
16630.2435b |
16694.6922 |
15247.9101 |
15308.5584 |
15373.0036 |
| 17 |
17935.2870b |
17999.7350b |
18067.9402 |
16580.2662 |
16644.6981 |
16712.9238 |
15259.3599 |
15323.8044 |
15392.0068 |
| 18 |
17946.0199 |
18014.2502 |
18086.2085b |
16591.8117b |
16660.0117 |
16732.0040 |
15271.7297 |
15339.9268 |
15411.9211 |
| 19 |
17957.6189b |
18029.6005b |
18105.3502 |
16604.1975 |
16676.1770b |
16751.9305 |
15284.9971 |
15356.9602 |
15432.7399 |
| 20 |
17969.9100 |
18045.6680 |
18125.1789 |
16617.4401 |
16693.1912 |
16772.7136 |
15299.1573 |
15374.8906 |
15454.4240 |
| 21 |
17983.0826b |
18062.6124b |
18145.8766 |
16631.5498 |
16711.0648 |
16794.3439 |
15314.2281 |
15393.7315 |
15477.0222 |
| 22 |
17997.0654 |
18080.4029 |
18167.3898 |
16646.5087 |
16729.7939 |
16816.8168 |
15330.1972b |
15413.4733 |
15500.5139 |
| 23 |
18011.8926 |
18099.0791 |
18189.7235 |
16662.3326 |
16749.4891 |
16840.1597b |
15347.0858 |
15434.1239 |
15524.9246wb |
| 24 |
18027.5385 |
18119.3843 |
18212.8737 |
16679.0067 |
16769.7712 |
16864.3394b |
15364.8940 |
15455.6780 |
15550.2386wb |
| 25 |
18044.1309 |
18137.7727b |
18236.9649 |
16696.5573 |
16791.0561 |
16889.3887b |
15383.6275 |
15478.1744b |
15576.4581wb |
| 26 |
18061.8968 |
18159.0512b |
18262.2549 |
16714.9513b |
16813.2121 |
16915.2774b |
15403.2833wb |
15501.6332 |
15603.6053wb |
| 27 |
18076.9080 |
18180.9483b |
18284.7404wb |
16734.2123b |
16836.2224 |
16942.0178b |
15423.9461w |
e
|
15631.7723w |
| 28 |
18097.1756 |
18203.6581 |
18312.4882wb |
16754.3424w |
16860.1012 |
16969.6086 |
15445.2634w |
15552.7612b |
15660.5543wb |
| 29 |
18117.0975b |
18227.4324 |
18339.8457w |
16775.3465w |
16884.8186 |
16998.0915b |
|
15576.7018wb |
|
| 30 |
18137.6823b |
18250.1705 |
18367.8876w |
16797.2108w |
16910.4095 |
17027.3687w |
|
15604.1346wb |
|
| 31 |
18159.0776wb |
18275.8613b |
18396.7270wb |
16819.9516wb |
16936.8710 |
|
|
15630.5207w |
|
| 32 |
18181.1794wb |
18301.8278w |
|
16843.5748w |
16964.1936 |
|
|
15660.4293wb |
|
| 33 |
18204.5622w |
18328.9618wb |
|
16868.2295w |
16992.3948 |
|
|
|
|
| 34 |
18227.8885w |
18356.0240wb |
|
16891.7250w |
17021.4713w |
|
|
|
|
| 35 |
18252.4990wb |
18384.3289w |
|
|
|
|
|
|
|
| 36 |
|
18413.4754w |
|
|
|
|
|
|
|
|
J′′ |
B1Σ+ → A1Π (0, 1)f |
B1Σ+ → A1Π (1, 5)f |
| P11ee(J′′) |
Q11ef(J′′) |
R11ee(J′′) |
P11ee(J′′) |
Q11ef(J′′) |
R11ee(J′′) |
| 1 |
|
|
|
|
|
|
| … |
|
|
|
|
|
|
| 21 |
|
|
|
|
17438.5662w |
|
| 22 |
|
|
|
|
17457.1157w |
|
| 23 |
|
|
|
|
17476.5644w |
|
| … |
|
|
|
|
|
|
| 35 |
|
21150.5933w |
|
|
|
|
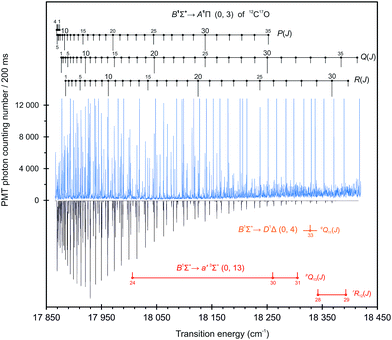 |
| | Fig. 1 High resolution emission spectra, recorded with the high-accuracy dispersive optical spectroscopy setup66 at an instrumental resolution of 0.15 cm−1, of the 12C17O B1Σ+ → A1Π (0, 3) band, with the perturber lines associated with the B1Σ+ → D1Δ (0, 4), and B1Σ+ → a′3Σ+ (0, 13) transitions (upper trace) together with the final branch assignments, calibrating Th atomic lines (going beyond the scale), as well as simulated spectra67 (lower trace). The ratio of the gas compositions used to obtain the molecular spectra was 12C17O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O = 1 12C16O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35. 0.35. | |
 |
| | Fig. 2 High resolution emission spectra, recorded with the high-accuracy dispersive optical spectroscopy setup66 at an instrumental resolution of 0.15 cm−1, of the 12C17O B1Σ+ → A1Π (0, 4) band, with the perturber lines associated with the B1Σ+ → e3Σ− (0, 7), B1Σ+ → I1Σ− (0, 6), and B1Σ+ → a′3Σ+ (0, 14) transitions (upper trace) together with the final branch assignments, calibrating Th atomic lines (going beyond the scale), as well as simulated spectra67 (lower trace). The ratio of the gas compositions used to obtain the molecular spectra was 12C17O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O = 1 12C16O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35. 0.35. | |
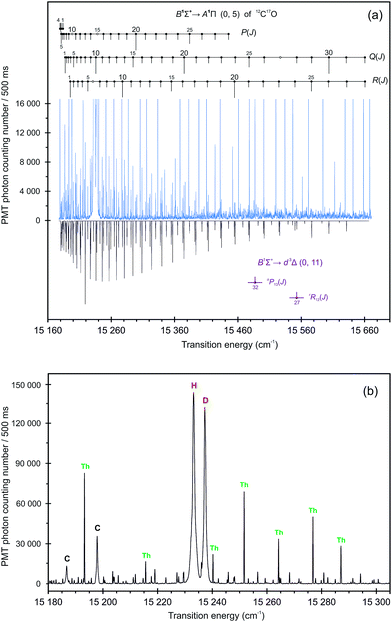 |
| | Fig. 3 High resolution emission spectra, recorded with the high-accuracy dispersive optical spectroscopy setup66 at an instrumental resolution of 0.15 cm−1, of the 12C17O B1Σ+ → A1Π (0, 5) band with the perturber lines associated with the B1Σ+ → d3Δ (0, 11) transition. The ratio of the gas compositions used to obtain the molecular spectra was 12C17O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O = 1 12C16O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35. (Panel (a)) An overview of the observed B1Σ+ → A1Π (0, 5) and B1Σ+ → d3Δ (0, 11) spectra (upper trace) together with the final branch assignments, calibrating Th atomic lines (going beyond the scale), as well as simulated spectra67 (lower trace). The empty circles indicate spectral lines of undetermined location due to overlap with much more intense atomic lines of carbon, hydrogen, and deuterium. (Panel (b)) Expanded view of the B → A (0, 5) band head region in 12C17O at an enlarged scale. 0.35. (Panel (a)) An overview of the observed B1Σ+ → A1Π (0, 5) and B1Σ+ → d3Δ (0, 11) spectra (upper trace) together with the final branch assignments, calibrating Th atomic lines (going beyond the scale), as well as simulated spectra67 (lower trace). The empty circles indicate spectral lines of undetermined location due to overlap with much more intense atomic lines of carbon, hydrogen, and deuterium. (Panel (b)) Expanded view of the B → A (0, 5) band head region in 12C17O at an enlarged scale. | |
Our deperturbation analysis allowed us to assign 24 rotational lines from 14 bands of the B1Σ+ → d3Δi, B1Σ+ → e3Σ−, B1Σ+ → a′3Σ+, B1Σ+ → I1Σ−, B1Σ+ → D1Δ, C1Σ+ → e3Σ−, C1Σ+ → a′3Σ+, and C1Σ+ → D1Δ systems in 12C17O. The transition frequencies and assignments are presented in Table 2. Since most of them are weak their accuracy is not better than 0.01 cm−1. The deperturbation included some lines from the 12C17O B1Σ+ → A1Π (0, 1) and (1, 5) bands which we have measured with an improved accuracy26–28 and reassigned. Lines in the B → A (1, 5) band originate from above the first dissociation limit of CO located at 90679.1 cm−1,64 and have low intensities due to the competition of emission with predissociation.70 The wavelengths for these lines are collected in Table 1. All high-J lines located in the perturbation regions, previously analysed26–28 in 12C17O, were checked carefully with regard to their quality, because these lines are usually weak. Those lines that were too weak and/or blended were removed from the deperturbation analysis. Also, we extended and corrected the assignment of some heavily perturbed or extremely weak lines located in the region of strong and multistate interactions. They are collected in Table 3.
Table 2 Transition frequencies of the (B1Σ+, C1Σ+) → (d3Δi, e3Σ−, a′3Σ+, I1Σ−, and D1Δ) extra-line bands in 12C17Oa,b
| System |
Band |
Branch |
J′′ |
Frequency (cm−1) |
B–A or C–A band of occurrence |
|
The estimated calibration 1σ uncertainty was 0.002 cm−1. The absolute accuracy of the significant majority of extra-lines should be assumed as not better than approximately 0.01 cm−1 due to their weakness.
Lines marked with ‘w’ were weak and with ‘b’ were blended in the spectra. The superscript o, p, r, s, or q preceding the main notation P, Q, R of the branch indicates the change in total angular momentum excluding spin for transition to the perturber state.68
|
| B1Σ+ → d3Δi |
(0, 7) |
qP13ee |
35 |
19632.935 |
B1Σ+–A1Π (0, 2) |
| (0, 11) |
oP11ee |
32 |
15487.171w |
B1Σ+–A1Π (0, 5) |
| |
rR12ee |
27 |
15552.369 |
|
| B1Σ+ → e3Σ− |
(0, 4) |
qQ12ef |
25 |
19460.541w |
B1Σ+–A1Π (0, 2) |
| |
qP11ee |
26 |
19463.325w |
|
| (0, 7) |
qQ12ef |
35 |
17002.628w |
B1Σ+–A1Π (0, 4) |
| |
sR11ee |
33 |
17098.203wb |
|
| B1Σ+ → a′3Σ+ |
(0, 10) |
pP12ee |
20 |
20761.828w |
B1Σ+–A1Π (0, 1) |
| |
pP12ee |
22 |
20820.661 |
|
| (0, 13) |
pQ13ef |
24 |
18005.897w |
B1Σ+–A1Π (0, 3) |
| |
pQ13ef |
30 |
18260.250w |
|
| |
pQ13ef |
31 |
18307.498w |
|
| |
rR12ee |
28 |
18342.563 |
|
| |
rR12ee |
29 |
18392.832 |
|
| (0, 14) |
rR12ee |
3 |
16658.293w |
B1Σ+–A1Π (0, 4) |
| B1Σ+ → I1Σ− |
(0, 3) |
qQ11ef |
7 |
19291.955 |
B1Σ+–A1Π (0, 2) |
| (0, 6) |
qQ11ef |
24 |
16783.703w |
B1Σ+–A1Π (0, 4) |
| B1Σ+ → D1Δ |
(0, 1) |
qQ11ef |
27 |
20986.818w |
B1Σ+–A1Π (0, 1) |
| (0, 4) |
qQ11ef |
33 |
18327.789wb |
B1Σ+–A1Π (0, 3) |
| C1Σ+ → e3Σ− |
(0, 4) |
qP11ee |
25 |
24430.966w |
C1Σ+–A1Π (0, 2) |
| |
qP11ee |
29 |
24578.958w |
|
| C1Σ+ → a′3Σ+ |
(0, 10) |
rQ11ef |
22 |
25952.917wb |
C1Σ+–A1Π (0, 1) |
| (0, 13) |
rQ11ef |
24 |
23111.431 |
C1Σ+–A1Π (0, 3) |
| C1Σ+ → D1Δ |
(0, 1) |
pP11ee |
26 |
25849.807w |
C1Σ+–A1Π (0, 1) |
Table 3 Extended and corrected assignmenta of some of heavily perturbed or extremely weak lines located mostly in the region of strong and multistate interactionsb,c
| System |
J′′ |
Branch |
Frequency (cm−1) |
|
Extended and corrected assignment of the lines already published in previous publication (ref. 26–28).
The estimated calibration 1σ uncertainty was 0.002 cm−1. The absolute accuracy of the significant majority of the lines should be assumed as not better than approximately 0.01 cm−1.
Lines marked with ‘w’ were weak and with ‘b’ were blended in the spectra.
|
| B1Σ+–A1Π (0, 1) |
1 |
Q11ef |
20701.471wb |
| 2 |
Q11ef |
20702.936w |
| 5 |
Q11ef |
20711.661b |
| 26 |
P11ee |
20855.286b |
| 26 |
R11ee |
21055.609b |
| 34 |
Q11ef |
21128.729b |
| B1Σ+–A1Π (0, 2) |
26 |
R11ee |
19640.375 |
| 28 |
Q11ef |
19587.541 |
| 29 |
Q11ef |
19600.539 |
| 30 |
Q11ef |
19624.714 |
| 31 |
Q11ef |
19648.885w |
| 31 |
P11ee |
19534.375wb |
| 32 |
Q11ef |
19673.557w |
| 32 |
P11ee |
19550.099wb |
| 33 |
Q11ef |
19698.930w |
| 33 |
P11ee |
19573.885w |
| B1Σ+–A1Π (1, 1) |
1 |
P11ee |
22754.143wb |
| 1 |
R11ee |
22765.387wb |
| B1Σ+–A1Π (1, 5) |
2 |
R11ee |
17257.095b |
| 21 |
P11ee |
17360.067wb |
| C1Σ+–A1Π (0, 1) |
26 |
P11ee |
25855.228wb |
| 26 |
Q11ef |
25953.327 |
| 26 |
R11ee |
26055.176w |
| C1Σ+–A1Π (0, 2) |
27 |
Q11ef |
24561.747b |
| 28 |
Q11ef |
24586.932wb |
| 29 |
Q11ef |
24599.645w |
| 30 |
Q11ef |
24623.687w |
| C1Σ+–A1Π (0, 3) |
11 |
P11ee |
22889.944b |
| 15 |
R11ee |
23035.165 |
| 16 |
P11ee |
22926.873b |
| 20 |
P11ee |
22970.859 |
| 25 |
R11ee |
23236.712w |
2.2. VUV-FTS of the B1Σ+ ← X1Σ+ and C1Σ+ ← X1Σ+ systems
We have measured photoabsorption spectra for two bands of 12C17O: B1Σ+ ← X1Σ+ (0, 0) and C1Σ+ ← X1Σ+ (0, 0). Their spectra, shown in Fig. 4 and 5, respectively, were recorded at the SOLEIL synchrotron utilising the tunable-undulator radiation source of the DESIRS beamline and its permanently-installed vacuum-ultraviolet Fourier-transform spectrometer. The characteristics of the beamline and spectrometer are described by Nahon et al.50 and de Oliveira et al.48,49 Two room-temperature spectra were recorded with approximate column densities of 2 × 1015 and 6 × 1013 cm−2, and have spectral resolutions of 0.32 and 0.21 cm−1 FWHM, respectively. The lower column density measurement was necessary to avoid saturation of the strongest rotational transitions of C1Σ+ ← X1Σ+ (0, 0) (as indicated in Fig. 5), and was also used by Stark et al.25 to determine the oscillator strength of this band.
 |
| | Fig. 4 High resolution absorption spectrum of the B1Σ+ → X1Σ+ (0, 0) Hopfield–Birge band system in the less-abundant 12C17O isotopologue recorded with the VUV-FTS setup at the SOLEIL synchrotron at an instrumental resolution of 0.20 cm−1. The estimated absolute calibration 1σ uncertainty was 0.005 cm−1. The 1σ uncertainty due to fitting errors of measured wavenumbers (exclusive of calibration uncertainty) was estimated from the least-squares optimisation algorithm and varies between 0.002 and 0.1 cm−1 for the strongest and weakest lines, respectively. The ratio of the gases used in the experiment was 12C17O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O 12C16O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C18O = 1 12C18O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.85 0.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.20. 0.20. | |
 |
| | Fig. 5 High resolution absorption spectra of the C1Σ+ → X1Σ+ (0, 0) Hopfield–Birge band system in the less-abundant 12C17O isotopologue recorded with the VUV-FTS setup at the SOLEIL synchrotron at an instrumental resolution of 0.20 cm−1. We used two scans at different column density for the lower (red spectrum) and higher (green spectrum) J to get the final list of transition wavenumbers. The estimated absolute calibration 1σ uncertainty was 0.005 cm−1. The 1σ uncertainty due to fitting errors of measured wavenumbers (exclusive of calibration uncertainty) was estimated from the least-squares optimisation algorithm and varies between 0.002 and 0.1 cm−1 for the strongest and weakest lines, respectively. The ratio of the gases used in the experiment was 12C17O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O 12C16O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C18O = 1 12C18O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.85 0.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.20. 0.20. | |
There is significant admixture of the 12C16O and 12C18O isotopologues in our gas sample25 and lines from these isotopologues frequently overlap the transitions of 12C17O. Despite this, we were able to fit wavenumbers with an accuracy better than 0.01 cm−1 for many 12C17O transitions by modelling the sinc-function line broadening inherent to Fourier-transform spectrometry, as previously implemented and shown with multiple independent codes.25,71–73 A brief summary of the steps involved in our spectral modelling is as follows:
• An initial wavenumber and integrated cross section was assigned to every observed rotational transition in a recorded B ← X or C ← X band, and assuming a column density for each isotopologue component of our spectrum.
• A Gaussian wavelength-dependent cross section for each simulated line was calculated from these values, assuming a Doppler width characteristic of the known experimental temperature (FWHM of 0.20 cm−1 for the case of 12C17O and 295 K). The summation of all lines provided a total cross section.
• The total cross section was converted into a transmission spectrum by the Beer–Lambert law, then convolved with a sinc function to represent the known instrumental broadening of the FTS, and multiplied by the slightly wavelength dependent synchrotron beam intensity, giving a completely simulated absorption spectrum.
• The simulated spectrum was compared with the raw experimental data and model line wavenumbers and cross sections, and isotopologue column densities, were adjusted to minimise the model-to-experiment difference in a pointwise least-squares sense.
The wavenumbers of 12C16O and 12C18O B ← X (0, 0) and C ← X (0, 0) transitions were determined by the analysis of separate spectra recorded with pure samples of those gases. Additionally, the oscillator strengths of the two bands were shown to be independent of isotopic composition and have the rotational dependence of unperturbed 1Σ+ ← 1Σ+ transitions.25 Thus, we could fix all details of the individual 12C16O and 12C18O lines in our mixed-gas spectrum while fitting the 12C17O lines. The final assessment of column densities allowed us to estimate the admixture of isotopologues in our mixed sample to be 12C17O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O
12C16O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C18O = 1
12C18O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.85
0.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.20. The residual error, after optimally fitting B ← X (0, 0), is nearly consistent with the statistical noise.
0.20. The residual error, after optimally fitting B ← X (0, 0), is nearly consistent with the statistical noise.
Absolute wavenumber calibrations of our spectra were made by comparing lines appearing from contaminant species with their literature wavenumbers: H2 (ref. 74), Xe (ref. 75 and 76), H (ref. 77), and O (ref. 77). The estimated absolute calibration 1σ uncertainty was 0.005 cm−1. The 1σ uncertainty due to fitting errors of measured wavenumbers (exclusive of calibration uncertainty) was estimated from the least-squares optimisation algorithm and varies between 0.002 and 0.1 cm−1 for the strongest and weakest lines, respectively. A listing of 122 measured transition wavenumbers is given in Table 4.
Table 4 Transition frequencies (in cm−1) of the 12C17O B1Σ+ ← X1Σ+, and C1Σ+ ← X1Σ+ absorption bands from the VUV-FTS measurementsa
|
J′′ |
B1Σ+ ← X1Σ+ (0, 0) |
C1Σ+ ← X1Σ+ (0, 0) |
| P(J′′) |
R(J′′) |
P(J′′) |
R(J′′) |
|
The estimated absolute calibration 1σ uncertainty was 0.005 cm−1. Lines marked with ‘w’ were weak, and with ‘b’ were blended in the spectra. Absolute accuracy of the line frequency measurements varies between 0.002 and 0.1 cm−1 for the strongest and weakest lines, respectively.
|
| 0 |
|
86920.218bw |
|
91922.750bw |
| 1 |
86912.686bw |
86924.067bw |
91915.194bw |
91926.567bw |
| 2 |
86908.974b |
86927.963b |
91911.507b |
91930.435b |
| 3 |
86905.328b |
86931.904b |
91907.829 |
91934.341b |
| 4 |
86901.729b |
86935.904 |
91904.201 |
91938.297b |
| 5 |
86898.177b |
86939.949 |
91900.614 |
91942.290b |
| 6 |
86894.685 |
86944.041 |
91897.078 |
91946.322b |
| 7 |
86891.238 |
86948.186 |
91893.580 |
91950.395 |
| 8 |
86887.842 |
86952.377 |
91890.124 |
91954.508 |
| 9 |
86884.500 |
86956.615 |
91886.709 |
91958.664 |
| 10 |
86881.206 |
86960.907 |
91883.337 |
91962.856 |
| 11 |
86877.962 |
86965.233 |
91880.012 |
91967.087 |
| 12 |
86874.775 |
86969.616 |
91876.725 |
91971.365 |
| 13 |
86871.626 |
86974.045 |
91873.481 |
91975.675 |
| 14 |
86868.537 |
86978.519 |
91870.286 |
91980.024 |
| 15 |
86865.497 |
86983.035 |
91867.128 |
91984.412 |
| 16 |
86862.507 |
86987.601 |
91864.012 |
91988.841 |
| 17 |
86859.563 |
86992.220 |
91860.940 |
91993.310 |
| 18 |
86856.674 |
86996.888 |
91857.913 |
91997.811 |
| 19 |
86853.842 |
87001.572 |
91854.931 |
92002.351 |
| 20 |
86851.065 |
87006.309 |
91851.987 |
92006.928 |
| 21 |
86848.308 |
87011.127 |
91849.087 |
92011.547 |
| 22 |
86845.611 |
87015.940 |
91846.230 |
92016.204 |
| 23 |
86843.001 |
87020.864w |
91843.421 |
92020.903 |
| 24 |
86840.392w |
87025.729w |
91840.656 |
92025.634 |
| 25 |
86837.900w |
87030.662w |
91837.939 |
92030.404 |
| 26 |
86835.356w |
87035.627w |
91835.262 |
92035.207 |
| 27 |
86832.887w |
|
91832.630 |
92040.062 |
| 28 |
86830.458w |
|
91830.039w |
92044.939bw |
| 29 |
|
|
91827.507w |
92049.860bw |
| 30 |
|
|
91825.005w |
92054.804bw |
| 31 |
|
|
91822.556w |
92059.793bw |
| 32 |
|
|
91820.138w |
92064.829bw |
| 33 |
|
|
91817.774w |
|
| 34 |
|
|
91815.466w |
|
3. Results
3.1. Level energies
Rovibronic term values of the B1Σ+ (υ = 0) and C1Σ+ (υ = 0) Rydberg states, with regard to the lowest X1Σ+ (υ = 0) rovibrational level of the 12C17O ground state, were calculated by using the B ← X (0, 0) and C ← X (0, 0) transition frequencies obtained from a VUV-FTS experiment and using the ground state molecular parameters by Coxon et al.,80 given for the 12C17O isotopologue. These data were combined with the B → A (this work, and ref. 26 and 27) as well as C → A28 transition wavenumbers to give term values of the A1Π (υ = 1, 2, 3, 4, and 5) levels as high as Jmax = 27–30. They were calculated as differences of values of the B1Σ+ (υ = 0), C1Σ+ (υ = 0) terms and B → A (0 − υ′′), C → A (0 − υ′′) transition frequencies. A similar procedure was adopted to determine terms of the D, I, e, a′, and d perturbers in 12C17O using the B1Σ+ (υ = 0) and C1Σ+ (υ = 0) level energies and (B1Σ+, C1Σ+) → (d3Δi, e3Σ−, a′3Σ+, I1Σ−, and D1Δ) extra-lines (listed in Table 2). The A1Π (υ) high-J level energies were calculated by means of the deperturbed Tυ rotationless energies of the A1Π (υ) state from Section 3.2 and relative terms of A1Π (υ) calculated on the basis of B–A26,27 and C–A28 bands by means of the linear least-squares method in the version given by Curl and Dane78 and Watson.79 The final values of the A1Π energy levels are obtained using the weighted average method and are collected in Tables 5 and 6.
Table 5 Rovibronic term values of the A1Π (υ = 1, 2, 3, 4, and 5), C1Σ+ (υ = 0), and B1Σ+ (υ = 0) levels in 12C17Oa,b
|
J
|
C1Σ+ (υ = 0) |
B1Σ+ (υ = 0) |
A1Π (υ = 1) |
A1Π (υ = 2) |
A1Π (υ = 3) |
A1Π (υ = 4) |
A1Π (υ = 5) |
| e |
e |
e |
f |
e |
f |
e |
f |
e |
f |
e |
f |
|
All values in cm−1.
Level energies were calculated relative to the lowest υ = 0 rovibrational level of the X1Σ+ ground state of 12C17O from the combined data sets of two experiments: the VUV-FTS study for the C1Σ+ (υ = 0) and B1Σ+ (υ = 0) levels, as well as VIS high-accuracy dispersive optical spectroscopy measurements for the A1Π (υ = 1, 2, 3, 4, and 5) levels. The final values of the terms were obtained using the weighted average method. See Section 3.1 for details.
Level energies obtained by means of the deperturbed Tυ rotation-less energies of A1Π (υ) state from Table 10 and the relative terms of the A1Π (υ) calculated on the basis of B–A26,27 and C–A28 bands by means of the least-squares method in the version given by Curl and Dane78 and Watson.79 The final values of the A1Π level energies are obtained using the weighted average method.
|
| 0 |
91918.942 |
86916.434 |
|
|
|
|
|
|
|
|
|
|
| 1 |
91922.750 |
86920.218 |
66218.823 |
66218.768 |
67646.816 |
67646.811 |
69042.885 |
69042.875 |
70404.726 |
70404.724 |
71732.502 |
71732.487 |
| 2 |
91930.315 |
86927.815 |
66224.934 |
66224.893 |
67652.915 |
67652.884 |
69048.887 |
69048.872 |
70410.616 |
70410.619 |
71738.304 |
71738.299 |
| 3 |
91941.679 |
86939.206 |
66234.132 |
66234.094 |
67662.016 |
67662.007 |
69057.847 |
69057.840 |
70419.456 |
70419.461 |
71747.005 |
71747.010 |
| 4 |
91956.828 |
86954.390 |
66246.395 |
66246.371 |
67674.177 |
67674.143 |
69069.812 |
69069.808 |
70431.250 |
70431.246 |
71758.624 |
71758.618 |
| 5 |
91975.774 |
86973.381 |
66261.742 |
66261.739 |
67689.355 |
67689.329 |
69084.774 |
69084.776 |
70445.991 |
70445.990 |
71773.132 |
71773.140 |
| 6 |
91998.503 |
86996.162 |
66280.161 |
66280.154 |
67707.592 |
67707.529 |
69102.724 |
69102.720 |
70463.666 |
70463.672 |
71790.546 |
71790.549 |
| 7 |
92025.018 |
87022.737 |
66301.660 |
66301.665 |
67728.816 |
67728.648 |
69123.664 |
69123.663 |
70484.296 |
70484.296 |
71810.861 |
71810.861 |
| 8 |
92055.319 |
87053.110 |
66326.238 |
66326.230 |
67753.123 |
67753.255 |
69147.591 |
69147.591 |
70507.864 |
70507.873 |
71834.067 |
71834.077 |
| 9 |
92089.403 |
87087.272 |
66353.897 |
66353.900 |
67780.432 |
67780.513 |
69174.504 |
69174.504 |
70534.378 |
70534.388 |
71860.180 |
71860.188 |
| 10 |
92127.273 |
87125.224 |
66384.639 |
66384.634 |
67810.788 |
67810.839 |
69204.407 |
69204.413 |
70563.834 |
70563.836 |
71889.180 |
71889.189 |
| 11 |
92168.921 |
87166.972 |
66418.438 |
66418.440 |
67844.167 |
67844.209 |
69237.299 |
69237.296 |
70596.226 |
70596.236 |
71921.079 |
71921.093 |
| 12 |
92214.350 |
87212.495 |
66455.330 |
66455.323 |
67880.575 |
67880.612 |
69273.175 |
69273.156 |
70631.561 |
70631.558 |
71955.868 |
71955.873 |
| 13 |
92263.561 |
87261.813 |
66495.280 |
66495.267 |
67919.992 |
67920.042 |
69312.017 |
69312.016 |
70669.816 |
70669.830 |
71993.544 |
71993.554 |
| 14 |
92316.544 |
87314.914 |
66538.300 |
66538.305 |
67962.454 |
67962.499 |
69353.848 |
69353.841 |
70711.020 |
70711.034 |
72034.102 |
72034.115 |
| 15 |
92373.300 |
87371.795 |
66584.391 |
66584.381 |
68007.923 |
68007.968 |
69398.653 |
69398.649 |
70755.147 |
70755.161 |
72077.551 |
72077.564 |
| 16 |
92433.829 |
87432.452 |
66633.546 |
66633.522 |
68056.394 |
68056.450 |
69446.422 |
69446.423 |
70802.202 |
70802.208 |
72123.885 |
72123.893 |
| 17 |
92498.128 |
87496.889 |
66685.753 |
66685.652 |
68107.913 |
68107.953 |
69497.171 |
69497.168 |
70852.185 |
70852.191 |
72173.094 |
72173.085 |
| 18 |
92566.198 |
87565.108 |
66740.992 |
66740.417 |
68162.407 |
68162.456 |
69550.873 |
69550.857 |
70905.086 |
70905.097 |
72225.167 |
72225.182 |
| 19 |
92638.026 |
87637.104 |
66799.255 |
66799.803 |
68219.900 |
68219.968 |
69607.503 |
69607.484 |
70960.910 |
70960.927 |
72280.107 |
72280.144 |
| 20 |
92713.617 |
87712.838 |
66860.352 |
66860.993 |
68280.389 |
68280.469 |
69667.176 |
69667.179 |
71019.655 |
71019.647 |
72337.941 |
72337.948 |
| 21 |
92792.967 |
87792.348 |
66927.043 |
66925.357 |
68343.852 |
68343.958 |
69729.750 |
69729.751 |
71081.294 |
71081.283 |
72398.616 |
72398.616 |
| 22 |
92876.077 |
87875.657 |
66993.251 |
66992.786 |
68410.260 |
68410.451 |
69795.297 |
69795.242 |
71145.844 |
71145.864 |
72462.156 |
72462.184 |
| 23 |
92962.941 |
87962.678 |
67063.585 |
67063.159 |
68479.559 |
68479.899 |
69863.749 |
69863.593 |
71213.330 |
71213.188 |
72528.577 |
72528.554 |
| 24 |
93053.559 |
88053.521 |
67137.064 |
67138.630 |
68551.373 |
68552.304 |
69935.138 |
69934.082 |
71283.672 |
71283.749 |
72597.782 |
72597.843 |
| 25 |
93147.920 |
88148.014 |
67213.596 |
67213.717 |
|
68627.604 |
70009.336 |
70010.255 |
71356.952 |
71356.958 |
72669.880 |
72669.840 |
| 26 |
93246.025 |
88246.282 |
67292.693 |
67292.699 |
68707.986 |
68705.698 |
70086.103 |
70087.264 |
71433.055 |
71433.070 |
72744.723 |
72744.649 |
| 27 |
93347.865 |
88348.285 |
67376.318 |
67376.227 |
68788.846 |
68786.116 |
70169.374 |
70167.337 |
71512.070 |
71512.063 |
72822.312c |
|
| 28 |
93453.457 |
|
67461.808 |
67461.748c |
68872.906 |
68866.525 |
70251.109 |
70250.435c |
71593.943 |
71593.998c |
72903.043c |
72901.288c |
| 29 |
93562.765 |
|
67550.486 |
67550.365c |
68960.079c |
68963.120 |
70336.996c |
70336.169c |
71678.752c |
71678.788c |
|
72986.858c |
| 30 |
93675.810 |
|
67642.094c |
67642.030c |
69050.105c |
69052.123 |
70425.920c |
70426.671c |
71766.396c |
71766.434c |
|
73072.667c |
| 31 |
93792.564 |
|
67736.801c |
67736.683c |
69142.454c |
69144.909c |
70517.765c |
70517.946c |
71856.892c |
71856.936c |
|
73163.250c |
| 32 |
93913.047 |
|
67834.509c |
67834.315c |
69243.696c |
69240.923c |
70612.627c |
70612.665c |
71950.232c |
71950.298c |
|
73254.031c |
| 33 |
94037.356 |
|
67935.175c |
67934.877c |
69340.595c |
69339.953c |
70709.931c |
70709.934c |
72046.262c |
72046.497c |
|
|
| 34 |
|
|
68038.858c |
68038.274c |
|
|
70811.007c |
70810.986c |
72147.166c |
72145.531c |
|
|
| 35 |
|
|
|
68148.228c |
|
|
70914.511c |
70914.501c |
|
|
|
|
| |
|
|
|
|
|
|
|
71020.875c |
|
|
|
|
Table 6 Rovibronic term values of the d3Δi (υ = 11), e3Σ− (υ = 4), a′3Σ+ (υ = 10, 13), I1Σ− (υ = 3, 6), and D1Δ (υ = 1) levels in 12C17Oa
| State |
υ
|
J
|
Energy |
Triplet component |
Electronic symmetry |
|
All values in cm−1. Level energies were calculated relative to the lowest υ = 0 rovibrational level of the X1Σ+ ground state of 12C17O from the combined data sets of two experiments: the VUV-FTS study for the C1Σ+ (υ = 0) and B1Σ+ (υ = 0) levels, as well as VIS high-accuracy dispersive optical spectroscopy measurements for the e3Σ− (υ = 4), a′3Σ+ (υ = 10, 13), I1Σ− (υ = 3, 6), and D1Δ (υ = 1) levels. The final values of the terms were obtained using the weighted average method.
|
| e3Σ− |
4 |
25 |
68622.59 |
F1 |
e |
| 4 |
26 |
68684.69 |
F1 |
e |
| 4 |
25 |
68687.47 |
F2 |
f |
| a′3Σ+ |
10 |
20 |
66875.28 |
F2 |
e |
| 10 |
22 |
66923.16 |
F1 |
f |
| 10 |
22 |
66971.69 |
F2 |
e |
| 13 |
24 |
69942.13 |
F1 |
f |
| 13 |
24 |
70047.62 |
F3 |
f |
| 14 |
3 |
70296.10 |
F2 |
e |
| I1Σ− |
3 |
7 |
67730.78 |
|
f |
| 6 |
24 |
71269.82 |
|
f |
| D1Δ |
1 |
26 |
67298.11 |
|
e |
| 1 |
27 |
67361.47 |
|
f |
In order to display a visual presentation of perturbations occurring in the 12C17O A1Π (υ = 1–5) rovibrational levels, we determined reduced term values T(J) − BAJ(J + 1) + DAJ2(J + 1)2 of the A1Π state with the hypothetical unperturbed and crossing perturber levels, where BA and DA refer to deperturbed rotational constants of the corresponding A1Π level. The reduced term values were calculated in relation to the lowest υ = 0 rovibrational level of the 12C17O X1Σ+ ground state by means of the term values given in Tables 5 and 6. Those among the reduced terms which we were not able to determine from the experimental data, were calculated on the basis of isotopically recalculated equilibrium molecular constants by Field30 for d3Δi, e3Σ−, a′3Σ+, and I1Σ− states and by Kittrell et al.81 for D1Δ state. The Te values were taken from ref. 81–83, and the G(υ = 0) value for the X1Σ+ state in 12C17O, 1068.0310 cm−1, from Coxon et al.80 The results are presented in Fig. 6. Identification of perturbers for both e and f Λ-doubling components of the A1Π (υ = 3, 4, and 5) levels are summarized in Table 7.
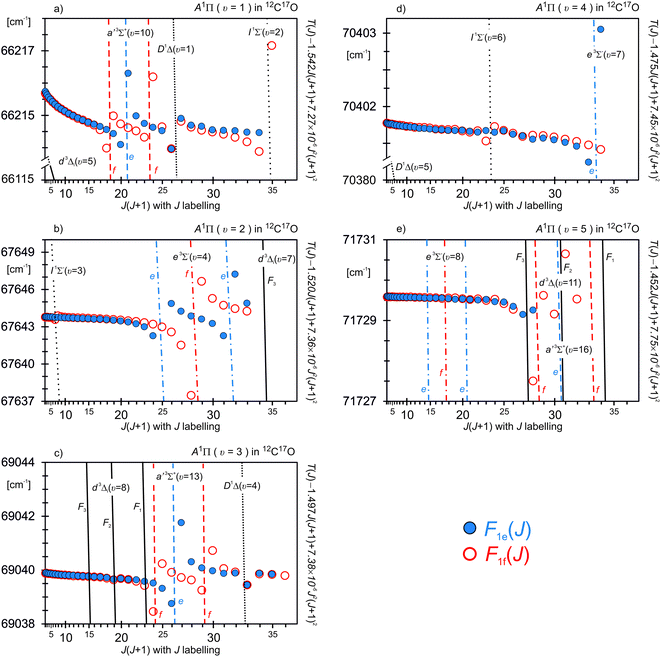 |
| | Fig. 6 The reduced T(J) − BAJ(J + 1) + DAJ2(J + 1)2 term values for the 12C17O A1Π (υ = 1–5) levels and for the hypothetical unperturbed crossing rovibronic levels of the perturbers. Filled and open circles indicate e and f electronic symmetry of the A1Π state, respectively. The reduced level energies (in cm−1) were calculated in relation to the lowest υ = 0 rovibrational level of the X1Σ+ ground state by means of terms calculated in this work (see Tables 5 and 6). Some reduced terms were calculated on the basis of isotopically recalculated equilibrium molecular constants given by Field30 for d3Δi, e3Σ−, a′3Σ+, and I1Σ− states and by Kittrell et al.81 for D1Δ state. The Te values were taken from ref. 81–83, and the G(υ = 0) value for the X1Σ+ state in 12C17O, 1068.0310 cm−1, from Coxon et al.80BA and DA symbols refer to deperturbed rotational constants of the respective A1Π rovibronic level, determined in this work (see Table 10). Note that different reduced-energy scales in cm−1 are used for different vibrational levels of A1Π. | |
Table 7 Observed and predicted perturbations in the A1Π, υ = 3, 4, and 5 rovibrational levels of the 12C17O isotopologuea
| Perturbed state |
Perturbing state |
J value for the maximum of perturbation in Λ-doubling components |
| Vibrational level |
Triplet component |
f |
e |
| Observed |
Calculated |
Observed |
Calculated |
|
The values in bold correspond to perturbations observed for the first time in 12C17O.
Theoretically predicted interaction of energetically remote states (for J < 0 or J > Jmax) without any observed crossing points with the A1Π state but the deperturbation fit shows that they have a noticeable influence on the A1Π (υ = 3, 4, or 5) levels (see Table 10).
See Table 10.
Perturbation difficult to identify on the basis of observations only (e.g.Fig. 6) due to much stronger interaction that exists in this region due to the a′3Σ+ (υ = 13) state. Its significance can be evaluated only on the basis of results of deperturbation fit provided in Table 10.
Perturbation difficult to identify on the basis of observations only (e.g.Fig. 6) due to stronger interaction that exists in this region deriving from the F1 term of the a′3Σ+ (υ = 16) state. Its significance can be evaluated only on the basis of results of deperturbation fit provided in Table 10.
Perturbation difficult to identify on the basis of observations only (e.g.Fig. 6) because of uncharacteristic behaviour of the rovibrational e-parity terms at J = 26–28 due to overlapping interaction with distant a substantially interaction with the F2 term of the a′3Σ+ (υ = 16) state.
|
| A1Π (υ = 3) |
e3Σ− (υ = 5) |
F(1) |
|
|
b
|
<1 |
| F(2) |
b
|
<1 |
|
|
| F(3) |
|
|
b
|
<1 |
| d3Δi (υ = 8) |
F(3) |
Negligibly smallc |
15–16 |
Negligibly smallc |
15–16 |
| F(2) |
19–20 (very weak)c |
19–20 |
19–20 (very weak)c |
19–20 |
| F(1) |
d
|
23–24 |
d
|
23–24 |
| a′3Σ+ (υ = 13) |
F(1) |
24–25 |
23–24 |
|
|
| F(2) |
|
|
26–27
|
26–27 |
| F(3) |
29–30 |
29–30 |
|
|
| D1Δ (υ = 4) |
|
33 (weak)c |
33 |
33 (weak)c |
33 |
| I1Σ− (υ = 5) |
|
b
|
40–41 |
|
|
| A1Π (υ = 4) |
a′3Σ+ (υ = 14) |
F(1) |
b
|
<1 |
|
|
| F(2) |
|
|
<1
|
<1 |
| F(3) |
<1
|
<1 |
|
|
| D1Δ (υ = 5) |
|
<1
|
<1 |
<1
|
<1 |
| I1Σ− (υ = 6) |
|
23–24
|
23 |
|
|
| e3Σ− (υ = 7) |
F(1) |
|
|
33–34
|
34 |
| F(2) |
b
|
37 |
|
|
| F(3) |
|
|
b
|
40 |
| a′3Σ+ (υ = 15) |
F(1) |
b
|
40–41 |
|
|
| F(2) |
|
|
b
|
43–44 |
| F(3) |
b
|
46–47 |
|
|
| d3Δi (υ = 10) |
F(3) |
b
|
40 |
b
|
40 |
| F(2) |
b
|
44 |
b
|
44 |
| F(1) |
b
|
48 |
b
|
48 |
| A1Π (υ = 5) |
e3Σ− (υ = 8) |
F(1) |
|
|
14 (very weak)c |
14 |
| F(2) |
17 (very weak)c |
17 |
|
|
| F(3) |
|
|
20 (very weak)c |
20 |
| d3Δi (υ = 11) |
F(3) |
e
|
26–27 |
f
|
26–27 |
| F(2) |
e
|
30–31 |
b
|
30–31 |
| F(1) |
b
|
34–35 |
b
|
34–35 |
| a′3Σ+ (υ = 16) |
F(1) |
28–29
|
27–28 |
|
|
| F(2) |
|
|
30–31
|
30–31 |
| F(3) |
b
|
33–34 |
|
|
| D1Δ (υ = 7) |
|
b
|
37 |
b
|
37 |
3.2. Deperturbation analysis of the A1Π state in 12C17O
In total, 982 transitions from 12 B–A, C–A, B–X, and C–X bands and their extra-lines of 12C17O were used in the global fitting procedure. This results in 72 molecular parameters fitted for this minor CO species. This analysis is performed, in analogy to deperturbation analyses of the main 12C16O isotopologue,44,51 using the Pgopher software.67 Applying this program we simulated each member of the B(υ′ = 0, 1) − A(υ′′) and C(υ′ = 0) − A(υ′′) progressions independently with a parameterised model of the A(υ) levels, perturber levels, and their interactions. The computed level positions, line frequencies, and intensities are the result of a matrix diagonalization including all interacting levels. The assignment of perturber levels, the selection of which parameters and interactions could be discriminated from our spectra, and the values of these parameters were iteratively optimised. The Pgopher program67 uses the effective Hamiltonian with matrix elements similar to Field,30 Bergeman et al.,84 and Le Floch et al.31 The model is presented in Table 8. The non-diagonal elements describe the interaction of the A1Π state with its perturbers, that is the d3Δi, e3Σ−, a′3Σ+, I1Σ−, and D1Δ states. Interactions between the perturbing states were neglected. For the A1Π diagonal element the ‘+’ and ‘−‘ signs relating to Λ-doubling refer to the e- and f-symmetry states, respectively. Tυ denotes the rotation-less energies calculated relative to the lowest rovibrational level of the X1Σ+ ground state, ηi is the spin–orbit interaction parameter, ξi is the L-uncoupling interaction parameter.
Table 8 Effective Hamiltonian and matrix elements for perturbation analyses of the A1Π (υ = 1, 2, 3, 4, and 5) rovibronic levels and their perturbers in 12C17Oa,b,c
| |
A1Π |
I1Σ− |
D1Δ |
e3Σ− |
a′3Σ+ |
d3Δi |
|
The model is consistent with that of Pgopher software.67
The matrix is symmetric, therefore, the lower left non-diagonal elements, which are not shown in the Hamiltonian, are equivalent to those of the corresponding upper right elements. The matrix elements set to zero are results of an approximation consisting in neglecting the mutual interaction between the perturbing states. For the A1Π diagonal element the ‘+’ and ‘−’ signs relating to Λ-doubling refer to the e- and f-symmetry states, respectively.
T
υ
– denotes the rotation-less energies calculated relative to the lowest rovibrational level of the X1Σ+ ground state, ηi – spin–orbit interaction parameter, ξi – L-uncoupling interaction parameter. The rest of the parameters used are defined in the open literature.68,86,87
|
| A1Π |
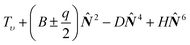
|
ξ
i(Iυ) × (![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) + +![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) − + − + ![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) − −![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) +) +) |
ξ
i(Dυ) × (![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) + +![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) − + − + ![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) − −![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) +) +) |
η
i(eυ)![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) ·Ŝ ·Ŝ |
η
i(a′υ)![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) ·Ŝ ·Ŝ |
η
i(dυ)![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) ·Ŝ ·Ŝ |
| I1Σ− |
|
T
υ
+ B![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 2 − D 2 − D![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 4 + H 4 + H![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 6 6 |
0 |
0 |
0 |
0 |
| D1Δ |
|
|
T
υ
+ B![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 2 − D 2 − D![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 4 + H 4 + H![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 6 6 |
0 |
0 |
0 |
| e3Σ− |
|
|
|

|
0 |
0 |
| a′3Σ+ |
|
|
|
|

|
|
| d3Δi |
|
|
|
|
|

|
The D1Δ and d3Δ states have nearly degenerate e and f Λ-doublet components. The e3Σ− state has two fine structure levels of e type and one f type, while the a′3Σ+ state has two fine structure levels of f type and one e type. By contrast, the I1Σ− state has only f levels. The interactions between the A1Π state and the e3Σ−, a′3Σ+, and d3Δ triplet states are caused by spin–orbit coupling, represented by J-independent matrix elements. Interactions of A1Π with the I1Σ− and D1Δ singlet states result from L-uncoupling and, therefore, produce heterogeneous interactions with J-dependent matrix elements.32
It was necessary to adopt some isotopically recalculated molecular constants, using Dunham's relationship within the Born–Oppenheimer approximation,85 of 12C16O d3Δi, e3Σ−, a′3Σ+, I1Σ−, and D1Δ states from ref. 30 and 81, because there are insufficient term-value data for these levels in 12C17O to determine these independently. These values were held fixed during the calculations. We only fitted molecular constants to those perturber states for which a sufficient number of transitions were observed in the present experiments. All possible vibrational levels of the perturbers which have a non-negligible influence on the A1Π, υ = 1, 2, 3, 4, and 5 levels were included in the calculation. Some of them do not have crossings with the A1Π state but still result in recognisable A-state energy level shifts.
The frequencies of strong and isolated lines were assigned relative weights of 1.0 during the fitting. However, the frequencies of weak and/or blended lines have lower accuracy, so they were individually weighted between 0.5 and 0.1, according to the degree of their weakening and/or overlap.
Initial fits were made by varying the B, D, H rotational constants and the q Λ-doubling constant of the A1Π (υ = 1–5) levels. This means that all parity-dependent interactions were included explicitly in the interactions contained in our deperturbation. Any additional Λ-doubling from remote perturbers was aliased by the interactions included in our perturbation. During the deperturbation, the rotational B and D parameters of the X1Σ+ (υ = 0) ground state were fixed to the values given by Coxon80 for 12C17O.
The unweighted obs-calc residuals of the fitting method are dominated by the uncertainties of the very weak and heavily perturbed lines that belong to the weakest B–A (1, 1) and (1, 5) bands. The weighted contribution to the root-mean-square (rms) residual value of high-accuracy dispersive optical spectroscopy and VUV-FTS data is 0.006 cm−1. This shows that the fitting model acceptably reproduces such a comprehensive experimental data set.
In a few cases, fitting of the interaction parameters was statistically unjustified because there was an insufficient quantity of experimental transitions in the vicinity of the avoided crossings of the perturbing states or because of the interaction of energetically remote states (for J < 0 or J > Jmax) without any observed crossing points with the A1Π state in 12C17O. In such cases we estimated the semi-empirical interaction parameters making use of the quality suggested in ref. 31, 41 and 88, which shows that for perturbation between vibronic levels of a given pair of electronic states, the perturbation matrix element (α, β) is the product of a vibrational factor and a constant electronic perturbation parameter (a, b). The effective perturbation parameters α and β, in the e/f basis set, are defined as follows:
| |  | (1) |
| |  | (2) |
| |  | (3) |
| | 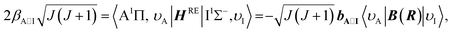 | (4) |
| |  | (5) |
where
HSO and
HRE are the spin–orbit and rotation-electronic operators, respectively, and
a = 〈2π|
al+|2
σ〉,
b = 〈2π|
l+|2
σ〉. It is then possible to calculate initial values of interaction parameters for any pair of levels whenever the relevant vibrational wavefunctions are known.
31 So, the missing perturbation parameters, which were fixed during the deperturbation calculation, were estimated on the basis of the isotopologue-independent purely electronic perturbation parameters
a and
b of Le Floch,
31 as well as 〈
υA|
υd,e,or a′〉 vibrational overlap integrals and the 〈
υA|
B(
R)|
υI or D〉 rotational operator integral in
12C
17O, according to
eqn (1)–(8). These parameters are presented in
Table 9. The vibrational integrals were calculated on the basis of
12C
17O RKRs of A, d, e, a′, I, and D states obtained from isotopically recalculated equilibrium constants of Field,
30 Field
et al.,
32,87 Le Floch
et al.,
31 and Kittrell
et al.81 and using the computer programs ‘LEVEL’ of Le Roy
89 as well as ‘FRACON’ of Jung
90 (later modified by Jakubek
91). Then, justification of the use of each of those estimated values in the fit was tested. Only those were used that led to noticeable improvements in the quality of the fit within the accuracy obtained.
Table 9 Perturbation parameters of the A1Π∼(d3Δi, e3Σ−, a′3Σ+, I1Σ−, and D1Δ) interactions, fixed in the 12C17O deperturbation analysis
| Interaction |
a
a (cm−1) |
〈υA|υpert〉b |
η
c (cm−1) |
|
The spin–orbit and rotation-electronic perturbation parameters a and b were taken from Le Floch et al.31 (Table 2).
The vibrational integrals were calculated on the basis of 12C17O RKRs of A, d, e, a′, I, and D states obtained from isotopically recalculated equilibrium constants of Field,30 Field et al.,32,87 Le Floch et al.,31 and Kittrell et al.81 and using the computer programs ‘LEVEL’ of Le Roy89 as well as ‘FRACON’ of Jung90 (later modified by Jakubek91). See Section 3.2 for details.
The perturbation parameters, fixed during the 12C17O deperturbation fits. They were calculated on the basis of eqn (1)–(8) using electronic perturbation parameters and vibrational integrals given in the current table.
|
| A1Π (υ = 3)∼d3Δ (υ = 8) |
95.3 |
−0.0026 |
0.15 |
| A1Π (υ = 4)∼d3Δ (υ = 10) |
95.3 |
−0.0295 |
1.72 |
| A1Π (υ = 1)∼e3Σ− (υ = 3) |
98.9 |
−0.0964 |
4.13 |
| A1Π (υ = 3)∼e3Σ− (υ = 5) |
98.9 |
−0.2061 |
8.83 |
| A1Π (υ = 5)∼e3Σ− (υ = 8) |
98.9 |
0.0001 |
−0.58 × 10−2 |
| A1Π (υ = 2)∼a′3Σ+ (υ = 11) |
83.4 |
−0.1937 |
−6.99 |
| A1Π (υ = 2)∼a′3Σ+ (υ = 12) |
83.4 |
0.1565 |
5.65 |
| A1Π (υ = 4)∼a′3Σ+ (υ = 15) |
83.4 |
−0.1931 |
−6.97 |
| Interaction |
b
a (unitless) |
〈υA|B|υpert〉b (cm−1) |
ξ
c (cm−1) |
| A1Π (υ = 3)∼I1Σ− (υ = 5) |
0.227 |
−0.2023 |
3.25 × 10−2 |
| A1Π (υ = 5)∼I1Σ− (υ = 8) |
0.227 |
−0.1230 |
1.98 × 10−2 |
| A1Π (υ = 2)∼D1Δ (υ = 2) |
0.11 |
0.0381 |
4.19 × 10−3 |
| A1Π (υ = 4)∼D1Δ (υ = 5) |
0.11 |
−0.3523 |
−3.88 × 10−2 |
| A1Π (υ = 5)∼D1Δ (υ = 7) |
0.11 |
0.3203 |
3.52 × 10−2 |
A careful examination of the correlation matrix shows satisfactorily low correlations between fitted model parameters. The final set of deperturbed molecular constants from the fits is presented mainly in Tables 10 and 11. The relationships between the η and α as well as ξ and β perturbation parameters result from their different definitions,30,67,94,95 which affect the interaction matrix elements, are as follows:
| |  | (6) |
| | 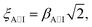 | (7) |
where subscript ‘i’ indicates A∼d, A∼e, as well as A∼a′ interactions.
Table 10 Deperturbed molecular constants (in cm−1) of the A1Π, υ = 1, 2, 3, 4, and 5 rovibronic levels and their perturbers in 12C17Oa
| Constant/level |
A1Π (υ = 1) |
A1Π (υ = 2) |
A1Π (υ = 3) |
A1Π (υ = 4) |
A1Π (υ = 5) |
The parameters without indicating uncertainties are taken from the literature and held fixed during the fitting. Tυ denotes the energy level separations between the ground state X1Σ+ (υ = 0, J = 0) and excited state (υ = 0, J = 0) of 12C17O, ηi – spin–orbit interaction parameter, and ξi – L-uncoupling interaction parameter.
Isotopically recalculated from Le Floch.42
Calculated on the basis of isotopically recalculated vibrational equilibrium constants of d3Δi by Field,30 X1Σ+ by Le Floch92 and Te of d3Δi from Huber and Herzberg.83
Isotopically recalculated from Field.30
Isotopically recalculated from spin–spin C constants of Field30 taking into account the equation  (see Table 3.4 in ref. 87).
Calculated on the basis of Field's data30 using the conversion 29979, 2458 MHz cm−1,92 isotopically recalculated to 12C17O.
Isotopically recalculated from Le Floch.31
Estimated on the basis of the isotopologue-independent purely electronic perturbation parameters a and b of Field32,41 and Le Floch,31 as well as 〈υA|υd,e or a′〉 and 〈υA|B|υI or D〉 in 12C17O from Table 9, according to the eqn (1)–(8). See Section 3.2 for details.
Calculated on the basis of isotopically recalculated vibrational equilibrium constants of a′3Σ+ by Field,30 X1Σ+ by Le Floch92 and Te of the perturber by Tilford et al.82
Calculated on the basis of isotopically recalculated vibrational equilibrium constants of I1Σ− by Field,30 X1Σ+ by Le Floch92 and Te of I1Σ− from Herzberg et al.93
Isotopically recalculated from Kittrell et al.81
Calculated on the basis of isotopically recalculated vibrational equilibrium constants of D1Δ by Kittrell et al.,81 X1Σ+ by Le Floch92 and Te of D1Δ by Kittrell et al.81 (see Table 3.4 in ref. 87).
Calculated on the basis of Field's data30 using the conversion 29979, 2458 MHz cm−1,92 isotopically recalculated to 12C17O.
Isotopically recalculated from Le Floch.31
Estimated on the basis of the isotopologue-independent purely electronic perturbation parameters a and b of Field32,41 and Le Floch,31 as well as 〈υA|υd,e or a′〉 and 〈υA|B|υI or D〉 in 12C17O from Table 9, according to the eqn (1)–(8). See Section 3.2 for details.
Calculated on the basis of isotopically recalculated vibrational equilibrium constants of a′3Σ+ by Field,30 X1Σ+ by Le Floch92 and Te of the perturber by Tilford et al.82
Calculated on the basis of isotopically recalculated vibrational equilibrium constants of I1Σ− by Field,30 X1Σ+ by Le Floch92 and Te of I1Σ− from Herzberg et al.93
Isotopically recalculated from Kittrell et al.81
Calculated on the basis of isotopically recalculated vibrational equilibrium constants of D1Δ by Kittrell et al.,81 X1Σ+ by Le Floch92 and Te of D1Δ by Kittrell et al.81
|
|
T
υ
|
66214.2529 (87) |
67643.9829 (31) |
69039.7043 (16) |
70401.6687 (63) |
71729.6882 (17) |
|
B
υ
|
1.541 758 (21) |
1.519 578 (11) |
1.497 130 4 (92) |
1.474 504 (15) |
1.451 844 (11) |
|
D
υ
× 106 |
7.275 (16) |
7.361 (11) |
7.383 (10) |
7.447 (13) |
7.754 (15) |
|
H
υ
× 1011 |
−1.26b |
−1.26b |
−1.26b |
−1.26b |
−1.26b |
| Constant/level |
d3Δi (υ = 5) |
d3Δi (υ = 7) |
d3Δi (υ = 8) |
d3Δi (υ = 10) |
d3Δi (υ = 11) |
|
T
υ
|
66117.62c |
68178.22c |
69180.76c |
71131.06c |
72079.01c |
|
B
υ
|
1.186 79d |
1.154 46d |
1.138 55d |
1.107 25d |
1.091 82d |
|
A
υ
|
−16.523d |
−16.830d |
−16.984d |
−17.291d |
−17.444d |
|
λ
υ
|
0.898e |
1.094e |
1.191e |
1.387e |
1.485e |
|
γ
υ
× 103 |
−8.13f |
−8.13f |
−8.13f |
−8.13f |
−8.13f |
|
D
υ
× 106 |
6.13d |
6.10d |
6.09d |
6.08d |
6.08d |
|
H
υ
× 1013 |
−7.41g |
−7.41g |
−7.41g |
−7.41g |
−7.41g |
|
A
Dυ
× 105 |
−4.94f |
−4.94f |
−4.94f |
−4.94f |
−4.94f |
|
η
|
−16.455 (54) |
10.21 (19) |
0.15h |
1.72h |
7.915 (44) |
| Constant/level |
e3Σ− (υ = 3) |
e3Σ− (υ = 4) |
e3Σ− (υ = 5) |
e3Σ− (υ = 7) |
e3Σ− (υ = 8) |
|
T
υ
|
66900.71i |
67924.973 (35) |
68930.84i |
70886.156 (13) |
71836.97i |
|
B
υ
|
1.191 69d |
1.175 145 (46) |
1.158 79d |
1.126 417d |
1.110 34d |
|
λ
υ
|
0.542e |
0.557 (11) |
0.576e |
0.611e |
0.628e |
|
D
υ
× 106 |
6.39d |
6.35d |
6.33d |
6.29d |
6.28d |
|
H
υ
× 1012 |
−1.85g |
−1.85g |
−1.85g |
−1.85g |
−1.85g |
|
η
|
4.13h |
12.981 (79) |
8.83h |
−6.792 (27) |
−0.0058h |
| Constant/level |
a′3Σ+ (υ = 10) |
a′3Σ+ (υ = 11) |
a′3Σ+ (υ = 13) |
a′3Σ+ (υ = 14) |
a′3Σ+ (υ = 16) |
|
T
υ
|
66398.5691 (51) |
67397.25i |
69339.963 (17) |
70284.08i |
72118.33i |
|
B
υ
|
1.137 90d |
1.122 35d |
1.091 481 (23) |
1.076 07d |
1.045 37d |
|
λ
υ
|
−1.131 4 (86) |
−1.126e |
−1.114 1 (75) |
−1.106e |
−1.092e |
|
γ
υ
× 103 |
−5.85 (34) |
−6.27f |
−6.19 (24) |
−6.27f |
−6.27f |
|
D
υ
× 106 |
5.95d |
5.94d |
5.93d |
5.93d |
5.92d |
|
H
υ
× 1013 |
−3.7g |
−3.7g |
−3.7g |
−3.7g |
−3.7g |
|
η
|
−4.918 (73) |
−6.99h |
7.091 (11) |
7.63 (15) |
−6.803 (31) |
| Constant/level |
|
a′3Σ+ (υ = 12) |
|
a′3Σ+ (υ = 15) |
|
|
T
υ
|
|
68377.68i |
|
71210.21i |
|
|
B
υ
|
|
1.106 87d |
|
1.060 72d |
|
|
λ
υ
|
|
−1.119e |
|
−1.099e |
|
|
γ
υ
× 103 |
|
−6.27f |
|
−6.27f |
|
|
D
υ
× 106 |
|
5.94d |
|
5.92d |
|
|
H
υ
× 1013 |
|
−3.7g |
|
−3.7g |
|
|
η
|
|
5.65h |
|
−6.97h |
|
| Constant/level |
I1Σ− (υ = 2) |
I1Σ− (υ = 3) |
I1Σ− (υ = 5) |
I1Σ− (υ = 6) |
I1Σ− (υ = 8) |
|
T
υ
|
66647.75j |
67664.68j |
69639.21j |
70596.1599 (73) |
72454.96j |
|
B
υ
|
1.195 01d |
1.177 87d |
1.143 67d |
1.126 67d |
1.092 91d |
|
D
υ
× 106 |
6.54g |
6.56g |
6.60g |
6.62g |
6.66g |
|
H
υ
× 1012 |
2.78g |
2.78g |
2.78g |
2.78g |
2.78g |
|
ξ × 102 |
−7.420 (15) |
−5.75 (10) |
3.25h |
−1.76 (11) |
1.98h |
| Constant/level |
D1Δ (υ = 1) |
D1Δ (υ = 2) |
D1Δ (υ = 4) |
D1Δ (υ = 5) |
D1Δ (υ = 7) |
|
T
υ
|
66458.5762 (48) |
67468.27l |
69429.99l |
70382.01l |
72228.37l |
|
B
υ
|
1.199 71k |
1.182 76k |
1.148 86k |
1.131 91k |
1.098 01k |
|
D
υ
× 106 |
6.69k |
6.65k |
6.62k |
6.60k |
6.56k |
|
H
υ
× 1013 |
−2.78g |
−2.78g |
−2.78g |
−2.78g |
−2.78g |
|
ξ × 102 |
−6.64 (23) |
0.42h |
−1.68 (23) |
−3.88h |
3.52h |
Table 11 Spin–orbit and rotation-electronic parameters obtained from deperturbation analysis of the A1Π, υ = 1–5 levels in 12C17Oa
| Interaction |
〈υA|υpert〉b |
η (cm−1) |
η/〈υA|υpert〉 (cm−1) |
a
c (cm−1) |
ā
d (cm−1) |
|
Uncertainties in parentheses correspond to one standard deviation.
The vibrational integrals were calculated on the basis of 12C17O RKRs of A, d, e, a′, I, and D states obtained from isotopically recalculated equilibrium constants of Field,30 Field et al.,32,87 Le Floch et al.,31 and Kittrell et al.81 and using the computer programs ‘LEVEL’ of Le Roy89 as well as ‘FRACON’ of Jung90 (later modified by Jakubek91).
The spin–orbit and rotation-electronic perturbation parameters a and b were calculated on the basis of eqn (1)–(8).
The weighted average values of the electronic perturbation parameters obtained in this work.
|
| A1Π (υ = 1)∼d3Δ (υ = 5) |
0.2803 |
−16.455 (54) |
−58.71 (19) |
95.87 (31) |
95.59 (27) |
| A1Π (υ = 2)∼d3Δ (υ = 7) |
−0.1763 |
10.21 (19) |
−57.9 (11) |
94.6 (18) |
|
| A1Π (υ = 5)∼d3Δ (υ = 11) |
−0.1362 |
7.915 (44) |
−58.12 (32) |
94.90 (53) |
|
| A1Π (υ = 2)∼e3Σ− (υ = 4) |
−0.2967 |
12.981 (79) |
−43.76 (27) |
101.05 (61) |
98.90 (33) |
| A1Π (υ = 4)∼e3Σ− (υ = 7) |
0.1600 |
−6.792 (27) |
−42.46 (17) |
98.05 (39) |
|
| A1Π (υ = 1)∼a′3Σ+ (υ = 10) |
−0.1371 |
−4.918 (73) |
35.87 (53) |
82.9 (12) |
83.62 (12) |
| A1Π (υ = 3)∼a′3Σ+ (υ = 13) |
0.1957 |
7.091 (11) |
36.226 (56) |
83.66 (13) |
|
| A1Π (υ = 4)∼a′3Σ+ (υ = 14) |
0.2098 |
7.63 (15) |
36.36 (72) |
84.0 (17) |
|
| A1Π (υ = 5)∼a′3Σ+ (υ = 16) |
−0.1883 |
−6.803 (31) |
36.12 (16) |
83.42 (38) |
|
| Interaction |
〈υA|B|υpert〉b (cm−1) |
ξ × 102 (cm−1) |
ξ/〈υA|B|υpert〉 (unitless) |
b
c (unitless) |
![[b with combining macron]](https://www.rsc.org/images/entities/b_i_char_0062_0304.gif) d (unitless)
d (unitless) |
| A1Π (υ = 1)∼I1Σ− (υ = 2) |
0.4618 |
−7.420 (15) |
−0.16067 (33) |
0.22722 (46) |
0.2274 (46) |
| A1Π (υ = 2)∼I1Σ− (υ = 3) |
0.3412 |
−5.75 (10) |
−0.1685 (31) |
0.2384 (43) |
|
| A1Π (υ = 4)∼I1Σ− (υ = 6) |
0.1065 |
−1.76 (11) |
−0.165 (10) |
0.234 (15) |
|
| A1Π (υ = 1)∼D1Δ (υ = 1) |
−0.5818 |
−6.64 (23) |
0.1142 (40) |
0.1142 (40) |
0.1103 (14) |
| A1Π (υ = 3)∼D1Δ (υ = 4) |
−0.1534 |
−1.68 (23) |
0.1098 (15) |
0.1098 (15) |
|
The spin–orbit and rotation-electronic parameters obtained from the 12C17O A1Π (υ = 1–5) deperturbation analysis are collected in Table 11. The isotopologue independent, electronic perturbation parameters a and b for the A1Π∼(d3Δi, e3Σ−, a′3Σ+, I1Σ−, and D1Δ) interactions are in very good agreement with the values given by Le Floch31 (see Table 9) Field,30 and Field et al.32,87
While performing the deperturbation calculations, we also obtained the rovibrational constants for the B1Σ+ (υ = 0 and 1) and C1Σ+ (υ = 0) Rydberg states in 12C17O. The results are given in Table 12. The constants for the B1Σ+ and C1Σ+ states are compared with analogous values derived in previous studies.26–28
Table 12 Molecular constants of the B1Σ+ (υ = 0, 1) and C1Σ+ (υ = 0) Rydberg states in 12C17Oa,b
| Level/constant |
B1Σ+ (υ = 0) |
B1Σ+ (υ = 1) |
C1Σ+ (υ = 0) |
|
All values in cm−1. Uncertainties in parentheses represent one standard deviation in units of the last quoted digit.
T
υ
denotes the energy level separations between a given excited state and the X1Σ+ (υ = 0, J = 0) ground state in 12C17O.
After Ubachs et al.22
After Hakalla et al.26
After Hakalla et al.27
After Hakalla.28
|
|
T
υ
|
86916.4256 (12) |
88972.9215 (22) |
91918.9337 (14) |
| |
|
91918.83 (8)c |
|
B
υ
|
1.898 934 5 (75) |
1.873 949 (21) |
1.894 573 1 (76) |
| 1.898 882 3 (41)d |
1.874 146 (22)e |
1.894 890 (11)f |
| |
|
1.895 0 (3)c |
|
D
υ
× 106 |
6.472 1 (88) |
7.395 (42) |
5.877 4 (77) |
| 6.428 3 (26)d |
6.937 (52)e |
6.187 (12)f |
| |
|
6.0c |
3.3. Equilibrium constants and transition probabilities in 12C17O
Equilibrium constants of the A1Π state in 12C17O were determined on the basis of the A1Π (υ = 1–5) deperturbed constants summarised in Table 10, using a weighted least-squares method. The results are collected in Table 13 and expressed as Dunham coefficients. Despite the fact that Dunham parameters do not include the parameters that describe perturbations between the zero-order states and they are not expected to fit the data to measurement accuracy, they are the most appropriate input to RKR and Franck–Condon Factors (FCF) calculations. It allowed for obtaining the FCF for the Ångström (B1Σ+–A1Π), Herzberg (C1Σ+–A1Π) and Fourth positive (A1Π–X1Σ+) systems using the deperturbed RKR potential energy curve parameters of the 12C17O A1Π (this work), B1Σ+ (ref. 27), C1Σ+ (ref. 28), and X1Σ+ (ref. 80) states. The FCFs in 12C17O are provided in Table 14.
Table 13 Deperturbed equilibrium molecular constants of the A1Π state in 12C17Oa,b,c
| Constant/state |
A1Π |
|
All values in cm−1 except re [Å]. Uncertainties of the Dunham parameters have not been included, because these are not the fitted parameters and they do not reflect inter-parameter correlations.
Values given in square brackets were held fixed during the calculation.
Values calculated within this work are given in bold.
Isotopically recalculated from the 12C18O parameters given by Beaty et al.52
Isotopically recalculated from the 12C16O parameters given by Le Floch.42
Isotopically recalculated from the 12C16O parameters given by Field.30
Calculated by Field30 for the 12C16O molecule.
Calculated by Beaty et al.52 for the 12C18O isotopologue.
|
|
Y
00
|
−0.57
|
|
Y
10
|
1497.61
|
| 1497.94d |
| 1497.70e |
| 1501.18f |
|
Y
20
|
17.15
|
| 17.23d |
| 17.43e |
| 19.54f |
|
Y
30 × 102 |
6.69
|
|
Y
40 × 103 |
[−8.82]d |
|
Y
50 × 104 |
[4.37]d |
|
Y
01
|
1.574 11
|
| 1.574 41d |
| 1.574 59e |
| 1.574 33f |
|
Y
11 × 102 |
2.059
|
| 2.172d |
| 2.175e |
| 2.067f |
|
Y
21 × 103 |
−0.961 |
| −0.953f |
| −0.11d |
| −0.10e |
|
Y
31 × 104 |
[2.862]f |
|
Y
41 × 105 |
[−5.085]f |
|
Y
51 × 106 |
[5.1251]f |
|
Y
61 × 107 |
[−2.930]f |
|
Y
71 × 109 |
[8.846]f |
|
Y
81 × 1010 |
[−1.106]f |
|
Y
02 × 106 |
7.03
|
| 6.97d |
| 6.91e |
|
Y
12 × 107 |
1.13
|
| 1.22e |
|
r
e
|
1.233 87 (19)
|
| 1.233 781 (25)g |
| 1.233 753 (86)h |
Table 14 Franck–Condon Factors (FCF) of the B1Σ+–A1Π, C1Σ+–A1Π, and A1Π–X1Σ+ band systems in the 12C17O isotopologue
| A1Π (υ′′) |
B1Σ+ |
C1Σ+ |
|
υ′ = 0 |
υ′ = 1 |
υ′ = 2a |
υ′ = 0 |
υ′ = 1 |
υ′ = 2a |
|
The vibrational levels, which have not been experimentally observed so far in 12C17O.
|
| 0a |
9.0101 × 10−2 |
0.2537 |
0.3176 |
9.0795 × 10−2 |
0.2373 |
0.2914 |
| 1 |
0.1849 |
0.1736 |
7.3587 × 10−3 |
0.1901 |
0.1741 |
1.3703 × 10−2 |
| 2 |
0.2135 |
2.7840 × 10−2 |
7.1057 × 10−2 |
0.2195 |
2.8173 × 10−2 |
6.2281 × 10−2 |
| 3 |
0.1840 |
5.5201 × 10−3 |
0.1122 |
0.1866 |
6.6188 × 10−3 |
0.1167 |
| 4 |
0.1323 |
5.6103 × 10−2 |
4.6893 × 10−2 |
0.1311 |
6.2383 × 10−2 |
5.2013 × 10−2 |
| 5 |
8.3982 × 10−2 |
9.9048 × 10−2 |
1.5129 × 10−3 |
8.0901 × 10−2 |
0.1075 |
1.7551 × 10−3 |
| 6a |
4.8926 × 10−2 |
0.1082 |
1.3889 × 10−2 |
4.5654 × 10−2 |
0.1145 |
1.5607 × 10−2 |
| X1Σ+ (υ′′) |
A1Π |
|
υ′ = 0a |
υ′ = 1 |
υ′ = 2 |
υ′ = 3 |
υ′ = 4 |
υ′ = 5 |
υ′ = 6a |
| 0 |
0.1173 |
0.2231 |
0.2333 |
0.1794 |
0.1139 |
6.3343 × 10−2 |
3.2546 × 10−2 |
| 1 |
0.2667 |
0.1511 |
8.9305 × 10−3 |
2.6220 × 10−2 |
9.5805 × 10−2 |
0.1267 |
0.1156 |
| 2 |
0.2903 |
1.9746 × 10−3 |
9.5116 × 10−2 |
0.1123 |
2.7289 × 10−2 |
1.8249 × 10−3 |
4.1426 × 10−2 |
| 3 |
0.2023 |
8.1391 × 10−2 |
0.1102 |
3.4831 × 10−5 |
6.3114 × 10−2 |
8.7219 × 10−2 |
3.3372 × 10−2 |
| 4 |
0.1018 |
0.1985 |
3.1476 × 10−3 |
9.1924 × 10−2 |
5.7717 × 10−2 |
4.1846 × 10−4 |
4.8918 × 10−2 |
| 5 |
3.9013 × 10−2 |
0.1899 |
6.2494 × 10−2 |
7.6121 × 10−2 |
9.1741 × 10−3 |
8.0194 × 10−2 |
3.3475 × 10−2 |
| 6 |
1.2109 × 10−2 |
0.1134 |
0.1696 |
1.3827 × 10−5 |
9.5519 × 10−2 |
1.6287 × 10−2 |
2.6512 × 10−2 |
| 7 |
3.0502 × 10−3 |
4.8889 × 10−2 |
0.1699 |
7.3344 × 10−2 |
4.2941 × 10−2 |
3.5060 × 10−2 |
6.4551 × 10−2 |
| 8 |
6.6337 × 10−4 |
1.6894 × 10−2 |
0.1051 |
0.1637 |
5.1326 × 10−3 |
8.6169 × 10−2 |
7.7229 × 10−7 |
| 9 |
1.2243 × 10−4 |
4.6161 × 10−3 |
4.5818 × 10−2 |
0.1508 |
9.4368 × 10−2 |
1.4775 × 10−2 |
6.3127 × 10−2 |
| 10 |
2.2279 × 10−5 |
1.0469 × 10−3 |
1.6225 × 10−2 |
8.9287 × 10−2 |
0.1601 |
2.3354 × 10−2 |
6.0487 × 10−2 |
4. Discussion
Fig. 6a–e show plots of the 12C17O A1Π, υ = 1–5 reduced term values together with a diabatic representation of the perturbers. The strongest perturbations occur because of the spin–orbit interactions with the d3Δi, a′3Σ+, and e3Σ− triplet states. They lead to clearly visible splitting of the Λ-doublet components in regions of avoiding crossings. This phenomenon is most visible for A1Π (υ = 1) at J = 18–24 caused by a′3Σ+ (υ = 10) with term shifts of ∼2.5 cm−1, A1Π (υ = 2) at J = 25–32 caused by e3Σ− (υ = 4) with maximum term shifts of ∼4 cm−1, A1Π (υ = 3) at J = 24–30 caused by a′3Σ+ (υ = 13) with maximum term shifts of ∼3 cm−1, and for A1Π (υ = 5) where we observe a complex perturbation pattern occurring at J = 28–32 resulting from the interactions with the three spin components of d3Δi (υ = 11) and a′3Σ+ (υ = 16) with maximum term shifts of about 2.5 cm−1. In contrast, for A1Π (υ = 1) we observe distinct upward shifts of only the lowest rovibronic levels, with no significant effects on the Λ-doublings, despite the fact that the interaction is of a spin–orbit type. The reason is that this perturbation is caused by the lower lying d3Δi (υ = 5) state, which rapidly diverges with increasing rotation from the 1Π partner. We deal with a similar situation for A1Π (υ = 4), where the perturbation is caused by the D1Δ (υ = 5) level, but this is far less noticeable in the presented scale of the plot. It is worth considering the effect of Λ-doubling caused by a state of Σ symmetry. However, interactions with the D1Δ and d3Δ states induce perturbations of both e and f – parity levels, so do not result in Λ-doubling.
We should also notice the cases of spin–orbit interactions between A1Π and its e3Σ−, a′3Σ+, d3Δi triplet perturbers, for which negligible Λ-doubling effects are observed, in spite of the fact that the crossings occur within the observed 0 < J < 35 region. We deal with such a case for the A1Π, υ = 3 and 5 levels where the perturbers are d3Δi (υ = 8), and e3Σ− (υ = 8), respectively. The reduced effects are in this case caused by the very small values of the vibrational integrals for the interacting levels in 12C17O (see Table 9). In turn, the L-uncoupling interactions between the A1Π state and I1Σ−, D1Δ singlet states are usually much weaker. We can notice these interactions distinctly in Fig. 6b–d, where there are interactions of A1Π (υ = 2) with I1Σ− (υ = 3), and A1Π (υ = 3) with D1Δ (υ = 4) as well as A1Π (υ = 4) with I1Σ− (υ = 6). In all these cases the largest term shifts do not exceed 0.5 cm−1, which can be classified as weak interactions.
In Table 12, with the high accuracy of the results obtained, we notice a slight inconsistency of rotational constants Bυ and Dυ of B1Σ+ (υ = 0 and 1) and C1Σ+ (υ = 0) in relation to those that were calculated in our previous works.26–28 This could be caused by the fact that the linear least-squares method in the version given by Curl and Dane78 and Watson79 takes no account of the impact of the Q(J) branches in the singlet–singlet fits. Improvement in the assignment of some of the heavily overlapped and/or extremely weak lines located in the region of strong and multistate perturbations, which was described in Section 2.1, could also be a reason for this inconsistency. It is worth noticing here that the deperturbation analysis conducted in this work was based on a global, three times more extensive experimental data set than was used in other works concerning the less-abundant 12C17O isotopologue.26–28
The present work also allowed for verification and improvement in the observed perturbations of the A1Π, υ = 1, and 2 rovibrational levels in 12C17O presented in ref. 26. For the A1Π, υ = 1 level, the A1Π (υ = 1)∼D1Δ (υ = 1) avoiding crossing occurs at J = 26–27, both for the e- and f-symmetry levels (see Fig. 6a). However, in the case of the A1Π, υ = 2 level, it turns out that in the perturbation analysis we must take into account small, but not negligible, impacts of the a′3Σ+ (υ = 11) and D1Δ (υ = 2) states on its band origin and the fact that the maximum of the A1Π (υ = 1)∼e3Σ− (υ = 4; F3) interaction for the e-symmetry levels falls at J = 31–32, and not at J = 30–31 as had been thought (see Fig. 6b).
It can be seen in Table 10 that the energy levels, Tυ, for A1Π (υ = 1) and A1Π (υ = 4) have larger uncertainties than the remaining rovibrational levels of this state. This could be due to uncertainties derived from interactions with the d3Δi (υ = 5) and D1Δ (υ = 5) states, respectively. It is important to note that the rotational progressions of these states do not cross the A1Π (υ = 1) and A1Π (υ = 4) states. The effects of such interactions result in global energy shifts of the A1Π (υ = 1, and 4) states, just as in the case of vibrational perturbations.86 Thus, these interactions translate directly into uncertainties in Tυ.
There is a very good agreement between the present and Le Floch's,31 Field's,30 and Field's et al.32,87 values of the isotopologue independent electronic perturbation parameters a and b for the A1Π∼(d3Δi, e3Σ−, a′3Σ+, I1Σ−, and D1Δ) interactions, highlighted in Tables 9 and 11. The obtained electronic perturbation parameters can be used to predict perturbations in other A1Π levels of all CO isotopologues. These parameters may be helpful in interpreting laboratory and astrophysical spectra of higher levels of the A1Π state.
5. Conclusion
Two different experimental methods, high-accuracy dispersive optical spectroscopy in the visible region and Fourier-transform spectroscopy in the vacuum ultraviolet region, were used to obtain high-resolution spectra of the B1Σ+ → A1Π, B1Σ+ ← X1Σ+, and C1Σ+ ← X1Σ+ systems in the less-abundant 12C17O isotopologue; a total of 429 high-accuracy transition frequencies were measured. The combined current data and our recent results,26–28 in total 982 lines in 12 bands (B–A, C–A, B–X, C–X) and 15 bands consisting of extra-lines, were used to perform deperturbation analysis of the A1Π state in 12C17O, taking into account the complete impacts of the d3Δi, e3Σ−, a′3Σ+, I1Σ−, and D1Δ states. As a result the accurate perturbation model describes our experimental findings to the quantum level energies of accuracy.
Acknowledgements
R. Hakalla expresses his gratitude to the LASERLAB-EUROPE for support of this research (grant no. 284464 within the EC's Seventh Framework Programme). R. W. Field thanks the US National Science Foundation (grant no. CHE-1361865) for support of this research. A. Heays was supported by grant no. 648.000.002 from the Netherlands Organisation for Scientific Research (NWO) via the Dutch Astrochemistry Network. J. Lyons and G. Stark acknowledge support from the NASA Origins program. S. Federman was supported by NASA grants NNG 06-GG70G and NNX10AD80G to the University of Toledo. We are grateful to the general and technical staff of SOLEIL synchrotron for providing beam time under projects no. 20090021, 20100018, 20110121, and 20120653. The Rzeszów group would like to express their gratitude for the support of the European Regional Development Fund and the Polish state budget within the framework of the Carpathian Regional Operational Programme (RPPK.01.03.00-18-001/10) for the period of 2007–2013 through the funding of the Centre for Innovation and Transfer of Natural Science and Engineering Knowledge of the University of Rzeszów.
Notes and references
- N. Neininger, M. Guelin, H. Ungerechts, R. Lucas and R. Wielebinski, Nature, 1998, 395, 871–873 CrossRef CAS.
- J. Bally, A. A. Stark, R. W. Wilson and W. D. Langer, Astrophys. J., Lett., 1987, 312, L45–L49 CrossRef CAS.
- J. R. Lyons and E. D. Young, Nature, 2005, 435, 317–320 CrossRef CAS PubMed.
- R. T. Garrod, S. L. Widicus Weaver and E. Herbst, Astrophys. J., 2008, 682, 283–302 CrossRef CAS.
- H. A. Weaver, P. D. Feldman, M. F. A'Hearn, N. Dello Russo and S. A. Stern, Astrophys. J., 2011, 734, L5–L9 CrossRef.
- Q. M. Konopacky, T. S. Barman, B. A. Macintosh and C. Marois, Science, 2013, 339, 1398–1401 CrossRef CAS PubMed.
- P. D. Feldman, E. B. Burgh, S. T. Durrance and A. F. Davidsen, Astrophys. J., 2000, 538, 395–400 CrossRef CAS.
- V. A. Krasnopolsky and P. D. Feldman, Icarus, 2002, 160, 86–94 CrossRef CAS.
- P. D. Feldman, H. A. Weaver and E. B. Burgh, Astrophys. J., 2002, 576, L91–L94 CrossRef CAS.
- J.-C. Gérard, B. Hubert, J. Gustin, V. I. Shematovich, D. Bisikalo, G. R. Gladstone and L. W. Esposito, Icarus, 2011, 211, 70–80 CrossRef.
- E. F. Ladd, Astrophys. J., 2004, 610, 320–328 CrossRef CAS.
- J. G. A. Wouterloot, J. Brand and C. Henkel, Astron. Astrophys., 2005, 430, 549–560 CrossRef CAS.
- Y. Sheffer, D. L. Lambert and S. R. Federman, Astrophys. J., 2002, 574, L171–L174 CrossRef CAS.
- F. Bensch, I. Pak, J. G. A. Wouterloot, G. Klapper and G. Winnewisser, Astrophys. J., Lett., 2001, 562, L185–L188 CrossRef CAS.
- R. L. Smith, K. M. Pontoppidan, E. D. Young, M. R. Morris and E. F. Van Dishoeck, Astrophys. J., 2009, 701, 163–175 CrossRef CAS.
- R. Visser, E. F. van Dishoeck and J. H. Black, Astron. Astrophys., 2009, 503, 323–343 CrossRef CAS.
- S. R. Federman, D. L. Lambert, Y. Sheffer, J. A. Cardelli, B.-G. Andersson, E. F. Van Dishoeck and J. Zsargó, Astrophys. J., 2003, 591, 986–999 CrossRef CAS.
- P. Sonnentrucker, D. E. Welty, J. A. Thorburn and D. G. York, Astrophys. J., Suppl. Ser., 2007, 168, 58–99 CrossRef CAS.
- P. J. Encrenaz, P. G. Wannier, K. B. Jefferts, A. A. Penzias and R. W. Wilson, Astrophys. J., 1973, 186, L77–L80 CrossRef CAS.
- G. Guelachvili, J. Mol. Spectrosc., 1979, 75, 251–269 CrossRef CAS.
- P. Cacciani, W. Hogervorst and W. Ubachs, J. Chem. Phys., 1995, 102, 8308–8320 CrossRef CAS.
- W. Ubachs, P. C. Hinnen, P. Hansen, S. Stolte, W. Hogervorst and P. Cacciani, J. Mol. Spectrosc., 1995, 174, 388–396 CrossRef CAS.
- W. Ubachs, I. Velchev and P. Cacciani, J. Chem. Phys., 2000, 113, 547–560 CrossRef CAS.
- A. Du Plessis, E. G. Rohwer and C. M. Steenkamp, J. Mol. Spectrosc., 2007, 243, 124–133 CrossRef CAS.
- G. Stark, A. N. Heays, J. R. Lyons, P. L. Smith, M. Eidelsberg, S. R. Federman, J. L. Lemaire, L. Gavilan, N. de Oliveira, D. Joyeux and L. Nahon, Astrophys. J., 2014, 788, 67–80 CrossRef.
- R. Hakalla, W. Szajna and M. Zachwieja, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 215102 CrossRef.
- R. Hakalla, M. Zachwieja and W. Szajna, J. Quant. Spectrosc. Radiat. Transfer, 2014, 140, 7–17 CrossRef CAS.
- R. Hakalla, J. Quant. Spectrosc. Radiat. Transfer, 2015, 164, 231–247 CrossRef CAS.
- P. Cacciani, F. Brandi, I. Velchev, C. Lyngå, C.-G. Wahlström and W. Ubachs, Eur. Phys. J. D, 2001, 15, 47–56 CrossRef CAS.
-
R. W. Field, Ph.D. thesis, Harvard University, 1971.
- A. C. Le Floch, F. Launay, J. Rostas, R. W. Field, C. M. Brown and K. Yoshino, J. Mol. Spectrosc., 1987, 121, 337–379 CrossRef CAS.
- R. W. Field, B. G. Wicke, J. D. Simmons and S. G. Tilford, J. Mol. Spectrosc., 1972, 44, 383–399 CrossRef CAS.
- C. Haridass, S. P. Reddy and A. C. Le Floch, J. Mol. Spectrosc., 1994, 167, 334–352 CrossRef CAS.
- B. A. Garetz, C. Kittrell and A. C. Le Floch, J. Chem. Phys., 1991, 94, 843–853 CrossRef CAS.
- R. Hakalla, W. Szajna, M. Zachwieja and R. Kepa, Acta Phys. Pol., A, 2012, 122, 674–682 CrossRef CAS.
- R. Hakalla, M. Zachwieja and W. Szajna, J. Phys. Chem. A, 2013, 117, 12299–12312 CrossRef CAS PubMed.
- R. Hakalla, RSC Adv., 2014, 4, 44394–44407 RSC.
- M. Ostrowska-Kopeć, I. Piotrowska, R. Kępa, P. Kowalczyk, M. Zachwieja and R. Hakalla, J. Mol. Spectrosc., 2015, 314, 63–72 CrossRef.
-
P. H. Krupenie, The Band Spectrum of Carbon Monoxide, National Bureau of Standards, Washington, DC, 1966 Search PubMed.
- J. D. Simmons, A. M. Bass and S. G. Tilford, Astrophys. J., 1969, 155, 345–358 CrossRef CAS.
- R. W. Field, S. G. Tilford, R. A. Howard and J. D. Simmons, J. Mol. Spectrosc., 1972, 44, 347–382 CrossRef CAS.
-
A. C. Le Floch, Ph.D. thesis, University Paris-Sud, 1989.
- A. Le Floch, J. Mol. Spectrosc., 1992, 155, 177–183 CrossRef CAS.
- M. L. Niu, E. J. Salumbides, D. Zhao, N. de Oliveira, D. Joyeux, L. Nahon, R. W. Field and W. Ubachs, Mol. Phys., 2013, 111, 2163–2174 CrossRef CAS.
- E. J. Salumbides, M. L. Niu, J. Bagdonaite, N. de Oliveira, D. Joyeux, L. Nahon and W. Ubachs, Phys. Rev. A, 2012, 86, 022510 CrossRef.
- M. L. Niu, F. Ramirez, E. J. Salumbides and W. Ubachs, J. Chem. Phys., 2015, 142, 044302 CrossRef CAS PubMed.
- W. Ubachs, K. S. E. Eikema, W. Hogervorst and P. C. Cacciani, J. Opt. Soc. Am. B, 1997, 14, 2469–2476 CrossRef CAS.
- N. de Oliveira, M. Roudjane, D. Joyeux, D. Phalippou, J.-C. Rodier and L. Nahon, Nat. Photonics, 2011, 5, 149–153 CrossRef CAS.
- N. de Oliveira, D. Joyeux, D. Phalippou, J. C. Rodier, F. Polack, M. Vervloet and L. Nahon, Rev. Sci. Instrum., 2009, 80, 043101 CrossRef CAS PubMed.
- L. Nahon, N. De Oliveira, G. A. Garcia, J.-F. Gil, B. Pilette, O. Marcouillé, B. Lagarde and F. Polack, J. Synchrotron Radiat., 2012, 19, 508–520 CrossRef CAS PubMed.
- M. L. Niu, E. J. Salumbides, A. N. Heays, N. de Oliveira, R. W. Field and W. Ubachs, Mol. Phys., 2016, 114, 627–636 CrossRef CAS.
- L. M. Beaty, V. D. Braun, K. P. Huber and A. C. Le Floch, Astrophys. J., Suppl. Ser., 1997, 109, 269–277 CrossRef CAS.
- C. Haridass, S. P. Reddy and A. C. Le Floch, J. Mol. Spectrosc., 1994, 168, 429–441 CrossRef CAS.
- R. Kępa and M. Rytel, J. Phys. B: At., Mol. Opt. Phys., 1993, 26, 3355–3362 CrossRef.
- R. Kępa, J. Mol. Spectrosc., 1989, 135, 119–130 CrossRef.
- R. Kępa, Can. J. Phys., 1988, 66, 1012–1024 CrossRef.
- R. Kępa, U. Domin and K. Porada, Acta Phys. Pol., A, 2003, 103, 441–451 CrossRef.
- R. Kępa, M. Ostrowska-Kopeć and I. Piotrowska, J. Mol. Spectrosc., 2011, 266, 104–112 CrossRef.
-
C. E. Moore and NIST ASD Team, NIST At. Spectra Database, National Institute of Standards and Technology, Gaithersburg, MD, 2014, http://physics.nist.gov/asd Search PubMed.
- G. Tachiev and C. F. Fischer, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 2419–2435 CrossRef CAS.
-
J. Baker and NIST ASD Team, NIST At. Spectra Database, National Institute of Standards and Technology, Gaithersburg, MD, 2014, http://physics.nist.gov/asd Search PubMed.
-
P. Zhao, W. Lichten, H. Layer, J. C. Bergquist and NIST ASD Team, NIST At. Spectra Database, National Institute of Standards and Technology, Gaithersburg, MD, 2014, http://physics.nist.gov/asd Search PubMed.
-
S. A. Mitchell and NIST ASD Team, NIST At. Spectra Database, National Institute of Standards and Technology, Gaithersburg, MD, 2014, http://physics.nist.gov/asd Search PubMed.
- R. Kępa, M. Ostrowska-Kopeć, I. Piotrowska, M. Zachwieja, R. Hakalla, W. Szajna and P. Kolek, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 045101 CrossRef.
- R. Bacis, J. Phys. E: Sci. Instrum., 1976, 9, 1081–1086 CrossRef CAS.
- R. Hakalla and M. Zachwieja, J. Mol. Spectrosc., 2012, 272, 11–18 CrossRef CAS.
-
C. M. Western, PGOPHER, a Program for Simulating Rotational, Vibrational and Electronic Structure, University of Bristol, 2015, http://pgopher.chm.bris.ac.uk Search PubMed.
- D. C. Morton and L. Noreau, Astrophys. J., Suppl. Ser., 1994, 95, 301–344 CrossRef CAS.
-
B. A. Palmer and R. Engleman, Atlas of the Thorium Spectrum, Los Alamos Report LA-9615, Los Alamos Scientific Laboratory, Los Alamos, New Mexico, 1983 Search PubMed.
- W.-Ü. L. Tchang-Brillet, P. S. Julienne, J.-M. Robbe, C. Letzelter and F. Rostas, J. Chem. Phys., 1992, 96, 6735–6745 CrossRef CAS.
- A. N. Heays, G. D. Dickenson, E. J. Salumbides, N. De Oliveira, D. Joyeux, L. Nahon, B. R. Lewis and W. Ubachs, J. Chem. Phys., 2011, 135, 244301 CrossRef CAS PubMed.
- M. Eidelsberg, J. L. Lemaire, S. R. Federman, G. Stark, A. N. Heays, Y. Sheffer, L. Gavilan, J.-H. Fillion, F. Rostas, J. R. Lyons, P. L. Smith, N. de Oliveira, D. Joyeux, M. Roudjane and L. Nahon, Astron. Astrophys., 2012, 543, A69 CrossRef.
- L. Gavilan, J. L. Lemaire, M. Eidelsberg, S. R. Federman, G. Stark, A. N. Heays, J.-H. Fillion, J. R. Lyons and N. de Oliveira, J. Phys. Chem. A, 2013, 117, 9644–9652 CrossRef CAS PubMed.
- D. Bailly, E. J. Salumbides, M. Vervloet and W. Ubachs, Mol. Phys., 2010, 108, 827–846 CrossRef CAS.
- K. Yoshino and D. E. Freeman, J. Opt. Soc. Am. B, 1985, 2, 1268–1274 CrossRef CAS.
- F. Brandi, I. Velchev, W. Hogervorst and W. Ubachs, Phys. Rev. A, 2001, 64, 032505 CrossRef.
-
NIST ASD Team, NIST At. Spectra Database, National Institute of Standards and Technology, Gaithersburg, MD, 2014, http://physics.nist.gov/asd Search PubMed.
- R. F. Curl and C. B. Dane, J. Mol. Spectrosc., 1988, 128, 406–412 CrossRef CAS.
- J. K. G. Watson, J. Mol. Spectrosc., 1989, 138, 302–308 CrossRef CAS.
- J. A. Coxon and P. G. Hajigeorgiou, J. Chem. Phys., 2004, 121, 2992–3008 CrossRef CAS PubMed.
- C. Kittrell and B. A. Garetz, Spectrochim. Acta, 1989, 45, 31–40 CrossRef.
- S. G. Tilford and J. D. Simmons, J. Phys. Chem. Ref. Data, 1972, 1, 147–188 CrossRef CAS.
-
K. P. Huber and G. Herzberg, Constants of diatomic molecules, Van Nostrand Reinhold, New York, 1979 Search PubMed.
- T. Bergeman and D. Cossart, J. Mol. Spectrosc., 1981, 87, 119–195 CrossRef CAS.
- J. L. Dunham, Phys. Rev., 1932, 41, 721–731 CrossRef CAS.
-
G. Herzberg, Molecular Spectra and Molecular Structure. I. Spectra of Diatomic Molecules, reprinted 1989 by Krieger, Van Nostrand-Reinhold, Princeton, New Jersey, Malabar, 1950 Search PubMed.
-
H. Lefebvre-Brion and R. W. Field, The Spectra and Dynamics of Diatomic Molecules, Elsevier Academic Press, Amsterdam, The Netherlands, 2004 Search PubMed.
- H. Lefebvre-Brion, Can. J. Phys., 1969, 47, 541–545 CrossRef CAS.
-
R. J. Le Roy, LEVEL 8.2: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels, University of Waterloo Chemical Physics Research Report CP-663, 2014, http://leroy.uwaterloo.ca/programs/ Search PubMed.
-
C. Jung, FRACON-Programmdokumentation Quantenchemie, Akademie der Wissenschaften der DDR, Berlin, 1979 Search PubMed.
-
C. Jung and Z. Jakubek, FRACONB-Programmdokumentation Quantenchemie FRACON (ver. B), Akademie der Wissenschaften der DDR and Pedagogical University of Rzeszów, Berlin – Rzeszów, 1988 Search PubMed.
- A. Le Floch, Mol. Phys., 1991, 72, 133–144 CrossRef CAS.
- G. Herzberg, J. D. Simmons, A. M. Bass and S. G. Tilford, Can. J. Phys., 1966, 44, 3039–3045 CrossRef CAS.
- K. F. Freed, J. Chem. Phys., 1966, 45, 4214–4241 CrossRef CAS.
- B. G. Wicke, R. W. Field and W. Klemperer, J. Chem. Phys., 1972, 56, 5758–5770 CrossRef CAS.
Footnote |
| † Previously at Paris Observatory, LERMA. |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
M. L.
Niu
b,
R. W.
Field
c,
E. J.
Salumbides
*a,
M. L.
Niu
b,
R. W.
Field
c,
E. J.
Salumbides
 bd,
A. N.
Heays
bd,
A. N.
Heays
 e,
G.
Stark
e,
G.
Stark
 f,
J. R.
Lyons
g,
M.
Eidelsberg
h,
J. L.
Lemaire†
i,
S. R.
Federman
j,
M.
Zachwieja
a,
W.
Szajna
a,
P.
Kolek
a,
I.
Piotrowska
a,
M.
Ostrowska-Kopeć
a,
R.
Kępa
a,
N.
de Oliveira
k and
W.
Ubachs
f,
J. R.
Lyons
g,
M.
Eidelsberg
h,
J. L.
Lemaire†
i,
S. R.
Federman
j,
M.
Zachwieja
a,
W.
Szajna
a,
P.
Kolek
a,
I.
Piotrowska
a,
M.
Ostrowska-Kopeć
a,
R.
Kępa
a,
N.
de Oliveira
k and
W.
Ubachs
 b
b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100–18
100–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 and 86
400 cm−1 and 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900–92
900–92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 regions with an absolute accuracy of up to 0.003 cm−1 and 0.005 cm−1 for the B–A, and B–X, C–X systems, respectively. These new experimental data were combined with data from the previously analysed C → A and B → A systems. The comprehensive data set, 982 spectral lines belonging to 12 bands, was included in a deperturbation analysis of the A1Π, υ = 1–5 levels of 12C17O, taking into account interactions with levels in the d3Δi, e3Σ−, a′3Σ+, I1Σ− and D1Δ states. The A1Π and perturber states were described in terms of a set of deperturbed molecular constants, spin–orbit and L-uncoupling interaction parameters, equilibrium constants, 309 term values, as well as isotopologue-independent spin–orbit and rotation-electronic perturbation parameters.
100 cm−1 regions with an absolute accuracy of up to 0.003 cm−1 and 0.005 cm−1 for the B–A, and B–X, C–X systems, respectively. These new experimental data were combined with data from the previously analysed C → A and B → A systems. The comprehensive data set, 982 spectral lines belonging to 12 bands, was included in a deperturbation analysis of the A1Π, υ = 1–5 levels of 12C17O, taking into account interactions with levels in the d3Δi, e3Σ−, a′3Σ+, I1Σ− and D1Δ states. The A1Π and perturber states were described in terms of a set of deperturbed molecular constants, spin–orbit and L-uncoupling interaction parameters, equilibrium constants, 309 term values, as well as isotopologue-independent spin–orbit and rotation-electronic perturbation parameters.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 grooves, blazed at 1.0 μm in 3rd and 4th order, giving reciprocal dispersion and resolving power in the ranges 0.11–0.19 nm mm−1 and 182
600 grooves, blazed at 1.0 μm in 3rd and 4th order, giving reciprocal dispersion and resolving power in the ranges 0.11–0.19 nm mm−1 and 182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–136
400–136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800, respectively. Discharge emission signals were recorded by means of a photomultiplier tube (HAMAMATSU R943-02) mounted on a linear stage (HIWIN KK5002) along the focal curve of the spectrograph. The input and exit slits were 35 μm in width. The intensities of the lines were measured by means of photon counting (HAMAMATSU C3866 photon counting unit and M8784 photon counting board) with a counter gate time of 200–500 ms (no dead time between the gates). The position of the exit slit was measured by means of a He–Ne laser interferometer (LASERTEX) synchronized with the photon counting board. During one exposure of the counter gate, the position was measured 64 times. Simultaneously recorded thorium atomic lines,69 obtained from an auxiliary water-cooled, hollow-cathode tube filled with Th foil were used for absolute CO wavenumber calibration.
800, respectively. Discharge emission signals were recorded by means of a photomultiplier tube (HAMAMATSU R943-02) mounted on a linear stage (HIWIN KK5002) along the focal curve of the spectrograph. The input and exit slits were 35 μm in width. The intensities of the lines were measured by means of photon counting (HAMAMATSU C3866 photon counting unit and M8784 photon counting board) with a counter gate time of 200–500 ms (no dead time between the gates). The position of the exit slit was measured by means of a He–Ne laser interferometer (LASERTEX) synchronized with the photon counting board. During one exposure of the counter gate, the position was measured 64 times. Simultaneously recorded thorium atomic lines,69 obtained from an auxiliary water-cooled, hollow-cathode tube filled with Th foil were used for absolute CO wavenumber calibration.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as well as count rates of up to about 16
1 as well as count rates of up to about 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–60
000–60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 photons per s for the 12C17O B1Σ+ (υ = 0) → A1Π (υ = 3, 4, and 5) bands. The absolute accuracy of the frequency measurements was 0.003 cm−1, corresponding to a relative accuracy of Δλ/λ = 2 × 10−7, for the 15
000 photons per s for the 12C17O B1Σ+ (υ = 0) → A1Π (υ = 3, 4, and 5) bands. The absolute accuracy of the frequency measurements was 0.003 cm−1, corresponding to a relative accuracy of Δλ/λ = 2 × 10−7, for the 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180–18
180–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 spectral region. However, weaker or blended lines have lower accuracy, at worst 0.07 cm−1 or Δλ/λ = 4 × 10−6.
400 cm−1 spectral region. However, weaker or blended lines have lower accuracy, at worst 0.07 cm−1 or Δλ/λ = 4 × 10−6.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O = 1
12C16O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35.
0.35.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O = 1
12C16O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35.
0.35.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O = 1
12C16O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35. (Panel (a)) An overview of the observed B1Σ+ → A1Π (0, 5) and B1Σ+ → d3Δ (0, 11) spectra (upper trace) together with the final branch assignments, calibrating Th atomic lines (going beyond the scale), as well as simulated spectra67 (lower trace). The empty circles indicate spectral lines of undetermined location due to overlap with much more intense atomic lines of carbon, hydrogen, and deuterium. (Panel (b)) Expanded view of the B → A (0, 5) band head region in 12C17O at an enlarged scale.
0.35. (Panel (a)) An overview of the observed B1Σ+ → A1Π (0, 5) and B1Σ+ → d3Δ (0, 11) spectra (upper trace) together with the final branch assignments, calibrating Th atomic lines (going beyond the scale), as well as simulated spectra67 (lower trace). The empty circles indicate spectral lines of undetermined location due to overlap with much more intense atomic lines of carbon, hydrogen, and deuterium. (Panel (b)) Expanded view of the B → A (0, 5) band head region in 12C17O at an enlarged scale.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C16O
12C16O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12C18O = 1
12C18O = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.85
0.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.20. The residual error, after optimally fitting B ← X (0, 0), is nearly consistent with the statistical noise.
0.20. The residual error, after optimally fitting B ← X (0, 0), is nearly consistent with the statistical noise.
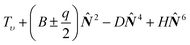
![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) +
+![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) − +
− + ![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) −
−![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) +)
+)![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) +
+![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) − +
− + ![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) −
−![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) +)
+)![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) ·Ŝ
·Ŝ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) ·Ŝ
·Ŝ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) ·Ŝ
·Ŝ![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 2 − D
2 − D![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 4 + H
4 + H![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 6
6![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 2 − D
2 − D![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 4 + H
4 + H![[N with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004e_0302.gif) 6
6





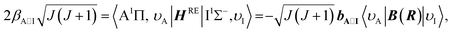


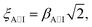
 (see Table 3.4 in ref. 87).
f Calculated on the basis of Field's data30 using the conversion 29979, 2458 MHz cm−1,92 isotopically recalculated to 12C17O.
g Isotopically recalculated from Le Floch.31
h Estimated on the basis of the isotopologue-independent purely electronic perturbation parameters a and b of Field32,41 and Le Floch,31 as well as 〈υA|υd,e or a′〉 and 〈υA|B|υI or D〉 in 12C17O from Table 9, according to the eqn (1)–(8). See Section 3.2 for details.
i Calculated on the basis of isotopically recalculated vibrational equilibrium constants of a′3Σ+ by Field,30 X1Σ+ by Le Floch92 and Te of the perturber by Tilford et al.82
j Calculated on the basis of isotopically recalculated vibrational equilibrium constants of I1Σ− by Field,30 X1Σ+ by Le Floch92 and Te of I1Σ− from Herzberg et al.93
k Isotopically recalculated from Kittrell et al.81
l Calculated on the basis of isotopically recalculated vibrational equilibrium constants of D1Δ by Kittrell et al.,81 X1Σ+ by Le Floch92 and Te of D1Δ by Kittrell et al.81
(see Table 3.4 in ref. 87).
f Calculated on the basis of Field's data30 using the conversion 29979, 2458 MHz cm−1,92 isotopically recalculated to 12C17O.
g Isotopically recalculated from Le Floch.31
h Estimated on the basis of the isotopologue-independent purely electronic perturbation parameters a and b of Field32,41 and Le Floch,31 as well as 〈υA|υd,e or a′〉 and 〈υA|B|υI or D〉 in 12C17O from Table 9, according to the eqn (1)–(8). See Section 3.2 for details.
i Calculated on the basis of isotopically recalculated vibrational equilibrium constants of a′3Σ+ by Field,30 X1Σ+ by Le Floch92 and Te of the perturber by Tilford et al.82
j Calculated on the basis of isotopically recalculated vibrational equilibrium constants of I1Σ− by Field,30 X1Σ+ by Le Floch92 and Te of I1Σ− from Herzberg et al.93
k Isotopically recalculated from Kittrell et al.81
l Calculated on the basis of isotopically recalculated vibrational equilibrium constants of D1Δ by Kittrell et al.,81 X1Σ+ by Le Floch92 and Te of D1Δ by Kittrell et al.81
![[b with combining macron]](https://www.rsc.org/images/entities/b_i_char_0062_0304.gif) d (unitless)
d (unitless)

