Methanol dissociation on bimetallic surfaces: validity of the general Brønsted–Evans–Polanyi relationship for O–H bond cleavage

Abstract

Density functional theory (DFT) calculations were employed to study the dissociation of the O–H bond in methanol on several planar and stepped bimetallic transition metal surfaces, composed of elements showing high or moderate activity towards this reaction, namely, Ni, Rh, Ru, Ir, Pd, Au, Zn and Cu. The activation energies for the O–H bond cleavage were compared with those estimated using a Brønsted–Evans–Polanyi (BEP) relationship for the RO–H bond breakage on pure metal transition surfaces, relating the activation energy for the reaction with the adsorption energies of the reaction products, RO˙ and H˙ adsorbed on the surface of the catalyst. Furthermore, the average differences between the values of the activation energies calculated with the exhaustive determination of the full reaction path and location of the transition state on each surface model and the activation energies obtained from the BEP relationship with the simple calculation of the adsorption energies of the RO˙ and H˙ species are ∼0.14 eV. This suggests that the BEP relationship developed upon the consideration of data for dissociation of the O–H bond in alcohols and water on pure metal surfaces is also valid for a qualitative prediction of the methanol activation energy on bimetallic surfaces.

---

1. Introduction

The reactions of light alcohols such as methanol or ethanol on surfaces are being deeply studied nowadays due to their crucial role in relevant processes such as, for instance, the steam reforming method for the production of H₂ from renewable sources, with the aim of obtaining hydrogen in sufficient amounts to feed proton exchange membrane fuel cells (PEMFC).^1,2 The interest in the study of the catalysis of these alcohols is also due to their consideration as fuels in direct alcohol fuel cells (DAFC).²

Technologies as partial oxidation (POX),³ steam reforming (SR),^4,5 or oxidative steam (OSR) or autothermal (ATR) reforming⁶ are the most common techniques used in the hydrogen production from alcohols and from fossil resources such as natural gas (mostly methane), the latter being the main hydrogen source nowadays.¹ POX yields H₂ and CO by partial oxidation of the alcohol or hydrocarbon on a catalyst with an oxidant, usually O₂.¹ The hydrogen stream obtained through this technique has a considerable concentration of CO, which is known to poison the platinum catalyst used in the PEMFC;⁷ thus, this process is not convenient for the hydrogen production for such purposes. In the SR technique, the alcohol or hydrocarbon reacts with water on the catalyst to yield hydrogen with a low CO concentration; this reaction is endothermic and, therefore, necessitates an external heat source.¹ The combination of SR and POX originates the OSR process, in which the substrate reacts with water and O₂ on the catalyst. The OSR combines the advantages of the SR process, i.e., high H₂/CO ratio, and of the POX technique, i.e., external heating is not required.¹ In any case, the implementation of the OSR technique is very expensive and, therefore, despite the disadvantages associated to the SR process, the latter is still the most appropriate technique to produce hydrogen for PEMFC.¹

The principal advantage of the hydrogen production from alcohols over that from fossil resources is because the former can be obtained from renewable supplies making it an environmental friendly process.^8–10 Notice that light alcohols are also used as feedstock for obtaining other chemicals such as aldehydes or ketones.¹¹

The catalysts routinely used in the processes mentioned above for hydrogen production present a considerable selectivity toward byproducts such as CO, CH₄, or coke. As happening with CO, the formation of the two latter species is also undesirable. The presence of coke on the catalyst surface blocks available reaction sites leading to its poisoning, while the formation of methane consumes hydrogen and, therefore, reduces the yields of hydrogen formed. Thus, the optimization of catalysts for reactions of alcohols on surfaces can have important industrial implications. The idea is to obtain more efficient catalysts in terms of products yields and selectivities, which will reduce the formation of contaminant byproducts, and also to obtain catalysts that can be recycled more efficiently, which will have obvious environmental impact.

Concerning the hydrogen production from methanol on solid catalysts, the usage of bimetallic catalysts can be an effective way to increase the hydrogen yields and selectivity.¹² In fact, bimetallic PdZn based catalysts were found to have an activity similar to that of copper based catalysts¹³ for methanol reforming, but being more thermally stable and also presenting a higher hydrogen selectivity.^14–16 Understandingly, several other bimetallic catalysts were investigated for hydrogen production; for instance, gold- and palladium based Au–Ru/Fe₂O₃, Au–Cu/TiO₂ and Au–Pd/ZnO,^3,17–19 or Pd–Cu/ZnAl₂O₄ (ref. 20) bimetallic catalysts were found to reduce the formation of CO, CH₄ or coke byproducts. In the case of catalysts incorporating gold atoms,^3,17–19 the improved catalytic performance was related with a smaller particle size of the bimetallic phase, while in the case of the Pd–Cu catalyst the performance was related with the synergic catalytic effects due to the formation of the alloy.²⁰ On the other hand, the decrease (especially at low temperature) of the selectivity of the Cu/CeO₂ catalyst toward CO species, which might be formed through the reverse water gas shift reaction, can be achieved by addition of Zn to the catalyst.²¹ It seems that Zn addition decreases the Cu²⁺ reducibility and increases the oxygen mobility of ceria, which promotes the water gas shift reaction with the concomitant reduction of CO.

In relation to the mechanisms of light alcohols reactions on surfaces, it is widely accepted that the first step in the decomposition of methanol and ethanol on most transition metal surfaces is the breakage of the O–H bond.^22–25 Still, under realistic conditions on the Pt(111) surface, some authors found that C–H bond breakage is also a possible way for methanol decomposition.^26,27 The balance between the energies of alcohol adsorption and of activation for breaking the O–H bond on a specific metal surface is associated with the ability of the latter to catalyze the reaction. While the adsorption energy can be calculated easily, the activation energy requires the determination of the full reaction path, which requires more computational resources and skills. Therefore, the usage of empirical relationships for easy estimation of the activation energies arises as a convenient practical solution, being examples the Brønsted–Evans–Polanyi (BEP) relationships relating reaction activation energies with descriptors that can be calculated easily.

Herewith, it is investigated whether BEP relationships²⁸ derived from calculated activation energies for the RO–H (in water or alcohols) bond rupture on several transition metal surfaces and adsorption energies of the corresponding products of reaction (RO + H), can be applied also to the prediction of the activation energy for the methanol O–H bond break on bimetallic surfaces. The bimetallic surfaces considered in this work are based on combinations of transition metals studied experimentally or on metals that seem to present more interesting activities for the dissociation of the RO–H bond as inferred from results in ref. 28. For consistency, the density functional theory calculations performed in this work for obtaining all the energetic data employed the same computational parameters used in that previous work.

2. Catalyst surface models and computational details

Structural models of the bimetallic catalytic surfaces were built in similar fashion to those considered in previous works,^28,29 and were based on some combinations of Pd, Zn, Au, Cu, Ru transition metals (TM) because catalysts based on these metals were already the focus of experimental studies concerning the hydrogen production from methanol.^3,13,17–19 The calculations considered also Ni, Rh and Ir because a previous computational study showed that surfaces based on these metals displayed low to moderate activation energy barriers for dissociating the O–H in methanol.²⁸ These transition metals were used to design a working set of bimetallic catalyst surface models. The majority of these models were derived from pure Ni and Cu surfaces because these metals are cheap and seem to be quite promising for SR reactions.³⁰

The bimetallic catalyst models, namely, Zn@Pd(111), Zn@Pd(110), Ru@Au(110), Au@Pd(111), Au@Cu(110), Pd@Cu(111), Pd@Cu(110), Ru@Cu(110), Rh@Cu(110), Rh@Ir(110), Rh@Ni(111), Ru@Ni(111), Rh@Ni(110) and Ru@Ni(110), were obtained by substitution of atoms of the pure metal surface (i.e., surfaces indicated after the @ symbol), by atoms of the metal indicated before the @ symbol. Therefore, in this notation, the Zn@Pd(111) surface was derived from a pure Pd(111) model, in which a single Pd atom from the outermost layer was substituted by a Zn atom. The pure metal surfaces used to derive the bimetallic models were built from slabs consisting in 2 × 2 unit supercell representations, with a thickness of four atomic layers and a vacuum region of at least 10 Å in the direction perpendicular to the surface. Notice that all the positions in the outermost layer of the (111) Miller index surfaces are equivalent, but that is not the case of the (110) ones because the atoms in the outermost layer are not equidistant, as it happens in (111) Miller index, being formed by protruding rows (crests) of metal atoms separated by valleys showing second-layer atoms that are accessible to small adsorbates like H adatoms. Thus, in the (110) surfaces, the dopant was introduced, again by atomic substitution, at a surface crest because these sites were found to be more accessible for the reactants.^28,29,31 TM(111) and TM(110) terminated slabs were considered because of the improved stability of the former and of the presence of catalytically active low coordinated atoms in the latter.²⁸ The different adsorption sites in the (111) and (110) Miller index surfaces are represented in Fig. 1.

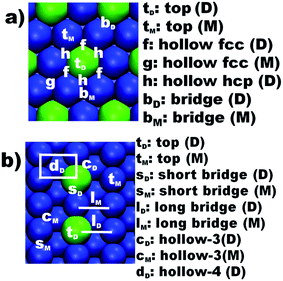Fig. 1 Representation of the adsorption positions in bimetallic surfaces: (a) flat-like (111) surfaces and (b) crested-like (110) surfaces. D and M represent dopant and matrix sites, respectively.

The most favorable adsorption sites and geometries for methanol (the reaction reactant) and for co-adsorbed methoxy and H species (the reaction products) were obtained by full optimization, using a conjugate gradient algorithm implemented in the VASP 5.3 computer code,^32–34 of the atomic coordinates of the adsorbates and of the two topmost surface layers. The two lowermost layers in each transition metal slab model were kept frozen with metal–metal distances at the bulk optimized values. The transition states (TS) for the methanol O–H bond breakage were located with the DIMER method.³⁵ After the analysis of the vibrational normal modes of the transition state, the existence of a single imaginary frequency with an associated motion toward products formation ensured the correct determination of the TS structure. The convergence criteria used in the calculations were 10⁻⁶ eV for the total energy change and 10⁻³ eV Å⁻¹ for the forces acting on the ions. The PW91 exchange correlation functional³⁶ based on the generalized gradient approximation (GGA) was considered in all the calculations. This functional is chosen in this work for consistency with the BEP relationship from ref. 28, and because this functional provided satisfactory data for the O–H bond dissociation in the water molecule.³⁷ Dispersion corrections were not considered in the present study.³⁸ The inclusion of dispersion corrections is expected to impact the magnitudes of the adsorption energies without changing the qualitative picture of the overall reaction.³⁹ Therefore, the main conclusions from the present study are expected to be unaltered by the consideration of such effects. The valence electrons were described by plane wave basis sets, employing a cutoff of 415 eV for the kinetic energy, while the inner electrons and their effects in the valence electron densities of the atoms were described by the projected augmented-wave (PAW) potentials as implemented in the VASP code.^40,41 A 7 × 7 × 1 Monkhorst–Pack grid of special k-points⁴² was employed for the numerical integration in the reciprocal space.

The energies from the DFT calculations were used in the determination of the adsorption and co-adsorption energies (E_ads), reaction energies (E_react), and activation energy barriers for the O–H bond breakage in methanol (E_act). Adsorption and co-adsorption energies were calculated as:

E_ads = E_{slab–adsorbate} − E_slab − E_adsorbate (1)

where E_slab refers to the energy of the metallic surface slab, E_adsorbate to the energy of the methanol molecule in the gaseous phase, and E_{slab–adsorbate} to the energy corresponding to the most favorable configuration(s) for the adsorbate species (cf. CH₃OH* or CH₃O* + H*, with * being an adsorption site available on the surface slab) interacting with the slab. In this notation, negative E_ads values mean favorable adsorption with respect to the undissociated methanol molecule in the gas phase.

The activation energy barrier for the methanol O–H bond break was determined as the energy difference between the transition state (TS) and the most favorable configuration for methanol adsorbed on each surface model (cf. the initial state, IS). The reaction energy is defined as the energy difference between the energies of the dissociated products of reaction on each surface model (cf. the final state, FS) and of the IS. These quantities were corrected with the zero point vibrational energy (ZPVE) that was numerically approximated from the vibrational frequencies of the selected configurations according to the harmonic oscillator approach.

Estimations of the transition state rate constants (k) at 463 K (operating temperature for the water gas shift reaction used to obtain H₂ from methanol SR⁴³), at 523 K (typical temperature for the methanol synthesis reaction⁴⁴), and at 503 K and 573 K (temperature interval limits in the opposite reaction of CO hydrogenation toward methanol)⁴⁵ were derived from transition state theory⁴⁶ employing the following equation.

where k_B is the Boltzmann constant, T is the absolute temperature, h is the Planck constant, and E_act is the zero point vibrational corrected activation energy barrier. In eqn (2), q^≠ and q are the vibrational partition functions for the TS and initial state, respectively, which were approximated from the vibrational frequencies.

3. Results

3.1. Molecular adsorption of methanol

The adsorption of methanol was studied on the different bimetallic surfaces for obtaining the structures and energetics of the initial state on each catalyst model. As common practice, several different starting geometries were considered. Herewith, for each adsorption site indicated in Fig. 1, methanol was placed above the different bimetallic catalyst models, either with the molecular axis parallel or normal to the surface. In the latter case, two different orientations were studied, i.e., configurations either with the OH or the CH₃ groups pointing towards the surface. On all the bimetallic catalyst models, methanol was found to be adsorbed preferentially with its O–H group pointing towards the surface. Numerical results for the most stable adsorption geometry on each surface are given in Table 1 (an extended version of this table is given in ESI, Table S1†) and a graphical representation can be seen in the leftmost panels of Fig. 2.

Table 1 Adsorption energies (E^o_ads eV) for methanol on several bimetallic surfaces

Surface	Adsorption site^a	E^oads^b	d^c
a Labels for adsorption sites are provided in Fig. 1.b Label ^o stands for ZPV corrected adsorption energy values.c Nearest-neighbor distance (Å) between methanol (HOH atom in the case of the undetermined adsorption site and O atom in the remaining cases) and an atom on the catalyst model surface.
Au@Cu(110)	tM	−0.19	2.24 (O)
Au@Pd(111)	Undetermined	−0.03	2.66 (H–(O))
Pd@Cu(110)	tD	−0.20	2.43 (O)
Pd@Cu(111)	Undetermined	0.00	2.76 (H–(O))
Rh@Cu(110)	tD	−0.31	2.31 (O)
Rh@Ir(110)	tD	−0.49	2.25 (O)
Rh@Ni(111)	Undetermined	−0.05	2.67 (H–(O))
Rh@Ni(110)	tD	−0.34	2.33 (O)
Ru@Au(110)	tD	−0.59	2.21 (O)
Ru@Cu(110)	tD	−0.49	2.25 (O)
Ru@Ni(111)	tD	−0.20	2.33 (O)
Ru@Ni(110)	tD	−0.43	2.30 (O)
Zn@Pd(111)	Undetermined	−0.04	2.69 (H–(O))
Zn@Pd(110)	tD	−0.34	2.22 (O)

---

Fig. 2 Most stable configurations for the initial (IS, panels in the left side column), transition (TS, panels in the central column) and final (FS, panels in the right side column) states for the reaction path with the lowest activation energy of CH₃OH* + * → CH₃O* + H* reaction on several bimetallic surfaces. (a) Rh@Ni(111); (b) Ru@Ni(111), (c) Rh@Ni(110); (d) Ru@Ni(110); (e) Ru@Cu(110); (f) Rh@Cu(110); (g) Rh@Ir(110); (h) Zn@Pd(111); (i) Zn@Pd(110); (j) Pd@Cu(110); (k) Pd@Cu(111); (l) Au@Cu(110); (m) Au@Pd(111) and (n) Ru@Au(110). Insets show the lengths of the O–H bond in Å.

The calculated adsorption energies for methanol on the bimetallic surfaces considered in this work vary between 0.00 eV, on the Pd@Cu(111) surface, and −0.59 eV, on the Ru@Au(110) surface. Besides the Pd@Cu(111) catalyst models, methanol also interacts weakly with the Rh@Ni(111), Zn@Pd(111), and Au@Pd(111) flat surfaces. In these cases, the methanol molecule is placed above the surface, with its O–H end pointing toward the surface. In the remaining surfaces, the adsorption energies are more negative than ∼−0.2 eV, and the methanol molecule is chemically bonded through its oxygen atom to a surface atom. With the exception of the Au@Cu(110) surface, in which the methanol molecule prefers to interact directly with the copper atoms, the chemical interaction of methanol occurs with the dopant atom.

The comparison of methanol adsorption on the (111) and (110) Miller index planes shows that the presence of low coordinated atoms in the latter surfaces leads to higher adsorption energies. In fact, the adsorption energies are nearly zero in all the (111) models, being an exception the Ru@Ni(111) surface, with an E^o_ads value of −0.20 eV.

The comparison of the energy values reported in Table 1 for methanol adsorption on the bimetallic surfaces with those corresponding to adsorption on the parent pure surfaces,²⁸ shows interesting variations. In the case of Cu(110), it is found that the methanol adsorption energies become less negative when copper atoms are replaced by Au or Pd to yield the Au@Cu(110) and Pd@Cu(110) surfaces, and become more negative when the doping is made with Ru and Rh atoms to provide the Ru@Cu(110) and Rh@Cu(110) surfaces, respectively. Cooperative effects are also found for methanol adsorption on the Ru@Ni(110), Rh@Ni(111) and Ru@Ni(111) surface models. In contrast with these observations, the adsorption energy was almost the same on the doped Rh@Ni(110), Zn@Pd(111) and Au@Pd(111), and on the parent pure Ni(110) and Pd(111) surfaces. It is also found that the doping of the Cu(111) surface with Pd atoms has a significant destabilizing effect on the interaction of methanol with the catalyst model surface.

3.2. Dissociative adsorption of methanol

The dissociative adsorption of methanol leads to the formation of co-adsorbed methoxy and hydrogen species on the catalyst surface. The most stable configurations for these co-adsorbed species are represented in the rightmost panels of Fig. 2 and the numerical results are given in Tables 2 and S2 of ESI.† As it can be seen, on the different (111) bimetallic catalyst models, the methoxy radical binds 3-fold hollow sites on the surface with its oxygen atom, while keeping its C–O axis almost perpendicular to the surface plane. On the (110) models, the interaction is also involving the oxygen atom end of the methoxy radical but, on those surfaces, the adsorbate interacts with the short-bridge sites and with its C–O axis significantly tilted from the normal to the surface plane. It is found also that the methoxy radical preferentially interacts with most surface models at adsorption sites containing the dopant element, being exceptions to this general behavior the Ag@Ni(111) and Ag@Ni(110) surfaces on which the adsorption occurs on sites exclusively delimited by Ni atoms.

Table 2 Co-adsorption energies (E^o_co-ads eV) for CH₃. O + H pair on several bimetallic surfaces

Surface	Adsorption site^a	E^oco-ads^b	d^c
a Labels for adsorption sites are provided in Fig. 1 (ordering is CH3O/H).b Label ^o stands for ZPV corrected values.c Shorter distance (Å) between the methoxy radical oxygen atom and a metal atom on the surface (in parentheses).
Au@Cu(110)	sD/sM	0.13	1.94 (Cu)
Au@Pd(111)	f/h	0.48	2.16 (Pd)
Pd@Cu(110)	sD/sM	−0.15	1.92 (Cu)
Pd@Cu(111)	f/h	0.31	2.03 (Cu)
Rh@Cu(110)	sD/sM	−0.50	1.96 (Cu)
Rh@Ir(110)	sD/sM	−1.02	2.02 (Ir)
Rh@Ni(111)	f/h	−0.24	2.00 (Ni)
Rh@Ni(110)	sD/sM	−1.02	1.90 (Ni)
Ru@Au(110)	tD/sM	−0.55	1.88 (Ru)
Ru@Cu(110)	sD/sM	−0.94	1.99 (Cu)
Ru@Ni(111)	f/h	−0.50	2.02 (Ni)
Ru@Ni(110)	sD/sM	−1.09	1.94 (Ni)
Zn@Pd(111)	g/f	−0.09	2.05 (Zn)
Zn@Pd(110)	sD/sM	−0.33	1.98 (Zn)

---

The calculated co-adsorption energies referenced to the energy of gas-phase methanol (cf. eqn (1)) vary in the range 0.48 eV, computed for the Au@Pd(111) surface, to −1.02 eV, calculated for co-adsorption on Rh@Ir(110), Table 2. Besides the Au@Pd(111) surface, the dissociative adsorption of methanol is thermodynamically unfavorable also in the cases of the Pd@Cu(111) and Au@Cu(110) surfaces, with co-adsorption energies of 0.31 eV and 0.13 eV, respectively. The co-adsorption of the methoxy and hydrogen species is favorable on the remaining bimetallic surface models (Table 2). Interestingly, in the cases of the Zn@Pd(111) and Ru@Cu(110) bimetallic models, the co-adsorption energies of methoxy and hydrogen become more negative than in the parent Pd(111) and Cu(110) surfaces, respectively.

3.3. Energy barriers for methanol O–H bond cleavage

Selected calculated parameters for the reaction of O–H bond dissociation in methanol are provided in Table 3 (an extended version of this table is given in ESI, Table S3†), while views of the TS geometries on the different bimetallic surfaces can be seen on the central panels of Fig. 2.

Table 3 Activation energy barriers (E^o_act, eV), reaction energies (E^o_react, eV) and O–H bond distances (d, Å) in the TS of the CH₃OH* + * → CH₃O* + H* reaction occurring on several bimetallic surfaces

Surface	dO⋯H^a	E^oact^b	E^o,BEPact^c (Δ)	E^o,BEPact^d (Δ)	E^oreact^b
a Length of the O–H breaking bond in the TS structure.b In activation and reaction energies ^o stands for ZPV corrected values.c Estimated activation energy barrier values using the general BEP relationship obtained in ref. 28 (cf. eqn (3)); values in parentheses are differences to the values obtained from the exhaustive location of the transition state structures with DFT.d Estimated activation energy barrier values using the BEP relationship obtained in this work (cf. eq (4)); values in parentheses are differences to the values obtained from the exhaustive location of the transition state structures with DFT.
Au@Cu(110)	1.54	0.96	0.85 (−0.11)	0.92 (−0.04)	0.48
Au@Pd(111)	1.77	1.25	1.00 (−0.25)	1.11 (−0.14)	0.54
Pd@Cu(110)	1.51	0.65	0.73 (0.08)	0.76 (0.11)	0.05
Pd@Cu(111)	1.72	1.16	0.93 (−0.23)	1.02 (−0.14)	0.34
Rh@Cu(110)	1.43	0.62	0.58 (−0.04)	0.56 (−0.06)	−0.20
Rh@Ir(110)	1.39	0.03	0.35 (0.32)	0.27 (0.24)	−0.53
Rh@Ni(110)	1.55	0.49	0.35 (−0.14)	0.27 (−0.22)	−0.68
Rh@Ni(111)	1.52	0.56	0.69 (0.13)	0.71 (0.15)	−0.18
Ru@Au(110)	1.63	0.57	0.56 (−0.01)	0.53 (−0.04)	0.04
Ru@Cu(110)	1.38	0.55	0.39 (−0.16)	0.31 (−0.24)	−0.45
Ru@Ni(111)	1.46	0.39	0.58 (0.19)	0.56 (0.17)	−0.30
Ru@Ni(110)	1.35	0.36	0.32 (−0.04)	0.23 (−0.13)	−0.67
Zn@Pd(111)	1.57	0.65	0.75 (0.10)	0.79 (0.14)	−0.03
Zn@Pd(110)	1.50	0.56	0.65 (0.09)	0.66 (0.10)	0.01

---

As can be seen, the activation energy barriers calculated with the PW91 exchange–correlation functional range in the interval from 0.03 eV, obtained on the Rh@Ir(110) surface, to 1.25 eV, in the case of dissociation on Au@Pd(111). The higher the activation energy, the longer the O–H bond distance in the TS structure. The reaction energies vary from −0.68 eV (exothermic reaction) on the Ru@Ni(110) surface to 0.54 eV (endothermic reaction) on the Au@Pd(111) surface. In general, surfaces displaying lower activation energy barriers are those where the dissociation reaction is exothermic, while the reactions become endothermic when the activation energies are larger than ∼0.55 eV. With the exceptions of the Pd@Cu(111) and Au@Pd(111) surfaces, the transition state rate constants determined according to eqn (2) are found to be moderate or high at all the temperatures. Also, it is found that the calculated activation energy barriers on most of the studied bimetallic surfaces are larger than on the corresponding pure metal surfaces. Combining this information with that from the (co)adsorption energies reported in the preceding sections, where it was found that surface doping with atoms of Rh, Ru, Zn or Ni was accompanied by more negative adsorption energies, it is possible to conclude that surface doping stabilizes better the reactants and the products of the methanol O–H bond dissociation than the transition states. These findings are similar to those obtained previously for the reaction of NO dissociation on bimetallic surfaces.⁴⁷ Furthermore, for the same combination of transition metal elements, the presence of low coordinated atoms on the (110) Miller index surfaces is found to lead to a decrease of the activation energy barriers for methanol dissociation when compared with the results obtained for the corresponding (111) surfaces. Such decrease is quite small in the case of the Zn@Pd, Rh@Ni, and Ru@Ni surfaces, i.e., with differences smaller than 0.1 eV, but in the case of Pd@Cu surfaces the difference is of approximately 0.5 eV.

From the comparison of the absolute values of the adsorption energies calculated for methanol adsorption on the bimetallic surfaces and the activation energy barriers on the corresponding surfaces, the dissociative adsorption of methanol is possible on the Ru@Ni(110), Rh@Ir(110) and Ru@Au(110) surfaces only. On the remaining surfaces, methanol will desorb intact from the catalyst surface without suffering O–H bond cleavage. In the case of the latter catalysts, O–H bond breakage may only occur in the case of the presence of more reactive surface defects or of other surface species that can aid the abstraction of the H atom from methanol.

The activation energy barriers for the reaction of methanol dissociation on the bimetallic surfaces were also estimated with a BEP relationship,

E^o,BEP_act = 0.4329 × E^o_{co-ads,RO*+H*} + 0.7942 (3)

obtained from DFT data calculated for the RO–H* → RO* + H* (R = H; CH₃; CH₃CH₂; HCO; and * is a free adsorption site on the catalyst surface) reaction on several different catalyst models.²⁸ The term E^o,BEP_act stands for the activation energy barrier estimated for the RO–H* → RO* + H* reaction, while the term E^o_{co-ads,RO*+H*} refers to the co-adsorption energy for the products of reaction with respect to the energies of the ROH molecule in the gaseous phase and of the clean catalyst model. The mean absolute error from 49 datapoints was 0.13 eV from data calculated with the PW91 exchange–correlation functional. Noteworthy, the maximum deviation between the activation energy barriers estimated with the same BEP relationship and data calculated with the PBE functional for the dissociation of the water molecule, i.e., H₂O* → OH* + H* reaction, on Ni(111), Ni(110) and Ni(100) surfaces was only 0.06 eV.⁴⁸

In Table 3 are reported the estimated barriers for the methanol dissociation on the fourteen bimetallic transition metal surface models, E^o,BEP_act, which were obtained with eqn (3) and the co-adsorption energies reported in Table 2. In general, the estimated and the DFT calculated barriers are in satisfactory agreement, with a mean absolute error of 0.14 eV. Still, in the case of the reaction occurring on the Rh@Ir(110) surface, the deviation between the estimated and the calculated values is 0.32 eV, which is the maximum deviation found.

E^{o,BEP,this work}_act = 0.5639 × E^o_{co-ads,MeO*+H*} + 0.8346 (4)

Based on the general agreement between the calculated and estimated barriers, it seems that the BEP relationship can be used for qualitative predictions of the activation energy barrier for the methanol O–H bond break on bimetallic surfaces. In fact, the equation for the BEP obtained in a previous study²⁸ (cf. eqn (3)) is similar to that obtained with the data from Table 2 (E^o_{co-ads,MeO*+H*}) and from Table 3 (E^o_act). The equation for the BEP relationship derived with such data has an associated mean absolute error equal to 0.14 eV, and is displayed in Fig. 3.

Fig. 3 Relationship between activation energy barrier (E_act) and co-adsorption energy of CH₃O and H species for the CH₃OH* + * → CH₃O* + H* reaction on bimetallic surfaces.

The observation of a similar slope, intercept and associated mean absolute error for the BEP relationship from the calculated data for the O–H bond dissociation of methanol on several bimetallic surfaces (this work) and from the calculated data for several O–H bond dissociation reactions on metal based catalyst models (previous work) suggests that these relationships can be successfully applied to other reactions involving the dissociation of the O–H bond.

Based on what has been exposed above and for a better understanding of the surface doping effects on the catalysis of the reaction of O–H bond dissociation, we extended the determination of the activation energy barriers to fifteen additional bimetallic surfaces, namely, Ag@Cu(111), Ag@Cu(110), Pt@Cu(111), Pt@Cu(110), Ru@Cu(111), Pt@Ni(111), Ag@Ni(111), Rh@Cu(111), Rh@Pd(111), Ru@Pd(111), Ag@Ni(110), Ni@Pd(110), Ni@Cu(111), Ni@Au(110), and Ir@Au(110). These bimetallic surface models were built as described Section 2. The estimation of the energy barriers was based on the calculated co-adsorption energies for the CH₃O and H which are reported in Tables 4 and S4 of ESI† (a representation of these configurations is given in Fig. 4) and on the BEP relationship from ref. 28. The energy barriers, which are also given in Table 4, suggest that the doping of metallic surfaces with Rh, Ru or Ni atoms is accompanied by substantial decrease of the activation energies and, in principle, will increase the catalytic reactivity toward the breakage of O–H bonds.

Table 4 Co-adsorption energies (E^o_co-ads) for CH₃O and H and estimated activation energy barriers (E^o,BEP_act) for the methanol O–H bond dissociation on bimetallic surfaces. Values in eV

Surface	Adsorption site^a	E^oco-ads^b	d^c	E^o,BEPact
a Labels for adsorption sites are provided in Fig. 1 (ordering is CH3O/H).b In adsorption energies ^o stands for ZPV corrected values.c Shorter distance (Å) between the methoxide and the surface; between parenthesis is given the surface atom interacting with the methoxide which interacts always through the O atom.
Ag@Cu(110)	sD/sM	−0.16	1.91 (Cu)	0.73
Ag@Cu(111)	f/h	0.59	2.05 (Cu)	1.05
Ag@Ni(111)	h/g	0.07	2.00 (Ni)	0.83
Ag@Ni(110)	lM/cM	−0.53	1.98 (Ni)	0.56
Ir@Au(110)	sD/sM	−0.21	1.96 (Ir)	0.70
Ni@Au(110)	sD/sM	0.02	1.86 (Ni)	0.80
Ni@Cu(111)	f/h	−0.33	1.98 (Ni)	0.65
Ni@Pd(110)	sD/sM	−0.63	1.87 (Ni)	0.52
Pt@Cu(110)	sD/sM	−0.11	1.98 (Cu)	0.74
Pt@Cu(111)	f/h	0.48	2.06 (Cu)	1.00
Pt@Ni(111)	f/h	0.72	1.98 (Ni)	1.11
Rh@Cu(111)	f/h	−0.25	2.08 (Cu)	0.69
Rh@Pd(111)	f/h	−0.20	2.05 (Rh)	0.71
Ru@Cu(111)	f/h	−0.68	2.05 (Ru)	0.50
Ru@Pd(111)	f/h	−0.52	2.01 (Ru)	0.57

---

Fig. 4 Most stable adsorption geometries for the methoxide plus H on the additional set of surfaces; (a) Ag@Cu(111), (b) Ag@Cu(110), (c) Pt@Cu(111), (d) Pt@Cu(110), (e) Ru@Cu(111), (f) Pt@Ni(111), (g) Ag@Ni(111), (h) Rh@Cu(111), (i) Rh@Pd(111), (j) Ru@Pd(111), (k) Ag@Ni(110), (l) Ni@Pd(110), (m) Ni@Cu(111), (n) Ni@Au(110), and (o) Ir@Au(110) surfaces.

4. Conclusions

In this work, DFT calculations were used to investigate the methanol O–H bond cleavage on bimetallic surfaces. The comparison of the activation energy barriers calculated with DFT by the explicit characterization of the full reaction path with those estimated using a BEP type relationship obtained in a previous work for the O–H bond breakage on metal based systems, shows that the relationship is valid for qualitative prediction of the activities of bimetallic surfaces for catalyzing the dissociation of the methanol O–H bond. The mean absolute error between calculated and estimated activation energy barriers is 0.14 eV. This result also suggests that the activity of bimetallic surfaces for O–H bond break in alcohols or water can be estimated from the general BEP relationship derived for pure metallic systems. This have important implications since the breakage of the O–H bond is quite common in catalytic processes and paves the way for obtaining similar relationships for other reactions aiming at fast and effective screenings of novel catalysts based on computational approaches.

Acknowledgements

This work was developed within the scope of the project CICECO-Aveiro Institute of Materials, POCI-01-0145-FEDER-007679 (FCT Ref. UID/CTM/50011/2013), financed by national funds through the FCT/MEC and when appropriate co-financed by FEDER under the PT2020 Partnership Agreement and also within the scope of the project UID/QUI/50006/2013 attributed to LAQV@REQUIMTE. JLCF and JRBG acknowledge FCT for the grant SFRH/BPD/64566/2009 co-financed by the Programa Operacional Potencial Humano (POPH)/Fundo Social Europeu (FSE)/Quadro de Referência Estratégico Nacional 2009–2013 do Governo da República Portuguesa and for the Programme Investigador FCT, respectively.

Notes and references

1. J. D. Holladay, J. Hu, D. L. King and Y. Wang, Catal. Today, 2009, 139, 244.
2. C. Bianchini and P. K. Shen, Chem. Rev., 2009, 109, 4183.
3. T.-C. Ou, F.-W. Chang and L. S. Roselin, J. Mol. Catal. A: Chem., 2008, 293, 8.
4. D. R. Palo, R. A. Dagle and J. D. Holladay, Chem. Rev., 2007, 107, 3992.
5. L. V. Mattos, G. Jacobs, B. H. Davis and F. B. Noronha, Chem. Rev., 2012, 112, 4094.
6. R. Pérez-Hernández, G. Mondragón-Galicia, A. Allende-Maravilla and J. Palacios, Phys. Chem. Chem. Phys., 2013, 15, 12702.
7. D. J. Suh, C. Kwak, J.-H. Kim, S. M. Kwon and T.-J. Park, J. Power Sources, 2005, 142, 70.
8. N. J. Divins, E. Lopez, A. Rodriguez, D. Vega and J. Llorca, Chem. Eng. Process., 2013, 64, 31.
9. H. Song, L. Zhang, R. B. Watson, D. Braden and U. S. Ozkan, Catal. Today, 2007, 129, 346.
10. T. Rampe, A. Heinzel and B. Vogel, J. Power Sources, 2000, 86, 536.
11. J. M. Thomas and W. J. Thomas, in Principles and Practice of Heterogeneous Catalysis, VCH, Verlagsgesellschaft mbH, Weinheim, 1997.
12. Z. H. Wei, J. M. Sun, Y. Li, A. K. Datye and Y. Wang, Chem. Soc. Rev., 2012, 41, 7994.
13. K. Liu, C. S. Song and V. Subramani, in Hydrogen and syngas production and purification technologies, Wiley, Hoboken, NJ, 2010, pp. 65–76.
14. S. Sá, H. Silva, L. Brandão, J. M. Sousa and A. Mendes, Appl. Catal., B, 2010, 99, 43.
15. B. Halevi, E. J. Peterson, A. Roy, A. DeLariva, E. Jeroro, F. Gao, Y. Wang, J. M. Vohs, B. Kiefer, E. Kunkes, M. Hävecker, M. Behrens, R. Schlögl and A. K. Datye, J. Catal., 2012, 291, 44.
16. C. Rameshan, W. Stadlmayr, C. Weilach, S. Penner, H. Lorenz, M. Hävecker, R. Blume, T. Rocha, D. Teschner, A. Knop-Gericke, R. Schlögl, N. Memmel, D. Zemlyanov, G. Rupprechter and B. Klötzer, Angew. Chem., Int. Ed., 2010, 49, 3224.
17. K. L. Hohn and Y. C. Lin, ChemSuChem, 2009, 2, 927.
18. F.-W. Chang, L. S. Roselin and T.-C. Ou, Appl. Catal., A, 2008, 334, 147.
19. J. Wang and L. A. Luo, Catal. Lett., 2008, 126, 325.
20. P. Mierczynski, K. Vasilev, A. Mierczynska, W. Maniukiewicz and T. P. Maniecki, Appl. Catal., A, 2014, 479, 26.
21. F. Tonelli, O. Gorriz, L. Arrúa and M. C. Abello, Quim. Nova, 2011, 34, 1334.
22. L. Xu, D. Mei and G. Henkelman, J. Chem. Phys., 2009, 131, 244520.
23. X. Wang, W.-K. Chen and C.-H. Lu, Appl. Surf. Sci., 2008, 254, 4421.
24. C. Pistonesi, A. Juan, A. P. Farkas and F. Solymosi, Surf. Sci., 2008, 602, 2206.
25. W. Liu, J.-G. Wang, X. Guo, W. Fang, M. Wei, X. Lu and L. Lu, Catal. Today, 2011, 165, 32.
26. J. Greeley and M. Mavrikakis, J. Am. Chem. Soc., 2004, 126, 3910.
27. S. Kandoi, J. Greeley, M. A. Sanchez-Castillo, S. T. Evans, A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, Top. Catal., 2006, 37, 17.
28. J. L. C. Fajín, M. N. D. S. Cordeiro, F. Illas and J. R. B. Gomes, J. Catal., 2014, 313, 24.
29. J. L. C. Fajín, M. N. D. S. Cordeiro and J. R. B. Gomes, J. Phys. Chem. C, 2012, 116, 10120.
30. L.-C. Chen, H. Cheng, C.-W. Chiang and S. D. Lin, ChemSusChem, 2015, 1787.
31. J. L. C. Fajín, M. N. D. S. Cordeiro, F. Illas and J. R. B. Gomes, J. Catal., 2010, 276, 92.
32. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mat, 1993, 47, 558.
33. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
34. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mat, 1996, 54, 11169.
35. G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010.
36. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mat, 1992, 46, 6671.
37. J. L. C. Fajín, F. Illas and J. R. B. Gomes, J. Chem. Phys., 2009, 130, 224702.
38. J. P. P. Ramalho, J. R. B. Gomes and F. Illas, RSC Adv., 2013, 3, 13085.
39. H. Prats, P. Gamallo, R. Sayós and F. Illas, Phys. Chem. Chem. Phys., 2016, 18, 2792.
40. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mat, 1994, 50, 17953.
41. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mat, 1999, 59, 1758.
42. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mat, 1976, 13, 5188.
43. J. L. Ayastuy, M. A. Gutiérrez-Ortiz, J. A. González-Marcos, A. Aranzabal and J. R. González-Velasco, Ind. Eng. Chem. Res., 2005, 44, 41.
44. M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893.
45. J. L. C. Fajín, J. R. B. Gomes and M. N. D. S. Cordeiro, J. Phys. Chem. C, 2015, 119, 16537.
46. K. J. Laidler, in Chemical Kinetics, Harper Collins, New York, third edn, 1987, p. 193.
47. J. L. C. Fajín, M. N. D. S. Cordeiro and J. R. B. Gomes, J. Chem. Phys., 2013, 138, 074701.
48. A. Mohsenzadeh, K. Bolton and T. Richards, Surf. Sci., 2014, 627, 1.

---

Footnote

† Electronic supplementary information (ESI) available: Extended versions of Tables S1–4 with adsorption, reaction and activation energies, selected geometrical data, and reaction rates. See DOI: 10.1039/c6ra01118g

---