Passive flow regulator for precise high-throughput flow rate control in microfluidic environments
Abstract
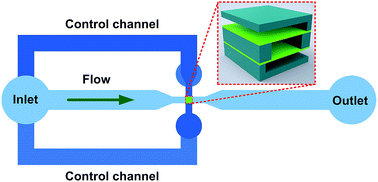
In this paper, we propose a passive flow regulator with a five-layer structure for high-throughput flow-rate control in microfluidic environments. The stacking architecture of the regulator effectively prevents the membrane breakage encountered in previously reported high-throughput flow regulators. To investigate the flow regulation characteristics of our passive flow regulator, a prototype device is integrated into the fluid circuit of a gas-driven flow system, and the flow rate outputs of the device under continuously increased gas pressures are measured. A three-phase regulation process, including an unstable phase, a saturated phase and a stable phase, is observed in the obtained flow-rate curves, and constant output flow rates are achieved at a low threshold pressure. In addition, we investigate the flow autoregulation capability of our flow regulator under periodically varied pressures. Good flow stabilization of the gas-driven flow system is achieved even under dramatically fluctuating pressures. Our passive flow regulator can be applied in many microfluidic environments where low-cost pressure sources (e.g., micropumps or gas tanks) are used while a precise flow rate is required.

 Please wait while we load your content...
Please wait while we load your content...