Hydrogen abstraction of carbon/phosphorus-containing radicals in photoassisted polymerization†
Hua Zhou‡
a,
Yugang Huang‡b,
Yun Zhang‡b,
Dandan Songb,
Hong Huangb,
Cheng Zhongc and
Guodong Ye*b
aKey Laboratory for Major Obstetric Diseases of Guangdong Province, The Third Affiliated Hospital of Guangzhou Medical University, Guangzhou 510150, People's Republic of China. E-mail: gzhygd@gzhmu.edu.cn; Fax: +86 2037103263; Tel: +86 13229494539
bDepartment of Chemistry, School of Pharmaceutical Sciences, Guangzhou Medical University, Guangzhou 511436, People's Republic of China
cCollege of Chemistry and Molecular Sciences, Wuhan University, Wuhan 430072, People's Republic of China
First published on 6th July 2016
Abstract
Free-radical-promoted photopolymerization has successfully improved the curing performance in cationic photopolymerization and is now employed in promoted autoxidation. The main objective was to investigate the photopolymerization kinetics of free-radical-promoted autoxidation by observing the effects of technological parameters such as the light intensity and the sources of the radicals on the rate profiles. The mechanisms of the reaction of a model alkyd monomer with a carbon-containing radical/phosphorus-containing radical, respectively, were also studied by density functional theory. The results showed that the reaction proceeds via hydrogen abstraction. The geometry of the transition states was simply analyzed in terms of a statistical thermodynamics method. A distortion/interaction model was used to understand the differences in energy between two transition states and helped to explain why the phosphorus-containing radical is highly reactive. A bond energy-bond order model and an Evans–Polanyi factor are available for analyzing the non-linear transition states in the carbon-containing radical system. Based on the results of quantum chemistry, Eyring transition state theory with the Wigner correction was employed to compute the pre-exponential factors and rate constants of the two reactions.
Introduction
Free-radical-promoted photopolymerization is an important auxiliary method of increasing the rate of polymerization. It uses free radicals generated by photoinitiators to improve the polymerization conditions, for example, increasing the wavelength flexibility, increasing the amount of primary radicals, and controlling the curing time. Many examples can be found in the literature, which are mostly based on free-radical polymerization of (meth)acrylates or cationic polymerization of epoxides or vinyl ethers.1,2Now, this technology has been extended to the autoxidation of an alkyd resin.3 According to the hydroperoxide theory, the mechanism of autoxidation involves hydrogen abstraction from a methylene group between two double bonds in a polyunsaturated fatty acid chain, and then a bisallylic methylene radical (R˙) is formed. After rearrangement to yield a conjugated structure, this radical reacts with triplet oxygen leading to an alkyl hydroperoxide intermediate (ROOH).4 The drying agent, which is usually a cobalt complex, exerts its activity mainly via the decomposition of alkyl hydroperoxides to form alkoxy radicals (RO˙) and subsequent alkoxy radical-driven polymerization.5,6 Among the different chemical processes involved, the formation of the alkyl hydroperoxide is the “bottleneck” step. Hence, the polymerization requires a long time at the initial stage. However, this problem cannot be solved simply by increasing the amount of the Co complex. A Co complex is not a “through” drier; that is, it will cause the surface to dry but will leave a wet film underneath.7 As a consequence, excessive amounts of Co complexes in the formulation will cause wrinkling or cracking of the film. From a medical point of view, the main drawback of using Co complexes is that they are regarded as substances that should be avoided or at least used sparingly owing to their latent carcinogenic effects.
Our suggestion for dealing with this dilemma is the use of free-radical-promoted autoxidation, which can increase the curing rate and reduce the risk simultaneously. Acylphosphine oxide photoinitiators (including BAPO, TPO, TPO-L, IPO, NPO, etc.) are most frequently employed because the carbonyl–phosphine oxide group [C(O)–P(O)] is an extraordinary functional group; for example, the absorption maximum of BAPO is around 400 nm and it generates an aroyl–phosphinoyl radical (C6H2(CH3)3C(O)–P(O)˙–C6H5, APAR) and a 2,4,6-trimethylbenzoyl radical (C6H2(CH3)3C(O)˙, TMBR) when irradiated with visible light (>400 nm). According to early reports, both radicals can also abstract hydrogen from appropriate donors (e.g. solvents or monomers).8 Moreover, acylphosphine oxide has an outstanding photobleaching effect and does not lead to yellowing of the cured layer. Some phosphorus-containing photoinitiators are shown in Fig. 1. In this work, firstly, in the experimental section we investigated the UV-vis spectra of a photoinitiator in combination with the corresponding steady-state photolysis. We also used time-resolved IR to investigate the kinetics of the curing process in the search for experimental proof of our theory. Then, in the calculations section we studied the mechanistic details using density functional theory. We investigated hydrogen abstraction between a model alkyd, 3,6-nonadiene, as a donor and radicals (APAR and TMBR) as acceptors from two points of view: geometry, including the conformation of the donor and the geometry of the transient state (TS), and energy, including the excitation energy of BAPO and thermodynamic parameters (such as the activation energy) of the reaction in combination with kinetic descriptors (such as rate constants).
We hope to provide detailed kinetic data about our novel approach with its corresponding mechanism to industrial users and scientific researchers in order to develop an environmentally friendly formulation.
Results and discussion
I. Experimental section
 | (1) |
 | (2) |
The kinetic profile of autoxidation assisted by BAPO is shown in Fig. 3. As can be seen in Fig. 3(a), the polymerization rate was particularly low for alkyd that was merely initiated by cobalt, which confirms the above statement that the formation of the alkyl hydroperoxide is the “bottleneck” step. Our RT-IR experiment revealed that BAPO definitely helped to increase the polymerization rate at the onset of polymerization, but the final conversion was low if the sample was merely initiated by BAPO, as shown in Fig. 3(b); the result shows that the best polymerization profile can be obtained by the combined use of BAPO and Co. It has been found that as the reaction proceeds Rp reaches a maximum very rapidly followed by a dramatic decrease. The maximum value of Rp is greater than the sum of the values of Rp produced by BAPO or cobalt separately. Fig. 4 shows plots of α versus t for alkyd resin using (a) different phosphorus-containing photoinitiators and (b) different light intensities. By comparing the four curves in Fig. 4(a), it can be found that the three photoinitiators containing phosphorus (marked as BAPO/TPO/TPO-L) provide better performance than with the blank sample merely initiated by cobalt (abbreviated AlkydCo). Fig. 4(b) also shows that the intensity of simulated daylight has a positive influence on the polymerization behavior.
II Calculations section
Conformation. We selected the diene 3,6-nonadiene (EL) as a model compound of alkyd resin. It has three possible stable conformers: (E,E), (E,Z) and (Z,Z). Therefore, the Boltzmann distribution formula of statistical mechanics was used for the theoretical determination of the conformational populations. The population ratios were obtained by using values of free energy according to eqn (3):
ΔG = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K
| (3) |
The results are 88% for E,E (ΔE = 0.00 kcal mol−1), 11% for E,Z (ΔE = 1.26 kcal mol−1), and 1% for Z,Z (ΔE = 2.28 kcal mol−1) relative to the most stable conformation (E,E), respectively. The results indicate that the E,E conformer is dominant because it has the lowest energy. We therefore selected the E,E conformer as a model in the following research.
It is noteworthy that EL is also a skipped diene.8 The two π orbitals in such a system are separated by a methylene group. Compared with a conjugated diene, it is highly non-planar owing to sp3 hybridization at the carbon (CD) of the methylene group. We observed that EL exists predominantly in a gauche conformation instead of a zigzag form. Moreover, the calculation shows that the two methyl groups at the terminal positions of the chain do not significantly affect the stability.
After an allylic hydrogen atom between the double bonds is abstracted, CD switches from sp3 to sp2 hybridization immediately, forming a bisallylic methylene radical (ELR). Because the unpaired electron is located between two π electron systems, ELR is a linear chain radical with five coplanar carbon atoms. Apparently, the linear axis is too stiff to deform if there is no extra energy input. As a result, there are two planes containing two double bonds, which meet at the bisallylic methylene group. The dihedral angles were 124.3° and 180.0°, respectively, before and after the hydrogen abstraction reaction. It is important to remember the conformation, because we will discuss it in more detail later in the section on bond order.
Bond dissociation energy (BDE). In a hydrogen abstraction process, hydrogen-containing (e.g. EL) and hydrogen-deficient reactants (e.g. TMBR or APAR) give rise to dehydrogenated (e.g. ELR) and hydrogenated products (e.g. TMB or APA). The crosslinking of alkyds starts with the abstraction of an allylic hydrogen (Ha) atom from a fatty acid, because there are two types of allylic hydrogen adjacent to a double bond, one being the central methylene hydrogens between the two non-conjugated double bonds, the other being lateral methylene hydrogens. All of these are possible sites for H abstraction; therefore, it is first necessary to compare their reactivity. For the sake of simplicity, 3-hexene, 3,6,9-dodecatriene and EL were chosen to represent oleic acid, linoleic acid and linolenic acid, respectively. By comparing their BDE, we observed that the BDEs of the central methylene hydrogens between the two double bonds were nearly the same, which indicates that the BDE is not very susceptible to the number of double bonds or even the chain length. Also, the BDE of the central hydrogens is, at about 69 kcal mol−1, lower than that of the lateral hydrogens (about 79 kcal mol−1), which implies that they predominantly participate in H transfer reactions. For monounsaturated lipids such as oleic acid the oxidizability is much reduced because the BDE of the lateral hydrogens (about 81 kcal mol−1) is higher.
It has been found that the oxidizability of polyunsaturated fatty acids is linearly dependent on the number of bisallylic methylenes present in the fatty acid.9,10 The total is greater than that of the lateral hydrogens.
Excitation energy. When BAPO is exposed to UV energy, the first excited singlet state is formed, followed by the triplet state after intersystem crossing. Bond breaking is known to occur from the later excited state.11 Because APAR and TMBR are generated after the excited state, we calculated the first vertical excitation energies of the singlet and triplet states for BAPO and its derivatives, as summarized in Table 1. The experimental results for the triplet energy (ET) were reported to be 62.6 kcal mol−1 for BAPO and 60.7 kcal mol−1 for TPO, respectively, by Jockusch et al.12 There is some discrepancy between the calculated values and the experimental results, which is because the vertical excitation energy is a virtual point on the potential energy surface. The results were equivalent or nearly so from an industrial user's point of view. They show that the results for the singlet state obtained by the B3LYP functional decrease in the order TPO > TPO-L > BAPO. This trend continues for the triplet states. It is well known that the B3LYP functional, which has only 20% short-range HF exchange, is unlikely to give satisfactory results for the excited state. Therefore, we also calculated these by using the M062X functional. The first vertical excitation energies of the singlet and triplet states display the same tendency but are higher than those from B3LYP.
| BAPO B3LYP/M062X kcal mol−1 | TPO B3LYP/M062X kcal mol−1 | TPO-L B3LYP/M062X kcal mol−1 | |
|---|---|---|---|
| a Evert: vertical excitation energy. | |||
| Evert (S1) | 69.7/70.8 | 73.2/72.3 | 72.6/71.4 |
| Evert (T1) | 58.5/61.4 | 61.5/62.8 | 60.5/61.8 |
Geometry. In our system, the central hydrogen migrates from the carbon atom in the alkyl chain (CD) to the carbon/phosphorus atom in the carbonyl-containing radical (CTMBR and PAPAR). The geometry of the TS after optimization is shown in Fig. 5. The phosphorus–carbon, carbon–carbon, and carbon–hydrogen distances for all compounds in the TS are reported in Table 2, which also contains the corresponding included angle data. These distances for the D–H and H–A bonds in the TS are significantly longer than those in the ground states, which indicates that they appear ready to be broken and formed, respectively. However, an obvious change in conformation was also observed. For example, the chain skeleton displayed a C-shaped curve with a linear portion in the middle before hydrogen abstraction, whereas now the linear section is distinctly bent with an angle/radian of about 177°. Obviously, H abstraction causes it to assume a crooked form. In view of the general character of both reactions, it is of interest to compare the structures of the TS.
| Distance Å | Dihedral angle (°) | Included angle (°) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| rD–Hc | rH–A | rD–A | rD–A | ∠C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–Cd–C C–Cd–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
∠D–H–Af | ∠H–Cd–Hd | ∠H–A–Oe | |||
| a rD–A is the sum of rD–H and rA–H according to the hydrogenation products; it is a virtual bond.b Elongation.c rD–H is the distance in the TS, whereas 1.1003 Å is the corresponding distance in the reactant EL.d The included angle is the angle between the two hydrogens in the methylene group surrounded by two double bonds in the TS, whereas 106.7152° is the corresponding angle in the reactant EL.e The included angle is the angle between the hydrogen and the oxygen in the acceptor.f This is a virtual angle assuming that the donor atom (CD in EL), migrating hydrogen and acceptor atom (C or P in the radical) lie in a straight line.g Abbreviations: APA and APAR: aroyl–phosphinoyl and its dehydrogenated radical; TMB and TMBR: 2,4,6-trimethylbenzaldehyde and 2,4,6-trimethylbenzoyl radical; B and BR: benzaldehyde and benzoyl radical; EL and ELR: 3,6-nonadiene and its dehydrogenated radical. | ||||||||||
| Reactant/product | APA | 1.4187 | 2.5190a | 124.3 for EL | 116.4 | |||||
| TMB | 1.1003 | 1.1053 | 2.2056a | 180.0 | 106.7 | 118.7 | ||||
| B | 1.1108 | 2.2111a | 180.0 for ELR | 120.4 | ||||||
| TS | APAR | +EL | 1.3954 | 1.6827 | 3.0728a | 3.0781 | 154.0 | 173.2 | 97.1 | 112.7 |
| TMBR | +EL | 1.3091 | 1.4789 | 2.7388a | 2.7880 | 155.2 | 158.4 | 96.4 | 111.6 | |
| BR | +EL | 1.3014 | 1.4943 | 2.7901a | 2.7957 | 141.1 | 172.7 | 101.3 | 116.2 | |
| Ratio (%) | APAR | +EL | 26.8b | 18.6b | 22.0b | 0.2 | ||||
| TMBR | +EL | 19.0b | 33.8b | 24.2b | 1.8 | |||||
| BR | +EL | 18.3b | 34.5b | 26.2b | 0.2 | |||||
Reaction: APAR and EL. The partial donor and acceptor bond lengths rD–H and rA–H are ca. 1.3954 Å and 1.6827 Å in the TS, respectively, which are longer than the values of ca. 1.1003 Å in EL and 1.4187 Å in APA. The corresponding elongations are 26.8% and 18.6%, respectively. The value of rD–A in the TS amounts to 3.0781 Å, which is about the same as the sum of the values of rD–H and rH–A (3.0728 Å). This is a virtual distance calculated from the sum of rD–H in EL and rH–A in APA; the percentage increase is merely 0.1%. This means that the migration trajectory of the H atom is almost along the PAPAR–CEL line. This was then confirmed by the corresponding angle (∠D–H–A), which has a value of 173.2°, which is closer to 180°. Because the three atoms P, H and CD are aligned along a straight line, the TS can be considered as pseudo-linear. This is often found in hydroxyl radical-induced lipid peroxidation.13
In such a system, if the distance between two groups is less than the sum of their van der Waals radii, then strong repulsion begins. For most groups this distance is between 3 and 4 Å, which is about twice the normal length of a C–C single bond of 1.54 Å. Intuitively, the measured direct distance in the TS is of nearly this size. It was expected that this would result in a reduction in the repulsive force. Moreover, the included angle of ∠H–CD–Hm (97.1°) in the methylene group between the two double bonds in the TS is fairly close to what was observed before H transfer (106.7°). This heightens the impression that the activation energy would be less.
A more in-depth analysis of the geometry found that the hydrogen atom being transferred is not located in the middle of two terminal atoms but is shifted toward the atom with a larger force constant (i.e., it is not halfway between the two terminal atoms). The result is that the unpaired spin density is not shared equally by CD and P in the TS. This is different from a thermoneutral/isoenergetic reaction, but is not so “early” (“early” means that the CD–H distance is barely larger than in the reactant, and the CA–H distance is still large).
Reaction: TMBR and EL. In the TS, the partial bond lengths rD–H for the donor and rA–H for the acceptor are ca. 1.3091 and 1.4789 Å, respectively, which are longer than the values of ca. 1.1003 Å in EL and 1.1053 Å in TMB. The corresponding elongations are 18.6% and 33.8%, respectively, which indicates that the elongations have opposite relative sizes to those in the case of APAR, but the length rD–A between CD and CA has an elongation (24.2%) that is greater than that in the APAR system (22.0%).
Two further aspects are notable deductions from this result of optimization. Firstly, TMBR adopted a perpendicular orientation with respect to the carbon skeletons of ELR. For reference, we used a benzoyl radical (BR) to react with EL. The aryl group of BR was shifted by about 90° from the original conformation. As a result, the benzene ring was almost parallel to the carbon skeletons of ELR.
As we know, bisacylphosphine oxides undergo facile solvolytic cleavage of a carbon–phosphorus bond in the presence of nucleophiles. Therefore, BAPO was deliberately prepared by introducing ortho substituents onto the benzoyl moiety in order to improve its stability to solvolysis during product development. The subtlety of the molecular design is that the carbonyl group is shielded from nucleophilic attack by the introduction of bulky groups.14 Steric hindrance by the methyl groups at the ortho positions obliged the EL molecule to adopt a pseudo-perpendicular arrangement with the TMBR radical, which was more favourable than the pseudo-parallel arrangement with the unsubstituted benzoyl radical. The result of RT-IR shows that the methyl groups on the benzene ring had only a small effect on the rates of the atom abstraction reactions of benzoyl radicals.15 Our results indicated that although the methyl groups at the ortho positions did not participate directly in the reaction, they had a definite influence on the evolution of the reaction, which consequently resulted in some divergence from the traditional scenarios.
Secondly, and more strikingly, the sum of rD–H (1.3091 Å) and rA–H (1.4789 Å) amounts to 2.7880 Å, which is 1.8% higher than the measured distance of rD–A (2.7388 Å). Moreover, the corresponding angle (∠D–H–A) was found to be 158.4°, which implies that the radical approached the EL molecule at an angle. This leads to a non-linear TS. The ortho methyl groups in the TS prevent the retention of the bond, which implies an increase in the steric energy owing to its angular configuration.16 However, the configuration of the reaction centre in the reactions of BR with EL is virtually linear, because the angle ∠D–H–A is 172.7°, as in the case of APAR. The geometry of the BR system is reminiscent of that of the APAR system; for example, the measured distance (2.7901 Å) approaches the sum of the distances from Hm to CD or CA (2.7957 Å). Because TMBR experiences difficulty in achieving the proper orientation for the reaction, this increases the impact parameter according to collision theory and then causes the formation of a sigma bond to be more difficult.
Descriptors.
Thermodynamic parameters. For simplicity in the subsequent processes, we used the free energy to obtain the value of Ea. A schematic list of the values of these energies is shown in Table 3.
| ΔrG kcal mol−1 | ΔrH kcal mol−1 | Ea kcal mol−1 | ν cm−1 | κ | A L mol−1 s−1 | k L mol−1 s−1 | |
|---|---|---|---|---|---|---|---|
| a Ea: activation energy; ΔrH: reaction enthalpy; ν: imaginary frequency; κ: tunneling coefficient; A: pre-exponential factor; k: rate coefficient; APAR: aroyl-phosphinoyl radical; TMBR: 2,4,6-trimethylbenzoyl radical; BR: benzoyl radical; EL: 3,6-nonadiene. | |||||||
| APAR + EL | −5.15 | −5.72 | 21.22 | 1438.23 | 3.04 | 5.25 × 106 | 0.254 |
| TMBR + EL | −14.76 | −16.33 | 23.48 | 1654.78 | 3.66 | 1.75 × 106 | 0.00676 |
| BR + EL | −19.05 | −19.62 | 18.25 | 1572.49 | 3.40 | 3.96 × 107 | 42.9 |
Calculations show that the Ea of APAR is slightly lower than that of TMBR. The values are 21.22 kcal mol−1 and 23.48 kcal mol−1, respectively, which results in a difference of 2.26 kcal mol−1. At room temperature, this difference in the height of the barrier means that APA is formed several times as rapidly as TMB, as confirmed by the reaction rate constants shown subsequently. According to the intersecting-state model, a decrease in the force constant should lead to a decrease in the activation energy.17 Because the force constant is also linked to the stability factor, the stability factor of the reactant will directly affect the height of the barrier. The phosphorus-centered radicals are high-energy reactants with no stabilizing factor. In APAR, the two rings are not arranged in one plane as in the case of biphenyl. Our calculation shows that the dihedral angle of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) and C
and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups in APAR was 169.9° in the trans conformation. This cannot form a conjugated system. Besides, bulky groups also affected the C
O groups in APAR was 169.9° in the trans conformation. This cannot form a conjugated system. Besides, bulky groups also affected the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group and benzene ring in APAR and made it difficult for them to form a conjugated system with a nonzero dihedral angle. In a sense, APAR can be considered as a radical with a restriction on deformation; its excess energy becomes stored without loss via deformation. In turn, it can react with hydrogen donors quickly and easily. Conversely, branched alkyl groups in the vicinity of the carbon atom can stabilize carbon-centered radicals relatively to APAR. As a consequence, this raises the barrier and reduces the reactivity of TMBR. It is noteworthy and surprising that the barriers are a substantial fraction (−20% for APAR-EL) of the energy of the C–H bond. In contrast, H abstraction reactions occur with barriers that are a small fraction (−8% for APAR-nonane) of the energy of the C–H bond in the donor.
O group and benzene ring in APAR and made it difficult for them to form a conjugated system with a nonzero dihedral angle. In a sense, APAR can be considered as a radical with a restriction on deformation; its excess energy becomes stored without loss via deformation. In turn, it can react with hydrogen donors quickly and easily. Conversely, branched alkyl groups in the vicinity of the carbon atom can stabilize carbon-centered radicals relatively to APAR. As a consequence, this raises the barrier and reduces the reactivity of TMBR. It is noteworthy and surprising that the barriers are a substantial fraction (−20% for APAR-EL) of the energy of the C–H bond. In contrast, H abstraction reactions occur with barriers that are a small fraction (−8% for APAR-nonane) of the energy of the C–H bond in the donor.
Another reason is that the sigma orbitals of the donor and acceptor must be aligned with each other and begin the bond breaking and formation processes at almost the same time, so that they can easily complete the H transfer process. The result for ΔrH is also similar to that for Ea. Both of the reactions are exothermic, which represents a negative change in enthalpy. More enthalpy will be provided in TMBR to compensate for the extra loss caused by the non-linear configuration, which will therefore lead to an increase in ΔH as in the case of Ea. The value of ΔrH of APAR was found to be −5.72 kcal mol−1, which was significantly less than that of TMBR (−16.33 kcal mol−1). It is likely that hydrogen transfer in the APAR system is a reaction in which bond breaking and formation occur at almost the same time. APAR is a special reactant with a low Ea and low ΔrH. Because more energy is required to break a bond and there had not yet been a gain in energy from bond formation, extra energy in the form of the TS was required to start the reaction.
Comparing the TS of TMBR with that of BR, it became obvious that the former requires that the reacting molecules must be aligned relative to each other in a specific conformation, and disorder is therefore sacrificed. Because a change in entropy is a measure of the degree of disorder in the TS, the value of the change in entropy will decrease or become negative. The result also shows that the value of ΔrG of APAR (−5.15 kcal mol−1) is notably less than that of TMBR (−14.76 kcal mol−1), which indicates that a large driving force is still stored in the product.
Rate constants. Kinetic data calculated from the optimization of the TS such as the rate constants might help us to understand the nature of the reaction processes. The rate constants were calculated using the conventional TST formula:
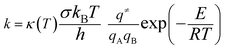 | (4) |
This equation does not include tunneling corrections, which may substantially increase the rates at low temperatures.18 The Wigner formula was employed for the tunneling factor κ(T):19
 | (5) |
The calculated values of k are 0.254 L mol−1 s−1 for APAR and 0.00676 L mol−1 s−1 for TMBR, which indicates that the activation energy was still the main factor governing the value of the reaction rate constant, although the pre-exponential factor (A) of APAR is higher (5.25 × 106) than that of TMBR (1.75 × 106), which is caused by the difference in the partition function. The rate constant for APAR is about two orders of magnitude higher than that for TMBR, which also suggests that APAR is more efficient in the hydrogen abstraction reaction. However, the most attractive is the benzoyl radical because it has the lowest Ea and highest A (3.96 × 107) among them. As we know, the value of a bimolecular A can be 1010 to 1011 L mol−1 s−1 regardless of the chemical nature of the reactants and products, which corresponds to a reaction upon every collision. Actually, this is of the correct order of magnitude for the frequency of a molecular vibration, which is obtained from kBT/h (=6.2 × 1012 s−1). The three pre-exponential factors are about three orders of magnitude lower than the above upper limit, which means that additional complications arise in estimating values of A for these reactions. The formation of a resonance-stabilized radical could restrict rotation about the centre of the radical, reducing the entropy of the transition state and correspondingly decreasing the value of A. Hydrogen abstraction reactions from aldehydes and carbon atoms adjacent to carbonyl groups also require special treatment.
The reactions, in combination with the previously noted mechanism of autoxidation, are briefly depicted in Fig. 6. The probable mechanism involves the photogeneration of APAR and TMBR in the first step. Subsequent abstraction of hydrogen from a bisallylic methylene group of the alkyd monomer promotes the formation of a bisallylic methylene radical.
Experimental
I. Measurements
The alkyd monomer and cobalt drying agent were obtained from AkzoNobel. UV/vis absorption spectra were recorded on a Varian Cary 100 spectrometer. The kinetic profiles were studied via real-time FTIR (RT-IR). Spectra were recorded on a modified Nicolet Magna 360 spectrometer designed to allow light to irradiate a horizontal sample using a fiber optic cable; the signal was detected using DTGS (quantum efficiency 6%) and recorded. The light source used for irradiation was a xenon lamp (Hamamatsu L9588). A filter was used to cut off light below 400 nm and to obtain a spectral window of 400–700 nm. The reaction rate was monitored via the cis H–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH stretching vibration at 3010 cm−1.
CH stretching vibration at 3010 cm−1.
II. Computational details
We restricted our attention to gases. All calculations were performed using Gaussian 09 software.20 Both geometry optimization and single point calculations were performed by the B3LYP method using the 6-311++g(d,p) basis set without the inclusion of any BSSE correction. The reaction transition states were located using QST3 for the saddle point search. We selected the B3LYP and M062X functionals to obtain the vertical excitation energies by TD-DFT with the 50–50 option for closed-shell systems. The rate constants and tunneling factors were obtained by KiSThelP from the results of quantum chemistry.21Conclusions
The promoting effect of free radicals originating from BAPO was confirmed by an RT-IR photopolymerization experiment. This was indicated by a red shift in its spectral features and a photobleaching effect, which was confirmed by a UV-vis experiment. Calculations show that significant steric hindrance between the methyl groups in TMBR and the EL chain occurs in the transition state. This leads to a non-linear TS. TMBR has earlier transition states than APAR, which results in lower distortion energy, but its activation barrier is higher than that of APAR owing to a near-zero interaction energy. The resulting effect is that APAR is more reactive than TMBR. The activation energies, rate constants, and distortion/interaction energies of the corresponding hydrogen abstraction reactions further support our prediction.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 21274032) and the Natural Science Foundation of Guangdong Province (Grant No. 2014A030313500). The corresponding author, Guodong Ye, thanks the above funds.Notes and references
- C. Dursun, M. Degirmenci, Y. Yagci, S. Jockusch and N. J. Turro, Polymer, 2003, 44, 7389 CrossRef CAS.
- T. W. M. Carine, B. L. Fernanda, P. Evandro and A. O. Fabrício, et al., Dent. Mater., 2014, 30(9), 945 CrossRef PubMed.
- G. D. Ye, F. Courtecuisse, X. Allonas, C. Ley, C. Croutxe-Barghorn, P. Raja, P. Taylor and G. Bescond, Prog. Org. Coat., 2012, 73(4), 366 CrossRef CAS.
- O. K. Guler, F. S. Guner and A. T. Erciyes, Prog. Org. Coat., 2004, 51, 365 CrossRef.
- R. Van Gorkum and E. Bouwman, Coord. Chem. Rev., 2005, 249, 1709 CrossRef CAS.
- S. M. P. Meneghetti, R. F. de Souza, A. L. Monteiro and M. O. de Souza, Prog. Org. Coat., 1998, 33, 219 CrossRef CAS.
- S. Tanase, E. Bouwman and J. Reedijk, Appl. Catal., A, 2004, 259, 101 CrossRef CAS.
- Y. Yagci, S. Jockusch and N. J. Turro, Macromolecules, 2010, 43, 6245 CrossRef CAS.
- A. Napolitano, O. Crescenzi, E. Camera, I. Giudicianni, M. Picardo and M. d'Ischia, Tetrahedron Lett., 1999, 40(40), 7179 CrossRef.
- J. P. Cosgrove, D. F. Church and W. A. Pryor, Lipids, 1987, 22, 299 CrossRef CAS PubMed.
- U. Kolczak, G. Rist, K. Dietliker and J. Wirz, J. Am. Chem. Soc., 1996, 118, 6477 CrossRef CAS.
- S. Jockusch, I. V. Koptyug, P. F. McGarry, G. W. Sluggett, N. J. Turro and D. M. Watkins, J. Am. Chem. Soc., 1997, 119, 11495 CrossRef CAS.
- I. Tejero and L. A. Eriksson, et al., J. Phys. Chem. B, 2007, 111, 5684 CrossRef CAS PubMed.
- W. Rutsch, K. Dietliker, D. Leppard and M. G. Rist, Prog. Org. Coat., 1996, 27, 227 CrossRef CAS.
- G. W. Sluggett, C. Turro, M. W. George, I. V. Koptyugs and N. J. Turro, J. Am. Chem. Soc., 1995, 117, 5148 CrossRef CAS.
- L. G. Arnaut, A. A. C. C. Pais and S. J. Formosinho, J. Mol. Struct., 2001, 563–564, 1 CrossRef CAS.
- P. Politzer, J. S. Murray and P. Jaque, J. Mol. Model., 2013, 19, 4111 CrossRef CAS PubMed.
- S. J. Formosinho, chapter Understanding Chemical Reactivity Through the Intersecting-State Model, in Theoretical and Computational Models for Organic Chemistry, ed. S. J. Formosinho, G. I. Csizmadia and L. G. Arnaut, Springer Science+Business Media, Dordrecht, 1991, p. 159 Search PubMed.
- R. G. Susnow, A. M. Dean and W. H. Green Jr, Chem. Phys. Lett., 1999, 312, 262 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel and G. E. Scuseria, et al., GAUSSIAN 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- S. Canneaux, F. Bohr and E. Henon, J. Comput. Chem., 2014, 35, 82 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra00156d |
| ‡ These authors contributed to the work equally and should be regarded as co-first authors. |
| This journal is © The Royal Society of Chemistry 2016 |






