Correlating the surface structure and hydration of a γ-Al₂O₃ support with the Ru_n (n = 1–4) cluster adsorption behavior: a density functional theory study

Abstract

The adsorption and nucleation behavior of Ru_n (n = 1–4) clusters deposited on absolutely dehydrated and hydroxyl-modified γ-Al₂O₃ (100) and (110) surfaces were studied using density functional theory slab calculations. The results indicated that the adsorption process was strongly sensitive to cluster size and surface structure, with deformation and metal–support interactions apparently related. A single Ru atom preferred to adsorb on the (100) surface with small deformation energies, while small interaction energies led to the adsorption of Ru₄ clusters on the (110) surface. When the surface was dehydrated, the adsorption of Ru_n (n = 2–4) clusters on the (110) surface was substantially more stable than that on the (100) surface. The stronger acceptor and almost equal donor sites present on the dehydrated (110) surface increased the bidirectional electron transfer between the clusters and surface sites, resulting in lower adsorption and interaction energies. When the surface was hydrated, the introduction of hydroxyl groups lowered the Ru_n (n = 2–4) clusters' adsorption ability on the hydrated (110) surface by decreasing the surface acidity and basicity, thereby weakening the driving force underlying electron transfer. However, for single Ru atoms, the opposite behavior was observed. In this case, the surface hydroxyl groups increased the stability of the adsorption of the Ru_n (n = 1–4) clusters on the hydrated (100) surface as surface H acted as an adsorption site, receiving an electron from the Ru atom because of its strong Lewis acidity. Further, the support can stabilize the Ru_n (n = 2–4) clusters by decreasing the binding energies of supported configurations lower than the corresponding gas phase. And the nucleation of Ru_n clusters on all surfaces is thermodynamically favourable. The hydration of the (110) surface facilitates agglomeration of Ru₄ clusters, while it is suppressed on the (100) surface. These results are relevant to understanding the interaction between surfaces and clusters.

---

1. Introduction

Economically sustainable development has driven the development of heterogeneous catalysis in the fields of oil refining,¹ exhaust gas treatment,^2–4 and organic degradation^5,6 to solve the energy crisis and environmental pollution problems. Heterogeneous catalysts consisting of metal clusters supported on metal oxides are widely recognized and very attractive because of their highly disperse active phases, resistance to loss of activity, and unique interface sites.^7–10 Conventionally, the support was believed to function only as an inert matrix, contributing to the dispersion and stability of the metal clusters, whereas the metal was the active phase during catalysis. However, by combining elegant experiments and state-of-the-art theory, researchers have shown that the chemical and physical properties of clusters and supports are changed by the interactions that occur when metal clusters are deposited and grown on oxide supports.^11–13 Consequently, the adsorption behavior, catalytic reactivity and catalytic selectivity can also be influenced, sometimes in unexpected ways.^14–23 For example, the bond length of Au₁₂ clusters increased after being supported on the (100) surface of MgO, increasing the ability to adsorb CO and O₂.^11,24 Rodríguez et al.²² suggested that when Ni covers only a small portion of the CeO₂ (111) surface, it exists in the +2 state, thereby inducing high selectivity for water–gas shift reactions. In contrast, however, for large coverage, Ni is present in a lower oxidation state, leading to the production of CH₄. These phenomena revealed that heterogeneous catalysts are complex and that it is necessary to systematically study metal–support interactions. Recently, Raróg-Pilecka et al.²⁵ generated Ru/Al₂O₃ with higher turnover frequencies (TOFs) than Ru/MgAl₂O₄, Ru/MgO, and Ru/C for CO_X methanation. Previously, Akane et al.¹⁴ observed that minimizing the interactions between Ru nanoparticles and the Al₂O₃ support led to high activity for ammonia synthesis. Unfortunately, the interaction mechanism was a difficult puzzle to solve. Therefore, theoretical studies of the interactions between Ru and Al₂O₃ should constitute an integral part of developing heterogeneous catalysts.

Currently, new discoveries are being made based on ongoing phenomenological studies. Recently, Kwak et al.²⁶ achieved a high CO yield via CO₂ reduction using low Ru loading on Al₂O₃ (≤0.5 wt%), whereas CH₄ formed when high Ru loading was used. These results indicated that the selectivity of CO₂ reduction was sensitive to cluster size. However, the original structure of Ru/Al₂O₃ was unknown. To the best of our knowledge, no theoretical study focused on the correlation between cluster size and metal–support interactions in Ru/Al₂O₃ has yet been published. It is well known that the exposed surface plays a pivotal role in these interactions and the subsequent reaction performance, which can be traced to the various geometries and electronic structures of the surface atoms in different surfaces.^27–30 For example, Wei et al.³⁰ suggested that the Ru/TiO₂ (101) surface had a higher activity than the Ru/TiO₂ (001) surface for CO₂ methanation because of the stronger interactions between Ru clusters and the TiO₂ (101) surface. Thus, a detailed analysis relating surface activity and such interactions is needed. In addition, the surface environment, which frequently contains hydroxyl groups,³¹ should trigger the electronic redistribution of atoms and surface reconstruction, thereby altering the active sites.³² Layman et al.³³ noted that the absorbance features of CO were red-shifted on hydrated 5 wt% Ru/Al₂O₃ compared to the dry condition, suggesting that water slightly altered the surface properties and thereby influenced the reactant adsorption. Behm et al.³⁴ recently observed that the presence of water decreased the mean Ru particle size in Ru/Al₂O₃ catalysts concomitant with decreased CO₂ dissociation activity. Therefore, the influence of water should not be neglected when in heterogeneous catalysis of this type. Therefore, connecting the quantum calculations with experiment results and determining the bases for these experimental observations to design an appropriate synthetic method for highly efficient catalysts are worthwhile activities.

In this paper, the structure sensitivity of γ-Al₂O₃ was studied by investigating the adsorption of Ru_n (n = 1–4) clusters on dehydrated and hydrated (110) and (100) surfaces using density functional theory (DFT) calculations. The results showed that the Ru_n adsorption process was strongly sensitive to the particle size and surface structure. Our work aimed to gain insights into the cluster size, surface sites, and effects of hydroxyl groups on adsorption behavior and provide a theoretical basis for the design of tailor-made catalysts. The paper is organized as follows: in the second section, the calculation methods and models are briefly described. In the third section, the Ru_n (n = 1–4) cluster adsorption on dehydrated and hydrated γ-Al₂O₃ surfaces is presented and discussed. Finally, in the fourth section, we summarize the main conclusions of our study.

2. Methods and models

All of the periodic DFT³⁵ calculations were conducted in the Cambridge Sequential Total Energy Package (CASTEP) program.¹² The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA)²⁸ was chosen to describe the exchange correlation energy. A plane wave basis set was implemented to expand the electron wave functions, and the interaction between ion cores and valence electrons was handled with ultrasoft pseudopotentials. For Ru, the 4s, 4p, 4d, and 5s states were treated as valence states, whereas for Al, the 3s and 3p states were treated as the valence states. A cutoff energy of 340 eV was used throughout our calculations. The convergence test for the cutoff energy is included in the ESI (Fig. S1†). The Monkhorst–Pack scheme k-point grids were set: 4 × 3 × 3 for the Al₂O₃ bulk, 3 × 3 × 1 for the (110) surface, and 2 × 3 × 1 for the (100) surface. The maximum force for the convergence criteria of geometry optimization was chosen as 0.03 eV Å⁻¹. The structure was relaxed until the total energy converged to less than 1.0 × 10⁻⁵ eV per atom, the stress was less than 0.05 GPa, and the displacement was less than 0.001 Å. For the energy calculation, a value of 1.0 × 10⁻⁶ was set for self-consistent field (SCF) tolerance. To improve the computational performance, a smearing of 0.1 eV was used. The Mulliken charge population and charge density difference for involved atoms was used to study the interactions between metal clusters and supports. Calculations show that the spin-polarized of Ru_n cluster has little effect on the adsorption energies and charge transfer for Ru_n cluster adsorption on Al₂O₃ support (Tables S3–S7, ESI†). Although the absolute values of the Mulliken charge have no actual meaning, the relative values could facilitate understanding the redistribution of charges and the strength of the forming bonds.

The non-spinel Al₂O₃ model was adopted to construct the surfaces in our work because the penta-Al sites on the (100) surface have detected experimentally.^36,37 The same unit cell size was used for the study of Ru deposition, as in previous works.^38,39 Based on our test (Fig. S3 and Table S1†) and previous report,³¹ O_4c–Al_3c–2O_2c terminated surfaces are chosen to model the (110) surface, meanwhile, Al_5c terminated surfaces are for (100) surface. This calculation yielded the lattice parameters of the bulk crystal structure: a = 5.60 Å, b = 8.43 Å, and c = 8.08 Å; α = β = γ = 90°. The (110) surface was modeled using a unit cell (1 × 1) with dimensions of 8.43 Å × 8.08 Å × 19.18 Å in six layers. In the calculations, the bottom atomic layers were frozen, but the four topmost layers and Ru_n were allowed to relax. The (100) surface was modeled by a supercell (2 × 1) with dimensions of 11.20 Å × 8.43 Å × 20.45 Å in ten layers. Because they were differentiated from the (110) surface, the bottom four layers were fixed. The hydrated surface was built by adsorbing H₂O, yielding a surface-adsorbed hydroxyl radical and a surface-terminated hydroxyl radical. The vacuum region was set to 12 Å in the z direction to separate the slabs; this distance is sufficient to shield the self-interaction of the periodic boundary conditions according to the convergence test presented in Fig. S2.†

As a standard for the relative stability of isolated Ru_n (n = 2–4) clusters, we took the average binding energy, E_bind(Ru_n), of a cluster, typically defined as follows:

E_bind(Ru_n) = [E(Ru_n) − n × E(Ru)]/n (1)

where E(Ru) and E(Ru_n) are the total energies of a single Ru atom and isolated Ru_n cluster, respectively; and n is the number of Ru atoms in the clusters (here, n = 2–4).

To evaluate the stability of the adsorption structure, the adsorption energy (E_ads) of a Ru_n (n = 1–4) cluster deposited on the substrate was defined as follows:

E_ads = E(Ru_n/γ-Al₂O₃) − E(γ-Al₂O₃) − E(Ru_n) (2)

where E(Ru_n/γ-Al₂O₃), E(γ-Al₂O₃), and E(Ru_n) are the total energies of the γ-Al₂O₃ with Ru_n cluster, the bare γ-Al₂O₃ slab, and the free Ru_n cluster, respectively. The deformation and interaction energy also contributed to this energy. The interaction energy, E_int, represents the interaction between clusters and the oxide surface as follows:

E_int = E(Ru_n/γ-Al₂O₃) − E(γ-Al₂O₃)′ − E(Ru_n)′ (3)

where E(γ-Al₂O₃)′ is the total energy of the deformed oxide surface when supporting a cluster, and E(Ru_n)′ is the total energy of a deformed cluster after being deposited on the substrate. Thus, E_def,surface represents the energy difference between the isolated γ-Al₂O₃ surface and the surface after adsorption, as defined by

E_def,surface = E(γ-Al₂O₃)′ − E(γ-Al₂O₃) (4)

Similarly, E_def,Run is the energy difference between free clusters and adsorbed clusters, as follows:

E_def,Run = E(Ru_n)′ − E(Ru_n) (5)

To explore the influence of surface structure and hydration on the stability of Ru_n (n = 1–4) cluster, the average binding energy, E_bind(Ru_n/γ-Al₂O₃), of supported Ru_n cluster on four different surfaces are calculated as follows:

E_bind(Ru_n/γ-Al₂O₃) = [E(Ru_n/γ-Al₂O₃) − n × E(Ru) − E(γ-Al₂O₃)]/n (6)

Based on the most preferable adsorption configurations of Ru_n (n = 1–4) clusters on γ-Al₂O₃ surface, we further investigated the nucleation of Ru_n cluster as follows:

E_nuc = E(Ru_n/γ-Al₂O₃) + E(γ-Al₂O₃) − E(Ru_n−1/γ-Al₂O₃) − E(Ru/γ-Al₂O₃) (7)

3. Results and discussion

3.1 Gas-phase clusters

To understand the adsorption of clusters on the substrate, we first explored the geometries and energies of isolated Ru_n (n = 2–4) clusters. The geometries of Ru_n (n = 2–4) clusters and bulk material are obtained using the methods described above and are presented in Fig. 1, which shows the one-dimensional (1D), two-dimensional (2D), and three-dimensional (3D) structures of Ru_n (n = 2–4) clusters. The stable geometries are summarized in Table 1. The Ru–Ru bond length in the linear Ru₂ cluster is 1.96 Å, and the formation process is exothermic by 3.81 eV. For the Ru₃ cluster, the average bond length is 2.28 Å in a triangle configuration, and the formation process of cluster is exothermic by 4.20 eV. For the Ru₄ cluster, the planar and spatial configurations were both investigated. Although the 3D tetrahedral configuration is less stable than the 2D planar one, the tetrahedral structure, as the smallest unit, can be used to examine the metal–metal and metal–support interactions. Thus, we employed the tetrahedral configuration in the subsequent study.

Fig. 1 The stable geometries of isolated Ru_n (n = 2–4) clusters.

Table 1 The geometry, average bond length, binding energy of Ru_n (n = 2–4) clusters

n	Geometry	d(Ru–Ru) (Å)	Ebind(Run) (eV)
2	D∞h	1.96	−3.81
3	D3h	2.28	−4.20
4	D4h	2.21	−5.20
4	Td	2.42	−5.00

---

As listed in Table 1, the Ru–Ru bond distance generally tends to increase with atomic coordination. However, the Ru–Ru bond distance of the clusters is smaller than that in the bulk (d_Ru–Ru = 2.66 Å). Additionally, the binding energies of Ru_n (n = 2–4) clusters decrease with the cluster size (except for the planar Ru₄ cluster), indicating that the Ru₄ tetrahedral cluster is the most stable.

3.2 γ-Al₂O₃ surface structures

The relaxed structure of the dehydrated γ-Al₂O₃ (110) surface is shown in Fig. 2 (D(110)) and consists of 3-fold-Al, 4-fold-coordinated Al, 2-fold-coordinated O, and 3-fold-coordinated O distributed across the uneven surface. For the flat dehydrated (100) surface, the 5-fold-coordinated Al, 3-fold-coordinated O, and 4-fold-coordinated O are exposed. Although both surfaces contain coordinately unsaturated Al and O sites, they differ in their geometry and electron structure because of the degree of surface unevenness and unsaturation. Thus, there are both similarities and differences in their adsorption performance toward Ru_n (n = 1–4) clusters.

Fig. 2 Top and side views of the dehydrated (110), dehydrated (100), hydrated (110), and hydrated (100) surfaces. Red, pink, and white balls represent O, Al, and H atoms, respectively.

Water, which is usually present on γ-Al₂O₃ surfaces during preparation, can influence the characteristics of surface sites and the material's adsorption ability or reactivity.^{10,28,40–42} Thus, in this study, we investigated the interaction of Ru_n (n = 1–4) clusters with hydrated γ-Al₂O₃ (110) and (100) surfaces. For the hydrated (110) and (100) surfaces, a single H₂O molecule was adsorbed on the surfaces to elucidate the partially hydroxylated structure. After testing hydroxylation process (Table S2, ESI†), a hydroxyl-covered (110) surface (θ = 2.94 OH per nm²) is obtained which is identical to the model in the works of Digne et al.³¹ and Ge et al.⁴³ Similarly, we obtained a (100) surface with θ = 2.12 OH per nm². These configurations are shown in Fig. 2 H(110) and H(100). The energy barriers for this dissociation pathway are shown in Fig. S4 and S5.† On the hydrated (110) surface, the dissociated H₂O molecule interacts with the surface by forming an O_w–Al_3c bond (1.71 Å) and a H_a–O_3c3 bond (1.03 Å). On the hydrated (100) surface, the favorable configuration consists of H_a adsorbing on the O_b (0.98 Å) and O_wH_b bonding to Al_5c2 (1.76 Å).

3.3 Ru_n (n = 1–4) cluster adsorption on γ-Al₂O₃ surfaces

In this section, we illustrate the surface-sensitive interactions between Ru_n (n = 1–4) clusters and the support. Ru_n clusters can interact with the γ-Al₂O₃ surface through different adsorption sites in different ways. We analyzed various adsorption configurations of Ru_n (n = 1–4) clusters (shown in ESI†) and obtained the corresponding energetic and structural parameters. Here, we only consider the favorable structures.

3.3.1 Ru_n (n = 1–4) cluster adsorption on dehydrated γ-Al₂O₃ (110) surfaces. First, we investigated the adsorption of Ru atoms on a clean γ-Al₂O₃ (110) surface. Two favorable geometries are shown in Fig. 3, and the calculated energy components and structural parameters are listed in Table 2. These configurations include Ru atom adsorption at the O_2c2⋯Al_4c⋯O_2c1 site (D(110)-1a) and at the O_3c3⋯Al_3c⋯O_3c2 site (D(110)-1b), with the D(110)-1a configuration being the most stable (exothermic by 4.33 eV). In the D(110)-1a configuration, the Ru atom bound at a hollow, forming the Ru–O_2c1, Ru–O_2c2, and Ru–Al_4c bonds with distances of 1.97 Å, 2.00 Å, and 2.47 Å, respectively. For the D(110)-1b configuration, the Ru atom interacts with the surface by binding to the Al_3c, O_3c2, and O_3c3 sites, with bond lengths of 2.63 Å, 2.09 Å, and 2.09 Å, respectively. The newly formed Al_3c–Ru bond induces a substantial rearrangement of the surface in which the Al_3c stretched out of the groove, achieving a height similar to those of O_2c3 and O_2c2. Although the interaction energy of the D(110)-1b configuration (−5.81 eV) is lower than that of the D(110)-1a configuration (−5.51 eV), its higher surface deformation energy (1.90 eV) causes its adsorption less stable than that of the D(110)-1a configuration.

Fig. 3 Top and side views of energetically favorable geometries of an Ru atom on the dehydrated γ-Al₂O₃ (110) surface: D(110)-1a Ru atom binding to the Al_4c site; D(110)-1b Ru atom located above the surface and binding to the Al_3c site.

Table 2 Structural parameters and corresponding energies of Ru_n (n = 1–4) adsorption in stable configurations on the dehydrated γ-Al₂O₃ (110) surface

Configuration	Eads	Eint (eV)	Edef,Run (eV)	Edef,surface (eV)	Ebind(Run/Al2O3) (eV)	Enuc (eV)	d(Ru–Ru) (Å)
D(110)-1a	−4.33	−5.51	—	1.18	—	—	—
D(110)-1b	−3.91	−5.81	—	1.90	—	—	—
D(110)-2a	−3.76	−5.76	0.40	1.60	−5.69	−2.73	2.12
D(110)-2b	−2.82	−4.52	0.08	1.62	−5.22	−1.79	2.01
D(110)-3	−4.73	−7.05	0.15	2.17	−5.78	−1.63	2.38
D(110)-4	−5.18	−7.60	0.42	2.00	−6.29	−2.76	2.44

---

To further illustrate the modes of cluster adsorption on the substrate, we performed population (Table 3) and electron density difference (Fig. S10†) analyses. Table 3 shows that the Ru atom has a charge of 0.25|e| in the D(110)-1a state, indicating that the charge migrated from the cluster to the surface. Moreover, the deposition of Ru atoms increases the charge density on Al_4c atoms and decreases the charge density on O_2c1 and O_2c2 atoms. Therefore, the observed interactions between Ru atoms and the surface are similar to back-donation interactions,¹⁵ where the Ru atom accepts the charge from the O_2c1 and O_2c2 sites and then donates it to the Al_4c site. The net effect of adsorption is that the Ru atom acts as a conduit and thus promotes the charge transfer from the O sites to the Al site. This phenomenon is qualitatively described by determining the charge density difference (Fig. S10†, D(110)-1a), which indicates that the Ru atom is electronically depleted and balanced by the accumulated charge density on the Ru–Al bond and reduced charge density on the Ru–O bonds. The same situation is observed for the D(110)-1b configuration, where Ru promotes the charge transfer from the O_3c3 and O_3c2 sites to the Al_3c site.

Table 3 Mulliken charges of Ru_n (n = 1–4) adsorption in stable configurations on the dehydrated γ-Al₂O₃ (110) surface

Mulliken charges, |e|	Run	O2c1	O2c2	O3c1	O3c2	O3c3	Al3c	Al4c
D(110)		−1.17	−1.16	−1.12	−1.13	−1.13	1.78	1.79
D(110)-1a	0.25	−0.97	−1.02	−1.11	−1.13	−1.13	1.74	1.40
D(110)-1b	0.17	−1.16	−1.14	−1.11	−0.94	−0.94	1.38	1.77
D(110)-2a	0.32	−1.07	−1.02	−1.10	−1.01	−1.10	1.39	1.50
D(110)-2b	0.26	−1.16	−1.14	−1.11	−0.99	−0.99	1.39	1.78
D(110)-3	0.37	−1.13	−1.02	−0.97	−0.98	−1.08	1.37	1.42
D(110)-4	0.48	−1.02	−1.04	−1.00	−1.01	−1.10	1.37	1.40

---

The above discussion indicates that the metal–substrate interactions lead to the formation of new bonds (Ru–O and Ru–Al) at the cluster–support interface and provide the impetus for electron movement from the O sites to the Al site. Among the other adsorption sites, Ru atoms prefer to adsorb at the O_2c2⋯O_2c1⋯Al_4c site to avoid the excessive energy resulting from surface deformation.

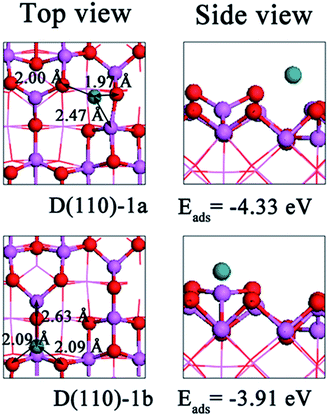
Next, Ru₂ adsorption on the dehydrated (110) surface was studied. We achieved two stable configurations, which are indicated as D(110)-2a and D(110)-2b. The geometries of the stable configurations are presented in Fig. 4, and the key energies and structural parameters are shown in Table 2. Fig. 4 shows that the adsorption sites of the Ru₂ cluster are similar to those of the isolated Ru atom and involve both metal and O atoms. Between the two stable configurations, D(110)-2a is the most stable structure, with an adsorption energy of −3.76 eV, resulting in the formation of Ru₁–O_2c1, Ru₁–O_2c2, Ru₁–Al_4c, Ru₂–Al_3c, and Ru₂–O_3c2 bonds. Unlike in the D(110)-2a configuration, the Ru₂ cluster interacts with the surface in the D(110)-2b configuration by forming Ru–Al_3c (2.55 Å), Ru–O_3c2 (2.15 Å), and Ru–O_3c3 (2.15 Å) bond and has an adsorption energy of −2.82 eV. The larger number of bonds formed in the D(110)-2a configuration is related to its lower interaction energy (−5.76 eV) relative to the D(110)-2b configuration (−4.52 eV). Because both configurations involve the Al_3c site, the surfaces experience similar deformation energies. After geometry optimization, the Ru–Ru distance is 2.01 Å in D(110)-2b configuration, which is shorter than that in the D(110)-2a configuration (2.12 Å) but longer than that of the isolated Ru₂ cluster (1.96 Å). Thus, the deformation energy of the Ru₂ cluster in D(110)-2b is lower than that in the D(110)-2a configuration. Therefore, the D(110)-2a configuration is more stable than D(110)-2b in terms of the adsorption energy. This difference is especially large in terms of the interaction energy but is balanced by the small difference in the deformation energy costs. Table 2 shows that although Ru₂ clusters interact with the surface more strongly than Ru atoms, its higher deformation energy largely neutralize the interaction energy, thereby increasing its adsorption energy. Therefore, the adsorption configuration of an Ru atom in D(110)-1a is more stable than that of an Ru₂ cluster in D(110)-2a.

Fig. 4 Top and side view of energetically favorable geometries of Ru₂ cluster on the dehydrated γ-Al₂O₃ (110) surface. D(110)-2a Ru₂ cluster was parallel to the surface, D(110)-2b Ru₂ cluster slanted on the surface.

The strong interactions in the D(110)-2a and D(110)-2b configurations are attributed to electron transfer between cluster and surface, where the Ru₂ cluster acts as a reservoir, receiving and donating electrons. Table 3 shows that in D(110)-2a and D(110)-2b, the electron density of the O_2c1, O_2c2, O_3c2, and O_3c3 sites bonding to the Ru₂ cluster is depleted, while that of Al_3c and Al_4c is enriched. Fig. S10† shows that for D(110)-2a and D(110)-2b, the Ru₂ cluster loses its electron, thereby increasing the Ru–Al bond density and decreasing the Ru–O bond density. These findings constitute a qualitative basis for understanding metal–substrate interactions.

Finally, we studied the adsorption of Ru₃ and Ru₄ clusters on the dehydrated (110) surface. Fig. 5 shows that in the most stable configuration (D(110)-3), the Ru₃ cluster is slanted on the surface, which is consistent with previous results obtained for Cu₃ clusters.²⁶ In this configuration, the three Ru atoms binds to the surface through Ru₁–O_2c2, Ru₁–Al_3c, Ru₂–Al_3c, Ru₂–O_3c2, Ru₃–O_3c1, and Ru₃–Al_4c bonds. The corresponding bond lengths are 2.09 Å, 2.66 Å, 2.65 Å, 2.09 Å, 2.16 Å, and 2.37 Å, respectively. The average Ru–Ru bond length is 0.10 Å longer than that of isolated Ru₃ clusters, resulting in deformation energy of 0.15 eV in the cluster. The increased number of bonds formed in D(110)-3 relative to D(110)-2a yields a stronger interaction between Ru₃ and the substrate, with an interaction energy of −7.05 eV. After the Ru₃ cluster is deposited, the original appearance of the surface changes, increasing in energy by 2.17 eV, more than D(110)-2a. Additionally, the interaction energy makes a major contribution to the adsorption energy, and as a result, the adsorption energy of the D(110)-3 configuration is 0.97 eV less stable than that of the D(110)-2a configuration. As listed in Table 3, the charge density of the Al atoms (Al_3c and Al_4c) is more positive and that of the O atoms (O_2c2, O_3c1, and O_3c2) is more negative than in the isolated surface. The total charge of the Ru₃ cluster is 0.37|e|, which exceeds that of the Ru₂ cluster. The charge density difference shown in Fig. S11† for D(110)-3 suggests that the Ru₃ cluster accepts the electron from the bound O atom and then donates it to the Al atoms.

Fig. 5 Top and side views of the most energetically favorable geometries of Ru₃ and Ru₄ clusters on the dehydrated γ-Al₂O₃ (110) surface.

For the Ru₄ cluster, the most stable structure is shown in Fig. 5 (D(110)-4), in which three Ru atoms interact directly with the surface, forming four Ru–O bonds and two Ru–Al bonds. The adsorption energy of the Ru₄ cluster is −5.18 eV, which lower than that of the Ru₃ cluster. The small difference in the adsorption energy between the Ru₄ and Ru₃ clusters is the result of its lower interaction energy and similar deformation energy, as shown in Table 3. These can be attributed to the fourth Ru atom that binds via the Ru–Ru interaction, while the third Ru atom binds via the Ru–support and Ru–Ru interactions. As for the Ru₄ cluster deposited on the substrate, the charge density is observed to increase on the Al sites (Al_3c and Al_4c) and decrease on the O sites (O_2c1, O_2c2, O_3c1, and O_3c2). Additionally, the characteristic of Ru₄ cluster changes to electropositive (0.48|e|) since adsorption on the surface. Thus, the Ru₄ cluster enhances the intensity of the electronic exchange between the O and Al sites. The charge density difference plots shown in Fig. S11† (D(110)-4) reveals increased charge density on the newly formed Ru–Al bond and decreased charge density on the Ru–O bond.

To evaluate the relative stability between different sizes, we also calculated the binding energies and nucleation energies of Ru_n (n = 2–4) clusters as shown in Table 2. It is observed that the support stabilizes the Ru_n clusters by decreasing the binding energies of supported configurations lower than that corresponding gas phase. Additionally, the nucleation process of Ru_n (n = 2–4) clusters is exothermic and thermodynamically favorable suggesting the critical cluster size is 2. This result is in accord with the previous studies on the growth of Rh,²⁷ Cu,³⁸ Ni²⁸ and Pd.⁴⁴

As stated above, the interaction energy makes a dominant contribution to the adsorption energy, while the deformation energy exerts an opposite effect. The adsorption energies are balanced by the decrease interaction energies and increase deformation energies. For the most stable configurations (D(110)-1a, D(110)-2a, D(110)-3, and D(110)-4), as the cluster size (n = 1–4) increases, the interaction energy decreases. However, this decreasing trend in the adsorption energy only occurs for clusters from Ru₂ to Ru₄. This is because every cluster adsorption configuration involves Al_3c and cluster deformation, except D(110)-1a. Therefore, the higher deformation energy for the surface and the cluster in D(110)-2a increases the adsorption energy relative to that of D(110)-1a. Additionally, the Ru–Ru bond length is extended compared to that of the isolated cluster but is always shorter than that of the bulk. The stable structures requires the cooperative effect of O and metal sites so that the Ru_n (n = 1–4) clusters receive electrons from oxygen sites and donate them to metal sites. Furthermore, the electron transfer increases as the interaction energy decreases (except in the D(110)-1b configuration); the D(110)-2b configuration exhibits the least electron transfer. Therefore, the presence of Ru_n is responsible for increasing the transfer of electrons from O sites to Al sites.

3.3.2 Ru_n (n = 1–4) clusters adsorption on dehydrated γ-Al₂O₃ (100) surface. In this section, we consider the adsorption of Ru_n (n = 1–4) clusters on the dehydrated (100) surface. The Ru_n (n = 1–4) clusters adsorbed on different sites of the dehydrated γ-Al₂O₃ (100) surface were analyzed, and the most stable configurations are shown in Fig. 6. These configurations are labeled as follows: a single Ru atom locates at the vacancy where it bonds with O_c, O_d, and Al_5c2 sites (D(100)-1), forming Ru–O_c (1.97 Å), Ru–O_d (2.00 Å) and Ru–Al_5c2 (2.31 Å); the Ru₂ cluster with Ru–Ru distance of 2.14 Å almost parallel to the dehydrated (100) surface (D(100)-2), forming Ru₁–O_c (2.00 Å), Ru₁–O_d (2.01 Å), Ru₂–O_b (2.19 Å) and Ru₁–Al_5c2 (2.46 Å) bonds; the Ru₃ cluster slants on the surface with two atoms interacting with the surface (D(100)-3), stretching the distance of Ru–Ru bond by 0.09 Å and forming two Ru₁–O bonds (2.03 Å and 2.05 Å), Ru₁–Al_5c2 bond (2.43 Å), Ru₂–O_b (2.03 Å) and Ru₂–Al_5c1 bond (2.62 Å); the adsorption of a Ru₄ cluster with two Ru atoms interacting directly with the surface and the third and fourth atoms distant from the surface (D(100)-4), forming Ru₁–O_c bond (2.11 Å), Ru₁–O_d (2.56 Å), Ru₁–Al_5c2 (2.56 Å), Ru₂–Al_5c1 (2.68 Å), Ru₃–Al_5c3 (2.75 Å) and Ru₂–O_b (2.10 Å) bonds. From the perspective of adsorption geometries, the situation of Ru_n (n = 1–4) clusters on the dehydrated (100) surface is similar to that on the dehydrated (110) surface, and both involve both metal and O sites. There are, however, subtle differences in the adsorption of Ru₃ and Ru₄ clusters relating to how the two species interact with the surface through two Ru atoms. Table 4 shows that on the dehydrated (100) surface, the Ru_n (n = 1–4) clusters become more positive charged by donating electrons to the surface. In this case, the surface O sites lose their electrons by bonding with the clusters. In contrast, the electron density of Al_5c1, Al_5c2, Al_5c3, and Al_5c4 sites increases because they accept electrons from the cluster. Based on our population analysis (Table 4) and charge density difference analysis (Fig. S12†), we find that the interactions between Ru atoms and γ-Al₂O₃ in these configurations are similar to donation and back-donation interactions where the Ru cluster acts as a media, accepting electrons from O sites and then donating them to Al sites.

Fig. 6 Top and side views of the most energetically favorable geometries of Ru_n (n = 1–4) clusters on the dehydrated (100) surface.

Table 4 Mulliken charges of Ru_n (n = 1–4) adsorption in stable configurations on the dehydrated (100) surface

Mulliken charges, |e|	Run	Oa	Ob	Oc	Od	Oe	Al5c1	Al5c2	Al5c3
D(100)	—	−1.17	−1.11	−1.11	−1.07	−1.10	1.70	1.65	1.66
D(100)-1	0.07	−1.15	−1.10	−0.97	−0.94	−1.10	1.67	1.32	1.63
D(100)-2	0.19	−1.14	−1.03	−0.99	−0.95	−1.14	1.70	1.46	1.68
D(100)-3	0.04	−1.14	−0.96	−0.99	−0.93	−1.12	1.50	1.36	1.66
D(100)-4	0.18	−1.15	−0.98	−1.01	−1.01	−1.04	1.52	1.36	1.48

---

In terms of the adsorption energy (Table 5), the D(100)-1 configuration is the most stable structure among the observed configurations and is exothermic by 4.62 eV. The reason for this stability is that its relatively small deformation energy (1.62 eV) only neutralizes part of the relatively interaction energy (−6.24 eV). In the adsorption of Ru₂ clusters, the Ru–Ru bond length is elongated to 2.14 Å with deformation energy of 0.53 eV. In addition, the adsorption of Ru₂ dimers induces a large rearrangement of the surface in which the Al_5c2 stretched out of the lattice, negatively affecting adsorption. Additionally, the Ru–Al₂O₃ interaction is 1.05 eV weaker than that in D(100)-1. These effects contribute to the higher adsorption energy of the D(110)-2 configuration compares with the D(100)-1 configuration. For Ru₃ cluster adsorption, the adsorption energy is −3.66 eV, more exothermic than the Ru₂ particle. This is because of its lower interaction energy and lower deformation energy cost. As for the Ru₃ cluster, the most favorable configuration for Ru₄ clusters is slant on the surface with two Ru atoms bound to the surface; this configuration is less exothermic (0.35 eV) than the D(100)-3 configuration. Although the deformation introduced by Ru₄ cluster adsorption is 0.37 eV smaller than that of the Ru₃ cluster, the interaction energy is 0.72 eV higher than in the D(100)-3 configuration, resulting in an adsorption energy (−3.31 eV) higher than that of the Ru₃ cluster but lower than that of the Ru₂ cluster. Additionally, as the cluster sizes increase, the binding energies decrease. Be similar to dehydrated (110), the critical size for cluster is 2. However, the nucleation reaction on dehydrated (110) surface is more favored than on (100) surface.

Table 5 Structural parameters and corresponding energies of Ru_n (n = 1–4) adsorption in stable configurations on the dehydrated (100) surface

Configuration	Eads (eV)	Eint (eV)	Edef,Run (eV)	Edef,surface (eV)	Ebind(Run/Al2O3) (eV)	Enuc (eV)	d(Ru–Ru) (Å)
D(100)-1	−4.62	−6.24	—	1.62	—	—	—
D(100)-2	−2.18	−5.19	0.53	2.48	−4.90	−0.59	2.14
D(100)-3	−3.66	−5.97	0.16	2.15	−5.42	−1.86	2.37
D(100)-4	−3.31	−5.25	0.17	1.77	−5.82	−2.41	2.43

---

The above results indicate that the adsorption energies are highly dependent on and increase with the interaction energies. Because of its relatively strong interactions and relatively small deformation, the D(100)-1 configuration is the most stable. Comparing the adsorption on the D(110) and D(100) surfaces reveals that the interaction energies and adsorption energies for Ru_n (n = 2–4) clusters on the D(110) surface are smaller than those on the D(100) surface, suggesting that the stronger metal–support interactions should occur on the D(110) surface. However, the opposite is observed for Ru atom adsorption. The population analysis and charge density difference analysis of the D(100) surface suggests that the interactions between Ru atoms and γ-Al₂O₃ in these configurations is similar a donation and back-donation interaction where the Ru cluster acts as a conduit, moving charge from O to Al sites. However, consistent with adsorption on the D(110) surface, the electron variation in the involved sites is relatively small. The origin of this phenomenon will be analyzed in detail in the Section 3.4.

3.3.3 Ru_n (n = 1–4) clusters adsorption on hydrated γ-Al₂O₃ (110) surfaces. In this section, we considered the adsorption of Ru_n (n = 1–4) clusters on the hydrated (110) surface. Various adsorption geometries were considered, and the most stable configurations are given in Fig. 7: a single Ru atom locates at the hollow where it bonds with O_w, O_3c2, and Al_4c (H(110)-1); the Ru₂ cluster parallel to the hydrated (110) surface (similar to adsorption on the dehydrated (110) surface) (H(110)-2); the Ru₃ cluster slants on the surface with the third atom above the surface (H(110)-3); the adsorption of Ru₄ cluster with three Ru atoms interacting directly with the surface while the fourth atom is distant from the surface (H(110)-4). Unlike adsorption on the dehydrated (110) surface, the surface hydroxyl groups affect this configuration by interacting with its O_w, concomitant with a charge redistribution and alteration of the energies. Table 6 shows that after being adsorbed on the hydrated (110) surface, the Ru_n (n = 1–4) clusters obtain positive charges by donating electrons to the surface. The surface O sites and the O_w sites both lose their electrons because through bonding with the cluster. In contrast, the electron densities of the Al_3c and Al_4c sites increase by accepting electrons from cluster. The variation for Mulliken charge of surface sites induced by surface hydroxyls is less than 0.07|e| on (110) surface, far below the charge transfer between Ru_n cluster and hydrated (110) surface. Therefore, the charge density difference (Fig. S13†) shows that the loss of some Ru d electrons resulted from the combined effects of the increased electron density on the Ru–Al bond and the decreased electron density on the Ru–O bond.

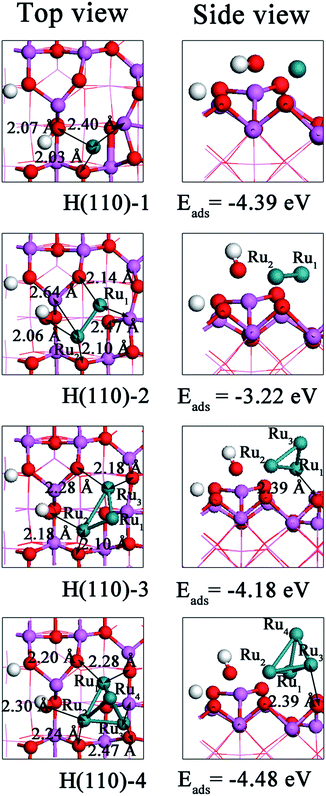Fig. 7 Top and side views of the most energetically favorable geometries of Ru_n (n = 1–4) clusters on the hydrated (110) surface.

Table 6 Mulliken charges of Ru_n (n = 1–4) adsorption in stable configurations on the hydrated (110) surface

Mulliken charges, |e|	Run	O2c1	O2c2	O3c1	O3c2	Ow	Al3c	Al4c
H(110)		−1.14	−1.20	−1.12	−1.13	−1.13	1.85	1.80
H(110)-1	0.22	−1.13	−1.18	−1.06	−0.96	−0.95	1.80	1.37
H(110)-2	0.35	−1.06	−1.05	−1.10	−0.99	−0.93	1.69	1.36
H(110)-3	0.33	−0.99	−1.06	−1.08	−1.00	−0.95	1.78	1.27
H(110)-4	0.36	−1.03	−1.06	−1.02	−1.01	−0.96	1.69	1.30

---

In terms of the adsorption energy (Table 7), the H(110)-4 configuration is the most stable structure among those shown in Fig. 7. Although the interaction energy in H(110)-4 is 0.24 eV higher than that in H(110)-1, its deformation energy is 0.33 eV lower. Thus, the deformation energy only neutralizes a small portion of the interaction energy, resulting in adsorption energy of −4.48 eV. For Ru atom adsorption, the Al_4c atom is distorted from its original location and is endothermic by 1.89 eV. Additionally, the interaction energy of H(110)-1 is the lowest. Thus, the H(110)-1 configuration has the second highest adsorption energy, behind H(110)-4. For the H(110)-2 configuration, although its deformation energy is lower than that of H(110)-1, there is a large difference in the interaction energies between these two configurations, and as a result, the adsorption energy of H(110)-2 is 1.17 eV less exothermic than that of H(110)-1. For Ru₃ cluster adsorption, the lower interaction energy in conjunction with the lower deformation energy lowers the adsorption energy below that of Ru₂ cluster adsorption. Moreover, the binding and nucleation energy for Ru₄ cluster on hydrated (110) surface is the lowest among others.

Table 7 Structural parameters and corresponding energies of Ru_n (n = 1–4) clusters adsorbing in stable configurations on the hydrated (110) surface

Configuration	Eads (eV)	Eint (eV)	Edef,Run (eV)	Edef,surface (eV)	Ebind(Run/Al2O3) (eV)	Enuc (eV)	d(Ru–Ru) (Å)
H(110)-1	−4.39	−6.28	—	1.89	—	—	—
H(110)-2	−3.22	−4.94	0.01	1.71	−5.42	−5.38	2.14
H(110)-3	−4.18	−5.83	0.16	1.49	−5.58	−5.62	2.37
H(110)-4	−4.48	−6.04	0.20	1.36	−6.11	−5.92	2.43

---

The above results indicates that the adsorption energy decreases as the cluster size increases, except for Ru atom adsorption, which is consistent with the trend observed for the interaction energy.

However, the deformation energy for Ru_n (n = 1–4) cluster adsorption configurations decreases as the cluster size increases. Comparing adsorption on the hydrated (110) and dehydrated (110) surfaces reveals that the adsorption energies for Ru_n (n = 1–4) clusters on the dehydrated (110) surface converges to within 0.4–1.42 eV, whereas the adsorption energies for Ru_n (n = 1–4) clusters on the hydrated (110) surface converges to within 0.09–1.26 eV. This finding suggests that the energy variations decrease because of the presence of surface hydroxyl groups. Additionally, the interaction energies of Ru_n (n = 2–4) clusters on the H(110) surface are higher than those on the D(110) surface, indicating that the presence of the hydroxyl groups on the (110) surface weakens the interactions. The opposite is observed for Ru atom adsorption. Because the O_w participated in the adsorption on the hydrated (110) surface instead of Al_3c, the increased interaction energy could not be “neutralizes” by decreased deformation energy. As a result, the adsorption of Ru_n (n = 2–4) clusters on the hydrated (110) surface is more stable than that on the dehydrated (110) surface. In contrast, the Ru atom adsorbs more stably on the hydrated (110) surface than on the dehydrated (100) surface. The interaction mechanism in which the Ru_n (n = 1–4) cluster acts as a medium to accelerate the transfer of electrons from the O sites to the Al sites is the same for both the hydrated and the dehydrated (110) surface. However, when the variation in the Mulliken charge is compared, we observe less electron movement on the hydrated surface. It is observed that the hydroxyls reduce the stability of Ru_n (n = 2–4) clusters on (110) surface. Therefore, the introduction of hydroxyl groups also introduces some changes.

3.3.4 Ru_n (n = 1–4) cluster adsorption on hydrated γ-Al₂O₃ (100) surfaces. After investigating the adsorption of Ru_n (n = 1–4) clusters on the hydrated (110) surface, we then address their deposition on the hydrated (100) surface. Various adsorption geometries were considered, and the most stable configurations are given in Fig. 8: the Ru atom locates at a hollow and bonding with H_a (H(100)-1); the Ru₂ cluster parallel to the surface (H(100)-2); the Ru₃ trimer slants above the surface and bonding with H_a and Al_5c4 (H(100)-3); the Ru₄ cluster contacting the surface through two atoms while the other two atoms are distant from the surface (H(100)-4a); and the Ru₄ cluster binding to the surface by three Ru atoms (H(100)-4b). Fig. 8 shows that H_a binds to the Ru atom far from the O_b site involved in the adsorption on the hydrated (100) surface. Consequently, the introduction of hydroxyl groups on the (100) surface affects the metal–support interaction mechanism. Based on the Mulliken charges listed in Table 8, we can see that the O sites bonding to the Ru atom all lose their electrons, whereas H_a receives them and becomes relatively negative in the H(100) configuration. Additionally, the electron density of Al_5c4 increases in the H(100)-3 and H(100)-4b configurations. The Ru_n (n = 1–4) clusters carry positive charges because they donate electrons to the surface. Thus, unlike the dehydrated (100) surface, in this case, the cluster–substrate interaction is based on charge transfer from the O sites to the H_a (Al_5c4) site with Ru_n clusters acting as the charge-transfer medium. A comparison of Mulliken charges for surface sites before and after hydrated indicates the difference of them is less than 0.08|e|. Therefore, the adsorption of Ru_n cluster is responsible for charge transfer in Fig. S14.† Moreover, the charge density differences reveals that Ru loses some d electrons and that this loss is compensated by an increase in the electron density of the Ru–H_a (Al_5c4) bond and a decrease in the electron density of the Ru–O bonds, which is consistent with the population analysis.

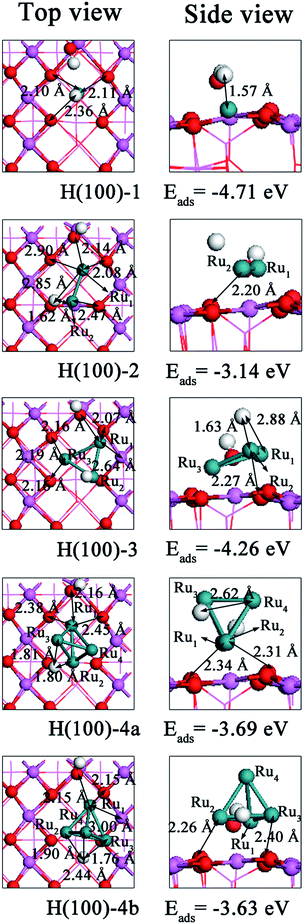Fig. 8 Top and side views of energetically favorable geometries of Ru_n (n = 1–4) clusters on the hydrated (100) surface.

Table 8 Mulliken charges of Ru_n (n = 1–4) adsorption in stable configurations on the hydrated (100) surface

Mulliken charges, |e|	Run	Oa	Ob	Oc	Od	Ow	Ha	Al5c4
H(100)		−1.17	−1.03	−1.12	−1.10	−1.11	0.48	1.68
H(100)-1	0.53	−1.06	−1.02	−1.01	−0.98	−1.04	−0.16	1.66
H(100)-2	0.60	−1.09	−0.99	−1.02	−1.07	−0.95	−0.20	1.68
H(100)-3	0.61	−1.05	−0.99	−0.96	−0.99	−0.94	−0.20	1.44
H(100)-4a	0.51	−1.05	−1.00	−1.04	−0.99	−0.95	−0.18	1.67
H(100)-4b	0.54	−1.05	−1.00	−0.99	−1.07	−0.95	−0.14	1.52

---

In terms of the adsorption energy (Table 9), H(100)-1 is the most stable structure among those shown in Fig. 8 and is exothermic by 4.71 eV. The underlying reason for this finding is that the cluster and surface suffer the smallest deformations possible and that the interaction energy (−10.36 eV) is the second lowest (second to that of H(100)-3: −11.09 eV). For Ru₂ cluster adsorption, the interaction energy is 0.94 eV higher than that of the H(100)-1 configuration. In addition, the surface and cluster both experience greater deformation than in the H(100)-1 configuration, which contributes 6.28 eV to the interaction energy. Therefore, the adsorption energy of the H(100)-2 configuration is higher than that involved in Ru atom adsorption. For Ru₃ cluster adsorption, the adsorption energy is −4.26 eV, the second lowest value. This value could be related to the large gap in interaction energy and the cluster's larger deformation energy and surface cost. Although the deformation energy for H(100)-4a is 0.57 eV lower than that of H(100)-3, it could not balance the 1.14 eV gap in the interaction energy. Thus, the adsorption energy of the H(100)-4a is 0.57 eV higher than that associated with Ru₃ cluster adsorption. Another stable configuration for Ru₄ cluster adsorption is the H(100)-4b configuration, in which the metal–support interaction energy is only −9.58 eV. This adsorption configuration needs to trap 5.95 eV to satisfy its deformation cost. Consequently, the deposition of Ru clusters causes the H(100)-4b configuration to be exothermic by 3.63 eV, 0.06 eV less than H(100)-4b. Additionally, the binding energies shown in Table 9 indicate the Ru₄ cluster is the most stable configurations than others. And it is thermodynamically favorable to grow Ru_n (n = 2–4) clusters on hydrated (110) surface.

Table 9 Structural parameters and corresponding energies of Ru_n (n = 1–4) cluster adsorption in stable configurations on the hydrated (100) surface

Configuration	Eads (eV)	Eint (eV)	Edef,Run (eV)	Edef,surface (eV)	Ebind(Run/Al2O3) (eV)	Enuc (eV)	d(Ru–Ru) (Å)
H(100)-1	−4.71	−10.36	—	5.65	—	—	—
H(100)-2	−3.14	−9.42	0.29	5.99	−5.38	1.34	2.08
H(100)-3	−4.26	−11.09	0.23	6.60	−5.62	−1.40	2.33
H(100)-4a	−3.69	−9.95	0.18	6.08	−5.92	−2.08	2.41
H(100)-4b	−3.63	−9.58	0.24	5.71	−5.90	−2.03	2.40

---

The above results indicate the adsorption energy is a combination of the interaction energy and the deformation energy. As shown in Table 8, we rank the adsorption energies of Ru_n (n = 1–4) clusters on the hydrated (100) surface as follows: H(100)-2 > H(100)-4b > H(100)-4a > H(100)-3 > H(100)-1. This suggests that the H(100)-1 configuration is the most stable structure. Comparing the data in Tables 4 and 8, the adsorption energies for Ru_n (n = 1–4) clusters on the dehydrated (100) surface converge to within 0.35–2.44 eV, whereas the adsorption energies for Ru_n (n = 1–4) clusters on the hydrated (100) surface converge to within 0.06–1.57 eV, indicating that introducing surface hydroxyl groups lessen the energy variation. Additionally, we observe that the adsorption energy and interaction energy of the hydrated (100) surface are more negative than those of the dehydrated (100) surface, suggesting that introducing hydroxyl groups to the (100) surface strengthen the interactions. We also find that in the adsorption configurations, the H_a tends to stay away from O_b but approach the Ru_n (n = 1–4) clusters. As a result, the hydrated surface undergoes greater deformation than the dehydrated (100) surface. In general, the introduction of the surface hydroxyl groups not only influences the adsorption energy but also affects the interaction mechanism. On the hydrated (100) surface, the interaction mechanism in which the Ru_n (n = 1–4) cluster acted as a medium to accelerate the electron transfer from the O sites to H_a (Al_4c) sites is different from that on the dehydrated surface. In addition, comparing the Mulliken charges, we find more electron migration occurs on the hydrated surface, which responsible for the red-shift of CO absorbance.³³ This result is in consistent with the previous study on Ru/silica and Ru/zeolite catalysts.⁴⁵ Clearly, given the information in provided in the section “Ru_n (n = 1–4) clusters adsorption on dehydrated γ-Al₂O₃ (100) surface”, the surface hydroxyl groups exert different effects on the adsorption behavior of Ru_n (n = 1–4) clusters on the hydrated (110) and (100) surfaces. Therefore, the population analysis and charge density difference analysis could not explain the differences. As a result, studies conducted from additional perspectives are needed. Moreover, the hydroxyls enhance the stability of clusters on (100) surface.

3.4 Site-dependent Lewis acidity and basicity of surface: PDOS analysis

Understanding cluster–support interactions will contribute to the design and fabrication of heterogeneous catalysts with desirable stability and activity properties. The above sections discussed in detail the adsorption configuration from the perspective of geometric structure and corresponding energies, and the population and charge density difference analyses provided information about metal–support interactions. However, the primary origin of the different adsorption behaviors remains to be determined.

It is well known that the atoms' intrinsic Lewis acid/basicity is associated with charge transfer. Therefore, a detailed investigation of the Lewis acid/basicity of that atoms that participate in the adsorption configurations was performed. Prior works have investigated the Lewis acidity of surface alumina sites in terms of the energy of unoccupied bands and have reported that lower energy levels correlate with alumina sites with stronger Lewis acidity, thereby increasing the atom's adsorption stability. Surface O anions usually act as “basic” centers that provide charges to clusters. The Lewis basicity of O sites can be evaluated in terms of the energy of the highest occupied bands: higher energies indicate stronger donor abilities.^46,47 Therefore, the projected electronic density of states (PDOS) was used to characterize the intrinsic reactivity of surface alumina and O sites. Because the Lewis acid acts as an electron acceptor, we only considered the PDOS of the 3s3p orbital of surface Al (the lowest unoccupied bands in alumina), and used the band center to describe its Lewis acidity as follows:

The Lewis basicity of O sites can be defined similarly by considering the PDOS of the 2s2p orbital (the highest occupied bands). The band center can be described as follows:

For Al sites, a lower value of ε indicates stronger acidity and, thus, a stronger ability to accept electrons from donors. Similarly, because the O anion 2s2p orbital has the highest energy, it is also the most basic. Thus, we determine the ε values for Al sites and O sites on different surfaces, as listed in Table 10 and 11. The calculated PDOS are presented in the ESI.†

Table 10 The ε values for Al atoms on the dehydrated (110), dehydrated (100), hydrated (110), and hydrated (100) surfaces

Dehydrated (110)	Al3c	Al4c
ε	5.37	5.64
Hydrated (110)	Al3c	Al4c	Ha
ε	6.61	5.26	6.87
Dehydrated (100)	Al5c1	Al5c2	Al5c3	Al5c4
ε	5.87	5.34	5.82	5.88
Hydrated (100)	Al5c1	Al5c2	Al5c3	Al5c4	Ha
ε	6.03	6.66	5.99	5.74	5.17

---

Table 11 The ε values for O atoms on the dehydrated (110), dehydrated (100), hydrated (110), and hydrated (100) surfaces

Dehydrated (110)	O2c1	O2c2	O3c1	O3c2	O3c3
ε	−6.71	−7.18	−7.62	−7.90	−7.90
Hydrated (110)	O2c1	O2c2	O3c1	O3c2	O3c3	Ow
ε	−7.86	−7.02	−7.75	−7.90	−8.04	−7.57
Dehydrated (100)	Oa	Ob	Oc	Od	Oe
ε	−7.81	−7.29	−7.49	−7.24	−7.49
Hydrated (100)	Oa	Ob	Oc	Od	Oe	Ow
ε	−7.78	−9.39	−6.86	−7.04	−7.56	−6.45

---

Our geometry and population analysis predict that the presence of electropositive Ru_n clusters was a result of accumulating charge density on the Ru–Al bond and depleting on the Ru–O bond. It is therefore qualitative reasonable to say that two Lewis acid–base pairs are on the system. In other words, a Ru_n cluster is an acid in Ru–O pair while be a base in Ru–Al bond.⁴⁸ The above data reveals that, as expected, the low-coordinated sites are more acidic than the highly coordinated sites on the dehydrated surface. Nevertheless, some exceptions are observed: the Al_5c2 site on the dehydrated (100) surface is more acidic than the Al_4c site on the dehydrated (110) surface, indicating that the coordinate number is not the only factor that influences the acidity. By analyzing and comparing the sites' Lewis acidities, the dehydrated (110) surface is more acidic than the (100) surface; namely, the aluminum sites on the (110) surface are better able to receive electrons from Ru atoms. Furthermore, the information in Table 11 allows the following ranking to be constructed with regard to basicity on the dehydrated surface: O_2c1 > O_2c2 > O_d > O_b > O_c = O_e > O_3c1 > O_3c2; only the sites involved in the most stable configuration are analyzed. After comparing the sites' average basicity values, a subtle difference between the two surfaces becomes evident. Although the average basicity of (110) is roughly equal to that of (100) surface, the absence of electron induced by Ru–Al bond turns the Ru_n cluster into a strong Lewis acid, strengthening the Ru–O bond.⁴⁹ Thus, the stronger acceptor and nearly equal donor sites on the dehydrated (110) surface drive more electron transfer between clusters and the surface, indicating that the adsorption of Ru_n (n = 2–4) clusters on the dehydrated (110) surface is stronger than that of Ru_n (n = 2–4) clusters on the dehydrated (100) surface. Considering the work of Akane et al.,¹⁴ if we want to minimize the cluster–support interactions for ammonia synthesis, we should expose the (100) surface more than others. The adsorption of Ru atoms is, of course, the exception to the rule. Comparing the ε values of O_2c1, O_2c2, Al_4c, O_c, O_d, and Al_5c2 sites involved in bonds in the D(110)-1a and D(100)-1 configurations reveals that O_2c1 and O_2c2 are more basic than O_c and O_d, but Al_4c is less acidic than Al_5c2. As a weak acid, Ru atom may be able to accept few electrons from O site; the existence of a stronger base (O_2c1 and O_2c2) makes subtle difference when compared to O_c and O_d in Ru–O bond.⁴⁹ Conversely, a more acid (Al_5c2 site) would increase the Ru–Al bond strength. Therefore, the relatively high level of electron movement on the dehydrated (110) surface relative to the dehydrated (100) surface represents the combine effects of higher donor ability and lower acceptor ability; this trend is opposite to that observed for the adsorption ability.

As shown in Table 10, the Al_3c ε value increases when hydroxyl groups adsorbed on the Al_3c site whereas that of Al_4c decreases. A similar situation appears to hold for the basicity of the O sites: the basicity of the O_2c1, O_3c1, and O_3c3 sites decreases, while that of the O_2c2 site increases. By comparing the variation in the ε value, we determine that the net electron acceptor ability for Al sites and donor ability for oxygen sites decreases because of the introduction of surface hydroxyl groups. Consequently, Ru_n (n = 2–4) clusters accepted less electrons from O sites and thereby was less basic in Ru–Al bond when compared to dry surface. Thus, these groups increases the adsorption energy and interaction energy of the adsorption of Ru_n (n = 2–4) clusters on the hydrated (110) surface. The opposite is observed for the adsorption of Ru atoms. Comparing the ε values of the O_3c2, O_w, Al_4c (hydrated), O_2c1, O_2c2, and Al_4c (dehydrated) sites involved in bonding in the H(110)-1 and D(110)-1a configurations reveals that O_3c2 and O_w sites are less basic than O_2c1 and O_2c2, whereas Al_4c (hydrated) is more acidic than Al_4c (dehydrated), which plays a dominant role. Therefore, more electron movement occurs when Ru atom adsorption took place on the hydrated (110) surface than on the dehydrated (110) surface, decreasing the adsorption energy and interaction energy.

Based on the above discussion of energies, the surface hydroxyl exerts different effects on the adsorption behavior on the (100) surface than on the (110) surface. Thus, the introduction of hydroxyl groups must have changed the surface in some way. The ε values shown in Table 6 indicates that the surface hydroxyl groups decrease the Lewis acidity of the hydrated (100) surface sites, except for the Al_5c4 site. However, the Lewis acidity of the H_a involved in bonding is stronger than that of the Al sites, which explains the cluster–substrate interactions based on electron transfer from the Ru atom to the H_a (Al) sites. The acidity of H_a is also stronger than that of the Al sites on the dehydrated (100) surface. It is therefore more electrons were migrated from Ru_n (n = 1–4) clusters to H_a atom than to Al atom on dehydrated (100) surface. Although the Lewis basicities of the O_b and O_e sites decrease, the hydrated (100) surface includes relatively strongly basic O_w, O_a, O_c, and O_d sites. Overall, the basicity of the hydrated (100) surface is stronger than that of the dehydrated (100) surface. As a result, more basic O sites together with stronger acid Ru_n clusters increase the stability of Ru–O bonds. Therefore, the stronger adsorption on the hydrated (100) relative to the dehydrated (100) surface represents a combined effect of the increased donor ability and acceptor ability. To support this claim, we calculated relationships between the average (ε_Al − ε_O) values of the O and Al atoms involved in bonding and interaction energies (as shown in Fig. S22†). The results clearly show that interaction energies increase with the (ε_Al − ε_O) values (i.e., stronger Lewis acid–basicity pair leads to stronger interaction).

It is found that the adsorption performance of a single Ru atom exhibits distinctive stability other than Ru_n (n = 2–4) clusters. This means the supported single-Ru atom catalyst would show characteristic reactivity and selectivity in chemical process; for instance, catalyzing the CO₂ into CO instead of CH₄.²⁶ Moreover, the remarkable performance of supported single-atom catalysts has attracted extensive attention.^50–52 For example, Zhang et al. reported the activity of Ir₁/FeO_x in water gas shift is 1 order of magnitude higher than its clusterpart.⁵⁰ Studies for catalysis performance of supported single-Ru atom are in progress.

4. Conclusions

In this work, to investigate the influence of cluster size, surface structure, and hydroxyl groups on adsorption behavior and interactions, DFT calculations were conducted to characterize the adsorption and nucleation of Ru_n (n = 1–4) clusters on γ-Al₂O₃ (110) and (100) surfaces. The results indicate that the adsorption process is strongly sensitive to the cluster size and the surface microstructure (atomic and electronic structure) and environment. The adsorption energy is the product of coordination between the deformation energy and interaction energy. A single Ru atom prefers to adsorb on the (100) surface in the presence of small deformation, whereas strong metal–support interactions lead to the adsorption of Ru₄ clusters on the (110) surface. When the surface is dehydrated, the adsorption energy and interaction energy of Ru_n (n = 2–4) clusters adsorbed on the (110) surface are smaller relative to those of the (100) surface, whereas the opposite is observed for single Ru atom adsorption. The population and charge density difference analyses shows that the adsorption is stabilized by the O (donor)–Ru–Al (acceptor) charge movement effect. The stronger acceptor and nearly equal donor sites on the (110) surface drive increased electron movement, making the (110) surface relatively favorable for Ru_n (n = 2–4) cluster adsorption.

The introduction of hydroxyl groups decrease the acceptor ability of the Al sites and the donor ability of the O sites in the (110) surface, thereby reducing the driving force for electron transfer and lowering the adsorption stability of Ru_n (n = 2–4) clusters on the hydrated (110) surface. However, single Ru atoms preferentially adsorbs on the hydrated (110) surface over the dehydrated (110) surface because of the increased acidity of the Al_4c site. Conversely, the H_a acts as an active site and increases the stability of Ru_n (n = 1–4) cluster adsorption on the (100) surface. Specifically, the overall basicity of the O sites increase because of the introduction of surface hydroxyl groups. Thus, the electron transfer from the O sites to the H_a site proceeds through Ru_n clusters acting as a medium. In summary, the present results demonstrates that the adsorption process of Ru_n (n = 1–4) clusters is surface dependent.

Although the nucleation of Ru_n (n = 2–4) cluster on all surfaces is thermodynamically favorable, the process on γ-Al₂O₃ support is less stable than in isolated state. The hydroxyls effect on the nucleation process is varied with the exposed surface accompanied with facilitate agglomeration for large cluster on the (110) surface while suppress it on the (100) surface. Moreover, it is obviously that the nucleation process for Ru₄ cluster has a larger tendency, namely, the three-dimensional particles will be easily transformed from the two-dimensional. This work provides a theoretical foundation for experimental results, contributing to the design and synthesis of effective catalysts.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (grant no. 21173131) and the Taishan Scholar Project of Shandong Province (China).

Notes and references

1. L. X. Cui, Y. H. Tang, H. Zhang, L. C. Ouyang Jr, S. Q. Shi, H. Li and L. Q. Chen, First-principles investigation of transition metal atom M (M = Cu, Ag, Au) adsorption on CeO₂(110), Phys. Chem. Chem. Phys., 2012, 14, 1923–1933.
2. Z. Y. Duan and G. Henkelman, CO oxidation at the Au/TiO₂ boundary: the role of the Au/Ti_5c site, ACS Catal., 2015, 1589–1595.
3. S. Aranifard, S. C. Ammal and A. Heyden, On the importance of metal-oxide interface sites for the water–gas shift reaction over Pt/CeO₂ catalysts, J. Catal., 2014, 309, 314–324.
4. Z. F. Qin, J. Ren, M. Q. Miao, Z. Li, J. Y. Lin and K. C. Xie, The catalytic methanation of coke oven gas over Ni–Ce/Al₂O₃ catalysts prepared by microwave heating: effect of amorphous NiO formation, Appl. Catal., B, 2015, 164, 18–30.
5. L. Ran, Z. Qin, Z. Y. Wang, X. Y. Wang and Q. G. Bai, Catalytic decomposition of CH₂Cl₂ over supported Ru catalysts, Catal. Commun., 2013, 37, 5–8.
6. S. Y. Wu, Y. R. Lia, J. J. Ho and H. M. Hsieh, Density functional studies of ethanol dehydrogenation on a 2Rh/γ-Al₂O₃(110) surfaces, J. Phys. Chem. C, 2009, 113, 16181–16187.
7. Z. Q. Wang, Z. N. Xu, S. Y. Peng, M. J. Zhang, G. Lu, Q. S. Chen, Y. M. Chen and G. C. Guo, High-performance and long-lived Cu/SiO₂ nanocatalyst for CO₂ hydrogenation, ACS Catal., 2015, 5, 4255–4259.
8. D. H. Mei, V. A. Glezakou, V. Lebarbier, L. Kovarik, H. Y. Wan, K. O. Albrecht, M. Gerber, R. Rousseau and R. A. Dagle, Highly active and stable MgAl₂O₄-supported Rh and Ir catalysts for methane steam reforming: a combined experimental and theoretical study, J. Catal., 2014, 316, 11–23.
9. C. M. Li, S. T. Zhang, B. S. Zhang, D. S. Su, S. He, Y. F. Zhao, J. Liu, F. Wang, M. Wei, D. G. Evans and X. Duan, Photohole-oxidation-assisted anchoring of ultra-small Ru clusters onto TiO₂ with excellent catalytic activity and stability, J. Mater. Chem. A, 2013, 1, 2461–2467.
10. D. H. Mei, J. H. Kwak, J. Z. Hu, S. J. Cho, J. Szanyi, L. Allard and C. F. Peden, Unique role of anchoring penta-coordinated Al³⁺ sites in the sintering of γ-Al₂O₃-supported Pt catalysts, J. Phys. Chem. Lett., 2010, 1, 2688–2691.
11. D. F. Mukhamedzyanova, N. K. Ratmanova, D. A. Pichugina and N. E. Kuzmenko, A structural and stability evaluation of Au₁₂ from an isolated cluster to the deposited material, J. Phys. Chem. C, 2012, 116, 11507–11518.
12. H. Deng, Y. B. Yu, F. D. Liu, J. Z. Ma, Y. Zhang and H. He, Nature of Ag species on Ag/γ-Al₂O₃: a combined experimental and theoretical, ACS Catal., 2014, 4, 2776–2784.
13. A. Bruix, J. A. Rodriguez, P. J. Ramírez, S. D. Senanayake, J. Evans, J. B. Park, D. Stacchiola, P. Liu, J. Hrbek and F. Illas, A new type of strong metal–support interaction and the production of H₂ through the transformation of water on Pt/CeO₂ (111) and Pt/CeO_x/TiO₂ (110) catalysts, J. Am. Chem. Soc., 2012, 134, 8968–8974.
14. M. Akane, B. Ioan, A. Ken-ichi and N. Yoshio, Preparation of Ru nanoparticles supported on γ-Al₂O₃ and its novel catalytic activity for ammonia synthesis, J. Catal., 2001, 204, 364–371.
15. J. D. Li, E. Croiset and L. Ricardez-Sandoval, Effect of metal–support interface during CH₄ and H₂ dissociation on Ni/γ-Al₂O₃: a density functional theory study, J. Phys. Chem. C, 2013, 117, 16907–16920.
16. G. Pacchioni, Electronic interactions and charge transfers of metal atoms and clusters on oxide surface, Phys. Chem. Chem. Phys., 2013, 15, 1737–1757.
17. S. T. Zhang, C. M. Li, H. Yan, M. Wei, D. Evans and X. Duan, Density functional theory study on the metal–support interaction between Ru cluster and anatase TiO₂(101) surface, J. Phys. Chem. C, 2014, 118, 3514–3522.
18. Y. G. Wang, Y. Yoon, V. A. Glezakou, J. Li and R. Rousseau, The role of reducible oxide-metal cluster charge transfer in catalytic process: new insights on the catalytic mechanism of CO oxidation on Au/TiO₂ from ab initio molecular dynamics, J. Am. Chem. Soc., 2013, 135, 10673–10683.
19. H. Y. Liu, B. T. Teng, M. H. Fan, B. J. wang, Y. L. Zhang and H. G. Harris, CH₄ dissociation on the perfect and defective MgO(001) supported Ni₄, Fuel, 2014, 123, 285–292.
20. C. T. Campbell, Catalyst–support interactions: electronic perturbations, Nat. Chem., 2012, 4, 597–598.
21. K. R. Hahn, A. P. Seitsonen, M. Lannuzzi and J. Hutter, Functionalization of CeO₂(111) by deposition of small Ni clusters: effect on CO₂ adsorption and O vacancy formation, ChemCatChem, 2015, 7, 625–634.
22. J. Carrasco, D. López-Durán, Z. Y. Liu, T. Duchoň, J. Evans, S. D. Senanayake, E. J. Crumlin, V. Matolín, J. A. Rodríguez and M. V. Ganduglia-Pirovano, In situ and theoretical studies for the dissociation of water on an active Ni/CeO₂ catalyst: importance of strong metal–support interactions for the cleavage of O–H bonds, Angew. Chem., Int. Ed., 2015, 54, 3917–3921.
23. N. LóPZ and f. Illas, Electronic effects in the activation of supported metal clusters: density functional theory study of H₂ dissociation on Cu/SiO₂, J. Phys. Chem. B, 1999, 103, 8552–8557.
24. M. Mavrikakis, P. Stoltze and J. K. Nørskov, Making gold less noble, Catal. Lett., 2000, 64, 101–106.
25. Z. Kowalczyk, K. Stolecki, W. Raróg-Pilecka, E. Miśkiewicz, E. Wilczkowska and Z. Karpinski, Supported ruthenium catalysts for selective methanation of carbon oxides at very low CO_x/H₂ ratios, Appl. Catal., A, 2008, 342, 35–39.
26. J. H. Kwak, L. Kovarik and J. Szanyi, CO₂ reduction on supported Ru/Al₂O₃ catalysts: cluster size dependence of product selectivity, ACS Catal., 2013, 3, 2449–2455.
27. X. R. Shi and D. Sholl, Nucleation of Rh_n (n = 1–5) clusters on γ-Al₂O₃ surfaces: a density functional theory study, J. Phys. Chem. C, 2012, 116, 10623–10631.
28. Z. X. Liu, Y. H. Wang, J. R. Li and R. G. Zhang, The effect of γ-Al₂O₃ surface hydroxylation on the stability and nucleation of Ni in Ni/γ-Al₂O₃ catalyst: a theoretical study, RSC Adv., 2014, 4, 13280–13292.
29. C. H. Hu, C. Chizallet, C. Mager-Maury, M. Corral-Valero, P. Sautet, H. Toulhoat and P. Raybaud, Modulation of catalyst particle structure upon support hydroxylation: ab initio insights into Pd₁₃ and Pt₁₃/γ-Al₂O₃, J. Catal., 2010, 274, 99–110.
30. F. Wang, S. T. Zhang, C. M. Li, J. Liu, S. He, Y. F. Zhao, H. Yan, M. Wei, D. G. Evans and X. Duan, Catalytic behavior of supported Ru nanoparticles on the (101) and (001) facets of anatase TiO₂, RSC Adv., 2014, 4, 10834–10840.
31. M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Toulhoat, Use of DFT to achieve a rational understanding of acid-basic properties of γ-alumina surfaces, J. Catal., 2004, 226, 54–68.
32. H. Petitjean, H. Guesmi, H. Lauron-Pernot, G. Costentin, D. Loffreda, P. Sautet and F. Delbecq, How surface hydroxyls enhance MgO reactivity in basic catalysis: the case of methylbutynol conversion, ACS Catal., 2014, 4, 4004–4014.
33. A. S. Baird, K. M. Kross, D. Gottschalk, E. A. Hinson, N. Wood and K. A. Layman, Attenuated Total Reflection Fourier Transform Infrared Spectroscopic Investigation of CO Adsorption on Hydrated Ru/Al₂O₃, J. Phys. Chem. C, 2007, 111, 14207–14214.
34. A. M. Abdel-Mageed, S. Eckle and R. J. Behm, High selectivity of supported Ru catalysts in the selectivity CO methanation-water makes the difference, J. Am. Chem. Soc., 2015, 137, 8672–8675.
35. M. C. Valero, P. Raybaud and P. Sautet, Influence of the hydroxylation of γ-Al₂O₃ surfaces on the stability and diffusion of single Pd atoms: a DFT study, J. Phys. Chem. B, 2006, 110, 1759–1767.
36. J. H. Kwak, J. Z. Hu, A. Lukaski, D. H. Kim, J. Szanyi and C. H. F. Peden, Role of pentacoordinated Al³⁺ ions in the high temperature phase transformation of γ-Al₂O₃, J. Phys. Chem. C, 2008, 112, 9486–9492.
37. J. H. Kwak, J. Z. Hu, D. H. Kim, J. Szanyi and C. F. Peden, Penta-coordinated Al³⁺ ions as preferential nucleation sites for BaO on γ-Al₂O₃: an ultra-high-magnetic field ²⁷Al MAS NNR study, J. Catal., 2007, 251, 189–194.
38. J. R. Li, R. G. Zhang and B. J. Wang, Influence of the hydroxylation of γ-Al₂O₃ surfaces on the stability and growth of Cu for Cu/γ-Al₂O₃ catalyst: a DFT study, Appl. Surf. Sci., 2013, 270, 728–736.
39. Y. X. Pan, C. J. Liu, T. S. Wiltowski and Q. F. Ge, CO₂ adsorption and activation over γ-Al₂O₃-supported transition metal dimers: a density functional study, Catal. Today, 2009, 147, 68–76.
40. R. G. Zhang, H. Y. Liu, B. J. Wang and L. X. Ling, Insights into the effect of surface hydroxyls on CO₂ hydrogenation over Pd/γ-Al₂O₃ catalyst: a computational study, Appl. Catal., B, 2012, 126, 108–120.
41. Y. X. Pan, C. J. Liu and Q. F. Ge, Effect of surface hydroxyls on selective CO₂ hydrogenation over Ni₄/γ-Al₂O₃: a density functional theory study, J. Catal., 2010, 272, 227–234.
42. R. G. Zhang, B. J. Wang, H. Y. Liu and L. X. Ling, Effect of surface hydroxyls on CO₂ hydrogenation over Cu/γ-Al₂O₃ catalyst: a theoretical study, J. Phys. Chem. C, 2011, 115, 19811–19818.
43. Y. X. Pan, C. J. Liu and Q. F. Ge, Adsorption and protonation of CO₂ on partially hydroxylated γ-Al₂O₃ surfaces: a density functional theory study, Langmuir, 2008, 24, 12410–12419.
44. M. C. Valero, P. Raybaud and P. Sautet, Nucleation of Pd_n (n = 1–5) clusters and wetting of Pd particles on γ-Al₂O₃ surface: a density functional theory study, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045427.
45. S. Scirè, C. Crisafulli, R. Maggiore, S. Minicò and S. Galvagno, Influence of the support on CO₂ methanation over Ru catalysts: an FT-IR study, Catal. Lett., 1998, 51, 41–45.
46. R. Wischert, P. Laurent, C. Copéret, F. Delbecq and P. Sautet, γ-Alumina: the essential and unexpected role of water for the structure, stability, and reactivity of “defect” sites, J. Am. Chem. Soc., 2012, 134, 14430–14449.
47. G. Jenness, M. A. Christiansen, S. Caratzoulas, D. Vlachos and R. J. Gorte, Site-dependent Lewis acidity of γ-Al₂O₃ and its impact on ethanol dehydration and etherification, J. Phys. Chem. C, 2014, 118, 12899–12907.
48. H. Metiu, S. Chrétien, Z. P. Hu, B. Li and X. Y. Sun, Chemistry of Lewis acid–base pairs on oxide surface, J. Phys. Chem. C, 2012, 116, 10439–10450.
49. S. Chrétien and H. Metiu, Enhanced adsorption energy of and on the stoichiometric surface by coadsorption with other molecules, J. Chem. Phys., 2008, 128, 044714.
50. J. Lin, A. Q. Wang, B. T. Qiao, X. Y. Liu, X. F. Yang, X. D. Wang, J. X. Liang, J. Li, J. Y. Liu and T. Zhang, Remarkable performance of Ir₁/FeO_x single-atom catalyst in water gas shift reaction, J. Am. Chem. Soc., 2013, 135, 15314–15317.
51. B. T. Qiao, J. X. Liang, A. Q. Wang, C. Q. Xu, J. Li, T. Zhang and J. Y. Liu, Ultrastable single-atom gold catalysts with strong covalent metal–support interaction (CMSI), Nano Res., 2015, 8, 2913–2924.
52. H. S. Wei, X. Y. Liu, A. Q. Wang, L. L. Zhang, B. T. Qiao, X. F. Yang, Y. Q. Huang, S. Miao, J. Y. Liu and T. Zhang, FeO_x-supported platinum single-atom and pseudo-single-atom catalysts for chemoselective hydrogenation of functionalized nitroarenes, Nat. Commun., 2014, 5, 5634–5641.

---

Footnote

† Electronic supplementary information (ESI) available: The convergence test for the cutoff energy, the convergence test of the vacuum slab for the (100) and (110) surfaces, the potential energy profiles for the dissociation of H₂O on the dehydrated (100) and (110) surfaces, the charge density difference for different configurations of Ru_n (n = 1–4) clusters adsorbed on the (100) and (110) surfaces, the PDOS of atoms of different surfaces involved in Ru_n (n = 1–4) cluster adsorption. See DOI: 10.1039/c5ra28173c

---