Observation of large dielectric permittivity and dielectric relaxation phenomenon in Mn-doped lanthanum gallate†
Abstract
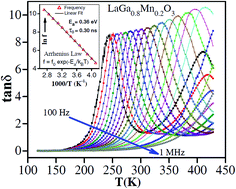
Polycrystalline LaGa1−xMnxO3 (x = 0, 0.05, 0.1, 0.15, 0.2 and 0.3) samples were prepared via the solid-state reaction method. These samples were characterized using synchrotron-based X-ray diffraction (XRD) and the X-ray absorption near edge structure (XANES). XRD studies confirm the orthorhombic structure for the prepared samples whereas XANES analysis reveals the co-existence of Mn3+ and Mn4+ in all Mn-doped samples. Dielectric relaxation is observed for all Mn-doped samples whereas a large dielectric constant (ε′) is perceived in samples with higher Mn doping (x = 0.2 and x = 0.3). Occurrence of a large ε′ is attributed to the huge decrease in impedance with increasing Mn doping which is governed by the hopping charge transport and extrinsic interface effects, whereas at high frequencies, this effect is observed possibly due to dipolar effects associated with the possible off-centrosymmetry of the MnO6 octahedron which is indicated by the pre-edge feature (Mn K-edge) in XANES and validated through P–E measurements. The appearance of dielectric relaxation was credited to the dipolar effects associated with the flipping of the Mn3+/Mn4+ dipole i.e., with the hopping of charge carriers between Mn3+ and Mn4+ under an external electric field. The value of activation energy (Ea = 0.36 eV), extracted from temperature-dependent dielectric data, reveals the polaron hopping mechanism.

 Please wait while we load your content...
Please wait while we load your content...