Quantitative description of the SABRE process: rigorous consideration of spin dynamics and chemical exchange

Abstract

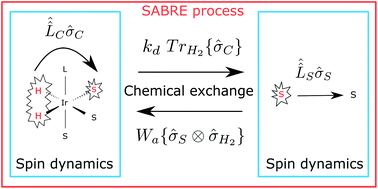
A consistent theoretical description of the spin dynamics and chemical kinetics underlying the SABRE (Signal Amplification By Reversible Exchange) process is proposed and validated experimentally. SABRE is a promising method for Nuclear Magnetic Resonance (NMR) signal enhancement, which exploits the transfer of strong non-thermal spin order from parahydrogen (the H₂ molecule in its singlet spin state) to a substrate in a transient organometallic complex. A great advantage of the SABRE method is that the substrate acquires strong nuclear spin polarization without being modified chemically, as it is only transiently bound to the complex. However, for the same reason theoretical treatment of SABRE meets difficulties because of the interplay of the spin dynamics with the association–dissociation reactions of the SABRE complex. Here we propose a quantitative model, which takes into account both the spin evolution in the SABRE complex and the substrate exchange between the free and bound forms. The model allows for the calculation of the substrate spin polarization dependency on various parameters, such as the external magnetic field strength and complex association–dissocation rates, and enables the simulation of experimental data for the SABRE time dependence. This investigation opens new insights into the SABRE process and can be generalized to treat more complex cases, such as SABRE facilitated by NMR pulses.

---

Introduction

The greatest impediment of Nuclear Magnetic Resonance (NMR) spectroscopy and imaging is low sensitivity. By making efficient use of strong non-thermal nuclear spin polarization, termed spin hyperpolarization, it is possible to boost weak NMR signals. One of the hyperpolarization methods is paraHydrogen Induced Polarization (PHIP),¹ which converts the non-thermal spin order of parahydrogen (pH₂, the H₂ molecule in its nuclear singlet state) into detectable magnetization.

In a recent version of PHIP known as Signal Amplification By Reversible Exchange (SABRE), introduced by Atkinson et al.² in 2009, a target substrate, S, is hyperpolarized at a complex, consisting of S, pH₂ and a suitable organometallic catalyst (Fig. 1). The non-hydrogenative and reversible nature of the complex formation enables the creation of continuously renewable polarization.^3–6

Fig. 1 Schematic representation of the exchange processes taking place in an Ir-based SABRE system. (a) Exchange of a substrate, S, between the bound form (left, see complex C) and the free form. Polarization of S is formed in complex C due to spin order transfer from Ir-HH; the polarized substrate is released in the course of dissociation of C to complex C₁ and free S. The rate constants of the dissociation–association process C ↔ C₁ + S are k_d and k_a. (b) H₂ exchange in the intermediate complex C₁. Here we assume that the reverse process is almost absent because pH₂ in the solution is very rapidly replenished. In the scheme, non-thermally polarized species are highlighted.

SABRE has developed into a versatile technique: it was extended to the polarization of heteronuclei,^7,8 used in quantitative trace analysis^5,9 and utilized for polarization of biologically relevant molecules.^10,11 Some of the limitations of the SABRE method, such as the use of organic solvents¹² or the requirement for low polarization fields, have been recently addressed.^4,5,13

A prerequisite for optimizing the performance of the SABRE method is developing a theoretical description of the underlying reaction and spin dynamics as well as their interplay. The theoretical treatment to this point, is mostly focused on the spin dynamics in the SABRE complex^6,14,15 and the magnetic field dependence of the SABRE polarization.¹⁶ Previous studies have revealed the importance of Level Anti-Crossings (LACs)^15,17 for a coherent transfer of spin order from pH₂ to substrate.

As far as the interplay of the spin dynamics with the chemical exchange kinetics is concerned it was, until recently, considered only by Adams et al.¹⁴ and Hövener et al.⁶ who suggested approximate methods to treat dissociation of the SABRE complex. Very recently, some of us have proposed¹⁸ a phenomenological approach, which assumes that kinetics and spin dynamics can be separated and which is focused on the steady-state equilibrium of the SABRE hyperpolarization process. In this work, the rates of the processes responsible for SABRE formation were derived, while the spin dynamics were considered by defining the amount of spin order transferred in the SABRE complex until it dissociates. Under these assumptions, a relatively simple analytical “SABRE formula”, i.e., an expression for the substrate spin polarization, was obtained.

A comparison of the capabilities of the different approaches is presented in the conclusions to this article.

Developments of the SABRE technique including RF-SABRE, applications to quantitative trace analysis, feasibility of time-dependent SABRE experiments (as presented in this work) as well as the need for the optimization of the SABRE chemical systems, result in the need for a rigorous quantitative approach to SABRE. The essence of this work is to address this need by introducing a theoretical model, using real NMR properties of the substrate and SABRE complex, and reaction rates rather than phenomenological parameters.

In this contribution we describe and experimentally verify a versatile model combining both the spin dynamics and chemical exchange kinetics underlying the SABRE process. We propose a set of equations for the spin density matrices of a polarized substrate and SABRE complex, which allows one to take into account the spin dynamics and reaction kinetics. Our model neither invokes any ad hoc procedures for treating association–dissociation of the SABRE complex nor does it require phenomenological assumptions for describing the interplay of the chemical reactions and spin dynamics. Consequently, with this model we are able to consider for the first time both steady-state and dynamic behavior of SABRE experiments.

By using this new model we calculate the dependence of the SABRE effect on the parameters describing the spin dynamics of the SABRE complex and chemical exchange rates and present a detailed discussion on the dependence of polarization on the relevant parameters. We demonstrate that our model correctly reproduces the magnetic field dependence of polarization and describes such peculiar features of the SABRE process as the non-monotonous dependence of the SABRE effect on the dissociation rate. Finally, we present an experimental example for validation of the theory.

Theory and methods

A. Chemical kinetics

We describe the SABRE-system as a pool of free substrate, complexes and pH₂. The treatment of the chemical kinetics follows closely the consideration of ref. 18.

Fig. 1 illustrates the exchange kinetics of the SABRE process which involve an intermediate complex C₁ (Fig. 1b) consisting of H₂ and the catalyst. C₁ exchanges two dihydride protons bound to iridium (denoted as Ir-HH) with the dihydrogen pool in solution. The intermediate complex later binds a substrate molecule, S, from the pool of free substrate, at one of the equatorial positions thereby forming the SABRE-complex C (Fig. 1a). These chemical exchange processes are described by the rate eqn (1):

where k_a and k_d are the association and dissociation rate constants and [X] denotes the concentration of the corresponding species, X. As chemical equilibrium is rapidly established in the system, we set d[S]/dt = d[C]/dt = 0 and obtain the following relation:Hereafter, we use the association rate W_a instead of the rate constant k_a and equilibrium concentrations [S], [C] and [C₁]. In the foregoing analysis we find it convenient to operate with the fractions of the complex C and free S (i.e. bound S and free S) instead of the concentration, which are f_S = [S]/([S] + [C]) and f_C = [C]/([S] + [C]). These new quantities obey eqn (3):Hereafter, for the sake of simplicity, we assume that the content of pH₂ is rapidly replenished in the reacting system (this is the case when pH₂, supplied by an external source, continuously and efficiently replaces H₂ in solution). In this situation the concentration [C₁] is the sum of concentrations of C₁ with pH₂ and orthohydrogen (oH₂, H₂ in its triplet state):

[C₁] = [C₁(pH₂)] + [C₁(oH₂)] = (f_pH2 + f_oH2)[C₁] (4)

Here f_pH2 and f_oH2 denote the fraction of pH₂ and oH₂ in the system, i.e., their fractions in the external H₂ source. For normal (thermally polarized) hydrogen f_pH2 : f_oH2 = 1 : 3. Therefore, at all times we have [C₁(pH₂)]/[C₁(oH₂)] = f_pH2/f_oH2. A more general and complex case is considered in ESI.†

B. SABRE kinetics equations

In order to treat not only the reaction dynamics, but also spin evolution, it is necessary to make a transition from the fractional probabilities f_S and f_C to the spin density matrices of S and C. The reason is that during the limited lifetime of the SABRE complex, there is a conversion of the singlet spin order from pH₂ into substrate polarization. As we show below, the resulting conversion efficiency is a complex function of the chemical rates and NMR parameters of the complex (notably, the spin order transfer is efficient only within a specific magnetic field range where the spin system has a LAC). Furthermore, because of the continued exchange, the polarization of the free substrate pool increases until a steady state is reached, that is limited by relaxation.

Let us now introduce a set of kinetic eqn (5) for the density matrices [small sigma, Greek, circumflex]_S and [small sigma, Greek, circumflex]_C of the free substrate in solution and of the SABRE-complex, respectively. Such equations allow for the analysis of the dynamic behavior. Furthermore, they enable the consideration of multiple association-dissociation events and polarization transfer from pH₂ to S in complex C. Therefore, the equations directly introduce averaging over the times of complex formation and dissociation. These kinetics equations can be written as follows:

In both equations we treat the spin dynamics by the Liouville super-operators and . Each Liouville operator describes coherent spin evolution (given by the corresponding Hamiltonian, ) and spin relaxation (given by the corresponding relaxation operator, ), i.e., The form of these operators is discussed later in the article and also in ESI.† In each equation the terms comprising the rate W_a take account of association of S with C₁ and terms with the rate k_d correspond to dissociation of SABRE-complexes, that leads to release of S. We choose the normalization such that Tr{[small sigma, Greek, circumflex]_S} + Tr{[small sigma, Greek, circumflex]_C} = 1; in this situation, the trace of [small sigma, Greek, circumflex]_S and [small sigma, Greek, circumflex]_C is equal to the probability of finding the substrate in the free and bound form, respectively, i.e., Tr{[small sigma, Greek, circumflex]_S} = f_S and Tr{[small sigma, Greek, circumflex]_C} = f_C. Consequently, when applying the trace operation to eqn (5) one obtains eqn (3). The state of H₂ in the complex is described by the density matrix of which is introduced in the following way:

because [small sigma, Greek, circumflex]_oH2 = (1̂ − [small sigma, Greek, circumflex]_pH2)/3, where 1̂ is the 4 × 4 unity operator; when the density matrices are normalized in such a way that Tr{σ_pH2} = Tr{σ_oH2} = 1.

The structure of the terms comprising the direct product and the trace operation in eqn (5) takes into account the fact that the dimensionality of [small sigma, Greek, circumflex]_S and [small sigma, Greek, circumflex]_C is different, because the SABRE-complex has at least two spins (i.e., the protons of Ir-HH) more than S. In the first equation, the dimensionality is reduced by taking the partial trace over the spin states of Ir-HH, this operation is denoted by Tr_H2. In the second equation the extra dimensionality is generated by the direct product with (spin density matrix of pH₂). Here we do not present the derivation of the kinetic equations, but mention that they can be obtained as the Markovian limit of the integral encounter theory^19,20 – a general and rigorous approach to chemical reactions of arbitrary complexity in the condensed phase. A similar treatment to describe exchange in NMR has been proposed by Alexander and Binsch;²¹ this theory was used later by Kühne et al.²² to describe manifestation of chemical exchange in NMR spectra. Buntkowsky et al.²³ have applied this approach to describe reaction pathway effects on PHIP.

To solve the set of eqn (5) we work in the Liouville space and define an analogue of the ‘density matrix’ of the entire system, comprising S and the complex, which is denoted as [small sigma, Greek, circumflex]. Using the original set of equations we obtain the following linear equation for [small sigma, Greek, circumflex] written in the matrix form:

with a generalized superoperator

In this formulation, the diagonal elements correspond to the spin dynamics, including coherent spin evolution and relaxation, as well as the reaction terms. The off-diagonal elements describe the exchange between the free substrate and the complex. The super-operators are unity matrices with dimensionality of either substrate or complex dimensionality squared.

The advantage of describing the system in this manner is the computationally efficient way of solving eqn (7), by calculating the propagator in eqn (9), instead of numerically integrating eqn (5):

In our model we assume that initially the spin system is non-polarized and is at chemical equilibrium, then [small sigma, Greek, circumflex](t = 0) is of the form:

We now discuss how the different terms in eqn (8) are constructed.

For the description of exchange, it is necessary to define both the partial trace superoperator, see eqn (11), which describes the dissociation of the complex, and the Liouville space representation of the direct product, describing the association of substrate and H₂:

We included these derivations, which are mainly based on index transformations, in ESI.† The partial trace operation is equivalent to a “quantum measurement” in removing all coherences between the substrate and Ir-HH. This is the basis of the quantum Zeno effect,^24,25 which manifests in our model (see Results).

C. Spin dynamics

In isotropic liquids, the coherent time evolution of a system of N scalar-coupled spins at an external magnetic field of a strength B is described by the following time-independent Hamiltonian²⁶where ω_i = γB(1 + δ_i) is the Lamor frequency of the i-th spin, δ_i is its chemical shift, γ is the proton gyromagnetic ratio and J_ij is the scalar spin–spin coupling constant between the i-th and j-th spin. The corresponding superoperator, which satisfies the relation is constructed as follows:

In order to find the steady-state solution of eqn (9), relaxation of both free and bound substrate as well as of hydrogen in the complex, needs to be taken into account.

For this contribution, we decided to employ a previously described method,^27,28 based on random fluctuations of local fields (experienced by each spin) in the extreme narrowing regime. In this approximation, the high-field relaxation rates and the parameters of the Hamiltonian, see eqn (12), are the only parameters required for the calculation of the relaxation superoperator , which describes relaxation of polarization to zero (here we neglect the small thermal polarization). The necessary steps for implementing this approach are described in ESI.† The Liouvillian combines relaxation and coherent evolution.

The parameters used in all simulations, unless otherwise specified, are listed in Table 1.

Table 1 J-Couplings, chemical shifts and relaxation times used as parameters in the presented model. Ha and Hb denote the Ir-HH protons, S stands for the substrate proton

---

For simplicity and clarity, we take into account only a single substrate spin and two hydrogen spins, resulting in a three-spin complex and single-spin free substrate. Generalization of our consideration to a multi-nuclear spin system is straightforward.

The magnetic field of the LAC can be found from the following expression:¹⁵

Using the constants in Table 1, this yields B_LAC ≅ 5.6 mT. Here, ν^LAC_HH and ν^LAC_S are the NMR frequencies of the Ir-HH protons and the substrate proton in the complex at the field B_LAC respectively, and δ_HH and δ_S denote their chemical shifts; J_HH is the J-coupling between the Ir-HH protons; J_Ha,S and J_Hb,S are the Ir-HH to substrate couplings. Unless otherwise specified, we assume 100% pH₂ enrichment (f_pH2 = 1).

To quantify SABRE polarization from [small sigma, Greek, circumflex](t), we computed [small sigma, Greek, circumflex]_S(t) and determined the populations (i.e., the diagonal elements of [small sigma, Greek, circumflex]_S), N_α and N_β, for the spin-up state, |α〉, and spin-down state, |β〉, of S. The polarization value, P_S, of the free substrate is then determined as follows:

D. Experimental methods

Data were acquired using a previously described^17,29 fast field-cycling setup, where the polarization field is set by moving the NMR probe with the sample in the fringe field of a superconducting magnet superimposed on the magnetic field of additional electromagnetic coils. The experimental setup is capable of transfer times below 0.3 s.

All data was acquired for the polarization field B_p = 7 mT. At this field, the H₂ gas (92% of pH₂; pH₂ Generator, Bruker, USA) was bubbled through the sample for a time interval varied from 7 s to 60 s. In the next step, the sample was shuttled into the NMR spectrometer within 0.5 s and an NMR spectrum was obtained at a field of 7 T by applying a 90° excitation pulse. The field profile, i.e., variation of the magnetic field as a function of time, was precisely controlled and reproducible.

The data presented were acquired with a solution of 1.2 mM IrImes(COD)Cl catalyst³⁰ in 1.5 ml 99.9% CD₃OD (Sigma-Aldrich) solvent using pyridine (Py, Sigma-Aldrich) as the substrate with variable concentration.

Because of the evaporation of methanol, concentrations are difficult to control over time; for this reason, they were later determined from the NMR spectra.

The enhancement factor, was calculated by dividing the line intensity integral, S_H, in a hyperpolarized spectrum by the corresponding integral, S_T, in the thermal spectrum (Fig. 2). In the experiments reported here, we present the enhancement evaluated for all protons of Py (including Py in the complex).

Fig. 2 Typical ¹H NMR spectra of thermally polarized (top) and SABRE-polarized (bottom) pyridine (14 mM) with IrImesCODCl complex (1.2 mM) in CD₃OD acquired at 7 T. For the SABRE spectrum the polarization field is B_p = 7 mT. Signal of the ortho-, meta- and para-protons of pyridine (Py) are indicated as o-Py, m-Py and p-Py, respectively; ePy denotes Py bound to the SABRE complex in the equatorial positions.

Results

A. SABRE magnetic field dependency

The polarization transfer mechanism acting in our model is the coherent evolution of the SABRE complex, facilitated by the Hamiltonan Ĥ defined in eqn (12). The calculated dependence of the free substrate polarization on the magnetic field (Fig. 3) has a single maximum. This feature does exhibit the same properties, with regard to the sign of polarization and position, as reported in previous studies.¹⁵ The magnetic field B_LAC, at which the polarization transfer is efficient, is given by the LAC at 5.6 mT. At this LAC, the energy levels corresponding to spin states |Sα〉 and |T₊β〉 come close together and become mixed in a coherent process. Consequently, the population from the |Sα〉 state (enriched due to the fact that we use pH₂) is transferred to the |T₊β〉 state (initially depleted in SABRE experiments) and the substrate proton is predominantly in the spin-down state, i.e., it becomes negatively polarized. The position of the LAC feature can be reproduced by calculations of spin dynamics only; however, such calculations cannot predict the absolute polarization level and the shape of the SABRE field dependence.

Fig. 3 Simulated steady-state free substrate polarization as a function of the polarization field B_p for different dissociation rates k_d. The ratio of the association-dissociation rates, is 0.1, all parameters except for W_a and k_d are listed in Table 1.

By introducing the interplay of exchange kinetics and relaxation, we obtain the value of polarization. Upon increase of W_a and k_d (at a constant ratio of rates, W_a/k_d), polarization first increases and then decreases (Fig. 3).

This effect is described in more detail in subsequent sections of the text. The field dependence of polarization always has one negative maximum at B_p = B_LAC, but the width of the maximum is sensitive to the exchange rates. The reason for such a dependency is the interference of the exchange processes with spin mixing at the LAC. At the center of the LAC, the mixing frequency is minimal (equal to ω_LAC) but the mixing amplitude is maximal.¹⁷ Consequently, the maximal polarization is always formed at B_p = B_LAC but the mixing efficiency becomes suppressed when ω_LAC ≪ k_d. Suppression of spin mixing in the SABRE complex at high k_d is less pronounced when the spin system is moved away from the LAC, but P_S remains lower than when B_p = B_LAC.

B. Exchange rate dependencies

Using the presented model, it is possible to describe the spin mixing in the SABRE complex under chemical exchange, a peculiarity of the SABRE technique that was not included in previous models.

First, we demonstrate the kinetic traces, i.e. the time dependence of SABRE polarization, P_S(t), see Fig. 4. We found that the build-up time and steady-state polarization level do not only depend on the spin relaxation rates but are also strongly affected by the exchange rates (Fig. 4 and 5).

Fig. 4 Polarization build-up for different W_a at B_p = B_LAC. We used fixed k_d value of 10 s⁻¹; all other parameters are listed in Table 1.

Fig. 5 The dependence of the steady-state polarization on the association rate W_a. Here k_d = 10 s⁻¹, B_p = B_LAC. All other parameters are listed in Table 1. Since W_a = k_d[C]/[S], we define the upper x-axis as [C]/[S].

The association rate, W_a, used in our model is proportional to the concentration of complexes and the inverse of the substrate concentration as shown in eqn (2). Fig. 5 illustrates this dependence for a fixed dissociation rate. At small W_a rates almost all substrate molecules are in the free form. Consequently, the polarization is strongly limited by spin relaxation. When the association rate is high, so too is the probability to find substrate in the complex. Therefore, the steady-state polarization level is determined by the efficiency of coherent evolution, i.e., by the k_d rate, and by spin relaxation rates of nuclei in the SABRE complex.

The behavior obtained upon varying the dissociation rate, is somewhat more complicated (Fig. 6).

Fig. 6 Simulated steady-state polarization as a function of the dissociation rate constant, k_d, for different ratios W_a/k_d = [C]/[S], at B_p = B_LAC. All other parameters are listed in Table 1.

There is a distinct maximum of polarization, the exact position of which is determined by the interplay of the coherent spin evolution, spin relaxation and chemical exchange. At low k_d rates exchange is too slow and the polarization is therefore limited by relaxation effects. Alternatively, when k_d is high, the coherent evolution responsible for polarization transfer is suppressed by the rapid dissociation of the complex. This is, in effect, a manifestation of the quantum Zeno effect which is facilitated by the loss of coherence in the system.

When the polarization transfer mechanism is cross-relaxation, the only important parameter is the ratio, W_a/k_d, of the association–dissociation rates, i.e., the relation between f_S and f_C. However, this is not true in the case of coherent evolution: when the parameter W_a/k_d is kept constant the resulting polarization depends on k_d (or W_a). The reason is that the fast exchange processes irreversibly destroys the spin coherence, which is formed at the LAC and is responsible for spin order transfer from pH₂. As a consequence, the transfer process is continuously interrupted and eventually will be suppressed at very large values of W_a or k_d. In other words, because of random reaction events, coherent evolution starts from the beginning. Effectively this is the same as performing “quantum measurements” on the spin system thereby continuously projecting it onto an eigen-state. Our results are in qualitative agreement with a study of SABRE enhancement for different catalysts with varying exchange rates, conducted by van Weerdenburg et al.,³¹ who found that the enhancement decreases for higher exchange rates.

In addition to the dependence on chemical exchange rates we analyzed the dependence of the SABRE polarization of the fraction of pH₂ in the external source of the H₂ gas. Our model predicts a different polarization dependence on the fraction of parahydrogen (Fig. 7) compared to hydrogenative PHIP, where a strictly linear dependence is expected.³²

Fig. 7 Polarization dependence on the fraction of parahydrogen for different values of W_a. Here k_d = 10 s⁻¹, all other parameters are taken from Table 1. Polarization was normalized by the factor P_S(f_pH2 = 1).

C. Optimal conditions for SABRE

The relaxation rates of the Ir-HH protons as well as of free and bound substrate are essential for reaching a high level of steady-state polarization. When relaxation in the complex is fast, the efficiency of polarization transfer is limited. In most cases however, the limiting factor is the relaxation of the free substrate, opposing the build-up of polarization.

In the case of the coherent transfer mechanism studied in this work, an increase of the exchange rates eventually quenches the coherent evolution and reduces polarization. Therefore our model can help in the design or choice of appropriate catalysts (regarding the exchange and relaxation rates).

A decrease of the substrate concentration and, hence, the increase of the association rate (relative to k_d, see eqn (2)) results in an increased enhancement (see below).

It should be noted that, for low relaxation rates, the model presented predicts polarization levels greater than the previously found limit¹⁸ of P_S = 0.5. This is because our model takes into account multiple association–dissociation events: when an already polarized substrate enters in the complex with pH₂ again, its polarization can be boosted further.

D. Experimental validation

To verify the predictive power of our model, we compared measured and theoretical polarization build-up curves for different concentrations of S (Fig. 8). The only free parameters considered in the fit are the association rates W_a for each dataset and a global efficiency factor, which gives the relation between simulated polarization and observed NMR enhancement. We used a fixed value k_d = 10 s⁻¹ for the simulations, in agreement with previous studies.^30,31

Fig. 8 Comparison of simulated and measured time-dependent enhancements, for different substrate (here Py) concentrations, as a function of the bubbling time (i.e., the time the sample was bubbled with pH₂ at the polarization field).

The rate constants determined as the free parameters of the fits shown in Fig. 8 are plotted in Fig. 9 and obey the predicted linear dependency of eqn (2). The slope of the W_a dependence on 1/[S] is 10.3 ± 0.9 s⁻¹ mM, i.e., it is indeed close to the product of k_d and [C]. A small deviation from proportionality between W_a and 1/[S] in Fig. 9 is attributed to the fact that after bubbling with pH₂ some time is needed so that the concentration of pH₂ in the solution can reach its steady-state value. The resulting transient effects give a slight experimental inaccuracy. Furthermore, solvent evaporation during each dataset acquisition leads to an increase of concentration of up to 5% during the experiment.

Fig. 9 Dependency of the association rates W_a (with error bars, as obtained by fitting the data in Fig. 8) as a function of the inverse substrate concentration. The data shows the expected linear behavior, see eqn (2), with the slope of k_d[C] = 10.3 ± 0.9 s⁻¹ mM.

Conclusions and outlook

In this contribution we present a theoretical model that treats both reaction and spin dynamics in SABRE experiments. Our consideration enables the description of the SABRE process with a set of equations avoiding phenomenological assumptions that were used previously for treating association–dissociation of the SABRE complex. In this model, relaxation effects are also taken into account, which is a prerequisite for reproducing correctly the steady-state polarization level.

We were able to calculate the SABRE dependence on time, external magnetic field and exchange rates. Dependence on the exchange rates exhibits a particularly interesting behavior: at high k_d rates the polarization transfer efficiency significantly decreases, which is a manifestation of the “quantum Zeno effect”. Furthermore, we provided experimental validation of the proposed theoretical treatment. The presented model is the most general approach to SABRE theory so far and overcomes many of the limitations inherent to previous descriptions (see Table 2). Previous approaches are limited and cannot be employed to describe, for example, the evolution of multi-spin systems, time dependent SABRE-polarization or SABRE formed under the action of RF-irradiation or NMR pulse sequences (RF-SABRE).

Table 2 Comparison of the capabilities of the spin dynamics based model proposed by Adams et al.,¹⁴ the analytical model of Barskiy et al.¹⁸ and the treatment suggested in this work

	Spin dynamics model^14	Analytical model^18	This work
a It should be noted that in principle relaxation can be included in the spin dynamics based treatment but, to the best of our knowledge, this has never been reported.
Coherent spin evolution	✓	✗	✓
Chemical exchange	✗	✓	✓
Relaxation	✗^a	✓	✓
Time dependence of polarization	✗	✓	✓
Multi-spin systems	✓	✗	✓
RF-SABRE	✗	✗	✓
Multiple association–dissociation events	✗	✗	✓

---

Our treatment paves the way to provide a quantitative description of SABRE and may be applied to address the following important challenges. Firstly, it can be used to efficiently design new SABRE catalysts, optimized in terms of exchange rates, spin relaxation rates and structure of the coupled spin networks in SABRE complexes. Secondly, we can calculate the entire field dependence of SABRE-derived polarization. In particular, polarization transfer to hetero-nuclei, occurring at very low fields (being in the range of several 100 nT to tens of μT) can be treated and optimal strength of the external magnetic field can be determined. Thirdly, we can extend our treatment to take into account the additional stages of chemical reactions underlying the SABRE process. Likewise, more transient SABRE complexes can be considered. Fourthly, we are able to extend the treatment to the cross-relaxation mechanism of polarization transfer. This is (most likely) the dominant transfer mechanism at high magnetic fields. Fifthly, it is possible to treat SABRE in the presence of resonant RF-fields, which is a method of choice to transfer polarization to protons⁴ and spin-1/2 hetero-nuclei^8,13 at high magnetic fields. Furthermore, we are able to treat polarization transfer by RF-pulse sequences, which can be done by solving the equations for σ_S and σ_C for a time-dependent Hamiltonian Ĥ.

Acknowledgements

Derivation of the general kinetic equations has been supported by the Russian Science Foundation (project number 14-13-01053). JBH wishes to acknowledge support by the DFG (HO-4604/2-1) and the German Consortium for Translational Cancer Research (DKTK). SK acknowledges the Russian Foundation for Basic Research for a travel grant (project 15-33-50136).

Notes and references

1. C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541–5542.
2. K. D. Atkinson, M. J. Cowley, P. I. P. Elliott, S. B. Duckett, G. G. R. Green, J. López-Serrano and A. C. Whitwood, J. Am. Chem. Soc., 2009, 131, 13362–13368.
3. J.-B. Hövener, N. Schwaderlapp, T. Lickert, S. B. Duckett, R. E. Mewis, L. A. R. Highton, S. M. Kenny, G. G. R. Green, D. Leibfritz, J. G. Korvink, J. Hennig and D. von Elverfeldt, Nat. Commun., 2013, 4, 2946.
4. A. N. Pravdivtsev, A. V. Yurkovskaya, H.-M. Vieth and K. L. Ivanov, J. Phys. Chem. B, 2015, 119, 13619–13629.
5. N. Eshuis, R. L. E. G. Aspers, B. J. A. van Weerdenburg, M. C. Feiters, F. P. J. T. Rutjes, S. S. Wijmenga and M. Tessari, Angew. Chem., Int. Ed., 2015, 54, 14527–14530.
6. J.-B. Hövener, S. Knecht, N. Schwaderlapp, J. Hennig and D. von Elverfeldt, ChemPhysChem, 2014, 15, 2451–2457.
7. T. Theis, M. L. Truong, A. M. Coffey, R. V. Shchepin, K. W. Waddell, F. Shi, B. M. Goodson, W. S. Warren and E. Y. Chekmenev, J. Am. Chem. Soc., 2015, 137, 1404–1407.
8. A. N. Pravdivtsev, A. V. Yurkovskaya, H. Zimmermann, H.-M. Vieth and K. L. Ivanov, RSC Adv., 2015, 5, 63615–63623.
9. N. Eshuis, B. J. A. van Weerdenburg, M. C. Feiters, F. P. J. T. Rutjes, S. S. Wijmenga and M. Tessari, Angew. Chem., Int. Ed., 2015, 54, 1481–1484.
10. H. Zeng, J. Xu, J. Gillen, M. T. McMahon, D. Artemov, J.-M. Tyburn, J. A. B. Lohman, R. E. Mewis, K. D. Atkinson, G. G. R. Green, S. B. Duckett and P. C. M. van Zijl, J. Magn. Reson., 2013, 237, 73–78.
11. J.-B. Hövener, N. Schwaderlapp, R. Borowiak, T. Lickert, S. B. Duckett, R. E. Mewis, R. W. Adams, M. J. Burns, L. A. R. Highton, G. G. R. Green, A. Olaru, J. Hennig and D. von Elverfeldt, Anal. Chem., 2014, 86, 1767–1774.
12. M. L. Truong, F. Shi, P. He, B. Yuan, K. N. Plunkett, A. M. Coffey, R. V. Shchepin, D. A. Barskiy, K. V. Kovtunov, I. V. Koptyug, K. W. Waddell, B. M. Goodson and E. Y. Chekmenev, J. Phys. Chem. B, 2014, 118, 13882–13889.
13. T. Theis, M. Truong, A. M. Coffey, E. Y. Chekmenev and W. S. Warren, J. Magn. Reson., 2014, 248, 23–26.
14. R. W. Adams, S. B. Duckett, R. A. Green, D. C. Williamson and G. G. R. Green, J. Chem. Phys., 2009, 131, 194505.
15. A. N. Pravdivtsev, A. V. Yurkovskaya, H.-M. Vieth, K. L. Ivanov and R. Kaptein, ChemPhysChem, 2013, 14, 3327–3331.
16. A. N. Pravdivtsev, K. L. Ivanov, A. V. Yurkovskaya, P. A. Petrov, H.-H. Limbach, R. Kaptein and H.-M. Vieth, J. Magn. Reson., 2015, 261, 73–82.
17. K. L. Ivanov, A. N. Pravdivtsev, A. V. Yurkovskaya, H.-M. Vieth and R. Kaptein, Prog. Nucl. Magn. Reson. Spectrosc., 2014, 81, 1–36.
18. D. A. Barskiy, A. N. Pravdivtsev, K. L. Ivanov, K. V. Kovtunov and I. V. Koptyug, Phys. Chem. Chem. Phys., 2016, 18, 89–93.
19. K. L. Ivanov, N. N. Lukzen, A. A. Kipriyanov and A. B. Doktorov, Phys. Chem. Chem. Phys., 2004, 6, 1706–1718.
20. K. L. Ivanov, N. N. Lukzen and A. B. Doktorov, J. Chem. Phys., 2004, 121, 5115–5124.
21. G. Binsch, J. Am. Chem. Soc., 1969, 91, 1304–1309.
22. R. O. Kühne, T. Schaffhauser, A. Wokaun and R. R. Ernst, J. Magn. Reson., 1969, 1979(35), 39–67.
23. G. Buntkowsky, J. Bargon and H.-H. Limbach, J. Am. Chem. Soc., 1996, 118, 8677–8683.
24. T. Nakanishi, K. Yamane and M. Kitano, Phys. Rev. A, 2001, 65, 013404.
25. B. Misra and E. C. G. Sudarshan, J. Math. Phys., 1977, 18, 756–763.
26. M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, John Wiley & Sons, Chichester, England, 2008.
27. K. Ivanov, A. Yurkovskaya and H.-M. Vieth, J. Chem. Phys., 2008, 129, 234513.
28. R. Freeman, S. Wittekoek and R. R. Ernst, J. Chem. Phys., 1970, 52, 1529–1544.
29. A. S. Kiryutin, A. N. Pravdivtsev, K. L. Ivanov, Y. A. Grishin, H.-M. Vieth and A. V. Yurkovskaya, J. Magn. Reson., 2016, 263, 79–91.
30. M. J. Cowley, R. W. Adams, K. D. Atkinson, M. C. R. Cockett, S. B. Duckett, G. G. R. Green, J. A. B. Lohman, R. Kerssebaum, D. Kilgour and R. E. Mewis, J. Am. Chem. Soc., 2011, 133, 6134–6137.
31. B. J. A. van Weerdenburg, S. Glöggler, N. Eshuis, A. H. J. (Ton) Engwerda, J. M. M. Smits, R. de Gelder, S. Appelt, S. S. Wymenga, M. Tessari, M. C. Feiters, B. Blümich and F. P. J. T. Rutjes, Chem. Commun., 2013, 49, 7388.
32. C. R. Bowers, Sensitivity Enhancement Utilizing Parahydrogen, in eMagRes, John Wiley & Sons, Ltd, 2007,  DOI:10.1002/9780470034590.emrstm0489.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra28059a

‡ These authors contributed equally to this work.

---