Iron-activated carbon nanocomposite: synthesis, characterization and application for lead removal from aqueous solution†
H. Sharififarda,
F. Pepe*b,
M. Soleimania,
P. Apreac and
D. Caputoc
aDepartment of Chemical Engineering, Amirkabir University of Technology, No. 424, Hafez Ave., Tehran, Iran
bDipartimento di Ingegneria, Università del Sannio, Piazza Roma 21, 82100 Benevento, Italy. E-mail: francesco.pepe@unisannio.it
cDipartimento di Ingegneria Chimica, dei Materiali e della Produzione Industriale, Università Federico II, P.le Tecchio 80, 80125, Napoli, Italy
First published on 25th April 2016
Abstract
The removal of Pb(II) ions from aqueous solution by adsorption on an Iron-Activated Carbon (IAC) nanocomposite was investigated. Removal studies were carried out in a batch system, and the effects of various operating parameters, such as solution pH, solid to liquid ratio and initial concentration were evaluated. Experimental design was carried out using central composite design (CCD) with response surface methodology (RSM). According to the RSM results, the optimum adsorption conditions for Pb(II) removal by IAC were pH = 6.5, solid to liquid ratio of 3 g L−1 and initial lead concentration of 10 mg L−1. Under these optimum operating conditions, 96.5% of Pb(II) was removed by the IAC nanocomposite. The equilibrium adsorption data were well described by the Freundlich isotherm. The maximum adsorption capacity of IAC was 121.9 mg g−1 for Pb(II). It was observed that the adsorption kinetics of Pb(II) on the IAC could be well analyzed with a pseudo-second-order model.
Introduction
Heavy metal contamination of water resources is a major source of concern because of its toxic effect on human health and on animals and plants in the environment. Lead is a heavy metal that is released to the environment through a number of industrial activities such as battery production, coating and painting industries, pulp and paper production, petrochemical industries, etc.1–6 The presence of lead in the environment, even at very low concentrations, is extremely harmful to the aquatic environment and human health. Lead can damage the nervous system, kidneys, reproductive system and other organs.7 The World Health Organization (WHO) and US Environmental Protection Agency (US EPA) have set a maximum guideline concentration of 0.01 and 0.015 mg L−1 for Pb in drinking water, respectively.8Several separation methods, such as chemical precipitation, electrocoagulation, ion exchange, membrane processes and adsorption have been suggested for heavy metal removal from industrial wastewater to decrease their impact on the environment.9–16 Among these, adsorption seems to be the most suitable technique for the removal of metals in low concentration, due to low cost and high efficiency.
Activated carbon has been chosen as an adsorbent for removal of different pollutants from liquid and gas systems due to its high adsorption capacity, high adsorption rate and good resistance to abrasion.17–20 However, its ability to adsorb inorganic ions is relatively low.21–24 To increase the adsorption capacity or making the process more economical, modification of the adsorbent has been proposed. Deposition of iron nanoparticles on activated carbon is a novel and promising way to modify activated carbon and overcome these limitations.
Iron-activated carbon (IAC) nanocomposite have been synthesized via anchorage of iron oxide–hydroxide nanoparticles onto the activated carbon surface. Different techniques have been tested with this aim, such as iron precipitation with alkaline solutions, evaporation of iron salt solution in the presence of activated carbon, and oxidation/precipitation of iron.25–27 However, since a large amount of energy is consumed with some techniques,24 synthesis of IAC by evaporation of iron salt solution appears the optimal one.22,28
In this work a IAC nanocomposite was synthesized and characterized using different techniques. The main objectives of the present study include the following:
(1) To present a facile, low temperature synthesis technique for the preparation of IAC nanocomposite with good adsorption properties.
(2) To investigate the performance of the synthesized IAC for Pb(II) removal from aqueous solutions under different operating conditions (pH, solid to liquid ratio, lead initial concentration and temperature).
(3) To analyze the kinetic and equilibrium data in order to better clarify the lead adsorption mechanisms on IAC.
Materials and methods
Materials
Commercial Norit ROY 0.8 activated carbon (AC) was used as template. Nitric acid (Merck Co., 63%) and Fe(NO3)3 (Merck Co.) were used to synthesize iron-activated carbon (IAC) nanocomposite. Pb(NO3)2 (Sigma-Aldrich Company) and deionized water were used to prepare the test solutions. The initial pH of the solution was adjusted by HCl and NaOH solutions (Sigma-Aldrich Co.).Preparation and characterization of adsorbent
• The pHZPC (point of zero charge) of sample was measured by the following method: 0.3 g of adsorbent was added to 50 mL of a 0.1 N NaCl solution, where the initial solution pH was adjusted using aqueous HCl or NaOH solutions. If the initial pH of the solution is equal to the pHZPC of the adsorbent, no change in the pH will be observed after adding adsorbent to the solution.29
• The porous texture and surface area of samples (AC and IAC) were determined from adsorption–desorption of N2 at 77 K using an automatic volumetric system (Quantachrome NOVA 1000). The surface area was calculated by applying the BET (Brunauer–Emmett–Teller) method. The volume (mL g−1) and width (Å) of micropore and mesopore were determined by HK (Horvath–Kawazoe) and BJH (Barrett, Joyner, and Halenda) methods, respectively.30,31 The total pore volume of the sample was determined from the amount of nitrogen adsorbed at the highest relative pressure examined.
• The surface chemistry of AC and IAC samples was determined by using Fourier transform infrared radiation (Nicolet FT-IR spectrophotometer, NEXUS 670, 4 cm−1 resolution, sample/KBr = 1/100) within the range of 400–4000 cm−1 wave number.
• The iron content of AC and IAC nanocomposite was determined by using X-ray fluorescence (XRF, Unisantis, XMF-104).
• The average particle size, the morphology of AC and IAC nanocomposite and the composition of IAC nanocomposite were determined by scanning electron micrography (SEM-EDS, Tescan).
• X-ray diffraction (XRD) spectra of AC and IAC nanocomposite were obtained using a high-resolution X-ray diffractometer (Philips X'Pert).
Effect of adsorption parameters
In this study the effects of three removal parameters such as solution pH, solid to liquid ratio and initial concentration were investigated. Lead removal experiments were performed in batch manner by adding a measured weight of IAC in 50 mL of Pb(II) solutions with a fixed initial concentration and pH in 100 mL Erlenmeyer flasks. These samples were shaken at 25 °C using an orbital shaker (FINEPCR-SH30) at 150 rpm for 6 h. At the end of the experiment, the adsorbent was separated by paper filter (Whatman no. 42), and the residual Pb(II) concentration in the solution was determined using ICP emission spectrometry. The removal percentage of Pb(II) was determined from eqn (1):
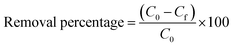 | (1) |
Kinetic studies
Adsorption kinetics were studied by placing 0.05 g of adsorbent in flasks containing 50 mL of 100 mg L−1 Pb(II) solution at pH 6.0. The flasks were agitated in an orbital shaker at 150 rpm for prescribed periods of time (2–360 min) at 25 °C. After these periods of time, solid and liquid were separated by filtration, and the solution concentration was analyzed using ICP emission spectrometry. The metal uptake capacity, q, was calculated as:
 | (2) |
ln(qe − qt) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe − k1t qe − k1t
| (3) |
On the other hand, the pseudo-second-order rate equation can be written as:
 | (4) |
Weber and Morris found that in many adsorption processes the initial solute uptake is almost proportional to t1/2, and interpreted this result by stating that the limiting step for the process is intra-particle diffusion.37 Their model can be described by the following equation:
| qt = kidt0.5 | (5) |
Eventually, the last model which was considered has been the Boyd model. This model too can be used to estimate the role of intra-particle diffusion with respect to film diffusion:38
| Bt = −0.4977 − ln(1 − F) | (6) |
Equilibrium studies
The equilibrium of Pb(II) adsorption by IAC nanocomposite was studied by placing 0.05 g of adsorbent in a series of flasks containing 50 mL of Pb(NO3)2 solution at different initial concentrations (10–220 mg L−1 of Pb(II)) and with an initial pH of 6.0. The flasks were agitated in an orbital shaker at 150 rpm for 24 h at various temperatures (25°, 45° and 60 °C). After this period, the metal solution was filtered and the residual concentration of the metal ions was determined. The amount of lead adsorbed by adsorbent, qe, was determined using eqn (2).
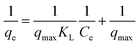 | (7) |
 | (8) |
If the RL value is between 0 and 1, the adsorption process is favorable.
The linear form of Freundlich model is:
 | (9) |
The Dubinin–Radushkevich (D–R) isotherm was applied since it allows to evaluate if the nature of adsorption as physical or chemical. The linear form of Dubinin–Raduskevich isotherm is:
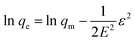 | (10) |
In this equation, qm is the theoretical saturation capacity (mol g−1), ε is the Polanyi potential, which is related to the equilibrium concentration as follows:
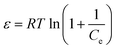 | (11) |
Results and discussion
Characterization of the adsorbents
The porosity parameters of both raw AC and IAC nanocomposite have been derived from N2 adsorption–desorption data (Table 1). It can be seen that the formation of iron nanoparticles inside and outside the porous structure of the AC causes a slight reduction in BET surface area and pore volume (both micro and mesopore), and a small increase in the average pore width, again both in the micro and meso ranges. As pointed out by Arcibar-Orozco et al.,28 the extent of BET area reduction can be taken as an indication of the fact that iron oxide–hydroxide nanoparticles, with sizes in the order of a few tens of nm, were formed. Indeed, large particles deposited on the AC surface would have blocked the pore entrances, leading to a significant reduction in N2 adsorption capacity. In turn, the formation of iron oxide–hydroxide nanoparticles is quite important, since the AC pores remain accessible, and the interaction between physical adsorption and chemisorption can enhance the separation process.
| Parameter | AC | IAC |
|---|---|---|
| BET Sp. Surf. area (m2 g−1) | 1062 | 890 |
| Total pore volume (mL g−1) | 0.66 | 0.545 |
| Micropore volume (mL g−1), HK method | 0.53 | 0.47 |
| Mesopore volume (mL g−1), BJH method | 0.13 | 0.080 |
| Volume occupied by micropores (%) | 80.0 | 86.2 |
| Average micropore width (Å), HK method | 15.5 | 16.7 |
| Average mesopore width (Å), BJH method | 22.5 | 26.4 |
Effect of separation parameters
| Removal percentage (%) = −20.02 + 13.90(X1) − 9.38(X2) + 0.44(X3) − 1.21(X1X2) − 0.12(X1X3) − 0.01(X2X3) + 0.75(X12) + 5.42(X22) + 1.65 × 10−4(X32) | (12) |
In this equation X1, X2 and X3 are solution pH, solid to liquid ratio (g L−1) and initial concentration of Pb(II) (mg L−1), respectively.
Eqn (12) shows that removal of Pb(II) is linear with respect to pH, solid to liquid ratio and initial concentration, and quadratic with respect to solid to liquid ratio and pH. This equation also indicates that there are interactions between pH and solid to liquid ratio and between pH and initial concentration on Pb(II) removal. The analysis of variance was applied in order to ensure a desirable model. The ANOVA results are shown in Table 2. According to the rule, the best regression model is determined by highest Fisher’s F value and lowest p-value.36,46 Data in Table 2 indicate that the quadratic model was significant at the 95% confidence level. As it can be seen from inspection of Table 2, F value for the model is 98.74 with corresponding P < 0.0001 and high SS (9264.55). This implies that the model is significant, and can appropriately explain the relationship between response and independent variables. This conclusion is also confirmed by the fact that both R2 and Radj2 approached unity.
| Source | Sum of squares | df | Mean square | F value | p-Value |
|---|---|---|---|---|---|
| Model | 9264.55 | 9 | 1029.39 | 98.74 | <10−4 |
| X1 | 7001.29 | 1 | 7001.29 | 671.53 | <10−5 |
| X2 | 218.27 | 1 | 218.27 | 20.94 | 0.0010 |
| X3 | 34.21 | 1 | 34.21 | 3.28 | 0.1002 |
| X1X2 | 92.96 | 1 | 92.96 | 8.92 | 0.0137 |
| X1X3 | 1245.25 | 1 | 1245.25 | 119.44 | <10−4 |
| X2X3 | 5.27 | 1 | 5.27 | 0.50 | 0.4936 |
| X12 | 55.95 | 1 | 55.95 | 5.37 | 0.0430 |
| X22 | 277.12 | 1 | 277.12 | 26.58 | 0.0004 |
| X32 | 0.66 | 1 | 0.66 | 0.063 | 0.8062 |
| Residual | 104.26 | 10 | 10.42 | ||
| Pure error | 2.58 | 5 | 0.52 |
p-Values that are lower than 0.05 allow to individuate the model terms which are significant, while values greater than 0.1 allow to individuate model terms are not significant, and can be omitted.47 Based on ANOVA table, the linear effects of pH (X1) and solid to liquid ratio (X2) and quadratic effects of solid to liquid ratio (X22) and pH (X12) are more significant. Table 2 also indicates that interactive effects between pH and solid to liquid ratio (X1X2) and pH and initial concentration (X1X3) have a significant influence on Pb(II) removal. Eliminating the less significant terms from eqn (12) and refining the model, eqn (12) may be simplified to:
| Removal percentage (%) = −20.02 + 13.90(X1) − 9.38(X2) − 1.21(X1X2) − 0.12(X1X3) + 0.75(X12) + 5.42(X22) | (13) |
It can be concluded that through response surface methodology it is possible to individuate a reasonable model for Pb(II) removal process, which can be used for prediction of removal efficiency. By applying the diagnostic plots, such as the predicted vs. actual value plots, the models adequacy can be assessed to verify if the selected models provide adequate approximation of the real system. Fig. 4 shows the relationship between predicted and actual values of Pb(II) removal using IAC.
It is clear that the predicted values are quite close to the actual experiments, which suggests that the model is accurate.
The perturbation plot (Fig. S2†) shows the comparative effects of all independent variables on Pb(II) removal efficiency. In Fig. S2† curvature in pH is the sharpest and effect of solid to liquid ratio is sharper than initial concentration: this indicates that Pb(II) removal efficiency is very sensitive to pH compared to solid to liquid ratio and initial concentration. This can be realized from ANOVA table as well. As it was indicated in Table 2, the F value of pH is higher than those relative to solid to liquid ratio and initial concentration.
Fig. 5a and b show the effect of solution pH on the removal efficiency. According to these figures, the removal efficiency of lead increased with pH ranging from 2 to 6.5 at any fixed initial concentration and solid to liquid ratio, even though this effect is smaller at higher initial concentrations. This trend may be the result of interaction of pH and initial concentration. Presumably the fact that the solution pH is one of the most influencing parameters of the lead removal process derives from it affecting the surface functional groups and the speciation of lead in solution. Indeed, the fact that pHZPC was 4.8 for IAC means that the surface charge of the adsorbent is positive and negative when pH < 4.8 and pH > 4.8, respectively. Since the dominant forms of lead at initial pH < 6–6.5 is Pb2+ cations,48,49 at pH < pHZPC, the surface of IAC is positive and electrostatic repulsion occurs between Pb2+ cations and positive adsorption sites of IAC, while at pH > pHZPC, the adsorbent surface is negative and it can more easily adsorb Pb2+.
According to Fig. 5a and b, the removal efficiency first decreased with increasing adsorbent dosage, and then increased. The presence of a minimum is quite difficult to address: it can be in principle due to some sort of interaction between the solution pH and the solid to liquid ratio, due to a not neutral hydrolysis of the adsorbent. Nevertheless, further investigation is needed in order to give a proper explanation of this particular response.
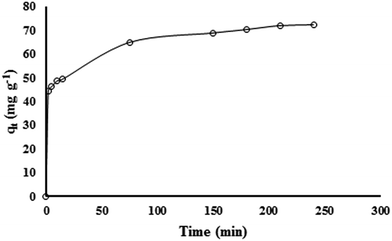
Adsorption kinetics
Fig. 6 reports an example of kinetic experiment for lead uptake by IAC nanocomposite. The other experiments gave similar results, so are not showed in this paper. The results demonstrate that the separation rate is fast for the first 5 min and then decreases, with the adsorption process reaching equilibrium at about 200 min. As mentioned above, the experimental data were analyzed in terms of pseudo-first-order, pseudo-second-order, intra-particle diffusion and Boyd kinetic models. The constants and regression coefficient (R2) for these models are presented in Table S2.† The R2 values indicate that the pseudo-second-order model is more appropriate than the pseudo-first-order model for description of the lead removal process. Also, from the table it appears that the calculated qe from the pseudo-second-order model is very closely similar to the experimental value of qe. These results confirm the validity of this model to the lead removal kinetics. This suggests that, under the experimental conditions taken into account, the lead removal by IAC is controlled by chemical sorption.According to data presented in Table S2,† the R2 value for the Weber–Morris model is 0.95; however, despite the high value of R2, it has to be observed that the intercept of the straight line relative to the plot of qt vs. t0.5 is significantly different from zero, suggesting that intra-particle diffusion is not the only rate controlling process.
A similar conclusion can be reached for what concerns the Boyd model: despite the fact that the R2 value is quite high (>0.97), the plots of −0.4977 − ln(1 − F) vs. t have an intercept significantly different from zero. Based on these results, the film diffusion may be important in lead adsorption by IAC. The B value was used to calculate the effective diffusion coefficient, Di (m2 s−1) using the following equation:
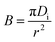 | (14) |
Adsorption equilibrium
Fig. 7a–c illustrate the predicted equilibrium adsorption values vs. equilibrium concentration at different temperatures using Langmuir, Freundlich and Dubinin–Raduskevich (D–R) isotherm models. Constant parameters and regression coefficient (R2) of these isotherms are presented in Table 3. Results show that Freundlich isotherm best fits the equilibrium data at all the temperatures. This may be attributed to the coexistence of different sorption sites and/or different sorption mechanisms or the sorption of different lead species that have led to a heterogeneous adsorption. The maximum adsorption capacity of IAC nanocomposite was 121.9 mg g−1. The maximum adsorption capacities reported for various adsorbents for lead are shown in Table 4. The comparison indicates that IAC nanocomposite exhibits a reasonably high capacity for lead adsorption from aqueous solutions. | ||
| Fig. 7 Adsorption isotherms of lead on IAC nanocomposite at different temperatures: (a) 25 °C, (b) 45 °C, (c) 60 °C. | ||
| Adsorbent | Adsorption capacity (mg g−1) | Ref. |
|---|---|---|
| Nanometer titanium dioxide immobilized on silica gel | 3.16 | 48 |
| Activated carbon | 147.06 | 49 |
| Activated carbon | 51.81 | 50 |
| Pine cone activated carbon | 27.53 | 51 |
| Fe3O4/SiO2 nanocomposite | 17.65 | 52 |
| Chemically treated pulp (1 M citric acid) | 34.6 | 53 |
| EDTA modified activated carbon | 60.03 | 54 |
| Activated carbon | 338 | 55 |
| Fe3O4@C | 71.42 | 56 |
| Fe3O4 nanospheres | 18.47 | 57 |
| (α,γ-FeOOH) nanoparticles | 820 | 58 |
| Co0.6Fe2.4O4 micro-particles | 80.32 | 59 |
| MHC/OMCNTs | 116.3 | 60 |
| IAC nanocomposite | 121.9 | This work |
The RL values for lead removal indicate that the adsorption isotherms are favorable at all temperatures considered. From the D–R isotherm parameters it is obtained that the mean free energy (E) of adsorption per molecule of the adsorbate was in the range of 9.22–15.8 kJ mol−1, suggesting that the process under consideration has a markedly chemical nature (chemisorption), rather than being a pure physical adsorption: this is in agreement with the results of kinetic studies, which indicate that the controlling step for the adsorption process is the adsorption pseudo-reaction.
Thermodynamic parameters
Inspection of Fig. 7 indicates that the adsorption capacity decreases as temperature increases. These equilibrium data were fitted by the Langmuir model, and the values of KL were used to determine the thermodynamic parameters according to the following equations:
ΔG° = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KL) ln(KL)
| (15) |
 | (16) |
| TΔS° = ΔH° − ΔG° | (17) |
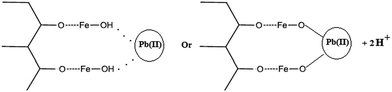
Mechanism of lead adsorption
There are two probable mechanisms for Pb(II) adsorption by IAC nanocomposite, both involving the abundant hydroxyl groups present on the surface of particles, either as hydroxyl groups of AC, or as hydroxyl groups of FeOOH structure. Indeed, such groups could either share their electron pairs to bind with Pb(II) ions and form complexes, or could lose one proton in the context of a ion exchange process involving Pb(II) ions.61,62 Fig. 8 illustrates the two possible mechanisms for lead removal by IAC nanocomposite.Conclusions
Commercial activated carbon (AC) was modified via anchorage of iron nanoparticles. Iron-activated carbon nanocomposite (IAC) was synthesized and used as adsorbent for Pb(II) removal from aqueous solution. Characterization tests proved that iron nanoparticles coated on activated carbon surface effectively. The ANOVA tables indicate that solution pH and solid to liquid ratio are the most significant removal parameters and that optimum operating conditions were pH = 6.5, solid to liquid ratio of 3 g L−1 and initial Pb(II) concentration = 10 mg L−1. Under optimum operation condition 96.5% of Pb(II) is removed from dilute solution by IAC. The maximum adsorption capacity of IAC was 121.9 mg g−1. Freundlich model was the best model to describe equilibrium adsorption of lead on IAC. Results showed that chemical adsorption is important in Pb(II) removal.Acknowledgements
The authors wish to acknowledge the Ministry for Foreign Affairs and International Cooperation of Italy and Amirkabir University of Technology of I.R.Iran for financial support.Notes and references
- K. K. Wong, C. K. Lee, K. S. Low and M. J. Haron, Chemosphere, 2003, 50, 23 CrossRef CAS PubMed.
- R. Jalali, H. Ghafourian, Y. Asef, S. J. Davarpanah and S. Sepehr, J. Hazard. Mater., 2002, 92, 253 CrossRef CAS PubMed.
- V. K. Gupta, M. Gupta and S. Sharma, Water Res., 2001, 35, 1125 CrossRef CAS PubMed.
- K. Conrad and H. C. B. Hansen, Sorption of zinc and lead on coir, Bioresour. Technol., 2007, 98, 89 CrossRef CAS PubMed.
- T. Bahadir, G. Bakan, L. Altas and H. Buyukgungor, Enzyme Microb. Technol., 2007, 41, 98 CrossRef CAS.
- L. Xingyue, A. Lunhong and J. Jing, Chem. Eng. J., 2016, 288, 789 CrossRef.
- R. Brooks, M. Bahadory, F. Tovia and H. Rostami, Int. J. Soil, Sediment Water, 2010, 3, 1 CAS.
- K. Li, Z. Zheng and Y. Li, J. Hazard. Mater., 2010, 181, 440 CrossRef CAS PubMed.
- M. J. González-Muñoz, M. A. Rodríguez, S. Luque and J. R. Álvarez, Desalination, 2006, 200, 742 CrossRef.
- E. Pehlivan and T. Altun, J. Hazard. Mater., 2007, 140, 299 CrossRef CAS PubMed.
- S. Vasudevan, J. Lakshmi and G. Sozhan, J. Hazard. Mater., 2011, 192, 26 CAS.
- S. Zhang, F. Xu, Y. Wang, W. Zhang, X. Peng and F. Pepe, Chem. Eng. J., 2013, 234, 33 CrossRef CAS.
- S. Hydari, H. Sharififard, M. Nabavinia and M. R. Parvizi, Chem. Eng. J., 2012, 193, 276 CrossRef.
- S. Hao, Y. Zhong, F. Pepe and W. Zhu, Chem. Eng. J., 2012, 189–190, 160 CrossRef CAS.
- H. Sharififard, F. Zokaee Ashtiani and M. Soleimani, Asia-Pac. J. Chem. Eng., 2013, 8, 384 CrossRef CAS.
- L. Xingyue, G. Xiaoyan, A. Lunhong and J. Jing, Chem. Eng. J., 2015, 274, 238 CrossRef.
- R. Chand-Bansal and M. Goyal, Activated Carbon Adsorption, Taylor & Francis, Boca Raton, 2005 Search PubMed.
- H. Marsh and F. Rodriguez-Reinoso, Activated Carbon, Elsevier, New York, 2006 Search PubMed.
- J. Yang and K. Qiu, Chem. Eng. J., 2010, 165, 209 CrossRef CAS.
- M. Kuppusamy, R. S. Somani and H. C. Bajaj, J. Environ. Chem. Eng., 2015, 3, 4 Search PubMed.
- A. M. Cooper, K. D. Hristovski, T. Möller, P. Westerhoff and P. Sylvester, J. Hazard. Mater., 2010, 183, 381 CrossRef CAS PubMed.
- J. H. Xu, N. Gao, Y. Deng and S. Xia, Chem. Eng. J., 2013, 222, 520 CrossRef CAS.
- X. Luo and L. Zhang, J. Hazard. Mater., 2009, 171, 340 CrossRef CAS PubMed.
- N. Yang, S. H. Zhu, D. Zhang and S. H. Xu, Mater. Lett., 2008, 62, 645 CrossRef CAS.
- H. Zhu, Y. Jia, X. Wu and H. Wang, J. Hazard. Mater., 2009, 172(2–3), 1591 CrossRef CAS PubMed.
- C. S. Castro, M. C. Guerreiro, L. C. A. Oliveira, M. Goncalves, A. S. Anastácio and M. Nazzarro, Appl. Catal., A, 2009, 367, 53 CrossRef CAS.
- E. Deliyanni and T. J. Bandosz, J. Hazard. Mater., 2011, 186, 667 CrossRef CAS PubMed.
- J. A. Arcibar-Orozco, J. Rene Rangel-Mendez and T. J. Bandosz, J. Hazard. Mater., 2013, 246–247, 300 CrossRef CAS PubMed.
- H. Sharififard and M. Soleimani, RSC Adv., 2015, 5, 80650 RSC.
- S. Lowell, J. E. Shields, M. A. Thomas and M. Thommes, Characterization of Porous Materials and Powders: Surface Area, Pore Size and Density, Springer, Dordrecht, 2004 Search PubMed.
- F. N. Aarden, Adsorption onto Heterogeneous Porous Materials: Equilibria and Kinetics, Ph.D. Dissertation, Technische Universiteit Delft, Eindhoven, 2001.
- R. Azargohar and A. K. Dalai, Microporous Mesoporous Mater., 2005, 85, 219 CrossRef CAS.
- M. Jain, V. K. Garg and K. Kadirvelu, Bioresour. Technol., 2011, 102, 600 CrossRef CAS PubMed.
- D. C. Montgomery, Design and Analysis of Experiments, John Wiley & Sons, New York, 5th edn, 2001 Search PubMed.
- R. H. Myers and D. C. Montgomery, Response Surface Methodology: Process and Product Optimization Using Designed Experiments, John Wiley & Sons, New York, 2nd edn, 2002 Search PubMed.
- M. Roso, A. Lorenzetti, S. Besco, M. Monti, G. Berti and M. Modesti, Comput. Chem. Eng., 2011, 35, 2248 CrossRef CAS.
- B. H. Hameed and A. A. Ahmad, J. Hazard. Mater., 2009, 164, 870 CrossRef CAS PubMed.
- G. E. Boyd, A. W. Adamson and L. S. Myers Jr, J. Am. Chem. Soc., 1947, 69, 2836 CrossRef CAS PubMed.
- S. Sanchez-Segado, T. Makanyire, L. Escudero-Castejon, Y. Hara and A. Jha, Green Chem., 2015, 17, 2059 RSC.
- S. J. Gregg and K. S. Sing, Adsorption, Surface Area, and Porosity, Academic Press, New York, 1982 Search PubMed.
- N. Asasian and T. Kaghazchi, Ind. Eng. Chem. Res., 2012, 51, 12046 CrossRef CAS.
- J. H. Chua, The Adsorption of Fatty Acids Using Metal Silica Complexes from Rice Husk Ash, Master's dissertation, UniversitiSains Malaysia, Penang, 2008 Search PubMed.
- N. Mehrabi, M. Soleimani, M. Madadi Yeganeh and H. Sharififard, RSC Adv., 2015, 5, 51470 RSC.
- P. Cambier, Clay Miner., 1986, 21, 191 CAS.
- Y. Li, C. Zhu, T. Lu, Z. Guo, D. Zhang, J. Ma and S. Zhu, Carbon, 2013, 52, 565 CrossRef CAS.
- R. A. Fischer, Statistical Methods for Research Worker, Oliver & Boyd, London, 1925 Search PubMed.
- K. Y. Nandiwale, N. D. Galande and V. V. Bokade, RSC Adv., 2015, 5, 17109 RSC.
- R. Liu and P. Liang, J. Hazard. Mater., 2008, 152, 166 CrossRef CAS PubMed.
- Y. Li, Q. Du, X. Wang, P. Zhang, D. Wang and Y. Xia, J. Hazard. Mater., 2010, 183, 583 CrossRef CAS PubMed.
- S. Z. Mohammadi, M. A. Karimi, D. Afzali and F. Mansouri, Desalination, 2010, 262, 86 CrossRef CAS.
- M. Momcilovic, M. Purenovic, A. Bojic, A. Zarubica and M. Randelovic, Desalination, 2011, 276, 53 CrossRef CAS.
- M. Mahdavi, M. B. Ahmad, M. J. Haron, Y. Gharayebi, K. Shameli and B. Nadi, J. Inorg. Organomet. Polym., 2013, 23, 599 CrossRef CAS.
- S. Pitsari, E. Tsoufakis and M. Loizidou, Chem. Eng. J., 2013, 223, 18 CrossRef CAS.
- C. Wei-fang, P. Ling, C. Li-fang, Y. Zhe, W. Qiong and Y. Chang-cheng, Appl. Surf. Sci., 2014, 309, 38 CrossRef.
- E. A. Deliyanni, G. Z. Kyzas, K. S. Triantafyllidis and K. A. Matis, Open Chem., 2015, 13, 699 CAS.
- B. Kakavandi, R. Rezaei Kalantary, A. Jonidi Jafari, S. Nasseri, A. Ameri, A. Esrafili and A. Azari, Clean: Soil, Air, Water, 2015, 43, 1157 CrossRef CAS.
- M. Kumari, C. U. Pittman Jr and D. Mohan, J. Colloid Interface Sci., 2015, 442, 120 CrossRef CAS PubMed.
- S. Rahimi, R. M. Moattari, L. Rajabi, A. Ashraf Derakhshan and M. Keyhani, J. Ind. Eng. Chem., 2015, 23, 33 CrossRef CAS.
- D. Shengxia, T. Rongfeng, X. Zechun, Z. Xianxi, Z. Yueying, Z. Wen, Z. Junhong, W. Bingquan, Z. Suyuan and S. Dezhi, Colloids Surf., A, 2015, 469, 211 CrossRef.
- Y. Wang, L. Shi, L. Gao, Q. Wei, L. Cui, L. Hu, L. Yan and B. Du, J. Colloid Interface Sci., 2015, 451, 7 CrossRef CAS PubMed.
- H. Abdel-Samad and P. R. Watson, Appl. Surf. Sci., 1998, 136, 46 CrossRef CAS.
- N. Pojananukij, K. Wantala, S. Neramittagapong and A. Neramittagapong, Desalin. Water Treat., 2015 DOI:10.1080/19443994.2015.1092890.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra27923b |
| This journal is © The Royal Society of Chemistry 2016 |