Comparative simulative analysis of single and double stranded truncated octahedral DNA nanocages

Abstract

An entirely double stranded truncated octahedral DNA nanocage structure has been modeled in silico and the molecular dynamics simulation technique has been used to characterize its dynamical properties. In this polyhedron, unlike other previously simulated truncated octahedral cages, the linker regions are represented by double helices. Simulations of nanocages, with single or double stranded linkers, have been carried out to evaluate differences in their dynamic behavior. The results indicate a higher rigidity of the double stranded nanocage in comparison with the structure sharing the same geometry but having single stranded linkers. In detail the highly constrained geometry of the entirely double stranded DNA cage generates a distortion of the polyhedron and a fixed orientation of the double helices that results in constant exposure of selected bases on the cage external surface. These bases may represent the preferential sites for chemical modifications endowing the structure with specific molecular recognition capabilities.

---

Introduction

In structural nanotechnology applications DNA has been employed as a building block to assemble complex nanostructures. Its high thermodynamic stability, together with the constrained auto-assembly characteristics due to its unique self-recognition properties, make this biopolymer an efficient material for bio-nanotechnological purposes.¹ Nadrian Seeman introduced this field in the '80s assembling two-dimensional nanostructures.² Some years later his group engineered and assembled the first three-dimensional nanostructure, namely a cube entirely consisting of B-DNA double helices,³ followed in 1994 by a truncated octahedron.⁴ These structures, however, presented many issues in the assembly phase and had quite a low production yield (i.e. 1% of product over the total of the oligonucleotides used for the assembling procedure). Due to the development of efficient experimental assembling methods and of computer-assisted design, an impressive variety of DNA cage structures including tetrahedra,^5,6 cubes,⁷ truncated octahedra,^8,9 trigonal bipyramids,¹⁰ dodecahedra,¹¹ icosahedra¹² and truncated icosahedra as well as hybrid structures with synthetic linkers and/or large DNA origami based structures have been presented during the last years.¹³ These structures are resistant to degradation in biological environment as demonstrated by the resistance to chemical and thermal denaturation of a covalently closed octahedral cage⁸ and the very long (42 hours) degradation half time of a tetrahedral DNA cage in 10% fetal bovine serum.¹⁴

During the past few years molecular dynamics (MD) atomistic simulations have been successfully used to characterize the structure and the dynamics of the Seeman DNA nanostructures,^15,16 to investigate the properties of a truncated octahedral DNA nanocage family,^17–19 to probe the stability and the dynamical properties of DNA nanocircles and supercoiled DNA structures,^20–22 to investigate the temperature dependent encapsulation mechanism of a DNA nanostructure²³ and of different DNA origami based assemblies.^24–27

Concerning the truncated octahedral cage a systematic investigation has been carried out to understand how the variation of specific geometrical parameters can modulate the yield of assembly and their mechanical–dynamical properties.^9,17–19,23 The truncated octahedral cages are composed by twelve double helices, each one connected to four single stranded linkers having different length and made by different bases.^17–19 Systematic and comparative simulative analyses indicate that the conformational variability of the cages are dependent on the number of bases composing the single stranded linkers, being larger in the 7T and 5T than in the 3T cage, and it is independent of the linker base composition.^18,19

In this paper, we attempt to decrease the conformational variability of the original truncated octahedral cages^18,19 introducing a double strand linker to confer a high degree of stiffness to the scaffold. For this purpose, we have modeled and simulated trough classical MD two cages with either single stranded linkers, composed by 9 nucleotides, or double stranded linkers composed by 9 base pairs. The results indicate that, compared to the cage with single stranded linkers, the presence of double stranded linkers strongly reduces the conformational variability of the cage giving rise to a more rigid nanocage that maintains a constant orientation of the structural double helices. This may permit selective introduction of chemical modifications on the external side for recognition purposes and selective cell targeting.

Computational methods

Model building of the double stranded DNA cage

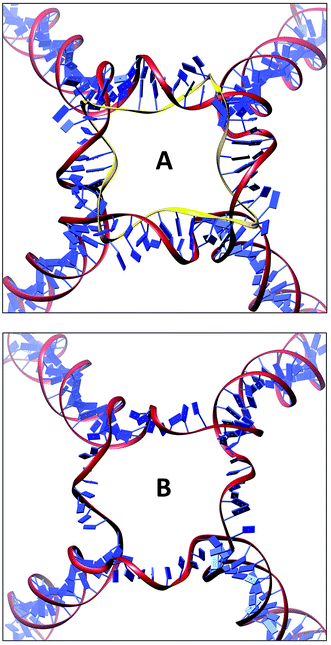
The DNA nanocages with single or double stranded linkers have been built starting from the first atomistic model generated by our group^17–19 and using oligonucleotides sequences previously designed to experimentally assemble truncated octahedral geometries.^8,9,23 To build the cage with double stranded linkers (named DSL), the 12 structural double helices (18 bp), corresponding to the truncated octahedron edges, have been connected using 24 double stranded linkers, each composed by 9 bp with the sequence GGGAAAACC and corresponding paired bases (Fig. 1). The single stranded linker cage (named SSL), with GGGAAAACC linkers, has been obtained by simply removing the six linkers' complementary DNA circles (Fig. 2A and B). The cage structure modelling has been executed using the SYBYL 6.0 program (TRIPOS, http://www.tripos.com). The clashes have been removed through the SYBYL Anneal module and then a first minimization of the entire structure has been performed using the SYBYL Maximin2 module. The system topologies and the coordinates, used as input for the NAMD 2.10 MD package,²⁸ have been obtained through the AmberTools14 tLeap module,²⁹ parameterizing the structures through the AMBER FF14SB force-field with the parmbsc0 (ref. 30) and εζ³¹ corrections. The structures have been immersed in an octahedral box filled with TIP3P water molecules,³² imposing a minimum distance between the solute and the box of 14 Å, whereas the charges have been neutralized adding, in electrostatically favorable positions, sodium counter-ions to the solvated systems (Table 1).

Fig. 1 Spacefill view of the DSL DNA nanocage. The red spacefill atoms represent the DNA oligos composing also the SSL nanocage, while the yellow spacefill atoms show the circular single stranded DNA oligo that, complementary to the sequence of the single strand linkers, shape the double stranded linkers.

Fig. 2 (A) Squared face of the truncated octahedron containing four double stranded linkers of the DSL DNA nanocage. The red ribbon indicates the DNA sugar-phosphate backbone while the blue squares show the orientation of the bases. The yellow ribbon shows the circular DNA single stranded oligo that, complementary to the sequence of the four single stranded linkers, shapes the double stranded linkers. (B) Squared face of the truncated octahedron containing four single stranded linkers of the SSL DNA nanocage.

Table 1 Simulation systems composition

Simulation system	DSL	SSL
Total number of atoms	473 358	464 016
DNA atoms	27 408	20 520
Water molecules (TIP3P)	148 362	147 616
Number of ions	864Na^+	648Na^+

---

Even if the use of the magnesium is more common in the experimental assembly of DNA nanostructures,^7,8,33 we used sodium ions in these simulations because it has been recently shown that the assembly DNA nano-structures occurs independently of the presence of monovalent or divalent ions.³⁴

Equilibration and MD protocol

The nanocages were subjected to two minimization runs. In the first one restraints of 500 kcal mol⁻¹ have been imposed on all the cages atoms to relax the water molecules and the ions, in the second one the cages have been minimized without any restraint to relax the entire system. A thermalization procedure, using the NVT ensemble has been carried out on the minimized structure gradually heating the systems from 0 K to 300 K, increasing temperature of 10 K every 30 ps. The optimized systems have been then simulated using periodic boundary conditions for 100 ns, with a 2.0 fs time-step, using the isobaric-isothermal ensemble (NPT). In our experience, 100 ns of classical MD are sufficient to sample the conformational properties of this class of nanostructures. The electrostatic interactions have been calculated every 4.0 fs, using a cut-off of 10 Å for the evaluation of short-range non-bonded interactions and the PME method for the long-range electrostatic interactions.^35,36 The SHAKE³⁷ and the SETTLE³⁸ algorithms have been used to constrain the nucleic acids and the water molecules, respectively. Temperature has been fixed at 300 K using Langevin dynamics,³⁹ while pressure has been held constant at 1 atm through the Langevin piston method.⁴⁰ The atomic positions have been saved every 500 steps (1.0 ps) for the analyses. The simulations have been performed using 256 nodes, for a total of 4096 CPUs, of the FERMI cluster hosted by CINECA.

Analyses

Root mean square deviation (RMSD), root mean square fluctuations (RMSF) projection over the first eigenvector, radii of gyration, cluster analysis and principal component analysis (PCA)⁴¹ have been calculated over the entire 100 ns trajectories by using the GROMACS 4.6.7 (ref. 42 and 43) integrated tools. The RMSF values obtained by the projection of the motions on the first eigenvector have been calculated taking into account the total cage motions. For each cage, the degree of conformational variability characterizing the linker regions has been evaluated by separately clustering each linker in the trajectories through the g_cluster program, using the clustering algorithm gromos⁴⁴ and a relative cut-off depending on the RMSD distribution relative to each structural element, as previously described.⁴⁴

The double helices rotation angles have been calculated aligning each helix to its principal axes using the VMD⁴⁵ orient plugin and singly fitting the trajectories using the conformation oriented on the helix principal axis (corresponding to the X-axis). After this coordinates transformation, the (3 × 3) helix rotation matrix has been computed by using the g_rotmat program of GROMACS^42,43 and the corresponding rotation angle over the X-axis of the molecule has been calculated and plotted as a function of time.

The structural images were obtained using the programs VMD⁴⁵ and UCSF Chimera,⁴⁶ while plots have been obtained through the Grace plotting tool (http://plasma-gate.weizmann.ac.il/Grace/).

Results

Comparison between DNA nanocages with single or double stranded linkers

Root mean square deviation and gyration radius. Fig. S1A† shows the total RMSD calculated as a function of time over all the atoms of the DSL and SSL nanocages, using as reference the final coordinates obtained from the equilibration procedure. The DSL and SSL RMSD values increase slightly differently in the first 55 ns, reaching the same value in the last 40 ns. The increase in the DSL cage is due to a rearrangement of the structural double helices, while in the SSL cage is due to the structural variability of the single stranded linkers, as evidenced comparing the RMSD values of the different structural elements (double helices and linkers, respectively). In the DSL nanocage the structural helices and the linkers have similar RMSD values, whilst in the SSL cage the linkers represent the structural elements having the largest deviation (Fig. S1B and C†).

For the entire trajectory the radius of gyration (RG) of the DSL nanocage is constantly larger than that of the SSL nanocage (Fig. S2†), the average RG values being approximately 6.7 and 6.4 nm for the DSL and SSL simulation, respectively. The average internal volumes are 560 and 330 nm³ for the DSL and SSL cages, respectively, indicating that the double helix linkers constantly maintain a larger cavity.

Conformational variability. Fig. 3 shows the RMSF, filtered along the first eigenvector, calculated for each strand composing the 12 structural helices. In the SSL cage the RMSF values of the helices have a sinusoidal trend indicating a rotational motion that roughly occurs, in spite of some inclination, around the double helix main axis. The sinusoidal trend, shown by almost all the double helices, indicates that the main component of the global cage motions is characterized by the rotation of the double helices, as already observed in previous simulations of nanocages with single stranded linkers.^17–19 In the DSL nanocage such sinusoidal trend is abolished and the extent of the fluctuation is much lower than in SSL (Fig. 3). The RMSF have also been calculated filtering the trajectories along the second and third eigenvectors for the DSL and SSL cages (Fig. S3†). The RMSF trend resembles that observed for the first eigenvector, thereby excluding the presence of a rotational motion at the level of the helices in the DSL cage. These results are confirmed by the measurement of the double helices rotation angles as a function of time for the SSL and DSL cage. As an example, Fig. S4† shows the rotation angles for the DH1, DH2, DH5, DH7, DH11 and DH12, for both cages together with a graphical representation of the Cartesian reference system used to compute the rotation angle of each double helix (Fig. S4A†). As can be observed in Fig. S4B,† representing the SSL cage, all the helices rotate around their axis, except DH1 a rigid helix that has been shown as a control. In the DSL cage, the corresponding helices instead show a negligible rotation angle (Fig. S4C†). This implies that in the DSL cage the DNA helices always have the same orientation. This permits the definition of specific bases that are always located on the external region of the cage and that can be chemically modified with specific ligands to allow the cage to interact with specific molecules.

Fig. 3 Per nucleotide RMSF projection along the first eigenvector for each of the two strands of the 12 structural DNA double helices (i.e. non linker helices) for the DSL (black and red lines) and the SSL (green and blue lines) nanocages.

For the two cages, the degree of conformational variability present in each linker region has been evaluated by separately clustering each linker in the trajectories. The percentages of the three most populated clusters, reported using three different colors in the bars representing each linker of the DSL and SSL nanocages (Fig. 4A and B, respectively), are largely different. In fact, due to the rigid constraints imposed by the double stranded linkers, in the DSL cage almost all the conformations are confined in a single cluster that can be described by a slightly distorted double helix conformation that is maintained during all the trajectory, shown by the red portion of the stacked bars (Fig. 4A). Despite these highly distorted conformations hydrogen bond breaking, that could induces events such as the base flipping,⁴⁷ have not been observed in the DSL linkers.

Fig. 4 Histograms representing the frequency distribution of the first three conformational clusters (red, green and blue, respectively), calculated for the 24 linkers of the DSL (A) and SSL (B) nanocages.

On the other hand, the SSL cage is characterized by the presence of several clusters represented by the red, green and blue colors (Fig. 4B), indicating a conformational variability larger than that previously observed in cages with shorter linkers.¹⁸ These reinforces the presence of a correlation between the conformational variability and linker length. In detail the histogram representing the average number of linkers clusters observed in the SSL, DSL and in previously published simulations of the truncated octahedral nanocages with 3, 5 or 7 thymidines linkers, indicates that in cages with single stranded linkers the conformational variability increases linearly with linkers length (Fig. 5). The conformational variability of the DSL cage having 9 base pairs linkers is comparable to that of the cage connected by 3 thymidines single stranded linkers, indicating that the cage rigidity can be increased either reducing the linkers length or introducing a double stranded linker.

Fig. 5 Average number of linker clusters evaluated as a function of the single stranded linker length in comparison with the double stranded linkers of the DSL cage.

The principal component analysis (PCA)⁴¹ based on the diagonalization of the covariance matrix, permits to identify the main 3N directions (eigenvectors) along which the majority of the motion is defined. The analyses, carried out on the phosphorus atoms of the DNA backbone, indicate that the first 10 eigenvectors describe 80% of the motion for both the DSL and SSL nanocages. The principal direction and amplitude of the motion described by the first eigenvector (corresponding to 35% of the total motion), has been projected and depicted over the phosphor atoms of the DSL (Fig. 6A) and SSL (Fig. 6B) cages. The amplitude of the motion is proportional to the width of the ribbon drawn by the contiguous lines while the motion direction is indicated by the color going from red to blue. The projections show an amplitude of motion much larger in the SSL than in the DSL validating that the double stranded linkers confer more rigidity to the DSL cage. The projections, calculated filtering the trajectories along the second and third eigenvectors for the DSL and SSL cages, confirm that the motion amplitudes are larger in the SSL (Fig. S5B and D†) than in the DSL cage (Fig. S5A and C†) and that the helices rotational motion is entirely abolished in the DSL cage.

Fig. 6 Tube representation of the motion projections along the first eigenvector for the DSL (A) and SSL (B) nanocage structures. The width of the ribbon, generated by the flanking tubes, indicates the amplitude of the motion, the direction going from the red to the blue color. This picture was produced using the VMD program.⁴⁵

Conclusions

The overall results of the simulations indicate a high rigidity of the DSL nanocage compared to the SSL one. The presence of double helix linkers imposes a large constraint to the nanostructure geometry, strongly limiting the sampled conformational space. Indeed, the helices RMSF values, evaluated filtering the trajectories along the first three eigenvectors, are lower in the DSL nanocage (Fig. 3 and S3†) and the sinusoidal trend of the RMSF values observed in the SSL cage is almost completely abolished in the DSL cage (Fig. 3). These findings indicate that the DSL helices do not undergo a rotational motion (Fig. S4†) at variance on what shown for both the SSL cage presented here and in previous published simulations.^17–19 In the SSL cage the conformations and local interactions sampled by the linkers do not significantly alter the octahedral geometry but induce rotations in the structural double helices resulting in nanocage contractions.^17–19 These effects disappear in the DSL simulation where the cage is rigid and slightly deformable (Fig. 3 and 6, S2–S5†). As a matter of fact, the linker represents the main feature modulating the conformational variability of the cage. Analysis of the linkers structural variability, evaluated by separately clustering each linker, indicates the presence in the SSL cage of three highly populated clusters showing a variability larger than that previously observed in the simulations of cages with single stranded linkers composed by 3, 5 or 7 bases (Fig. 5). On the contrary, the conformational variability is strongly reduced in the DSL cage, indicating that the presence of double stranded elements as linkers strongly stiffens the cage scaffold, since the entire conformational panorama can almost be described by a single cluster. This rigidity also imposes a defined orientation to all the helices of the cage so that a specific nucleotide portion is always oriented on the external region of the cage, in contrast to what is observed for the SSL, where the position of the helices can not be defined due to the described rotational motion (Fig. 6 and S5†).

The fixed helices orientations permit to uniquely define the bases that are always located on the internal or external surface of the cage. This will enable the introduction of spectroscopic probes at specific positions and to attach ligands or antibodies on the external face for a selective interaction with receptors overexpressed in defined pathologies.

Acknowledgements

We acknowledge PRACE (Partnership for Advanced Computing in Europe) for awarding us the access to the FERMI supercomputer (CINECA, Italy), where under the PRACE Project No. 2014112630 (10^th PRACE call) the MD calculations have been carried out.

References

1. S. Biocca and A. Desideri, Nano LIFE, 2015, 5, 1541004.
2. N. C. Seeman, J. Theor. Biol., 1982, 99, 237–247.
3. J. Chen and N. C. Seeman, Nature, 1991, 350, 631–633.
4. Y. Zhang and N. C. Seeman, J. Am. Chem. Soc., 1994, 116, 1661–1669.
5. R. P. Goodman, I. A. T. Schaap, C. F. Tardin, C. M. Erben, R. M. Berry, C. F. Schmidt and A. J. Turberfield, Science, 2005, 310, 1661–1665.
6. C. M. Erben, R. P. Goodman and A. J. Turberfield, Angew. Chem., Int. Ed., 2006, 45, 7414–7417.
7. T. G. W. Edwardson, K. M. M. Carneiro, C. K. McLaughlin, C. J. Serpell and H. F. Sleiman, Nat. Chem., 2013, 5, 868–875.
8. F. F. Andersen, B. Knudsen, C. L. P. Oliveira, R. F. Frohlich, D. Kruger, J. Bungert, M. Agbandje-McKenna, R. McKenna, S. Juul, C. Veigaard, J. Koch, J. L. Rubinstein, B. Guldbrandtsen, M. S. Hede, G. Karlsson, A. H. Andersen, J. S. Pedersen and B. R. Knudsen, Nucleic Acids Res., 2007, 36, 1113–1119.
9. C. L. P. Oliveira, S. Juul, H. L. Jørgensen, B. Knudsen, D. Tordrup, F. Oteri, M. Falconi, J. Koch, A. Desideri, J. S. Pedersen, F. F. Andersen and B. R. Knudsen, ACS Nano, 2010, 4, 1367–1376.
10. C. M. Erben, R. P. Goodman and A. J. Turberfield, J. Am. Chem. Soc., 2007, 129, 6992–6993.
11. J. Zimmermann, M. P. J. Cebulla, S. Mönninghoff and G. von Kiedrowski, Angew. Chem., Int. Ed., 2008, 47, 3626–3630.
12. D. Bhatia, S. Mehtab, R. Krishnan, S. S. Indi, A. Basu and Y. Krishnan, Angew. Chem., Int. Ed., 2009, 48, 4134–4137.
13. E. Benson, A. Mohammed, J. Gardell, S. Masich, E. Czeizler, P. Orponen and B. Högberg, Nature, 2015, 523, 441–444.
14. J.-W. Keum and H. Bermudez, Chem. Commun., 2009, 7036.
15. P. K. Maiti, T. a. Pascal, N. Vaidehi, J. Heo and W. a. Goddard, Biophys. J., 2006, 90, 1463–1479.
16. M. Santosh and P. K. Maiti, Biophys. J., 2011, 101, 1393–1402.
17. M. Falconi, F. Oteri, G. Chillemi, F. F. Andersen, D. Tordrup, C. L. P. Oliveira, J. S. Pedersen, B. R. Knudsen and A. Desideri, ACS Nano, 2009, 3, 1813–1822.
18. F. Oteri, M. Falconi, G. Chillemi, F. F. Andersen, C. L. P. Oliveira, J. S. Pedersen, B. R. Knudsen and A. Desideri, J. Phys. Chem. C, 2011, 115, 16819–16827.
19. F. Iacovelli, C. Alves, M. Falconi, F. Oteri, C. L. P. De Oliveira and A. Desideri, Biopolymers, 2014, 101, 992–999.
20. F. Lankaš, R. Lavery and J. H. Maddocks, Structure, 2006, 14, 1527–1534.
21. J. S. Mitchell, C. a. Laughton and S. a. Harris, Nucleic Acids Res., 2011, 39, 3928–3938.
22. I. D'Annessa, A. Coletta, T. Sutthibutpong, J. Mitchell, G. Chillemi, S. Harris and A. Desideri, Nucleic Acids Res., 2014, 42, 9304–9312.
23. S. Juul, F. Iacovelli, M. Falconi, S. L. Kragh, B. Christensen, R. Frøhlich, O. Franch, E. L. Kristoffersen, M. Stougaard, K. W. Leong, Y.-P. Ho, E. S. Sørensen, V. Birkedal, A. Desideri and B. R. Knudsen, ACS Nano, 2013, 7, 9724–9734.
24. J. Yoo and A. Aksimentiev, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20099–20104.
25. H. Joshi, A. Dwaraknath and P. K. Maiti, Phys. Chem. Chem. Phys., 2014, 17, 1424–1434.
26. J. Yoo and A. Aksimentiev, J. Phys. Chem. Lett., 2015, 6, 4680–4687.
27. F. Iacovelli and M. Falconi, FEBS J., 2015, 282, 3298–3310.
28. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
29. R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210.
30. A. Pérez, I. Marchán, D. Svozil, J. Sponer, T. E. Cheatham, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829.
31. M. Zgarbová, F. J. Luque, J. Šponer, T. E. Cheatham, M. Otyepka and P. Jurečka, J. Chem. Theory Comput., 2013, 9, 2339–2354.
32. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926.
33. E. S. Andersen, M. Dong, M. M. Nielsen, K. Jahn, R. Subramani, W. Mamdouh, M. M. Golas, B. Sander, H. Stark, C. L. P. Oliveira, J. S. Pedersen, V. Birkedal, F. Besenbacher, K. V Gothelf and J. Kjems, Nature, 2009, 459, 73–76.
34. T. G. Martin and H. Dietz, Nat. Commun., 2012, 3, 1103.
35. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089.
36. N. Spackova, I. Berger and J. Sponer, J. Am. Chem. Soc., 2000, 122, 7564–7572.
37. J. Ryckaert, G. Ciccotti and H. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
38. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
39. S. Nose, J. Chem. Phys., 1984, 81, 511.
40. S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613.
41. A. Amadei, A. B. M. Linssen and H. J. C. Berendsen, Proteins: Struct., Funct., Genet., 1993, 17, 412–425.
42. B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
43. S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
44. X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. Van Gunsteren and A. E. Mark, Angew. Chem., Int. Ed., 1999, 38, 236–240.
45. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
46. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
47. P. Imhof and M. Zahran, PLoS One, 2013, 8, e53305.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra27591a

---