Atomistic investigation into the mechanical behaviour of crystalline and amorphous TiO2 nanotubes
Yanan Xua,
Mingchao Wanga,
Ning Hub,
John Bella and
Cheng Yan*a
aSchool of Chemistry, Physics and Mechanical Engineering, Science and Engineering Faculty, Queensland University of Technology (QUT), Brisbane, QLD 4001, Australia. E-mail: c2.yan@qut.edu.au
bDepartment of Engineering Mechanics, College of Aerospace Engineering, Chongqing University, Chongqing, China
First published on 10th March 2016
Abstract
Titanium dioxide (TiO2) nanotubes are appealing to research communities due to their excellent functional properties. However, there is still a lack of understanding of their mechanical properties. In this work, we conduct molecular dynamics (MD) simulations to investigate the mechanical behaviour of rutile and amorphous TiO2 nanotubes. The results indicate that the rutile TiO2 nanotube has a much higher Young's modulus (∼800 GPa) than the amorphous one (∼400 GPa). Under tensile loading, rutile nanotubes fail in the form of brittle fracture but significant ductility (up to 30%) has been observed in amorphous nanotubes. This is attributed to a unique ‘repairing’ mechanism via bond reconstruction at under-coordinated sites as well as bond conversion at over-coordinated sites. In addition, it is observed that the fracture strength of rutile nanotubes is strongly dependent on their free surfaces. These findings are considered to be useful for development of TiO2 nanostructures with improved mechanical properties.
1. Introduction
TiO2 is a multifunctional semiconductor material with a large refractive index,1 high energy conversion efficiency2–5 and high photocatalytic activity.6–9 Nanosized TiO2 has also demonstrated unique physical and chemical properties. For example, owing to the quantum-size effect,10 the energy gap between the conduction and valence bands of TiO2 nanoparticles exhibits a blue shift,11 as compared to bulk TiO2.12 Different opto-electronic properties have also been observed for TiO2 nanotubes.13 TiO2 with distinctive nanostructures were synthesized by various methods.14–16 Recently, TiO2 nanotube arrays have demonstrated great potential for applications in sensors,17 dye-sensitized solar cells,18,19 drug delivery and tissue engineering.20–23 To take full advantage of the superior electrical and biomedical properties of TiO2 nanotubes, it is critical to maintain the mechanical integrity in relevant structures and devices. A better understanding of the mechanical performance of TiO2 nanotubes is essential. Recently, nanoindentation technique has been adapted to explore the mechanical behaviour of TiO2 nanotube arrays.24,25 Significant densification and fracture of nanotubes were observed in these experiments. Hirakata et al. proposed a stress-based fracture model to estimate the fracture strength of TiO2 nanotube arrays.26For individual TiO2 nanotubes, owing to nanoscale dimensions, it is still a challenge to experimentally evaluate their mechanical properties, and corresponding deformation and failure mechanisms. On the other hand, atomistic simulations provide an alternative approach. In this work, we conducted MD simulations to investigate the mechanical properties (i.e. Young's modulus, fracture strength and yield strength), and deformation and failure mechanisms of individual TiO2 nanotubes. The effects of crystal structures and geometrical parameters on the mechanical properties of single TiO2 nanotube were also discussed.
2. Simulation methods
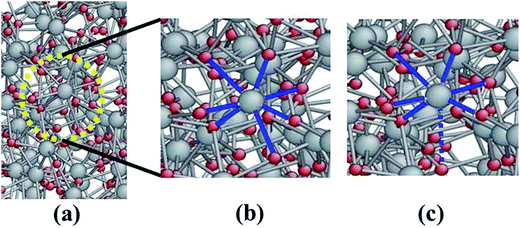
TiO2-nanotube models with different geometrical parameters (i.e. inner radius and wall thickness) and microstructures (i.e. rutile crystal and amorphous) were built by seamlessly wrapping TiO2 thin films in a self-programmed code, as shown in Fig. 1. Such code implements the spatial transformation method to convert thin films into nanotubes. The axis of rutile nanotube is aligned with [001] direction. The geometrical parameters of these TiO2-nanotube models are listed in Table 1. It is found that there are minor differences between the thicknesses and inner radii of thin films before wrapping and corresponding nanotubes. The nanotube lengths in all simulation models were chosen as 30 nm. Periodic boundary conditions were applied to all simulation models along the length direction.| Rutile | Inner radius Rin (Å) | Thickness h (Å) | Amorphous | Inner radius Rin (Å) | Thickness h (Å) |
|---|---|---|---|---|---|
| No. 1 | 7.6756 | 8.56510 | No. 1 | 7.27395 | 10.07025 |
| No. 2 | 7.4366 | 13.6460 | No. 2 | 7.19950 | 14.7030 |
| No. 3 | 7.2829 | 18.5438 | No. 3 | 6.88030 | 19.7068 |
| No. 4 | 26.575 | 13.7300 | No. 4 | 25.3300 | 14.7000 |
| No. 5 | 37.475 | 13.1100 | No. 5 | 36.6850 | 14.3800 |
| No. 6 | 48.420 | 13.2900 | No. 6 | 47.4650 | 14.1600 |
The amorphous structure in the TiO2 models was achieved via a melt-and-quench procedure, which is very popular for formation of amorphous solids.27,28,32 Firstly, rutile TiO2 thin films were melted from 300 K to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K under the Nosé–Hoover NVT ensemble.29,30 After reaching to 10
000 K under the Nosé–Hoover NVT ensemble.29,30 After reaching to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, the Nosé–Hoover NPT ensemble29,30 with a constant pressure of 1 bar was performed to further equilibrate the system. Then, rapid quenching at a rate of 4.85 × 1013 K s−1 was applied to the TiO2 thin films under the Nosé–Hoover NVT ensemble until 300 K. The finally obtained simulation models, which are equilibrated under the Nosé–Hoover NPT ensemble at 300 K, indicate that atomistic structures of amorphous TiO2 thin films are approximately independent of quench rates in the range of ∼1012 to 1014 K s−1. Hence, only one quench rate was considered here.
000 K, the Nosé–Hoover NPT ensemble29,30 with a constant pressure of 1 bar was performed to further equilibrate the system. Then, rapid quenching at a rate of 4.85 × 1013 K s−1 was applied to the TiO2 thin films under the Nosé–Hoover NVT ensemble until 300 K. The finally obtained simulation models, which are equilibrated under the Nosé–Hoover NPT ensemble at 300 K, indicate that atomistic structures of amorphous TiO2 thin films are approximately independent of quench rates in the range of ∼1012 to 1014 K s−1. Hence, only one quench rate was considered here.
Matsui and Akaogi proposed a pairwise potential (MA potential), which is derived from typical Born–Huggins–Meyer (BHM) potential,31 for the simulations of TiO2 materials.33 Numerous computational studies have demonstrated that MA potential can accurately describe geometries and properties of TiO2 crystal (i.e. rutile, anatase and brookite) as well as amorphous TiO2 structures.33–36 It has also been applied to simulations of both nanophase solid TiO2 (ref. 37) and nanophase liquid TiO2.38 Comparing different potentials for TiO2 simulation, Collins et al.39 pointed out that MA potential is the most suitable one for TiO2 simulation. The MA potential is also a type of ionic model, it includes Buckingham interaction (first and second terms in eqn (1)) and pairwise coulombic interaction (third term in eqn (1)), which can be expressed in the following formula:33,37,38
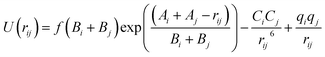 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to keep all models' charge neutral. In this work, the cut-off distances for both Buckingham and pairwise coulombic interactions were chosen as 8.0 Å.
2 to keep all models' charge neutral. In this work, the cut-off distances for both Buckingham and pairwise coulombic interactions were chosen as 8.0 Å.
| Ion | A (Å) | B (Å) | C (Å3 kJ1/2 mol−1/2) |
|---|---|---|---|
| Ti | 1.1823 | 0.077 | 22.5 |
| O | 1.6339 | 0.117 | 54.0 |
All MD simulations were carried out using the large-scale atomic/molecular massively parallel simulator (LAMMPS)40 with the MA potential, which has been used for simulating mechanical properties of nanomaterials in our previous works.41–43 TiO2-nanotube models were firstly relaxed to a minimum energy state using the conjugate gradient energy minimization method until the maximum atomic force was brought below 10−8 eV Å−1. Tensile loadings were then carefully applied by stretching nanotube models along their longitudinal directions at a strain rate of 0.1% ps−1 and with a time step of 0.5 fs. The Nosé–Hoover NVT ensemble was performed to maintain nanotube models at 300 K. Since the dimensions of all nanotube models are large enough to satisfy the thermodynamic limit, the virial theorem44,45 can be used to evaluate the atomic stress and determine stress–strain (σ–ε) curves under tensile loadings. Specifically, the atomic stress can be expressed as:
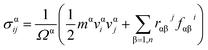 | (2) |
3. Results and discussions
3.1. Structural characteristics of crystalline and amorphous TiO2 nanotubes
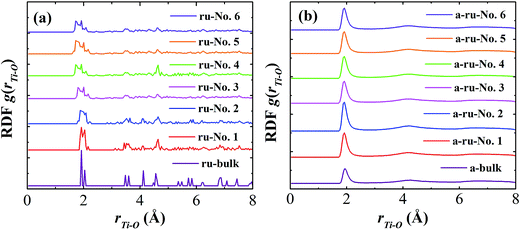
The structural characteristics of rutile and amorphous TiO2 nanotubes obtained at 300 K have been compared with bulk rutile TiO2 at the same temperature. Here, the bulk rutile TiO2 model was built with the dimensions of 10 nm × 10 nm × 10 nm and applied with periodic boundary conditions along all directions. As observed in radial distribution functions (RDFs) (Fig. 2), bulk rutile has two obvious sharp peaks within the bond cut-off radius of RTi–O = 3.0 Å.34 These two peaks correspond to two different Ti–O bond lengths (1.9486 Å and 1.9802 Å) in rutile TiO2, in agreement with the experiment.47 In Fig. 2(a), the RDFs of rutile nanotubes have more small sharp peaks compared with that of bulk rutile TiO2, within the cut-off radius of RTi–O = 3.0 Å. Here the peak sharpness can be attributed to the crystalline arrangement of rutile nanotubes. And more sharp peaks result from a large number of under-coordinated Ti and O atoms on the existing free surfaces of nanotubes, which have different Ti–O bond lengths from those inside nanotubes. The RDFs of rutile nanotubes are also insensitive to the nanotube wall thickness and inner radius, indicating little variation of bond length distribution.In contrast, smooth RDF peaks are observed in amorphous TiO2 (bulk and nanotubes), as shown in Fig. 2(b). Generally, it is difficult to estimate the accurate atoms distributions in amorphous material. Petkov et al.48 investigated the atomic structure of amorphous TiO2 by electron and X-ray diffraction. They found that the first smooth peak in RDFs of amorphous TiO2 centered at around 1.96 Å. Our simulation also indicates the first smooth peak in RDFs located around 1.96 Å, confirming the validation and accuracy of current models. Smooth peaks observed in RDFs are common for amorphous materials.49–53 The smooth peaks for amorphous nanotubes can be well explained by the disordered reconstruction of both inner and surface Ti–O bonds during amorphization, which have wide-range bond length distribution. In addition, Fig. 2(b) also indicates the RDFs of amorphous nanotubes are independent of nanotube sizes.
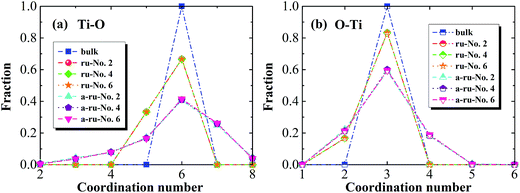
We also investigated the coordination number distributions of both Ti and O atoms in rutile and amorphous TiO2 nanotubes, kTi–O (Ti as the central atom) and kO–Ti (O as the central atom). As shown in Fig. 3, only coordination number kO–Ti = 3 and kTi–O = 6 exist in rutile bulk TiO2, which is in accordance with Ti3O6 unit cell of rutile. In rutile nanotubes, the fractions of kO–Ti = 3 and kTi–O = 6 decrease and the fractions of under-coordination numbers such as kO–Ti = 1, 2 and kTi–O = 3 become non-zero. This is due to that the structure of rutile nanotube gets truncated by the free surfaces, causing many under-coordinated atoms on the free surfaces. To achieve energy minimization, these under-coordinated Ti or O atoms tend to interact with nearby O or Ti atoms, causing distortion and reconstruction of surface microstructure. In amorphous TiO2 nanotube, the fractions of kO–Ti = 3 and kTi–O = 6 decrease more as compared to rutile nanotube. This is because that a number of under-coordinated and over-coordinated atoms are introduced to the amorphous TiO2 nanotubes, resulting from the amorphization process. The corresponding non-zero coordination numbers (e.g. kO–Ti = 2, 4 and kTi–O = 5, 7) are shown in Fig. 3. The mean coordination numbers ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) Ti–O = 5.89 and
Ti–O = 5.89 and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) Ti–O = 2.88 are in good agreement with those in previous results.48,52
Ti–O = 2.88 are in good agreement with those in previous results.48,52
3.2. Mechanical properties of crystalline and amorphous TiO2 nanotubes
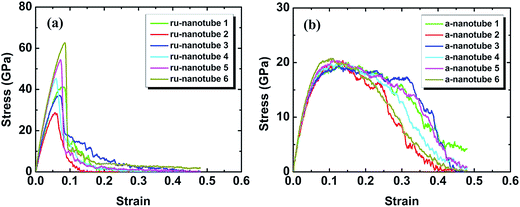
To understand the mechanical performance of rutile and amorphous TiO2 nanotubes, σ–ε curves under tensile loadings are analyzed in Fig. 4. From these σ–ε curves, we can see approximately linear behavior when the strain is in the range of 0–3%, where the slopes denote the Young's moduli of TiO2 nanotubes. For rutile nanotubes (Fig. 4(a)), their Young's moduli are insensitive to inner radius and thickness (about 800 GPa). The modulus of rutile TiO2 nanowires estimated by MD simulation is about ∼688 GPa.54 Normally, the significant free-surface effect due to large surface-to-volume ratio can lead to much higher Young's moduli of nanostructured materials than those of bulk counterparts.55,56 Hence rutile TiO2 nanotubes possess larger surface-to-volume ratios due to the existence of inner wall surface, thereby having a higher Young's moduli than those of rutile TiO2 nanowires. For all amorphous TiO2 nanotubes (Fig. 4(b)), their Young's moduli (approximate 400 GPa) is independent of inner radius and thickness, only half value of the rutile nanotubes. The decrease of Young's modulus is associated with the structural disorder introduced during the amorphization process, which has also been observed in other materials.57,58 Under the tensile loading up to the critical (yield or fracture) strain, the stress distribution in amorphous nanotubes is more non-uniform than that in rutile ones. This means amorphous nanotubes contain more Ti–O bonds which cannot efficiently bear external loading, and thus possesses lower Young's moduli than rutile ones.Considering the structure evolution during loading, rutile nanotubes generate reversible elastic deformation within a small strain range and no structural failure can be observed, as shown in Fig. 5(a). Then, a drop of stress σ occurs, triggered by crack initiation in nanotube walls, as shown in Fig. 5(b). Obviously, the fracture strength of rutile nanotubes, namely the maximum stresses in σ–ε curves (Fig. 4(a)), is determined by the elastic limit before the crack initiation. The crack propagates across the cross-section area of the nanotubes, as shown in Fig. 5(c). After reaching fracture strength, the nanotube starts to lose the load capacity until the complete failure, Fig. 5(d). As shown in Table 3, the fracture strength of rutile nanotubes is in the range of σf = 28.55–62.58 GPa, which are greater than those of rutile nanowires (∼10 GPa).54 Remarkably, except for rutile nanotube no. 2, increase of the average inner and outer radii (see Table 3) results in the enhancement of fracture strength. This trend unveils the possible strong free-surface effect on fracture strengths of rutile nanotubes. The atoms near the surface of the crystalline nanotube reside in a local environment different from the interior, which can result in the non-zero surface stress.59 With increasing the average radius, such surface stress is reduced, leading to increased fracture strength.60 Similar free-surface effect also appears in metal nanowires, where non-zero tensile surface stress can enhance their tensile yield stress.61,62
| (GPa) | No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | No. 6 |
|---|---|---|---|---|---|---|
| Rutile | 40.95 | 28.55 | 36.63 | 45.34 | 54.37 | 62.58 |
| Amorphous | 18.60 | 18.91 | 18.18 | 18.65 | 19.28 | 20.15 |
As shown in Fig. 4(b), all amorphous TiO2 nanotubes deform elastically within the strain range of 0–10%. Different from σ–ε curves of rutile nanotubes, however, significant ductility (about 30%) is observed in their σ–ε curves after the yielding. The corresponding yield stress σy and εy are around 19 GPa and 10%, respectively. Similar to the Young's modulus, the yield stresses of amorphous nanotubes are lower than fracture strengths of rutile ones. During yielding no obvious cracks can be observed in Fig. 6(b). As shown in Fig. 6(c), the nanotube starts to experience necking at about 30% strain. This is followed by final failure via shear deformation, corresponding to a failure strain of about 45%, Fig. 6(d). As compared to rutile type nanotubes, these amorphous nanotubes demonstrate significant ductility. Note that the fracture strength and yield stress obtained from MD simulations are generally higher than those from experiments.63 This is attributed to the large number of structural defects in TiO2 nanotubes formed during synthesis process.
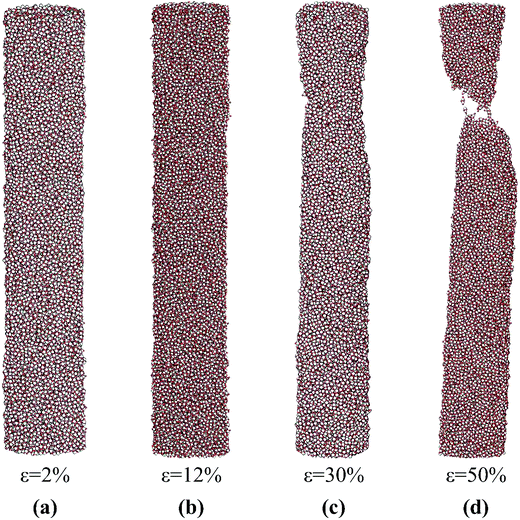 | ||
| Fig. 6 Snap shots of tensile deformation of amorphous TiO2 nanotube no. 2 under the tensile strain of (a) 2%, (b) 12%, (c) 30% and (d) 50%. | ||
3.3. Deformation mechanisms of TiO2 nanotubes
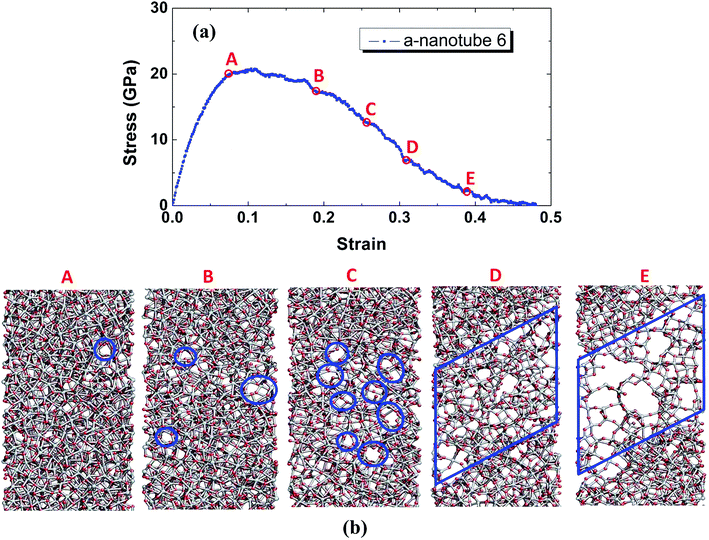 | ||
| Fig. 8 (a) Stress–strain (σ–ε) curve of amorphous TiO2 nanotube no. 6, and (b) evolution of atomic structure under tensile loading (insets A–E correspond to points A–E in the σ–ε curve). | ||
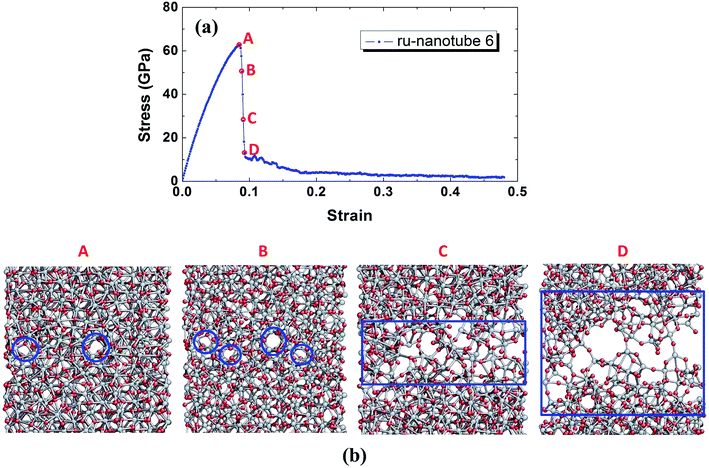
Note that some newly-formed nanovoids disappear during the tensile loading. For example, those nanovoids shown in inset A in Fig. 8(c) disappear but other nanovoids emerge at different locations, inset B Fig. 8(c). In other words, these nanovoids can be repaired during deformation. To understand this repairing mechanism, the evolution of Ti–O bonds with loading is examined, as illustrated in Fig. 9. In a localized area (point G, highlighted by the blue circle), the T–O bond shown in Fig. 9(a) is broken under tensile loading, Fig. 9(b). This is also accompanied by the formation of new bonds, shown in green in Fig. 9(c). The nanovoid at point G can be repaired via the formation of new bonds, as shown in Fig. 9(d).
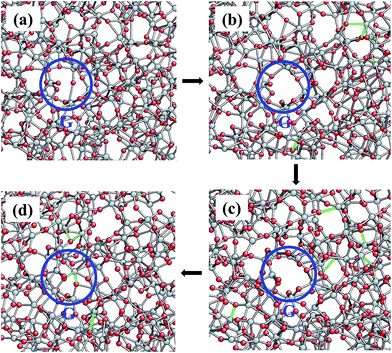 | ||
| Fig. 9 (a) Localized Ti–O bonds (highlighted by the blue circle), (b) bond breaking under loading, (c) new bonds formation (highlighted in green), and (d) repaired bonds. | ||
The under-coordinated atoms in the amorphous TiO2 nanotube may contribute to such repairing mechanism. Randomly organized Ti–O bonds in the amorphous nanotube are stretched, rotated or broken under loading. On the other hand, the under-coordinated O atoms or surface dangling O atoms are inclined to react with nearby under-coordinated Ti atoms, leading to the formation of new bonds. The breaking or forming of bonds will change the local structure and atom distribution, as well as the local stress and strain distribution. For example, if a bond gets broken, this will release the tensile stress to the section close to it. If this happens near a nanovoid, it will cause the shrinkage of the nanovoid. This can benefit the formation of new Ti–O bonds across the nanovoid and the repairing of it. The competition between the breaking and formation of new bonds may delay the formation of nanovoids with critical sizes required for brittle fracture, contributing to the ductility observed in the σ–ε curves. With the increase of tensile loading, more nanovoids are formed but less are repaired in amorphous nanotubes. In such case, the coalescence of neighboring nanovoids starts, and the stress begins to drop gradually (Fig. 8(b)). When the tensile loading further rising, the coalescence of a series of nanovoids occurs (inset D in Fig. 8(c)), which leads to the total failure of amorphous nanotubes, shown in inset E in Fig. 8(c).
The over-coordinated (such as 7-fold) Ti sites also attribute to the ductility observed in the amorphous nanotubes. As shown in Fig. 10, the over-coordinated sites can be converted into the regular-coordinated (6-fold) Ti sites during tensile deformation, which can create new bonds, increase strain energy dissipation and ductility beyond the elastic limit.65 Since a small fraction of over-coordinated Ti sites exist in the amorphous structure, the breaking of excessive Ti–O bonds at those 7-fold coordination sites enables the plastic deformation through such strain energy dissipation process. Similar phenomena have been observed at over-coordinated Si sites in amorphous silica glass.65–67 Therefore, although the disordered structure of amorphous TiO2 nanotube lowers the Young's modulus, its under- and over-coordinated atomic structure contribute to the ‘repairing’ and ‘conversion’ mechanism, which promotes new bond formation and breaking, and associated strain energy dissipation and ductility under loading.
4. Conclusions
In present work, we have conducted MD simulations to investigate the mechanical behaviour of both rutile and amorphous TiO2 nanotubes, with a focus on the effects of geometric parameters and crystal structure. The results demonstrate that rutile nanotubes have higher Young's modulus and fracture strength than those of amorphous TiO2 nanotubes. This can be attributed to the regular crystalline structure in the rutile TiO2 nanotubes. However, amorphous TiO2 nanotubes surprisingly exhibit greater ductility via a ‘repairing’ mechanism. In other words, the external loading can effectively promote bond reconstructions at under-coordinated Ti sites and strain energy dissipation at over-coordinated Ti sites, increasing the overall ductility. Furthermore, we find that fracture strengths of rutile TiO2 nanotubes strongly depend on their free surfaces. The decrease of induced surface stress can render the enhancement of their fracture strength.Acknowledgements
This research was supported by the Australian Research Council Discovery Project (DP150101717). Y. N. Xu acknowledges the financial support from the China Scholarship Council and a Top-Up scholarship from Queensland University of Technology.References
- J. H. Braun, A. Baidins and R. E. Marganski, Prog. Org. Coat., 1992, 20, 105–138 CrossRef CAS.
- U. Bach, D. Lupo, P. Comte, J. E. Moser, F. Weissortel, J. Salbeck, H. Spreitzer and M. Gratzel, Nature, 1998, 395, 583–585 CrossRef CAS.
- L. Etgar, P. Gao, Z. Xue, Q. Peng, A. K. Chandiran, B. Liu, M. K. Nazeeruddin and M. Grätzel, J. Am. Chem. Soc., 2012, 134, 17396–17399 CrossRef CAS PubMed.
- E. J. W. Crossland, N. Noel, V. Sivaram, T. Leijtens, J. A. Alexander-Webber and H. J. Snaith, Nature, 2013, 495, 215–219 CrossRef CAS PubMed.
- J. T.-W. Wang, J. M. Ball, E. M. Barea, A. Abate, J. A. Alexander-Webber, J. Huang, M. Saliba, I. Mora-Sero, J. Bisquert, H. J. Snaith and R. J. Nicholas, Nano Lett., 2014, 14, 724–730 CrossRef CAS PubMed.
- J. Wang, D. N. Tafen, J. P. Lewis, Z. Hong, A. Manivannan, M. Zhi, M. Li and N. Wu, J. Am. Chem. Soc., 2009, 131, 12290–12297 CrossRef CAS PubMed.
- S. N. Habisreutinger, L. Schmidt-Mende and J. K. Stolarczyk, Angew. Chem., Int. Ed., 2013, 52, 7372–7408 CrossRef CAS PubMed.
- J. Yu, J. Low, W. Xiao, P. Zhou and M. Jaroniec, J. Am. Chem. Soc., 2014, 136, 8839–8842 CrossRef CAS PubMed.
- B. Qiu, M. Xing and J. Zhang, J. Am. Chem. Soc., 2014, 136, 5852–5855 CrossRef CAS PubMed.
- A. J. Nozik and R. Memming, J. Phys. Chem., 1996, 100, 13061–13078 CrossRef CAS.
- N. Satoh, T. Nakashima, K. Kamikura and K. Yamamoto, Nat. Nanotechnol., 2008, 3, 106–111 CrossRef CAS PubMed.
- N. Sakai, Y. Ebina, K. Takada and T. Sasaki, J. Am. Chem. Soc., 2004, 126, 5851–5858 CrossRef CAS PubMed.
- J. Yan, S. Feng, H. Lu, J. Wang, J. Zheng, J. Zhao, L. Li and Z. Zhu, Mater. Sci. Eng., B, 2010, 172, 114–120 CrossRef CAS.
- M. Liu, H. Wang, C. Yan, G. Will and J. Bell, Appl. Phys. Lett., 2011, 98, 133113 CrossRef.
- D. Regonini, C. Bowen, A. Jaroenworaluck and R. Stevens, Mater. Sci. Eng., R, 2013, 74, 377–406 CrossRef.
- M. Liu, H. Wang, C. Yan and J. Bell, Mater. Focus, 2012, 1, 136–141 CrossRef CAS.
- J. Tang, B. Kong, Y. Wang, M. Xu, Y. Wang, H. Wu and G. Zheng, Nano Lett., 2013, 13, 5350–5354 CrossRef CAS PubMed.
- W. Guo, X. Xue, S. Wang, C. Lin and Z. L. Wang, Nano Lett., 2012, 12, 2520–2523 CrossRef CAS PubMed.
- M. Ye, D. Zheng, M. Lv, C. Chen, C. Lin and Z. Lin, Adv. Mater., 2013, 25, 3039–3044 CrossRef CAS PubMed.
- J. Lu, H. Li, D. Cui, Y. Zhang and S. Liu, Anal. Chem., 2014, 86, 8003–8009 CrossRef CAS PubMed.
- Y.-Y. Song, F. Schmidt-Stein, S. Bauer and P. Schmuki, J. Am. Chem. Soc., 2009, 131, 4230–4232 CrossRef CAS PubMed.
- J. Park, S. Bauer, A. Pittrof, M. S. Killian, P. Schmuki and K. von der Mark, Small, 2012, 8, 98–107 CrossRef CAS PubMed.
- K. Gulati, S. Ramakrishnan, M. S. Aw, G. J. Atkins, D. M. Findlay and D. Losic, Acta Biomater., 2012, 8, 449–456 CrossRef CAS PubMed.
- Y. N. Xu, M. N. Liu, M. C. Wang, A. Oloyede, J. M. Bell and C. Yan, J. Appl. Phys., 2015, 118, 145301 CrossRef.
- G. A. Crawford, N. Chawla, K. Das, S. Bose and A. Bandyopadhyay, Acta Biomater., 2007, 3, 359–367 CrossRef CAS PubMed.
- H. Hirakata, K. Ito, A. Yonezu, H. Tsuchiya, S. Fujimoto and K. Minoshima, Acta Mater., 2010, 58, 4956–4967 CrossRef CAS.
- F.-L. Arthur, B. Etienne, A. Tristan, M. Samy, L. David and T. Konstantinos, J. Phys.: Condens. Matter, 2014, 26, 055011 CrossRef PubMed.
- Y. Qi, T. Çağın, Y. Kimura and W. A. Goddard, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3527–3533 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford university press, 1989 Search PubMed.
- M. D. Kluge, J. R. Ray and A. Rahman, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 4234–4237 CrossRef CAS.
- M. Matsui and M. Akaogi, Mol. Simul., 1991, 6, 239–244 CrossRef.
- H. Vo Van, Nanotechnology, 2008, 19, 105706 CrossRef PubMed.
- K. h. Thomas, T. Marcus, E. Henrik, L. Marc, R. Detlev and F. Thomas, J. Phys. D: Appl. Phys., 2013, 46, 325302 CrossRef.
- C. F. Valeria, F. A. N. Christian, M. B. n. Oviedo, P. B. Franco, Y. O. Fabiana and G. S. n. Cristin, J. Phys.: Condens. Matter, 2013, 25, 115304 CrossRef PubMed.
- V. N. Koparde and P. T. Cummings, J. Phys. Chem. B, 2005, 109, 24280–24287 CrossRef CAS PubMed.
- V. Hoang, H. Zung and N. H. B. Trong, Eur. Phys. J. D, 2007, 44, 515–524 CrossRef CAS.
- D. Collins and W. Smith, Council for the Central Laboratory of Research Councils, Daresbury Research Report DL-TR-96–001, 1996 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- M. C. Wang, C. Yan, L. Ma, N. Hu and M. W. Chen, Comput. Mater. Sci., 2012, 54, 236–239 CrossRef CAS.
- M. C. Wang and C. Yan, Sci. Adv. Mater., 2014, 6, 1501–1505 CrossRef CAS.
- M. C. Wang, Z. B. Lai, D. Galpaya, C. Yan, N. Hu and L. M. Zhou, J. Appl. Phys., 2014, 115, 123520 CrossRef.
- M. Zhou, Proc. R. Soc. London, Ser. A, 2003, 459, 2347–2392 CrossRef CAS.
- D. H. Tsai, J. Chem. Phys., 1979, 70, 1375–1382 CrossRef CAS.
- L. Ju, Modell. Simul. Mater. Sci. Eng., 2003, 11, 173–177 CrossRef.
- D. T. Cromer and K. Herrington, J. Am. Chem. Soc., 1955, 77, 4708–4709 CrossRef CAS.
- V. Petkov, G. Holzhüter, U. Tröge, T. Gerber and B. Himmel, J. Non-Cryst. Solids, 1998, 231, 17–30 CrossRef CAS.
- M. J. Demkowicz and A. S. Argon, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 245206 CrossRef.
- A. Kerrache, N. Mousseau and L. J. Lewis, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014110 CrossRef.
- A. J. Kulkarni, M. Zhou and F. J. Ke, Nanotechnology, 2005, 16, 2749 CrossRef CAS.
- V. Van Hoang, Phys. Status Solidi B, 2007, 244, 1280–1287 CrossRef.
- M. M. J. Treacy and K. B. Borisenko, Science, 2012, 335, 950–953 CrossRef CAS PubMed.
- L. Dai, C. Sow, C. Lim, W. Cheong and V. Tan, Nano Lett., 2009, 9, 576–582 CrossRef CAS PubMed.
- J. Diao, K. Gall and M. L. Dunn, J. Mech. Phys. Solids, 2004, 52, 1935–1962 CrossRef CAS.
- C. Q. Chen, Y. Shi, Y. S. Zhang, J. Zhu and Y. J. Yan, Phys. Rev. Lett., 2006, 96, 075505 CrossRef CAS PubMed.
- K. Xue and L.-S. Niu, J. Appl. Phys., 2009, 106, 083505 CrossRef.
- K. Xue and L.-S. Niu, J. Appl. Phys., 2010, 107, 083517 CrossRef.
- G.-F. Wang and X.-Q. Feng, Appl. Phys. Lett., 2009, 94, 141913 CrossRef.
- X.-Y. Sun, Y. Xu, G.-F. Wang, Y. Gu and X.-Q. Feng, Phys. Lett. A, 2015, 379, 1893–1897 CrossRef CAS.
- K. Gall, J. Diao and M. L. Dunn, Nano Lett., 2004, 4, 2431–2436 CrossRef CAS.
- Z. Yang, Z. Lu and Y.-P. Zhao, Comput. Mater. Sci., 2009, 46, 142–150 CrossRef CAS.
- M. C. Wang, C. Yan, D. Galpaya, Z. B. Lai, L. Ma, N. Hu, Q. Yuan, R. X. Bai and L. M. Zhou, J. Nano Res., 2013, 23, 43–49 CrossRef.
- T. Dumitrica, M. Hua and B. I. Yakobson, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6105–6109 CrossRef CAS PubMed.
- F. Yuan and L. Huang, Sci. Rep., 2014, 4, 5035 CAS.
- Y.-C. Chen, Z. Lu, K.-I. Nomura, W. Wang, R. K. Kalia, A. Nakano and P. Vashishta, Phys. Rev. Lett., 2007, 99, 155506 CrossRef PubMed.
- K.-I. Nomura, Y.-C. Chen, R. K. Kalia, A. Nakano and P. Vashishta, Appl. Phys. Lett., 2011, 99, 111906 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |