Anomalous mechanical strengths and shear deformation paths of Al2O3 polymorphs with high ionicity
Z. Zhangab,
Z. H. Fuab,
R. F. Zhang*ab,
D. Legutcd and
H. B. Guo*a
aSchool of Materials Science and Engineering, Beihang University, Beijing 100191, P. R. China. E-mail: zrf@buaa.edu.cn; guo.hongbo@buaa.edu.cn
bCenter for Integrated Computational Engineering, International Research Institute for Multidisciplinary Science, Beihang University, Beijing 100191, P. R. China
cIT4 Innovations Center, VSB-Technical University of Ostrava, CZ-70833 Ostrava, Czech Republic
dCharles University, Faculty of Mathematics and Physics, Department of Condensed Matter Physics, Ke Karlovu 5, CZ-12 116 Prague 2, Czech Republic
First published on 15th January 2016
Abstract
Alumina (Al2O3) formed by selective oxidization provides an effective way to protect aluminide alloys against corrosion for sustainable applications. Despite a broad interest and investigations on Al2O3 polymorphs such as α-Al2O3 and θ-Al2O3, their intrinsic mechanical strengths and atomic deformation mechanisms are not yet fully understood. In this research, density functional theory is used to show that the calculated shear moduli and mechanical strengths of θ-Al2O3 are substantially lower than those of α-Al2O3, and this explains why θ-Al2O3 is much weaker than α-Al2O3. An analysis of shear deformation paths and electronic structure indicates that the longest Al–O ionic bonds are responsible for the lattice instability of both polymorphs during shear, showing they have different anisotropic features. This study gives a novel view on the failure of thermally grown α-Al2O3 and θ-Al2O3, and it should help to improve the performance of thermal barrier coatings.
1. Introduction
Alumina (Al2O3) polymorphs are important ceramic materials with many desirable properties such as high hardness, chemical inertness, thermal shock resistance and wear resistance, which makes them useful for many technological applications such as protective coatings, abrasives, insulators, and catalysts.1–4 The most stable form of alumina is α-Al2O3, which is described as a quasi-harmonic crystal with negligible intrinsic anharmonic effects.5 The α-Al2O3, alumina may also adopt a series of metastable transition polymorphs such as γ, η, θ, γ′ and δ structures with different fcc packing of oxygen, and α, κ, κ′ and ι structures based on hcp packing lattice.6,7 Some other structures include θ′, θ′′, λ, U and χ have also been reported.6,7 When Al2O3 adopts the fcc packing lattice, a phase transformation of alumina may occur by the reactions shown in the following four sequences:7
 | (i) |
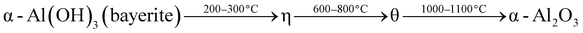 | (ii) |
| Amorphous (anodic film) → γ → δ → θ → α-Al2O3 | (iii) |
| Melt → γ → δ, θ → α-Al2O3 | (iv) |
With the alumina polymorphs and hydroxides as input, Peintinger et al.6 systematically investigated their relative stability using hybrid density functional theory (DFT), and then obtained the following energetic order: gibbsite < bayerite < boehmite < akdalaite < α-Al2O3 < κ-Al2O3 < θ-Al2O3 < δ-Al2O3 < γ-Al2O3 < η-Al2O3 < ι-Al2O3. Lee et al.8 compared the band gap of some aluminas and provided an order of α > κ > θ > γ, which is agreement with the most recent results by Museur et al.9
Among these alumina polymorphs, the α-Al2O3 and κ-Al2O3 are used as protective coatings against wear on tools because of their superior mechanical properties, whereas the metastable γ-Al2O3 and θ-Al2O3 are used as catalytic supports because of their lower surface energy.10 It is generally known that the α- and θ-Al2O3 play an important role in the performance of the early oxidation of nickel–aluminium alloys in thermal barrier coatings (TBCs), whereas the others are generally regarded as defectively metastable ones.11–13 However, the stress concentration because of the fast phase transformation of θ-Al2O3 to α-Al2O3 is an important factor that leads to alumina scale cracking and spallation at Al2O3/alloy interface in TBCs.14,15 To better understand the effect of metastable θ-Al2O3 on the performance of TBCs, much effort has been made to evaluate the properties of θ-Al2O3 both practically and using theoretical calculations. However, only limited equilibrium data, such as structural stability, electronic structure and elastic constants, have been reported so far. Therefore, in the present study, the former two polymorphs were the ones that were focused on. In the previous theoretical studies, the band gaps of α-Al2O3 were calculated to be about 6.72 eV,8 6.1 eV (ref. 16) and 6.24 eV,17 which underestimate the experimental value of 8.8 eV.16,18 The indirect band gaps of 5.04 eV (ref. 8) and 4.98 eV (ref. 17) were also reported for θ-Al2O3, which are about 1.3–1.7 eV smaller than that of α-Al2O3. Although the calculated site- and orbital-resolved partial electronic density of states (EDOS) show profound dependence on local coordination of Al and oxygen (O) atoms, the derived effective charge and bond order are similar for both θ-Al2O3 and α-Al2O3.17 These results suggest a fundamental question about whether both polymorphs could possess comparable mechanical properties.
For this purpose, a comparative mechanical test of α-Al2O3 and θ-Al2O3 was performed by Shang et al.19 several years ago. They obtained a positive value of c14 for α-Al2O3 by means of ab initio DFT calculations, and these results were in good agreement with the results obtained in previous experiments and theoretical studies by Gladden et al.20 and Hovis et al.21 With this validation, the derived bulk moduli and shear moduli of α-Al2O3 are shown to be much higher than those of θ-Al2O3, and this provides guidance for understanding the failure origin of the TBCs. In Shang's later work,22 the calculated temperature-dependent elastic constants enable a more realistic stress analysis at elevated temperatures in thermally grown oxides containing α-Al2O3 and θ-Al2O3, which provide a deeper understanding of the failure of TBCs in gas turbine engines.
Although numerous investigations have been performed on the structure and elastic properties of Al2O3 polymorphs, relatively little work has been devoted to the calculations of ideal strength and deformation paths which are critical for an in-depth understanding of the failure of turbine parts operating under extreme conditions. In general, a higher elastic modulus does not guarantee a higher strength because the former one describes only the reversible response of a crystal to a small strain, whereas the ideal strength gives an upper limit of stress that an ideal crystal can sustain at large strain.23,24 In the present paper, α-Al2O3 and θ-Al2O3 polymorphs are used to illustrate that, although both are experimentally accessible and have similar effective charge and ionicity,17 their mechanical strengths and shear deformation paths are substantially different.
Recent advancements in computational techniques have made it the routine method to calculate the ideal strengths in a reasonably precise way using first principle methods and have provided a method to analyze the deformation paths and electronic instabilities under various loadings.23,25,26 It is generally recognized that the ideal strength is a fundamental indicator of material strength,27 which is defined as the minimum stress required to plastically deform an ideal crystal and the stress required for the formation of stacking faults.28 A close connection between Peierls–Nabarro stress of dislocations and ideal shear strength has also made it possible to evaluate the mechanical strength of a real material via a comprehensive analysis of two intrinsic mechanical parameters: shear moduli and shear strength.25,29 In addition, the ideal shear strength has attracted much more attention with the progress of nanotechnology, which provides a way to quantitatively measure the near ideal strength, which can be obtained from modern first principle calculations.27,30
2. Computational methods
The ab initio DFT calculations31,32 were performed using the Vienna ab initio simulation package (VASP) with the Perdew–Burke–Ernzerhof (PBE)33 version of the generalized gradient approximation (GGA) for the exchange–correlation functional. For the EDOS calculations, the screened hybrid functional (HF) of Heyd, Scuseria, and Ernzerhof (HSE06)34 was chosen, where correlation is described in GGA (PBE) and the exchange is a mixture of 25% exact (HF) exchange and 75% PBE exchange. The integration in the Brillouin zone was done on special k points of 9 × 9 × 9 grids for the phases under consideration, with an energy cutoff of 600 eV, which was sufficient to keep the total energy convergence at 10−3 meV per atom or less. The atomic positions were relaxed using the conjugate gradient method until the forces on all the atoms were converged to less than 10−3 eV Å−1.As a further check of the validity of the applied projected augmented wave (PAW)-PBE potentials, the elastic constants and moduli were determined by applying a set of small deformations, δ, between −0.02 and +0.02, and then the second order coefficients in a polynomial fit of the total energy as a function of the distortion δ were calculated. Atomic relaxations were allowed when straining the cell. The applied strain configurations and the corresponding strain–energy density variations, ΔE/V0, for hcp α-Al2O3 structure were: ε = (δ, δ, 0, 0, 0, 0) with ΔE/V0 = (c11 + c12)δ2, ε = (0, 0, 0, 0, 0, δ) with ΔE/V0 = 1/4(c11 − c12)δ2, ε = (0, 0, δ, 0, 0, 0) with ΔE/V0 = 1/2c33δ2, ε = (0, 0, 0, δ, 0, 0) with ΔE/V0 = 1/2c44δ2, and ε = (δ, δ, δ, 0, 0, 0) with ΔE/V0 = (c11 + c12 + 2c13 + 1/2c33)δ2. For θ-Al2O3, ε = (δ, 0, 0, 0, 0, 0) with ΔE/V0 = 1/2c11δ2, ε = (0, δ, 0, 0, 0, 0) with ΔE/V0 = 1/2c22δ2, ε = (0, 0, δ, 0, 0, 0) with ΔE/V0 = 1/2c33δ2, ε = (0, 0, 0, δ, 0, 0) with ΔE/V0 = 1/2c44δ2, ε = (0, 0, 0, 0, δ, 0) with ΔE/V0 = 1/2c55δ2, ε = (0, 0, 0, 0, 0, δ) with ΔE/V0 = 1/2c66δ2, ε = (δ, δ, 0, 0, 0, 0) with ΔE/V0 = (1/2c11 + c12 + 1/2c22)δ2, ε = (δ, 0, δ, 0, 0, 0) with ΔE/V0 = (1/2c11 + c13 + 1/2c33)δ2.
The ab initio DFT calculations of stress–strain dependences conducted in this research are technically similar to those performed in previous studies by Zhang et al.35–39 and these should be referred to for further details. The atomic basis vectors of a given unit cell were firstly projected onto the Cartesian coordinate system with one cell axis vector being parallel to the strain direction for the tension loading. For the shear deformation, one cell axis vector was perpendicular to the slip plane and another one was parallel to the slip direction in that plane. Afterwards, the crystal was incrementally deformed by transforming the unstrained cell basis vector matrices to the strained ones using the deformation matrices. In order to keep the crystal under a stress state of uniaxial tension or shear, the strained cell was relaxed for both the cell basis vectors and for the atom position inside the unit cell by keeping the applied strain component fixed and relaxing the other five strain components until their conjugate stress components, i.e., the Hellmann–Feynman stresses reached negligible values.
3. Results and discussion
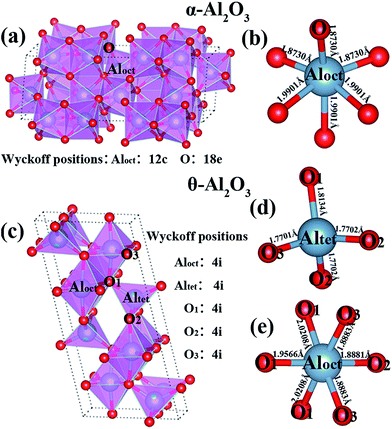
The α-Al2O3 with a space group of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c has the most symmetric ordering of Al atoms, which gives it a higher density compared to other polymorphs. The relaxed topological bond structure of α-Al2O3 is shown in Fig. 1(a); the Al cations and the O anions are located at the 12c (0, 0, z) and 18e (x, 0, 0.25) Wyckoff positions, respectively. The obtained values of the x- and z-coordinates are 0.306 and 0.352, respectively, which are in good agreement with those results obtained previously (x = 0.306 and z = 0.347).40 The α-Al2O3 can also be represented in a hexagonal lattice with six layers of close packed O atoms filled by Al atoms at the octahedral hole sites. Each Al atom is bonded to six O atoms with two non-equivalent bond distances, and each O atom has four neighbor Al atoms [see Fig. 1(b)]. Fig. 1(c) shows the crystal structure and local coordination of anions of θ-Al2O3 that belong to the monoclinic system with a space group of C2/m, with all the ions located at 4i (x, 0, z) Wyckoff positions. Our calculated coordinates of O are: (0.160 0 0.109), (0.495 0 0.257), (0.826 0 0.433), and those of Al are: (0.090 0 0.796) (0.342 0 0.683), and these values agree with the previous values of O: (0.163 0 0.123), (0.489 0 0.261), (0.830 0 0.439) and those of Al: (0.101 0 0.794) (0.352 0 0.687).41 The Al atoms occupy four octahedral and four tetrahedral interstitials of the O sublattice42 [see Fig. 1(d) and (e)]. The calculated lattice parameters of α-Al2O3 are a = 4.806 Å, c/a = 2.7285 and those of θ-Al2O3 are a = 11.922 Å, b = 2.940 Å, c = 5.668 Å, β = 104.0°. They are in agreement with the available theoretical and experimental values (a = 4.8195 Åa, 5.180 Åb, c/a = 2.7284a for α-Al2O3 and a = 11.923Åb, 11.8530c; b = 2.941 Åb, 2.904c; c = 5.671 Åb, 5.622c, β = 103.90°b, 103.8°c for θ-Al2O3) (a ref. 43, b ref. 19, c ref. 44). There is only one type of O coordination in α-Al2O3, but θ-Al2O3 has three different types of O coordination, which produce a more complicated bond anisotropy. Fig. 1(c) shows that O1 is bonded to one Altet and three Aloct cations, where Aloct (Altet) stands for the Al in octahedral (tetrahedral) coordination. It can be further seen in Fig. 1(c) that O2 is bonded to two Altet and one Aloct cations, and O3 is bonded to one Altet and two Aloct cations.17 The Al–O bond lengths of 1.9901 (1.969d) Å and 1.8730 (1.857d) Å (d ref. 17) for α-Al2O3 [see Fig. 1(b)] show some differences from those of θ-Al2O3 in which seven equivalent Al–O bond lengths are 1.7701, 1.7702, 1.8134, 1.8881, 1.8883, 1.9566, 2.0208 Å [see Fig. 1(d) and (e)], which are in agreement with the previous values of 1.710, 1.745, 1.896, 1.904, 1.936, 2.025 Åd, respectively, (d ref. 17). The difference of local coordination between α-Al2O3 and θ-Al2O3, especially the bond anisotropy and the longest Al–O bonds are responsible for the different mechanical properties and the deformation paths during shear, as will be shown later in this paper.
c has the most symmetric ordering of Al atoms, which gives it a higher density compared to other polymorphs. The relaxed topological bond structure of α-Al2O3 is shown in Fig. 1(a); the Al cations and the O anions are located at the 12c (0, 0, z) and 18e (x, 0, 0.25) Wyckoff positions, respectively. The obtained values of the x- and z-coordinates are 0.306 and 0.352, respectively, which are in good agreement with those results obtained previously (x = 0.306 and z = 0.347).40 The α-Al2O3 can also be represented in a hexagonal lattice with six layers of close packed O atoms filled by Al atoms at the octahedral hole sites. Each Al atom is bonded to six O atoms with two non-equivalent bond distances, and each O atom has four neighbor Al atoms [see Fig. 1(b)]. Fig. 1(c) shows the crystal structure and local coordination of anions of θ-Al2O3 that belong to the monoclinic system with a space group of C2/m, with all the ions located at 4i (x, 0, z) Wyckoff positions. Our calculated coordinates of O are: (0.160 0 0.109), (0.495 0 0.257), (0.826 0 0.433), and those of Al are: (0.090 0 0.796) (0.342 0 0.683), and these values agree with the previous values of O: (0.163 0 0.123), (0.489 0 0.261), (0.830 0 0.439) and those of Al: (0.101 0 0.794) (0.352 0 0.687).41 The Al atoms occupy four octahedral and four tetrahedral interstitials of the O sublattice42 [see Fig. 1(d) and (e)]. The calculated lattice parameters of α-Al2O3 are a = 4.806 Å, c/a = 2.7285 and those of θ-Al2O3 are a = 11.922 Å, b = 2.940 Å, c = 5.668 Å, β = 104.0°. They are in agreement with the available theoretical and experimental values (a = 4.8195 Åa, 5.180 Åb, c/a = 2.7284a for α-Al2O3 and a = 11.923Åb, 11.8530c; b = 2.941 Åb, 2.904c; c = 5.671 Åb, 5.622c, β = 103.90°b, 103.8°c for θ-Al2O3) (a ref. 43, b ref. 19, c ref. 44). There is only one type of O coordination in α-Al2O3, but θ-Al2O3 has three different types of O coordination, which produce a more complicated bond anisotropy. Fig. 1(c) shows that O1 is bonded to one Altet and three Aloct cations, where Aloct (Altet) stands for the Al in octahedral (tetrahedral) coordination. It can be further seen in Fig. 1(c) that O2 is bonded to two Altet and one Aloct cations, and O3 is bonded to one Altet and two Aloct cations.17 The Al–O bond lengths of 1.9901 (1.969d) Å and 1.8730 (1.857d) Å (d ref. 17) for α-Al2O3 [see Fig. 1(b)] show some differences from those of θ-Al2O3 in which seven equivalent Al–O bond lengths are 1.7701, 1.7702, 1.8134, 1.8881, 1.8883, 1.9566, 2.0208 Å [see Fig. 1(d) and (e)], which are in agreement with the previous values of 1.710, 1.745, 1.896, 1.904, 1.936, 2.025 Åd, respectively, (d ref. 17). The difference of local coordination between α-Al2O3 and θ-Al2O3, especially the bond anisotropy and the longest Al–O bonds are responsible for the different mechanical properties and the deformation paths during shear, as will be shown later in this paper.
Based on the reaction 4Al + 3O2 = 2Al2O3, the calculated energy difference per formula unit between α-Al2O3 and θ-Al2O3 is 0.047 eV, which is consistent with results from previous reports where the following values were reported: ΔE(θ − α) = 0.03 eV per formula unit in42 and 0.04 eV per formula unit in45 thus confirming that α-Al2O3 is thermodynamically more stable than θ-Al2O3.
The elastic constants were determined by applying an appropriate set of distortions within elastic limits.46,47 Table 1 shows the calculated and measured values of the elastic constants cij for α-Al2O3 and θ-Al2O3. The elastic constants satisfy the Born stability criteria,43,48,49 thus confirming that both hexagonal α-Al2O3 and monoclinic θ-Al2O3 are mechanically stable. Voigt average bulk modulus, BV, of α-Al2O3 (235.6 GPa) is much larger than that of θ-Al2O3 (187.4 GPa), i.e., α-Al2O3 is more incompressible than θ-Al2O3. Additionally, it is found that the anisotropy ratio between c11 and c33 is nearly unity for α-Al2O3, whereas it is about 1.5 for θ-Al2O3, suggesting a higher elastic anisotropy for θ-Al2O3. A well-established consideration of whether a crystalline solid is intrinsically ductile or brittle50–52 can be characterized approximately by using the ratio of the shear modulus to the bulk modulus, G/B, by considering B as the resistance to fracture and G as the resistance to plastic deformation.52–54 The critical G/B ratio which separates ductile and brittle materials is around 0.57, i.e., if G/B < 0.57 the material behaves in a ductile manner, otherwise the material is brittle. The relatively high ratio of G/B ≈ 0.63 for α-Al2O3 reveals that it is intrinsically brittle, and this in agreement with the results of the experiments. The somewhat lower value of 0.58 for θ-Al2O3 is closer to the boundary of brittleness/ductility.
| Property | α-Al2O3 | θ-Al2O3 | |||||
|---|---|---|---|---|---|---|---|
| This work | GGA | LDA | Experimental | This work | GGA | LDA | |
| a Ref. 43.b Ref. 21.c Ref. 44.d Ref. 17.e Ref. 48. | |||||||
| c11 | 455.2 | 437.2a, 451.5b | 476.8a, 497.1b | 497.5c, 497d, 497.4e | 268.0 | 269.1b | 283.8b |
| c22 | 389.7 | 389.3b | 420.4b | ||||
| c33 | 457.1 | 443.3a, 454.9b | 476.6a, 492.5b | 503.3c, 501d, 499.1e | 405.8 | 404.2b | 435.3b |
| c44 | 132.6 | 125.5a, 131.7b | 145.5a, 154.2b | 147.4c, 147d, 147.4e | 72.5 | 74.2b | 86.8b |
| c55 | 102.0 | 102.2b | 104.3b | ||||
| c66 | 151.6 | 146.4a | 159.6a | 122.3 | 126.0b | 124.5b | |
| c12 | 152.0 | 144.3a, 148.4b | 157.6a, 164.7b | 162.7c, 163d, 164.0e | 112.2 | 113.2b | 119.3b |
| c13 | 112.2 | 101.5a, 107.6b | 119.4a, 129.5b | 115.5c, 116d, 112.2e | 135.5 | 132.2b | 159.8b |
| BV | 235.6 | 223.4a, 231.7b | 246.9a, 259.3b | 252.3e | 187.4 | 186.9b | 207.1b |
| GV | 149.4 | 143.0a, 149.3b | 158.5a, 165.8b | 166.0e | 109.5 | 110.7b | 114.9b |
| E | 370.0 | 353.6a | 391.6a | 403.0e | 274.9 | ||
| ν | 0.238 | 0.2362a | 0.2356a | 0.23e | 0.256 | ||
Next the ideal strengths of both Al2O3 polymorphs were investigated. For α-Al2O3, the ab initio DFT calculations were performed with a unit cell along the 〈0001〉, 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 and 〈10
0〉 and 〈10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 directions for tension and on the (0001) 〈
0〉 directions for tension and on the (0001) 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉, (0001) 〈10
0〉, (0001) 〈10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 and (10
0〉 and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) 〈
0) 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 slip systems for shear. The crystallographic directions of 〈010〉 and 〈001〉 of monoclinic θ-Al2O3 are parallel to the y and z axes in the Cartesian coordinate system. Fig. 2(a) shows the calculated stress–strain curves for α-Al2O3. The ideal tensile strength of α-Al2O3 along the 〈0001〉 direction of about 58.3 GPa is much larger than in the two other directions. The anisotropy ratio of tensile strengths for α-Al2O3 of σ〈0001〉 = 58.3
0〉 slip systems for shear. The crystallographic directions of 〈010〉 and 〈001〉 of monoclinic θ-Al2O3 are parallel to the y and z axes in the Cartesian coordinate system. Fig. 2(a) shows the calculated stress–strain curves for α-Al2O3. The ideal tensile strength of α-Al2O3 along the 〈0001〉 direction of about 58.3 GPa is much larger than in the two other directions. The anisotropy ratio of tensile strengths for α-Al2O3 of σ〈0001〉 = 58.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ〈10
σ〈10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 = 36.5
0〉 = 36.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ〈
σ〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 = 26.3 GPa ≈ 2.22
0〉 = 26.3 GPa ≈ 2.22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.39
1.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is slightly larger than those of θ-Al2O3 [see Fig. 2(b)]: σ〈010〉 = 28.9
1 is slightly larger than those of θ-Al2O3 [see Fig. 2(b)]: σ〈010〉 = 28.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ{001}normal = 14.8
σ{001}normal = 14.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ〈100〉 = 13.9 GPa ≈ 2.08
σ〈100〉 = 13.9 GPa ≈ 2.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.06
1.06![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. It is interesting to note that the anisotropy of ideal tensile strengths does not follow the previously mentioned elastic anisotropy for both Al2O3 polymorphs. The tensile strength of 26.3 GPa along the weakest 〈
1. It is interesting to note that the anisotropy of ideal tensile strengths does not follow the previously mentioned elastic anisotropy for both Al2O3 polymorphs. The tensile strength of 26.3 GPa along the weakest 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 direction of α-Al2O3 is comparable to the maximum value of 28.9 GPa of θ-Al2O3 along the 〈010〉 direction. Because plastic deformation occurs in shear, the calculated anisotropic ideal shear strengths must be compared.35,36,55,56 The lowest shear strength of 14.4 GPa of α-Al2O3 is found in the (0001) 〈
0〉 direction of α-Al2O3 is comparable to the maximum value of 28.9 GPa of θ-Al2O3 along the 〈010〉 direction. Because plastic deformation occurs in shear, the calculated anisotropic ideal shear strengths must be compared.35,36,55,56 The lowest shear strength of 14.4 GPa of α-Al2O3 is found in the (0001) 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 slip system [Fig. 2(a)]. This value is about 67% higher than the lowest shear strength of 4.7 GPa found for θ-Al2O3 [Fig. 2(b)], and this provides direct theoretical evidence that θ-Al2O3 is intrinsically much weaker than α-Al2O3.
0〉 slip system [Fig. 2(a)]. This value is about 67% higher than the lowest shear strength of 4.7 GPa found for θ-Al2O3 [Fig. 2(b)], and this provides direct theoretical evidence that θ-Al2O3 is intrinsically much weaker than α-Al2O3.
To further understand the deformation paths of both Al2O3 polymorphs in shear, the change of Al–O bond length and valence charge density differences (VCDD) during shear deformation are compared in Fig. 3. The VCDD is defined as the difference between the calculated total valence charge density of the crystal minus the superposition of the valence charge densities of neutral atoms39). A negative value (yellow color in Fig. 3) means a depletion of charge when compared to neutral atoms (bond weakening). To emphasize the variation of charge depletion between Al–O bonds, only the negative isosurface of VCDD is shown in Fig. 3. Note that the expansion of the negative VCDD isosurface between Al–O bonds indicates their weakening during shear deformation. Although both α-Al2O3 and θ-Al2O3 have similar ionic bonds, their bond deformation paths and electronic instability modes are substantially different as can be seen from the change of bond topology and deformed VCDD isosurfaces shown in Fig. 3. Fig. 3(b) and (c) show the typical Al–O bond length and VCDD at shear strain of γ = 0.1934 (before) and γ = 0.3400 (after instability) for α-Al2O3, and Fig. 3(e) and (f) show them at a shear strain of γ = 0.0924 (before) and γ = 0.1366 (after instability) for θ-Al2O3. For α-Al2O3, the shear instability occurs between Al {0001} and O {0001} planes [Fig. 3(b) and (c)] with an increase of Al–O bond length from 2.33 to 3.04 Å, whereas for θ-Al2O3, the shear instability appears between Al/O {001} planes with the Al–O bond lengths increasing from 2.23 to 2.73 Å [Fig. 3(e) and (f)]. In Fig. 3, it can also be seen that the dramatic change of VCDD before and after the instability of α-Al2O3 and θ-Al2O3 (see the yellow isosurface marked by big blue arrows), which shows that the process of Al–O bond strength becomes too weak for bond cleavage.
To quantify the electronic origin of distinct mechanical strength in both Al2O3, the quantum theory of atoms in molecules proposed by Bader57,58 is first used to quantitatively determine the change of charge transfer during shearing. The calculated non-equivalent values of Bader charges are: for α-Al2O3, at equilibrium: (Al−2.4751)2(O+1.6501)3, at γ = 0.1934 (before instability): (Al−2.4732)2(O+1.6488)3, at γ = 0.3400 (after instability): (Al−2.4640)2(O+1.6427)3; for θ-Al2O3, at equilibrium: (Al−2.4442/−2.4637)2(O+1.6431/+1.6346/+1.6303)3, at γ = 0.0924 (before instability): (Al−2.4451/−2.4749)2(O+1.6481/+1.6359/+1.6360)3, at γ = 0.1366 (after instability): (Al−2.4479/−2.4733)2(O+1.6340/+1.6442/+1.6431)3. It is seen that the highly ionicity of α-Al2O3 and θ-Al2O3 are nearly identical. The minor difference of the Bader charges between α-Al2O3 and θ-Al2O3 provides an electronic explanation on the significant differences of their ideal tensile and shear strengths. Further consideration of the distributions of non-equivalent, highly ionic Al–O bonds for θ-Al2O3 may give an explanation of the choice of deformation paths of both structures during the shear loadings (see the change of bond lengths and VCDD isosurface marked in Fig. (3).
In order to develop a deeper understanding of the mechanical properties of α-Al2O3 and θ-Al2O3, the EDOS and localized charge accumulation between Al–O bonds was next analyzed. Fig. 4(a) and (b) shows the total EDOS which presents three distinct regions: the lower part of the valence bands is dominated by O 2s states and the upper part by O 2p- and Al 3s-, 3p-like states. Both α-Al2O3 [Fig. 4(a)] and θ-Al2O3 [Fig. 4(b)] are insulators with band gaps of about 7.6 and 6.2 eV, respectively. The previously calculated band gaps of α-Al2O3 are 8.6 eV,6 9.1 eV,59 and 8.5 eV,60 and that of θ-Al2O3 is 6.9 eV,6 by utilizing the HSE functional. A higher value of the band gaps of α-Al2O3 was reported by Weber et al.,59 because the Hartree–Fock mixing parameter in the HSE calculation is 32%, which is higher than the standard HSE06 (25%). Note that the calculated band gap for α-Al2O3 using HSE06 pseudopotentials is much more close to the experimental value (∼8.8 eV) when compared to the previous studies.16,18 The upper valence band width (from −7.5 eV to 0 eV) of α-Al2O3, which is dominated by overlapping of O 2p and Al 3p orbitals, shows strong similarity to that of θ-Al2O3. To obtain the difference of bond strength between α-Al2O3 and θ-Al2O3, Fig. 4(c) and (d) show the contour plot of the VCDD cross section for α-Al2O3 and θ-Al2O3. The circled regions between the longest Al–O bonds in Fig. 4(c) and (d) indicate the magnitude of charge depletion. It can be clearly seen that the longer Al–O bonds for θ-Al2O3 corresponds to a higher depletion of valence charge density between them and a significant bond weakening, providing a physical explanation why α-Al2O3 is stronger than θ-Al2O3.
4. Conclusions
In conclusion, the structural, thermodynamic, mechanical, electronic properties and shear deformation paths of α-Al2O3 and θ-Al2O3 have been studied using ab initio DFT calculations. The resulting equilibrium properties of α-Al2O3 and θ-Al2O3 obtained are consistent with the experimental and theoretical data. The relatively high bulk modulus of α-Al2O3 confirms that it is a low compressible material, whereas the relatively low ratio of the shear modulus to bulk modulus shows that it is still intrinsically brittle, and somewhat more brittle than θ-Al2O3. The shear strength of θ-Al2O3 is much lower than that of α-Al2O3 because of the highly ionic Al–O bonds with the longest bond length being more intense for θ-Al2O3. The longest Al–O bond lengths determine the deformation paths in both of the Al2O3 polymorphs.Acknowledgements
This research is sponsored by National Basic Research Program (973 Program) of China under Grant No. 2012CB625100, the National High-tech R&D Program (863 project) No. 2012AA03A512, and the Nature Science Foundations of China (NFSC) under Grant No. 51231001 and No. 51425102. R. F. Zhang is supported by the Fundamental Research Funds for the Central Universities, NFSC with No. 51471018, and the National Thousand Young Talents Program of China. D. Legut acknowledges financial and computational support from the IT4 Innovations Centre of Excellence project (CZ.1.05/1.1.00/02.0070), funded by the European Regional Development Fund and the national budget of the Czech Republic (Large Research, Development and Innovations Infrastructures project, LM2011033). We would like to thank Prof. Dr. Stan Veprek for constructive comments and suggestions, and Prof. G. Kresse for valuable advice for the application of VASP.References
- N. P. Padture, M. Gell and E. H. Jordan, Science, 2002, 296, 280 CrossRef PubMed.
- A. Stierle, F. Renner, R. Streitel, H. Dosch, W. Drube and B. C. Cowie, Science, 2004, 303, 1652 CrossRef PubMed.
- G. Kresse, M. Schmid, E. Napetschnig, M. Shishkin, L. Köhler and P. Varga, Science, 2005, 308, 1440 CrossRef CAS PubMed.
- Z. Łodziana, N. Y. Topsoe and J. K. Norskov, Nat. Mater., 2004, 3, 289 CrossRef PubMed.
- A. Erba, J. Maul, R. Demichelis and R. Dovesi, Phys. Chem. Chem. Phys., 2015, 17, 11670–11677 RSC.
- M. F. Peintinger, M. J. Kratz and T. Bredow, J. Mater. Chem. A, 2014, 2, 13143–13158 CAS.
- I. Levin and D. Brandon, J. Am. Ceram. Soc., 1998, 81, 1995–2012 CrossRef.
- C. K. Lee, E. Cho, H. S. Lee, K. Seol and S. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245110 CrossRef.
- L. Museur, M. Bouslama, M. Amamra and A. Kanaev, Phys. Status Solidi RRL, 2013, 7, 1026–1029 CrossRef CAS.
- J. M. McHale, A. Auroux, A. J. Perrota and A. Navrotsky, Science, 1997, 277, 788 CrossRef CAS.
- K. M. N. Prasanna, A. S. Khanna and R. Chandra, Oxid. Met., 1996, 46, 465–480 CrossRef CAS.
- J. Doychak and M. Rühle, Oxid. Met., 1989, 31, 431–452 CrossRef CAS.
- S. H. Cai, S. N. Rashkeev, S. T. Pantelides and K. Sohlberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 224104 CrossRef.
- E. Schumann, Oxid. Met., 1995, 43, 157–172 CrossRef CAS.
- D. M. Lipkin, D. R. Clarke, M. Hollatz, M. Bobeth and W. Pompe, Corros. Sci., 1997, 39, 231–242 CrossRef CAS.
- R. H. French, J. Am. Ceram. Soc., 1990, 73, 477 CrossRef CAS.
- S. D. Mo and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 15219 CrossRef CAS.
- B. D. Evans, G. J. Pogatshnik and Y. Chen, Nucl. Instrum. Methods Phys. Res., Sect. B, 1994, 91, 258–262 CrossRef CAS.
- S. L. Shang, Y. Wang and Z. K. Liu, Appl. Phys. Lett., 2007, 90, 101909 CrossRef.
- J. R. Gladden, J. H. So, J. D. Maynard, P. W. Saxe and Y. L. Page, Appl. Phys. Lett., 2004, 85, 392 CrossRef CAS.
- D. B. Hovis, A. Reddy and A. H. Heuer, Appl. Phys. Lett., 2006, 88, 131910 CrossRef.
- S. L. Shang, W. Y. Wang, Y. Wang, Y. Du, J. X. Zhang, D. Patel and Z. K. Liu, J. Phys.: Condens. Matter, 2012, 24, 155402 CrossRef CAS PubMed.
- Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2015, 115, 185502 CrossRef PubMed.
- S. Ogata, J. Li and S. Yip, Science, 2002, 298, 807–811 CrossRef CAS PubMed.
- R. F. Zhang, D. Legut, Z. H. Fu, S. Veprek, Q. F. Zhang and H. K. Mao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 104107 CrossRef.
- R. F. Zhang, D. Legut, Z. J. Lin, Y. S. Zhao, H. K. Mao and S. Veprek, Phys. Rev. Lett., 2012, 108, 255502 CrossRef CAS PubMed.
- S. L. Shang, W. Y. Wang, B. C. Zhou, Y. Wang, K. A. Darling, L. J. Kecskes, S. N. Mathaudhu and Z. K. Liu, Acta Mater., 2014, 67, 168–180 CrossRef CAS.
- M. Jahnátek, J. Hafner and M. Krajčí, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 224103 CrossRef.
- M. Zhang, H. Yan, B. Zheng and Q. Wei, Sci. Rep., 2015, 5, 15481 CrossRef CAS PubMed.
- F. Liu, P. Ming and J. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 064120 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- R. F. Zhang, S. H. Sheng and S. Veprek, Appl. Phys. Lett., 2007, 90, 191903 CrossRef.
- R. F. Zhang, S. H. Sheng and S. Veprek, Appl. Phys. Lett., 2007, 91, 031906 CrossRef.
- R. F. Zhang, S. Veprek and A. S. Argon, Appl. Phys. Lett., 2007, 91, 201914 CrossRef.
- R. F. Zhang, S. H. Sheng and S. Veprek, Appl. Phys. Lett., 2009, 94, 121903 CrossRef.
- R. F. Zhang, D. Legut, X. D. Wen, S. Veprek, K. Rajan, T. Lookman, H. K. Mao and Y. S. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 094115 CrossRef.
- L. Lutterotti and P. Scardi, J. Appl. Crystallogr., 1990, 23, 246–252 CrossRef CAS.
- E. Husson and Y. Repelin, J. Solid State Chem., 1996, 33, 1223–1231 CAS.
- Z. Łodziana and K. Parlinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 174106 CrossRef.
- H. Z. Yao, L. Z. Ouyang and W. Y. Ching, J. Am. Ceram. Soc., 2007, 90, 3194–3204 CrossRef CAS.
- R. S. Zhou and R. L. Snyder, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 617 CrossRef.
- C. Wolverton and K. C. Hass, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 024102 CrossRef.
- A. F. Wright, J. Appl. Phys., 1997, 82, 2833 CrossRef CAS.
- S. Q. Wang and H. Q. Ye, J. Phys.: Condens. Matter, 2005, 17, 4475 CrossRef CAS.
- G. B. Brook, in Smithells Metals Reference Book, 8, ed. E. A. Brandes, 1983 Search PubMed.
- M. Born, Proc. Cambridge Philos. Soc., 1940, 36, 160 CrossRef CAS.
- G. Xu, A. S. Argon and M. Ortiz, Philos. Mag. A, 1997, 75, 341 CAS.
- G. Xu, A. S. Argon and M. Ortiz, Philos. Mag. A, 1995, 72, 415 CAS.
- S. F. Pugh, Philos. Mag., 1954, 45, 823 CrossRef CAS.
- M. Mattesini, R. Ahuja and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 184108 CrossRef.
- J. R. Rice, G. E. Beltz and Y. Sun, in Topics in Fracture and Fatigue, ed. A. S. Argon, Springer, New York, 1992, pp. 1–58 Search PubMed.
- J. Haines, J. M. Leger and G. Bocquillon, Annu. Rev. Mater. Res., 2001, 31, 1 CrossRef CAS.
- J. J. Gilman, Electronic Basis of the Strength of Materials, Cambridge University Press, United Kingdom, 2003, pp. 1–4 and 201–225 Search PubMed.
- R. F. W. Bader, Atoms in Molecules - A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 254 CrossRef.
- J. R. Weber, A. Janotti and C. G. van de Walle, J. Appl. Phys., 2011, 109, 033715 CrossRef.
- S. Park, B. Lee, S. H. Jeon and S. Han, Curr. Appl. Phys., 2011, 11, S337–S340 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |