Localized surface plasmon resonance on Au nanoparticles: tuning and exploitation for performance enhancement in ultrathin photovoltaics
Abstract
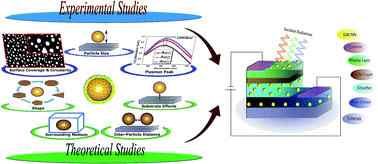
We report a detailed correlation analysis of the size, shape, and distribution of Au nanoparticles (NPs) on fine-tuning of localized surface plasmon resonance and optical absorption cross-section. Experimental analysis of annealing temperature and initial Au layer thickness on NP parameters such as size, interparticle distance, surface coverage, and circularity factor has been studied. The effect of annealing on the morphological, structural, dielectric, and elemental behavior of Au NPs has been reported. Theoretically, we have analyzed the tuning of LSPR and absorption cross-section peaks by varying NP parameters, surrounding medium, and substrate. This report is critical in terms of predicting performance enhancement of ultrathin photovoltaics with varied cell architectures.

 Please wait while we load your content...
Please wait while we load your content...