Capillary filling dynamics of polymer melts in nanopores: experiments and rheological modelling
Bing-Yang Cao*,
Min Yang and
Guo-Jie Hu
Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, P. R. China. E-mail: caoby@tsinghua.edu.cn; Fax: +86-10-6279-4531; Tel: +86-10-6279-4531
First published on 14th January 2016
Abstract
Understanding capillary filling dynamics in nanoconfined geometries is crucial in the nanotechnology field, such as nanofluidic devices, lab-on-a-chip, 3D printers, porous nanomaterials. The spontaneous capillarity-driven flow behaviors of polyethylene (PE) melts through anodized aluminum oxide (AAO) nanopores are investigated experimentally by using the nanoporous template wetting technique first in our study. The diameter of the pores is 100 nm and 200 nm. The displacement of the polymer melts is measured by the thickness of the fabricated nanowire array as a function of time. Besides, considering the effect of the shear rate on the polymer viscosity in the capillary nanoflow, a theoretical model, i.e. a modified Lucas–Washburn law that combines the Lucas–Washburn law with the polymer rheological model, is established. Based on the experimental results it is speculated that the rise of the meniscus agrees with the modified Lucas–Washburn law. It also suggests that the zero-shear-rate viscosity of the PE melts decreases in their flows through the nanopores and the induced unconventional rheological behavior may be caused by nanoconfinement of the nanopores.
I. Introduction
The capillary flow of liquids through nanochannels plays a decisive role in a broad range of natural and industrial applications, such as nanofluidic devices, lab-on-a-chip systems and porous nanomaterials. In recent years, with the progress in micro/nanofluidics and nanotechnology, nanofluidic devices and nanostructures manufactured based on it have drawn more and more attention. Among them, polymer nanostructures, with several advantages over other materials, such as low cost, simple processing techniques and accurate repeatability in mass-production, have offered potential applications in many areas, such as photonics,1,2 mechatronics,3,4 medicine and fluidic nanodevices.5,6 For the fabrication of these nanoproducts, a set of processing approaches, such as photolithography, scanning beam lithography,7 moulding,8 embossing,9 printing10 and electrospinning11 have been reported. Among these techniques, moulding offers a wide application and has the potential to be the ultimate low-cost method for manufacturing.12 Besides, the thermal conductivity of the fabricated polymer nanowire arrays were found to be about 2 orders of magnitude higher than their bulk counterparts, and with the morphology of the micro- and nanostructures on the surface superhydrophobicity of polymers has been obtained.13,14 As to fabricate high-quality polymer nanoproducts by nanomoulding, accurately controlling the flow behaviors of polymer melts through nanochannels is a key point.15For the capillary flow behaviors of liquids through pores, lots of theoretical, numerical and experimental studies16–21 have been done in search of a thorough physical understanding of the basic mechanisms involved. Almost a century ago, Lucas and Washburn established the basic capillarity law for newtonian liquids, i.e. the Lucas–Washburn equation (LWE)16
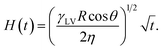 | (1) |
Actually whether the Lucas–Washburn equation or the modified formulas are applicable at micro- or nanoscale is still under discussions. Some experiments and numerical simulations have been carried out in recent years. Geromichalos et al.22 investigated the spontaneous imbibition of water and 1-undecanol fronts between two roughened glass plates with the separation between 10 and 50 μm, while Gruener and Huber23 studied the capillary filling behavior of water, liquid n-tetracosane and liquid crystal octyloxycyanobiphenyl in Vycor. Both of their work confirmed the LWE. Meanwhile, Oh et al.24 found that the dynamics of the filling of nanochannels using mixtures of ethanol and water followed the (time)1/2 dependence but the prefactor of the algebraic relation greatly deviated from the predictions based on the LWE with the bulk properties. The (time)1/2 dependence of the filling height but quantitative deviation of the prefactor from the LWE were also reported by Engel and Stuhn25 in their experimental measurements of the filling process in nanopores of polymer melts which appeared as newtonian liquids in the shear experiment since their molar masses were well below the critical molecular mass of entanglement.
More numerical studies have been done but no consistent description of the filling behavior at nanoscale has been got. Quirke et al.26,27 found out the penetration length was a linear function of time for short time and tended to a (time)1/2 dependence at long time based on their molecular dynamics (MD) simulations of carbon nanotubes imbibing decane. They believed that the linear time dependence at short time was due to the formation of a precursor film which spread at a much greater speed in advance of the main wetting line. However, Chibbaro et al.28 found that the dynamics of the precursor films obeyed a square-root law although with a larger prefactor by both hydrokinetic and MD approaches. Martic et al.29 demonstrated a reduction in the rate of penetration for a simple Lennard-Jones (LJ) fluid by using MD simulations and believed the reduction was caused by the contact angle that depended on the rate of wetting, especially during the early stages of capillary filling. There were lots of studies30–36 on the filling of various liquids (e.g. LJ fluid, polymer, liquid propane and water) into nanochannels (e.g. nanopores, patterned channels and carbon nanotubes) by using MD or lattice Boltzmann simulations. They observed the deviation of the kinetics of imbibition from the LWE and demonstrated the neglection of the DCA in the LWE is responsible for the deviation. Besides the DCA correction, some researchers investigated the effects of slip on the capillary dynamics and proposed the modifications to the LWE. Dimitrov et al.,37 using MD simulations, found for both the simple LJ fluid and polymer melts the meniscus rose according to the LWE after a transient period of a few nanoseconds. For the polymer melt, however, a slip length exhibited. Joly38 even believed the standard description of capillary filling dynamics had to be modified to account for the liquid/solid slip in nanometric pores based on their MD simulations of dynamics of water uptake by carbon nanotubes. Recently, Bakli and Chakraborty39 derived a universal analytical depiction of capillary imbibition characteristics of water in nanoscale pores through the realization of a molecularly sensitive closure model for dynamic slip length and they believed the DCA did not play any significant role in their work based on the simulation data of the contact angles which relaxed to the static value within a very short time span.
Few reports on non-newtonian liquids in nanoscale pores can be found in literature, especially experimental work, although it is a significant topic. There exists no description of the capillary flow behaviors of non-newtonian liquids like polymer melts through nanopores that is experimentally and theoretically consistent. In our previous paper,40 the preliminary study showed that the capillary filling of PE melts into nanopores followed the LW model, in which we did not take into account the non-newtonian characteristics of PE melts. Here we get more fruitful experimental data, and the aim of the present paper is to further clarify the problem of capillary filling of polymer melts in nanopores. We investigate the flow behaviors of the PE melt in AAO nanoporous templates experimentally, and develop a modified LW model of the capillary flow of polymer melts through nanopores based on the experimental results considering the non-newtonian characteristics. Here, our experiments are on much longer time scale compared with the existing MD studies, which is more instructive to practical applications.
II. Experimental details
Here we use the nanoporous template wetting technique to investigate the capillary flows of PE melts through nanopores. The AAO nanoporous templates used here are purchased from Whatman, Inc. The templates are freestanding disks with a diameter of 13 mm. Their pores are all through-holes with a length of 60 μm and two batches of diameters of 200 nm and 100 nm. The top view and cross-section images, characterized by scanning electron microscopy (SEM, Hitachi S-5500), of the AAO nanoporous template with the pore diameters of 200 nm are given in Fig. 1(a) and (b), respectively. The PE films with thickness of about 300 μm, density of 0.945 g cm−3 are obtained from Qilu Petroleum and Chemical Co. of China.In the experiments, a PE film is placed on the top of the template with a good contact and then put into a chamber in vacuum with the temperature of 130 °C at which the PE film will melt and infiltrate into the nanopores of the template. After a period of time the PE nanowire array with certain thickness can be produced. Choosing different wetting time we get the nanowire arrays with different thicknesses, i.e. the different wetting displacements of the PE melt. Then, the sample is taken out of the chamber and cooled down to ambient temperature. After that, the PE nanowire array is released by removing the template in NaOH aqueous solution and being rinsed with deionized water and ethanol in sequence. At last, the sample is dried at 30 °C in vacuum. Here, the thicknesses of the nanowire arrays are surely reflect the nanoflow velocity of the PE melt.
The top view and cross-section SEM images of the as-fabricated PE nanowire array generated within the AAO nanoporous template with a pore diameter of 200 nm after being heated at the wetting temperature of 130 °C for 30 min are shown in Fig. 1(c) and (d), respectively. By measuring the cross-section SEM image, we can get the thickness of the nanowire array. As to ensure the accurately of our results, three repeatability experiments for each wetting time are carried out and the final data are obtained by averaging over the three samples as well as more than five positions on each sample. Using this method, we also get the thicknesses of the nanowire arrays generated at other different wetting time.
Besides, the dependence of the viscosity of the PE sample used in our experiment on the shear rate at 130 °C is measured by a standard rotor rheometer (Physica MCR300) and the detailed results can be found in ref. 40. The range of the stress strain rate that the rotor rheometer applies on the sample is consistent with that exists in the nanoflow in our experiment. A comparison is made between the measured values and the Carreau model (CM),41,42
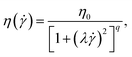 | (2) |
III. Results and discussion
In order to discuss the experimental data of the displacements of the PE melt, we develop a theoretical model first since the classical LWE is applicable only for newtonian fluids. As shown in Fig. 2, the effect of the shear rate on the viscosity should be considered for the PE sample which exhibits shear thinning behavior. Thus, the LWE that is a Newton dynamics equation19 is not applicable here and we should derive the dynamics equation for Carreau fluids. Based on the assumption of a quasi-steady process and unidirectional flow, the equation of motion44 reads
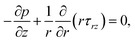 | (3) |
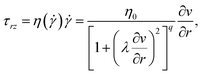 | (4) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate, v is the velocity in the axial direction. By substituting eqn (4) into eqn (3), the equation of motion can be rewritten as
is the shear rate, v is the velocity in the axial direction. By substituting eqn (4) into eqn (3), the equation of motion can be rewritten as
 | (5) |
 | ||
| Fig. 2 Dependence of displacements of the PE melt on the square root of the wetting time obtained in our experiments and predicted by the MLWE. | ||
In capillary, the pressure gradient is obtained by taking into account that p|z=0 = 0 and p|z=H(t) = 2γLV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/R:
θ/R:
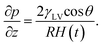 | (6) |
In a quasi-steady process, at certain time t the meniscus height H(t) is a given value. Therefore the pressure gradient will be a constant. Then, by integrating eqn (5), we get
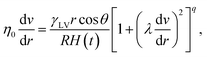 | (7) |
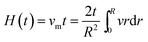 with the mean velocity vm. The solution of eqn (7) can be carried out numerically through finite differences. Comparing the above derivation with that of the LWE, it can be seen that if the effect of the shear rate is neglected the solution of eqn (7) will reduce to the LWE. The solution is a modified LWE (MLWE) combining the LWE with the rheological model.
with the mean velocity vm. The solution of eqn (7) can be carried out numerically through finite differences. Comparing the above derivation with that of the LWE, it can be seen that if the effect of the shear rate is neglected the solution of eqn (7) will reduce to the LWE. The solution is a modified LWE (MLWE) combining the LWE with the rheological model.
To obtain the theoretical results, it is crucial to determine the parameters firstly. Here, R is the pore radius (100 nm or 50 nm). The surface tension of polymer melts can be measured by the pendant drop method which was firstly reported by Wu.45 He measured the surface tensions of polymer melts in the temperature range of 100 °C to 200 °C and the results could be expressed as a function of temperature. For PE, the function is
| γLV = 35.562 − 0.057(T − 20), | (8) |
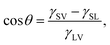 | (9) |
As can be seen in Fig. 2, the H(t)–t0.5 dependence is not linear for both our experimental data and the theoretical solutions of the MLWE. For the LWE, the viscous drag is a linear function of velocity, which results in a linear relationship between H(t) and t0.5,19 while for Carreau fluids the viscous drag is a nonlinear function of velocity, and the dependence of H(t) on t0.5 will be nonlinear. Thus, our MLWE instead of the LWE can model the capillary filling dynamics of polymer melts in nanopores. However, it also can be seen in Fig. 2 that the nanoflow velocity of polymer melts measured in our experiments is much larger than that predicted by the MLWE using the measured parameters. As mentioned before, some corrections, such as the slip37–39 and DCA,29,30,33 have already been proposed and we will analyze their effects on the nanoflows of polymer melts here.
Assuming the wall slip ls exists in the flow, the velocity at the position apart ls from the capillary wall equals zero. It is believed that the slip length vanishes for a completely wetting surface, but increases with the contact angle. When the contact angle goes to 180°, the slip length diverges as47,48
| ls/σ ∼ 1/(π − θ)4, | (10) |
 | ||
| Fig. 3 Dependence of displacements of the PE melt on the square root of the wetting time predicted by the MLWE considering the effect of the wall slip or DCA and our experiment data. | ||
To discuss the effect of the DCA, two commonly used models (i.e. hydrodynamic and molecular-kinetic models) are employed to calculate the DCA. In the context of the hydrodynamic model, the most complete analysis is the Cox equation50 as follows:
 | (11) |
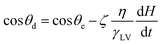 | (12) |
 is a coefficient of friction per length of the contact line depending on both fluid viscosity and liquid solid interaction, where n is the number of adsorption sites per unit area, kB is the Boltzmann constant, T is the absolute temperature, ΩL is the volume of the ‘unit of flow’, h is Planck's constant, λ is the length of the individual molecular displacements near the contact line, κS is the frequency of the individual molecular displacements that occur along its length. Then, by replacing θ in eqn (7) with θd obtained in eqn (11) or (12), we can obtain the theoretical solution of the MLWE considering the DCA. The slip length of the meniscus δ in the Cox equation and dimensionless parameter ζ in the MK model are the adjustable parameters. Here, we just present one case for each DCA model, which is δ of d/4 and ζ of 10. The results are presented in Fig. 3. As shown in Fig. 3, the theoretical solutions for the two DCA models both deviate far from the experimental data. In our calculations, we also obtain the solutions with the parameters δ and ζ taking other values. The extreme cases are that δ = d/2 and ζ = 0 where the DCA is reduced to the ECA. The solutions show that H(t) rises slower in all other cases than in those extreme cases, which is consistent with the reports29,30,33 and reasonable since the DCA is larger than the ECA. However, even the rise obtained in those extreme cases is found to be much slower than that observed in our experiments. Thus, it is believed the rise predicted by the theoretical solutions considering the DCA cannot be consistent with our experiment results no matter what the values of the parameters δ and ζ take.
is a coefficient of friction per length of the contact line depending on both fluid viscosity and liquid solid interaction, where n is the number of adsorption sites per unit area, kB is the Boltzmann constant, T is the absolute temperature, ΩL is the volume of the ‘unit of flow’, h is Planck's constant, λ is the length of the individual molecular displacements near the contact line, κS is the frequency of the individual molecular displacements that occur along its length. Then, by replacing θ in eqn (7) with θd obtained in eqn (11) or (12), we can obtain the theoretical solution of the MLWE considering the DCA. The slip length of the meniscus δ in the Cox equation and dimensionless parameter ζ in the MK model are the adjustable parameters. Here, we just present one case for each DCA model, which is δ of d/4 and ζ of 10. The results are presented in Fig. 3. As shown in Fig. 3, the theoretical solutions for the two DCA models both deviate far from the experimental data. In our calculations, we also obtain the solutions with the parameters δ and ζ taking other values. The extreme cases are that δ = d/2 and ζ = 0 where the DCA is reduced to the ECA. The solutions show that H(t) rises slower in all other cases than in those extreme cases, which is consistent with the reports29,30,33 and reasonable since the DCA is larger than the ECA. However, even the rise obtained in those extreme cases is found to be much slower than that observed in our experiments. Thus, it is believed the rise predicted by the theoretical solutions considering the DCA cannot be consistent with our experiment results no matter what the values of the parameters δ and ζ take.
It is reported that the nanoflow that is constrained by the nanoconfinement of the pore will strongly influence transport coefficients. Cao et al.13 presented that the thermal conductivities of the PE nanowire arrays prepared in the same way were about 2 orders of magnitude higher than their bulk counterparts. Considering the relevance of the thermal conductivity and viscosity, we believe the zero-shear-rate viscosity of the PE melt will decrease in nanoflows. By fitting the MLWE with the experimental data, we get the zero-shear-rate viscosity η0 are about 6.35 × 104 Pa s and 5.25 × 104 Pa s for the pores with diameters of 200 nm and 100 nm, respectively, which are both smaller than that of the bulk sample measured by rotor rheometer. As can be seen in Fig. 2, good agreement is observed between the fitted MLWE and the experimental data and the zero-shear-rate viscosity for the pore with a diameter of 100 nm is smaller than that for the 200 nm pore. We believe that the unconventional rheological behavior is induced by the nanoconfinement, i.e. the interaction between polymer chains and the alumina pore's wall with high surface energy, and the confinement is stronger for smaller pores. Based on the investigation of the morphologies of polymers in nanotubes and nanorods, the effect of the spatial confinement on the orientation of the polymer crystals has been reported. It was found that the PE crystals developed in the AAO nanoporous template grew along the long axis of cylindrical nanopores restricted.51 In addition, it was observed that the crystallites of poly(vinylidene difluoride) (PVDF) grew preferentially in the tube direction when the nanotubes were prepared by wetting the template with PVDF melts and the orientation of the PVDF chains prior to crystallization was speculated to be responsible for the difference in the crystallinity observed.52 It has also been reported that the PVDF crystallized in the nanotrenches orients with the chain axis parallel to the walls.53 Besides, the molecular simulations of polymer crystallization confined in rigid nanotubes also showed that the crystal orientation was uniform and parallel to the tube axis.54 Given the anisotropic structure of polymer crystals described above, the orientation contributed to the nanoconfinement will decrease the viscosity, just like shear thinning.
IV. Concluding remarks
In this paper, we have studied the flow behaviors of PE melts through nanopores experimentally by using the nanoporous template wetting technique. Based on the experimental results we find the displacement of polymer melts changes nonlinearly with (time)1/2, indicating the breakdown of the LWE that predicts a linear relationship between the displacement and (time)1/2. A modified LWE is proposed by combining the rheological model of shear rate dependent viscosity. Comparing the experimental results and the theoretical solution of the MLWE quantitatively, we observe the decrease of the zero-shear-rate viscosity of polymer melts during their flows through nanopores, which means the polymer melts exhibit unconventional rheological behavior except the shear thinning in the nano-wetting process. As for the underlying mechanism of the unconventional rheological behavior we believe the intrinsic confinement of nanopores plays a dominant role.Acknowledgements
This work is financially supported by National Natural Science Foundation of China (No. 51322603, 51136001, 51356001), Science Fund for Creative Research Groups (No. 51321002).References
- G. Li, V. Shrotriya, J. Huang, Y. Yao and T. Moriarty, et al., High-efficiency solution processable polymer photovoltaic cells by self-organization of polymer blends, Nat. Mater., 2005, 4, 864–868 CrossRef CAS.
- Z. Nie and E. Kumacheva, Patterning surfaces with functional polymers, Nat. Mater., 2008, 7, 277–290 CrossRef CAS PubMed.
- C. Liu, Recent developments in polymer MEMS, Adv. Mater., 2007, 19, 3783–3790 CrossRef CAS.
- A. J. Ryan, Nanotechnology: Squaring up with polymers, Nature, 2008, 456, 334–336 CrossRef CAS PubMed.
- M. Bruening and D. Dotzauer, Polymer films: Just spray it, Nat. Mater., 2009, 8, 449–450 CrossRef CAS PubMed.
- K. Zhou, X. G. Zhu, Y. Li and J. Liu, Fabrication of PDMS micro through-holes using micromolding in open capillaries, RSC Adv., 2014, 4, 31988–31993 RSC.
- D. B. Gates, Q. Xu, M. Stewart, D. Ryan and C. G. Willson, et al., New approaches to nanofabrication: molding, printing, and other techniques, Chem. Rev., 2005, 105, 1171–1196 CrossRef PubMed.
- Y. N. Xia, E. Kim, X. M. Zhao, J. A. Roger and M. Prentiss, et al., Complex optical surfaces formed by replica molding against elastomeric masters, Science, 1996, 273, 347–349 CAS.
- S. Y. Chou, P. R. Krauss and P. J. Renstrom, 25-nanometer resolution, Science, 1996, 272, 85–87 CAS.
- Y. Xia, J. A. Rogers, K. E. Paul and G. M. Whitesides, Unconventional methods for fabricating and patterning nanostructures, Chem. Rev., 1999, 99, 1823–1848 CrossRef CAS PubMed.
- D. Li and Y. Xia, Direct fabrication of composite and ceramic hollow nanofibers by electrospinning, Nano Lett., 2004, 4, 933–938 CrossRef CAS.
- U. M. Attia, S. Marson and J. R. Alcock, Micro-injection moulding of polymer microfluidic devices, Microfluid. Nanofluid., 2009, 7, 1–28 CrossRef CAS.
- B. Y. Cao, Y. W. Li, J. Kong, H. Chen and Y. Xu, et al., High thermal conductivity of polyethylene nanowire arrays fabricated by an improved nanoporous template wetting technique, Polymer, 2011, 52, 1711–1715 CrossRef CAS.
- B. Y. Cao, J. Kong, Y. Xu, K. L. Yung and A. Cai, Polymer nanowire arrays with high thermal conductivity and superhydrophobicity fabricated by a nano-molding technique, Heat Transfer Eng., 2013, 34, 131–139 CrossRef CAS.
- J. D. Beard, D. Rouholamin, B. L. Farmer, K. E. Evans and O. R. Ghita, Control and modelling of capillary flow of epoxy resin in aligned carbon nanotube forests, RSC Adv., 2015, 5, 39433–39441 RSC.
- E. W. Washburn, The dynamics of capillary flow, Phys. Rev., 1921, 17, 273–283 CrossRef.
- P. Joos, P. Remoortere and M. Bracke, The kinetics of wetting in a capillary, J. Colloid Interface Sci., 1990, 136, 189–197 CrossRef CAS.
- T. D. Blake and J. M. Haynes, Kinetics of liquidliquid displacement, J. Colloid Interface Sci., 1969, 30, 421–423 CrossRef CAS.
- B. V. Zhmud, F. Tiberg and K. Hallstensson, Dynamics of capillary rise, J. Colloid Interface Sci., 2000, 228, 263–269 CrossRef CAS PubMed.
- S. Levine, J. Lowndes, E. J. Watson and G. Neale, A theory of capillary rise of a liquid in a vertical cylindrical tube and in a parallel-plate channel: Washburn equation modified to account for the meniscus with slippage at the contact line, J. Colloid Interface Sci., 1980, 73, 136–151 CrossRef CAS.
- R. M. Digilov, Capillary rise of a non-newtonian power law liquid: impact of the fluid rheology and dynamic contact angle, Langmuir, 2008, 24, 13663–13667 CrossRef CAS PubMed.
- D. Geromichalos, F. Mugele and S. Herminghaus, Nonlocal dynamics of spontaneous imbibition fronts, Phys. Rev. Lett., 2002, 89, 104503 CrossRef PubMed.
- S. Gruener and P. Huber, Spontaneous imbibition dynamics of an n-alkane in nanopores: Evidence of meniscus freezing and monolayer sticking, Phys. Rev. Lett., 2009, 103, 174501 CrossRef PubMed.
- J. M. Oh, T. Faez, S. de Beer and F. Mugele, Capillarity-driven dynamics of water–alcohol mixtures in nanofluidic channels, Microfluid. Nanofluid., 2010, 9, 123–129 CrossRef CAS.
- M. Engel and B. Stuhn, In situ small angle x-ray scattering measurements of the filling process of polyisobutylene and poly-epsilon-caprolactone in ion track etched polycarbonate nanopores, J. Chem. Phys., 2010, 132, 54–58 CrossRef PubMed.
- S. Supple and N. Quirke, Rapid Imbibition of Fluids in Carbon Nanotubes, Phys. Rev. Lett., 2003, 90, 214501 CrossRef CAS PubMed.
- M. Whitby and N. Quirke, Fluid flow in carbon nanotubes and nanopipes, Nat. Nanotechnol., 2007, 2, 87–94 CrossRef CAS PubMed.
- S. Chibbaro, L. Biferale, F. Diotallevi, S. Succi and K. Binder, et al., Evidence of thin-film precursors formation in hydrokinetic and atomistic simulations of nano-channel capillary filling, Europhys. Lett., 2008, 84, 605–609 CrossRef.
- G. Martic, F. Gentner, D. Seveno, D. Coulon and J. D. Coninck, et al., A molecular dynamics simulation of capillary imbibition, Langmuir, 2002, 18, 7971–7976 CrossRef CAS.
- M. R. Stukan, P. Ligneul, J. P. Crawshaw and E. S. Boek, Spontaneous imbibition in nanopores of different roughness and wettability, Langmuir, 2010, 26, 13342–13352 CrossRef CAS PubMed.
- H. Kusumaatmaja, C. M. Pooley, S. Girardo, D. Pisignano and J. M. Yeomans, Capillary filling in patterned channels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 601–611 CrossRef PubMed.
- C. Cupelli, B. Henrich, T. Glatzel, R. Zengerle and M. Moseler, et al., Dynamic capillary wetting studied with dissipative particle dynamics, New J. Phys., 2008, 10, 1131–1137 CrossRef.
- S. Ahadian and Y. Kawazoe, A molecular dynamics approach to examine the kinetics of the capillary imbibition of a polymer at nanoscale, Colloid Polym. Sci., 2009, 287, 961–967 CAS.
- S. Ahadian, H. Mizuseki and Y. Kawazoe, Prediction and analysis of flow behavior of a polymer melt through nanochannels using artificial neural network and statistical methods, J. Colloid Interface Sci., 2010, 352, 319–329 CrossRef PubMed.
- F. G. Wolf, L. O. E. dos Santos and P. C. Philippi, Capillary rise between parallel plates under dynamic conditions, J. Colloid Interface Sci., 2010, 344, 171–179 CrossRef CAS PubMed.
- W. Stroberg, S. Keten and W. K. Liu, Hydrodynamics of capillary imbibition under nanoconfinement, Langmuir, 2012, 28, 14488–14495 CrossRef CAS PubMed.
- D. I. Dimitrov, A. Milchev and K. Binder, Capillary rise in nanopores: molecular dynamics evidence for the Lucas–Washburn equation, Phys. Rev. Lett., 2007, 99, 054501 CrossRef CAS PubMed.
- L. Joly, Capillary filling with giant liquid/solid slip: dynamics of water uptake by carbon nanotubes, J. Chem. Phys., 2011, 135, 214705 CrossRef PubMed.
- C. Bakli and S. Chakraborty, Capillary filling dynamics of water in nanopores, Appl. Phys. Lett., 2012, 101, 153112 CrossRef.
- G. J. Hu and B. Y. Cao, Flows of polymer melts through nanopores: Experiments and modelling, J. Therm. Sci. Technol., 2013, 8, 363 CrossRef.
- P. J. Carreau, Rheological equations from molecular network theories, Trans. Soc. Rheol., 1972, 16, 99–127 CrossRef CAS.
- B. Y. Cao and R. Y. Dong, Nonequilibrium molecular dynamics simulation of shear viscosity by a uniform momentum source-and-sink scheme, J. Comput. Phys., 2012, 231, 5306–5316 CrossRef.
- Q. Y. Wu and J. A. Wu, Polymer Rheology, Higher Education Press, Beijing, 2002 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Pergamon, Oxford, 1959 Search PubMed.
- S. Wu, Surface and interfacial tensions of polymer melts. II. Poly (methyl methacrylate), poly(n-butyl methacrylate), and polystyrene, J. Phys. Chem., 1970, 74, 632–638 CrossRef CAS.
- T. Young, Analysis of Interfacial Forces, Philos. Trans. R. Soc. London, 1805, 95, 65–69 CrossRef.
- N. V. Priezjev and S. M. Troian, Molecular origin and dynamic behavior of slip in sheared polymer films, Phys. Rev. Lett., 2004, 92, 018302 CrossRef PubMed.
- B. Y. Cao, J. Sun, M. Chen and Z. Y. Guo, Molecular momentum transport at fluid-solid interfaces in MEMS/NEMS: a review, Int. J. Mol. Sci., 2009, 10, 4638–4706 CrossRef CAS PubMed.
- H. Benoit, Determination of polymer chain conformation in amorphous polymers, J. Macromol. Sci., Part B: Phys., 1976, 12, 27–40 CrossRef.
- R. G. Cox, The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow, J. Fluid Mech., 1986, 168, 169–194 CrossRef CAS.
- K. Shin, E. Woo, Y. G. Jeong, C. Kim and J. Huh, et al., Crystalline structures, melting, and crystallization of linear polyethylene in cylindrical nanopores, Macromolecules, 2007, 40, 6617–6623 CrossRef CAS.
- M. Steinhart, S. Senz, R. B. Wehrspohn, U. Gosele and J. H. Wendorff, Curvature-directed crystallization of poly (vinylidene difluoride) in nanotube walls, Macromolecules, 2003, 36, 3646–3651 CrossRef CAS.
- Z. J. Hu, G. Baralia, V. Bayot, J. F. Gohy and A. M. Jonas, Nanoscale control of polymer crystallization by nanoimprint lithography, Nano Lett., 2005, 5, 1738–1743 CrossRef CAS PubMed.
- Y. Ma, W. Hu, J. Hobbs and G. Reiter, Understanding crystal orientation in quasi-one-dimensional polymer systems, Soft Matter, 2008, 4, 540–543 RSC.
| This journal is © The Royal Society of Chemistry 2016 |

