An analytical solution to the kinetics of growth of gold nanorods
Neethu Thomas and
Ethayaraja Mani*
Polymer Engineering and Colloid Science Laboratory, Department of Chemical Engineering, Indian Institute of Technology Madras, Chennai-600 036, India. E-mail: ethaya@iitm.ac.in
First published on 10th March 2016
Abstract
We present the analytical solution of a mathematical model to explain the growth kinetics of gold nanorods grown via seed mediated synthesis. In the synthesis process, pre-formed gold nanoseeds are added to a solution containing cylindrical surfactant micelles, gold salt and a reducing agent. A mechanism is proposed based on several control experiments to understand the role of each species. Surfactant micelles act as a template for one-dimensional growth and solubilize the gold salt; the reducing agent partially reduces gold salt and the seed particles auto-catalytically reduce the partially reduced salt into metallic atoms. Based on this mechanism a mathematical model has been developed. Our model based on this physically relevant mechanism shows a bound exponential growth of nanorod length. The analytical model captures quantitatively the growth curves obtained in our experiments and the kinetic data of others under different synthesis conditions reported in the literature. The model can be appropriately modified to explain the growth kinetics of other seed-mediated growth processes of metallic nanorods.
1 Introduction
One dimensional metallic nanomaterials such as nanowires, nanorods, nanobelts and nanotubes have tremendous potential applications in diverse fields due to their unique physico-chemical properties which are affected by their size, shape and aspect ratio.1,2 Exploiting these nanomaterials for technological applications requires tight control of their physical dimensions and uniformity. In bottom-up approaches such as wet-chemical methods, the size and shape of nanoparticles can be controlled by tuning the synthetic conditions. The majority of synthesis protocols are based on the reduction of metal salt using a reducing agent in the presence of specific shape directing agents (templates) and other additives to facilitate anisotropic growth.3,4 In this context, mathematical modelling can be useful in providing insight into the rational synthesis of nanorods if the model is developed based on the correct mechanism and be able to quantitatively predict growth kinetics.In this article, we develop a mathematical model and solve it analytically to explain the growth kinetics of nanorods. Gold nanorods have been chosen as a model system for the present study because of their diverse applications ranging from medical photothermal therapy, bio-sensing, bio-imaging,5 surface enhanced Raman scattering,6 solar cells,7 to drug delivery.8 Perhaps the most notable aspect is the optical properties of gold nanorods. They exhibit longitudinal and transverse surface plasmons in the near infrared (NIR) and ultraviolet-visible (UV-Vis) range, respectively, due to the quantum confinement along the length and diameter of nanorods. Notably, the longitudinal plasmon resonance is adjustable by varying the aspect ratio. Although several synthesis methods have been reported in the literature, seed-mediated growth is a popular known method as it allows variation of aspect ratio, affords high yield and involves room temperature conditions. In this method, surfactant or citrate capped gold nanoseeds are first synthesized separately and then introduced into a growth solution which contains gold salt, surfactant, mild reducing agent and an additive like silver nitrate.9–11 This method involves a singular recipe of different chemical species and their role is only qualitatively hypothesized. Modelling of this growth process is essential in producing gold nanorods with tight control on aspect ratio.
Several reports have addressed the mechanistic details of the process from a kinetic and thermodynamic point of view. These can be broadly classified into three classes. (1) Molecular aspects of adsorption of surfactant to nanoseed and to the growing nanorod, (2) chemical reaction kinetics involved in the synthesis and (3) empirical fitting of growth curves with a mathematical function without regarding the actual mechanism of the growth process. Wang et al. proposed a charge transfer model based on the reactions involved during the growth and predicted the time evolution of concentration of Au(0) formation in the growth solution.12 Perez-Juste et al. argued that the flux of Au(I) ions at the tip of the growing nanorod is at a maximum due to the highest gradient of electrical double layer potential. This model explains that the proneness of one dimensional growth is due to electrostatic interactions.
Henkel et al. fitted their growth kinetics data with an empirical equation leading to a bounded exponential function.14 Their model does not include any physical mechanism involved in the growth process as it was purely an empirical fitting. A kinetic model referring to the surface area limited theory of growth was reported by Seyed-Razavi et al.15 to address the kinetics of facetted nanoparticles into various shapes by considering the surface diffusion of atoms, rate of step growth and the availability of surface sites. Due to the assumed step growth kinetics, the evolution of aspect ratio increases step-wise with time, which is not observed in the growth of gold nanorods. Takenaka and Kitahata16 presented a population balance based equation to account for the growth of both length and diameter of gold nanorods. This model was solved numerically and the parameters of the model were fitted to match their experimental data. This model is like that of Seyed-Razavi et al.15 in the sense that both of them are geometrical growth models: the detailed mechanisms of the reaction, role of template, seed and surfactant do not appear in the model. Thermodynamics of facetted nanoparticles, adsorption–desorption behavior of surfactants and other additives to the nanoparticle facets have been addressed in MD simulations.17–19
An analytical solution for the growth of gold nanorods via seed-mediated synthesis would be of great use for experimentalists to explain their experimental data. The model should be in consistency with experimental conditions and have quantitative predictive capability. With this motivation, we propose a multi-step mechanism and a kinetic model based on the experimental facts inferred from control experiments. The model incorporates a series of diffusion processes and reactions of gold ions in the surfactant environment before converting into zero valent metal atoms prior to deposition on the growing particle. The model addresses the role of the initial concentration of gold salt in the growth solution, the amount of seed particles added to the growth solution and size of the seed, which are the main variables in controlling the aspect ratio of gold nanorods. It predicts the time evolution of the length of nanorods of our experimental data and that of others reported in the literature.
2 Experimental section
2.1 Materials used and physical characterization
HAuCl4·3H2O (99.99%, Alfa Aesar), cetyltrimethyl ammonium bromide (CTAB) (99%, Sigma), NaBH4 (<95%, Merck), L-ascorbic acid (99%, Rankem), Na2S (98%, Merck) and AgNO3 (99%, Alfa Aesar) were purchased and used without further purification. Deionized water was used in all experiments. The UV-Vis absorption spectra of the solutions were recorded in the range of 200–1100 nm using Specord 200 Plus Analytikjena. Transmission Electron Microscopy (TEM) images of nanoparticles and nanorods were recorded on a Philips CM12 with an Energy Dispersive X-ray analysis (EDAX) attachment. Carbon coated copper grids of mesh size 200 were used for sample preparation. The samples were dried under ambient conditions.2.2 Formation of HAuCl4–CTAB complex
To investigate the formation of gold salt–CTAB complexes, we add aqueous CTAB solutions of various concentrations ranging from 0.05 mM to 0.5 M to an aqueous gold salt solution of 1 mM concentration. These two solutions are mixed in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio. The UV-Vis absorption spectra were taken for a total of 18 samples. For comparison, absorption spectra of pure aqueous solution of HAuCl4 at 1 mM concentration was also recorded. We also recorded the absorption spectra of gold–surfactant (formed by mixing 5 mL of 0.2 M CTAB and 5 mL of 1 mM HAuCl4 solutions) after reducing it with ascorbic acid (0.078 M of 70 μL).
1 volume ratio. The UV-Vis absorption spectra were taken for a total of 18 samples. For comparison, absorption spectra of pure aqueous solution of HAuCl4 at 1 mM concentration was also recorded. We also recorded the absorption spectra of gold–surfactant (formed by mixing 5 mL of 0.2 M CTAB and 5 mL of 1 mM HAuCl4 solutions) after reducing it with ascorbic acid (0.078 M of 70 μL).
2.3 Reduction of HAuCl4 with ascorbic acid in the absence of CTAB
To understand the role of CTAB in the formation of nanoparticles, we reduce an aqueous solution of HAuCl4 (5 mL, 1 mM) with ascorbic acid (70 μL, 0.0788 M) in the absence of CTAB surfactant. UV-Vis absorption spectra were recorded immediately after mixing and TEM images of the resulting solution were recorded.2.4 Synthesis of gold nanoseeds
5 mL of 0.5 mM HAuCl4 was mixed with 5 mL of 0.2 M CTAB solution. To this mixture, 0.6 mL of 0.01 M ice-cold NaBH4 solution was added while vigorously stirring for 2 min. The resultant yellow brownish solution was kept at 25 °C for 2 h.2.5 Synthesis of gold nanorods
We follow the experimental protocol of Nikoobakht and El-Sayed11 to synthesize gold nanorods with slight modifications. Aqueous CTAB solution (5 mL, 0.2 M) was mixed with 0.40 mL of 4 mM AgNO3 and 5 mL of 1 mM HAuCl4 solution at 25 °C. A further 70 μL of 0.0788 M ascorbic acid was added as a mild reducing agent to the above solution while mixing the contents of the solution. Next 12 μL of pre-synthesized seed solution is added to this growth solution at 28 °C and kept undisturbed for three hours for the growth of nanorods. For the kinetics of the growth of nanorods, the growth solutions were prepared and treated with 15 mL of 0.233 mM Na2S at different times ranging from 5 to 180 minutes after the addition of seed solution. The mole ratio of sulfide to total metal content (Au and Ag) was kept at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in each growth solution. Na2S treated nanorods were centrifuged and resuspended in deionized water.20 In each sample, at least 50 particles were sampled to measure the mean length and diameter of the nanorods. Using UV-Vis absorption spectra, the aspect ratio (AR) of nanorods was also calculated from the longitudinal peak by using the linear relation λ = 90.6AR + 445.4.21
2 in each growth solution. Na2S treated nanorods were centrifuged and resuspended in deionized water.20 In each sample, at least 50 particles were sampled to measure the mean length and diameter of the nanorods. Using UV-Vis absorption spectra, the aspect ratio (AR) of nanorods was also calculated from the longitudinal peak by using the linear relation λ = 90.6AR + 445.4.21
3 Results and discussion
3.1 Mechanism of the growth of gold nanorods
The results of various control experiments are discussed here to understand the role of different reagents used in the synthesis of gold nanorods. Fig. 1(a) shows the photograph of gold salt–CTAB complexes formed when different amounts of CTAB are mixed with aqueous gold salt. CTAB concentration in the first 5 vials are 0.05 mM, 0.1 mM, 0.2 mM, 0.5 mM and 0.8 mM, which were below the first CMC of CTAB in water (0.98 mM). In this pre-micellar region, we observe that the color of the solution transforms from pale yellow to deep yellow with visible sediment at the bottom of the vial. Under these pre-micellar conditions, gold–CTAB complexes are formed due to electrostatic interactions, with sediment at higher CTAB concentrations. The solutions in the vials from 6 to 9, in which CTAB concentration was varied as 2 mM, 5 mM, 8 mM and 0.02 M, were observed as a thick solution with sediment and the colour changed from deep yellow to orange. The concentration of CTAB (in vials 6 to 9) were between the first and second CMC of CTAB in water. In this concentration range spherical micelles are formed, and they solubilize some of the gold–CTAB complexes and the remaining aggregates form as sediment.Golden yellow coloured solutions with no sediment were obtained in vials 10 to 18, where the CTAB concentration is varied as 0.05 M, 0.08 M, 0.1 M, 0.15 M, 0.2 M, 0.25 M, 0.3 M, 0.4 M and 0.5 M and all samples appeared similar. Beyond the second CMC of CTAB (0.02 M),22–24 cylindrical or worm-like micelles of size 2.5 nm × 4 nm with an aggregation number of 200–250 form in the solution.25 As a result, the gold–surfactant complexes are solubilized into the excess cylindrical micelles. As more cylindrical micelles are formed when the CTAB concentration is increased, the CTAB–gold complexes are solubilized by these micelles. From Fig. 1(a), we see that the solutions appear clear in these vials. In the synthesis of gold nanorods, typically the concentration of CTAB is kept at 0.2 M (vial 14), and in this case, the gold salt exists in the form of a complex and solubilized in the cylindrical micelle. Therefore, we think that the role of CTAB is to form a template (cylindrical micelle) and serve as a reservoir of gold salt for the growth of gold nanorods.
Fig. 1(b) shows UV-Vis absorption spectra of aqueous gold salt solution, CTAB solution and a mixture of 0.2 M CTAB and 1 mM gold salt solution, corresponding to the sample labelled as 14 in Fig. 1(a). The 1 mM aqueous HAuCl4 solution shows peaks at 235 nm and 309 nm due to a ligand-to-metal charge transfer band and a ligand field band of species AuCl4− and these peak positions are closer to the values reported by Torigoe and Esumi.26 Pure CTAB solution has a peak at 207 nm due to the bromide ion. On mixing 1 mM HAuCl4 solution with 0.2 M CTAB solution, the first peak shifted to 256 nm, and the second peak shifted to a new position at 395 nm due to the formation of a large scattering species by the electrostatic interaction between the cationic part of CTAB monomer with the AuCl4− anion.26,27 In the presence of excess CTAB, the structure of this gold–CTAB complex was reported to be CTA+–AuBr4−.28,29 These results suggest that in the prevailing conditions of seed-mediated synthesis, gold salt is complexed with CTAB and internalized within the cylindrical micelles.
On adding 78.8 mM ascorbic acid to the solution containing 0.2 M CTAB and 1 mM HAuCl4, the growth solution immediately became colorless. As shown in Fig. 1(b), up on adding ascorbic acid, the first UV-Vis peak at 256 nm of the surfactant–gold complex remained unaltered but the second absorbance peak (at 395 nm) disappeared due to the loss of charge transfer to the solvent band.27 This result indicates that in the presence of excess CTAB, the complex (CTA+–AuBr4−) formation prevents the direct reduction of CTA+–AuBr4− to Au(0) by ascorbic acid and gets reduced only to CTA+–AuBr2− by a two electron process.28 If the ascorbic acid reduction generated gold atoms, they might undergo nucleation and growth to form Au nanoparticles and their signature would have been reflected in the UV-Vis spectrum.
To confirm the above arguments, aqueous HAuCl4 solution (1 mM) was reduced by ascorbic acid (78.8 mM) in the absence of CTAB. Upon reduction, a light purple-brownish colour solution was obtained. The UV-Vis spectrum of this solution showed a single peak at 560 nm as shown in Fig. 2 implying the formation of gold spherical nanoparticles. TEM image of this sample (inset) showed the formation of quasi-spherical nanoparticles of 45 nm average diameter. EDAX study revealed the presence of pure Au0 in this sample. Therefore we deduce that the role of CTAB is also to serve as a complexing agent with gold ions in kinetically controlling the direct reduction of Au3+ ions to Au0 by ascorbic acid, in addition to offering a template for the growth of nanorods and this kinetic control is one of the key steps in promoting anisotropic growth.
Fig. 3 shows the UV-Vis absorption spectrum of pre-synthesized gold nanoseeds (aged 2 h prior to the addition to the growth solution). The peak around 470 nm indicates the presence of particles of size less than 10 nm.30 The TEM image of the nanoseeds is shown in the inset of Fig. 3, and the mean seed size is found to be 6 nm. When this seed solution is mixed with the solution containing ascorbic acid, CTAB and gold salt, the UV-Vis spectrum shows two peaks at 515 nm and 780 nm, respectively. The TEM image of the nanorods (after 3 h growth) is shown in the inset of Fig. 3. The average aspect ratio calculated from the TEM images in this case is 4.1.
 | ||
| Fig. 3 UV-Vis absorption spectrum of gold nanoseeds (aged for 2 h) and nanorods (after 3 h growth). Insets show their TEM images. | ||
As the ascorbic acid reduces Au3+ ions into Au1+ ions during nanorod synthesis, further reduction of Au1+ to Au0 in the growth solution is triggered by the addition of gold seed particles. We think that the added seed particles are bound at one end of the worm-like micelles. The Au1+ ions diffuse on the micelle surface and reach the surface of the seed particle, where it is auto-catalytically reduced to Au0 and deposited on the seed particle.31,32 This freshly formed metal atom is now available for growth of the seed, guided by the micelle as a template in directing the flux of Au0 atoms in one dimension. In addition to this, the free micelles from the solution preferentially adsorbed on the newly formed Au surface and stabilized those faces by forming as a bilayer.33 It was shown previously that the growth rate of Au nanorods vs. the concentration of metallic Au0 followed a sigmoidal shaped curve, indicating that the formation of Au0 is an autocatalytic reaction.12,34,35
3.2 Proposed mechanism
Here we propose a mechanism for the kinetically controlled growth of gold nanorods from the seed particles, based on the insight from the control experiments discussed in the last section. The schematic of the proposed mechanism is shown in Fig. 4. The gold salt first forms a surfactant–gold complex and gold is present in the Au3+ ionic state. This complex is present both as free monomer in the solution and on the cylindrical micelle surface [see Fig. 4(1)], and there is a dynamical exchange of surfactant–gold complex between the micelles and the bulk solution. Upon addition of ascorbic acid, the surfactant–gold complex gets reduced from the Au3+ state to the Au1+ state [see Fig. 4(2)]. This reduction reaction happens both in the bulk solution and on the micelle surface. Upon the addition of seed nanoparticles, they are captured on one end of the cylindrical micelle due to the collision between the micelles and seed particles [see Fig. 4(3)]. After this step, the gold ions in the Au1+ state from the micelle surface diffuse to the seed particle, where they get reduced auto-catalytically to Au0. Then the metallic gold grows on the seed particle guided through the templating effect of the cylindrical micelle leading to the growth of a nanorod. Each seed-carrying micelle develops into a nanorod.3.3 Mathematical model
Based on the proposed mechanism a mathematical model is developed to address the growth of Au nanorod via seed mediated growth. The following assumptions are considered in the model:(1) Single particle level approach is considered, where each nanorod is identical to each other.
(2) Quasi-steady state conditions are assumed, as only 15% of initial gold ions are reduced to form nanorods.36
(3) Growth rate of length of the nanorod is much faster than that of the diameter,14 and therefore, the diameter of the nanorod is considered to be constant.
(4) All seeds are grown into nanorods and we neglect the possibility of secondary nucleation. That is, the number of rods obtained is the same as that of seeds. Nrods = Nseeds.
The total molar rate of gold–surfactant complex diffusing to the micelle surface JC1 can be written as
| JC1 = F1(C1 − C2)aM | (1) |
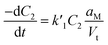 | (2) |
 | (3) |
Substituting C2 in eqn (1), and noting that the flux of gold–surfactant complex per Vt volume of growth solution to the micelle surface is equal to the rate of disappearance of gold–surfactant complex in the bulk, we get
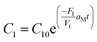 | (4) |
Here, we assumed k′1≫F1. On adding seed, it attaches to one end of the micelle and Au1+ ions diffused through the micelle to the seed surface. This diffusion flux can be written as
| JC3 = F2(C3 − C4)aS | (5) |
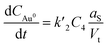 | (6) |
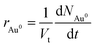 | (7) |
Thus in a quasi-steady state, the overall rate of change of gold atoms in the system can be written as
 | (8) |
Units of F1, F2, k′1 and k′2 are nm min−1. Writing C4 as a function of C1,
 | (9) |
Rate of change of number of moles of Au0 in N number of rods is given by
 | (10) |
 | (11) |
 and
and
 | (12) |
 | (13) |
From eqn (8), 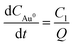 , where C1 is the concentration of gold ions available for the growth in the growth solution. Here Q is considered as the combined resistance for the entire growth process in the growth solution which is equivalent to
, where C1 is the concentration of gold ions available for the growth in the growth solution. Here Q is considered as the combined resistance for the entire growth process in the growth solution which is equivalent to  Thus, in the mathematical model developed, eqn (11) predicts the length of nanorods with time using a seed mediated method under different experimental conditions. The value of the parameter A can be obtained once the seed size is known. The other two parameters P and Q are fitted to match the experimental kinetics data. The TEM analysis of growing nanorods showed that short rods were formed within 2–3 minutes after the addition of seed and over a period of 1–3 h nanorods grow to their final length.34,38
Thus, in the mathematical model developed, eqn (11) predicts the length of nanorods with time using a seed mediated method under different experimental conditions. The value of the parameter A can be obtained once the seed size is known. The other two parameters P and Q are fitted to match the experimental kinetics data. The TEM analysis of growing nanorods showed that short rods were formed within 2–3 minutes after the addition of seed and over a period of 1–3 h nanorods grow to their final length.34,38
We first validate the model with our experimental data, followed by the data of others available in the literature. Fig. 5 shows the TEM images of nanorods at various growth times up to 3 h. The temporal variation of mean length and mean diameter of nanorods are given in Fig. 6. Fig. 7 shows the time evolution of the length obtained from experiments and the model prediction [eqn (11)]. The diameter of the growing particle is taken as the average diameter of the rods at the end of the growth period (i.e., 3 h). The model shows reasonable agreement with the experimental data with two fitting parameters P and Q. The parameter A is calculated from the molar density, volume of the growth solution, diameter of the nanorod and number of seed particles. The number of seed particles added to the growth solution are calculated by a method proposed by Takenaka and Kitahata.16 The basic volume unit of a gold seed is considered as a cube with an edge of 0.5 nm with the characteristic distance between Au atoms in a crystal is about 0.3 nm. So one basic volume unit contains  = 5 atoms. The number of Au atoms in one seed particle is obtained as 4479, which is calculated by using the characteristic size of the seed particle prior to the addition to growth solution (5.98 nm). The number of seed particles added is obtained by dividing the number of Au atoms added to the growth solution by the number of atoms in one seed particle. L0 is approximated as the particle size at time t = 0 min. The fitting was done using the MATLAB routine lsq. Parameters used were: D = 11.14 nm, L0 = 5.98 nm, N = 3.8 × 1011, C10 = 4.86 × 10−4 and Vt = 10.482 mL. The estimated values of parameters from the fitting are P = 0.0655 min−1 and Q = 588.06 min, respectively.
= 5 atoms. The number of Au atoms in one seed particle is obtained as 4479, which is calculated by using the characteristic size of the seed particle prior to the addition to growth solution (5.98 nm). The number of seed particles added is obtained by dividing the number of Au atoms added to the growth solution by the number of atoms in one seed particle. L0 is approximated as the particle size at time t = 0 min. The fitting was done using the MATLAB routine lsq. Parameters used were: D = 11.14 nm, L0 = 5.98 nm, N = 3.8 × 1011, C10 = 4.86 × 10−4 and Vt = 10.482 mL. The estimated values of parameters from the fitting are P = 0.0655 min−1 and Q = 588.06 min, respectively.
As the model is shown to explain our experimental data satisfactorily, we further compare experimental data from the literature10,11,13,14,38 with the model predictions. The model showed reasonable comparison with the literature data as shown in Fig. 8. The list of parameters used in the model are calculated from the corresponding experimental conditions and given in Table 1 along with the fitted parameters: P and Q. The seed size and concentration of seed solutions of the experiments reported by Park et al.38 and Nikoobakht and El-Sayed11 are same as in our experiments. The experimental conditions of Park et al.38 differ from ours in three ways: volume of the solution (ten times greater), number of seed particles added (220 times greater) and the average diameter of the rods (30% larger). Although the experimental conditions of Nikoobakht and El-Sayed11 are similar to that of ours, there is one difference: the volume of AgNO3 aqueous solution used is one half of the volume we used in our experiments. Due to this reason, the length of nanorod in their case is smaller than the length observed in our experiment provided all other conditions remain same. Additionally the dimensions of the nanorods were obtained from UV-Vis spectra in their experiments. The average length of nanorods reported by Henkel et al.14 is comparable to our experimental data. The gold ion concentration in the growth solution is the same for the first three cases (A–C) and our experiment. Concentration of gold salt in the growth solution and the volume of the growth solution are lower in the experiments of Sau and Murphy10 in comparison with our experimental conditions. In the experiments of Perez-Juste et al.,13 these authors first synthesized 3.5 nm citrate capped seed, and later exchanged citrate with CTAB molecules from the surface. The concentration of gold salt in the growth solution, the number of seed particles are lesser in this case compared to our conditions. Although the experimental conditions of the above studies are different from one another, the simple model that is derived based on the mechanistic insights from control experiments explains the data satisfactorily. The parameters in the model P is found to be less than unity and Q is observed to be in a range from 2 min to 50 min for the different cases considered. The observed differences in the value of P and Q are due to the difference in the experimental conditions. In all of these literature examples and in our kinetic experiment also, it is observed that the elongation of nanorods in the length direction is much faster at the initial stage and it attains a saturation level. The kinetic data is also shown a similar trend as that of the growth curve plotted. This indicates that in the entire growth process, the growth of rods in the length direction is more dominant and this observation is verified that one of our assumptions for the model is true.
 | ||
| Fig. 8 Comparison between the model prediction and experimental data available in the literature. (A) Park et al.,38 (B) Nikoobakht and El-Sayed,11 (C) Henkel et al.,14 (D) Sau and Murphy10 and (E) Perez-Juste et al.13 | ||
| Literature | A | B | C | D | E |
|---|---|---|---|---|---|
| a D: average diameter of the growing particle, L0: length of particle at time = 0 min (nm), N: number of seed particles added to growth solution, C10: initial concentration of Au3+ in molarity and Vt: volume of growth solution in mL, P & Q are fitting parameters. | |||||
| D | 14.27 | 8 | 11.3 | 20.82 | 15 |
| N | 8.45 × 1013 | 1.10 × 1013 | 6.02 × 1012 | 3.18 × 1012 | 8.17 × 1011 |
| V(t) | 101.23 | 10.284 | 10.142 | 5.022 | 10.035 |
| C(10) | 4.94 × 10−4 | 4.86 × 10−4 | 5 × 10−4 | 3.98 × 10−4 | 1.25 × 10−4 |
| L(0) | 3 | 3 | 3.83 | 3.8 | 3.54 |
| P | 0.073 | 0.092 | 0.1654 | 0.146 | 0.0748 |
| Q | 9.55 | 48.92 | 13.01 | 2.25 | 13.54 |
Henkel et al.14 fitted the time evolution of length of nanorods by an empirical correlation as:
 | (14) |
As time, t → ∞ we obtain from our model,
 | (15) |
4 Conclusion
We presented a model for the kinetics of growth of gold nanorods grown in a seed-mediated synthesis. The model was developed based on mechanistic insights obtained from control experiments. The mechanism involves the diffusion of gold salt from the bulk to the micelle surface, diffusion through the micelle surface, intermediate chemical reduction and auto-catalytic reduction on seed surface. The analytical solution of the model compares well with our experimental data and others data available in the literature. While the model is developed for gold nanorods, it can be used as it is or with proper modifications for the growth of other kinds of nanorods that are synthesized using seeded growth.Acknowledgements
The authors would like to thank the TEM facility at the Dept. of Metallurgical and Material Engineering and DST Unit of Nanoscience at IIT Madras.References
- Y. Xia, P. Yang, Y. Sun, Y. Wu, B. Mayers, B. Gates, Y. Yin, F. Kim and H. Yan, Adv. Mater., 2003, 15, 353–389 CrossRef CAS.
- M.-C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293–346 CrossRef CAS PubMed.
- N. R. Jana, L. Gearheart and C. J. Murphy, Adv. Mater., 2001, 13, 1389 CrossRef CAS.
- Y. Xiong, I. Washio, J. Chen, H. Cai, Z.-Y. Li and Y. Xia, Langmuir, 2006, 22, 8563–8570 CrossRef CAS PubMed.
- J. Becker, A. Trügler, A. Jakab, U. Hohenester and C. Sönnichsen, Plasmonics, 2010, 5, 161–167 CrossRef CAS.
- C. Gui and D.-x. Cui, Cancer Biol. Med., 2012, 9, 221 CAS.
- D. Kozanoglu, D. H. Apaydin, A. Cirpan and E. N. Esenturk, Org. Electron., 2013, 14, 1720–1727 CrossRef CAS.
- A. Wijaya, S. B. Schaffer, I. G. Pallares and K. Hamad-Schifferli, ACS Nano, 2008, 3, 80–86 CrossRef PubMed.
- N. R. Jana, L. Gearheart and C. J. Murphy, J. Phys. Chem. B, 2001, 105, 4065–4067 CrossRef CAS.
- T. K. Sau and C. J. Murphy, Langmuir, 2004, 20, 6414–6420 CrossRef CAS PubMed.
- B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15, 1957–1962 CrossRef CAS.
- Y.-y. Wang, B.-x. Li, S. Vdovic, X.-f. Wang and A.-d. Xia, Chin. J. Chem. Phys., 2012, 25, 135–141 CrossRef CAS.
- J. Perez-Juste, L. Liz-Marzan, S. Carnie, D. Y. Chan and P. Mulvaney, Adv. Funct. Mater., 2004, 14, 571–579 CrossRef CAS.
- A. Henkel, O. Schubert, A. Plech and C. Sonnichsen, J. Phys. Chem. C, 2009, 113, 10390–10394 CAS.
- A. Seyed-Razavi, I. K. Snook and A. S. Barnard, Cryst. Growth Des., 2010, 11, 158–165 Search PubMed.
- Y. Takenaka and H. Kitahata, Phys. Rev. E, 2009, 80, 020601 CrossRef PubMed.
- A. S. Barnard and L. A. Curtiss, J. Mater. Chem., 2007, 17, 3315–3323 RSC.
- G. Grochola, I. K. Snook and S. P. Russo, J. Chem. Phys., 2007, 127, 194707 CrossRef PubMed.
- S. K. Meena and M. Sulpizi, Langmuir, 2013, 29, 14954–14961 CrossRef CAS PubMed.
- D. A. Zweifel and A. Wei, Chem. Mater., 2005, 17, 4256–4261 CrossRef CAS PubMed.
- P. K. Jain, K. S. Lee, I. H. El-Sayed and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 7238–7248 CrossRef CAS PubMed.
- M. Törnblom and U. Henriksson, J. Phys. Chem. B, 1997, 101, 6028–6035 CrossRef.
- O. R. Miranda, N. R. Dollahon and T. S. Ahmadi, Cryst. Growth Des., 2006, 6, 2747–2753 CAS.
- P. Ekwall, L. Mandell and P. Solyom, J. Colloid Interface Sci., 1971, 35, 519–528 CrossRef CAS.
- V. Aswal, P. Goyal, H. Amenitsch and S. Bernstorff, Pramana, 2004, 63, 333–338 CrossRef CAS.
- K. Torigoe and K. Esumi, Langmuir, 1992, 8, 59–63 CrossRef CAS.
- V. Sharma, K. Park and M. Srinivasarao, Mater. Sci. Eng., R, 2009, 65, 1–38 CrossRef.
- L. G. Abdelmoti and F. P. Zamborini, Langmuir, 2010, 26, 13511–13521 CrossRef CAS PubMed.
- N. Garg, C. Scholl, A. Mohanty and R. Jin, Langmuir, 2010, 26, 10271–10276 CrossRef CAS PubMed.
- W. Haiss, N. T. Thanh, J. Aveyard and D. G. Fernig, Anal. Chem., 2007, 79, 4215–4221 CrossRef CAS PubMed.
- C. J. Murphy, T. K. Sau, A. M. Gole, C. J. Orendorff, J. Gao, L. Gou, S. E. Hunyadi and T. Li, J. Phys. Chem. B, 2005, 109, 13857–13870 CrossRef CAS PubMed.
- H. M. Chen, R.-S. Liu, K. Asakura, L.-Y. Jang and J.-F. Lee, J. Phys. Chem. C, 2007, 111, 18550–18557 CAS.
- J. Gao, C. M. Bender and C. J. Murphy, Langmuir, 2003, 19, 9065–9070 CrossRef CAS.
- J. A. Edgar, A. M. McDonagh and M. B. Cortie, ACS Nano, 2012, 6, 1116–1125 CrossRef CAS PubMed.
- C. Bullen, P. Zijlstra, E. Bakker, M. Gu and C. Raston, Cryst. Growth Des., 2011, 11, 3375–3380 CAS.
- C. J. Orendorff and C. J. Murphy, J. Phys. Chem. B, 2006, 110, 3990–3994 CrossRef CAS PubMed.
- M. Luty-Błocho, K. Pacławski, M. Wojnicki and K. Fitzner, Inorg. Chim. Acta, 2013, 395, 189–196 CrossRef.
- K. Park, L. F. Drummy, R. C. Wadams, H. Koerner, D. Nepal, L. Fabris and R. A. Vaia, Chem. Mater., 2013, 25, 555–563 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |






