 Open Access Article
Open Access ArticleEffect of shape and bending modulus on the properties of nematic lyotropic liquid crystals
A. R.
Ruiz-Fernández
ab,
J. J.
López-Cascales
*b,
J. J.
Giner-Casares
d,
R.
Araya-Maturana
e,
F. G.
Díaz-Baños
c,
D.
Muñoz-Gacitúa
a and
B. E.
Weiss-López
*a
aUni. de Chile, Fac. de Ciencias, Departamento de Química, Casilla 653, Santiago, Chile. E-mail: bweiss@uchile.cl
bUni. Politécnica de Cartagena, Grupo de Bioinformática y Macromoléculas (BioMac), Campus de Alfonso XIII, Aulario II, 30203 Cartagena, Murcia, Spain. E-mail: javier.lopez@upct.es
cUni. de Murcia, Fac. de Química, Dep. de Química Física, Campus de Espinardo, 30100 Espinardo, Murcia, Spain
dCIC biomaGUNE, Biofunctional Nanomaterials – Laboratory 6 Parque tecnológico de San Sebastián, Ed. Miramón 182, Guipúzcoa, 20009 Donostia – San Sebastián, Spain
eUni. de Talca, Inst. de Química de Recursos Naturales, Casilla 747, Talca, Chile
First published on 7th January 2016
Abstract
Synovial liquid is a natural lubricant of articular joints, such as shoulders, knees and hips. Thus, the development of biocompatible lubricants that can be employed in medical prosthesis for artificial implants, and eventually in certain therapies against osteo-arthritis or rheumatoid-arthritis diseases, is of an undoubted importance. Lyotropic liquid crystals have been used in the synthesis of silica and metals containing regularly oriented nanoporous, to obtain oriented carbon nanotube materials, in several pharmaceutical applications, as membrane mimetics and in lubrication applications. In this context, a new nematic lyotropic liquid crystal has been developed based on tetradecyltrimethyl ammonium chloride (TTAC), decanol (DeOH), a natural mixture of lipids (PL) extracted from soybean and sodium chloride (NaCl), all dissolved in water. A 30% w/w increase in TTAC content respect a certain composition of reference produces a more than 24-fold increase in the macroscopic viscosity of the solution. To understand the molecular principles that explain this behavior, several experimental and theoretical studies have been carried out. In this regard, 2H-NMR quadrupole splittings of fully deuterated sodium dodecyl sulphate (SDS-d25) introduced as molecular probe, transmission electron microscopy (TEM), freeze fracture transmission electron microscopy (FF-TEM), cryogenic transmission electron microscopy (Cryo-TEM) and polarized light microscopy (PLM) were obtained. In addition, hydrodynamic studies determined how the enhancement in viscosity requires a change in the shape of the aggregate, from circular to elliptic. Finally, molecular dynamics simulations allowed to estimate how variations in the bending modulus, kb, can explain the observed tendency of the quadrupole splittings, on the basis of a modification in the flexibility of the aggregate.
1 Introduction
Synovial liquid plays a crucial role as a natural lubricant and shock absorption of articular joins such as hips, shoulders and knees, where an optimal lubrication is required for the proper joint mobility and a reduction in cartilages degradation.1,2 In this regard, a deficiency in hyaluronic acid as a consequence of degradation in chronic diseases, such as osteo-arthritis and rheumatoid-arthritis, reduces the lubrication ability of synovial liquid, increasing the wearing of cartilages in knees, shoulders and hips.1–5 Furthermore, the sphingolipid and cholesterol composition of synovial liquid have been investigated with the goal of deciphering the role of these lipids in the lubrication of natural joints.1,2By increasing the concentration of amphiphiles in aqueous solution above certain value, known as critical micellar concentration (CMC), it is possible to observe the formation of a variety of different molecular organizations or phases. The main forces that drive these aggregation processes are of hydrophobic and electrostatic nature. These materials have been used in the synthesis of silica and metals containing regularly oriented nanoporous,6–11 to obtain oriented carbon nanotube materials,12–14 as carriers in pharmaceutical formulations,15–17 as membrane mimetics18–20 and in lubrication applications.21
In this context, Kupchinov et al.4 determined that synovial liquid contains about 2% nematic liquid crystals, to which important lubrication effects have been associated. The particular rheological properties and bio-compatibility of nematic lyotropic liquid crystals made of natural phospholipids makes them excellent candidates to be used as lubricants in joints of medical prosthesis for artificial implants and in potential therapeutic applications. Nematic lyotropic liquid crystals of finite size can be spontaneously generated in the laboratory when amphiphiles are dissolved in water in the presence of aliphatic alcohols and salt. Thus, at least two types of aggregates can be spontaneously generated: calamitic (NC) derived from hexagonal phases with prolate average symmetry, and discotic (ND), derived from the lamellar phase with oblate average symmetry.22–24 Searching for the development of an artificial and bio-compatible nematic liquid crystal that can be used as lubricant in prosthetic joints for medical applications, and eventually as substitute of synovial liquid in certain therapeutic applications,25 different liquid crystals have been prepared from the mixture of tetradecyltrimethyl ammonium chloride (TTAC), decanol (DeOH), a natural mixture of phospholipids (PL) extracted from soybean and sodium chloride (NaCl), all in aqueous solution. Few mg of fully deuterated sodium dodecylsulphate (SDS-d25) were added as a probe to test for the mobility of the aliphatic chains towards the interior of the hydrophobic core. The main advantage of using these liquid crystals as lubricant is that it is possible to modulate its lubricating power. In effect, an increase of 30% w/w in TTAC content, produces a more than 24-fold increase in the solution viscosity. Thus, small variations in TTAC composition allows to modulate the lubricating properties of the solution within a wide range of values.
In this article, we focused our efforts on explaining how the kinematic viscosity of the liquid crystal is related to the size, shape and flexibility of the molecular aggregate. To characterize the structure of the aggregates, different experimental and theoretical studies have been carried out. Thus, to observe the order degree of the molecular packing along the aliphatic chains of the aggregate, a 2H-NMR study was performed in the presence of SDS-d25, used as molecular probe. The kinematic viscosity of the solutions were measured at 298 K in all the studied concentration range. To explore the shape and size of the molecular aggregates, Transmission Electron Microscopy (TEM), freeze fracture transmission electron microscopy (FF-TEM) and Cryo-transmission electron microscopy (Cryo-TEM) images of selected samples were obtained. To assist with the characterization of the phases, polarized light microscopy (PLM) textures were also observed. With the aim of obtaining detailed insights into the properties of these liquid crystals, several molecular dynamics (MD) simulations were carried out with atomic detail. Finally, on the basis that our MD simulations are not capable to provide information related with the molecular rearrangements that should take place to explain the increase in viscosity with the increase in TTAC, a hydrodynamic modeling study was performed to explain the experimental observations.
2 Materials and methods
2.1 Mesophase preparation
PL from soybean, SDS-d25, TTAC and DeOH were purchased from Aldrich and used as received. Water of HPLC grade and NaCl at the highest purity available were purchased from Merck and used as received. The liquid crystal solutions were prepared by initially dissolving 0.2140 g of TTAC, 0.1165 g of PL, 0.012 g of SDS-d25, 0.0912 g of NaCl and 58 μl of DeOH in 1 ml of H2O. Furthermore, the TTAC concentration was increased up to a total of 0.2930 g of TTAC, maintaining the other components constant. This TTAC content corresponds the range of TTAC concentrations in which the liquid crystal generated exists. All mesophases were allowed to equilibrate at least 48 hours at 300 K before any measurements were made. These mesophases displayed thermal stability up to 315 K.2.2 2H-NMR spectra
All NMR spectra were obtained at 300 K in a Bruker Avance 400 NMR spectrometer, located at the Universidad de Santiago de Chile, using a broadband probe tuned to 61.425 MHz. The 2H 90° pulse was 19 μs long and more than 1000 transients from a spectral window of 40 kHz were accumulated in 32 kB files.2.3 Polarized light microscopy (PLM) and viscosity (η)
A Motic series B microscope equipped with crossed polarizers was employed to observe the textures. The samples were placed in a concave slide with a depth of 1 mm and were allowed to orient in a 2.35 T magnet for 15 min; longer periods in the field had no effects on the textures. The photos were taken at 300 K with a 20-fold magnification, from the center of the concavity, avoiding variations in the thickness of the sample due to the curvature of the slide.Kinematic viscosities of the liquid crystals, η, were measured using a standard Ubbelohde viscometer at 298 K and 1 atmosphere. Within the range of TTAC content, a noticeable change in the slope of the plot viscosity vs. TTAC concentration was observed. This is attributed to a change of phase and is corroborated with the PLM textures modification, observed at the same TTAC concentration. In this context, an special interest was paid on the following three experimental samples, which correspond to different phases of the synthesized liquid crystals:
Sample 1: this sample was prepared with 0.2250 g of TTAC, 0.1165 g of PL, 0.012 g of SDS-d25, 0.0912 g of NaCl and 58 μl of DeOH in 1 ml of H2O.
Sample 2: this sample was prepared with 0.2930 g of TTAC, 0.1165 g of PL, 0.012 g of SDS-d25, 0.0912 g of NaCl and 58 μl of DeOH in 1 ml of H2O. In summary, this phase was prepared starting from sample 1 in which the TTAC content was increased by 30% w/w and the rest of the components were maintained constant.
Sample 3: this sample was prepared with 0.2250 g of TTAC, 0.1165 g of PL, 0.012 g of SDS-d25, 0.1048 g of NaCl and 58 μl of DeOH in 1 ml of H2O. We note that sample 3 and 1 are of equal composition except that the NaCl content was increased by 15% w/w.
2.4 Transmission electron microscopy (TEM)
TEM images were collected with a JEOL JEM-1400PLUS instrument operating at 120 kV, using carbon coated 400 square mesh copper grids. Samples were drop casted onto the TEM grids.2.5 Freeze fracture transmission electron microscopy (FF-TEM)
FF-TEM samples were prepared according to a previously described methodology.26 The solution was deposited between two copper platelets using a 400-mesh gold grid spacer. The samples were frozen by immersion in liquid propane, at −189 °C, and fractured at −150 °C and 10−8 mbar in a BAF 060 freeze-etching system (Leica Microsystems, Vienna). The replicas were obtained by unidirectional shadowing at 45° with 2 nm of Pt/C and at 90° with 20 nm of C; they were floated on distilled water during 5 min and observed at 120 kV in a Tecnai Spirit microscope (FEI Company, Eindhoven, Netherlands).2.6 Cryo-transmission electron microscopy (Cryo-TEM)
Dipping and withdrawing a bare glow-discharged holey carbon grid from the solution a thin film was formed. The grid was blotted against filter paper, leaving thin sample films spanning the grid holes. These films were vitrified from room temperature by dipping into boiling ethane, using a Vitrobot (FEI Company, Eindhoven, Netherlands). The sample was kept at 100% humidity before freezing. Then it was transferred to a Tecnai F20 microscope (FEI Company, Eindhoven, Netherlands) using a Gatan cryoholder (Gatan, Pleasanton, CA). Images were taken at 200 kV, below −170 °C, using low-dose imaging conditions and an Eagle 4k × 4k CCD camera (FEI Company, Eindhoven, Netherlands).2.7 Setting up the computational boxes
To explore the effects of TTAC concentration and ionic strength on the properties of these liquid crystals, we have performed 3 simulations, representing sample 1, 2 and 3 as bilayer fragments. Consequently, three computational boxes were generated, with periodic boundary conditions in all directions of space.(1) System 1: this system was constituted by 392 tetradecyltrimethyl ammonium ion (TTA+) + 72 phosphatidylcholine (DOPC) + 32 phosphatidylethanolamine (POPE) + 200DeOH + 32 dodecylsulphate ion (DS−) + 32 cis-10-octadecanoic acid (AOL) + 32 sodium ions (Na+) + 392 chloride ions (Cl−). We must mention in this point, that Na+ and Cl− are not balanced in the system, because they were introduced only for maintaining the electroneutrality of the system (392Cl− are required to balance the 392TTA+ and 32Na+ are required to balance the 32DS−). The dimensions of the original computational box were 10.3, 10.3 and 9.5 nm for the x, y, and z axis, respectively, and the molecular ratios among TTA+, DOPC, POPE, DeOH and DS− were close to the experimental values. This computational box is a representation of the experimental sample 1 (see Section 2.3), corresponding to the liquid crystal with 0.2250 g of TTAC.
(2) System 2: in this system, the number of TTAC was increased by 30% with respect to system 1. Thus, the total number of molecules that constituted this system resulted as follows: 512TTA+ + 72DOPC + 32POPE + 200DeOH + 32DS− + 32AOL + 32Na+ + 512Cl−. The starting dimensions of the computational box were 12.2, 12.2 and 10.6 nm, for the x, y and z axis, respectively. In this case, this computational box is a representation of the experimental sample 2 (see Section 2.3), which corresponds to the liquid crystal with 0.2930 g of TTAC.
(3) System 3: in this case, system 1 was simulated including NaCl at 1 M concentration. The dimensions of the starting computational box were 10.4, 10.4 and 9.6 nm, for the x, y and z axis, respectively. In this case, this computational box is a representation of the experimental sample 3 (see Section 2.3), which corresponds to the liquid crystal with 0.2250 g of TTAC (sample 1) with an increase in the ionic strength.
In all three system described above, the species were symmetrically distributed between the two leaflets that constitute the bilayer. Fig. 1 shows a snapshot of system 1 and system 2 after 100 ns of trajectory.
2.8 MD simulation parameters
Once all three systems mentioned above were generated, the steepest descent minimization method was applied to remove the excess of energy associated with the overlapping between adjacent atoms. Once the energy achieved a minimum, 200 ns of trajectory length were simulated for each one of the systems previously described. GROMACS package 4.5.3 was used to carry out the molecular dynamics simulations. In this regard, an integration time step of 4 fs was employed. van der Waals interactions were simulated using the Lennard Jones potential (LJ), and long range electrostatic interactions were calculated using the Particle Mesh Ewald (PME) method.27,28 In both cases, for the LJ and the electrostatic interactions, a cut-off of 1.2 nm was employed. The bond lengths were restrained using the LINCS algorithm.29 All simulations were carried out in a NPT ensemble at 300 K and 1 atm, coupled to weak temperature and pressure baths algorithms,30 with time constants of 0.1 ps and 1 ps for temperature and pressure, respectively. The Ryckaert–Bellemans potential31 was used in all torsions along the aliphatic chains, for a better reproduction of cis–trans transitions.The Lennard-Jones parameters were the same than those specified in a previous work,32 along with the standard GROMOS 54a7 force field.33 The atomic charges distribution of TTA+, DS−, DeOH, DOPC, POPE and AOL were calculated using the semi-empirical Complete Neglect of Differential Overlap (CNDO) method.34Table 1 shows the atomic charge distributions (in e units), considering the atom numeration of Fig. 2. Such as argued in a previous work,32 the charge distributions of all species with net charge were halved, to consider the absence of polarizability in all molecules involved and the constancy of the dielectric medium.32,35–40 Simple Point Charge (SPC) water model41 was employed in all simulations.
| Atom number | TTA+ | DOPC | POPE | DeOH | DS− | AOL |
|---|---|---|---|---|---|---|
| 1 | 0.400 | 0.40 | 0.645 | 0.426 | −0.404 | 0.24 |
| 2 | 0.400 | 0.40 | 0.148 | −0.722 | −0.404 | −0.24 |
| 3 | 0.400 | 0.40 | 0.005 | 0.329 | −0.404 | 0.41 |
| 4 | −0.500 | −0.50 | −0.383 | −0.033 | 0.418 | −0.304 |
| 5 | 0.300 | 0.30 | 0.447 | 0.0 | −0.286 | −0.106 |
| 6 | 0.0 | 0.40 | −0.256 | 0.0 | 0.108 | 0.0 |
| 7 | 0.0 | −0.80 | −0.259 | 0.0 | −0.028 | 0.0 |
| 8 | 0.0 | 1.70 | −0.347 | 0.0 | 0.0 | 0.0 |
| 9 | 0.0 | −0.80 | 0.060 | 0.0 | 0.0 | 0.0 |
| 10 | 0.0 | −0.80 | 0.109 | 0.0 | 0.0 | 0.0 |
| 11 | 0.0 | −0.70 | −0.232 | 0.0 | 0.0 | 0.0 |
| 12 | 0.0 | 0.40 | 0.380 | 0.0 | 0.0 | 0.0 |
| 13 | 0.0 | 0.30 | −0.344 | — | 0.0 | 0.0 |
| 14 | 0.0 | −0.70 | 0.027 | — | 0.0 | 0.0 |
| 15 | 0.0 | 0.070 | 0.0 | — | 0.0 | 0.0 |
| 16 | 0.0 | −0.70 | 0.0 | — | 0.0 | 0.0 |
| 17 | 0.0 | 0.0 | 0.0 | — | 0.0 | 0.0 |
| 18–21 | — | 0.0 | 0.0 | — | — | 0.0 |
| 22–30 | — | 0.0 | 0.0 | — | — | 0.0 |
| 31 | — | 0.0 | 0.121 | — | — | — |
| 32 | — | 0.0 | −0.233 | — | — | — |
| 33 | — | 0.0 | 0.426 | — | — | — |
| 34 | — | 0.50 | −0.341 | — | — | — |
| 35 | — | −0.70 | 0.027 | — | — | — |
| 36 | — | 0.8 | 0.0 | — | — | — |
| 37 | — | −0.6 | 0.0 | — | — | — |
| 38–53 | — | 0.0 | 0.0 | — | — | — |
| Total charge | 1.0 | 0.0 | 0.0 | 0.0 | −1.0 | 0.0 |
3 Results and discussion
3.1 Characterization of the molecular aggregates
Fig. 3 shows the 2H-NMR spectra of SDS-d25 dissolved in sample 1 (A) and in sample 2 (B). The presence and magnitude of the quadrupole splittings along with the line shape of both spectra, strongly suggests that the aggregates correspond to bilayer structured micelles with nematic order.42–46 It is important to emphasize that these aggregates can not be spherical micelles since they can not generate 2H-NMR quadrupole splittings.Table 3 shows the experimentally measured quadrupole splittings of SDS-d25 in samples 1, 2 and 3 (sample compositions were described in Section 2.3). A significant decrease in the splittings is observed when increasing the TTAC content, however both spectra are very similar. Accepting that in the range of studied concentrations the average orientation of the aggregate in the magnetic field is not modified, the value of the observed 2H-NMR quadrupole splitting of a given C–D bond in a deuterated probe, such as SDS-d25, is a measurement of the alignment of that C–D bond with the spectrometer magnetic field; in other words it is representative of the mobility of the C–D bond. Therefore we can test for modifications in the dynamics of the aliphatic chains at different depths towards the interior of the hydrophobic core. A significant decrease in the general alignment is observed when augmenting the TTAC content. In addition, both mesophases display a region, near the interface, that shows similar mobility; in particular, this region increases from C1 to C5 in sample 1 to C1 to C7 in sample 2.
Despite the similarities between the 2H-NMR spectra of sample 1 and sample 2, they present very different polarized light microscopy textures (see Fig. 3C and D). This observation evidences the existence of two different nematic mesophases, necessarily arising from structural changes in the aggregates. However, this change does not seems to affect the bilayer structure of the micelles, as evidenced from the 2H-NMR spectra. The oily streaks texture observed in Fig. 3C usually appears as a consequence of homeotropic order, generally observed in lamellar phases, however, sometimes it is displayed by nematic discotic lyotropic liquid crystals, such as in this case. The texture observed in Fig. 3D is the typical schlieren texture, usually observed in nematic mesophases.47 These textures can not arise from smectic phases since these phases display a 2H-NMR spectrum typical of a powder pattern; smectic phases do not orient in the spectrometer magnetic field. All discussed evidence strongly suggest that the structure of the aggregates should be associated to some type of bilayer structured micelles.
Fig. 4 shows Cryo-TEM (A) and FF-TEM (B) images of sample 1. Both figures corroborate the existence of individual aggregates of finite size, strongly suggesting the presence of a nematic phase. In particular, aggregates of about 2 to 5 nm can be observed from both figures, however clusters of aggregates can also be observed, which could be the origin of the oily streaks observed in PLM. In an effort to experimentally explore variations in the size of the aggregates with the modification in TTAC content, TEM images of samples 1 and 2 were also obtained (Fig. 5). All TEM results, allow to discard the presence of lamellar or hexagonal smectic phases, usually surrounding the nematic region of the phase diagram.48 A simple comparison of the images in Fig. 5A and B show that aggregates of roughly 10–20 nm are observed in sample 2, large when compared with the image of sample 1, in which aggregates of scarcely 1–2 nm diameter can be observed. These experimental results are in excellent agreement with a hydrodynamic modeling calculation presented below.
 | ||
| Fig. 4 (A) Cryo-TEM image of sample 1 and (B) FF-TEM image of sample 1. Sample compositions were described in Section 2.3. | ||
 | ||
| Fig. 5 TEM images corresponding to (A) sample 1 and (B) sample 2. Sample compositions were described in Section 2.3. | ||
3.2 Aggregate bending modulus (kb)
The flexibility of the molecular aggregates that constitute the liquid crystal were estimated through the calculation of the bending modulus, kb, defined as:49 | (1) |
 | (2) |
Unfortunately, no experimental values to validate the bending modulus listed in Table 3 were found. However the values obtained here are in reasonable agreement with bending modulus obtained for lipid bilayers of different composition, where values from 15 to 30 kBT have been measured using X-ray, pipette aspiration and neutron spin echo experiments,50–54 and from MD simulations.55
From the results shown in Table 3, we observe a reduction of more than 50% in the bending modulus of the bilayer with an increase of 30% w/w in TTAC content (or in other words, the flexibility of the aggregate becomes doubled with the increase in TTAC content). Furthermore, we observe how a moderate increase in ionic strength (which corresponds to system 3 of Section 2.7) produces less than 20% increment in the bending modulus, relative to system 1. Therefore, as expected, an increase in ionic strength produces a moderate increase in the stiffness of the bilayer, in good agreement with the experimental results reported by Claessens et al.56 for a DOPG and DOPC bilayers at different ionic strength of the aqueous solution, and from molecular dynamics simulations of binary DPPC/DPPS bilayers in presence and absence of salt.55 Thus, this increase in bending modulus in system 3 is related with the fact that an increase in the ionic strength produces an additional stabilization of the interface, as expected from a counterion neutralization, that is reflected into an increase in the stiffness of the molecular aggregates.
From Table 3 we see how this increase in flexibility in sample 2 respect to sample 1, arises mainly from a reduction in the thickness of the bilayer. This decrease is associated with an increase in the interdigitation degree of the TTA+ hydrocarbon tails, since KA and A both remained almost invariable for all three studied cases.
3.3 Viscosity
Fig. 6 shows the kinematic viscosity of the liquid crystal as a function of TTAC content in the composition window in which the liquid crystal remains, outside of this windows it changes to a different isotropic phase. From Fig. 6 we appreciate a change in the slope of the viscosity with TTAC composition at a certain critical concentration of TTAC. Thus, values of 12.90 ± 0.06 and 310 ± 4 mPa s were obtained for samples 1 and 2 respectively (see Section 2.3 for their composition). For the case of sample 3 (in which NaCl increased 15% w/w respect to the sample 1), a viscosity of 10.28 ± 0.06 mPa s was measured, showing a moderate dependence on ionic strength. These results show an increase in the solution viscosity with TTAC content, where an increase in TTAC of scarcely 30% w/w in sample 1 produces an increase of more than 24 times in viscosity of sample 2 respect to the measured in sample 1. From Fig. 6, the composition at which the slopes change corresponding to 0.234 g in TTAC, is coincident with the concentration at which changes in the PLM textures were observed, corroborating the occurrence of a phase transition. | ||
| Fig. 6 Viscosity of the liquid crystal as a function of TTAC content (in grams) maintaining constant the rest of the components. | ||
This change in the viscosity slope will be associated to a change in size and shape of the molecular aggregates, such as it will be discussed in the section below.
The intrinsic viscosity, [η], provides information related to the shape and flexibility of the species dissolved, such as synthetic polymers, macromolecules, nanoparticles, aggregates or colloids,57,58 where [η] can be written as follows:
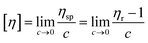 | (3) |
Solomon-Ciuta59eqn (4), provides a relation between the intrinsic viscosity [η] of a solute and the viscosity η of the solution:
 | (4) |
Therefore, the Solomon-Ciuta equation can be rewritten as follows:
 | (5) |
The ratio between the intrinsic viscosities of two liquid crystals with different TTAC content can be calculated from eqn (6):
 | (6) |
Assuming that η0 is the viscosity of pure water at 298 K (η0 = 1 mPa s), and η1 = 12, 9 mPa s and η2 = 310, 2 mPa s for samples 1 and 2 respectively, eqn (6) can be reduced to the following expression:
 | (7) |
From results of TEM microscopy, and considering that the size of the molecular aggregates for sample 2 is roughly 10 times bigger than for sample 1 and that TTAC composition increased scarcely a 30% w/w from sample 1 to sample 2, we can assume that c1 ≃ 10c2, and then, eqn (7) can be re-written as follows,
 | (8) |
In general, the intrinsic viscosity [η] depends on the shape and size of the macromolecule or colloid in solution. At this point, the main goal is try to reproduce the ratio between intrinsic viscosities for liquid crystals of different TTAC content, using hydrodynamic calculations based on molecular aggregates of different size and shape.
Thus, the program HYDRO60 (available from http://leonardo.inf.um.es/macromol), allows to calculate a dimensionless intrinsic viscosity. A model composed of two layers of 244 hard spheres each, forming a circular monoaxial structure, such as the one depicted in Fig. 7 was constructed. For this model, an intrinsic viscosity of [η]*1,circular = 1.39 (where the star means that we are working in dimensionless units) was calculated. To explain the increase in the viscosity of sample 2, the intrinsic viscosity was calculated for two different shapes, circular and elliptic (with a ratio in its semi-axes a/b = 20), with 2440 hard spheres that reproduce an increase in the surface area 10 times bigger than the corresponding to the circular shape in sample 1. From these calculations, a [η]*2,circular = 6.25 and [η]*2,elliptic = 75 were obtained, which provide a [η]*2/[η]*1 ratio of [η]*2,circular/[η]*1,circular = 4.5 and [η]*2,elliptic/[η]*1,circular = 54, considering that the aggregates adopt an circular and elliptic shape in sample 2. From these calculations, we can assert that the increase in TTAC content, not only increases the size but also induce changes in the shape of the molecular aggregates that form the liquid crystal, going from a circular to an elliptic symmetry, and that this change in the shape in the molecular aggregates is the main responsible of the increase in the viscosity of the liquid crystal.
3.4 2H-NMR study
Table 2 shows the 2H-NMR quadrupole splittings (ΔνQ) of SDS-d25 dissolved in samples 1, 2 and 3 (samples details were described in Section 2.3).| Carbon | Sample 1, ΔνQ (Hz) | Sample 2, ΔνQ (Hz) | Sample 3, ΔνQ (Hz) |
|---|---|---|---|
| 1 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232 232 |
| 2 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232 232 |
| 3 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232 232 |
| 4 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232 232 |
| 5 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232 232 |
| 6 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 783 783 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 489 |
| 7 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 734 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564 564 |
| 8 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 386 386 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 663 663 |
| 9 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 016 016 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 094 094 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951 951 |
| 10 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815 815 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710 710 |
| 11 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 852 852 |
9046 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792 792 |
| 12 | 2889 | 2383 | 2854 |
| System | A (nm2) | d/nm | K A/(J m−2) | k b/(kBT) |
|---|---|---|---|---|
| 1 | 0.5361 ± 0.0007 | 3.7 | 0.181 ± 0.019 | 12.9 ± 1.4 |
| 2 | 0.574 ± 0.003 | 2.6 | 0.25 ± 0.06 | 6.1 ± 1.4 |
| 3 | 0.537 ± 0.007 | 3.8 | 0.24 ± 0.08 | 16 ± 3 |
Table 2 shows how the quadrupole splittings of SDS-d25 significantly decreased with the increase in TTAC content. This indicates a significant decrease in the alignment of the aliphatic chains with the magnetic field, which could have different origins, including electrostatic repulsions among the ammonium head groups. On the other hand, an increase of 15% w/w in NaCl (sample 3) has no significant effect on the experimental splittings, showing that the integrity of aggregates does not depend markedly on ionic strength.
Values of ΔνQ obtained from 2H-NMR are related to deuterium order parameters, SCD, through the following expression:
 | (9) |
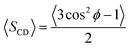 | (10) |
Here ϕ is the angle between the C–D bond and the bilayer normal, and the average is carried out over the simulation time and the number of identical molecules in the computational box. However, and bearing in mind that hydrogens from methylene groups have not been explicitly considered, the order parameters corresponding to a given C–D bond, can be calculated employing a well described methodology, exhaustively explained elsewhere.32,38 Consequently, order parameter for C12–D bond can not be calculated. Table 4 shows the quadrupole splittings obtained from simulations, corresponding to the systems 1, 2 and 3 (described in Section 2.7) which correlate with the experimental samples 1, 2 and 3 described in Section 2.3.
| Carbon | System 1, ΔνQ (Hz) | System 2, ΔνQ (Hz) | System 3, ΔνQ (Hz) |
|---|---|---|---|
| 1 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 ± 525 467 ± 525 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975 ± 816 975 ± 816 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 183 ± 391 183 ± 391 |
| 2 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 ± 663 639 ± 663 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 596 ± 844 596 ± 844 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 ± 589 483 ± 589 |
| 3 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 ± 670 260 ± 670 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 ± 1110 415 ± 1110 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 ± 559 721 ± 559 |
| 4 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 651 ± 678 651 ± 678 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414 ± 1254 414 ± 1254 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 ± 583 390 ± 583 |
| 5 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858 ± 716 858 ± 716 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 949 ± 1360 949 ± 1360 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ± 622 600 ± 622 |
| 6 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 652 ± 659 652 ± 659 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 162 ± 1354 162 ± 1354 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 566 ± 692 566 ± 692 |
| 7 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 699 ± 647 699 ± 647 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 067 ± 1439 067 ± 1439 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299 ± 717 299 ± 717 |
| 8 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 268 ± 619 268 ± 619 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 ± 1390 755 ± 1390 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864 ± 690 864 ± 690 |
| 9 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572 ± 568 572 ± 568 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091 ± 1388 091 ± 1388 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 ± 711 019 ± 711 |
| 10 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904 ± 410 904 ± 410 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 ± 1236 831 ± 1236 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 ± 586 489 ± 586 |
| 11 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 389 ± 223 389 ± 223 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 ± 1020 688 ± 1020 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 038 ± 557 038 ± 557 |
An inspection to Tables 2 and 4 shows that a semi-quantitative agreement between calculated splittings of SDS-d25 in system 1 and the experimental measured values in sample 1, is obtained for the first few carbon atoms of the aliphatic chain, near the interface. However, a significant deviation emerged when we look at the last C–D bonds of the chain. This discrepancy could arise either from the fact that our simulations corresponds to bilayer fragments, neglecting completely the curved rims which can be particularly important for small aggregates, or from molecules present as impurities in the PL mixture, which perturb the order of the hydrophobic core.
The observed 2H quadrupole splitting along the SDS-d25 tail are not significantly altered by an increase in the solution ionic strength, as shown in Table 2 for samples 1 and 3. This behavior is reproduce by the simulation, as shown in Table 4, for systems 1 and 3 respectively.
As mentioned before, comparing systems 1 and 2 with their corresponding experimental samples 1 and 2, a noticeable discrepancy between simulation and experiment arises. Experimentally it is observed how a moderate increase in TTAC content produces a reduction of about 19% in the quadrupole splitting for the first methylene groups of SDS-d25. This results clearly diverge from the results obtained from simulations, in which the same increase in TTAC content, produces no variation in the quadrupole splittings of the first C–D bonds, but a significant increment at the interior of the hydrophobic core.
This discrepancy between experiment and simulation can be explained on the basis of changes in the shape and flexibility of the aggregates when increasing the TTAC content, such as it was deduced in the previous Sections 3.2.1 and 3.2.2. Therefore, due to the increase in size and symmetry modifications of the aggregate, to a larger and elongated shape, there appear collective motions, similar to undulations observed in extended lamellar phases, which could increase the mobility of all C–D bonds, decreasing the quadrupole splittings without affecting their average orientation. Thus, to explore the effect of undulations on ΔνQ, values of ΔνQ have been recalculated considering four different tilt angles between the C–D bonds and the magnetic field, and the results are displayed in Table 5. It is observed that an angle deviation of ≃15°, such as it is represented in Fig. 8, is sufficient to reduce the values of ΔνQ close to the experimental values, as observed from Table 5. Therefore, undulations with oscillations of 15° amplitude around the average orientation should be enough to explain the decrease in ΔνQ. This result evidences how considerations of flexibility and size of the molecular aggregates are of crucial importance for the correct interpretation of the experimental data.
| Carbon | (ΔνQ (Hz))a | (ΔνQ (Hz))b | (ΔνQ (Hz))c | (ΔνQ (Hz))d |
|---|---|---|---|---|
| 1 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 183 ± 391 183 ± 391 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 302 ± 1211 302 ± 1211 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 ± 1425 440 ± 1425 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845 ± 1718 845 ± 1718 |
| 2 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 ± 589 483 ± 589 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 557 ± 1354 557 ± 1354 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 603 ± 1575 603 ± 1575 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 917 ± 1882 917 ± 1882 |
| 3 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 ± 559 721 ± 559 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 633 ± 1268 633 ± 1268 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 ± 1465 525 ± 1465 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 ± 1752 645 ± 1752 |
| 4 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 ± 583 390 ± 583 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229 ± 1253 229 ± 1253 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 ± 1455 048 ± 1455 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 ± 1755 080 ± 1755 |
| 5 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ± 622 600 ± 622 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 ± 1237 448 ± 1237 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235 ± 1433 235 ± 1433 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 226 ± 1726 226 ± 1726 |
| 6 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 566 ± 692 566 ± 692 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 381 ± 1231 381 ± 1231 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178 ± 1423 178 ± 1423 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 183 ± 1720 183 ± 1720 |
| 7 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299 ± 717 299 ± 717 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 ± 1246 132 ± 1246 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 955 ± 1436 955 ± 1436 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 943 ± 1724 943 ± 1724 |
| 8 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864 ± 690 864 ± 690 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 ± 1199 733 ± 1199 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599 ± 1393 599 ± 1393 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695 ± 1681 695 ± 1681 |
| 9 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 ± 711 019 ± 711 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 ± 1183 960 ± 1183 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910 ± 1368 910 ± 1368 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 115 ± 1646 115 ± 1646 |
| 10 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 ± 586 489 ± 586 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 596 ± 1123 596 ± 1123 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 ± 1298 720 ± 1298 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 ± 1561 146 ± 1561 |
| 11 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 038 ± 557 038 ± 557 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 524 ± 1063 524 ± 1063 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 036 ± 1217 036 ± 1217 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 942 ± 1443 942 ± 1443 |
4 Conclusions
The use of molecular dynamics in conjunction with hydrodynamic calculations have proven to be very useful in the interpretation of the experimental results.From the change in the slope of the plot of kinematic viscosity vs. TTAC content, a phase transition process between different bilayer structured aggregates is evidenced. Additional experimental evidence to support this hypothesis arises from the observation of PLM texture modification, at the same concentration where the slope of viscosity vs. TTAC content is observed. Cryo-TEM, FF-TEM and room temperature TEM images point in the same direction.
Hydrodynamic calculations support a phase transition from disk shaped mono-axial aggregates to bigger elliptic shaped bi-axial aggregates, explaining the viscosity increase. A decrease in bending modulus going from system 1 to system 2 is predicted by MD simulations. This increase in flexibility, which arises from the inter-digitation of TTA+ hydrocarbon chains, also contributes to increase the viscosity.
Finally, the increase in size and flexibility of the aggregates allows collective motions to occur, which decreases the alignment of the C–D bonds with the magnetic field, decreasing the values of ΔνQ. MD simulations indicates that oscillation amplitudes which deviates by 15° the alignment with the field, should be sufficient to explain the observed splittings.
Acknowledgements
The authors are pleased to acknowledge financial support from Fondecyt-Chile (Grant No. 1150135), Universidad de Chile (VID Grant ENL-003 and Facultad de Ciencias). The authors also acknowledge the invaluable assistance from the staff and facilities at the Computing Center of the Universidad Politecnica de Cartagena and the National Laboratory for High Performance Computing (NLHPC), Universidad de Chile. ARRF acknowledges a doctoral fellowship from Conicyt. JJLC acknowledges the financial support from Fundación Séneca (19353/PI/14).References
- S. Sivan, A. Schroeder, G. Verberne, Y. Merkher, D. Diminsky, A. Priev, A. Maroudas, G. Halperin, D. Nitzan, I. Etsion and Y. Barenholz, Langmuir, 2009, 26, 1107–1116 CrossRef PubMed.
- M. Knosinska, G. Liebisch, G. Lochnit, J. Wilhelm, H. Klein, U. Kaesser, G. Lasczkowski, M. Rickert, G. smitz and J. Steinmeyer, PLoS One, 2014, 9, e91769 Search PubMed.
- E. Waters, P. Spedding, A. Doherthy and R. Spedding, Asia-Pac. J. Chem. Eng., 2009, 4, 80–89 CrossRef CAS.
- B. Kupchinov, S. Ermakov, V. Rodnenkov, S. Bobrysheva, E. Beloenko and V. Kestelman, Smart Mater. Struct., 1993, 2, 7–12 CrossRef CAS.
- C. Myant and P. Cann, J. Mech. Behav. Biomed. Mater., 2014, 34, 338–348 CrossRef PubMed.
- A. Takai, Y. Yamauchi and K. Kuroda, J. Am. Chem. Soc., 2009, 132, 208–214 CrossRef PubMed.
- S. Warren and U. Wiesner, Pure Appl. Chem., 2009, 81, 73–84 CrossRef CAS.
- X. Zhang, W. Lu, J. Dai, L. Bourgeois, J. Yao, H. Wang, J. Friend, D. Zhao and D. MacFarlane, Sci. Rep., 2014, 4, 7420 CrossRef CAS PubMed.
- S. Che, Z. Liu, T. Ohsuna, K. Sakamoto, O. Terasaki and T. Tatsumi, Nature, 2004, 429, 281–284 CrossRef CAS PubMed.
- H. Lin and C. Mou, Acc. Chem. Res., 2002, 35, 927–935 CrossRef CAS PubMed.
- S. Umadevi, H. Lee, V. Ganesh, X. Feng and T. Hegmann, Liq. Cryst., 2014, 41, 265–276 CrossRef CAS.
- G. Scalia, ChemPhysChem, 2010, 11, 333–340 CrossRef CAS PubMed.
- D. Vijayaraghavan, J. Mol. Liq., 2014, 199, 128–132 CrossRef CAS.
- M. Casavant, D. Walters, J. Schmidt and R. Smalley, J. Appl. Phys., 2003, 93, 2153–2156 CrossRef CAS.
- M. Cohen-Avrahami, A. Shames, M. Ottaviani, A. Aserin and N. Garti, Colloids Surf., B, 2014, 122, 231–240 CrossRef CAS PubMed.
- C. Guo, J. Wang, F. Cao, R. Lee and G. Zhai, Drug Discovery Today, 2010, 15, 1032–1040 CrossRef CAS PubMed.
- M. Ki, J. Lim, J. Ko, S. Park, J. Kim, H. Cho, E. Park and D. Kim, J. Controlled Release, 2014, 185, 62–70 CrossRef CAS PubMed.
- V. Bahamonde-Padilla, J. López-Cascales, R. Araya-Maturana, M. Martínez-Cifuentes and B. Weiss-López, ChemPhysChem, 2014, 15, 1422–1431 CrossRef CAS PubMed.
- U. Dürr, M. Gildenberg and A. Ramamoorthy, Chem. Rev., 2012, 112, 6054–6074 CrossRef PubMed.
- D. Warschawski, A. Arnold, M. Beaugrand, A. Gravel, É. Chartrand and I. Marcotte, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 1957–1974 CrossRef CAS PubMed.
- L. Pinchuk, Y. Chernyakova and V. Goldade, J. Frict. Wear, 2008, 29, 224–233 CrossRef.
- A. Nesrullajev, F. Tepehan and N. Kazanci, Mater. Chem. Phys., 2002, 73, 74–77 CrossRef CAS.
- R. Montecinos, H. Ahumada, R. Araya-Maturana, A. Olea and B. Weiss-López, J. Colloid Interface Sci., 2007, 316, 126–131 CrossRef CAS PubMed.
- A. Neto and S. Salinas, The Physics of Lyotropic Liquid Crystals: Phase Transitions and Structural Properties: Phase Transitions and Structural Properties, Oxford University Press, 2005 Search PubMed.
- J. Lagerwall and G. Scalia, Curr. Appl. Phys., 2012, 12, 1387–1412 CrossRef.
- O. López, A. de la Maza, L. Coderch, C. López-Iglesias, E. Wehrli and J. Parra, FEBS Lett., 1998, 426, 314–318 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. Berkowitz, T. Darden, H. Lee and L. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- B. Hess, H. Bekker, H. Berendsen and J. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- H. Berendsen, J. Postma, W. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- J. Ryckaert and A. Bellemans, Faraday Discuss. Chem. Soc., 1978, 95–106 RSC.
- V. Bahamonde-Padilla, J. Espinoza, B. Weiss-Lopez, J. L. Cascales, R. Montecinos and R. Araya-Maturana, J. Chem. Phys., 2013, 139, 14703–14711 CrossRef CAS PubMed.
- N. Schmid, A. Eichenberger, M. Winger, A. Mark and W. van Gunsteren, Eur. Biophys. J., 2011, 7, 843–856 CrossRef PubMed.
- J. Pople and G. Segal, J. Chem. Phys., 1966, 44, 3289 CrossRef CAS.
- B. Jonsson, O. Edholm and O. Teleman, J. Chem. Phys., 1986, 85, 2259–2271 CrossRef.
- E. Egberts, S. Marrink and H. Berendsen, Eur. Biophys. J., 1994, 22, 423–436 CrossRef CAS PubMed.
- P. Ahlstrom and H. Berendsen, J. Phys. Chem., 1993, 97, 13691–13702 CrossRef CAS.
- J. J. López Cascales, J. García de la Torre, S. Marrink and H. Berendsen, J. Chem. Phys., 1996, 104, 2713–2720 CrossRef.
- P. David, W. van Gunsteren and A. Mark, J. Comput. Chem., 2010, 31, 1117–1125 CrossRef PubMed.
- T. Heinz, W. van Gunsteren and P. Hünenberger, J. Chem. Phys., 2001, 115, 1125–1136 CrossRef CAS.
- H. Berendsen, J. Postma, W. van Gunsteren and J. Hermans, Intermolecular Forces, D. Reidel Publishing Company, 1981 Search PubMed.
- G. Raffard, S. Steinbruckner, A. Arnold, J. H. Davis and E. J. Dufourc, Langmuir, 2000, 16, 7655–7662 CrossRef CAS.
- L. S. Vermeer, B. L. de Groot, V. Réat, A. Milon and J. Czaplicki, Eur. Biophys. J., 2007, 36, 919–931 CrossRef CAS PubMed.
- M. Bloom, J. H. Davis and A. L. Mackay, Chem. Phys. Lett., 1981, 80, 198–202 CrossRef CAS.
- Biological Membranes. A Molecular Perspective from Computation and Experiment, ed. K. Merz and B. Roux, Birkhäuser, Boston, 1996 Search PubMed.
- M. Brown, R. Thurmond, S. Dodd, D. Otten and K. Beyer, J. Am. Chem. Soc., 2002, 124, 8471–8484 CrossRef CAS PubMed.
- H. Stegemeyer and H. Behret, Liquid Crystals, Steinkopff, 1994 Search PubMed.
- A. A. de Melo Filho, A. Laverde and F. Y. Fujiwara, Langmuir, 2003, 19, 1127–1132 CrossRef CAS.
- M. Orsi, D. Haubertin, W. Sanderson and J. Essex, J. Phys. Chem. B, 2008, 112, 802–815 CrossRef CAS PubMed.
- N. Chu, N. Kucerka, Y. Liu, S. Tristram-Nagle and J. Nagle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 71.041904 CrossRef PubMed.
- W. Rawicz, K. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed.
- H. Petrache, S. Tristram-Nagle, K. Gawrisch, D. Harries, V. Parseguian and J. Nagle, Biophys. J., 2004, 86, 1574–1586 CrossRef CAS PubMed.
- J. Pan, S. Tristram-Nagle, N. Kucerka and J. Nagle, Biophys. J., 2008, 94, 117–124 CrossRef CAS PubMed.
- H. Seto, N. Yamada, M. Nagao, M. Hishida and T. Takeda, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 217–223 CrossRef CAS PubMed.
- J. J. Lopez Cascales, S. D. Oliveira Costa, A. Garro and R. D. Enriz, RSC Adv., 2012, 2, 11743–11750 RSC.
- M. Claessens, B. van Oort, F. Leermakers, F. Hoekstra and M. C. Stuart, Biophys. J., 2004, 87, 3882–3893 CrossRef CAS PubMed.
- H. Elias, Macromolecules: structure and properties, Plenum Press, 1984, vol. 1, p. 7420 Search PubMed.
- S. Harding, Prog. Biophys. Mol. Biol., 1997, 68, 207–262 CrossRef CAS PubMed.
- R. Pamies, J. H. Cifre, M. L. Martínez and J. de la Torre, Colloid Polym. Sci., 2008, 286, 1223–1231 CAS.
- J. García de la Torre, S. Navarro, M. L. Martínez and J. J. López Cascales, Biophys. J., 1994, 67, 530–531 CrossRef.
- A. Seelig and J. Seelig, Biochemistry, 1974, 13, 4839–4845 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |





