Designing binder-free, flexible electrodes for high-performance supercapacitors based on pristine carbon nano-onions and their composite with CuO nanoparticles†
Debananda Mohapatra,
Subramanya Badrayyana and
Smrutiranjan Parida*
Department of Metallurgical Engineering and Materials Science, Indian Institute of Technology, Bombay, Mumbai-400076, India. E-mail: paridasm@iitb.ac.in
First published on 19th January 2016
Abstract
The increasing demand for energy has triggered tremendous research efforts for the development of light-weight and durable energy storage devices. This requires exploring simple and economical methods to prepare the active materials and to design lightweight, flexible, free-standing supercapacitor electrodes in an inexpensive binder-free process. Herein, we try to address both these critical issues using CNOs and their composite with CuO as the active material. Active materials were supported on cotton wipes by a simple “sonication and drying” process to obtain light-weight, flexible and free-standing binder-free electrodes. In a symmetrical two-electrode cell, a pristine CNO electrode delivers a specific capacitance of 102.16 F g−1 (20 mV s−1), an energy density of 14.18 W h kg−1 and a power density of 2448 W kg−1, which are the highest values reported so far for CNO-based materials. CNO–CuO nanocomposites demonstrate a very significant specific capacitance of 420 F g−1 (10 mV s−1) with deliverable energy and power density at 58.33 W h kg−1 and 4228 W kg−1, respectively. Electrodes of both the active materials show an excellent cyclic performance and stability, retaining up to 90–95% of their initial capacitance after 5000 charge–discharge cycles at a current density of 5 A g−1. A simple cost estimation indicates that our device can deliver an energy density of 58.33 W h kg−1 at an estimated cost of less than 1 $.
1. Introduction
In recent years, there have been tremendous research efforts with the objective of increasing the energy density, power density and cyclic performance of supercapacitors to reach the level of batteries at a lower fabrication cost. Supercapacitors, also known as ultracapacitors or electrochemical capacitors, have attracted attention from both industry and academia due to their superior rate capability, high power density, long cyclic performance, simple principle and low maintenance cost.1 There is a fast-growing market for portable electronic devices, such as smartphones, notebooks and cameras, which are becoming more multifunctional and require novel, lightweight, inexpensive, flexible and wearable electronic devices.2,3It has been strongly recommended that it is critical to follow the best practices and methods to obtain reliable performance data using experimental devices that mimic the real ones. These include (1) measuring performances with not a too low scan rate or discharge current and (2) using two-electrode practical testing cells instead of three-electrode measurements, which could result in the intrinsic result being overestimated.4,5 We want to emphasize that our performance data are based on practical industry devices with electrode capacitance calculated using the most reliable method recommended rather than the three-electrode configuration. Voltage scan rates of at least 20 to 40 mV s−1 are needed to maintain discharge times of the order of a minute and to adequately reflect a material's performance. Moreover, very low rates of discharge lead to large errors.
The materials used for state-of-art supercapacitors include three main components, an active material, a conductive filler to enhance the overall conductivity and a binder material. It is noted that the conductive filler and binder make up about 10–20% of the total electrode weight but hardly contribute to the capacitance. Hence, it is essential to design and develop new, versatile and flexible binder-free electrodes for supercapacitor devices following the best practice methods to evaluate their performance.
As an important member of the fullerene family, CNOs, consisting of multiple concentric graphitic shells, forming encapsulated structures, have been envisioned to be a promising supercapacitor electrode material with a high power density due to nonporous outer shells that are easily accessible to electrolyte ions.6 Despite their outstanding electrochemical properties, CNOs have not received adequate attention as an electrode material for supercapacitors because of the lack of a convenient, cost-effective technique for preparing them in high yield. The methods developed so far to synthesize carbon onions suffer issues relating to purity, quantity and quality. Ugarte showed that irradiating carbon soot with high-energy electron irradiation could result in carbon onions with closed-caged cores that varied from a few layers to a few microns in size.7 The drawbacks of the method included the requirement for a high energy input and the yield was very low. Thermal annealing of nanodiamond particles generated CNOs8 and the need to use vacuum at high temperatures, which required specialized equipment, was the only drawback. Carbon arc plasma is utilized in another approach, in which one can fabricate gram amounts of onions; however, they are always contaminated by undesired byproducts, e.g. catalyst particles encapsulated in carbon cages.9 Carbon arc discharges submerged in deionized water represented a step forward because the use of metallic catalysts was eliminated.10,11 However, the products were a mixture of CNOs and nanotubes. A catalytic chemical vapor deposition route can also be a method for CNO production;12 however, the products are always contaminated by encapsulated carbon, similarly to synthesis using carbon arcs. However, all these methods for carbon nanostructure synthesis require high energy input and either their yield of CNOs is low or other species are obtained as a byproduct, which cannot be easily separated from the product. Therefore, large-scale applications require a simple, continuous and energy-efficient method to synthesize nanostructures. A flame can naturally and easily produce an appropriate high-temperature environment with the high radical concentrations required for the growth of CNOs. Therefore, flame synthesis shows more potential for inexpensive mass production of high-purity CNOs than other synthesis methods. Unfortunately, the use of CNOs as the main electrode material for carbon supercapacitors results in only a moderate electrochemical performance (<10 F g−1).13 Even activation and functionalization of CNOs failed to improve the performance of supercapacitors beyond 45 F g−1.6,14
To address these issues, the focus is on designing and synthesizing composite electrode materials to fully exploit their advantages and overcome their individual disadvantages. Previous work shows that a high specific capacitance can be obtained if metal oxides are uniformly dispersed on carbon materials with high surface areas.15–17 Combining carbon nanomaterials with metal oxides to prepare composites could enhance the specific surface areas, induce high porosity, facilitate electron and proton conduction, expand active sites, extend the potential window, protect active materials from mechanical degradation, improve cycling stability and improve the capacitive performance.16,17 Among the transition metal oxides, CuO is noteworthy as a promising supercapacitor material due to its low cost, abundant resources, non-toxicity, chemical stability, easy preparation and high theoretical capacitance (1800 F g−1).18,19 However, the poor electronic conductivity of CuO leads to poor stability during repetitive cycling. By adding conductive carbon nanomaterials, the electronic conductivity of the CuO electrodes can be increased. Several journal articles on the fabrication of copper oxide composites with various carbon allotropes for supercapacitor applications are available in the literature.20–22 The challenge, however, is to synthesize composites that are highly dispersible in polar solvents and can be easily loaded onto the substrate. Also, highly dispersible composite nanoparticles improve the wettability of the electrodes. To address the aforementioned issues, we synthesized novel composites consisting of CNO and CuO nanoparticles. Combining CNOs with copper oxide should lead to the manifestation of synergistic electrochemical properties. To the best of our knowledge, the synthesis of CNO–CuO nanocomposites and the study of their electrochemical performance has not been reported in the literature to date.
The other critical aspect in supercapacitor design is the way electrodes are prepared using particulate active materials. Pristine CNO powder is very difficult to handle and the process of fabrication into an electrode is tedious. Conductive agents (e.g. carbon black) and binders (e.g. poly(tetrafluoroethylene)) are always needed and have been used by many authors.23–25 The use of binder masks the electrochemically active surface area and reduces the conductivity of the active material.26 Recently, binder-free electrodes on conductive substrates for energy-storage have been explored.27,28 However, complicated and costly synthesis processes have been used, which are not suitable for large-scale production of supercapacitor devices. Therefore, it remains a great challenge to develop high-performance supercapacitor electrodes by a binder-free process that is facile, low-cost and scalable at room temperature.
In the present work, CNO and CNO–CuO nanocomposites were prepared by simple and economical methods. The composites were characterized by SEM, TEM, XRD, Raman and BET analysis. The supercapacitor performance of the flexible electrode materials was studied in a symmetrical two-electrode cell using aqueous electrolytes.
2. Experimental
2.1 Flame synthesis of CNOs
A simple flame synthesis method was implemented for the preparation of CNOs using clarified butter (also known as ghee in the Indian sub-continental region) as a precursor material.29 In a typical experiment, a cotton wick, known as lamp wick, was soaked in clarified butter by placing it in a spirit lamp. The exposed end of the lamp wick was ignited in the ambient atmosphere. A clean, polished bronze plate was placed in the upper part of the flame to collect the soot. The soot from the flame was deposited on the surface of the polished bronze plate. The yield depends on the duration of the collection (soot deposition on the collector) and the amount of precursor material (clarified butter). This method is capable of producing CNOs at a rate of several grams of CNOs per hour.2.2 Preparation of CNO–CuO composite
The CNO–CuO composite was prepared by a hydrothermal reaction. 50 mg of CNO powder was dispersed in 50 mL of DI water, 25 mg of copper acetate monohydrate was added to it and then the complete mixture was sonicated for 1 h. The obtained mixture was transferred to a Teflon-lined stainless steel autoclave and heated for six hours at 150 °C. After completion of the chemical reaction, the black suspension formed was washed and centrifuged several times. After washing, the precipitate was oven-dried for 8 h at 70 °C.2.3 Fabrication of free-standing, flexible, binder-free electrodes
Free-standing, flexible, binder-free electrodes are prepared by a simple “sonication and drying” method, using cotton wipes as a support for the active materials. 20 mg of CNO–CuO composite powder was dispersed in 10 mL of ethanol to maintain a concentration of 2 mg mL−1. The dispersion was sonicated for 30 minutes in a bath sonicator to form a binder-free CNO–CuO ink. A 2 × 2 cm cotton wipe was dipped into the binder-free CNO–CuO ink and soaked for a few minutes. The wipe soaked in ink was then sonicated for a fixed time. During this process, the active materials uniformly and conformally coated the fabric of the wipe. The mass loading of CNO–CuO composite on the wipe depends on the time of sonication, which was optimized to obtain the required mass loading. After the loading process, the electrode was completely dried at 70 °C in a hot air oven. The mass of the loaded CNO–CuO was obtained by calculating the difference in weight before and after loading. A similar procedure was followed to prepare CNO electrodes.The active material loaded on the cotton-wipe electrodes showed excellent mechanical properties; the wipes could be folded and stretched without detachment of the CNOs or the composite particles from the electrode (Fig. S1†).
2.4 Materials characterizations
The microscopic morphology of pristine CNOs and composite electrodes was characterized using a Hitachi Model S-3400N field-emission gun scanning electron microscope (FEG-SEM) and a JEOL TEM-2100 high-resolution transmission electron microscope (HR-TEM) with 0.19 nm point resolution. Raman spectra were obtained from 100 to 4000 cm−1 using a Horiba HR8000 spectrometer equipped with an argon laser with wavelength 514.4 nm. Nitrogen adsorption and desorption experiments were carried out at 77 K on an ASAP 2020 V3.05 H volumetric adsorption analyzer. Before the collection of the isotherm data, the sample was degassed at 300 °C for 20 h under vacuum. The specific surface area (SSA) was calculated using the multipoint Brunauer–Emmett–Teller (BET) method. The pore-size distribution was obtained from the adsorption data using the Barrett–Joyner–Halenda (BJH) method.2.5 Electrochemical measurements
All the electrochemical measurements were performed in a two-electrode symmetric cell configuration assembled into a Swagelok cell. Two active electrodes were separated by a tea-bag cloth soaked in 1 M Na2SO4, which acts as a separator. The electrochemical performance of the device was studied by cyclic voltammetry (CV) and galvanostatic charge–discharge (GCD) measurements using a Biologic Potentiostat SP-300 instrument. All the CV tests were done between −1 and +1 V at scan rates of 10–200 mV s−1. Galvanostatic charge/discharge curves were measured in the potential range −1 to +1 V at current densities of 2–15 A g−1. The cyclic stability of the supercapacitor was tested at a constant applied current density of 5 A g−1 in the voltage range −1 to +1 V for 5000 cycles.3. Results and discussion
3.1 Morphological and structural characterization
SEM micrographs of a cotton wipe before and after composite coating are presented in Fig. 1A and B. The wipe textile consists of numerous interwoven cellulose fibers, forming a hierarchical structure with a complicated surface morphology, resulting in pores of various lengths. The hierarchical porous structure of the wipe allows high mass loading of the active material. The SEM image reveals a uniform conformal coating of pristine CNOs (Fig. S2†) and CNO–CuO composite particles (Fig. 1B) on the fibers of the cotton wipe. The cotton fibers in the wipe are primarily made of cellulose and contain hydroxy functional groups.28 The CNO particles used in this study are also functionalized with oxygen-containing functional groups, which form hydrogen bonds with the –OH groups of the fiber. There are also van-der-Waals interactions between the active materials and the fibers.28 Because of these two types of interactions, CNO and CNO–CuO nanoparticles are conformally coated on the fibers of the cotton wipe. | ||
| Fig. 1 SEM images showing the cotton wipe (A) without active material coating and (B) with conformal CNO–CuO coating. HRTEM micrographs of as-prepared (C) CNOs and (D) CNO–CuO composite. | ||
The microstructural features of the as-prepared CNOs and CuO–CNO composite have been investigated by HR-TEM analysis and are presented in Fig. 1C and D, respectively. As shown in Fig. 1C, the concentric shells of graphitic layers are visible with an interlayer spacing of 0.334–0.353 nm, which is a characteristic feature of CNOs. The average size of the CNO nanoparticles varies between 35–40 nm. On examining the composite (Fig. 1D), the presence of different phases (i.e. CNOs and CuO) is evident, which is an indication of composite formation. The lattice spacing was measured to be 0.228 nm, corresponding to the (111) planes of monoclinic CuO.30 The intershell spacing between the concentric graphitic layers in the composite was same as that in pure CNOs.
The crystal structure and phase purity of the active materials were investigated by XRD. The XRD patterns of the as-prepared composite material and pristine CNOs (Fig. 2) show a prominent graphitic peak at 2θ = 25.5°, corresponding to the (002) reflection of graphite. The broadness of the (002) peak for the CNOs can be attributed to their small size and the relatively short domain order of the stacked graphitic layers.31 The low intense peak between 2θ = 40° and 50° in the XRD pattern of CNOs corresponds to either the (100) or the (101) reflection. In the composite, observed peaks can be indexed to the monoclinic phase of CuO (JCPDS card no. 05-661).20 The existence of traces of the Cu2O phase in the XRD pattern of the composite was detected, which may have formed due to the low reaction temperature (150 °C) used in our experiment.
The formation mechanism of CuO can be explained on the basis of different growing rates of various crystal facets. The coordination number of Cu2+ is generally six in a hydrolysis reaction. Each Cu2+ ion is surrounded by six water molecules when a copper salt is dissolved in water, of which four water molecules surround Cu2+ to form a planar square structure and the other two are located at its axis, leading to octahedral Cu(OH)64− growth units. The binding energies of the two OH− located at the axis is lower than those of OH− located in the plane.32 So, the two OH− located at the axis are easily replaced during dehydration to form CuO crystallites, i.e. the growth rate of CuO crystals along the axis are higher than in the plane. Therefore, a difference in growth rates in various directions emerges, leading to the formation of anisotropic CuO nanocrystals. Furthermore, during the process of crystal growth, the Gibbs free energies of crystallite surfaces are usually very high and the crystallites have a tendency to aggregate to decrease the Gibbs free energies of the surfaces.33 Consequently, secondary aggregation of small CuO crystallites leads to the formation of aggregated spherical structures. The CNOs prepared by flame synthesis of clarified butter are highly dispersible in water, i.e. hydrophilic, hence do not precipitate during the hydrothermal process. Hence the doping efficiency can be easily controlled and quantified.
Raman analyses of the CNOs and CNO–CuO composite are presented in Fig. 3A and B, respectively. Raman analysis allows identification of various forms of carbon as well as fingerprinting for single layers, bilayers and a few layers, reflecting changes in the electron bands of graphitic carbon.34 A peak positioned at 1344 cm−1, designated as the D-band, arises from various defects present in the CNO lattice. The peak positioned at 1582 cm−1 originates from ordered sp2 hybridized carbon. The narrowness of the G-band in CNOs points to a high degree of perfection in the graphitic network in the concentric shells. The broad nature of the D and G-bands of the CNO–CuO composite indicates the presence of smaller graphitic fragments, which is in agreement with XRD results. The degree of disorder in spherical graphitic nanostructures can also be estimated by the intensity ratio of the D and G-bands (ID/IG). ID/IG for CNOs is 0.94, indicating surface defects due to various oxygen-containing functional groups.35 For the composite, this ratio decreases to 0.92, indicating a decrease in the surface defects due to the reaction of oxygen-containing functional groups with copper acetate, forming CuO nanoparticles. This suggests that the composite materials have fewer defects, indicating that they have better electrical conductivity than the pristine CNOs. The composite formation is confirmed by the appearance of bands at 290, 337 and 625 cm−1 (Fig. 3B), which are due to vibrations in the CuO lattice.22 With reference to the vibration spectrum of a single CuO crystal, the peak at 290 cm−1 can be assigned to the Ag mode, whereas peaks positioned at 337 and 625 cm−1 can be assigned to the Bg modes.30
N2 adsorption/desorption isotherms obtained at −196 °C were employed to estimate the SSA and pore size distribution of CNOs and the CNO–CuO composite. From multipoint BET measurements, the SSA of the as-prepared CNOs was found to be 144.26 m2 g−1. It is seen that the as-prepared CNOs exhibit a type-IV isotherm with a hysteresis loop at higher relative pressures, indicating the presence of mesopores (Fig. S4A†).25 The pristine CNOs exhibit a bimodal pore size distribution i.e., they contain mesopores and macropores ranging from 2–100 nm, with the majority of pores having a diameter around 2–10 nm and 30–100 nm (Fig. S4B†). The presence of macropores in the sample may be due to the existence of inter-cluster and intra-cluster pores in the CNO nanoparticles. After composite formation with CuO, the corresponding BET surface area slightly decreases to 60.7 m2 g−1 (Fig. S4C†) but the pore-size distribution (Fig. S4D†) indicates a majority of micropores (from 0.6 to 1 nm), which is an added advantage as it will enhance the capacitance.36
3.2 Electrochemical characterization
Fig. 4 shows cyclic voltammograms of as-obtained flexible CNO electrodes as well as CNO–CuO composite electrodes in 1 M Na2SO4 at different sweep rates within the potential range −1 to +1 V in a two-electrode symmetrical cell configuration (Fig. 4A and C).It is observed that the voltammograms of pristine CNOs from a scan rate of 20 mV s−1 to 200 mV s−1 in Fig. 4A do not show any redox peaks, which evidently establishes that the supercapacitive behavior is free from any faradaic reactions. The quasi-rectangular shapes of the CV curves are an indication of ideal electrical double-layer capacitive behavior with excellent electrochemical stability under given conditions. The symmetry and shape of the curve remain unaffected even at a high scan rate of 200 mV s−1 (Fig. 4A), indicating excellent rate capability. The symmetric rectangular nature of the CV curves indicates compatibility of electrolyte ion size/pore size.13
The specific capacitance has been calculated using eqn (1);
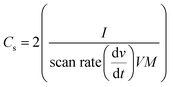 | (1) |
In a symmetrical 2-electrode cell configuration, the flexible and binder-free CNO electrodes demonstrated a specific capacitance of 102.16 F g−1. This is the highest value reported for pristine CNOs in a two-electrode cell configuration. It is important to note that these reported capacitance values are at 20 mV s−1, which is considerably higher than the reported scan rates in the literature.15,37 As reported by Stoller and Ruoff, for any practical application, a higher capacitance at a higher scan rate is desired.4 For non-functionalized, non-activated pristine CNOs, our result is highly competitive and higher by several orders of magnitude than those reported in the literature.6,15,24,38–42 The as-synthesized CNOs are highly hydrophilic and hence can easily be dispersed in water to form an ink, which can be conformally coated onto cotton fabric by a simple “sonication and drying” process. The wipe textile consists of numerous interwoven cellulose fibers, forming a hierarchical structure with a complicated surface morphology resulting in pores of various lengths. The hierarchical porous structure of the wipe allows a higher mass loading of CNOs per square centimetre. Both these factors contribute to the CNOs having a higher capacitance than other reported materials. It is important to note that most of the specific capacitance values reported in the literature are measured in three-electrode configurations, which results in the capacitance value being overestimated by a factor of two.4
As shown in Fig. 4A and B, when the scan rate increases, the capacitive current increases, causing a slight asymmetry in the CV curve. The asymmetry in the CV curves at higher scan rates may be due to saturation of ions inside the pores of the CNO electrode, which increases the internal resistance of the electrode, preventing faster ion diffusion. On the other hand, at low scan rates, the charge accumulation process is slow, allowing the electrolyte to access most of the surface area of the electrode. This increase in the electro-active surface area results in a high specific capacitance.
Fig. 4C depicts the CV profile of the CNO–CuO composite at different scan rates from 10 to 200 mV s−1. As we observe from the obtained CV curves, there is a pseudocapacitive contribution from CuO, along with a double-layer contribution from CNOs in the composite electrode. Specific capacitances as high as 420 F g−1 were obtained for the CNO–CuO, which is by far the highest value reported to date for any composite based on CuO and carbon nanomaterials following best-practice methods of evaluation. This remarkable enhancement in the specific capacitance of the composite material can be attributed to the synergistic effect of both components, i.e. the high electrical conductivity of CNOs and the pseudocapacitance of CuO. The intact assembly between the CNOs and the CuO nanoparticles after composite formation results in an intimate interaction of both components, enhancing charge transfer between the two components by introducing new paths for electron transfer and leading to rapid redox reactions of the CuO nanoparticles. The effective charge transfer in the electrode played an important role in enhancing the specific capacitance and rate capability. Furthermore, the microporous nature (pore size < 1 nm) of the composite material also contributes to the enhanced capacitance.36
In all measurements, there is a common trend of decreasing Cs values with increasing scan rates (Fig. 4B and D). It is well-known that, for very low scan rates, the Cs is higher because the ions have a much longer time to penetrate and populate all the available electrode surface and form electric double layers, which are needed to generate higher capacitance.43
There is a linear dependence of capacitive current on sweep rate in the case of CNOs (Fig. 4B). In other words, the voltammetric currents are almost directly proportional to the sweep rates, which is an indication of pure double-layer capacitive behavior. For the CNO–CuO composite, the capacitive current does not change linearly with the scan rate (Fig. 4D), indicating a faradaic contribution to the capacitive behavior.
Galvanostatic charging/discharging was carried out within the potential range −1 to +1 V with varying current densities from 2–15 A g−1. The measured results are shown in Fig. 5. A symmetrical and near-linear slope was observed in the case of CNOs at all current densities, indicating pure double-layer formation (Fig. 5A). The electrodes show a coulombic efficiency greater than 90%, demonstrating excellent electrochemical reversibility throughout the entire charge–discharge process. The GCD curves of the CNO–CuO composite electrode (Fig. 5C) show discharge curves that are slightly distorted and slightly unsymmetrical with their corresponding charging counterparts, indicating a pseudocapacitive contribution.
The electrochemical stability of CNO and CNO–CuO composite electrodes was evaluated by performing charge–discharge experiments for 5000 cycles at a current density of 5 A g−1, as shown in Fig. 5B and D. After 5000 cycles, the specific capacitance retention values for the CNO and CNO–CuO composite electrodes are 95% and 90%, respectively, demonstrating excellent cyclic stability with a high degree of reversibility in a repetitive charge/discharge process. The marginal capacitance loss may be due to a charge transfer limiting process, which increases the internal resistance and eventually decreases the initial capacitance over repetitive cycling. In other words, there may be a blockage of electroactive sites due to electrolyte flooding or mass transport issues.13
The energy density and power density are very significant parameters for any energy storage device. Ragone plots are used to illustrate the energy density of a supercapacitor as a function of power density. The energy density and power density of pristine CNO and CNO–CuO composite electrodes are calculated as per eqn (2) and (3), respectively.
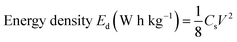 | (2) |
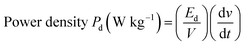 | (3) |
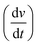 = scan rate (V s−1).
= scan rate (V s−1).
CNO electrodes show a maximum performance with the highest energy density of 14.18 W h kg−1 at a power density of 510.66 W kg−1 at 20 mV s−1, which gradually reduces to 6.8 W h kg−1 at 2448 W kg−1 at a current density of 200 mV s−1 as depicted in the Ragone plot (Fig. 5E). However, the CNO–CuO composites show an enhanced deliverable energy density of up to 58.33 W h kg−1 at a scan rate of 10 mV s−1 and a power density of 4228 W kg−1 at a scan rate of 200 mV s−1 (Fig. 5F). The values obtained for the composite are higher than those reported for either CNOs or CuO till date.6,14,19,20
To further investigate the redox behavior of the composite electrode, we measured the electrochemical response in 1 M NaOH electrolyte (Fig. 6). Starting from a scan rate of 5 mV s−1 to 200 mV s−1, we observe a symmetric pair of both anodic and cathodic peaks over the entire scan range (Fig. 6A). This result indicates that there is a reversible faradaic reaction of CuO during the charging and discharging process. The main pseudocapacitive behavior of the composite sample can be attributed to the reversible redox transition of Cu2+ to Cu+ and vice versa.37 Furthermore, there is an almost linear dependence of capacitive current on scan rate (Fig. 6B).
The CNO–CuO composite showed a maximum specific capacitance of 638.09 F g−1 with a deliverable energy density of 31.9 W h kg−1 and a maximum power density of 2360.7 W kg−1 in a symmetrical 2-electrode cell configuration (Fig. 6C). This can be attributed to the homogeneous distribution of CuO nanoparticles over the CNO network, which introduces new paths for electron transport and hence improves the conductivity and the capacitive behavior of the electrode.
We have successfully demonstrated for the first time that free-standing, flexible and binder-free CNO-based supercapacitor electrodes can be prepared by a simple, cost-effective fabrication method. To the best of our knowledge, there is no other reported device that uses simple and easily available materials and shows such high-performance characteristics. Based on the cost analysis (Table 1), we can claim that our device can deliver an energy density of 58.33 W h kg−1 at an estimated cost of less than 1 $.
| Material | Cost (INR) |
|---|---|
| Cotton wipe (substrate) | 01 |
| Tea bag (separator) | 01 |
| Active material (CNO–CuO composite) | 50 |
| Electrolyte | 05 |
| Total | 57 (<1 $) |
4. Conclusions
By employing a simple active material preparation technique and a novel electrode fabrication method, we have successfully enhanced the capacitance of pristine CNOs and a CNO–CuO composite, following best-practice methods of evaluation. We have demonstrated for the first time a facile and scalable flame synthesis method to prepare highly dispersible and functionalized CNO nanoparticles. An extremely simple “sonication and drying” technique was used to develop binder-free flexible electrodes using cotton wipes. A high specific capacitance of 102.16 F g−1, a deliverable energy density of 14.18 W h kg−1 and a power density of 2448 W kg−1 was achieved for pristine CNOs. The addition of redox surface functionality (CuO) led to a composite with more conductive networks, which exhibits higher capacitance (420 F g−1), energy density (58.33 W h kg−1), power density (4228 W kg−1) and cyclic stability (5000 cycles with more than 90% capacitance retention at 5 A g−1) in 1 M Na2SO4 electrolyte. By changing the electrolyte to 1 M NaOH, the CNO–CuO composite showed a maximum specific capacitance of 638.09 F g−1 with a deliverable energy density of 31.9 W h kg−1 and a maximum power density of 2360.7 W kg−1 in a symmetrical 2-electrode cell configuration. The novelty of this work is that our device can deliver an energy density of 58.33 W h kg−1 at an estimated cost of less than one dollar.Acknowledgements
This work was supported by financial assistance from the Industrial Research and Consultancy Center (IRCC), IIT-Bombay and DST (SERC). The authors acknowledge the access to experimental facilities at the Centre for Research in Nanotechnology and Science (CRNTS) and the Metallurgical Engineering and Materials Science (MEMS) Dept., IIT Bombay. We express our gratitude to Mrs Aaradhana Pant for HRTEM imaging at CRNTS.Notes and references
- J. Yan, Q. Wang, T. Wei and Z. Fan, Adv. Energy Mater., 2014, 4, 1300816 Search PubMed.
- Y. Liang, Z. Wang, J. Huang, H. Cheng, F. Zhao, Y. Hu, L. Jiang and L. Qu, J. Mater. Chem. A, 2015, 3, 2547–2551 CAS.
- S. E. Moosavifard, M. F. El-Kady, M. S. Rahmanifar, R. B. Kaner, M. F. Mousavi, X. Tian, M. Shi, X. Xu, M. Yan, L. Xu, A. Minhas-Khan, C. Han, L. He and L. Mai, Adv. Mater., 2015, 7, 7476–7482 Search PubMed.
- M. D. Stoller and R. S. Ruoff, Energy Environ. Sci., 2010, 3, 1294–1301 CAS.
- Y. Gogotsi and P. Simon, Science, 2011, 334, 917–918 CrossRef CAS PubMed.
- Y. Gao, Y. S. Zhou, M. Qian, X. N. He, J. Redepenning, P. Goodman, H. M. Li, L. Jiang and Y. F. Lu, Carbon, 2013, 51, 52–58 CrossRef CAS.
- D. Ugarte, Nature, 1992, 359, 707–709 CrossRef CAS PubMed.
- V. L. Kuznetsov, A. L. Chuvilin, Y. V. Butenko, I. Y. Mal'kov and V. M. Titov, Chem. Phys. Lett., 1994, 222, 343–348 CrossRef CAS.
- R. Selvan, R. Unnikrishnan, S. Ganapathy and T. Pradeep, Chem. Phys. Lett., 2000, 316, 205–210 CrossRef CAS.
- N. Sano, H. Wang and M. Chowalla, et al., Nature, 2001, 414, 506 CrossRef CAS PubMed.
- H. Lange, M. Sioda, A. Huczko, Y. Q. Zhu, H. W. Kroto and D. R. M. Walton, Carbon, 2003, 41, 1617–1623 CrossRef CAS.
- C. He, N. Zhao, C. Shi, X. Du, J. Li, L. Cui and F. He, Scr. Mater., 2006, 54, 1739–1743 CrossRef CAS.
- M. E. Plonska-Brzezinska and L. Echegoyen, J. Mater. Chem. A, 2013, 1, 13703 CAS.
- R. Borgohain, J. Li, J. P. Selegue and Y.-T. Cheng, J. Phys. Chem. C, 2012, 116, 15068–15075 CAS.
- M. E. Plonska-Brzezinska, D. M. Brus, A. Molina-Ontoria and L. Echegoyen, RSC Adv., 2013, 3, 25891–25901 RSC.
- X. Zhang, W. Shi, J. Zhu, D. J. Kharistal, W. Zhao, B. S. Lalia, H. H. Hng and Q. Yan, ACS Nano, 2011, 5, 2013–2019 CrossRef CAS PubMed.
- A. Allagui, T. Salameh and H. Alawadhi, J. Electroanal. Chem., 2015, 750, 107–113 CrossRef CAS.
- B. Vidyadharan, I. I. Misnon, J. Ismail, M. M. Yusoff and R. Jose, J. Alloys Compd., 2015, 633, 22–30 CrossRef CAS.
- S. E. Moosavifard, M. F. El-Kady, M. S. Rahmanifar, R. B. Kaner and M. F. Mousavi, ACS Appl. Mater. Interfaces, 2015, 7, 4851–4860 CAS.
- V. Senthilkumar, Y. S. Kim, S. Chandrasekaran, B. Rajagopalan, E. J. Kim and J. S. Chung, RSC Adv., 2015, 5, 20545–20553 RSC.
- D. P. Dubal, D. S. Dhawale, R. R. Salunkhe, V. S. Jamdade and C. D. Lokhande, J. Alloys Compd., 2010, 492, 26–30 CrossRef CAS.
- A. Pendashteh, M. F. Mousavi and M. S. Rahmanifar, Electrochim. Acta, 2013, 88, 347–357 CrossRef CAS.
- F. Béguin, K. Szostak, G. Lota and E. Frackowiak, Adv. Mater., 2005, 17, 2380–2384 CrossRef.
- M. E. Plonska-Brzezinska, M. Lewandowski, M. Błaszyk, A. Molina-Ontoria, T. Luciński and L. Echegoyen, ChemPhysChem, 2012, 13, 4134–4141 CrossRef CAS PubMed.
- B. Zhang, D. Wang, B. Yu, F. Zhou and W. Liu, RSC Adv., 2014, 4, 2586 RSC.
- C. Yuan, J. Li, L. Hou, X. Zhang, L. Shen and X. W. Lou, Adv. Funct. Mater., 2012, 22, 4592–4597 CrossRef CAS.
- G. Q. Zhang, H. Bin Wu, H. E. Hoster, M. B. Chan-Park and X. W. Lou, Energy Environ. Sci., 2012, 5, 9453 CAS.
- L. Hu, M. Pasta, F. La Mantia, L. Cui, S. Jeong, H. D. Deshazer, J. W. Choi, S. M. Han and Y. Cui, Nano Lett., 2010, 10, 708–714 CrossRef CAS PubMed.
- N. C. Ganguli and M. K. Jain, J. Dairy Sci., 1973, 56, 19–25 CrossRef CAS.
- T. Wen, X.-L. Wu, S. Zhang, X. Wang and A.-W. Xu, Chem.–Asian J., 2015, 10, 595–601 CrossRef CAS PubMed.
- V. Eswaraiah, S. S. Jyothirmayee Aravind and S. Ramaprabhu, J. Mater. Chem., 2011, 21, 6800 RSC.
- J. Zhu, H. Bi, Y. Wang, X. Wang, X. Yang and L. Lu, Mater. Lett., 2007, 61, 5236–5238 CrossRef CAS.
- H. Wang, J. Z. Xu, J. J. Zhu and H. Y. Chen, J. Cryst. Growth, 2002, 244, 88–94 CrossRef CAS.
- A. Ferrari, J. C. Meyer, C. Scardaci, C. Casiraghi and M. Lazzeri, Phys. Rev. Lett., 2006, 97(4), 187401 CrossRef CAS PubMed.
- J. Cebik, J. K. McDonough, F. Peerally, R. Medrano, I. Neitzel, Y. Gogotsi and S. Osswald, Nanotechnology, 2013, 24, 205703 CrossRef PubMed.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760–1763 CrossRef CAS PubMed.
- J. Huang, H. Li, Y. Zhu, Q. Cheng, X. Yang and C. Li, J. Mater. Chem. A, 2015, 3, 8734–8741 CAS.
- M. E. Plonska-Brzezinska, A. Palkar, K. Winkler and L. Echegoyen, Electrochem. Solid-State Lett., 2010, 13, K35–K38 CrossRef CAS.
- J. Breczko, K. Winkler, M. E. Plonska-Brzezinska, A. Villalta-Cerdas and L. Echegoyen, J. Mater. Chem., 2010, 20, 7761–7768 RSC.
- M. E. Plonska-Brzezinska, J. Mazurczyk, B. Palys, J. Breczko, A. Lapinski, A. T. Dubis and L. Echegoyen, Chem.–Eur. J., 2012, 18, 2600–2608 CrossRef CAS PubMed.
- E. Grądzka, K. Winkler, M. Borowska, M. E. Plonska-Brzezinska and L. Echegoyen, Electrochim. Acta, 2013, 96, 274–284 CrossRef.
- O. Mykhailiv, M. Imierska, M. Petelczyc, L. Echegoyen and M. E. Plonska-Brzezinska, Chem.–Eur. J., 2015, 21, 5783–5793 CrossRef CAS PubMed.
- C. Xu, J. Sun and L. Gao, J. Mater. Chem., 2011, 21, 11253–11258 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Fabrication of free-standing, flexible and binder-free electrodes, morphology of CNO, mechanical conditions of the electrodes after charge–discharge process, N2 adsorption/desorption isotherms and pore size distribution of CNO and CNO–CuO composite, synthesis and morphology of CuO nanoparticle. See DOI: 10.1039/c5ra23700a |
| This journal is © The Royal Society of Chemistry 2016 |





