The microscopic mechanism in the realization of ultra-wide temperature range stability in Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system
Bowen Zhang and
Lingxia Li*
School of Electronic and Information Engineering, Tianjin University, Tianjin 300072, China. E-mail: llxtju@126.com; Fax: +86 22 27402838; Tel: +86 22 27402838
First published on 22nd February 2016
Abstract
A novel lead-free, ultra-wide temperature range stable dielectric ceramic with a high dielectric constant was prepared by a traditional solid-state reaction method. The microscopic mechanism, and the electric and dielectric properties of the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system were investigated for the first time. X-ray diffraction revealed that Bi3+,Na+,Zn2+,Nb5+ and BaTiO3 form a solid-solution with a pseudo-cubic structure. The thermal vibration and interactions between the dipoles contributing to the realization of an ultra-wide temperature range stability, were discussed. The microscopic model based on the bond energy and coordination number, was used to research the changes of the dielectric stability. In this paper, the relationship between microscopic mechanism and the macroscopic dielectric properties in the ultra-wide temperature range stable dielectric ceramics was established, thereby paving the way for achieving ultra-wide temperature range capacitors. In addition, fine dielectric properties of (Na0.015Bi0.3Ba0.685)(Zn0.2Nb0.115Ti0.685)O3 with an εr of 700, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of 0.00535 can be obtained over an ultra-wide temperature range (−53 to 350 °C). These features give the ceramic system high practical value in miniaturization and increasing applications in harsh environments.
δ of 0.00535 can be obtained over an ultra-wide temperature range (−53 to 350 °C). These features give the ceramic system high practical value in miniaturization and increasing applications in harsh environments.
1. Introduction
The rapid development of the electronics industry leads to higher requirements for the next generation of dielectric ceramic materials.1–4 With the increasing integration of components, more circuits and devices are integrated in a limited space. A high dielectric constant is required for capacitors, so that they can meet the requirements of miniaturization. What’s more, the need for short circuit lengths forces us to make circuit modules near or directly in the work environment. Harsh working conditions, such as in automobile engines and rockets, as well as outer space, require that the components can be stable in an ultra-broad temperature scope.1–4 The ceiling working temperature of the dielectric materials has been raised from 125 °C (Electronic Industries Alliance X7R) to 150 °C (EIA-X8R) and now reaches 200 °C (EIA-X9R).5–9With their high dielectric constants, excellent insulation properties, non-toxicity and low cost, BaTiO3 based ceramics have become one of the major dielectric ceramic materials.10 The ceiling temperature of present BaTiO3 based dielectric materials only reaches 125–200 °C. When the temperature increases to over 200 °C a sharp decline occurs. However, even X9R materials would not fulfill the requirements of some harsh conditions, such as in oil drilling, aerospace and automotive environments. For example, anti-lock brake system sensors on wheels are required to work at a temperature range of 150–250 °C and in the cylinder the ambient temperature is 200–300 °C.11–13 The mismatch between the narrow effective temperature range (125–200 °C) and the high operating temperature requirements (over 200 °C) severely limits the use of dielectric components (e.g. MLCC). Thus, it is of great significance to develop temperature stable dielectric materials with a high dielectric constant, and low dielectric loss over a wide temperature range (−55 to 350 °C).14–17
Currently, there is much research on the development of stable dielectric materials over a wide temperature range. However, few studies have been done on the microscopic mechanisms in the materials, which benefit the realization of ultra-wide temperature range stability. In this paper, we report a Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system, which had a high dielectric constant, and a low dielectric loss over a wide temperature range (−53 to 350 °C). The thermal vibrations and the interactions between the dipoles contributing to the realization of the ultra-wide temperature range stability are discussed. What’s more, the bond energy and coordination number model were used to research the movements of the stable temperature range. This work has high practical value in the development of ultra-wide temperature range stable dielectric ceramics.
2. Experimental procedures
Reagent-grade BaTiO3, Na2CO3, Bi2O3, ZnO, and Nb2O5 were used as raw materials. Firstly, reagent-grade oxides and carbonate of Bi2O3, ZnO and Nb2O5 were weighed with a mole ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and mixed using ball-milling in deionized water for 4 h. Then the mixture was calcined in air at 800 °C to synthesize a Bi(Zn2/3Nb1/3)O3 phase. Secondly, stoichiometric proportions of Na2CO3 and Nb2O5 were mixed by ball milling in deionized water for 4 h. The mixture was dried and calcined at 900 °C in a covered alumina crucible for 4 h to synthesize a NaNbO3 phase. Bi(Zn2/3Nb1/3)O3 and NaNbO3 have a similar structure to BaTiO3.36,38–47 In the sintering process, it is more convenient for Bi3+, Na+, Zn2+, and Nb5+ to diffuse into the crystal lattice, rather than the oxide forms, such as Bi2O3, ZnO and Nb2O5. Subsequently, (1 − x)BaTiO3–xBi(Zn2/3Nb1/3)O3–0.015NaNbO3 (0.22 ≤ x ≤ 0.30) powders were weighed and milled in deionized water using zirconia balls for 4 h. The locations of the compositions in the (1 − x)BaTiO3–xBi(Zn2/3Nb1/3)O3–0.015NaNbO3 system are shown in Fig. 1. After drying, the mixed powders were added in 7 wt% binder wax, and then cold isostatically pressed into discs under a pressure of 200 MPa with a 20 mm diameter and 1 mm thickness. The samples were sintered at 1200 °C for 2 h. The samples with x = 0.22, 0.24, 0.0.27, and 0.30 were named sample 1, sample 2, sample 3, and sample 4, respectively.
1 and mixed using ball-milling in deionized water for 4 h. Then the mixture was calcined in air at 800 °C to synthesize a Bi(Zn2/3Nb1/3)O3 phase. Secondly, stoichiometric proportions of Na2CO3 and Nb2O5 were mixed by ball milling in deionized water for 4 h. The mixture was dried and calcined at 900 °C in a covered alumina crucible for 4 h to synthesize a NaNbO3 phase. Bi(Zn2/3Nb1/3)O3 and NaNbO3 have a similar structure to BaTiO3.36,38–47 In the sintering process, it is more convenient for Bi3+, Na+, Zn2+, and Nb5+ to diffuse into the crystal lattice, rather than the oxide forms, such as Bi2O3, ZnO and Nb2O5. Subsequently, (1 − x)BaTiO3–xBi(Zn2/3Nb1/3)O3–0.015NaNbO3 (0.22 ≤ x ≤ 0.30) powders were weighed and milled in deionized water using zirconia balls for 4 h. The locations of the compositions in the (1 − x)BaTiO3–xBi(Zn2/3Nb1/3)O3–0.015NaNbO3 system are shown in Fig. 1. After drying, the mixed powders were added in 7 wt% binder wax, and then cold isostatically pressed into discs under a pressure of 200 MPa with a 20 mm diameter and 1 mm thickness. The samples were sintered at 1200 °C for 2 h. The samples with x = 0.22, 0.24, 0.0.27, and 0.30 were named sample 1, sample 2, sample 3, and sample 4, respectively.
The crystal structure of the samples was identified at room temperature using an X-ray diffractometer (D8-Focus, Bruker AXS GmbH, German). To reduce noise, all data have been smoothed by an adaptive smoothing method and had background deducted. All parameters including background, zero-point, scale factors for all phases, half-width, asymmetry parameters, unit-cell parameters, atomic positional coordinates, and temperature factors are refined step-by-step to avoid correlations by the soft-ware of Fullprof-suite. The microstructure of the ceramic samples was observed by field emission scanning electron microscopy (FE-SEM, S-4800, Hitachi, Ltd. Japan). Dielectric loss and capacitance were measured with the use of a capacitance meter (HP4278A) at 1 kHz to 1 MHz, with a temperature range of −55 °C to 350 °C. Insulation resistance was measured using a high resistance meter (Agilent 4339B) at room temperature.
3. Results and discussion
3.1 The micro-mechanism and the dielectric properties
Fig. 2(a–c) shows the temperature dependence of the dielectric constant and capacitance variation rate based on C25 °C with various amounts of Bi3+,Na+,Zn2+,Nb5+, sintered at 1200 °C, and measured at 1 kHz to 1 MHz. As Fig. 2 shows, there is only one dielectric dispersion peak at low temperature (∼25 °C) and the dielectric constant varies with frequency, which is consistent with the relaxation ferroelectrics. The “modified Curie–Weiss law”34 is a method commonly used in the study of ferroelectric materials, which is expressed by the following equation:where ε is the relative permittivity, Tm is the temperature, εm is the maximum ε value at T = Tm, C is the modified Curie–Weiss constant, and r is a measurement of diffusivity. The material with r = 1 fits a normal ferroelectric behavior, with r = 2 it fits the ideal relaxation ferroelectric system,35 and between 1 and 2 it indicates a diffuse ferroelectric characteristic, which has the characteristics of “relaxorlike” behavior. Fig. 2(d) shows that the diffuse exponent r is about 1.4–1.5 for the (1 − x)BaTiO3–xBi(Zn2/3Nb1/3)O3–0.015NaNbO3 (0.22 ≤ x ≤ 0.30) ceramics, which confirmed that (1 − x)BaTiO3–xBi(Zn2/3Nb1/3)O3–0.015NaNbO3 exhibit the “relaxorlike” behavior. It was the special structure—“relaxorlike”—that gives the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system special dielectric properties. The details are shown below.35
Spontaneous polarization occurred in the ferroelectric BaTiO3 and the long-range interactions between the dipoles promoted the dipoles to form ferroelectric domains. When an external electric field was applied, the ferroelectric domains would be extended along the external electric field, which is the reason for a high dielectric constant in BaTiO3. Meanwhile, long-range interactions between dipoles were destroyed by the doping of external additives. The macroscopic ferroelectric domains gradually decreased and randomly distributed micro-domains formed.18–20 Fig. 3 shows a micro-mechanism in the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system, which benefits the realization of an ultra-wide temperature range stability.
 | ||
| Fig. 3 The micro-mechanism in the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system, which benefits the realization of an ultra-wide temperature range stability. | ||
When an external electric field was applied, there were three forces involved in the phase change process, the external electric field force (Fe), the interaction between the polarized micro-domains (Fi) and the thermal vibration force (Fv), which occurred throughout the whole temperature range. The interaction between the polarized micro-domains and the thermal vibration make the polarized micro-domains distribute randomly and macroscopic polarization is reduced. Meanwhile, the external electric field force (Fe) makes the polarized micro-domains distribute along the external electric field and the macroscopic polarization is increased. Local polarization regions formed at the Burns temperature (Td). At ambient temperatures, T ≫ Td, no polarization existed and the dielectric system was in a paraelectric phase. The Burns temperature is generally higher than the temperature Tc of the maximum dielectric constant.21,22
In a high temperature range (T ≤ Td), thermal vibration is very strong. The interactions of different polarization regions (Fi) are so weak they can be ignored. The thermal vibration force (Fv) is greater than the external electric field force (Fe). The polarized micro-domains can vibrate in several equivalent directions. The orientation of each polarized micro-domain is insulated from the others. The macroscopic polarization was close to zero.
In the temperature region of Tc < T ≪ Td, the polarized micro-domains gradually increased. The thermal vibration (Fv) reduced and gradually became less than the external electric field force (Fe). The interactions of different polarization regions (Fi) remain so weak that they can be ignored. Since the temperature is still relatively high, the degree of freedom of the polarized micro-domains is high and the external electric field force (Fe) makes the polarized micro-domains distribute along the external electric field quickly. As a result, the dielectric constant increases and the relaxivity is low.
In the temperature region of Tf ≪ T < Tc, the polarized micro-domains are large, and the interaction between the polarized micro-domains is strong. Because the temperature is relatively low, the thermal vibration energy is small and it can be ignored. The polarized micro-domains gradually increase and the interactions of micro-domains strengthen as the temperature declines. The electric field directional force (Fe) gradually becomes lower than the interaction between the polarized micro-domains (Fi). As a result, the dielectric constant is decreased, and dielectric loss and relaxivity are enhanced.
In the temperature region of T ≥ Tf, the polarized micro-domains become larger and the interaction between the dipoles (polarized micro-domains) (Fi) is larger than the electric field directional force (Fe) which leads to the dipoles being distributing randomly. The ambient temperature is so low that thermal vibration can be ignored. As a result, the macroscopic polarization is close to zero.
Accordingly, the dielectric constant increased firstly and then decreased, and significant dielectric relaxation appeared in the low temperature region.
3.2 Bond energy and coordination number relaxor model and the dielectric stability
In the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system, relaxation arises from the inert substitution of A, B site ions. Bi3+,Na+,Zn2+,Nb5+ diffuses into the cell and the dielectric system changes from normal ferroelectric to diffuse ferroelectric. The relaxation behavior can be described by the relationship of Vogel–Fulcher:
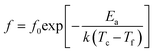 | (1) |
According to the bond energy and coordination number model, the Vogel–Fulcher formula can be expressed as follows:23,24
 | (2) |
 | (3) |
In the crystal of BaTiO3, one Ti4+ ion and six O2− ions form the special octahedral structure of [TiO6], which can be seen in the Fig. 1. In the octahedron, Ti4+ deviates from the center position of the octahedron and a dipole forms. So, each [TiO6] octahedron can be seen as one dipole.
In the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system, Bi3+,Na+,Zn2+,Nb5+ diffuses into the cell. Because of the different radii and valence with Ba2+ and Ti4+, the doping ions (Zn2+,Nb5+) locate at the center of the oxygen octahedra. As a result, a dipole cannot form.
What’s more, the original polarized [TiO6] octahedra in BaTiO3 are separated by the non-polarized area (the doping area). As a result, the interactions between the dipoles are weakened.
In summary, the inert substitution of A, B site ions makes the number of neighboring dipoles decrease and the interactions (which we call bond energy in this paper) between the dipoles weaken. Due to the non-uniform distribution of dopant ions,37 each different dipole has its own surroundings. Thus, the coordination number and bond energy of each dipole can be described as follows:
| Z = Z0 + ΔZ | (4) |
| E = E0 + ΔE | (5) |
When the bond energy and coordination number follow Gaussian distribution25
 | (6) |
| ΔE/E0 = γ·ΔZ/Z0 | (7) |
When γ = 1, formula (7) can be expressed as26
 | (8) |
In the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system, the substitution of doping ions within the crystal is non-uniform.37 The non-uniform distribution of the crystals inside leads to large fluctuations in bond energy (ΔE). From eqn (8), we can conclude that relaxation behavior will be enhanced with the increase of doping content.
What’s more, due to the non-uniform distribution of the substitutional ions, the surroundings of each dipole are different. Different areas have their own activation energy. So, different areas have different responses to temperature. As a result, the dielectric peak was broadened and dielectric stability was enhanced. The mechanism is shown in Fig. 2.
The results of Fig. 2 and 3 and Table 1 are consistent with the discussion above. Fig. 2 and Table 1 show that from sample 1 to sample 4, the dielectric stability gradually increased from the range of −55 to 245 °C, to −53 to 350 °C. What’s more, according to eqn (8), if the measuring frequency (f) remains constant, Tc will move to a higher temperature with the increasing of the doping content (ΔE is increased). Table 1 shows the dielectric properties of samples 1–4. When the doping content increased from x = 0.24 to x = 0.30, Tc increased from ∼25 °C to ∼50 °C. The movement of Tc makes the temperature stable range move to a higher temperature which we can see from Fig. 2 and Table 1.
| Sample | εr at 25 °C | tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ δ |
ΔC/C25 °C (%) ≤ ±15% | Curie temperature (Tc/°C) | Bulk density (g cm−3) | Insulation resistance (ρv 1010 Ω cm) | |
|---|---|---|---|---|---|---|---|
| 1 | 721 | 0.00539 | −55 °C | 245 °C | 25 | 5.729 | 2.78 |
| 2 | 704 | 0.00773 | −50 °C | 250 °C | 25 | 5.727 | 3.74 |
| 3 | 678 | 0.01005 | −50 °C | 300 °C | 25 | 5.817 | 1.41 |
| 4 | 630 | 0.01069 | −53 °C | 350 °C | 50 | 5.777 | 4.25 |
3.3 Structure of Bi3+,Zn2+,Nb5+ doped BaTiO3 solid solution
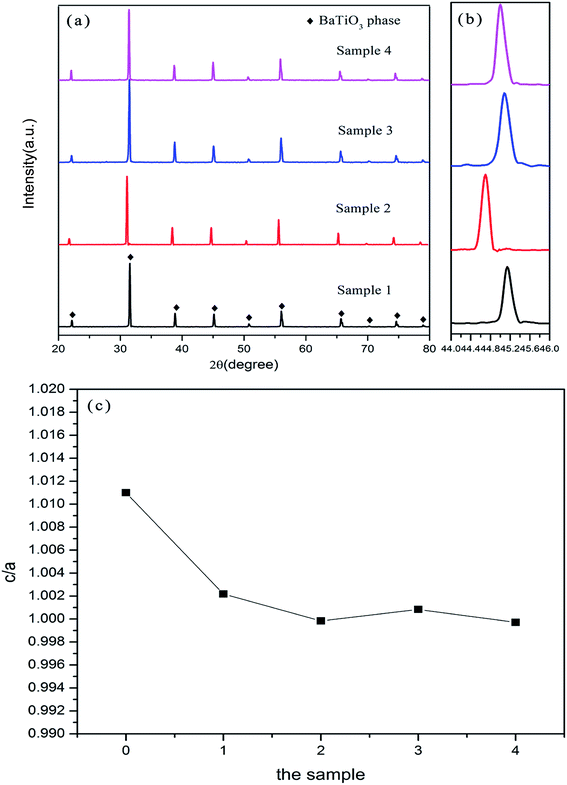
Fig. 4(a) shows the X-ray diffraction patterns of (1 − x)BaTiO3–xBi(Zn2/3Nb1/3)O3–0.015NaNbO3 doped with varying content of Bi(Zn2/3Nb1/3)O3 and sintered at 1200 °C. All samples show a perovskite phase, which means that there is formation of a solid solution between Bi3+,Na+,Zn2+,Nb5+ and BaTiO3. No second phase exists. The enlarged XRD patterns in the range of 2θ from 44° to 46° are illustrated in Fig. 4(b). It is clearly visible that there is a merging of the (002)/(200) (2θ = 45°) diffraction peaks of the pure barium titanate into a single (200) peak, indicating a transformation from a tetragonal phase (P4mm) to pseudocubic symmetry. Just as we can see from the dielectric constant–temperature curve mentioned above, the Curie peak at ∼120 °C (pure BaTiO3) disappeared. In addition, the dielectric anomaly peak occurs at the low temperature of ∼25 °C. With the increase of the doping concentration of Bi(Zn2/3Nb1/3)O3, the (200) diffraction peak shifted toward lower angles firstly (from x = 0.22 to x = 0.24) and then the (200) diffraction peak shifted higher accompanied by gradually enhancing Bi(Zn2/3Nb1/3)O3 concentration (from x = 0.24 to x = 0.27, and x = 0.30). This behavior demonstrates that the lattice parameters of solid solutions increased firstly and then decreased slightly. According to the principles of crystal chemistry and the radius-matching rule,30,31 the incorporation of the radii of Na+ (1.39 Å) and Bi3+ (1.30 Å) is nearly comparable to the value of Ba2+ (1.61 Å) owing to the 12-fold coordination in the A-site.27 Meanwhile, the B-site ions Zn2+ (0.74 Å) and Nb5+ (0.64 Å) have considerably larger radii than that of Ti4+ (0.605 Å) in a six-fold coordination.28,32 The substitution of the B-site is the main influencing factor on the crystal lattice in this paper. When there is a further increase in Bi(Zn2/3Nb1/3)O3 (e.g. sample 3), the content of Zn2+ and Nb5+ that diffuses into the cell is abnormally reduced. This phenomenon is due to the produced pinning effect by the heavily doped Bi(Zn2/3Nb1/3)O3, which inhibits the grains’ growth. What’s more, excessive increase in the content of Bi(Zn2/3Nb1/3)O3 (e.g. sample 4) will generate a lot of liquid phase in the sintering process; the content of Zn2+ and Nb5+ that diffuses into the lattice will increase. The lattice parameters (a and c) of the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 solid solution are calculated based on XRD results using High-Score plus software. Fig. 4(c) illustrates the compositional dependence of the tetragonality factor (c/a). The c/a ratio reduced from 1.011 for x = 0 to 1.0002 for x = 0.27 and 0.9971 for x = 0.30, and became equal to 1. The decreased c/a is inherently associated with the lower tolerance factor of Zn2+ and Nb5+, which is significantly lower than Ti4+ for the pure BaTiO3.3.4 Microstructure of the BaTiO3–Bi(Zn2/3Nb1/3)O3–NaNbO3 ceramics
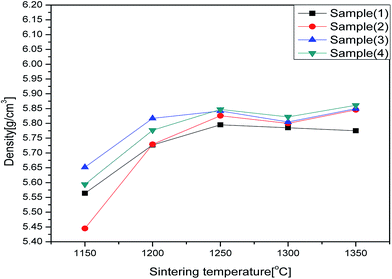
Fig. 5 shows the relationships between sintering temperatures and densities of all the studied samples. It can be observed that increasing the Bi(Zn2/3Nb1/3)O3 content could increase the density while no significant change occurred in the sintering temperature. Fig. 6 shows the SEM micrographs for the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric system. As shown here, the grains are well developed in all the samples. All of the samples show a uniform grain distribution and the size of the grain is about 2–3 μm. There is no second phase in this report. Fig. 7 shows the distribution of the grain size obtained by the software of Nano measure. Just as we can see, with the increase of the Bi(Zn2/3Nb1/3)O3 content, the densification and the grain size increased firstly, then decreased, and increased finally. As mentioned above, the Zn2+ ions will enter into the lattice to substitute for Ti4+ ions; the imbalance of ion valence will lead to the creation of oxygen vacancies,32,33 which enhances the transfer of mass and energy between the reactants. This improved the sintering process inducing an increase in the densification of grain distribution. However, a further increase in Bi(Zn2/3Nb1/3)O3 (x = 0.30) has an adverse effect on the densification of the samples, as illustrated in Fig. 6(c). This phenomenon is due to the produced pinning effect. When the doping amount is less, the distribution of Bi3+,Na+,Zn2+,Nb5+ is uniform. However, when the doping increases, an increase in the number of substitutional ions and lattice distortion occurs which is harmful to the diffusion process. Fig. 6(d) shows that the densification and the grain size increased again. This may be due to excess doping. A large amount of liquid phase occurred in the sintering process and accumulated in the grain boundaries. The right amount of liquid benefits the dissolution/precipitation process.27–29,33 | ||
| Fig. 6 SEM micrographs of natural surfaces for (1 − x)BaTiO3–xBi(Zn2/3Nb1/3)O3–0.015NaNbO3 ceramics with x = 0.22, 0.24, 0.27, and 0.30: (a)–(d). | ||
 | ||
| Fig. 7 (a)–(d) The distribution of the grain size in (1 − x)BaTiO3–xBi(Zn2/3Nb1/3)O3–0.015NaNbO3 ceramics with x = 0.22, 0.24, 0.27, and 0.30; (e) compositional dependence of the grain size. | ||
4. Conclusion
The crystal structure and dielectric properties of Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric systems were investigated. The relationship between the microscopic structure and the dielectric properties was discussed systematically. The microscopic model based on bond energy and coordination number, was proposed and used to investigate the changes of the dielectric stability in the Bi3+,Na+,Zn2+,Nb5+ doped BaTiO3 dielectric systems. The obtained results indicated that doping with Bi3+,Na+,Zn2+,Nb5+ can alter the temperature dependence of the dielectric constant markedly both in the high and low temperature range, which played a decisive role in the realization of wide temperature range stability. Dielectric measurements showed that doping with Bi3+,Na+,Zn2+,Nb5+ can make the dielectric system change from a normal ferroelectric to a diffusive ferroelectric (1 < r < 2) system, which has the characteristics of a normal ferroelectric system and ideal relaxation. The temperature coefficient of capacitance was flat in the temperature range of −53 to 350 °C. Moreover, the system had a relatively higher dielectric constant and lower dielectric loss (εr = ∼700, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 0.00535) over an ultra-wide temperature range. These features suggest that the ceramic system can be considered as a promising candidate material for the next generation of MLCCs used in harsh conditions (over 300 °C).
δ = 0.00535) over an ultra-wide temperature range. These features suggest that the ceramic system can be considered as a promising candidate material for the next generation of MLCCs used in harsh conditions (over 300 °C).
References
- W. Johnson, J. L. Evans, P. Jacobsen, J. R. Thompson and M. Christopher, The changing automotive environment: high-temperature electronics, IEEE Trans. Electron. Packag. Manuf., 2004, 27, 164–176 CrossRef.
- R. Werner and W. R. Fahrner, Review on materials, microsensors, systems and devices for high-temperature and harsh-environment applications, Industrial Electronics, IEEE Trans. Ind. Electron. Control Instrum., 2001, 48, 249–257 CrossRef.
- Y. Yuan, C. J. Zhao, X. H. Zhou, B. Tang and S. R. Zhang, High-temperature stable dielectrics in Mn-modified (1 − x)Bi0.5Na0.5TiO3–xCaTiO3 ceramics, J. Electroceram., 2010, 25, 212–217 CrossRef CAS.
- J. B. Lim, S. Zhang, N. Kim and T. R. Shrout, High-temperature dielectrics in the BiScO3–BaTiO3–(K1/2Bi1/2)TiO3 ternary system, J. Am. Ceram. Soc., 2009, 92, 679–682 CrossRef CAS.
- S. Wang, J. Li, Y. Hsu, Y. Wu, Y. Lai and M. Chen, Dielectric properties and microstructures of non-reducible high-temperature stable X9R ceramics, J. Eur. Ceram. Soc., 2013, 33, 1793–1799 CrossRef CAS.
- G. Yao, X. Wang, Y. Zhang, Z. Shen and L. Li, Nb-modified 0.9BaTiO3–0.1(Bi0.5Na0.5)TiO3 ceramics for X9R high-temperature dielectrics application prepared by coating method, J. Am. Ceram. Soc., 2012, 95, 3525–3531 CrossRef CAS.
- B. Tang, S. Zhang, X. Zhou, Y. Yuan and L. Yang, Preparation and modification of high Curie point BaTiO3-based X9R ceramics, J. Electroceram., 2010, 25, 93–97 CrossRef CAS.
- S. Gao, S. Wu, Y. Zhang, H. Yang and X. Wang, Study on the microstructure and dielectric properties of X9R ceramics based on BaTiO3, Materials Science and Engineeing B: Advanced Functional Solid-State Materials, 2011, 176, 68–71 CrossRef CAS.
- L. Li, Y. Han, P. Zhang, C. Ming and X. Wei, Synthesis and characterization of BaTiO3-based X9R ceramics, J. Mater. Sci., 2009, 44, 5563–5568 CrossRef CAS.
- A. Patterson and D. P. Cann, Relaxor to ferroelectric transitions in (Bi1/2Na1/2)TiO3–Bi(Zn1/2Ti1/2)O3 solid solutions, J. Am. Ceram. Soc., 2012, 95, 3509–3513 CrossRef.
- N. Raengthon, H. J. Brown-shaklee and G. L. Brennecka, Dielectric properties of BaTiO3–Bi(Zn1/2Ti1/2)O3–NaNbO3 solid solutions, J. Mater. Sci., 2013, 48, 2245–2250 CrossRef CAS.
- C. Jeon, C. S. Lee and S. J. L. Kang, The mechanism of core/shell structure formation during sintering of BaTiO3-based ceramics, J. Am. Ceram. Soc., 2012, 95, 2435–2438 CrossRef.
- A. Zeb and S. J. Milne, Stability of High Temperature Dielectric Properties for (1 − x)Ba0.8Ca0.2TiO3–xBi(Mg0.5Ti0.5)O3 Ceramics, J. Am. Ceram. Soc., 2013, 96, 2887–2892 CrossRef CAS.
- (a) A. Zeb and S. J. Milne, Low variation in relative permittivity over the temperature range 25–450 °C for ceramics in the system (1 − x)[Ba0.8Ca0.2TiO3]–x[Bi(Zn0.5Ti0.5)O3], J. Eur. Ceram. Soc., 2014, 34, 1727–1732 CrossRef CAS; (b) L. Zhang, O. P. Thakur, A. Feteira, G. M. Keith, A. G. Mould, D. C. Sinclair and A. R. West, Comment on the use of calcium as a dopant in X8R BaTiO3-based ceramics, Appl. Phys. Lett., 2007, 90, 142914 CrossRef.
- S. Wang, S. Zhang, X. Zhou, B. Li and Z. Chen, Influence of sintering atmosphere on the microstructure and electrical properties of BaTiO3-based X8R materials, J. Mater. Sci., 2006, 41, 1813–1817 CrossRef CAS.
- L. Li, R. Fu, Q. Liao and L. Ji, Doping behaviors of NiO and Nb2O5 in BaTiO3 and dielectric properties of BaTiO3-based X7R ceramics, Ceram. Int., 2012, 38, 1915–1920 CrossRef CAS.
- K. Yasukawa, M. Nishimura and Y. Nishihata, et al., Core–shell structure analysis of BaTiO3 ceramics by synchrotron X-ray diffraction, J. Am. Ceram. Soc., 2007, 90, 1107–1111 CrossRef CAS.
- C. J. Stringer, T. R. Shrout and C. A. Randall, High-temperature perovskite relaxor ferroelectrics: A comparative study,, J. Appl. Phys., 2007, 101, 054107 CrossRef.
- V. A. Isupov, Causes of Phase-Transition Broadening and the Nature of Dielectric Polarization Relaxation in Some Ferroelectrics, Phys. Solid State, 1963, 5, 136–140 Search PubMed.
- G. A. Smolenski, Physical Phenomena in Ferroelectrics With Diffused Phase Transition, J. Phys. Soc. Jpn., 1970, 28, 26–37 Search PubMed.
- D. Völtzke and H. Abicht, Mechanistic investigations on the densification behaviour of barium titanate ceramics, Solid State Sci., 2001, 3, 417–422 CrossRef.
- V. A. Isupov, Causes of Phase-Transition Broadening and the Nature of Dielectric Polarization Relaxation in Some Ferroelectrics, Phys. Solid State, 1963, 5, 136–140 Search PubMed.
- G. A. Smolenski, Physical Phenomena in Ferroelectrics With Diffuse d Phase Transition, J. Phys. Soc. Jpn., 1970, 28, 26–37 Search PubMed.
- M. Aniya, J. Therm. Anal. Calorim., 2002, 69, 971 CrossRef CAS.
- T. A. Vilgis, J. Phys.: Condens. Matter, 1990, 2, 3667 CrossRef.
- Q. Cao and M. F. Shu, Bond energy and coordination number model for relaxor ferroelectrics, Acta Phys. Sin., 2013, 62, 017701 Search PubMed.
- Y. Sun, H. Liu, H. Hao and L. Zhang, The role of Co in the BaTiO3–Na0.5Bi0.5TiO3 based X9R ceramics, Ceram. Int., 2015, 41, 931–939 CrossRef CAS.
- T. Wang, L. Li, C. Li, Q. Y. Hu and X. Y. Wei, Relaxor Ferroelectric BaTiO3–Bi(Mg2/3Nb1/3)O3 Ceramics for Energy Storage Application, J. Am. Ceram. Soc., 2014, 1–8 Search PubMed.
- C. Jeon, B. K. Yoon, K. H. Kim and S. J. L. Kang, Effects of core/shell volumetric ratio on the dielectric-temperature behavior of BaTiO3, J. Adv. Ceram., 2014, 3(1), 76–82 CrossRef.
- R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- D. Hennings, Barium titanate based ceramic materials for dielectric use, Int. J. High Technol. Ceram., 1987, 3, 91–111 CrossRef CAS.
- N. Zhang, L. Li, J. Chen and J. Yu, ZnO doped BaTiO3–Na0.5Bi0.5TiO3–Nb2O5-based ceramics with temperature-stable high permittivity from −55 °C to 375 °C, Mater. Lett., 2015, 138, 228–230 CrossRef CAS.
- T. Zhang, X. Tang, Q. Liu, Y. Jiang and X. Huang, Oxygen-Vacancy-Related High Temperature Dielectric Relaxation in (Pb1−xBax)ZrO3 Ceramics, J. Am. Ceram. Soc., 2014, 1–8 Search PubMed.
- H. Cheng, H. Du, W. Zhou, D. Zhu, F. Luo and B. Xu, Bi(Zn2/3Nb1/3)O3–(K0.5Na0.5)NbO3 High-Temperature Lead-Free Ferroelectric Ceramics with Low Capacitance Variation in a Broad Temperature Usage Range, J. Am. Ceram. Soc., 2013, 96, 833–837 CrossRef CAS.
- A. Bokov and Z.-G. Ye, Recent progress in relaxor ferroelectrics with perovskite structure, J. Mater. Sci., 2006, 41, 31–52 CrossRef CAS.
- X. Chen, J. Chen, D. Ma, L. Fang and H. Zhou, Thermally Stable BaTiO3–Bi(Mg2/3Nb1/3)O3 Solid Solution with High Relative Permittivity in a Broad Temperature Usage Range, J. Am. Ceram. Soc., 2015, 98, 804–810 CrossRef CAS.
- G. A. Smolensky, Physical phenomena in ferroelectrics with diffuse phase transition, J. Phys. Soc. Jpn., 1970, 28, 26–37 Search PubMed.
- H. Arvind, K. Umesh, R. E. Newnham and L. E. Cross, Stabilization of the Perovskite Phase and Dielectric Properties of Ceramics in the Pb(Zn1/3Nb2/3)O3–BaTiO3 System, Am. Ceram. Soc. Bull., 1987, 66, 671–676 Search PubMed.
- Z. Li, Q. Li, L. Zhang and X. Yao, Dielectric Properties and Transition Temperature of Ceramics in the Pb(Mg1/3Nb2/3)O3–BaTiO3 System, Ferroelectrics, 2001, 262, 47–52 CrossRef CAS.
- C. C. Huang and D. P. Cann, Phase Transition and Dielectric Properties in Bi(Zn1/2Ti1/2)O3–BaTiO3, J. Appl. Phys., 2008, 104, 024117 CrossRef , 4pp.
- M. R. Suchomel and P. K. Davies, Enhanced Tetragonality in (x)PbTiO3–(1 − x)Bi(Zn1/2Ti1/2)O3 and Related Solid Solution System, Appl. Phys. Lett., 2005, 86, 262905 CrossRef , 3pp.
- B. Xiong, H. Hao, S. J. Zhang, H. X. Liu and M. H. Cao, Structure, Dielectric Properties and Temperature Stability of BaTiO3–Bi(Mg1/2Ti1/2)O3 Perovskite Solid Solutions, J. Am. Ceram. Soc., 2011, 94, 3412–3417 CrossRef CAS.
- J. Chen, X. L. Tan, W. Jo and J. R. €odel, Temperature Dependence of Piezoelectric Properties of High–Tc (1 − x)Bi(Mg1/2Ti1/2)O3–xPbTiO3, J. Appl. Phys., 2009, 106, 034109 CrossRef , 7pp.
- T. Le ist, J. Chen, W. Jo, E. Aulbach, J. Suffner and J. R €ode, Temperature Dependence of the Piezoelectric Coefficient in BiMeO3–PbTiO3 (Me = Fe, Sc, (Mg1/2Ti1/2)) Ceramics, J. Am. Ceram. Soc., 2012, 95, 711–715 CrossRef CAS.
- S. M. Choi, C. J. Stringer, T. R. Shrout and C. A. Randall, Structure and Property Investigation of A Bi-Based Perovskite Solid Solution: (1 − x)Bi(Ni1/2Ti1/2)O3–xPbTiO3, J. Appl. Phys., 2005, 98, 034108 CrossRef , 4pp.
- Y. L. Wang, X. L. Chen, H. F. Zhou, L. Fang, L. J. Liu and H. Zhang, Evolution of Phase Transformation Behavior and Dielectric Temperature Stability of BaTiO3–Bi(Zn0.5Zr0.5)O3 Ceramics System, J. Alloys Compd., 2013, 551, 365–369 CrossRef CAS.
- A. Zeb and S. J. Milne, Temperature-Stable Dielectric Properties From −20 to 430 °C in the System BaTiO3–Bi(Mg0.5Zr0.5)O3, J. Eur. Ceram. Soc., 2014, 34, 3159–3166 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |