Enhancement of the oxygen evolution reaction in Mn3+-based electrocatalysts: correlation between Jahn–Teller distortion and catalytic activity

Abstract

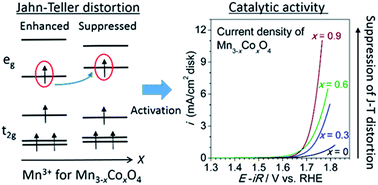
We systematically studied the catalytic activity of the oxygen evolution reaction (OER) for the tetragonal spinel oxide Mn_3−xCo_xO₄ (0 ≤ x < 1 and 1 < x ≤ 1.5). The OER catalytic activity of Mn_3−xCo_xO₄ (0 ≤ x < 1) dramatically improved with an increase in Co content. We found that the OER activity of Mn_3−xCo_xO₄ (0 ≤ x < 1) increased linearly with the suppression of the Jahn–Teller distortion. We therefore propose that the Jahn–Teller distortion plays an important role in the OER activities of compounds containing Mn³⁺. Mn_3−xCo_xO₄ (0 ≤ x < 1) provides a rare case for directly studying the effect of the Jahn–Teller distortion on OER activity.