Porous carbon nanoflakes with a high specific surface area derived from a kapok fiber for high-performance electrode materials of supercapacitors†
Abstract
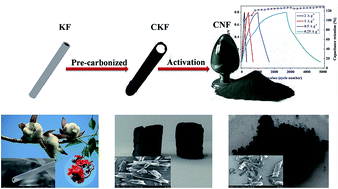
Well-defined porous carbon nanoflakes with a high specific surface area have been successfully prepared via pyrolytic carbonization and alkali activation treatment of an easily available kapok fiber. The details of alkali–carbon ratio, activation temperature, and activation time are optimized according to the specific surface area and the specific capacitance of the as-prepared samples. The porous carbon nanoflakes prepared at 700 °C for 2 h with an alkali carbon ratio of 5 : 1 possess a high specific surface area of 1634.5 m2 g−1. The specific capacitance can reach 430 F g−1 at a current density of 0.5 A g−1 in a 1.0 M H2SO4 electrolyte, and an excellent cycle stability with no obvious decrease is observed after 5000 cycles. In addition, the assembled symmetrical supercapacitor base on the sample exhibits an energy density of 7.85 W h kg−1 at a power density of 125 W kg−1. The favourable capacitive performances indicate that the low-cost kapok fiber can serve as a new resource of carbonaceous materials for high-performance supercapacitors.

 Please wait while we load your content...
Please wait while we load your content...