The molecular mechanism of secondary sodium symporters elucidated through the lens of the computational microscope

Abstract

Transport of molecules across cellular membranes is a key biological process for normal cell function. As such, secondary active transporters exploit electrochemical ion gradients to carry out fundamental processes, i.e. nutrients uptake, ion regulation, neurotransmission, and substrate extrusion. Despite their modest sequence similarity, several Na⁺ symporters share the same fold of LeuT (leucine transporter), a prokaryotic member of the neurotransmitter-sodium symporter family, pinpointing to a common structural/functional mechanism of transport. This is associated with specific conformational transitions occurring along a so-called alternating access mechanism. Thanks to recent advances in computer simulation techniques and the ever-increasing computational power that has become available in the last decade, molecular dynamics (MD) simulations have been largely employed to provide atomistic insights into mechanistic, kinetic, and thermodynamic aspects of this family of transporters. Here we report a detailed overview of selected Na⁺-symporters belonging to the LeuT-fold superfamily for which different aspects of the transport mechanism have been addressed using both experimental and computational studies. The aim of this review is to describe current state-of-the-art knowledge on the mechanism of these transporters showing how molecular simulations have contributed to elucidate mechanistic aspects and can provide nowadays a spatial and temporal resolution, allowing the interpretation of experimental findings, complementing biophysical methods, and filling the gaps in fragmentary experimental information.

---

1 Introduction

The transport of materials across cellular membranes is a fundamental event for cell survival and maintenance. To this end, living cells exploit membrane proteins, macromolecular machineries associated or embedded in cellular membranes.¹ Among these proteins, transporters are involved in the translocation of small organic molecules across membranes, coupling the energetically disfavored transport of their substrates to various sources of energies. While primary active transporters work by directly using the energy released by chemical reactions (i.e. ATP hydrolysis) or by light, secondary active transporters exploit energy stored as a transmembrane electrochemical gradient of ions (mostly Na⁺ or H⁺). These proteins can transport two or more molecules and ions in the same direction (symporters) or in opposite directions (antiporters). Sodium symporters, in particular, use Na⁺ ion(s) to cotransport a variety of substrates (sugars, amino acids, neurotransmitters, nucleobases)^2,3 against their chemical concentration gradient. These play a crucial role in the physiology of the brain, intestines, kidneys, thyroid and skin, thus being targets therapeutic intervention in the treatment of depression, diabetes, obesity, etc.^2,3 Despite belonging to different gene families, and their modest sequence identity (10–16%), these symporters share a common structural core of 10 transmembrane (TM) helices composed of two five-helix inverted repeat (5HIR) motifs, referred to from now on as ‘LeuT-fold’ (Fig. 1). Moreover, their active transport is believed to occur via a common alternating access mechanism,^2,5 during which substrate accessibility changes from one side to the other of the cellular membrane. Namely, the ion(s) and substrate bind to one face (extracellular, EC) of the transporter. This event induces some conformational changes in the protein, which are followed by the translocation of ion(s) and the substrate to the opposite face (intracellular, IC) of the membrane. Hence, during transport these proteins switch from an outward-facing (OF) to an inward-facing (IF) conformation via a complex set of structural transitions, occurring at both local and global levels, which thus range from between the micro- to millisecond timescale. During these large conformational rearrangements the transporters are believed to take on several possible intermediate structures, which are difficult to capture experimentally due to their short life-times (Fig. 2).

Fig. 1 The vSGLT structure and helix numbering for the LeuT-fold members. (A) The structure is colored as a rainbow from the N-terminus (red) to the C-terminus (purple). The blue and red trapeziums represent the inverted topology of TMs 1–5 and TMs 6–10. The extra- and intracellular halves of TM1 and TM6 are connected through unstructured regions. Galactose is shown as a gray hexagon with red trim. Residues involved in sugar recognition, gate residues, and a proposed ion site are shown (in cyan, gray, yellow circles, respectively). (B) The whole tertiary structure viewed in the membrane plane, with the same coloring scheme and numbering of helices as in (A). Galactose (black and red spheres) and proposed Na⁺ (blue sphere) are shown. Image from ref. 4 reprinted with permission from AAAS. (C) Numbering of the TMs of the transporters considered in this review indicating the position of the core domain (TMs 1–10) with respect to the other helices. HP stands for helical hairpin.

Fig. 2 Hypothesized alternating access mechanism and available crystallographic structures. (A) A schematic model showing the hypothesized possible conformational states of a generic symporter and the role of gates in transport. In the first state (apo) no ligands are bound to the transporter. Once the ion(s) and the substrate bind from the extracellular side (OFop), the external gate closes (OFoccl). Conformational switching leads to the closure of the external vestibule (closed) and to the subsequent opening of the internal vestibule (IFoccl). Opening of the internal gate permits the substrate and sodium ion(s) to dissociate and exit towards the intracellular face of the membrane (IFop). The cycle is completed by the closure of the internal vestibule and a return to the apo state. The abbreviations used are: inward-facing (IF) and outward-facing (OF) states; the gates can be open (op) or closed (occl); the intermediate structure (both gates closed) is referred to as the closed state. (B) Table reporting some examples of the available crystallographic structures of the LeuT-fold members (PDB access code specified) with the corresponding conformational states.

In the last few years several atomistic structures of secondary symporters have been obtained by X-ray studies (Fig. 2B). These structures comprise: (i) the leucine transporter, LeuT, a member of the Neurotransmitter Sodium Symporter (NSS) family,^6,7 which allows the selective reuptake of molecules within the synapse, and is therefore a target for neurological disorders (epilepsy, depression, anxiety, Parkinson’s) and substance addiction disorders; (ii) the benzyl-hydantoin transporter Mhp1, a member of the Nucleobase Cation Symporter-1 (NCS1) family,⁸ widely found in plants and bacteria. This plays an important role in salvage pathways for nitrogen balance. Moreover, transporters from the NCS1 family are important in the toxicity of antifungal agents,⁹ and mutations in these proteins can lead to drug resistance; (iii) the betaine transporter, BetP, a member of the Betaine Carnitine Choline Transporter (BCCT) family, which is a family of prokaryotic proteins that specifically mediate the transport of compounds containing a quaternary nitrogen atom, allowing living cells to adapt to variation in osmolarity and temperature;^10,11 (iv) the glutamate transporter, GltPh, a member of the Excitatory Amino Acids Transporter (EAAT),¹² which propagates signals along neural paths, by regulating the concentration of neurotransmitters in the synaptic cleft. Unbalanced concentrations of neurotransmitters lead to Alzheimer’s or Parkinson’s disease, and finally, (v) the bacterial homologue of the sodium/galactose transporter (vSGLT), a member of the Sodium Solute Symporter (SSS) family. In addition to the transport of sugar into cells, this transporter plays a role in water absorption. Thus, the human homologue (hSGLT), besides being a target for type II diabetes, also provides a basis for oral rehydration therapy.⁴ These structures provide insight into the molecular architecture of symporters at different stages of the transport cycle,^2,3,13–15 unveiling some common structural and functional characteristics.

However, this structural information, even supplemented by electrophysiological, biochemical and spectroscopy experiments, is still too fragmentary and incomplete to fully elucidate the general mechanism of this class of transporters. Thus, critical aspects of their molecular mechanism remain not completely understood. In fact, it is often not clear to which stage of the transport cycle that the solved crystal structures refer, or how the different sets of experimental structures are structurally and dynamically linked during the transport cycle. The static picture provided by X-ray crystallography has been recently complemented by distance measurements relying on pairs of spin labels based on a double electron–electron resonance (DEER)-EPR technique. These provide important experimental dynamics insight into the ion-coupling mechanism and time-sequence events of the conformational changes occurring along the transport cycle of different transporters.^16,17

Thanks to recent advances in force field accuracy, the enormous increase of computer power, specifically tuned computational platforms, as well as the development of sophisticated state-of-the-art computational methods, which allow to extend enormously the timescale accessibility, molecular simulations can provide increasingly quantitative information on the kinetic and thermodynamic features of biological systems, becoming a fundamental tool to comprehend at an atomistic level of detail the mechanism of complex biological macromolecules.^18–22 In this respect, a plethora of studies has focused on addressing unclear aspects of the mechanism of the symporters. Sharing the LeuT-fold transporters as a common general mechanism, a single focused study can be translated into a more general omics perspective, providing a unifying mechanistic picture of the Na⁺-symporter superfamily. In the following, we provide an overview of computational studies carried out on the five transporters (SGLT, LeuT, Mhp1, BetP and GltPh) for which experimental datasets have benefited subsequent computationally driven insights, focusing, in particular, on three relevant aspects: (i) the identification and description of sodium-binding sites; (ii) the cooperativity of Na⁺ and substrates at different stages of the binding/releasing mechanism to/from the transporter, and (iii) the large conformational changes underlying the alternating access mechanism.

To facilitate comparisons between these transporters, we used the helix numbering of ref. 6, i.e. starting from the two repeats (TMs 1–5 and TMs 6–10). The additional N-terminal helices are numbered TM(<0) and those at the C-terminal TM(>10), Fig. 1C.

2 Computational methods

In molecular dynamics (MD) a molecule is studied by following its behaviour in time. As such, the forces acting on a system’s particles are calculated, and their time evolution is obtained using a suitable equation of motion. The thermodynamic properties of the system are then computed from averages over sufficiently long trajectories. In classical MD simulations the underlying potential energy surface is an effective empirical potential or force field (FF) approximated by additive (parameterized) many-body terms. MD simulations have found widespread application in computational biology. Despite the use of a simple underlying and computationally cost-effective predefined empirical potential, one of the main limitations of MD remains the limited timescale accessibility of the simulations. Indeed, the standard timescale exploration of a MD run is in the order of tens of nanoseconds or microseconds, while several relevant and interesting biological processes occur on remarkably longer timescales ranging from milliseconds to seconds. A clear example of this is the timescale required by the conformational changes occurring during the inward-to-outward switch of transporters, or more generally, protein folding, biochemical reactions, etc. Indeed, it is very difficult to obtain statistically significant data from full atomic MD simulations alone, although the use of supercomputers specifically designed for biomolecular simulations^23,24 has allowed an enormous extension of the timescale accessible and, therefore, the potentialities of MD simulations. In the present case, long MD simulations may be integrated with elastic network models, which allow unravelling of the intrinsic dynamics of proteins. The latter has been demonstrated to have a role in driving protein/substrate interactions.²⁵ However, plain MD simulations are still unable to overcome large free energy barriers and are thus unable to efficiently explore the free energy landscape. For this reason, computational methods have been developed to overcome free energy barriers in shorter simulation times, and to reconstruct the free energy landscape out of non-equilibrium simulations. Here we will briefly describe some of the methods mentioned in this review.

2.1 Umbrella sampling (US)^26,27

In this approach, a series of initial configurations along a specific reaction coordinate is generated. Each of these states corresponds to a point along the selected degree of freedom, wherein the molecule of interest is harmonically restrained using an umbrella biasing potential. This restraint allows the system to sample the configurational space in a defined region along the reaction coordinate. Each simulated window must slightly overlap with the adjacent ones for a proper reconstruction of the Potential of Mean Force (PMF) curve by using the Weighted Histogram Analysis Method (WHAM).²⁷ One should note that the construction of the umbrella requires prior knowledge of the conformations of interest, which in many cases is not an obvious task.

2.2 Thermodynamic integration (TI)²⁸

This method is used to compute the free energy difference between two states (e.g. A and B) whose potential energies have different dependencies on the spatial coordinates. A coupling parameter λ (with values between 0 and 1) is defined and a series of simulations is set up corresponding to discrete λ values. Thus, the potential energy as a function of λ varies from the energy of system A for λ = 0 to system B for λ = 1.

2.3 Steered molecular dynamics (SMD)^29–31

This method applies an external force to manipulate biomolecules. In SMD the system is pulled along a selected degree of freedom. SMD simulations are equivalent to umbrella sampling when the applied forces are weak, thus change very slowly in time and induce minor overall changes. In contrast, when the forces applied are large the system is out of equilibrium and it is possible to employ a non-equilibrium description for analysis of the free energy. Indeed, in 1997 Jarzynski^32,33 demonstrated that free energy differences can be obtained through exponential averages of irreversible work.

2.4 Targeted molecular dynamics (TMD)³⁴

This approach induces a transition of a subset of atoms of the system from an initial to a final known target structure by applying a steering time-dependent force. At each time step, the Root Mean Square (RMS) distance between the current coordinates and those of the target structure is computed and the force applied depends on the difference between the actual RMS and that calculated evolving linearly from the initial to the target structure.

2.5 Metadynamics (MTD)³⁵

This method was developed in order to escape from local minima in the free energy surface (FES). This allows efficient exploration of the FES, while simultaneously picturing free energy differences/barriers. It is based on the addition of an external history-dependent potential (constructed as a sum of Gaussians) acting on a small number of collective variables (CVs). It has been demonstrated that, in the limit in which the CVs evolve according to Langevin dynamics, the average of the biasing potential added converges to the negative of the free energy, thus providing an optimal bias to enhance transition events.^36,37 A limitation of this method is that the performance of the algorithm rapidly deteriorates as the dimensionality of the CV space increases, since the time required to reconstruct a free energy surface scales exponentially with the number of CVs.

2.6 Bias-exchange metadynamics (BE-MTD)^38,39

To overcome the limitation of MTD simulations, several approaches have been proposed.^38,40–42 Among these, BE-MTD allows reconstructing the free energy using a virtually unlimited number of CVs.³⁸ Namely, this is based on the simulation of several replicas of the system at the same temperature, each biased by a time-dependent potential acting on a different CV. Exchanges of conformations among pairs of replicas are attempted according to the replica-exchange method.^40,42

2.7 Accelerated molecular dynamics (aMD)⁴³

In this method the potential energy landscape is altered by adding a bias potential, which accelerates the escape rates from potential wells, extending in turn the timescale accessible to MD simulations. A continuous non-negative bias boost potential function is defined such as if the true potential is lower than a selected value E, named as the boost energy, then the simulation is performed on the modified potential; while if the true potential is larger than E, then the simulation is performed on the true potential. An evolution of this method consists of a so-called dual-boost mode, where aMD simulations are performed not only boosting the total potential of all atoms but also the dihedral angles.^44,45 This method has been recently applied on a homology model of the human dopamine transporter (hDAT) built on Drosophila melanogaster DAT,^46,47 and has proven to be successful in describing the most important events characterizing the transport process of dopamine and in confirming relevant structural changes observed in the several crystallographic structures described in this review. This approach may represent a fruitful way for future mechanistic investigations of this type of transporters.

2.8 Dynamic importance sampling MD (DIMS-MD)⁴⁸

In this method, bias is dynamically adjusted to enhance sampling of the events of interest, namely, transitions between states separated by relevant free energy barriers. A soft-ratcheting biasing scheme works by a Monte Carlo-like procedure, where each MD step is accepted if it moves the system towards a target state (after defining a progress variable that unambiguously indicates the progression of the system towards the desired state).

2.9 Weighted ensemble path sampling^49,50

This is an enhanced sampling technique that tracks the evolution of a statistical ensemble of trajectories in the conformational space. It is based on the simulation of several stochastic MD runs and on the projection of the coordinates of the selected progress coordinate, assigning them into bins. By iterating the procedure it is possible to reach the target state B from the initial state A in an unbiased manner.⁵¹

Beside the limitation in timescale accessibility, a second delicate issue of classical MD simulations is the reliability and transferability of force fields and, thus, the choice of a specific force field among those available.¹ This choice requires particular care in the modeling of membrane proteins as they need to be simulated in a lipidic environment. Several force field parameters for different kinds of lipids (i.e. POPC, POPE, DOPC, DPPC) have been developed^52,53 along with a suitable computational method for simulating stable membranes (i.e. using semi-isotropic pressure control, surface tension parameters).¹ In the works mentioned in this review, the force fields adopted were mainly CHARMM27 or CHARMM36 with CMAP corrections^54–57 (for both proteins and lipids), or GAFF⁵⁸ (lipids) and AMBER⁵⁹ (protein).

3 In silico identification of sodium-binding sites

The binding of Na⁺ ions (one, two or even three, depending on the transporter type) is a crucial event for secondary transporter function, as it allows progression along the mechanistic cycle. However, the location and the atomistic details of Na⁺ ion binding sites are often unclear. This is in part due to the limited resolution of the currently available crystallographic structures and also to the similarity of the scattering factors between Na⁺ ions and oxygen atoms of water molecules. MD simulations have largely contributed to provide structural insight on the location of Na⁺ binding sites at different stages of the transport cycle. The nomenclature of these binding sites is Na1, Na2, and Na3. Interestingly, from the X-ray structures available to date it appears that these ions are tightly bound by protein residues in the OFop and OFoccl conformations, while they are difficult to detect in the IF ones. Moreover, in the case of binding sites in IF conformations, suggested on the basis of bioinformatics considerations, the ions are loosely surrounded by transporter residues.

In this section we will briefly review some of the recent studies addressing this important aspect for different LeuT-fold members.

3.1 Symporters working with one Na⁺ ion

vSGLT. As mentioned above, the Na⁺ stoichiometry of sodium symporters ranges from 1 to 3 ions. vSGLT and Mhp1 transporters belong to the simplest case with only the Na2 site occupied by a Na⁺ ion. This site is conserved among many distantly related families of secondary symporters (vSGLT, Mhp1, BetP, GltPh) and it is believed to be at the basis of the molecular mechanism of cotransport.

In the crystal structure of vSGLT, obtained from Vibrio parahaemolyticus and captured in an IF conformation,⁴ galactose (Gal) binds to the protein (Fig. 1), while the Na⁺ ion was not detected and a plausible ion-binding site was proposed on the basis of a structural comparison with the LeuT structure and by mutational analysis.^4,6 MD simulation studies, however, suggested that the crystal structure represents an ion-releasing state of the transporter since Na⁺ departs from the proposed binding site after a few ns of MD simulation (within 10 ns).^60–62

Recently, we proposed an ion-retaining state of the transporter, identifying a stable Na⁺ binding site by metadynamics simulations (Fig. 3). Starting from the experimentally proposed binding site, we explored the FES looking for a stable minimum representing the Na⁺ binding site. At this minimum, a Na⁺ ion is coordinated by A62, I65 and S365, which bind to Na⁺ with their carbonyl oxygens (the first two) and hydroxyl oxygen (the latter). Three water molecules complete the Na⁺ coordination sphere.⁶³ The coordination distances Na⁺–O are in the range of 2.3–2.6 Å and a water molecule H-bonds simultaneously to D189. Besides some small local rearrangements of the residues, this ion-retaining state (named hereafter as LC1) is obtained thanks to a kink in TM1 with respect to the structure captured crystallographically (Fig. 3). This site is consistent with the observation of Faham et al.⁴ pointing to a key role of S365 in the Na⁺-dependent transport of Gal.

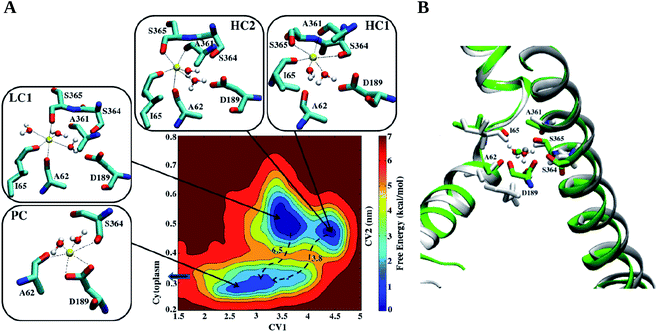Fig. 3 Na⁺ binding site in an IF conformation of vSGLT. (A) Free energy surface of vSGLT in an IF conformation with the structural features of the Na⁺ coordination states shown for the three minima. The axes are: CV1, the coordination number of the Na⁺ ion with the five closest residues of the binding site (A62, I65, A361, S364, and S365) and CV2, the distance between Na⁺ and D189. Among the different states, LC1 was found to be the most stable. Here, the ion is coordinated by 3 residues (A62, I65, and S365) and 3 water molecules. Except for the hydroxyl oxygens (Oγ) of the serines, the other residues coordinate the ion with carbonyl oxygens. The barriers on the path arrows are expressed in kcal mol⁻¹. (B) Overlap of crystal structure, colored in light gray, and LC1 conformation, in green. The most remarkable difference concerns the position of D189, much closer to the binding site in LC1. Reprinted with permission from ref. 63. Copyright 2013 American Chemical Society.

Mhp1. In the OFoccl crystal structure of Mhp1 a single positive peak in the electron density difference map was observed at a position structurally equivalent to Na2 of LeuT (surrounded by carbonyl oxygens of A38, I41, A309, and the side chain hydroxyl atoms from S312 and T313 in TM8) (Table 1). The Na⁺ positioned at this density remained bound during 100 ns MD simulations.⁶⁴ In contrast, multiple MD simulations conducted on the Mhp1 IF crystal structure and with the Na⁺ ion positioned on the basis of structural comparisons with the LeuT structure, showed that Na⁺ dissociation occurs within 2 ns, consistent with what was observed for vSGLT.⁶⁴

Table 1 Distances (expressed in Å) for sodium binding sites in the crystal structures of several Na⁺ symporters. We report the residues identified in the crystal structures within 3 Å from the ion. DAT is the very new crystal structure of the dopamine transporter from Drosophila melanogaster.⁴⁶ Adapted with permission from ref. 63. Copyright 2013 American Chemical Society

Symporter	Source	Ion	Crystallographic distances between Na^+ ion and coordinating ligands
a The sixth coordinating ligand in LeuT Na1 site is represented by the substrate, Leu (2.52 Å).
LeuT^a			A22 (O)	N27 (Oδ)	T254 (Oγ)	T254 (O)	N286 (Oδ)
	2A65 (out)	Na1	2.11	2.18	2.28	2.39	2.54
			G20 (O)	V23 (O)	A351 (O)	T354 (Oγ)	S355 (Oγ)
	2A65 (out)	Na2	2.21	2.11	2.25	2.21	2.32
GltPh			G306 (O)	N310 (O)	N401 (O)	D405 (Oδ1)	D405 (Oδ2)
	2NWX (out)	Na1	2.70	2.61	2.73	2.71	2.77
GltPh			T308 (O)	M311 (S)	S349 (O)	T352 (O)
	2NWX (out)	Na2	2.75	3.43	1.96	2.48
GltPh			G306 (O)	N310 (O)	N401 (O)	D405 (Oδ1)
	3KBC (inw)	Na1	2.16	2.50	2.99	2.66
GltPh			T308 (O)	M311 (S)	S349 (O)	T352 (O)	I350 (O)
	3KBC (inw)	Na2	2.66		2.26	2.58	2.65
Mhp1			A38 (O)	I41 (O)	A309 (O)	S312 (Oγ)	T313 (Oγ)
	2JLN (out)	Na2	2.62	2.66	2.09	2.53	2.77
	2JLO (occl)	Na2	2.84	2.79	2.56	2.62	2.65
	2X79 (inw)	Na2	Residues far apart from each other, no ion
BetP			A147 (O)	M150 (O)	F464 (O)	T467 (Oγ)	S468 (Oγ)
	4AIN	Na2	2.17	2.48	2.33	2.31	2.36
DAT			A44 (O)	N49 (Oδ)	S320 (Oγ)	S320 (O)	N352 (Oδ)
	4M48 (out)	Na1	2.31	2.73	2.44	2.40	3.00
			G42 (O)	V45 (O)	L417 (O)	D420 (Oδ)	S421 (Oγ)
	4M48 (out)	Na2	2.28	2.29	2.34	2.56	2.36

---

3.2 Symporters working with two Na⁺ ions

LeuT. Structural studies on LeuT revealed the existence of an OFoccl state where two Na⁺ ions bind at sites Na1 and Na2 and the cotransported solute structurally couples to Na1 (Table 1).⁶ In order to elucidate the role of these sites in the conformational dynamics of ion/substrate uptake/release, extensive MD simulations have been done.^65,66 These revealed that Na⁺ at the Na2 site was stable over 100 ns long MD simulations either in the presence or absence of the substrate. Moreover, PMF calculations and quasi-harmonic analysis of LeuT showed that in the presence of Na⁺ at Na2, the conserved residue T354 adopts a single, stable rotameric conformation (free energy barrier, ΔG^#, for the rotation up to 25 kcal mol⁻¹), while two degenerate states are adopted in its absence (ΔG^# up to 10 kcal mol⁻¹).⁶⁵ Thus, the release of the Na⁺ ion from Na2 is modulated by the rotameric flexibility of T354 and also by local hydration effects, since a wire of water molecules spanning from the cytoplasm to the Na2 site was observed. This may facilitate ion release and may lead to the rearrangement of the interhelical network. Importantly, these simulations also showed that the absence of Na⁺ at Na2 increases the fluctuations of Na⁺ at Na1 and of the substrate, hence facilitating the opening of the LeuT intracellular thin gate (formed by R5 and D369).

In a later study,⁶⁶ Zhao et al. addressed the role of Na⁺ bound to Na1 in the conformational dynamics of the OFop and OFoccl states of LeuT. μs-Long MD simulations starting from the OFoccl state with Na⁺ ions coordinated in both Na1 and Na2 and in the absence of substrate showed a spontaneous transition of the extracellular vestibule to the OFop conformation. The probability of assuming this conformation is enhanced by the absence of Na⁺ at Na1, suggesting that this ion contributes to stabilizing the OFoccl conformation.⁶⁶ PMF calculations show that in the absence of the substrate (leucine), Na⁺ can still bind to Na1 in the OFop conformation, although the free energy minimum is about 6 kcal mol⁻¹ higher than in the presence of the substrate. Binding enthalpies for the two ions obtained with Molecular Mechanics Poisson Solver Surface Area (MM/PBSA) calculations show a similar binding affinity of Na⁺ for the two sites, but a significant correlation exists between large scale conformational changes (from occluded to open state) and the Na⁺ binding affinity towards Na1, with the first being thermodynamically favored.⁶⁶

Lately, Zomot et al.⁶⁷ performed extensive MD simulations (>20 μs) on an OF conformation of LeuT, directly observing the series of events which leads from OFop to OFoccl transition, along with substrate binding/dissociation from/towards the extracellular site. Interestingly, they pinpointed that this process is mediated by the coupled dynamics between substrate and ion binding and that the binding of Na⁺ ions switches among several peripheral sites named here as Na1′ and Na1′′. These simulations observed Na⁺ in Na2 to be the first ion that dissociates completely in the OFoccl conformation (0.25 μs) either in the presence or absence of the substrate. In contrast, Na⁺ in Na1 either remained bound (1–1.5 μs) or it moved towards a different site, designated as Na1′, composed by the carboxylate of E290, the side chain of N27 and N286, and the hydroxyls of Y47 and/or T254. This site is occupied only along the exit route from Na1, while in the entry pathway from the extracellular side a second new Na⁺ binding site (named Na′′) was identified. The latter is located in the same cavity of the substrate binding site; it is 5 Å away from the Na1 and Na2 sites and is composed of the hydroxyls of S256, S355, and by N21 backbone and/or side chains.

BetP. Khafizov et al.⁶⁸ employed MD simulations in parallel with biochemical and electrophysiological measurements (mutagenesis, transport and binding assays) to characterize Na⁺-binding sites in the closed state of BetP for which experimental information was lacking. They initially placed Na⁺ in the Na2 site according to the position of a distinct positive peak revealed by the analysis of the F_o − F_c difference density map of the occluded conformation X-ray structure. Multiple 70 ns-long MD simulations confirmed the presence of the Na2 site between the TM1 and TM8 helices. This was also supported by the fact that the single and the double mutations T467A and S468A lead to a decrease in the affinity of Na⁺ (an increase of the Michaelis–Menten (K_m) and the dissociation (K_d) constants was observed), and a complete abrogation of Na⁺ binding, respectively. In contrast, for the location of Na1 there were no experimental hints and they proposed its location on the basis of the transporter pseudosymmetry (i.e. the five-helix inverted repeat fold). MD simulations revealed that in the closed state Na⁺ remains coordinated in this putative site (formed by the side chains of T246 and T250, the backbone carbonyl of T246) establishing a cation–π interaction with F380 and binding a single water molecule (Fig. 4). Mutagenesis experiments of residues T246, T250 and F380 showed remarkable variation of K_m, confirming their involvement in Na⁺ binding.

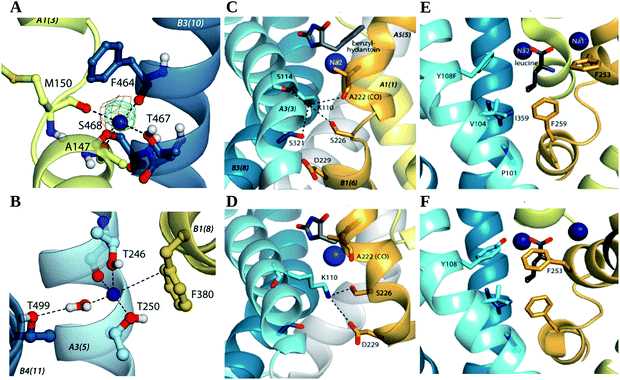Fig. 4 Ion binding sites of Betp, Mhp1 and LeuT. (A and B) Sodium binding sites in BetP predicted from structural analysis and MD simulations. Close-up views of simulation snapshots. (A) Simulation snapshot of the Na2 site overlaid with the F_o − F_c difference density map before placing the ion (contoured at 3.0σ, green) and the 2F_o − F_c map (contoured at 1.0σ, purple) for PDB 4AIN. (B) Simulation snapshot of the Na1′ site. (C and D) Na⁺-binding sites in structures of OFop and IFop conformations (PDB 2JLN and 2X79) of Mhp1, focusing on the location equivalent to that of Na1′ in BetP. The substrate benzylhydantoin (gray sticks) and one sodium ion (blue sphere) from an OFoccl (PDB 2JLO) are included for reference. (E and F) Structures of LeuT; (E) in OFop (PDB 3TT1) and (F) a Na2-deletion mutant of LeuT bound to an antibody fragment in an IFop (PDB 3TT3). Bound leucine (gray sticks) and two sodium ions (blue spheres) from an OFoccl conformation (PDB 2A65) are shown for reference. The position approximately equivalent to that of Na1′ in BetP is between residues P101, V104, F259, and I359 of LeuT. Image from ref. 68.

In a later study,⁶⁹ Perez et al. characterized the sequential formation of substrate and sodium binding sites in the OFop state of BetP. Using a combination of structural studies and MD simulations, they unveiled that the binding of the substrate leads to the occlusion of the Na⁺ sites, especially of Na2, leading to its progressive dehydration and reshaping.

3.3 Symporters working with three Na⁺ ions

GltPh. Glutamate transport by the human excitatory amino acid transporters (EAAT1) and their archaeal counterpart (GltPh) depends on three Na⁺ ions. However, only two ion binding sites have been identified in its crystal structure (Table 1). MD simulations combined with free energy perturbation (FEP) calculations pinpointed a third Na⁺ binding site (Na3) with a Na⁺ coordination shell composed by oxygens from the T92, S93, N310, and D312 (one oxygen) side chains and the backbone of Y89.⁷⁰ The authors also confirmed by site-directed mutagenesis and transport experiments the importance of T92 and S93 and their involvement in Na3 for GltPh and its human counterpart, EAAT1.

4 Cooperativity and role of Na⁺ in the binding and releasing mechanism of substrates to/from their transporters

An in depth comprehension of the synergism played by the ions and the ligand in the translocation mechanism across symporters is still far from being fully understood. In this respect in silico studies can offer unique atomistic insights to directly observe whether the ions may induce local and/or distal conformational changes, reshaping the free energy landscape, allowing the binding/dissociation of the substrates to/from their binding sites, and how Na⁺/ligand interplay occurs at different stages of the transport cycle.

4.1 vSGLT

The dissociation mechanism of galactose from the IF conformation of vSGLT has been addressed by MD simulations.^61,62,71,72 In these studies, Gal release can occur either spontaneously around 100 ns or by applying an external force. These works led also to contradictory conclusions on the free energy profile associated with substrate dissociation from the binding site identified crystallographically and on the role of Y263 as a possible inner gate.^61,62,71 Zomot et al. showed that Gal exited the protein only by applying an external force (SMD simulations) to the substrate, and after a rotameric transition of the Y263 side chain. This residue was, therefore, believed to be the first gate along the dissociation path, while the role of the second gate was attributed to Y269 encountered later along the path.⁶¹ Consistent with these findings, Watanabe et al. hypothesized that sodium exit triggers substrate release after the new rotameric conformation acquired by Y263 and that Gal has to overcome a very small barrier (ΔG^# ∼ 2 kcal mol⁻¹) to be released towards the cytosol.⁶² In contrast, Li and Tajkhorshid depicted a strikingly different scenario.⁷¹ By combining unbiased MD and SMD simulations, they identified a curved translocation pathway for Gal dissociation. In this path Gal moves around Y263, and its exit requires no gating event. This finding led to the conclusion that the crystal structure represents an IFop state of the transporter.⁷¹ Unfortunately, experiments do not help in solving this puzzling mechanism of substrate/ion release, as data on these controversial points as well as on the order of dissociation of the two ligands towards the cytosol are fragmentary.⁷³

In an attempt to shed light on this intricate scenario, we performed extensive BE-MTD simulations for a total of 1400 ns.⁷⁴ By biasing several collective variables to simultaneously promote the dissociation of both Na⁺ and Gal, we established on the fly the reciprocal influence of the cotransported ligands during their dissociation, also characterizing at the same time the kinetic and thermodynamic signatures of the process.⁷⁴ Importantly, the starting structure of our study is that of the IFoccl conformation in an ion-retaining state obtained in our previous study.⁶³ Our simulations unambiguously show that the Na⁺/Gal interplay along the dissociation path is minimal and limited only to the initial displacement of both Na⁺ and Gal from their binding sites (Fig. 5). This suggests that the binding of the ion in a stable site helps hamper the release of the substrate towards the intracellular side. Surprisingly, our simulations also reveal that the dissociation of both Na⁺ and Gal occurs with a ΔG^# of about 11–12 kcal mol⁻¹, and that at the rate limiting transition state both ligands are more than 10 Å apart from their binding sites (Fig. 5D and E). For these reasons, we updated the hypothesized alternating access mechanism by adding a branch path to account for the independent, uncorrelated and energetically competitive dissociation of Na⁺ and the substrate towards the cytoplasm. Moreover, our simulations of the Y263F mutant showed that Y263 has no gating role, although the mutant reshapes the free energy landscape of the first (main) minimum, affecting in turn Gal dissociation.⁷⁴

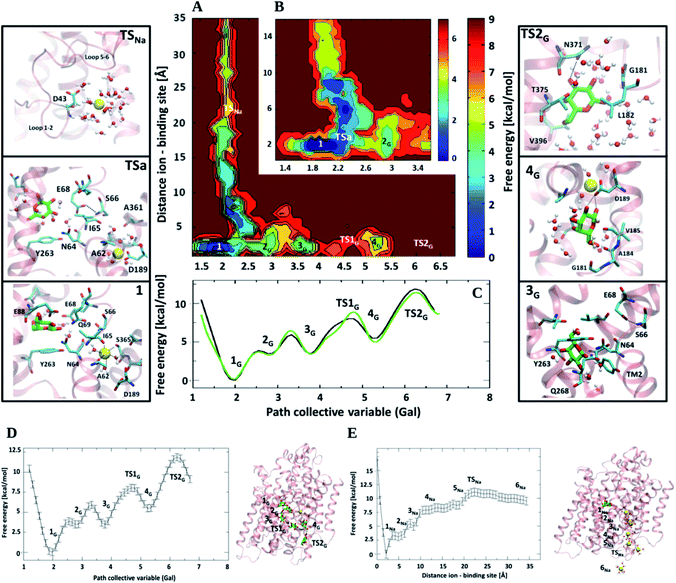Fig. 5 Cooperativity in the release mechanism of vSGLT. (A) 2D-free energy surface (kcal mol⁻¹) depicted with respect to the distance between Na⁺ and its binding site, and the galactose exit path. (B) Close-up view of the initial part of the FES. On the two sides of the image, the most relevant structures corresponding to minima and transition states (TS) are depicted (Gal in green and red sticks). (C) Projection of the free energy (kcal mol⁻¹) along the path collective variable representing Gal exit. Black and green lines correspond to the simulations carried out in the presence or absence of Na⁺. (D) Exit pathway of galactose. On the left is shown the free energy profile along the path collective variable representing Gal exit. On the right, the position of Gal at different minima along the exit pathway on the top of the protein is reported. The latter is depicted by pink cartoons, the substrate as a licorice color, while Na⁺ is depicted as a yellow sphere. The dissociation path is connected by dark dashed lines. (E) Exit pathway of the Na⁺ ion. Free energy profile projected along the distance ion-center of mass of its binding site is displayed. On the right the position of the different states along the exit path of Na⁺ are shown on the top of the protein. Image from ref. 74.

In very recent work, Li et al. observed the presence of a second Gal binding site in vSGLT.⁷⁵ Indeed, while the crystallographically identified Gal binding site, S1, aligns to a more extracellular position compared to the central binding site of LeuT, the second Gal site (named S2, in a binding pocket below Y263) aligns to the central site of LeuT. The two sites have different TM compositions. By using computational modeling (i.e. induced fit docking and 100 ns-long unbiased MD simulations) together with experiments to estimate the molar binding stoichiometry, Li et al. indicated that vSGLT can simultaneously bind two substrates. Mutations of residues in S2 lead to a reduction of binding stoichiometry.⁷⁵ These findings were also observed for a proline transporter (PutP), suggesting that substrate transport by these proteins may require both substrate binding sites.

4.2 Mhp1

Simmons et al. combined MD simulations with experimental studies (crystallography, biochemical assays, design/synthesis of novel ligands and mutagenesis) to elucidate substrate binding events in Mhp1.⁷⁶ They showed that a 5-substituted hydantoin substrate binds at the interface of the bundle (TMs 1, 2, 6, 7) and hash (TMs 3, 4, 8, 9) domains. PMF calculations indicate that in this site the substrate preferentially assumes an extended conformation with respect to the U-shaped one. This study also revealed that upon substrate binding, TM10 (the thin extracellular gate) has to bend over the substrate, assuming a closed position (i.e. occluded conformation), which allows transport to occur. Instead, the binding of a bulky inhibitor locks TM10 in the open position. In this manner transport does not take place and the structure captured in the presence of the inhibitor represents a non-active conformational state of Mhp1. Simmons et al. observed that the substrate interacts mainly with the hash motif, different to other 5HIRT superfamily members for which specific interactions between the substrate and the bundle were also observed.^4,6,11 As a consequence of this limited interaction pattern, most probably the switch from an OF to an IF conformation is determined by a predominant rigid body rotation of the hash motif relative to the bundle domain, in contrast to other LeuT-fold family members where a larger flexibility of the bundle domain helices around the unstructured regions of TM1 and TM6 is present and more complex conformational changes are at the basis of the OF-to-IF conformational switch (Fig. 1). Consistent with these findings, a recent study based on double electron–electron resonance (DEER) spectroscopy revealed that IF and OF structures of the Mhp1 transporter are indeed intermediate states of the transport cycle.¹⁶ This study pointed out that Na⁺ binding to Na2 at the IF conformation does not change the energetics of the IF to OF transition, in contrast to what is observed for LeuT. This suggests that the mechanism of single and double Na⁺-dependent transporters may differ in terms of how transport depends on ion gradient/ion binding.

Zhao et al. characterized how substrate and ion binding drives the conformational changes necessary for substrate transport.⁷⁷ By using TMD to generate large structural transitions of the transporter, followed by a multi-dimensional path sampling (string-method) and by US free energy simulations, the authors pinpointed the main thermodynamic and kinetic features governing the ion-dependent conformational dynamics of the Mhp1 transport cycle. They observed that: (i) the free energy difference between the IF and OF conformations in the absence of substrate and ions is very little, pointing to a stochastic gating of the transporter in the apo form; (ii) Na⁺ binding at the Na2 site reshapes the FES and modulates substrate binding; (iii) substrate binding determines the closure of the extracellular thin gate and hampers Na⁺ dissociation towards the extracellular side; (iv) substrate binding also stabilizes the binding of Na⁺, which otherwise is energetically disfavored in the OF apo form; (v) the Na2 site may also play a key role in intracellular thin gate modulation by altering its interactions with TM5 (in particular with N168, a residue reminiscent of the role assigned to D189 in vSGLT transporters⁶³ and E192 in LeuT); (vi) in analogy to LeuT, two possible substrate binding sites (S1 and S2) were identified, with S2 being less thermodynamically stable by 5 kcal mol⁻¹, and (vii) the transporter rearranges from the IFoccl to the IFop conformation where Na⁺ dissociates towards the intracellular side and the transporter opens its thick gate in a concerted manner (Fig. 6).⁷⁷

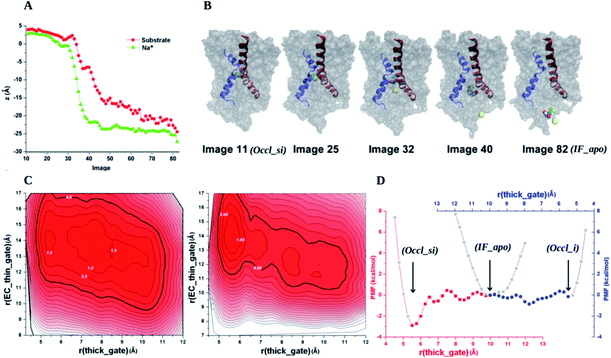Fig. 6 (A) Sequence of Na⁺ and substrate release for the transition from an occluded state with both substrate and ion bound (Occl_si) to an IF apo state (IF_apo) from the path obtained with a string method with swarms of trajectories. In this label, the s and i subscripts are present if the substrate and/or the ion are bound to the transporter, respectively. Occl refers to an occluded state. The path consists of 72 images with Image 11 in Occl_si and Image 82 in IF_apo states. The values of the z-coordinates as a function of the image number are shown for Na⁺ (green triangles) and the substrate (red circles). (B) Some images are shown. TM1 (residue 23 to 55) and TM8 (residue 296 to 329) are shown in blue and red cartoons respectively, with the remainder of the Mhp1 protein shown as a grey surface representation. Na⁺ (yellow ball) and the substrate (cyan, white, and red balls) are also shown. (C) Conformational stability vs. gating dynamics. 2D-PMF profiles on the thick gate, r(thick_gate) (whose values around 5.5 Å indicate an OF state, those around 10 Å an IF state), and EC thin gate, r(EC_thin_gate) (that accounts for the movement of this gate, the higher the more open) are calculated from umbrella sampling MD simulations. The transitions between Occl_si and IF_apo and between IF_apo and OF with only the ion bound (Occl_i) are shown in the left and central panel respectively. Darker colors indicate more favorable conformations (contour lines of 1 kcal mol⁻¹). The areas that are within 4 kcal mol⁻¹ are circled by darker contours. (D) 1D-PMF profiles integrated from the panels in (C) are shown as red squares and blue circles (red and blue x-coordinates correspond to the red and blue profile, respectively). The profiles represent the stability of the transporter as a function of the r(thick_gate) during the two transitions. The two profiles are placed side to side with an overlap around the IF_apo state, which is set to 0 for PMF, so that they provide an overall stability picture for the transitions from Occl_si (r(thick_gate) 5.3 Å in the crystal structure, red) to IF_apo (r(thick_gate) 10.2 Å in the crystal structure, red and blue) to Occl_i (r(thick_gate) 5.4 Å in crystal structure, blue). Image adapted from ref. 77.

4.3 LeuT

The LeuT transporter is probably the best structurally characterized member of the LeuT-fold family as it has been captured in three different conformational states (OFop, OFoccl and IF) in the apo form as well as in the presence of several substrates, inhibitors and natural ligands. In a recent review, Loland gave a comprehensive picture of the binding sites and binding modes of the substrates and inhibitors of the protein.⁷⁸ A second substrate binding site was suggested for the OF conformation by computational studies. Indeed, SMD simulations in which the ligand was pulled from the principal binding site (S1) towards the extracellular environment identified a peripheral site (S2), around 10 Å above S1.⁷⁹ S2 was confirmed by binding and flux experiments. This S2 site seems to be homologously corresponding to that of Mhp1.⁷⁷ Indeed, for both these transporters the S2 site is located around 9–10 Å above the S1 site (proteins in an OF state). Concerning vSGLT (IF conformation), instead, the location of the sites is not the same, as previously mentioned. S2 is indeed below S1, probably due to a different state of the transporter. Although observed in different experimental and computational studies, the existence of S2 is still a matter of debate.⁷⁸

30 ns-long MD simulations⁷⁹ in the apo and holo forms for the substrate and in the presence and absence of Na⁺ revealed that sodium ion binding opens up substrate access to S1. Binding of the leucine substrate to S1 further stabilizes this site and screens it from the entrance of water molecules. MD simulations (10 ns) revealed that two leucines can simultaneously occupy both S1 and S2 sites, and that upon binding to S2 the substrate allosterically triggers the intracellular release of sodium ions and the second substrate molecule from S1. According to this study, the following events take place: (i) Na⁺ binding increases the affinity of the substrate for S1 (i.e. no substrate binding is observed in the absence of Na⁺); (ii) upon leucine binding to S1 the extracellular gate (F253, R30, and D404) closes, trapping the substrate in S1; (iii) Na⁺ and the substrate are thus occluded in Na1 and S1 sites, while the second Na⁺ can be released from Na2 towards the intracellular side, and (iv) Na⁺ and leucine remain in Na1 and S1 until a second substrate molecule binds to S2, coadjuvating their dissociation.

In a subsequent study Zhao et al., by performing μs-long MD simulations, hypothesized that the binding of the Na⁺ ion in Na2 leads LeuT to a more OF open state, facilitating the entrance of the substrate to S1.^65,66 Instead, the release of Na⁺ from Na2 enhances the closing of the extracellular thin gate and the opening of the intracellular one.⁶⁵

Starting from LeuT in an OF conformation, Cheng et al. characterized the sequence of events from substrate binding to an OF state to its release from an IF conformation by using a complex computational protocol based on TMD, aMD, and unbiased MD simulations (up to a total of μs-long MD).⁸⁰ In particular, they focused on the binding of the alanine substrate, which is transported by LeuT more efficiently than leucine, to both S1 and S2 sites in the OF state. Interestingly, this study pinpointed S1 as a high affinity binding site, and showed that alanine binding to S1 determines a closure of extracellular gate (by a rotation of F253 and the formation of the salt bridge R30–D404). They also revealed that the binding affinity of the substrate in S2 depends on the conformational state of the transporter, this affinity being larger in the IF conformation. In a subsequent study the same authors completed the characterization of the substrate translocation mechanism, elucidating the series of events associated with substrate and ion translocation to the cell.⁸¹ These involve: (i) substrate recognition, (ii) the closure of the extracellular gate upon substrate/cation binding, (iii) a series of structural rearrangements of TM helices to proceed to a holo-occluded state, (iv) opening of the intracellular gate, release of substrate and ions, (v) closure of the intracellular gate, and (vi) transition back to a highly stable apo-occluded state, which is proposed to precede the final transition to an OFop state, resuming the transport cycle (Fig. 7). In this study the holo-occluded and apo-occluded states were identified for the first time. The authors also highlighted the involvement of the N-terminal segment in stabilizing, and possibly regulating, the functional transitions taking place along the transport cycle. Remarkably, in this study, the release of the substrate occurs before that of ions during the transition from the IFoccl to IFop, differing from what was observed for other transporters (vide infra).

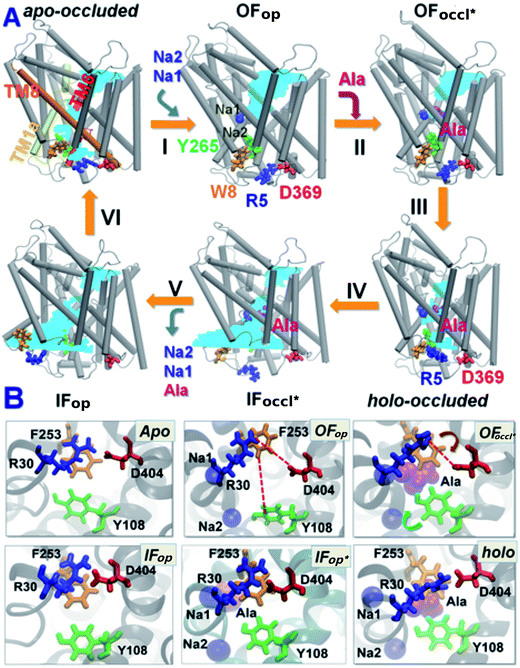Fig. 7 Conformational states visited by LeuT during its transport cycle and corresponding hydration patterns and changes in interactions at IC and EC gates. (A) Six states, labeled, are distinguished, including three newly determined ones: holo-occluded, inward-facing substrate-bound open (IFoccl*), and apo-occluded. The association/dissociation of the two putative IC gating pairs, R5–D369 and W8–Y268–Y265 (shown in licorice), distinguishes the OF and IF states, along with changes in TM1 and TM6 orientations. Hydrated regions are indicated by blue shaded areas. (B) Two EC gates R30–D404 and F253–Y108 exhibit closed or open (indicated by red dashed line) conformations depending on the LeuT state. At least one of the EC gates is closed in all states, except in OFop. In holo-occluded and apo-occluded states, the substrate binding site is practically occluded to both EC and IC environments, with at least one EC gate and one IC gate being closed concurrently. An asterisk indicates substrate/ion-bound states. Image adapted from ref. 81.

Finally, Zomot et al. observed an increased occupancy of several sodium binding sites in the OF conformation of LeuT.⁶⁷ In their extensive MD simulations they showed that Na⁺ binding to Na1′′ induced an opening of the extracellular vestibule, which is mostly closed in its absence, while Na⁺ binding to Na2 had no effect on the dissociation of either leucine or alanine from S1. Interestingly, alanine, which binds to LeuT with a lower affinity than leucine (but, as previously mentioned, is translocated with a higher turnover rate), escapes from the OFop conformation within 50 ns, never occupying S2. In contrast, leucine departs after 1 μs from S1, exiting the protein or binding in the S2 region. When alanine is bound to S1, Na⁺ remains coordinated at Na1 for the entire simulation time (0.5 μs), while Na⁺ dissociates from Na2 within 10–100 ns and remains in the Na1′′ site for 0.2 μs after the dissociation of alanine. In the presence of leucine, Na1 remains stably bound or moves transiently to Na1′ during substrate dissociation, while Na⁺ dissociates from Na2 after the substrate.⁶⁷

4.4 GltPh

In one of the first studies on the GltPh transporter, Shrivastava et al. described a series of occurrences that drive the recognition and binding of a substrate to the OF conformation of the transporter by performing classical MD simulations.⁸² They identified a helical hairpin (HP2) as the extracellular gate, which undergoes large movements and modulates the diffusion of the substrate towards the binding site.⁸² In subsequent work, PMF calculations along the path identified by SMD simulations revealed two free energy barriers, each of 15 kcal mol⁻¹.⁸³ The first barrier is overcome thanks to the interaction between the substrate (here, aspartate) α-carboxylate group with the sodium ion in Na2. This is modulated by a momentary departure of Na⁺ from its binding site. Na⁺ in Na1, instead, comes into play in the second phase, and remains “coupled” to the substrate until its release towards the cytoplasm.

A very detailed study, based on metadynamics simulations, characterized the mechanism of substrate uptake from the synaptic cleft, internalization and release in the intracellular medium, together with the role of the ions during these processes.⁸⁴ Grazioso et al. assigned different roles to the two ions: while Na⁺ in Na1 along with the substrate stabilizes the closed conformation of HP2, Na⁺ in Na2 locks GltPh in a conformation competent for substrate internalization (Fig. 8). A set of metadynamics simulations based on path collective variables⁸⁵ were done to study the transition from OFop to OFoccl, as well as from IFoccl to IFop, while simultaneously considering the dissociation of aspartate towards the synaptic cleft and the intracellular medium, respectively. The simulations were done on both the apo or holo forms of the transporter and in the presence and absence of Na⁺ ions at the different binding sites. Interestingly, the binding of Na⁺ in Na1 induces a remarkable change of the free energy surface leading to a conformational change between OFop and OFoccl states, which facilitates substrate uptake. The subsequent binding of aspartate determines a modest stabilization of the OFoccl conformation, while only the binding of Na⁺ at Na2 locks the substrate in a conformation competent for its internalization. The release of aspartate from the IF conformation occurs in reverse order. The binding of the substrate and both ions lead to a very stable IFoccl conformation; the release of Na⁺ from Na2 induces a rearrangement of HP2 and allows HP1 to assume an intermediate conformation between the open and closed states. The release of aspartate further increases the mobility of HP1, and finally the dissociation of both ions leads HP1 to fluctuate between conformations ranging from IFoccl to IFop. Interestingly, aspartate binding from the extracellular side comes along with the formation of metastable states, while these states do not appear during its release towards the cytoplasm. Remarkably, the authors of this study have also calculated the free energy profile which comes along with the transport events described above (Fig. 8).

Fig. 8 The FES at various stages of the Asp and Na⁺ ion binding process. The FESs of the OFoccl-to-OFop transition using different stoichiometry of ligands bound to GltPh are shown. Left (external cycle): (A) transporter only, (B) transporter and an internal sodium ion (Na1 site), (C) transporter, one sodium ion (Na1 site), and Asp, (D) transporter, Asp, and both sodium ions (in Na1 and Na2 sites). Right (internal cycle): (A) transporter, Asp, and two Na⁺ ions, (B) transporter, Asp, and one Na⁺ at Na1, (C) transporter and one Na⁺ at Na1, and (D) transporter without any ligand. The energy separation between contours is 1 kcal mol⁻¹. Each tick mark on the x axis represents one s unit. All FESs are represented in a y range of 0 to 5.5 Å. Adapted with permission from ref. 84. Copyright 2012 American Chemical Society.

5 Alternating access mechanism

Understanding at an atomistic level of detail the mechanism of the outward-to-inward facing conformational switch of sodium symporters is the most challenging mechanistic objective to address computationally concerning this type of proteins. These indeed do undergo large conformational transitions coupled to small local rearrangements. Several groups have focused on this issue for different LeuT-fold family members.^{7,11,51,64,76,81,86–92} However, computational studies of this process are still fragmentary and hampered by the timescale accessible to classical MD simulations. In fact, this large conformational transition occurs in the range of between hundreds of ms to seconds, which is currently not reachable by standard MD simulations. Biased MD simulations have been extensively used to address this problem, but the complexity of the conformational transitions occurring during OF to IF switching requires an oppositely tuned biasing protocol, and in some cases system-specific reaction coordinates in order to characterize the process at a qualitative or semi-quantitative level. Some hints on the structural determinants driving these complex conformational changes can be provided by a detailed analysis of protein internal dynamics,²⁵ recently applied to the dimeric form of this kind of transporters.⁹³

5.1 LeuT

Forrest et al. proposed a simple mechanism named ‘rocking bundle model’ to explain how ion-coupled solute flux works in symmetrical transporters.^86,87 Observing the OF structure of LeuT, they defined a four-helix bundle, consisting the first two helices of each repeat (TMs 1, 2, 6, 7), and a scaffold (TMs 3, 4, 8, 9) that surrounds the bundle protecting it from the lipidic membrane (see Fig. 1). Based on the intrinsic symmetry of LeuT, they generated a model of IF conformation (which was unknown at that time) simply by swapping the conformation of the two repeats. The greatest change they faced in comparing the OF crystal structure and the modeled IF conformation was the different tilt (about 25°) of the bundle with respect to the scaffold. According to the rocking bundle model, the binding sites should be located at the interface between the moving bundle and the stationary scaffold, so that the ligand can control the orientation of the bundle through direct interactions. The bundle, characterized by TM2 and TM7 (as semi-rigid splints) behind the broken TM1 and TM6 helices, has short loops, quite packed, that move essentially as a unit and thus ensure the integrity of the closer binding sites. The long, tilted TM3 and TM8 curve slightly towards or away the binding site in the IF model or the OF crystal structure, respectively.

The first computational attempt at addressing the OF to IF transition by computer simulation was done by Shaikh et al.⁸⁹ before the structure of the LeuT IF conformation was solved crystallographically. The authors built the IF conformation by homology modeling using vSGLT as a template structure.⁸⁹ Then, by doing TMD (50 ns) followed by 20 ns of classical MD, they forced the switch from the OF to the IF conformation to occur. Interestingly, they observed that: (i) two salt bridges (R5–D369 and E6–R375) have to break to allow the formation of the IF conformation; (ii) large motion of TM1 and TM6 occurs during the switch and, besides the helices lining the lumen, TM2 and TM7 may also facilitate the movement of TM1 and TM6; (iii) a conformational coupling of the symmetry-related subunits, and (iv) during the switch, structural modification occurred in only one of the two domains (TMs 1–5), suggesting that conformational change in one of the two inverted repeat units may be sufficient to induce a transition in the rest of the protein.

In 2012 Krishnamurthy et al. solved the structure of LeuT in the IF conformation.⁷ In line with previous findings this structure confirmed the rocking bundle hypothesis, although embedded in a more complex framework where both local conformational changes and rigid body movements of groups of helices are associated with transport.⁷ By comparing the LeuT crystal structures in the OF and IF states, they revealed that only a portion of the core moves as a unit and that there is no strict adherence to the pseudo-fold symmetry. Indeed, the transition is characterized by multiple adjustments in individual TMs: the bending of TM2 and TM7 and the independent movement of TM1 and TM6 (intracellular halves) (Fig. 9).

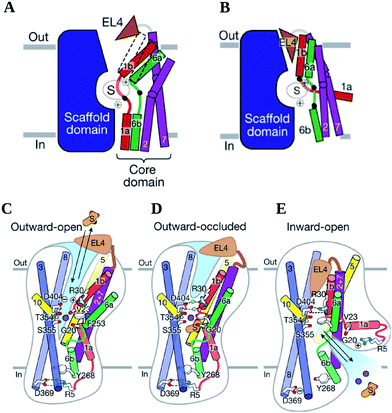Fig. 9 Schematic views of transport in LeuT. (A and B) Sketch of the IF and OF and their associated helices conformations. (C–E) Structural elements and gating residues instrumental to conformational changes associated with the transition from the (C) OFop to (D) OFoccl state and (E) to the IFop are shown. At present there is no crystal structure for an IFoccl state and thus no scheme is provided. Image reprinted by permission from Macmillan Publishers Ltd: Nature ref. 7, copyright 2012.

In a recent review, Loland presented a detailed comparison of the models and crystal structures of LeuT in OF and IF conformations.⁷⁸ The main differences between the IF models built according to the rocking bundle model and the crystallographic structure are observed in the cytoplasmatic halves of TM1 and TM6 (i.e. TM1a and TM6b). Indeed, the tilt of the crystal structure is markedly asymmetrical with respect to the IF conformation predicted on the basis of the rocking bundle model. This observation apparently rules out the rocking bundle mechanism (based exclusively on the symmetry of the repeats), supporting instead the hinge bending hypothesis. However, one should take into account that the OF and IF crystal structures do not provide direct information about the dynamic transitions interconnecting the different conformational states. The rocking bundle or the hinge bending mechanisms are thus not necessarily mutually exclusive. Indeed, the solved IF structures can be intermediates structurally close to the actual IF state. Namely, the rocking bundle model may involve the passage through an intermediate in which a bending of the hinge regions in TM1 and/or TM6 occurs.

5.2 Mhp1

Analysis of three crystal structures (OF, OFoccl, IF) of Mhp1 together with MD simulations have been used by Shimamura et al. to study the transitions from the OF to the IF conformation, passing through OFoccl state.^64,88 Using DIMS-MD the authors found an inversion mechanism consistent with the rocking bundle model. The scaffold, referred to as the hash motif (TMs 3, 4, 8, 9), undergoes a rigid body movement relative to the rest of protein. The TM5 and TM10 helices (considered to be flexible helices that bend) represent the thin extra- and intracellular gates, respectively. During the switch (RMSD of the OF and IF structures Cα = 3.3 Å) the hash motif acts as a thick gate, rotating by about 30° with respect to the bundle. Subsequently, the extracellular cavity is filled by TM3 and TM9, while TM4 and TM8 open towards the cytoplasm forming an inward cavity. No large steric or energetic barriers accompany the transition. Unbiased MD simulations, instead, show that the thin gate spontaneously opens and closes regardless of the starting conformation, suggesting that its opening is stochastically regulated on the sub-μs timescale. Interestingly, the movement of the intracellular thin gate appears to be independent to that of the thick gate, while the extracellular thin gate is connected to the thick gate by the movement of TM9 towards the bundle, which locks the extracellular gate into its closed position. No spontaneous transitions of the thick gate were observed in 1.6 μs. Thus, the opening of the thick gate appears to be the rate-limiting event of the transport process. In this study, the rigid body model proposed by Forrest^86,87 appears more likely than for LeuT. However, even for Mhp1 some discrepancies are present with respect to the rocking bundle model. Analyses of the helices differ between the OF, OFoccl and IF conformations obtained from non-equilibrium MD simulations, pointing out that although the bundle (TMs 1, 2, 6, and 7) and hash motif (TMs 3, 4, 8, and 9) move relative to each other mainly as rigid bodies, the helices of the thin gate (TM5 and TM10) move independently, with their position being linked to the motion of the thick gate.

In a subsequent study Adelman et al., starting from the crystallographic OF and IF structures of Mhp1, characterized the alternating access mechanism using a weighted ensemble path-sampling method based on the coarse grained (Go-like) model.⁵¹ By considering several reaction coordinates to enhance the sampling of the transport mechanism (i.e. distance-RMSD to the target (inward) state, movement of the inner and outer gates, etc.), they found that two transport mechanisms may take place according to: (i) the strict alternating access mechanism; (ii) a mechanism in which both gates are simultaneously open, creating a transient continuous permeation pathway through the transporter. Concerning the OF to IF switch, they confirmed the rocking bundle hypothesis, observing a rigid body motion of the hash motif relative to the bundle. They also calculated the rate of the transport cycle to be around 24 ms⁻¹.

Consistent with the above mentioned studies, Simmons et al. established that in Mhp1 the switch mechanism predominantly occurs via a rigid body rotation of the hash domain relative to the bundle one.⁷⁶ One of the reasons for the more rigid movement of the two domains with respect to each other is probably due to the fact that the substrate interacts mainly with the hash domain in Mhp1, while specific interactions of a substrate with the bundle were also observed in other structures of LeuT-fold family.^4,6,11

6 Water permeation

An important process associated with this type of symporters is the transport of water molecules.⁹⁴ Understanding the water transport mechanism is particularly relevant for SGLT symporters, since these proteins play a key role in water absorption in the human body, promoting the uptake of about 6 liters per day in normal adult intestines. As mentioned above, this function is exploited in oral rehydration therapy for the treatment of secretory diarrhea.^95,96 Two mechanisms for water permeation are considered to be viable: (i) active cotransport,^97,98 where water flux is stoichiometrically coupled to ion/solute flux, and (ii) passive osmosis-driven permeation,⁹⁹ where the accumulation of solutes near the intracellular side of the membrane during solute transport induces a flux of water as a response to the local osmotic gradient. While passive water diffusion appears to be an operative mechanism, active cotransport, in which a large amount of water enters into the transporter lumen along with the substrate and is pushed towards the cytoplasm, is still the subject of debate.

In this respect, MD simulations are of the utmost importance as they can complement the static picture drawn by X-ray studies, where at most a few water molecules are co-crystallized with the protein, with the dynamic properties of the transporter and water. In line with the passive mechanism, water molecules permeate easily through the whole protein during the several steps of the transport process.^72,74,94 In an interesting study, Li et al. provided a detailed comparison of different membrane transporters by performing extensive MD simulations (hundreds of ns to μs-long) (Fig. 10).⁹⁴ They showed that in 1.5 μs-long simulations on the IF form of vSGLT a large number of water permeation events occurred.⁹⁴ These are mediated by small fluctuations in the radius of the constriction point within the lumen (Y87, F424, the putative extracellular gate, and Q428). This point acts as a gate for water transport allowing the formation of water transient states.⁹⁴ In a later study focalized on vSGLT, Adelman et al.⁷² observed again the spontaneous formation of water conducting channels, in which the residues of the extracellular gate undergo a conformational transition connecting the lumen to the extracellular part (tens of μs-long MD simulations). In general, they observed that galactose binding can reduce permeability, even if the formation of a water transient state also occurs in its presence.

Fig. 10 (A and B) Water-conducting states and water transport in vSGLT. (C) Water-conducting states for GltPh (EAAT) of the SLC1 family (upper) and GlpT from the MFS superfamily (lower). (D) Water-conducting states for Mhp1 (upper) and maltose transporter of the ABC superfamily (lower). Image from ref. 94.

A similar formation of water transient states was observed for 1.2 μs-long MD simulations of the Mhp1 OF conformation. In line with these findings, 160 ns MD simulation of the trimeric state of Gltph, considering one monomer to be in an intermediate state and the other two to be in an OF conformation, showed that the formation of a water conduction state for the monomer in the intermediate state is associated with larger conformational changes than for vSGLT.⁹⁴ Thus, it has been proposed that the formation of water conducting states is a general feature of transporters and most probably relies on small imperfections in their overall gating motion (Fig. 10). Water transport appears to be independent from that of the substrate, but is sensitive to the conformational state of the transporter. Short-lived water-conduction states are clearly difficult to capture experimentally as they occur on a time resolution not accessible by experimental techniques. As such, molecular simulations have clearly provided an important contribution to this field.

7 Conclusions

Transport of molecules such as nutrients, precursors, and reaction products across cell membranes is at the basis of the living mechanism of cells. Ion-coupled secondary active transporters are involved in the mechanism of cellular uptake and release of various substrates against their concentration gradient by converting ion binding and transport along their concentration gradient into useful work. Understanding the molecular mechanism of these fascinating membrane proteins is clearly challenging from both experimental and computational aspects, as it relies on global and local conformational changes, which are interconnected in an intricate network of interactions and which drive/are driven by the stabilization/destabilization of several binding sites for both ions and substrates in a strictly interconnected time series of events. The sodium/solute symporters belonging to the LeuT-fold superfamily rely on an alternating access model of transport, in which the membrane proteins switch from an OF to an IF conformation, allowing the exposure of their substrate binding site to either side of the cellular membrane and permitting as a consequence its transport. The large number of crystallographic structures that have appeared in recent years for this superfamily’s members have provided compelling support to understand the atomistic details of the transport mechanism. Moreover, plain or biased molecular simulations have been widely employed to complement the static picture provided by X-ray crystallography and to characterize molecular events of the transport mechanism ranging from a sub-μs to 10 s μs timescale. With respect to ion binding sites, classical MD simulations have been of help in identifying the Na⁺ site for several members of the LeuT-fold family for which this site was either not solved or its assignation based on similarity sequence was ambiguous. Moreover, they allowed the identification of several possible metastable Na⁺ binding sites which are occupied upon substrate binding/release. They pinpointed also the existence of multiple substrate binding sites both at the OF and IF conformational states of the transporters, which may play a role in allosterically regulating the conformational changes occurring along with transport. From the studies reviewed here, it emerges clearly that despite the overall mechanistic similarity, one or two/three Na⁺-dependent transporters differ in some (important) mechanistic details. Concerning the ligand/ion-dependent conformational changes occurring at the OF conformation, it is clear that Na⁺ binding at the Na1 site contributes to reshaping the free energy landscape, stabilizing the OF conformation and creating and/or stabilizing substrate binding, while the role of Na⁺ in Na2 determines a complete closure of the gate in two/three Na⁺ binding transporters. On the other hand, in the transporters depending on one Na⁺ ion, both roles are played by Na⁺ in Na2, but it is believed that this ion mainly stabilizes substrate binding, playing a more marginal role in the conformational selection of the transporter. Conversely, when the transition to an IF conformation has occurred, it has been recently reported that the stabilization of the ion can be either mediated by local conformational changes, which allow the trapping of the transporter in an IFoccl conformation, or by the binding of a second substrate molecule. For one Na⁺-dependent transporter it is not fully established if a stable IFoccl conformation of the transporter exists. This state has been identified only by a metadynamics-based simulation study.⁷⁴ The existence of this state is instead clear for two/three Na⁺-dependent transporters. For both types of transporters, however, the order of Na⁺/substrate dissociation events at the intracellular side is still controversial.

The diversity among one or two/three-Na⁺ ion-dependent transporters is present also in OF to IF conformational switching. The simple rocking bundle mode originally proposed by symmetry considerations seems to be violated and integrated by local hinge bending motions. This occurs to a different extent in one and two Na⁺-dependent transporters. In the latter case the discrepancy from the rocking bundle model is clearly larger.

Remarkably, investigation of the water transport mechanism by μs-long MD simulations has revealed the presence of water conducting events in which the channels can open. These are cross-linked to the conformational state of the transporter and regulated by substrate load. This feature appears to be shared by the whole LeuT-fold superfamily.

While MD simulations have greatly contributed to elucidate water permeation and local structural rearrangements occurring during transport, the characterization of the coupled global/local conformational changes occurring in this mechanism is refractory to MD simulations as they occur on a timescale beyond that accessible even to specialized labs. The use of sophisticated enhanced sampling methods has so far provided only a qualitative picture of the underlying structural changes.¹⁰⁰ State of the art non-equilibrium MD techniques are needed for a more quantitative description of these complex phenomena to clarify if, how and why a divergent alternating access mechanism may take place depending on the ion load of the symporter.

An aspect which has only recently aroused the interest of computational studies is the characterization of membrane composition on the structure of the transporter and, thus, on its transport mechanism. We expect that interest in this aspect is going to increase.

Nowadays, computational studies based on different levels of theory have permeated all fields of biomolecular studies (including biocatalysis, biomaterial design, and drug design).^101–103 These studies are more often grounded on close integration between molecular simulations and experiments to fully elucidate atomistic details, which are often too difficult, too expensive or simply not accessible experimentally. Thus, molecular simulations are expected to become an essential tool in biophysical, biochemical, and biomaterial science studies in the near future, contributing also to fully elucidating the mechanism of the LeuT symporter superfamily.

References

1. C. Kandt, W. L. Ash and D. Peter Tieleman, Methods, 2007, 41, 475–488.
2. J. Abramson and E. M. Wright, Curr. Opin. Struct. Biol., 2009, 19, 425–432.
3. H. Krishnamurthy, C. L. Piscitelli and E. Gouaux, Nature, 2009, 459, 347–355.
4. S. Faham, A. Watanabe, G. M. Besserer, D. Cascio, A. Specht, B. A. Hirayama, E. M. Wright and J. Abramson, Science, 2008, 321, 810–814.
5. O. Jardetzky, Nature, 1966, 211, 969–970.
6. A. Yamashita, S. K. Singh, T. Kawate, Y. Jin and E. Gouaux, Nature, 2005, 437, 215–223.
7. H. Krishnamurthy and E. Gouaux, Nature, 2012, 481, 469–474.
8. S. Weyand, T. Shimamura, S. Yajima, S. Suzuki, O. Mirza, K. Krusong, E. Carpenter, N. Rutherford, J. Hadden and J. O’Reilly, Science, 2008, 322, 709.
9. J. P. Paluszynski, R. Klassen, M. Rohe and F. Meinhardt, Yeast, 2006, 23, 707–715.
10. S. Ressl, A. van Scheltinga, C. Vonrhein, V. Ott and C. Ziegler, Nature, 2009, 458, 47–52.
11. C. Perez, C. Koshy, Ö. Yildiz and C. Ziegler, Nature, 2012, 490, 126–130.
12. D. Yernool, O. Boudker, Y. Jin and E. Gouaux, Nature, 2004, 431, 811–818.
13. I. Zdravkovic, C. Zhao, B. Lev, J. E. Cuervo and S. Y. Noskov, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 337–347.
14. Y. Shi, Annu. Rev. Biophys., 2013, 42, 51–72.
15. S. A. Shaikh, J. Li, G. Enkavi, P.-C. Wen, Z. Huang and E. Tajkhorshid, Biochemistry, 2013, 52, 569–587.
16. K. Kazmier, S. Sharma, S. M. Islam, B. Roux and H. S. Mchaourab, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14752–14757.
17. K. Kazmier, S. Sharma, M. Quick, S. M. Islam, B. Roux, H. Weinstein, J. A. Javitch and H. S. Mchaourab, Nat. Struct. Mol. Biol., 2014, 21, 472–479.
18. L. Delemotte, M. A. Kasimova, M. L. Klein, M. Tarek and V. Carnevale, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 124–129.
19. A. V. Vargiu, P. Ruggerone, T. J. Opperman, S. T. Nguyen and H. Nikaido, Antimicrob. Agents Chemother., 2014, 58, 6224–6234.
20. S. Vanni, M. Neri, I. Tavernelli and U. Rothlisberger, PLoS Comput. Biol., 2011, 7, e1001053.
21. L. M. R. Napolitano, I. Bisha, M. de March, A. Marchesi, M. Arcangeletti, N. Demitri, M. Mazzolini, A. Rodriguez, A. Magistrato and S. Onesti, et al., Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E3619–E3628.
22. S. Furini, P. Barbini and C. Domene, Biophys. J., 2015, 108, 490a.
23. http://www.psc.edu/index.php/computing-resources/anton.
24. D. E. Shaw, R. O. Dror, J. K. Salmon, J. Grossman, K. M. Mackenzie, J. A. Bank, C. Young, M. M. Deneroff, B. Batson and K. J. Bowers, et al., High Performance Computing Networking, Storage and Analysis, Proceedings of the Conference on, 2009, pp. 1–11.
25. I. Bahar, M. H. Cheng, J. Y. Lee, C. Kaya and S. Zhang, Biophys. J., 2015, 109, 1101–1109.
26. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
27. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021.
28. D. L. Beveridge and F. DiCapua, Annu. Rev. Biophys. Biophys. Chem., 1989, 18, 431–492.
29. H. Grubmüller, B. Heymann and P. Tavan, Science, 1996, 271, 997–999.
30. B. Isralewitz, M. Gao and K. Schulten, Curr. Opin. Struct. Biol., 2001, 11, 224–230.
31. M. Sotomayor and K. Schulten, Science, 2007, 316, 1144–1148.
32. C. Jarzynski, Phys. Rev. Lett., 1997, 78, 2690.
33. C. Jarzynski, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5018.
34. J. Schlitter, M. Engels, P. Krüger, E. Jacoby and A. Wollmer, Mol. Simul., 1993, 10, 291–308.
35. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
36. A. Laio, A. Rodriguez-Fortea, F. L. Gervasio, M. Ceccarelli and M. Parrinello, J. Phys. Chem. B, 2005, 109, 6714–6721.
37. G. Bussi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2006, 96, 090601.
38. S. Piana and A. Laio, J. Phys. Chem. B, 2007, 111, 4553–4559.
39. F. Marinelli, F. Pietrucci, A. Laio and S. Piana, PLoS Comput. Biol., 2009, 5, e1000452.
40. Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151.
41. Y. Sugita, A. Kitao and Y. Okamoto, J. Chem. Phys., 2000, 113, 6042–6051.
42. G. Bussi, F. L. Gervasio, A. Laio and M. Parrinello, J. Am. Chem. Soc., 2006, 128, 13435–13441.
43. D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929.
44. D. Hamelberg, C. A. F. de Oliveira and J. A. McCammon, J. Chem. Phys., 2007, 127, 155102.
45. Y. Miao, S. E. Nichols, P. M. Gasper, V. T. Metzger and J. A. McCammon, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10982–10987.
46. A. Penmatsa, K. H. Wang and E. Gouaux, Nature, 2013, 503, 85–90.
47. M. H. Cheng and I. Bahar, Structure, 2015, 23, 2171–2181.
48. O. Beckstein, E. J. Denning, J. R. Perilla and T. B. Woolf, J. Mol. Biol., 2009, 394, 160–176.
49. G. A. Huber and S. Kim, Biophys. J., 1996, 70, 97.
50. B. W. Zhang, D. Jasnow and D. M. Zuckerman, J. Chem. Phys., 2010, 132, 054107.
51. J. Adelman, A. Dale, M. Zwier, D. Bhatt, L. Chong, D. Zuckerman and M. Grabe, Biophys. J., 2011, 101, 2399–2407.
52. A. Cordomí, G. Caltabiano and L. Pardo, J. Chem. Theory Comput., 2012, 8, 948–958.
53. C. J. Dickson, L. Rosso, R. M. Betz, R. C. Walker and I. R. Gould, Soft Matter, 2012, 8, 9617–9627.
54. A. D. MacKerell Jr, D. Bashford, M. Bellot, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, W. Watanabe, J. Wiorkiewicz-Kunczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616.
55. A. D. MacKerell, M. Feig and C. L. Brooks, J. Comput. Chem., 2004, 25, 1400–1415.
56. J. B. Klauda, R. M. Venable, J. A. Freites, J. W. OăĂŹConnor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell Jr and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843.
57. R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. MacKerell Jr, J. Chem. Theory Comput., 2012, 8, 3257–3273.
58. J. Wang, R. Wolf, J. Caldwell, P. Kollman and D. Case, J. Comput. Chem., 2004, 25, 1157–1174.
59. Y. Duan, C. Wu, S. Chowdhury, M. Lee, G. Xiong, W. Zhang, R. Yang, P. Cieplak, R. Luo and T. Lee, J. Comput. Chem., 2003, 24, 1999–2012.
60. J. Li and E. Tajkhorshid, Biophys. J., 2009, 97, 29–31.
61. E. Zomot and I. Bahar, Mol. BioSyst., 2010, 6, 1040–1046.
62. A. Watanabe, S. Choe, V. Chaptal, J. M. Rosenberg, E. M. Wright, M. Grabe and J. Abramson, Nature, 2010, 468, 988–991.
63. I. Bisha, A. Laio, A. Magistrato, A. Giorgetti and J. Sgrignani, J. Chem. Theory Comput., 2013, 9, 1240–1246.
64. T. Shimamura, S. Weyand, O. Beckstein, N. Rutherford, J. Hadden, D. Sharples, M. Sansom, S. Iwata, P. Henderson and A. Cameron, Science, 2010, 328, 470–473.
65. C. Zhao and S. Noskov, Biochemistry, 2011, 50, 1848–1856.
66. C. Zhao, S. Stolzenberg, L. Gracia, H. Weinstein, S. Noskov and L. Shi, Biophys. J., 2012, 103, 878–888.
67. E. Zomot, M. Gur and I. Bahar, J. Biol. Chem., 2015, 290, 544–555.
68. K. Khafizov, C. Perez, C. Koshy, M. Quick, K. Fendler, C. Ziegler and L. Forrest, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E3035–E3044.
69. C. Perez, B. Faust, A. R. Mehdipour, K. A. Francesconi, L. R. Forrest and C. Ziegler, Nat. Commun., 2014, 5, 4231.
70. T. Bastug, G. Heinzelmann, S. Kuyucak, M. Salim, R. Vandenberg and R. Ryan, PLoS One, 2012, 7, e33058.
71. J. Li and E. Tajkhorshid, Biochim. Biophys. Acta, 2012, 1818, 263–271.
72. J. L. Adelman, Y. Sheng, S. Choe, J. Abramson, E. M. Wright, J. M. Rosenberg and M. Grabe, Biophys. J., 2014, 106, 1280–1289.
73. M. Sala-Rabanal, B. A. Hirayama, D. D. Loo, V. Chaptal, J. Abramson and E. M. Wright, Am. J. Physiol.: Cell Physiol., 2012, 302, C1293.
74. I. Bisha, A. Rodriguez, A. Laio and A. Magistrato, PLoS Comput. Biol., 2014, 10, e1004017.
75. Z. Li, A. S. Lee, S. Bracher, H. Jung, A. Paz, J. P. Kumar, J. Abramson, M. Quick and L. Shi, J. Biol. Chem., 2015, 290, 127–141.
76. K. J. Simmons, S. M. Jackson, F. Brueckner, S. G. Patching, O. Beckstein, E. Ivanova, T. Geng, S. Weyand, D. Drew and J. Lanigan, et al., EMBO J., 2014, 33, 1831–1844.
77. C. Zhao and S. Y. Noskov, PLoS Comput. Biol., 2013, 9, e1003296.
78. C. J. Loland, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 500–510.
79. L. Shi, M. Quick, Y. Zhao, H. Weinstein and J. A. Javitch, Mol. Cell, 2008, 30, 667–677.
80. M. H. Cheng and I. Bahar, Biophys. J., 2013, 105, 630–639.
81. M. H. Cheng and I. Bahar, PLoS Comput. Biol., 2014, 10, e1003879.
82. I. H. Shrivastava, J. Jiang, S. G. Amara and I. Bahar, J. Biol. Chem., 2008, 283, 28680–28690.
83. Y. Gu, I. Shrivastava, S. Amara and I. Bahar, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 2589–2594.
84. G. Grazioso, V. Limongelli, D. Branduardi, E. Novellino, C. de Micheli, A. Cavalli and M. Parrinello, J. Am. Chem. Soc., 2011, 134, 453–463.
85. D. Branduardi, F. L. Gervasio and M. Parrinello, J. Chem. Phys., 2007, 126, 054103.
86. L. R. Forrest, Y.-W. Zhang, M. T. Jacobs, J. Gesmonde, L. Xie, B. H. Honig and G. Rudnick, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 10338–10343.
87. L. Forrest and G. Rudnick, Physiology, 2009, 24, 377–386.
88. S. Weyand, T. Shimamura, S. Yajima, S. Suzuki, O. Mirza, K. Krusong, E. P. Carpenter, N. G. Rutherford, J. M. Hadden and J. O’Reilly, et al., Science, 2008, 322, 709–713.
89. S. Shaikh and E. Tajkhorshid, PLoS Comput. Biol., 2010, 6, e1000905.
90. N. Reyes, C. Ginter and O. Boudker, Nature, 2009, 462, 880–885.
91. N. Akyuz, R. B. Altman, S. C. Blanchard and O. Boudker, Nature, 2013, 502, 114–118.
92. G. Verdon and O. Boudker, Nat. Struct. Mol. Biol., 2012, 19, 355–357.
93. M. Gur, E. Zomot, M. H. Cheng and I. Bahar, J. Chem. Phys., 2015, 143, 243134.
94. J. Li, S. A. Shaikh, G. Enkavi, P.-C. Wen, Z. Huang and E. Tajkhorshid, Proc. Natl. Acad. Sci. U. S. A., 2013, 201218986.
95. E. Wright, B. Hirayama and D. Loo, J. Intern. Med., 2007, 261, 32–43.
96. E. M. Wright, D. D. Loo and B. A. Hirayama, Physiol. Rev., 2011, 91, 733–794.
97. T. Zeuthen, A. Meinild, D. Loo, E. Wright and D. Klaerke, J. Physiol., 2004, 531, 631–644.
98. T. Zeuthen and N. MacAulay, Wiley Interdiscip. Rev.: Membr. Transp. Signaling, 2012, 1, 373–381.
99. L. Sasseville, J. Cuervo, J. Lapointe and S. Noskov, Biophys. J., 2011, 101, 1887–1895.
100. J. Li, P.-C. Wen, M. Moradi and E. Tajkhorshid, Curr. Opin. Struct. Biol., 2015, 31, 96–105.
101. P. Vidossich and A. Magistrato, Biomolecules, 2014, 4, 616–645.
102. F. de Leo, A. Magistrato and D. Bonifazi, Chem. Soc. Rev., 2015, 44(19), 6916–6953.
103. A. V. Vargiu and A. Magistrato, ChemMedChem, 2014, 9, 1966–1981.

---