Density functional theory study of hydrogenation of S to H2S on Pt–Pd alloy surfaces†
Yunjie Liua,
Wenyue Guo*a,
Xiaoqing Lua,
Wei Gaoa,
Guixia Lia,
Yahui Guoa,
Jun Zhub and
Lanzhong Hao*a
aCollege of Science, China University of Petroleum, Qingdao, Shandong 266580, People's Republic of China. E-mail: haolanzhong@upc.edu.cn; wyguo@upc.edu.cn
bState Key Laboratory of Electronic Thin Films and Integrated Devices, University of Electronic Science and Technology of China, Chengdu 610054, People's Republic of China
First published on 4th January 2016
Abstract
In this work, the adsorption of S-containing species (S, HS, and H2S) and the hydrogenation of S on the Pt–Pd alloy were investigated by using the periodic density functional theory (DFT). The energy minimum of the adsorbed S, HS, and H2S were identified to bind preferentially on the fcc, bridge and top sites, respectively. Compared to single metal surfaces, the adsorption energies of adsorbates were calculated to be larger on the Pt–Pd alloy surfaces and adsorbed preferably on the sites with a majority of Pt atoms. The reaction pathways and energy profiles for the conversion of adsorbed S and H into gas phase H2S were determined. The results showed that both the S + H and HS + H reactions on Pt–Pd alloy surfaces were endothermic. The energy for the overall reaction on Pt–Pd alloy surfaces decreased significantly by 0.30–0.55 eV compared to pure Pt(111) surface. In addition, the energy barrier on Pt–1Pd(111) (one Pt atom was replaced by Pd atom on Pt(111) surface) was lower than that on other studied alloy surfaces. The above characteristics revealed that the hydrogenation of S to H2S was easier on Pt–1Pd(111) surface than on the other alloy surfaces. The partial density of states was utilized to illustrate the interaction mechanisms between S-containing species and surface atoms.
1. Introduction
Platinum catalysts have received much attention due to their high activity towards the hydrodesulfurization (HDS) of organic sulfur compounds and their wide application in the area of the petrochemical processes.1 However, the catalysts could be easily poisoned and deactivated under sulfuric conditions. The previous studies indicated that sulfur containing molecules in feedstock, even in small levels of S impurities, can drastically reduce the catalytic efficiency of transition metal surfaces.2–4 Therefore, many attempts have been made to enhance sulfur resistance of platinum catalysts. Recent studies show that the addition of a second transition metal into platinum catalysts may effectively improve catalytic activity and sulfur resistance.5,6 In particular, Pt–Pd alloy catalysts have received a lot of attention since they have exhibited superior sulfur resistance.7–10 The Pt–Pd alloy catalysts perform better than either of the monometallic catalysts in selectivity, activity as well as resistance to poisoning. Lee et al. investigated the sulfur tolerance of bimetallic Pd–Pt/H-Beta catalysts for the isomerization of n-hexane in the presence of thiophene.11 The results showed that Pd–Pt/H-Beta catalysts were more sulfur resistant than Pd/H-Beta and Pt/H-Beta, regardless of the preparation method and the Pd–Pt atomic ratio. This suggests that the Pt–Pd bimetallic interaction could increase the amount of electron-deficient metal sites and the sulfur tolerance could be enhanced due to the reduction of the irreversible electrophilic sulfur adsorption. Yasuda et al. confirmed that tetralin hydrogenation could be enhanced largely due to the coexistence of Pt and Pd. The high sulfur tolerance of the Pt–Pd system could be attributed to the structural and electronic effects.12 Niquille-Röthlisberger et al. thought that high hydrogenation activity of Pt–Pd alloy catalysts originated from the new active sites in the Pt–Pd catalysts.13In spite of large quantities of experimental works about the Pt–Pd alloy catalysts, to our knowledge, little theoretical work has been carried out. Jiang et al. studied the adsorption of S, HS and H2S on Pt–Pd alloys metal.14 They thought the structure changes in Pt–Pd bimetallic catalysts gave rise to different active sites that made the adsorption of H2 more competitive to the adsorption of H2S and S. However, little is known about electron structure of S on the different active sites and the mechanism of hydrogenation reaction of S on Pt–Pd alloy surfaces. Undoubtedly, it is important to understand these elementary reactions for a number of industrial processes. In this paper, the hydrogenation reactions of sulfur were examined with density functional theory (DFT) to determine the catalytic effect of alloying Pt with Pd on the Pt–Pd catalysts. The optimized adsorption configurations, adsorption energies and partial density of states (PDOS) analyses of S, HS, H2S and H were presented. The main reaction pathways were obtained on the targeted metal surfaces.
2. Computation details
The calculations were performed in the framework of DFT with program package DMol3 and CASTEP in Materials Studio of Accelrys Inc.15–17 The exchange–correlation energy was calculated within the generalized gradient approximation (GGA) using the form of the function proposed by Perdew and Wang, usually referred as to Perdew-Wang 91.18,19 The PW91 functional has the shortcoming that does not contain dispersion contribution to some systems, but the contribution of van der Waals (vdW) dispersion term is small. Garćla-Muelas et al. reported that the inclusion of vdW interactions could enhance the adsorption energies by 0.01–0.20 eV using applying Grimme's DFT-D2 method for the reactants, products and decomposition on Cu, Ru, Pd and Pt surfaces.20 Furthermore, we calculated the adsorption energy of H adsorption at the top site on Pt(111) with the PBE exchange–correlation functional. The adsorption energy (2.77 eV) were almost equal with the energy (2.80 eV) calculated with PW91 functional, suggesting that dispersion effects have little influence to the results.The density functional semicore pseudopotential (DSPP) method was employed for the metal atoms,21 and the all-electron basis set was used to treat the incorporated atoms, such as H and S atom. The valence electron functions were expanded into a set of numerical atomic orbital by a double-numerical basis with polarization functions (DNP). A Fermi smearing of 0.136 eV was used to improve the computational performance. Spin-polarization was performed during the whole computations.
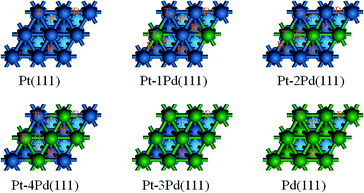
Here, we choose the (111) of Pt as the initial surface because it is the most stable crystal planes in the exposed basal planes of nanoparticles. The Pt(111) surface is modelled using a four-layer slab model with four atoms per layer representing a (2 × 2) surface unit cell and a 14 Å vacuum region. The reciprocal space is sampled by a grid of (5 × 5 × 1) k-points generated automatically using the Monkhorst–Pack method.22 A single adsorbate is allowed to adsorb on one side of the (2 × 2) unit cell, corresponding to a surface coverage of 1/4 ML. Full-geometry optimization is performed for all relevant adsorbates and the upper most two layers without symmetry restriction, while the bottom two layer Pt atoms are fixed to their calculated bulk positions. The tolerances of energy, gradient, and displacement convergence are 1.0 × 10−5 Hartree, 2.0 × 10−3 Hartree per Å, and 5 × 10−3 Å, respectively. In order to study the alloy effects, Pt atoms on the first layer of the Pt(111) surface are replaced by Pd atoms as our computational models, which are described as Pt–nPd(111) (n = 1–4). The atomic ratio between Pt and Pd on the first layer was thus 3/1, 2/2, 1/3, and 0/4, respectively. The computational model is in consistent with previous work.14 The Pd(111) model is built of all the Pd atoms, using a four-layer slab model with four atoms per layer representing a (2 × 2) surface unit cell and a 14 Å vacuum region. The slab models of Pt(111), four kinds of bimetallic surfaces and the Pd(111) are shown in Fig. 1. On the (111) facet of a face-centered cubic structure, the surface sites include top (T), bridge (B), fcc (F), and hcp (H), only one equivalent site for the adsorption of species on each of the T, B, F, and H sites on Pt(111), Pd(111), and Pt–4Pd(111), while on the other alloy surfaces, each of these sites can be classified into two or three catalogs, differentiated by footnotes 1, 2, and 3, in which the smaller footnote number denotes the corresponding site is relevant to more Pt atoms, while the situation of the larger footnote number is the reverse.
The bulk lattice constants and adsorption energies were calculated to ensure the reliability of the computational results. The calculated lattice constant of the bulk Pt and Pd were 4.006 and 3.983 Å, respectively, which are in good agreement with the experimental values (3.912 and 3.883 Å)23,24 and other theoretical values (3.971 and 3.965 Å).25,26 The adsorption energies of H adsorbed on Pt(111) and Pd(111) were calculated. H can adsorb at all site on Pt(111) with a similar energy, with 2.80 eV at the T site, 2.71 eV at the F site, 2.68 eV at the H site and 2.71 eV at the B site. The results agree very well with previous calculations.27 On Pd(111), the most favourable site for H is found to be at the F site and the adsorption energies are calculated to be 2.82 eV. The result are in very good agreement with previous experimental study (2.80 eV).28
The adsorption energies reported here were calculated using the equation:
| Eads = Eadsorbate + Eslab − Eadsorbate/slab | (1) |
Transition state (TS) searches were performed at the same theoretical level with the complete LST/QST method.15,16,29 Vibrational frequencies were calculated for all the initial state (IS) and final state (FS) as well as the TSs from the Hessian matrix with the harmonic approximation. The zero-point energy (ZPE) was calculated from the resulted frequencies. The reaction energy (ΔE) and energy barrier (Ea) of a step on Pt–Pd alloys can be calculated by the following formulas,
| ΔE = EFS − EIS | (2) |
| Ea = ETS − EIS | (3) |
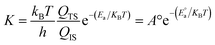 | (4) |
3. Results and discussion
This part is divided into four sections. In Section 3.1, the structures of metal surfaces are described. In Section 3.2, the adsorptions of S and surfaces species involved are discussed. In Section 3.3, electronic states of adsorption structures are analyzed. In Section 3.4, the reaction paths of the hydrogenation of S are elaborated.3.1 Structures of metal surface
The geometric and electronic structures of the surfaces with different Pt/Pd ratios are calculated and the obtained parameters are summarized in Table 1. The Pt(111) surface is flat with the distance of 2.38 Å between the most upper two layers. After Pd doping, due to the difference of lattice constant, the surface Pt atoms move inward by 0.02–0.08 Å and the Pd atoms yield a height of about 0.10 Å higher than the surrounding Pt atoms. The distance of the first and second layer Pt–Pt in pure Pt(111) is 2.875 Å. After Pd doping, the Pt–Pt bonds are shortened about 0.02–0.07 Å and the distance of Pt–Pd decreases from 2.916 to 2.845 Å with the increasing of the Pd number. Furthermore, the electrons transfer from Pd to Pt in the upper layer due to their different electronegativities. The transferred charges of Pt atom increase with increasing of the Pd atoms. The Pt atoms of the second layer get electron after Pd atoms doping. The overlap population values in Table 2 indicates the interactions in the upper layer are more strongly covalent than the first–second interlayer bonds, which are weakly covalent (Pt–Pt) or antibonding (Pd–Pt) interactions. The covalent components of the bonds in the uppermost layer follows the order of Pt–Pt (0.54–0.75) > Pt–Pd (0.24–0.45) > Pd–Pd (0.04–0.34), and the values for each type of the bonds increase with increasing the alloying atom number. These results are well consistent with the results of the corresponding bond lengths.| System | Atom | Charge | dPt–Pt/Pd (Å) | |
|---|---|---|---|---|
| Pt–Pta/Pd–Pda | Pd–Pta | |||
| a a second layer Pt or Pd atoms. Pd is nearest the site of S atom. | ||||
| Pt | Pt | −0.016 | 2.875 | |
| Pta | 0.013 | |||
| Pt–1Pd | Pt | −0.068 | 2.851 | 2.916 |
| Pd | 0.190 | |||
| Pta | 0 | |||
| Pt–2Pd | Pt | −0.122 | 2.828 | 2.894 |
| Pd | 0.148 | |||
| Pta | −0.014 | |||
| Pt–3Pd | Pt | −0.180 | 2.808 | 2.865 |
| Pd | 0.099 | |||
| Pta | −0.030 | |||
| Pt–4Pd | Pd | 0.047 | 2.845 | |
| Pta | −0.048 | |||
| Pd | Pd | −0.013 | 2.842 | |
| Pda | 0.011 | |||
| System | Surface | 1st–2nd layer | ||||
|---|---|---|---|---|---|---|
| Pt–Pt | Pt–Pd | Pd–Pd | Pt–Pta | Pd–Pta | Pd–Pda | |
| a a second layer Pt or Pd atoms. Pd is the closest to S atom. | ||||||
| Pt(111) | 0.54 | 0 | ||||
| Pt–1Pd(111) | 0.65 | 0.24 | 0.06 | −0.09 | ||
| Pt–2Pd(111) | 0.75 | 0.35 | 0.04 | 0.11 | −0.05 | |
| Pt–3Pd(111) | 0.45 | 0.14 | 0.12 | −0.02 | ||
| Pt–4Pd(111) | 0.23 | 0.03 | ||||
| Pd(111) | 0.34 | −0.01 | ||||
The partial density of states (PDOS) for metal surfaces is shown in Fig. 2. We find that with the increase of the Pd atoms (1) the range of the PDOS is successfully narrowed, i.e., from −13.0 eV to −5.87 eV for Pt(111) to −10.2 eV to −5.22 eV for Pd(111); (2) the Fermi level is higher located, that is, −5.87 eV for Pt(111) to −5.22 eV for Pd(111).
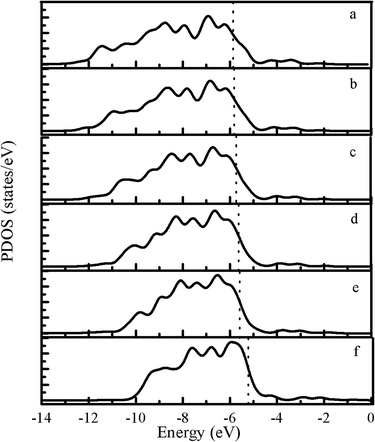 | ||
| Fig. 2 PDOS for different clean surfaces: (a) Pt(111), (b) Pt–1Pd(111), (c) Pt–2Pd(111), (d) Pt–3Pd(111), (e) Pt–4Pd(111), (f) Pd(111). | ||
3.2 Adsorptions of the S hydrogenation intermediates
To explore the hydrogenation of S, the preferential adsorption site for S, HS, H2S and H should be determined firstly. In this section, the adsorption geometries of all the intermediates are described. Table 3 lists some important parameters for these intermediates, and the most stable adsorption configurations are shown in Fig. 3.| Species | Slab | Sites | Eads (eV) | dS–Pt (Å) | dS–Pd (Å) | dS–H (Å) | Anglesa (°) |
|---|---|---|---|---|---|---|---|
| a Values are angles between the surface normal and the H–S axis when HS adsorption and the H–S–H angles when H2S adsorption. | |||||||
| S | Pt | F | 4.45 | 2.322, 2.322, 2.323 | |||
| H | 4.30 | 2.326, 2.329, 2.339 | |||||
| Pt–1Pd | F1 | 4.67 | 2.315, 2.317, 2.318 | ||||
| H1 | 4.52 | 2.323, 2.323, 2.324 | |||||
| F2 | 4.43 | 2.302, 2.303 | 2.344 | ||||
| H2 | 4.31 | 2.305, 2.305 | 2.355 | ||||
| Pt–2Pd | F1 | 4.65 | 2.300, 2.301 | 2.337 | |||
| H1 | 4.53 | 2.304, 2.306 | 2.337 | ||||
| F2 | 4.37 | 2.289 | 2.325, 2.326 | ||||
| H2 | 4.28 | 2.284 | 2.332, 2.333 | ||||
| Pt–3Pd | F1 | 4.59 | 2.281 | 2.325, 2.323 | |||
| H1 | 4.49 | 2.284, | 2.332, 2.333 | ||||
| F2 | 4.28 | 2.308, 2.308, 2.309 | |||||
| H2 | 4.21 | 2.310, 3.211, 2.313 | |||||
| Pt–4Pd | F | 4.69 | 2.304, 2.305, 2.306 | ||||
| H | 4.66 | 2.310, 2.312, 2.315 | |||||
| Pd | F | 4.42 | 2.301, 2.304, 2.306 | ||||
| H | 4.34 | 2.308, 2.308, 2.309 | |||||
| HS | Pt | B | 2.31 | 2.380, 2.378 | 1.377 | 104.3 | |
| Pt–1Pd | B1 | 2.77 | 2.371, 2.370 | 1.376 | 106.0 | ||
| B2 | 2.57 | 2.353 | 2.430 | 1.373 | 102.2 | ||
| Pt–2Pd | B1 | 2.89 | 2.364, 2.364 | 1.377 | 99.4 | ||
| B2 | 2.72 | 2.348 | 2.414 | 1.376 | 101.2 | ||
| B3 | 2.50 | 2.380 | 1.372 | 101.6 | |||
| Pt–3Pd | B1 | 2.86 | 2.340 | 2.405 | 1.376 | 104.4 | |
| B2 | 2.64 | 2.378, 2.379 | 1.373 | 103.3 | |||
| Pt–4Pd | B | 2.78 | 2.368, 2.368 | 1.376 | 99.3 | ||
| Pd | B | 2.49 | 2.373, 2.368 | 1.377 | 102.5 | ||
| H2S | Pt | T | 0.77 | 2.387 | 1.367 | 91.4 | |
| Pt–1Pd | T1 | 0.80 | 1.367 | 91.2 | |||
| T2 | 0.67 | 2.372 | 2.444 | 1.361 | 91.6 | ||
| Pt–2Pd | T1 | 0.83 | 2.358 | 1.367 | 91.1 | ||
| T2 | 0.71 | 2.417 | 1.362 | 91.6 | |||
| Pt–3Pd | T1 | 0.88 | 2.346 | 1.368 | 91.1 | ||
| T2 | 0.75 | 2.201 | 1.364 | 91.2 | |||
| Pt–4Pd | T | 0.80 | 2.373 | 1.365 | 91.2 | ||
| Pd | T | 0.74 | 2.386 | 1.366 | 91.5 | ||
We also study the S adsorption when H absorbed the surface. The adsorption energy on Pt(111), Pt–1Pd(111), Pt–2Pd(111), Pt–3Pd(111), Pt–4Pd(111) and Pd(111) are 4.31, 4.30, 4.29, 4.25, 4.22 and 3.89 eV, respectively. The adsorption energies are 0.14–0.53 eV less stable than that only S adsorb on the metal surface, indicating a slight repulsive interaction between S and H. Our main goal in this work is to describe the potential energy surface (PES) of the hydrogenation reaction to compare the reaction rate on the different metal surface. So we think the effect is very small.
Structurally, the S–H bonds in all cases are very similar, 1.372–1.377 Å, irrespective of the large difference in adsorption energies. This value is close to the value (∼1.360 Å) for the gas phase. On pure metal surfaces, the S–Pt distance (∼2.380 Å) is a little larger than the S–Pd distance (∼2.370 Å), surface alloying results in the tendency of shortening the S–Pt distance as well as stretching the S–Pd distance. HS was observed on Pt(111) by HREELS to be stable on the surface up to 150 K.31 It was suggested that HS may be inclined on Pt(111) based on the HREELS analysis.
| Species | Sites | Eads (eV) | dH–Pt (Å) | dH–Pd (Å) |
|---|---|---|---|---|
| Pt | T | 2.80 | 1.554 | |
| F | 2.71 | 1.872, 1.876, 1.879 | ||
| H | 2.68 | 1.873, 1.878, 1.880 | ||
| B | 2.71 | 1.751, 1.761 | ||
| Pt–1Pd | T1 | 2.83 | 1.555 | |
| T2 | 2.28 | 1.538 | ||
| F1 | 2.76 | 1.867, 1.872, 1.895 | ||
| H1 | 2.70 | 1.875, 1.879, 1.889 | ||
| F2 | 2.78 | 1.796, 1.808 | 2.050 | |
| H2 | 2.76 | 1.786, 1.788 | 2.144 | |
| B1 | 2.77 | 1.758, 1.760 | ||
| B2 | 2.71 | 1.667 | 1.921 | |
| Pt–2Pd | T1 | 2.86 | 1.556 | |
| T2 | 2.33 | 1.541 | ||
| F1 | 2.82 | 1.794, 1.807 | 2.074 | |
| F2 | 2.81 | 1.724 | 1.932, 1.960 | |
| H2 | 2.79 | 1.708 | 1.958, 1.985 | |
| B1 | 2.82 | 1.759, 1.759 | ||
| B2 | 2.78 | 1.668 | 1.918 | |
| Pt–3Pd | T1 | 2.89 | 1.559 | |
| T2 | 2.36 | 1.543 | ||
| F1 | 2.86 | 1.715 | 1.955, 1.956 | |
| F2 | 2.77 | 1.821, 1.821, 1.822 | ||
| H1 | 2.81 | 1.704 | 1.967, 2.008 | |
| H2 | 2.76 | 1.821, 1.824, 1.827 | ||
| Pt–4Pd | T | 2.40 | 1.551 | |
| F | 2.82 | 1.822, 1.822, 1.826 | ||
| H | 2.78 | 1.826, 1.831, 1.832 | ||
| Pd | T | 2.42 | 1.546 | |
| F | 2.82 | 1.814, 1.814, 1.816 | ||
| H | 2.76 | 1.814, 1.822, 1.824 |
3.3 Electronic structure
To clarify the surface alloying effect, PDOS for adsorbed S, HS and H2S was analyzed. Since Pt–nPd(111) (n = 1–3) show similar adsorption effect, i.e., the F1 site is more stable than F2 for S and the T1 site is more stable than T2 for H2S on the different alloy surfaces. For simplicity, we discuss only the PDOS of S, HS and H2S adsorbed on Pt–1Pd surface. PDOS for S adsorbed on the F1 and F2 sites was analyzed as shown in Fig. 4. After S adsorption, d states of Pt or Pd atom spread out into lower energies and broaden, where the electron density overlaps with the p states of S. The density of d states of Pt or Pd atom close to the Fermi level is reduced relative to the before adsorption. These results indicate rehybridization of the surface atoms d states and the S atom p states form strong covalent bonds. In Fig. 4c, the two overlap areas of the density of states of the F1 located at around −11.5 and −19.7 eV, respectively, are lower than those of the F2 counterparts (Fig. 4c, at around −11.2 and −19.4 eV, respectively), indicating a stronger interaction between the S and surface atom result in a larger adsorption energy of when S is adsorbed at the F1 site. The overlap population values of S at the F1 and F2 sites on Pt–1Pd(111) surface as shown in Table 5. The overlap population value for Pt–Pt and Pt–Pd bonds on the first layer decrease when S is adsorbed on the first layer decrease when S is adsorbed on the pt–1Pd(111) surface. This suggests that the Pt–Pt and Pt–Pd bonds of the surface weakened due to the adsorption of S atom. The Pt–S bond is stronger than Pd–S bond as shown the overlap population value when S adsorb at the F2 site. The result is agreed with the bond length (0.53 for Pt–S and 0.27 for Pd–S). | ||
| Fig. 4 Partial density of states (PDOS) of S adsorption on Pt–1Pd(111): (a) isolated S, (b) S at the F1 site, (c) S at the F2 site. | ||
| System | Surface | |||||
|---|---|---|---|---|---|---|
| PtS–PtS | PtS–Pt | Pt–Pd | PtS–Pd | PtS–S | Pd–S | |
| a S atom of connecting with S atom. | ||||||
| F1 | 0.24 | 0.17 | 0.51 | |||
| F2 | 0.24 | 0.53 | 0.12 | −0.13 | 0.53 | 0.27 |
We calculated the Hirshfeld atomic charges for different atoms after S adsorption on metal surface as shown in Table 6. When S is adsorbed on the Pt(111) surface, the electronic charge of surface Pt atom connecting with S atom is decreased 0.033e−. S atom gains a negative charge 0.020e−, so there is transference of electron density from the Pt of surface atoms to the adsorbed S atom. When S is adsorbed on the Pt–nPd(111) (n = 1–3) surface, the electronic charge of surface Pt atom is reduced about 0.039e−,0.052e− and 0.069e− comparing with the clean alloy surface, respectively. The electronic charge of Pd atom has a small decrease, especially the Pd atom connecting with the S atom. The electron transference towards S atom is 0.040e−, 0.088e− and 0.137e− (more than on Pt (111) surface), respectively. When S is adsorbed on the Pt–4Pd (111) and Pd (111) surface, the electronic charge of surface Pd atom connecting with S atom decreases 0.07e− and 0.073e−. The electron transference toward S atom (0.189e− and 0.190e−) is higher than in the previous case. The electronic charges of second layer atoms have increase when S is adsorbed on (111) surface.
| System | Atom | Charge |
|---|---|---|
| a a second layer atom. s atom of connecting with S atom. Values in parentheses are charges of no adsorption. | ||
| S/Pt | Pts | 0.017(−0.016) |
| Pt | −0.027(−0.016) | |
| Pta | −0.04(0.013) | |
| S | −0.020(0) | |
| S/Pt–1Pd | Pts | −0.029(−0.068) |
| Pd | 0.187(0.190) | |
| Pta | −0.015(0) | |
| S | −0.040(0) | |
| S/Pt–2Pd | Pts | −0.070(−0.122) |
| Pds | 0.189(0.148) | |
| Pd | 0.150(0.148) | |
| Pta | −0.028(−0.014) | |
| S | −0.088(0) | |
| S/Pt–3Pd | Pts | −0.111(−0.180) |
| Pds | 0.153(0.099) | |
| Pd | 0.112(0.099) | |
| Pta | −0.043(−0.030) | |
| S | −0.137(0) | |
| S/Pt–4Pd | Pds | 0.117(0.047) |
| Pd | 0.072(0.047) | |
| Pta | −0.058(−0.048) | |
| S | −0.189(0) | |
| S/Pd | Pds | 0.060(−0.013) |
| Pd | 0.008(−0.013) | |
| Pda | −0.002(0.011) | |
| S | −0.190(0) | |
The PDOS of HS adsorbed at the B1 and B2 sites on Pt–1Pd surface is given in Fig. S1 of the ESI.† The same as S adsorption, d states of Pt or Pd atom spread out into lower energies and broaden, where the electron density overlaps with the p states of S. In Fig. S1a,† the two overlap areas of the density of states are about −12.5 and −19.8 eV, respectively, are lower than in Fig. S1b† (about −12.3 and −19.4 eV, respectively), indicating a stronger interaction between the HS and surface when HS is adsorbed at the B1 site.
The PDOS of H2S adsorbed at the T1 and T2 sites on Pt–1Pd surface is shown in Fig. 5. The H2S molecule possesses C2v symmetry; four valence states of H2S are marked 4a1, 2b2, 5a1, and 2b1 according to their orbital symmetries. The PDOS indicates that states 4a1 and 2b1 are contributed mainly from atomic orbitals 3s and 3p of the S atom, whereas 2b2 and 5a1 states arise from the hybridization of orbital 3p of the S atom and 1s of the H atom. From the Fig. 5a, we can see that the two sp states in gas phase H2S corresponding to S–H σ bond overlap the clean surface atom d-band. After S adsorption, the S 3p electron peak broadens and is shifted to the lower energy overlapping the d-orbital states of the surface atoms which itself shifts to lower energies, especially H2S at the T1 site. And all S 3p atomic orbital of adsorbed H2S have significant overlaps with the d orbital of the atom that is bound to the H2S molecule, especially the Pt atom. This indicates that the occupancies of the metal d states and S 3p states have redistributed to an increased occupancy at lower energies due to the interaction of S and surface atoms. These results are consistent with the previous studies of H2S adsorption on Pd–Ni and Pd–Cu alloys.39 As shown in Fig. 5b, the overlap peak appeared at around −21.0 and −10.2 eV when H2S on the T1 site, lower than that of the T2 site, −20.4 and −9.5 eV (Fig. 5c), indicating a strong interaction and more adsorption energy of H2S on the T1 site on the T1 site. The calculated charges of the molecule H2S on the T1 and T2 are 0.1402e− and 0.0896e−, respectively. The results indicate that H2S → Pt charge transfer is stronger than that of H2S → Pd. From the above the analysis, we can conclude that the interaction of H2S with Pt atom is stronger than that of the Pd atom, explaining the fact that the T1 site is more stable than T2 for the adsorption of H2S.
 | ||
| Fig. 5 PDOS of H2S adsorption on Pt–1Pd(111): (a) gas H2S, (b) H2S at the T1 site, (c) H2S at the T2 site. | ||
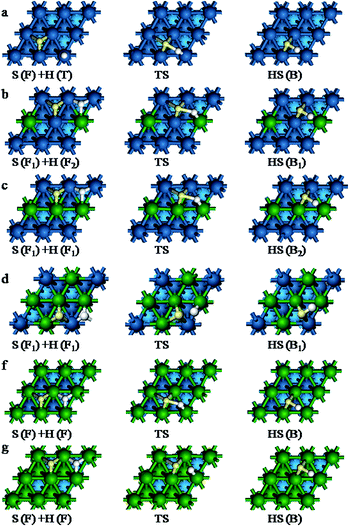
3.4 Hydrogenation of sulfur
After determined the preferable adsorption sites for S, HS, H2S and H, we also explore the possible reaction pathways for the full hydrogenation of S to H2S. Because alloys break up the homogeneity of the surface, modelling surface reactions on alloys is more complex than on pure metals.40 Thus, only the important reactions are considered. The vibrational frequencies of all transition states are listed in Table S1 of the ESI.†| Reaction | Ea (eV) | ΔE (eV) | dS–H (Å) | dS–Pt (Å) | dS–Pd (Å) |
|---|---|---|---|---|---|
| Pt | |||||
| S + H → HS | 0.92 | 0.65 | 1.641(1.377) | 2.357(2.380) | |
| HS + H → H2S | 0.59 | 0.44 | 1.906(1.366) | 2.332(2.386) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Pt–1Pd | |||||
| S(F1) + H → HS | 0.91 | 0.47 | 1.779(1.375) | 2.356(2.370) | |
| HS (B1) + H → H2S | 0.62 | 0.41 | 1.803(1.367) | 2.345(2.372) | |
| S(F2) + H → HS | 0.72 | 0.51 | 1.711(1.376) | 2.337(2.371) | |
| HS (B2) + H → H2S | 0.58 | 0.40 | 1.733(1.367) | 2.362(2.370) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Pt–2Pd | |||||
| S(F1) + H → HS | 0.96 | 0.52 | 1.764(1.375) | 2.336(2.343) | 2.343(2.414) |
| HS (B1) + H → H2S | 0.62 | 0.55 | 1.746(1.367) | 2.388(2.358) | |
| S(F2) + H → HS | 0.74 | 0.52 | 1.626(1.376) | 2.336(2.348) | 2.376(2.414) |
| HS (B2) + H → H2S | 0.71 | 0.52 | 2.315(1.368) | 2.334(2.355) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Pt–3Pd | |||||
| S(F1) + H → HS | 0.74 | 0.36 | 1.752(1.377) | 2.331(2.341) | 2.332(2.404) |
| HS (B1) + H → H2S | 0.67 | 0.50 | 1.812(1.364) | 2.413(2.401) | |
| S(F2) + H → HS | 0.76 | 0.55 | 1.625(1.373) | 2.352(2.379) | |
| HS (B2) + H → H2S | 0.85 | 0.56 | 1.631(1.362) | 2.344(2.388) | |
| 0.5 | |||||
| Pt–4Pd | |||||
| S + H → HS | 0.69 | 0.40 | 1.746(1.376) | 2.313(2.369) | |
| HS + H → H2S | 0.70 | 0.45 | 1.810(1.365) | 2.482(2.373) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Pd | |||||
| S + H → HS | 0.61 | 0.35 | 1.747(1.377) | 2.324(2.373) | |
| HS + H → H2S | 0.79 | 0.42 | 2.249(1.365) | 2.362(2.392) | |
Our calculation demonstrates that the reactions on different surfaces are all endothermic and the predicted energy change varies from 0.35 to 0.65 eV. The barrier is found to be moderately higher on Pt(111) and the path (I) of the Pt–nPd(111) (n = 1–2). On Pt(111), the reaction energy of S hydrogenation is 0.65 eV which is 0.10–0.20 eV higher than on Pt–Pd alloys metal and Pd(111). On Pt–nPd(111) (n = 1–2), the barrier of the path (II) is 0.72 and 0.74 eV, respectively, which is lower than that of the reaction path (I). On the different alloy surfaces, the transition states are structurally more product-like than reactant-like. At the transition state, the S–H distance is 1.625–1.779 Å, longer by 0.235–0.404 Å compared to the product. For the S–Pt and S–Pd corresponding bond length are 2.331–2.357 Å and 2.313–2.343 Å, and they are reduced by 0.01–0.05 Å.
To determine whether the incorporation of Pd into Pt could increase the ability of the catalyst to hydrogenation reaction of S, we need to consider how the alloying affects the following: (a) the overall reaction energy, (b) the energy change associated with each step, and (c) the activation energy barriers. This can be done by comparing the energetic pathways for each of the metal surfaces.34 A detailed energy profile for the hydrogenation reaction of S is presented in Fig. 8. The hydrogenation of the adsorbed S and H to H2S is a quite difficult process due to its overall endothermicity of >2.00 eV on the different alloy surface. The energy of the overall reaction significantly decreased by 0.30–0.55 eV comparing with pure Pt(111) due to doping Pd. This suggests that the addition of Pd into Pt can improve the reactivity for the hydrogenation of S. In the S + H → HS reaction, the barrier of all Pt–Pd alloys decrease except for the path (I) on Pt–2Pd(111) compared to the Pt(111). In the HS + H → H2S reaction, there are lower barrier on Pt–1Pd(111). As shown in Table 7, the barriers of Pt–1Pd(111) are 0.58 and 0.62 eV almost equalling with on Pt(111). From above analysis, we can see that Pt–1Pd alloy will enhance the active of the catalyst and promote the hydrogenation reaction of S.
The lower barriers on the Pt–1Pd(111) indicate that the hydrogenation reaction should proceed at lower temperatures. However, the reverse reaction dehydrogenation on Pt–1Pd(111) from H2S → H + HS and HS → H + S have low barriers of 0.42 and 0.21 eV in path (I), 0.21 and 0.18 eV in path (II), respectively. This indicates that the reverse process is more likely to occur, especially below room temperature. On Pt–1Pd(111), the reaction barrier of the path (I) is 0.91 eV which is 0.19 eV higher than the path (II) in S + H → HS reaction. The smaller barrier for path (II) can be attributed to the fact that the adsorption energy of the initial states is smaller and the weaker S–surface bond before dissociation. In the HS + H → H2S reaction, both the barriers in the path (I) and path (II) are almost equal with each other, about 0.62 and 0.58 eV. To elaborate the most likely pathway of the S hydrogenation reaction on Pt–1Pd(111), the rate constants when S on F1 site and F2 site are calculated according to the previous reports, respectively.42 We calculate that the rate constants k of the path (II) are 2.6 × 107 and 3.7 × 107, 7 and 5 orders larger than that of the path (I) in S + H → HS and HS + H → H2S reaction at 300 K, respectively. This suggests that the rate of the path (II) in the S hydrogenation is quicker than path (I).
4. Conclusion
Density functional theory calculations were employed to investigate possible adsorption structures and the mainly reaction pathways for the hydrogenation reactions of the S at the different adsorption sites on Pt(111), Pt–nPd(111) (n = 1–4) and Pd(111). H2S molecule was quite weakly adsorbed, favouring the top site and with the molecular plane lying parallel to the surface. HS and S interact strongly with the surfaces comparing with H2S and were adsorbed preferentially on the bridge, fcc and top sites. On Pt–nPd(111) (n = 1–3), the preferred adsorption site for S, HS and H2S was on the F1, B1 and T1 sites, respectively. H was preferentially adsorbed on the T and T1 site. On the Pt(111) and Pt–nPd(111) (n = 1–3), respectively. While on Pt–4Pd(111) and Pd(111), H was preferentially adsorbed on the F site. The adsorption energy of S, HS, H2S and H was weaker on Pt(111) than on Pt–nPd(111) (n = 1–4). It has been found that Pd atom has a lower attraction to S, HS, H2S and H compared to Pt atom. PDOS analysis indicated that the width of the occupied portion of the d-band of Pt atom is wider than Pd atom. Pt atom and adsorbate have significant overlapping than Pd atom.Our calculation demonstrated energy barriers for the formation of HS on the Pt–Pd(111) alloy surface are lower than on Pt(111). We think the result is due to the new sites with high hydrogenation activity were probably created in the Pt–Pd catalyst. The energy of the overall reaction significantly decreased on Pt–Pd alloy surface comparing with pure Pt(111), suggesting the lower energy for the hydrogenation reaction. From the above, the Pt–Pd alloy catalysts enhanced the hydrogenation activity. On Pt–1Pd(111), there are two reaction paths, the reaction barrier of the path (I) is 0.91 eV which is 0.18 eV higher than path (II) in the S + H → HS reaction. In the HS + H → H2S reaction, both the barriers in the path (I) and path (II) are almost equal with each other, about 0.62 and 0.58 eV. From our calculated potential energy surfaces and the rate constant, the path (II) would be preferable in theory. However, adsorption energy of S at the F1 is larger than that for S at the F2 site, making the reaction of the path (I) might show its possibility as a competitive pathway.
This theoretical work provides a systematic study to understand the effect of alloying elements, by analyzing the adsorption energy, electric structure and hydrogenation reaction. Our calculation results show that Pt–Pd alloy catalysts, especially Pt–1Pd catalyst, can enhance the hydrogenation activity of S. This could provide the guide to the development of highly active catalysts.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 51502348) and the Fundamental Research Funds for the central Universities (R1510062A, 14CX05038A and 13CX02018A).References
- B. C. Gates, Catal. Chem., Wiley, New York, 1992 Search PubMed.
- R. I. Masel, Principles of Adsorption and Reaction on Solid Surfaces, Wiley, New York, 1996 Search PubMed.
- M. Kiskinova, Surf. Sci. Rep., 1998, 8, 359 CrossRef.
- D. W. Goodman, J. Phys. Chem., 1996, 100, 13090 CrossRef CAS.
- L. I. Ali, A. A. Ali, S. M. Aboul-Fotouh and A. K. Aboul-Gheit, Appl. Catal., A, 1999, 177, 99 CrossRef CAS.
- V. G. Baldovino-Medrano, S. A. Giraldo and A. Centeno, Fuel, 2010, 89, 1012 CrossRef CAS.
- J. R. Chang and S. L. J. Chang, Catal., 1998, 176, 42 CrossRef CAS.
- C. Song and A. D. Schmitz, Energy Fuels, 1997, 11, 656 CrossRef CAS.
- A. Corma, A. Martínez and V. J. Martínez-Soria, Catal., 1997, 169, 480 CrossRef CAS.
- M. Vaarkamp, W. Dijkstra, B. H. Reesink and P. H. Berben, Prepr.–Am. Chem. Soc., Div. Pet. Chem., 1998, 43, 77 CAS.
- J. Lee and H. J. Rhee, Catal., 1998, 177, 208 CrossRef CAS.
- H. Yasuda and Y. Yoshimura, Catal. Lett., 1997, 46, 43 CrossRef CAS.
- A. Niquille-Röthlisberger and R. Prins, J. Catal., 2006, 242, 207 CrossRef.
- H. Jiang, H. Yang, R. Hawkins and Z. Ring, Catal. Today, 2007, 125, 282 CrossRef CAS.
- B. J. Delley, Chem. Phys., 1990, 92, 508 CAS.
- B. J. Delley, Chem. Phys., 1996, 100, 610 Search PubMed.
- X. Q. Gong, A. Selloni, M. Batzill and U. Diebold, Nat. Mater., 2006, 5, 665 CrossRef CAS PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- R. Garćla-Muelas, Q. Li and N. Lopez, ACS Catal., 2015, 5, 1027 CrossRef.
- B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155125 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- C. Popa, W. K. Offrmans, R. A. V. Santen and A. P. Jansen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 155428 CrossRef.
- B. R. Coles, J. Inst. Met., 1956, 84, 346 CAS.
- A. Michaelides and P. Hu, J. Chem. Phys., 2001, 115, 8570 CrossRef CAS.
- D. R. Alfonso, A. V. Cugini and D. C. Sorescu, Catal. Today, 2005, 99, 315 CrossRef.
- H. Y. Zhu, W. Y. Guo, R. B. Jiang, L. M. Zhao, X. Q. Lu, M. Li, D. L. Fu and H. H. Shan, Langmuir, 2010, 26, 12017 CrossRef CAS PubMed.
- D. R. Papai and C. M. Salahub, Surf. Sci., 1999, 236, 241 CrossRef.
- T. A. Halgren and W. N. Lipscomb, Chem. Phys. Lett., 1977, 49, 225 CrossRef.
- W. F. K. Wynne-Jones and H. Eying, J. Chem. Phys., 1935, 3, 492 CrossRef.
- R. J. Koestner, M. Salmeron, E. B. Kollin and J. L. Gland, Chem. Phys. Lett., 1986, 125, 134 CrossRef.
- R. C. Shiell, X. K. Hu, Q. J. Hu and J. W. Hepburn, J. Phys. Chem. A, 2000, 104, 4339 CrossRef.
- J. A. Rodriguez, S. Chaturvedi, M. Kuhn and J. Hrbek, J. Phys. Chem. B, 1998, 102, 5511 CrossRef.
- E. J. Albenze and A. Shamsi, Surf. Sci., 2006, 600, 3202 CrossRef.
- V. Mokrushin, V. Bedanov, W. Tsang, M. Zachariah and V. Knyazev, ChemRate, version 1.5.2, National Institute of Standards and Technology, Gaithersburg, MD, 2006 Search PubMed.
- D. R. Alfonso, A. V. Cugini and D. C. Sorescu, Catal. Today, 2005, 99, 315 CrossRef.
- G. Papoian, J. K. Nørskov and R. J. Hoffmann, J. Am. Chem. Soc., 2000, 122, 4129 CrossRef.
- L. J. Richter and W. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 9797 CrossRef.
- E. Ozdogan and J. Wilcox, J. Phys. Chem. B, 2010, 114, 12851 CrossRef CAS PubMed.
- M. P. Hyman, B. T. Loveless and J. W. Medlin, Surf. Sci., 2007, 601, 5382 CrossRef CAS.
- A. Michaelides and P. Hu, J. Chem. Phys., 2001, 115, 8570 CrossRef CAS.
- T. S. Rufael, J. Prasad, D. A. Fischer and J. L. Gland, Surf. Sci., 1992, 78, 4 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra20087c |
| This journal is © The Royal Society of Chemistry 2016 |