Theoretical evaluation of lanthanide binding tags as biomolecular handles for the organization of single ion magnets and spin qubits†
Lorena E.
Rosaleny
and
Alejandro
Gaita-Ariño
*
Instituto de Ciencia Molecular, Universitat de València, c/ Catedrático José Beltrán, 2, 4980, Paterna, Spain. E-mail: alejandro.gaita@uv.es; Fax: +34 96354 3273; Tel: +34 96354 4421
First published on 20th October 2015
Abstract
Lanthanoid complexes are amongst the most promising compounds both in single ion magnetism and as molecular spin qubits, but their organization remains an open problem. We propose to combine Lanthanide Binding Tags (LBTs) with recombinant proteins as a path for an extremely specific and spatially-resolved organisation of lanthanoid ions as spin qubits. We develop a new computational subroutine for the freely available code SIMPRE that allows an inexpensive estimate of quantum decoherence times and qubit–qubit interaction strengths. We use this subroutine to evaluate our proposal theoretically for 63 different systems. We evaluate their behavior as single ion magnets and estimate both decoherence caused by the nuclear spin bath and the interqubit interaction strength by dipolar coupling. We conclude that Dy3+ LBT complexes are expected to behave as SIMs, but Yb3+ derivatives should be better spin qubits.
Introduction
The spatially controlled positioning of functional building blocks by self-assembly is one of the fundamental visions of nanotechnology. The organisation of devices with a resolution scale below the nanometer and total sizes above the micrometer is a characteristic of molecular biology. Since the first use of ferritin as a template for magnetic nanoparticles,1 major steps towards this goal have been achieved as a part of what has been called synthetic biology.2 DNA has been used as a programmable building block,3 while short, self-assembling peptides have been shown to form a variety of stable nanostructures which have already been used for the rational design of functional devices.4This bio-nanotechnological strategy will eventually be applied for quantum computing purposes, where the challenging goal of scalability requires the ability to organize different kinds of quantum building blocks. Obviously, the use of biopolymers to control quantum effects in complex organized systems is still a long-term goal. Nevertheless, the nascent field of quantum biology, devoted to the study of coherent quantum effects in processes as diverse as photosynthesis in plants,5 geolocation in birds6 and possibly smell in insects,7 shows that this complex organization of quantum coherent processes already takes place in nature. The challenge is then to achieve this artificially.
Spin-carrying metalloproteins, which are already being studied by manipulating their quantum states via pulsed EPR,8 are promising systems for this synthetic quantum biology. We will focus on magnetic lanthanoid complexes because of the interest they awaken both as Single Ion Magnets (SIMs) and as spin qubits, that is, because of their favourable magnetic and quantum properties.9
A key experimental advance in this context is Lanthanide Binding Tags (LBTs). These are oligopeptides based on calcium-binding motifs of EF-hand proteins10 that have been designed to interact very specifically with lanthanoids.11
These new building blocks constitute a key advance towards an interdisciplinary region, since an LBT can be seen not only as a small part of a protein but also as a standard coordination complex. LBTs are easily incorporated at the DNA level into any recombinant protein, a potential route to highly complex organisation, e.g. via histones (Fig. 1).14
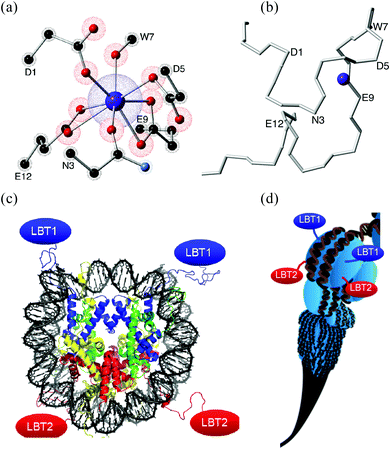 | ||
| Fig. 1 (a) Coordination environment created by a 17 aminoacid-long LBT. Only the coordinating lateral residues are shown, α-carbons are labeled. (b) Polypeptidic chain of the LBT without lateral residues, the α-carbons of aminoacids involved in the coordination sphere are labeled. (c) Each nucleosome (8 histones) could organise up to 8 LBTs (4 shown). (d) Nucleosome Positioning Sequences12 could organise a scalable sequence of nucleosomes. (c) & (d) Reproduced with permission from ref. 13. | ||
The first goal of this work is the development of a new computational subroutine to allow an inexpensive estimate of decoherence times and interaction strengths. A tool of this kind is lacking in the field: while wavefunctions are routinely calculated, only general arguments are given concerning the tunneling gap and its relation to decoherence, but detailed numbers are rarely offered. A second purpose will be to theoretically explore the possibility of using LBT for organising the lanthanoid ions, either for their use as SIMs or as spin qubits. This necessarily includes obtaining realistic estimates for decoherence times and interaction strengths that pave the way for the first experimental studies.
Results and discussion
We used SIMPRE, a tool commonly applied in the field of magnetic lanthanoid complexes, to study Ln–LBT complexes for the nine published crystallographically different LBT coordination environments (see Methods: Structures), using Ln = Nd, Tb, Dy, Ho, Er, Tm, Yb. Five of them correspond to LBTs designed for the exclusion of water and have analogous 8-coordinated environments: two bidentate carboxylates, three monodentate carboxylates, and a carbonyl group belonging to the LBT backbone. The remaining four, designed for an efficient interchange of water for their use as NMR contrast agents, are remarkably diverse, with a variable number of carboxilate groups and water molecules in the vicinity of the lanthanoid.First we analyzed the aptitude of these systems as single ion magnets. Next, we started from this set of energy levels and wavefunctions and used a specially crafted version of SIMPRE to calculate the expected quantum decoherence due to interaction of the electron spin qubit with the nuclear spins in the biomolecule, both in the native form and after deuteration (see Methods: Calculations). Finally we calculated interqubit coupling, which needs to be strong enough for two-qubit quantum gates to happen within the coherent time window.
Single molecule magnet behavior
We obtained the energy level scheme and the wavefunctions in a moderate field (0.32 T), to get rid of the hyperfine crossings due to the interaction with the lanthanoid nuclear spins, which our current model does not take into account. Note that this method cannot by itself predict SMM behavior, as this depends on many effects not included in the model, such as Raman processes. Nevertheless, the energy level scheme can be related to the single ion magnet potential, considering that it is more common to find SIM behavior in two-level systems with a marked Ising character. Thus, we calculated (a) the expectation values (〈Jz〉), which should be a maximum for an Ising character and (b) the ratio between the energy barrier (Ω) to the first excited state and the gap (Δ) within the ground doublet, which should be a maximum for a two-level system. Note that large tunneling energies tend to result in fast temperature-independent spin dynamics, while the presence of low-lying excited states tends to favour a fast thermal relaxation. Thus, complexes with low Ω/Δ ratios are not expected to present slow relaxation of the magnetization. We represent the results grouped by metal in box-and-whisker diagrams, which graphically divide the data into four quartiles, in order to give a visual idea of the expected character of LBT complexes and of the robustness of these expectations. The expectation values of 〈Jz〉 are a maximum for Dy and Er (Fig. 2, other metals in Fig. S1†). The most favourable Ω/Δ ratios are obtained for Yb, Nd and Dy (Yb and Dy in Fig. 3, other metals in Fig. S2†).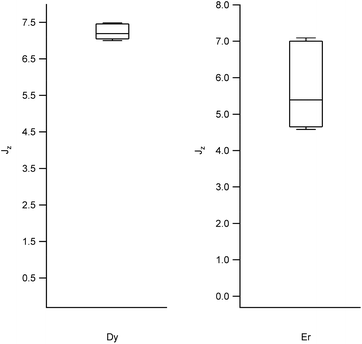 | ||
| Fig. 2 Box plots with the full distribution of expectation values 〈Jz〉 for diverse LBT structures substituted by Dy (left) and Er (right). | ||
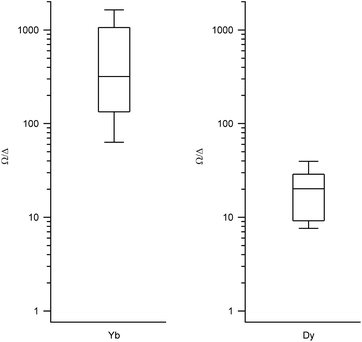 | ||
| Fig. 3 Box plots with the full distribution of Ω/Δ ratios for diverse LBT structures substituted by Yb (left) and Dy (right). | ||
In all the structures studied, the expectation values 〈Jz〉 stay close to the maximum theoretical values for both Dy and Er, that is, an almost pure Ising behavior is obtained for those two metals. This contrasts with the rest of the series, where a dispersion of behaviors is obtained. The second relevant parameter is the energy level scheme, here summarized in the Ω/Δ ratio. From this point of view, Yb and Nd are unrivalled, with values that routinely go over a 100 and never below 10, and Dy is an acceptable compromise, with a rather narrow distribution around Ω/Δ = 10. This means that, within the expected variation of coordination environments in LBT complexes, only Dy is consistently expected to show single molecule magnet behavior.
Decoherence from the nuclear spin bath
We work with the same set of energy level schemes and wavefunctions at 0.32 T, which is a typical value for the X-band in a pulse EPR setup. As quantitative estimates of the qubit potential of the different complexes, we take into account both (a) the previously calculated Ω/Δ ratio, which in this context quantifies the separation of the qubit states from the rest of the spectrum, and (b) the decoherence time τ considering only the coupling with the nuclear spin bath. As this is controlled by the tunneling gap, this is expected to be roughly proportional to the coupling with magnons, which are the second source of decoherence. The third main source of decoherence, namely the coupling with phonons, is related with the rigidity of the coordination environment, and thus is expected to be approximately constant. Again, we represent the results grouped by metal in box-and-whisker diagrams, in order to give a visual idea of the expected quality as spin qubits of LBT complexes and of the robustness of these expectations. The estimated ranges of τ are wide and tend to reach higher values in the best cases for Yb, Tb, Tm and Ho, while being consistently narrow and grouped around low values for Dy, Er and Nd (Tb and Yb in Fig. 4, other metals in Fig. S3†). According to this methodology and because of the different magnetogyric ratios in H and D, deuteration extends decoherence time by a factor of 15.2 in all cases, meaning all calculated times in Fig. 4 and S3† can be extended by up to an order of magnitude, but only if fully deuterated peptides were used. The vast number of experimental possibilities that ranges from labeling of the closest protons to perdeuteration results in a range of calculated decoherence times.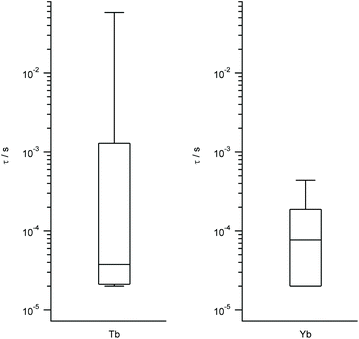 | ||
| Fig. 4 Box plots with the full distribution of estimates decoherence times τ for diverse LBT structures substituted by Tb (left) and Yb (right). | ||
Interqubit coupling
Let us use 2OJR, a polypeptide with a double-lanthanide-binding tag (see Methods) as an example to estimate the expected order of magnitude for the interqubit coupling in these kinds of systems. In 2OJR, the two lanthanoid ions bound to the same polypeptide are at a distance of r = 19.1 Å.Because of the nature of dipolar coupling, the relative orientation between the magnetic axes and the field establishes a vanishing lower bound for the coupling between two ions. Therefore, we estimate here the upper bounds for interqubit coupling in double-lanthanide-binding tags, assuming an optimal alignment between the magnetic axes of two neighbouring magnetic complexes. We do this for two extreme examples: Tm and Dy. Both ions present an adequate energetic isolation of the ground doublet: (Ω/Δ)Tm = 7.97, (Ω/Δ)Dy = 26.69, but, as discussed below, are practically opposite in the nature of their ground doublets.
In the case of Tm[2OJR], the ground doublet has an easy plane character, and as a result the expectation values are dominated by the x orientation (see Table 1). In turn, these result in the following differences (Δ01Hα) between the fields (Hα) created by the two qubit states |Ψ0〉, |Ψ1〉 of a Tm site on a neighbouring Tm site: Δ01Hx = 1.10 mT, Δ01Hy = 0.99 mT, Δ01Hz = 0.29 mT. This means an upper limit of 0.198 μeV for the interqubit coupling.
| Main MJ components (weight) | 〈J〉 | |
|---|---|---|
| |0, Dy〉 | |−15/2〉 (95%) | 〈Jxy〉 = 0.59 |
| 〈Jz〉 = 7.29 | ||
| |1, Dy〉 | |+15/2〉 (95%) | 〈Jxy〉 = 0.61 |
| 〈Jz〉 = −7.28 | ||
| |0, Tm〉 | |−3〉 (10%), |0〉 (58%), |+3〉 (10%) | 〈Jxy〉 = 3.29 |
| 〈Jz〉 = 0.03 | ||
| |1, Tm〉 | |−4〉 (8%), |−2〉 (32%), |+2〉 (32%), |+4〉 (8%) | 〈Jxy〉 = 6.40 |
| 〈Jz〉 = −0.01 |
For Dy[2OJR], the ground doublet has a marked easy axis character, with almost maximal expectation values 〈Jz〉 (see Table 1). These relatively high magnetic moments result in correspondingly larger differences Δ01Hα between the field created by the two qubit states |Ψ0〉, |Ψ1〉 of a Dy site on a neighbouring Dy site: Δ01Hx = 4.20 mT, Δ01Hy = 2.17 mT, Δ01Hz = 1.49 mT. This means an upper limit of 3.54 μeV for the interqubit coupling.
A dipolar interaction that cannot be switched off (“always-on”) in the order of the μeV means times for swap operations in the order of the nanosecond, which is also the order of magnitude for pulsed EPR operations. It is also within technologically accessible limits (1–100 GHz, i.e. 4–400 μeV or 0.05–5 K). According to this estimate and considering decoherence times as calculated above, this approach is then theoretically feasible. The ability of proteins to produce an on-demand spatial distribution of qubits means any conceivable scheme of dipolar couplings is available. Of course, in order to actually exploit polypeptide-organized qubits for a scalable quantum information processor, a new operating scheme would need to be developed. Lloyd's proposal, based on a periodic organisation of three different qubit types, would probably be a good start for this, as it is based on energetic, rather than spatial, addressing of the qubits.15
Conclusions
Including lanthanide binding tags in recombinant proteins constitutes a very promising pathway for the engineering of highly complex quantum structures, especially given the power of combinatorial peptide libraries.16 The calculations performed in this work allowed a general estimate of the crystal field created by these polypeptides, and thus an order-of-magnitude prediction of the magnetic and quantum properties in analogous complexes. This is needed both to guide the preparation of new LBT complexes and to prioritize the experimental study of those cases where it has not yet been possible to obtain crystals, a common problem with biopolymers. Thus, out of Nd, Tb, Dy, Ho, Er, Tm and Yb, we were able to confirm that only Dy is consistently expected to produce single molecule magnet behavior in a biological context; as LBTs are chiral these are expected to behave as chiral magnets. We also have determined that Yb is the best spin qubit candidate, combining a good isolation of the ground doublet from the first excited state and a certain protection from dipolar decoherence. From the methodological point of view, we have developed an extension to the freely distributable tool SIMPRE which adds the capability of inexpensively offering an inexpensive estimate of both (i) the decoherence time originated by the hydrogen nuclear spin bath and (ii) the through-space qubit–qubit interaction strength. It has to be remarked that this is a first effort and that more refined computational methods will need to be developed to calculate all sources of decoherence, in particular phonon-caused decoherence.Methods
Structures: from X-ray to coordination sphere
The structures used for SIMPRE calculations were downloaded from the Protein Data Bank (PDB) and are identified by their PDB Ids, as follows.1TJB is a 2.0 Å resolution X-ray crystal structure of a 17-residue lanthanide-binding peptide, complexed with Tb3+, which excludes water molecules from the primary coordination sphere.17 There are two crystallographically independent metal sites, corresponding to two separate copies of the same LBT.
2OJR is a construct of a double-lanthanide-binding tag as an N-terminal fusion of ubiquitin complexed with Tb3+, with a 2.60 Å resolution.18
3LTQ is a 2.1 Å X-ray crystal structure of a construct containing an LBT insert between the middle S-loop residues of interleukin-1β complexed with Tb3+.19 There is only one crystallographically independent metal site.
3VDZ is a 2.4 Å X-ray crystal structure of a modified dLBT-ubiquitin chimera complexed with Gd3+. The LBT sequence was modified to (a) enhance the exchange of water molecules in the vicinity of the magnetic site, (b) keep a high affinity for the lanthanoid and (c) favour crystallization. There are four crystallographically independent metal sites, corresponding to two separate copies of a “dinuclear” peptide.20
For all metal sites in 1TJB, 2OJR and 3LTQ, we considered eight oxygen atoms in the coordination sphere: two bidentate carboxylates, three monodentate carboxylates, and a carbonyl group belonging to the LBT backbone.
In contrast, the coordination spheres in 3VDZ are more diverse and less well-defined, up to the point where the considered coordination number is somewhat arbitrary. A r < 3.5 Å criterion results in eight oxygen atoms in the coordination sphere. One of these always belongs to a backbone carbonyl group, while the rest, depending on the cases, are from three to five carboxilate groups and either zero or one water molecule.
Hydrogen atoms were not resolved crystallographically, and instead their positions were estimated with Mercury software. As our purpose is to estimate the order of magnitude effect of a hydrogen cloud in peptide-coordinated lanthanoid ions, this lack of precision in the coordinates of each particular H atom is not considered critical.
Lanthanoid complexes are commonly isostructural to each other, with the metal–ligand bond distance being the main structural parameter that varies with the nature of the metal. Thus, we adapted the coordination environment from the original Ln = Tb/Gd structures to the complete series Ln = Nd, Tb, Dy, Ho, Er, Tm, Yb by changing the radial coordinates in the coordination sphere according to the variation in the ionic radii (see Table S1†).
Calculations: expectation values, decoherence times
The crystal field Hamiltonian was solved with SIMPRE,21 building upon previous results so that we are able to work with no adjustable parameters (see Table S2†).22 A minor modification allows the introduction of the magnetic field as a diagonal component in the Hamiltonian. We use the energy level structure in the presence of this field to define, for the purposes of this paper, Δ as the energy difference between the ground state and the first excited state and Ω as the energy difference between the ground state and the second excited states. This has the advantage of allowing an automated processing of the data. In terms of evaluating Two-Level Systems (TLSs), this simple definition means that those among the non-Kramers systems which do not actually present a TLS are instead considered as merely low-quality TLSs because of their very low (Ω/(Δ ratio.Note also that the current version of SIMPRE automatically chooses the orientation of the coordinate axes that correspond to the most simple expression of the wavefunction, and applies the magnetic field in this z direction. We maintain the standard definition of Δ as an extradiagonal term in the qubit basis, meaning that we redefine the qubit states and that they do not necessarily correspond to the spin being aligned with the easy axis of magnetization. In turn, this results in sub-optimal decoherence times. As a test case, we chose the case of Yb[3VDZ4], as Yb3+ is the ion for which we calculated the longest decoherence times and Yb[3VDZ4] is the LBT complex where Yb3+ is expected to present the most marked Ising behavior: MJ = +7/2 accounts for 92% of the wavefunction, resulting in an expectation value 〈Jz〉 = 3.2 and a decoherence time due to the nuclear spin bath τ = 5.2 × 10−5 s, which is among the lowest calculated for Yb[LBT] complexes. After a 90° rotation of the molecule, the field is along a hard axis and therefore there is a quenching of the expectation value 〈Jz〉 = 0.33. As a consequence, the calculated decoherence time rises to τ = 5.7 × 10−4 s which is among the highest calculated for Yb[LBT] complexes. This is comparable with Yb[3VDZ5], the LBT complex described as an easy-plane behavior, with MJ = +1/2 accounts for 92% of the wavefunction, resulting in an expectation value 〈Jz〉 = 0.3 and decoherence time due to the nuclear spin bath τ = 4.7 × 10−4 s.
SIMPRE was further adapted to extract the expectation values of 〈Jα〉 (with α = x, y, z) from the wavefunctions, using the Pauli matrices σα:
| 〈Jα〉 = 〈ψ|σα|ψ〉 | (1) |
As we mainly intend to distinguish between Ising and non-Ising character here, in Table 1 we present 〈Jxy〉 = (〈Jx〉2 + 〈Jy〉2)1/2.
Moreover, this specially crafted version of SIMPRE also takes the coordinates of the hydrogen atoms as an input. Of course, there are an effectively infinite number of hydrogen nuclei in a crystal structure. A cutoff radius for the hydrogen nuclei to be included in our calculation is needed. We neglect every hydrogen nucleus which, on average, is expected to produce 1/100th of the effect produced by the hydrogen nucleus closest to the metal. As the hyperfine interaction falls with the third power of the distance, this means the cutoff radius is a factor of 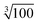 farther away than the nearest hydrogen atom.
farther away than the nearest hydrogen atom.
From the expectation values of 〈Jx〉, 〈Jy〉, 〈Jz〉 and these coordinates, the dipolar magnetic field (H) felt by each nucleus and the hyperfine interaction energy (E) can be trivially calculated, for each of the two states of the qubit.
 | (2) |
Of course, by including the nearest magnetic ion, this procedure can be immediately used to estimate the (dipolar) interqubit interaction strength. From the set of hyperfine interactions, we also estimate the nuclear spin bath decoherence time using the standard equation (eqn (3)).23 This estimate of decoherence depends on the sum of the energy differences, for each proton i between the two qubit states |0〉, |1〉. The decoherence time is then estimated as a function of the tunneling gap Δ and this energy sum (ωi = E0 − E1):
 | (3) |
Note that this model is only valid at low temperatures and in the cases where the tunneling splitting is much larger than the hyperfine couplings, something that is generally verified for lanthanoid ions, and fields of the order of hundreds of mT.25
For the representation of the results, box plots24 were generated with Wavemetrics’ IgorPro and include the full range of values.
Notes and references
- S. Mann, D. D. Archibald, J. M. Didymus, T. Douglas, B. R. Heywood, F. C. Meldrum and N. J. Reeves, Science, 1993, 261, 1286–1292 CAS.
- Y. Ding, F. Wu and C. Tan, Life, 2014, 4, 1092–1116 CrossRef CAS PubMed.
- T. Tørring, N. V. Voigt, J. Nangreave, H. Yan and K. V. Gothelf, Chem. Soc. Rev., 2011, 40, 5636–5646 RSC.
- A. Lakshmanan, S. Zhang and C. A. E. Hauser, Trends Biotechnol., 2012, 30, 155–165 CrossRef CAS PubMed.
- G. S. Engel, T. R. Calhoun, E. L. Read, T.-K. Ahn, T. Mancal, Y.-C. Cheng, R. E. Blankenship and G. R. Fleming, Nature, 2007, 446, 782–786 CrossRef CAS PubMed.
- N. Lambert, Y.-N. Chen, Y.-C. Cheng, C.-M. Li, G.-Y. Chen and F. Nori, Nat. Phys., 2013, 9, 10–18 CrossRef CAS.
- E. R. Bittner, A. Madalan, A. Czader and G. Roman, J. Chem. Phys., 2012, 137, 22A551 CrossRef PubMed.
- S. Lyubenova, T. Maly, K. Zwicker, U. Brandt, B. Ludwig and T. Prisner, Acc. Chem. Res., 2010, 43, 181–189 CrossRef CAS PubMed.
- R. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley, 2015 Search PubMed.
- M. Elbanowski and B. M
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) kowska, J. Photochem. Photobiol., A, 1996, 99, 85–92 CrossRef CAS.
kowska, J. Photochem. Photobiol., A, 1996, 99, 85–92 CrossRef CAS. - M. Nitz, K. J. Franz, R. L. Maglathlin and B. Imperiali, ChemBioChem, 2003, 4, 272–276 CrossRef CAS PubMed.
- K. Tóth, V. Böhm, C. Sellmann, M. Danner, J. Hanne, M. Berg, I. Barz, A. Gansen and J. Langowski, Cytom. Part J. Int. Soc. Anal. Cytol., 2013, 83, 839–846 CrossRef PubMed.
- (c) Modified with permission from Richard Wheeler (CC by-sa 3.0) Nucleosome_1KX5_colour_coded (d) Image modified with permission (CC by) from Marian L. Miller (Journal-Cover-Art.com), PLoS Genetics Issue Image, Vol. 4, 2008. PLoS Genet 4(3): ev04.i03.
- M. M. Müller and T. W. Muir, Chem. Rev., 2015, 115, 2296–2349 CrossRef PubMed.
- S. Lloyd, Science, 1993, 261, 1569–1571 CAS.
- B. P. Gray and K. C. Brown, Chem. Rev., 2014, 114, 1020–1081 CrossRef CAS PubMed.
- M. Nitz, M. Sherawat, K. J. Franz, E. Peisach, K. N. Allen and B. Imperiali, Angew. Chem., Int. Ed., 2004, 43, 3682–3685 CrossRef CAS PubMed.
- N. R. Silvaggi, L. J. Martin, H. Schwalbe, B. Imperiali and K. N. Allen, J. Am. Chem. Soc., 2007, 129, 7114–7120 CrossRef CAS PubMed.
- K. Barthelmes, A. M. Reynolds, E. Peisach, H. R. A. Jonker, N. J. DeNunzio, K. N. Allen, B. Imperiali and H. Schwalbe, J. Am. Chem. Soc., 2011, 133, 808–819 CrossRef CAS PubMed.
- K. D. Daughtry, L. J. Martin, A. Sarraju, B. Imperiali and K. N. Allen, ChemBioChem, 2012, 13, 2567–2574 CrossRef CAS PubMed.
- (a) J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2013, 34, 1961–1967 CrossRef; (b) J. J. Baldoví, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2014, 35, 1930–1934 CrossRef PubMed.
- (a) J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Dalton Trans., 2015, 44, 12535–12538 RSC; (b) J. J. Baldoví, J. M. Clemente-Juan, E. Coronado, Y. Duan, A. Gaita-Ariño and C. Giménez-Saiz, Inorg. Chem., 2014, 53, 9976–9980 CrossRef PubMed.
- S. Takahashi, I. S. Tupitsyn, J. van Tol, C. C. Beedle, D. N. Hendrickson and P. C. E. Stamp, Nature, 2011, 476, 76–79 CrossRef CAS PubMed.
- R. McGill, J. W. Tukey and W. A. Larsen, Am. Stat., 1978, 32, 12–16 Search PubMed.
- P. C. E. Stamp and I. S. Tupitsyn, Phys. Rev. B: Condens. Matter, 2004, 69, 014401 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: For all Ln3+ not included in Fig. 1, 2 and 3, results are in Fig. S1, S2 & S3. Parameters relevant to the calculations are in Tables S1 & S2. See DOI: 10.1039/c5qi00127g |
| This journal is © the Partner Organisations 2016 |
