Insights into structure and redox potential of lignin peroxidase from QM/MM calculations

Abstract

Redox potentials are computed for the active form (compound I) of lignin peroxidase (LiP) using a suitable QM/MM methodology (B3LYP/SDD/6-311G**//BP86/SVP:CHARMM). Allowing for dynamic conformational averaging, a potential of 0.67(33) V relative to ferrocenium/ferrocene is obtained for the active form with its oxoiron(IV) core. The computed redox potential is very sensitive to the charge distribution around the active site: protonation of titratable residues close to the metal center increases the redox potential, thereby rationalising the known pH dependence of LiP activity. A simple MM-charge deletion scheme is used to identify residues that are critical for the redox potential. Two mutant proteins are studied through homology modelling, E40Q and D183N, which are predicted to have an increased redox potential by 140 mV and 190 mV, respectively, relative to the wild type. These mutant proteins are thus promising targets for synthesis and further exploration toward a rational design of biocatalytic systems for oxidative degradation of lignin.

---

Dwelling in all vascular plants, lignin is one of the most abundant renewable sources of polymers on earth, making it an indispensable feedstock for carbon recycling. However, lignin is extremely recalcitrant to degradation because of its complex and heterogeneous structure, derived from oxidative-coupling of monolignols.¹ Most microorganisms are ineffective for such matter as anaerobic processes do not attack the aromatic rings of the polymer and aerobic processes are slow. In nature, only basidiomyceteous white-rot fungi can degrade lignin in an effective way.² It has indeed been demonstrated that some white-rot fungi prefer to attack lignin rather than cellulose in wood,³ leaving the latter pale and fibrous because of oxidative bleaching. This selectivity is extremely interesting for industrial applications since many wood processes consist of the removal of lignin only (e.g. in biopulping).

Lignin peroxidase (or ligninase, LiP) is one of the enzymes produced by white-rot fungi for the degradation of lignin. LiP belongs to class II peroxidases.⁴ These enzymes can oxidise substrates by multi-step electron transfers (Fig. 1).¹ The general LiP catalysed reaction is a two-step mechanism⁵ involving (1) the ferric resting state of the native enzyme, (2) the radical-cation oxoferryl intermediate compound I (Cpd I), and (3) the neutral oxoferryl intermediate compound II (Cpd II).

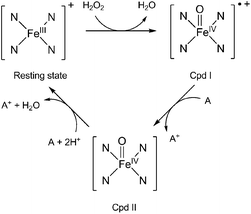Fig. 1 Catalytic cycle of lignin peroxidase. The four N atoms stand for the porphyrin ring and A is an electron-donating substrate.

LiP is able to catalyse the H₂O₂-dependent oxidative depolymerisation of lignin⁶ and is also known to oxidise non-phenolic aromatic substrates and organic compounds presenting high redox potentials (up to 1.4 V versus the standard hydrogen electrode (SHE)) when H₂O₂ is present, which is quite uncommon among peroxidases.⁷ As for the P450 enzyme, the reactive species of the catalytic cycle is assumed to be Cpd I. In the case of LiP, the reduction of Cpd I by an electron-donating substrate to yield Cpd II is pH-dependent, the rate of the reaction increasing when the pH is low.⁸ Kersten et al. compared the activity of lignin peroxidase, horseradish peroxidase and laccase regarding the oxidation of a series of methoxybenzenes presenting a range of redox potentials (from 0.81 V to 1.76 V versus the saturated calomel electrode).⁹ The authors show that LiP can oxidise 10 out of 12 congeners used in the study, while laccase and horseradish peroxidase can respectively oxidise only 1 and 4 out of 12 congeners (the ones with the lowest redox potentials), making LiP a stronger oxidant. The broad substrate specificity of the enzymes, and in particular of LiP, suggest that they do not have specific binding sites and that the redox potentials of the enzymes are mostly responsible for their activity. The authors also demonstrate a very important pH-dependency for the three enzymes, with a maximum of activity around pH 3 and a very sharp decrease when the pH increases. They estimate the redox potential of LiP as more than 1.2 V/SHE at pH 3.¹⁰

The present theoretical paper gives some insights about the redox potential of the Cpd I/Cpd II couple of LiP. The calculations of redox potentials for molecular systems in solution are usually carried out with the use of a thermodynamic Born–Haber cycle, using quantum mechanics (QM) methods such as density functional theory (DFT) to evaluate the free energy of electron uptake by the oxidant (Cpd I in our case) in solution (more details in the ESI†). As LiP is too big for full QM calculations, the steric and electrostatic contributions of the surrounding environment on the active site are modelled through combined quantum mechanical/molecular mechanical (QM/MM) calculations, which have become a powerful theoretical tool to study proteins and enzymes.¹¹ In such calculations, the active site of the enzyme can be treated at a QM level while the protein environment and the solvent are simulated by means of molecular mechanics (MM). QM/MM calculations on LiP have been reported before, but with different focus (namely the role of Trp radicals in the long-range electron transfer).¹² We now present the first QM/MM simulations of the redox potentials of the active Cpd I in LiP.¹³

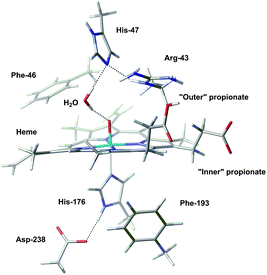
The geometries of Cpd I and Cpd II were optimised after 1000 ps of equilibration using classical MD; results obtained with the largest QM region (presented in Fig. 2) will be discussed preferentially. Geometrical differences between Cpd I and Cpd II are very subtle (see ESI† for details); also, formation of Cpd I from the wild type does not involve very important changes in the global structure of the enzyme (Fig. 3).

Fig. 2 The largest QM region used in this study, carbon: grey, hydrogen: white, oxygen: red, nitrogen: blue, iron: turquoise). The “outer” propionate is protonated in order to form an H-bond with Asp183.

Fig. 3 Superposition of the optimised structure of Cpd I (in blue) and the experimental structure of the resting state (in red). A zoom into the active site is depicted; for a view of the full structure see Fig. S3 in the ESI.†

The redox potentials have been calculated for a range of different QM regions. The size of the QM region does not have a large influence on the redox potentials. The latter have been computed with BP86/Def2-SVP at the QM/MM level and single-point calculations have then been carried out with B3LYP/SDD/6-311G** and the same QM/MM setup. Because both levels afford the same trend (see Fig. S4 in the ESI†), we can either discuss BP86 or B3LYP computed redox potentials. From here on, we will only discuss the B3LYP results for consistency with QM/MM calculations in the literature.¹⁴ They will be given relative to the absolute redox potential (ARP) of the ferrocenium/ferrocene redox couple in water, calculated as 5.03 V.

For the “neutral” Cpd I/Cpd II couple, where all residues were in their “normal” protonation states expected for pH 7, a relative redox potential (RRP) of 0.48 V is computed (Table S3 in the ESI†).^15,16 Averaging over a number of snapshots increases this value to 0.67(33) V, which is in good qualitative agreement with the experimental estimate⁹ (see Table S4 and discussion in the ESI†). In order to gain some insights into the relationship between the activity of the enzyme and the pH, we performed additional QM/MM calculations for systems where specific residues have been protonated. Three such systems have been prepared, with Asp238, or His47, or both protonated.¹⁶ The concomitant predicted increase in the redox potential is 1.14 V, 1.22 V, and 1.73 V, respectively.¹⁵ This increase arises because Cpd I is destabilised by the close proximity between the protonated residue and the electron-deficient porphyrin (see ESI† for details).

In order to gain deeper insights into the impact of local charge distributions on the RRPs and to identify potential targets for subsequent mutation studies, we devised a simple protocol for rapid screening: we performed single-point B3LYP/SDD/6-311G** calculations on the optimised geometries of Cpd I and Cpd II deleting the MM charges of individual specific residues. The QM region of the system used for this test only includes the heme and His176, employing the geometry from the QM/MM optimisation with BP86, Def2-TZVPP for iron and Def2-SVP for all other atoms. With this methodology, the calculated B3LYP RRP with the complete set of charges is equal to 0.29 V. Calculated RRPs with selected charges deleted are compiled in Tables S5–S7 in the ESI.†

When charges from neutral residues are deleted, the RRP is affected by only 0.14 V or less. When the charges of negatively charged residues (aspartates and glutamates) are deleted, the effect is stronger (see plot in Fig. 4a). Overall, the deletion of these negatively charged residues increases the redox potential of the Cpd I/Cpd II couple, suggesting that these residues stabilise Cpd I due to electrostatic interactions. As expected, the increase is larger when the residue is closer to the active site, but is still noticeable at long range. However, the magnitude of this effect is quite surprising. If it was possible to “knock out” the residue located at 6 Å away from Fe, the RRP could exceed 2 V (leftmost data point in Fig. 4a). Deleting charges from negatively charged residues (equivalent to neutralising them) as far as 27 Å away from Fe should still strongly affect the RRP, since we still find an increase of ca. 0.5 V (rightmost data point in Fig. 4a).

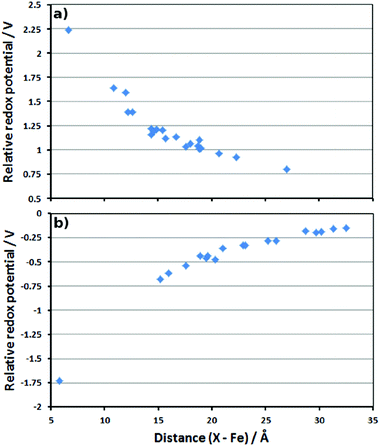Fig. 4 Plots of the distance between the deleted residue charges and Fe (in Å) versus the calculated RRP (in V). (a) Asp and Glu residues; (b) Arg and Lys residues.

Similarly, the deletion of the charges of positively charged residues leads to a decrease of the calculated redox potentials. This means these residues destabilise Cpd I because of electrostatic repulsions. Their absence stabilises Cpd I and decreases the redox potential. As for the negative residues, the effect is larger at short distance, but can be seen even at long range (Fig. 4b).

All these results show that the electrostatic interactions between the active site and the protein residues have a very important influence on the stability of Cpd I with respect to Cpd II, and thus on the redox potential of the Cpd I/Cpd II couple. For example, a low pH will have the effect to protonate deeply buried residues such as Asp238. The neutralisation of the negative charge of these residues destabilises Cpd I and thus increases the redox potential substantially. This is most likely one of the reasons for the increase of activity of lignin peroxidase at low pH (another being the protons required to convert Cpd II back to the resting state, cf. Fig. 1). Whether this increase is due to protonation of a single residue close to the active site or to protonation of several ones further away is difficult to determine at this point. Site-specific targeted protonation is not possible experimentally. An alternative way to design an enzyme with increased activity would be to perform mutations by replacing negatively charged residues by neutral ones, for examples Asp by Asn and Glu by Gln. In order to test this idea, mutations have been carried out in silico. For this purpose, we looked for suitable residues to mutate. Since these have to be negatively charged residues, they are usually implicated in hydrogen bonds which are important for the integrity of the enzyme. Only two suitable residues have been found: Asp183 and Glu40 (ca. 11 Å and 12 Å, respectively, away from Fe, see Table S6 in the ESI†). Asp183 forms an H-bond with the protonated propionate of the porphyrin ring, as well as H-bond interactions with surrounding water molecules. Replacing it by Asn183 still maintains the H-bond between the propionate of the heme and the oxygen of the asparagine and the solvent can rearrange in order to form new interactions with the NH₂ group. The carboxylic group of Glu40 only interacts with water molecules so replacing it by Gln40 should not be problematic. For each of these residues, the structure of the enzyme was changed (Asp183 to Asn183 or Glu40 to Gln40) from the geometry corresponding to the 1000 ps snapshot. Then we performed QM/MM optimisations with these two mutant proteins, using the smallest QM region.¹⁷ As expected, the global structures of these mutant proteins (D183N and E40Q respectively) are essentially unchanged from that of the wild type (see comparison of local optimised structures in Fig. 5 and S7†). Single-point B3LYP/6-311G**/SDD calculations were carried out on the optimised geometries and the redox potentials for D183N and E40Q were found to be 0.57 V and 0.52 V, respectively. By comparing them with the redox potential of the wild type at the same level of theory (0.38 V), it is clear that the mutations lead to a slight, but noticeable increase of the redox potential. However, the magnitude of this increase is clearly lower than the one induced by the protonation of the residues directly interacting with the active site, like His47 and Asp238. The actual, predicted effect of this mutation is also less pronounced than expected from the simplistic charge-deletion scheme in Fig. 4a (where RRPs around 1.6 V were computed for Asp183 and Glu40). However, a predicted increase in oxidative power by up to ca. 200 mV could result in substantially increased activity toward lignin degradation (or alleviate the harsh pH requirement). The two mutant proteins that we have identified are thus promising targets for synthesis and further engineering.

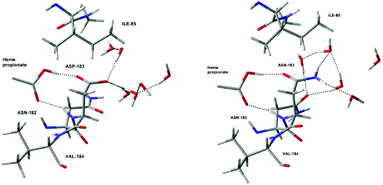Fig. 5 Optimised local structures of Cpd I (left) and the D183N mutant protein (right) around residue 183.

In summary, we have presented the first QM/MM study of the redox potential of lignin peroxidase (LiP) in its active form. This form corresponds to the famous compound I in cytochrome P450 enzymes with a heme-based oxoiron(IV) core. The computed redox potential is very sensitive to the charge distribution around the active site. Protonation of titratable residues close to the metal centre results in a substantial increase in the redox potential, qualitatively consistent with the observation that LiP has its highest oxidative power at low pH. An increase in the computed redox potential is also predicted upon “knocking out” negatively charged residues, either using a simple charge-deletion scheme (namely setting the MM charges of individual residues in the QM/MM minima to zero), or through actual homology modelling of suitable mutant proteins (i.e. by replacing negatively charged residues with neutral analogues). Two mutant proteins were identified, which are predicted to have an increased redox potential by up to 190 mV relative to the wild type (while maintaining the structural integrity of the enzyme). Because such an increase could translate into significant enhancement of activity, or the requirement of less harsh pH conditions, these mutants are promising targets for synthesis and further exploration.

The oxidative power of LiP is arguably just one piece in the puzzle of lignin degradation by this enzyme, and much further work will be needed to deduce the detailed mechanism of this important process. As the present paper shows, quantum-chemical calculations can be a valuable tool along this way, and may ultimately be useful in the design of new and improved biocatalytic systems that can degrade lignin and tap into this vast, and vastly underused resource.

Experimental section

Starting from the experimental crystal structure of the major LiP isozyme from Phanerocheate chrysosporium,¹⁸ QM/MM calculations were performed using ChemShell,¹⁹ where the QM part was treated with DFT while the MM part was described by the CHARMM force field. Geometry optimisations were carried out at the BP86/Def2-SVP level. The energies were recomputed by single-point calculations of the QM region surrounded by the optimised MM point charges using B3LYP functional, the Stuttgart–Dresden pseudopotential in combination with its adapted basis set for Fe, and 6-311G** basis set for all other atoms. For details and references see ESI.†

Acknowledgements

We wish to thank EaStCHEM, the School of Chemistry and the EPSRC (grant code EP/J018139/1) for funding, and Prof. Paul Kamer for encouragement and discussions during conception of this project. Computations were carried out on local Xeon PC clusters maintained by Dr H. Früchtl.

Notes and references

1. D. W. S. Wong, Appl. Biochem. Biotechnol., 2009, 157, 174–209.
2. (a) T. K. Kirk, W. J. Connors, R. D. Bleam, W. F. Hackett and J. G. Zeikus, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 2515–2519; (b) T. K. Kirk, W. J. Connors and J. G. Zeikus, Appl. Environ. Microbiol., 1976, 32, 192–194.
3. (a) T. Mester, E. Varela and M. Tien, Wood degradation by brown-rot and white-rot fungi. The Mycota II: genetics and biotechnology, Springer-Verlag, Berlin-Heidelberg, 2nd edn, 2004; (b) R. A. Blanchette, Appl. Environ. Microbiol., 1984, 48, 647–653; (c) L. Otjen and R. A. Blanchette, Holzforschung, 1987, 41, 343–349.
4. K. G. Welinder, Curr. Opin. Struct. Biol., 1992, 2, 388–393.
5. V. Renganathan and M. H. Gold, Biochem., 1986, 25, 1626–1631.
6. (a) M. Tien and T. K. Kirk, Science, 1983, 221, 661–663; (b) K. E. Hammel, K. A. Jensen Jr., M. D. Mozuch, L. L. Landucci, M. Tien and E. A. Pease, J. Biol. Chem., 1993, 268, 12274–12281.
7. K. Valli, H. Wariishi and M. H. Gold, Biochem., 1990, 29, 8535–8539.
8. (a) L. Marquez, H. Wariishi, H. B. Dunford and M. H. Gold, J. Biol. Chem., 1988, 263, 10549–10552; (b) M. Tien, T. K. Kirk, C. Bull and J. A. Fee, J. Biol. Chem., 1986, 261, 1687–1693.
9. P. J. Kersten, B. Kalyarnaraman, K. E. Hammel and B. Reinhammar, Biochem. J., 1990, 268, 475–480.
10. This estimate is associated with a large uncertainty because it involves redox couples measured at different pH.
11. For selected reviews see e.g.: (a) H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229; (b) A. Warshel, Angew. Chem., Int. Ed., 2014, 53, 10020–10031.
12. (a) C. Bernini, R. Pogni, R. Basosi and A. Sinicropi, Proteins: Struct., Funct., Bioinf., 2012, 80, 1476–1483; (b) Y. Miki, R. Pogni, S. Acebes, F. Lucas, E. Fernandez-Fueyo, M. C. Baratto, M. I. Fernandez, V. de los Rios, F. J. Ruiz-Dueñas, A. Sinicropi, R. Basosi, K. E. Hammel, V. Guallar and A. T. Martinez, Biochem. J., 2013, 452, 575–584.
13. QM/MM-based approaches have been used to calculate redox potentials of (a) Cpd I in cytochrome P450: A. Altun and W. Thiel, J. Phys. Chem. B, 2005, 109, 1268–1280; and of multi-copper oxidases: (b) G. Hong, D. M. Ivnitski, G. R. Johnson, P. Atanassov and R. Pachter, J. Am. Chem. Soc., 2011, 133, 4802–4809; (c) J. Li, M. Farrokhnia, L. Rulisek and U. Ryde, J. Phys. Chem. B, 2015, 119, 8268–8284.
14. For instance: (a) A. Altun, D. Kumar, F. Neese and W. Thiel, J. Phys. Chem. A, 2008, 112, 12904–12910; (b) K.-B. Cho, H. Hirao, H. Chen, M. A. Carvajal, S. Cohen, E. Derat, W. Thiel and S. Shaik, J. Phys. Chem. A, 2008, 112, 13128–13138 , and references cited therein.
15. Effects on dynamic averaging were evaluated for a smaller QM region through optimisations starting from different snapshots from the MD equilibration; RRPs of 0.67(33) V were obtained for the “neutral” form (ten structures in total, every 100 ps), and 2.70(45) V for the “doubly protonated” system (5 structures every 200 ps, standard deviation over all snapshots in parentheses; see ESI† for details).
16. In principle, the optimised QM/MM energies could be used to determine relative populations of individual structures from different snapshots (for a weighted average of the ARP), or to identify the most favourable sites of protonation. However, in practice this is not possible with our methodology, because the individual minima have a different equilibration history and the total energies are dominated to a large extent by the individual electrostatic and H-bonding interactions involving the many thousands of solvent molecules. Free-energy MD simulations would have to be performed for this purpose, which are, however, very expensive with our QM/MM approach.
17. For direct comparison with the snapshot from the wild type, no MD equilibration was performed in these cases. When the mutant proteins are properly equilibrated (at the MM level), the structural integrity of the enzyme is preserved (see overlay of structures in Fig. S8 of the ESI†).
18. T. L. Poulos, S. L. Edwards, H. Wariishi and M. H. Gold, J. Biol. Chem., 1993, 268, 4469–4440 . At 2.03 Å the resolution of this structure is not very high, but sufficient to ensure that our protocol for solvation and equilibration is appropriate.
19. P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjovoll, A. Fahmi, A. Schafer and C. Lennartz, Comput. Theor. Chem., 2003, 632, 1–28.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details and additional graphical and tabular material. See DOI: 10.1039/c6ob00037a. For access to research data and metadata see DOI: 10.17630/fdd19974-1189-4dc3-a219-9e8ab6394382.

---