The effects of an ionic liquid on unimolecular substitution processes: the importance of the extent of transition state solvation

Abstract

The reaction of bromodiphenylmethane and 3-chloropyridine, which proceeds concurrently through both unimolecular and bimolecular mechanisms, was examined in mixtures of acetonitrile and an ionic liquid. As predicted, the bimolecular rate constant (k₂) gradually increased as the amount of ionic liquid in the reaction mixture increased, as a result of a minor enthalpic cost offset by a more significant entropic benefit. Addition of an ionic liquid had a substantial effect on the unimolecular rate constant (k₁) of the reaction, with at least a 5-fold rate enhancement relative to acetonitrile, which was found to be due to a significant decrease in the enthalpy of activation, partially offset by the associated decrease in the entropy of activation. This is in contrast to the effects seen previously for aliphatic carbocation formation, where the entropic cost dominated reaction outcome. This change is attributed to a lessened ionic liquid–transition state interaction, as the incipient charges in the transition state were delocalized across the neighbouring π systems. By varying the mole fraction of ionic liquid in the reaction mixture the ratio between k₁ and k₂ could be altered, highlighting the potential to use ionic liquids to control which pathway a reaction proceeds through.

---

Introduction

In recent years ionic liquids (salts that are molten below 100 °C) have received much attention in areas including electrochemistry,^1–4 biomass processing^1,5–7 and, in particular, as alternative solvents for organic reactions.^8,9 Utilising ionic liquids as solvents for organic processes is attractive due to their low flammability and vapour pressure,^10–13 the ability to fine tune their physical and chemical properties and the potential to achieve reaction outcomes different to those in typical molecular solvents.^8,9

There has been much experimental^8,9 and computational^14–18 work aimed at understanding the interactions that exist between the component ions of ionic liquids and the species along the reaction coordinate, and how these interactions determine the observed ionic liquid solvent effects. While a number of interactions have now been identified, it has become apparent that these interactions contribute in opposing ways to the change in activation energy on introducing an ionic liquid solvent. Further, the magnitude of these interactions have a significant impact on the overall ionic liquid effect observed.

This limitation is best exemplified by a number of studies on the effect of an ionic liquid solvent on bimolecular nucleophilic substitution (S_N2) processes, where it has been found that there is an interaction between the ionic liquid cation and the nucleophile. Generally, for a reaction featuring a charged nucleophile^19–22 (or electrophile²³) the strong electrostatic interactions between the ionic liquid components and the charged reagent resulted in a significantly increased activation enthalpy, relative to non-polar and polar aprotic molecular solvents, reducing the rate constant of the reaction. For S_N2 processes involving neutral reagents, interaction between the ionic liquid cation and the reactive centre on the nucleophile also results in a significant enthalpic cost, relative to polar aprotic solvents.^24–29 Yet, importantly, for these cases there was an increased rate constant in the ionic liquid solvent. This change is likely due to differences in the strength of the ionic liquid–reagent interaction, and hence the magnitude of the associated enthalpic cost, as well as differences in the extent of transition state solvation by the ionic liquid components resulting in differences in the entropy of activation.

This idea is further reinforced by studies of the effect of changing the nature of the cation³⁰ and anion³¹ of the ionic liquid solvent for a condensation reaction, which allowed the strength of the cation – nucleophile interaction to be varied. Changing the magnitude of this interaction resulted in systematic changes in the activation enthalpy and entropy, but changes in the overall activation energy (and hence rate constant) were less predictable.^30,31 Clearly, identifying the main interactions between the ionic liquid components and species along the reaction coordinate is possible, but predicting how the differing strengths of these interactions affect the rate constant still remains elusive.

The importance of such an understanding has also become apparent for unimolecular nucleophilic substitution (S_N1) reactions, as these reactions involve carbocation formation and hence feature considerable charge separation in the transition state.^32,33 For an aliphatic substrate, use of mixtures containing high proportions of the ionic liquid 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([Bmim][N(SO₂CF₃)₂], 1) resulted in a decreased rate constant relative to methanol (Scheme 1).^34,35 Detailed kinetic studies showed that this was due to the significant increase in solvent ordering about the relatively charge-separated transition state (which is enthalpically favourable, but has a more significant entropic cost).³⁵ A decrease in k₁ for adamantyl carbocation formation was also seen in ionic liquid solvents, relative to polar protic solvents.³⁶

Scheme 1 The unimolecular substitution reaction between the linalool derivative 2 and methanol, which proceeds through the intermediate carbocation 3; this has been investigated in the ionic liquid 1 and methanol.^34,35

Conversely, for S_N1 processes that involve carbocation formation at the benzylic position (resulting in delocalisation of the net positive charge across the neighbouring π systems), both experimental³⁷ and kinetic³⁸ studies have found that there is an increase in the rate of reaction in ionic liquids relative to polar aprotic solvents. It could be speculated that this is due to a lessened extent of solvation by the ionic liquid about the more charge delocalized transition state, relative to the aliphatic case described above; this would result is a less significant entropic cost associated with the use of an ionic liquid. That is, the difference in reaction outcome for these two cases arises from differing strengths of an interaction that is of the same nature. Currently this proposal remains conjecture as activation parameters for such an S_N1 reaction, involving a more charge delocalized transition state, are yet to be determined in an ionic liquid solvent.

The main conclusion from the previous work described above is that to allow for predictions of the overall ionic liquid solvent effect to be made, it is essential to have a thorough understanding of both the interactions that exist between the ionic liquid and species along the reaction coordinate, and the relative strengths of these different interactions. To contribute to this developing understanding, this manuscript describes the effect of the ionic liquid [Bmim][N(SO₂CF₃)₂] 1 on both the rate constant and activation parameters of the reaction between bromodiphenylmethane 5 and 3-chloropyridne 6a (Scheme 2), relative to acetonitrile. This reaction proceeds through both a unimolecular pathway involving formation of a benzylic carbocation, with the transition state leading to this carbocation involving an extent of charge delocalisation across the π systems,^33,39 and a bimolecular pathway. Menschutkin reactions similar to the latter pathway between pyridine 6c and benzyl halides have been extensively studied in ionic liquids^{24–27,38,40} providing a further basis for comparison with previous work. It was predicted that the effect of the ionic liquid on the bimolecular reaction would be of comparable magnitude and have the same microscopic origins as has been described previously.^{24–27,35,39}

Scheme 2 The reaction between bromodiphenylmethane 5 and either 3-chloropyridine 6a, 2-chloropyridine 6b or pyridine 6c to produce the salts 7a–c, respectively.

By investigating the unimolecular reaction we hope to gain a better understanding of how the magnitude of the ionic liquid–transition state interaction affects the ionic liquid solvent effect. The overarching aim of this work is to continue developing our understanding of ionic liquid solvent effects so that it is possible to predict the effect an ionic liquid will have on the rate constant of a process, based on an understanding of the magnitude of the solvent–reagent interactions along the reaction coordinate.

Experimental

3-Chloropyridine 6a, 2-chloropyridine 6b and pyridine 6c were all commercially available, and were distilled under reduced pressure and stored over 4 Å molecular sieves at 253 K prior to use. Analytical grade deuterated acetonitrile was dried over 3 Å molecular sieves for at least 48 h before use. Bromodiphenylmethane 5 was synthesised by reacting benzhydrol with phosphorus(III) bromide to give the compound of interest 5. The ionic liquid [Bmim][N(CF₃SO₂)₂] 1 was prepared according to literature methods,^41,42 where 1-methylimidazole was treated with butyl bromide to afford the intermediate bromide salt, followed by salt metathesis with lithium bis(trifluoromethanesulfonyl)imide to give [Bmim][N(CF₃SO₂)₂] 1. The ionic liquid 1 was dried at 70 °C under reduced pressure immediately before use, and was found to have <200 ppm water using Karl Fischer titration methodology and contained <0.1 mol% residual halide by ion chromatography. The details of all preparations can be found in the ESI.†

Kinetic analyses were carried out in solutions containing the electrophile 5 (ca. 0.01 mol L⁻¹) and the nucleophile of interest (at either ca. 0.1, 0.2, 0.3 or 0.4 mol L⁻¹, see ESI† for further details) at a given temperature and specific mole fraction of the ionic liquid, with the remaining solvent being made up by deuterated acetonitrile. Reaction progress was monitored using ¹H NMR spectroscopy, and the pseudo-first order rate constant (k_obs) for the reaction in each solvent mixture was calculated using integrations of the signal corresponding to the benzylic proton in the electrophile 5 at δ ca. 6.5. This subsequently allowed determination of the unimolecular and bimolecular rate constants (k₁ and k₂, respectively). All experimental details for the kinetic analyses can be found in the ESI.†

Where appropriate, the activation enthalpy and entropy were then determined through fitting the obtained rate constants to either the unimolecular or bimolecular Eyring equations.^24,43 A complete description of this method, along with tables containing the exact mole fractions of ionic liquid 1 used in the reaction mixture, the nucleophile concentrations, temperature and rate constants for all the systems described below can be found in the ESI.†

Results and discussion

As discussed in the Introduction, the reaction outlined in Scheme 2 proceeds concurrently through unimolecular and bimolecular pathways. It should be noted that it was necessary to choose a suitable combination of reagents to ensure that there was a significant contribution from the unimolecular process to the overall reaction profile, the details of which are included in the ESI.†

Initially the effect of changing the amount of the ionic liquid [Bmim][N(SO₂CF₃)₂] 1 in the reaction mixture with acetonitrile was investigated; ionic liquids are often used in mixtures with other solvents, so it is important to know how the rate constant is affected by changing the mole fraction of ionic liquid in the reaction mixture. The reaction of bromodiphenylmethane 5 and 3-chloropyridine 6a was conducted at eight different mole fractions of the ionic liquid [Bmim][N(SO₂CF₃)₂] 1 (χ_IL) and acetonitrile at 47.5 °C (as this temperature resulted in the reaction progressing at a convenient rate across the different solvent compositions). For each mole fraction the reaction was conducted in triplicate at four different nucleophile concentrations allowing k₁ and k₂ to be determined across a range of solvent compositions (eqn (S1),† an exemplar plot for this type of study is shown in Fig. 1).

Fig. 1 The dependence of the observed pseudo first order rate constant (k_obs) on the concentration of the nucleophile 3-chloropyridine 6a, for the reaction between the bromide 5 and the pyridine 6a at 47.5 °C in either acetonitrile (black) or mixtures containing [Bmim][N(SO₂CF₃)₂] 1; χ_IL = 0.1 (green) and χ_IL = 0.88 (red). Values for k₁ and k₂ were determined from the intercept and slope, respectively, for each case.

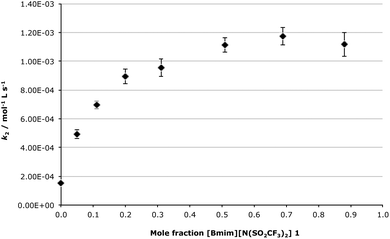
Discussion is first going to focus on the bimolecular mechanism, as this data can be readily compared with previous work on S_N2 processes.^{24–27,35,39} As the amount of the ionic liquid 1 in the reaction mixture was increased it was found that there was a gradual increase in k₂ (Fig. 2), with the main changes in k₂ occurring between χ_IL = 0 and 0.3. The rate constant then reached a plateau at higher mole fractions, with a maximum increase in k₂, relative to acetonitrile, of ca. 7-fold occurring between χ_IL = 0.5 and 0.88. This trend, as well as the magnitude of the rate enhancement when using the ionic liquid 1 relative to acetonitrile, was expected based on previous work examining S_N2^{24–27,38,40} and addition-elimination processes,^30,31,44 in which the rate-determining step of the processes also involved nucleophilic attack by a nitrogen-containing nucleophile. In this previous work the mole fraction dependence plot followed a similar trend, and the overall rate enhancement ranged from ca. 4 to ca. 8, depending on the reaction and the temperature used. In this current work, the comparable change in the bimolecular rate constant as the composition of the reaction mixture was varied further reinforces the validity of the predictive rationale being developed for ionic liquid solvent effects, as a predictable ionic liquid solvent effect is seen with this system.

Fig. 2 The dependence of the bimolecular rate constant (k₂) of the reaction between 3-chloropyridine 6a and bromodiphenylmethane 5 as the mole fraction of [Bmim][N(SO₂CF₃)₂] 1 in acetonitrile was increased, at 47.5 °C. Error bars represent the uncertainties from the linear regression from which k₂ was determined.

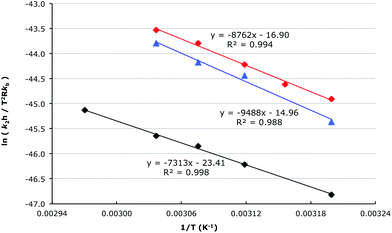
To further understand the microscopic origin of these changes in the rate constant of the process, temperature dependent kinetic studies were performed in acetonitrile, a mixture of acetonitrile and [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.20) and [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.88, in which the ionic liquid 1 was diluted only by reagents) to allow the activation parameters to be determined. For each temperature the reaction of species 5 and 6a was conducted in triplicate at four different nucleophile concentrations (an exemplar plot is shown in Fig. 3), allowing k₁ and k₂ to be determined across a range of temperatures (eqn (S1)†) for the different solvent compositions. This data was then used in combination with the bimolecular Eyring equation (eqn (S3)†) to determine both the enthalpy and entropy of activation for the process (Fig. 4 and Table 1).

Fig. 3 The dependence of the observed pseudo first order rate constant (k_obs) on the concentration of the nucleophile 3-chloropyridine 6a, for the reaction between the bromide 5 and the pyridine 6a in acetonitrile at either 39.4 °C (black), 47.5 °C (red) or 52.0 °C (green). Values for k₁ and k₂ were determined from the intercept and slope, respectively, for each case.

Fig. 4 The Eyring plot of the bimolecular rate constant (k₂) for the reaction between bromodiphenylmethane 5 and 3-chloropyridine 6a in acetonitrile (black), a mixture of acetonitrile and [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.20, blue) or [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.88, red) from which the activation parameters were determined.

Table 1 The activation parameters for the bimolecular reaction between bromodiphenylmethane 5 and 3-chloropyridine 6a, in either acetonitrile, a mixture of acetonitrile and [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.20) or [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.88)

χ IL	ΔH^‡/kJ mol^−1 ^a	ΔS^‡/J K^−1 mol^−1 ^a
a Uncertainties quoted are from the fit of the linear regression.
0	60.8 ± 1.5	−194.6 ± 4.6
0.20	78.9 ± 6.1	−124 ± 19
0.88	72.8 ± 3.3	−140 ± 10

---

It can clearly be seen that on moving from acetonitrile to [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.20) there was an increase in both the enthalpy and entropy of activation, with insignificant changes occurring when moving from χ_IL = 0.20 to χ_IL = 0.88, given the experimental uncertainties. Clearly, the main effects of the ionic liquid 1 are introduced by χ_ILca. 0.2, with further increases in the amount of [Bmim][N(SO₂CF₃)₂] 1 in the reaction mixture having little to no effect on the second order rate constant and the activation parameters. Once again, this effect was predicted by the framework that has been developed based on previous work, where interaction between the ionic liquid cation and the nitrogen lone pair on the nucleophile has been shown to be important.^24–26,30 For this case, it is likely that there is again an interaction between the ionic liquid cation and the lone pair on the nucleophile 6a, which would stabilise (and hence deactivate) this nucleophile, resulting in an increased enthalpy of activation relative to acetonitrile. On moving to the transition state, where this lone pair is no longer available to interact with the cation, there is an increase in solvent disorder, resulting in an increased entropy of activation relative to acetonitrile. The entropic effects of this phenomenon dominate reaction outcome, resulting in an increase in the rate constant when using the ionic liquid 1.

Overall, the ionic liquid solvent effects were as expected for the S_N2 component of the reaction between bromodiphenylmethane 5 and 3-chloropyridine 6a, based on the framework for predicting ionic liquid solvent effects that is being developed by our group. This is important as it further reinforces the validity of this rationale, and demonstrates that this model can be effectively applied to a variety of reactions.

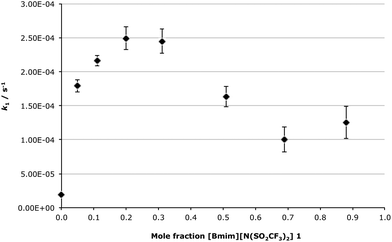
Attention now turns to the unimolecular mechanism of the reaction between compounds 5 and 6a; firstly the effect of changing the mole fraction of ionic liquid 1 in the reaction mixture on the unimolecular rate constant of the process will be considered (Fig. 5).

Fig. 5 The dependence of the unimolecular rate constant (k₁) of the reaction between 3-chloropyridine 6a and bromodiphenylmethane 5 as the mole fraction of [Bmim][N(SO₂CF₃)₂] 1 in acetonitrile was increased, at 47.5 °C. Error bars represent the uncertainties from the linear regression from which k₁ was determined.

Interestingly, the rate constant of the unimolecular process is affected very differently to that of the bimolecular mechanism when the solvent composition is varied. Initially there is a rapid increase in k₁ when moving from acetonitrile to χ_ILca. 0.20, where there is a peak rate enhancement of ca. 13-fold, relative to acetonitrile. This significant increase is then followed by a gradual decrease in the rate constant with increasing amounts of [Bmim][N(SO₂CF₃)₂] 1 in the reaction mixture, with k₁ remaining constant above χ_ILca. 0.7. Importantly, even at χ_IL = 0.7, where the lowest k₁ value for a mixture containing the ionic liquid 1 was obtained, there is still a rate enhancement of ca. 5-fold relative to acetonitrile. This result is very significant as it demonstrates that use of the ionic liquid 1, across all mixtures with acetonitrile, results in a substantial increase in the rate constant when compared to acetonitrile. This highlights that using the ionic liquid 1 in the solvent mixture is advantageous for this unimolecular reaction featuring an extent of charge delocalisation in the transition state.

This trend in the rate constant resembles the mole fraction dependency plot for the unimolecular reaction of the aliphatic species 2 (Scheme 1).^34,35 For both cases there is an initial increase in the rate constant on addition of a small amount of the ionic liquid 1, followed by a decrease in k₁ at higher mole fractions of [Bmim][N(SO₂CF₃)₂] 1 in the reaction mixture. The key difference between these two reactions is that for the aliphatic case the maximum rate constant increase occurs at χ_ILca. 0.02, and that increase is only 2-fold relative to methanol. At higher concentrations of the salt 1 in the reaction mixture the rate constant was less than that in methanol. Overall, for the reaction of the chloride 2 use of the ionic liquid 1 had comparatively little effect, and use of a high mole fraction of [Bmim][N(SO₂CF₃)₂] 1 in the reaction mixture was not beneficial to the rate constant. For the reaction of the benzylic species 5 examined in this work, the maximum rate enhancement was much more significant (ca. 13-fold at χ_IL = 0.20), and the rate constant remained significantly larger than that in acetonitrile for all solvent mixtures containing the ionic liquid 1. That is, across all solvent compositions use of [Bmim][N(SO₂CF₃)₂] 1 might be considered advantageous, as there was at least a 5-fold increase in the rate constant relative to acetonitrile.

The difference in the mole fraction dependency plots for these cases clearly suggest that the ionic liquid 1 affects the formation of an aliphatic carbocation differently to a benzylic carbocation. To allow the origin of these differences to be probed it is essential to now consider the activation parameters of the process (Fig. 6 and Table 2), which were determined in acetonitrile, a mixture of acetonitrile and [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.20) and [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.88, which was diluted only by reagents) through the temperature dependent kinetics studies that were described earlier.

Fig. 6 The Eyring plot of the unimolecular rate constant (k₁) for the reaction between bromodiphenylmethane 5 and 3-chloropyridine 6a in acetonitrile (black), a mixture of acetonitrile and [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.20, blue) or [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.88, red) from which the activation parameters were determined.

Table 2 The activation parameters for the unimolecular reaction between bromodiphenylmethane 5 and 3-chloropyridine 6a, in either acetonitrile, a mixture of acetonitrile and [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.20) or [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.88)

χ IL	ΔH^‡/kJ mol^−1 ^a	ΔS^‡/J K^−1 mol^−1 ^a
a Uncertainties quoted are from the fit of the linear regression.
0	69.4 ± 3.5	−119 ± 11
0.20	62.3 ± 5.6	−120 ± 17
0.88	47.1 ± 6.0	−174 ± 19

---

It is first important to highlight that as this is a unimolecular process, any interactions between the ionic liquid 1 and the nucleophile 6a are irrelevant when considering the kinetics of the process, as this reagent is not involved in the rate determining step of the reaction. Hence, only interactions between the ionic liquid 1 and either the bromide 5 or the transition state leading to the carbocation intermediate 8 can be used to rationalise the activation parameters determined for the unimolecular mechanism (Scheme 3).

Scheme 3 The unimolecular mechanism being considered, which involves dissociation of the bromide 5 to give the carbocation intermediate 8 (which is the rate determining step); this intermediate subsequently reacts with 3-chloropyridine 6a to give the product 7a.

On addition of a small amount of ionic liquid 1 to the reaction mixture (χ_IL = 0.20) there was a significant increase in the rate constant, indicating a change in the activation parameters of the process. Unfortunately the determined activation parameters in acetonitrile and χ_IL = 0.20 were the same within experimental uncertainty, so the microscopic origin of the rate increase could not be determined. The same was observed in the reaction of the chloride 2 through a unimolecular process.^34,35 In the case where the ionic liquid 1 was diluted only by reagents (χ_IL = 0.88) a decrease in both activation parameters, relative to acetonitrile, was observed. A decreased enthalpy of activation could either arise from: (1) the ionic liquid components ordering about and stabilising the incipient charges in the transition state to a greater extent than acetonitrile; or (2) from destabilisation of the bromide 5 by the ionic liquid 1, relative to acetonitrile. Considering the extent of charge development in the transition state, leading to the intermediate carbocation 8, the former is more likely. This is also consistent with the decreased entropy of activation; greater stabilisation of the incipient charges in the transition state by the ionic liquid 1 would result in a greater increase in ordering of the ionic liquid about the transition state, relative to the starting material 5, causing a decrease in the activation entropy in comparison to acetonitrile.

The observed change in the activation parameters when using an ionic liquid solvent (χ_IL = 0.88) is in the same direction as that seen for the unimolecular reaction of the linalool derivative 2 with methanol (Scheme 1); for that case there was also a decrease in both the enthalpy of activation (an enthalpic benefit) and the entropy of activation (an entropic cost) on moving from the molecular solvent methanol to the ionic liquid 1.³⁵ Importantly, the magnitude of these changes in the activation parameters is different for these two reactions; for the S_N1 reaction of the aliphatic substrate 2 there was ca. 50 kJ mol⁻¹ decrease in the enthalpy of activation and ca. 170 J K⁻¹ mol⁻¹ decrease in the entropy of activation,³⁵ whereas for the S_N1 reaction of the benzylic substrate 5 there was only ca. 25 kJ mol⁻¹ decrease in the enthalpy of activation and ca. 55 J K⁻¹ mol⁻¹ decrease in the entropy of activation, when moving from the polar organic solvent to [Bmim][N(SO₂CF₃)₂] 1. While it is difficult to compare the absolute changes in the activation parameters on moving from the molecular solvent to the ionic liquid 1 as these are different reactions, and the polar organic solvent used is different for each case, it is still reasonable to conclude that the enthalpic and entropic changes seen when moving from a polar organic solvent to the ionic liquid 1 are significantly larger for the aliphatic substrate 2 than for the benzylic substrate 5.

This conclusion is further reinforced by the magnitude of the changes in the rate constant for each process when using an ionic liquid solvent. For the aliphatic case 2 use of high concentrations of ionic liquid 1 results in a decrease in the rate constant relative to methanol,^34,35 while for the reaction considered here there is an increase in the rate constant of the reaction (Fig. 5). Clearly, for the aliphatic case the entropic cost dominates reaction outcome in the ionic liquid 1, resulting in the decreased rate constant; while for the benzylic case the entropic cost is less significant, resulting in the enthalpic benefit dominating reaction outcome and driving the increase in the rate constant in [Bmim][N(SO₂CF₃)₂] 1, relative to the polar organic solvent. This can be readily rationalised by considering the extent to which the incipient charges in the transition state will be delocalized for each of these cases, and how this would affect the magnitude of the interactions along the reaction coordinate. The transition state associated with the S_N1 reaction of bromodiphenylmethane 5 to give the intermediate carbocation 8 will feature a significant degree of charge delocalisation across the neighbouring π systems, resulting in a decreased extent of charge localisation and hence a decrease in the magnitude of the electrostatic interactions between the ionic liquid 1 and the transition state. Conversely, the reaction of the aliphatic substrate 2 to produce the intermediate carbocation 3 will feature very little, if any, charge delocalisation in the transition state, resulting in a much more charge localised transition state, and stronger ionic liquid–transition state interactions.‡ The activation parameters determined in this current work clearly demonstrate that differences in the magnitude of the electrostatic interactions between the ionic liquid and the transition state can have a substantial effect on the overall ionic liquid solvent effect: for the reactions considered above, when the ionic liquid–transition state interactions are large, the entropic cost dominates reaction outcome and there is a decrease in the reaction rate; yet when there are weaker ionic liquid–transition state interactions the enthalpic benefit dominates resulting in a rate enhancement, relative to a polar organic solvent.

It is worth revisiting the data for the mixture of acetonitrile and [Bmim][N(SO₂CF₃)₂] 1 (χ_IL = 0.20); although the change of solvent from acetonitrile to χ_IL = 0.20 caused a significant rate enhancement, the resulting changes in the activation parameters were within the uncertainties of those values. As was the case for the linalool derivative 2, it is likely that this rate enhancement is a result of stabilisation of the transition state (enthalpic benefit) overcoming any increase in order as a result (entropic cost). Considering the trend in the rate constant (Fig. 5), it is likely that the extent of solvent reorganisation on moving to the transition state is less significant at lower mole fractions of 1 in the reaction mixture, and at higher mole fractions of 1 solvent reorganisation becomes more substantial, increasing the entropic cost and causing the decreased rate constant at higher mole fractions.

The significantly larger rate constant at lower mole fractions reinforces the importance of the balance of the opposing enthalpic and entropic effects, rather than simply the magnitude of the change in each parameter. For this case a decrease in the enthalpy of activation is associated with a decrease in the entropy of activation (enthalpy–entropy compensation), hence the changes in the enthalpic and entropic contributions have opposite effects on the overall activation energy. As such, if there are large changes in both parameters but the magnitude of the change in each parameter is the same, these opposing effects will cancel each other out and result in negligible differences in the observed rate constant. Relating this now to what was observed in this work, the change in the activation parameters when moving from acetonitrile to χ_IL = 0.20 was much smaller than that seen when going from acetonitrile to χ_IL = 0.88, however the balance must be different to explain the observed rate constants. At χ_IL = 0.88, the balance of the changes in the activation parameters results in a smaller rate enhancement than that observed at χ_IL = 0.20. That is, large changes in the activation parameters don't necessarily result in a large change in the rate constant, it is the relative change in each parameter that is important. Clearly, understanding the balance between the opposing enthalpic and entropic effects is essential when trying to predict the overall change in the rate constant. The fact that the change in the activation parameters on moving from acetonitrile to χ_IL = 0.20 are within the uncertainties of the experiments demonstrates the difficulties in understanding solvent effects, except in cases where the changes in the activation parameters are large, as is the case at higher proportions of the salt 1 in the reaction mixture.

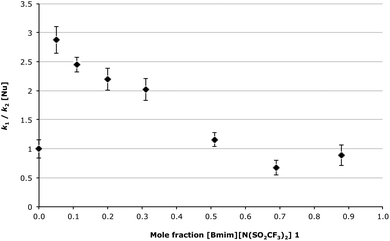
Finally, it is worth considering another interesting outcome from this work; that by changing the solvent composition one mechanism can be favoured over the other. At lower mole fractions of [Bmim][N(SO₂CF₃)₂] 1 in the reaction mixture the unimolecular mechanism is favoured, yet at higher mole fractions the bimolecular mechanism is preferred. This is most clearly seen in Fig. 7, where the ratio between k₁ and k₂[Nu]§ is plotted against the mole fraction of the ionic liquid 1 in the reaction mixture. Such a phenomenon has been observed in previous work examining competing mechanisms,³⁸ and further highlights the possibility of using ionic liquids to control reaction outcomes.

Fig. 7 The ratio between k₁ and k₂[Nu] for the reaction between bromodiphenylmethane 5 and 3-chloropyridine 6a across various mole fractions of [Bmim][N(SO₂CF₃)₂] 1 in acetonitrile at 47.5 °C. The nucleophile 6a concentration was arbitrarily set to 0.1268 mol L⁻¹ so that the data can be readily interpreted (as the ratio = 1 in acetonitrile). Errors bars represent the uncertainties from the linear regression, compounded from the division.

Conclusions

In summary, this work demonstrated a predictable ionic liquid solvent effect on the bimolecular mechanism of the reaction between the diphenyl species 5 and 3-chloropyridine 6a, further validating the framework for predicting ionic liquid solvent effects that is being developed. For the unimolecular mechanism of this reaction, it was demonstrated for the first time that use of an ionic liquid solvent can be beneficial for benzylic carbocation formation; this effect was confirmed to be enthalpically driven, due to the favourable ionic liquid–transition state interactions.

Much previous work has identified the importance of understanding the different interactions between the ionic liquid and species along the reaction coordinate. In this current work, the importance of understanding the strength of these interactions has been revealed: the charge delocalisation in the transition state for the benzylic system 5 resulted in a reduced extent of ionic liquid–transition interaction, relative to aliphatic carbocation formation, resulting in a significant change in the balance between the opposing enthalpic and entropic effects associated with the use of an ionic liquid, resulting in a substantial, enthalpically driven, rate increase. Overall, changes in the extent of solvation of species along the reaction coordinate by the ionic liquid can have marked effects on the overall activation energy, due to subtle differences in the enthalpic and entropic changes induced by an ionic liquid solvent. This work clearly highlights that the magnitude of the different interactions along the reaction coordinate need to be carefully considered; this is particularly important when trying to make predictions about how an ionic liquid might effect the rate constant of other reaction types.

A final interesting outcome from this work was the differences in how the unimolecular and bimolecular mechanisms were affected by changing the amount of ionic liquid 1 in the reaction mixture. For this case the unimolecular pathway was favoured at lower mole fractions of the salt 1, and the bimolecular case favoured at higher mole fractions. This demonstrates the potential to use ionic liquids to control which pathway a reaction proceeds through, which could have implications in areas such as asymmetric synthesis and for reactions where there are competing pathways, resulting in unwanted by-products. This is a potentially useful concept, and we hope this current work stimulates further research into the possible applications of ionic liquids in such areas.

Acknowledgements

STK acknowledges the support of the Australian government through the receipt of an Australian Postgraduate Award. JBH acknowledges financial support from the Australian Research Council Discovery Project Funding Scheme (Project DP130102331). The authors would like to acknowledge the NMR Facility within the Mark Wainwright Analytical Centre at the University of New South Wales for NMR support.

Notes and references

1. S. Zhang, J. Sun, X. Zhang, J. Xin, Q. Miao and J. Wang, Chem. Soc. Rev., 2014, 43, 7838–7869.
2. M. C. Buzzeo, R. G. Evans and R. G. Compton, ChemPhysChem, 2004, 5, 1106–1120.
3. D. R. MacFarlane, M. Forsyth, P. C. Howlett, J. M. Pringle, J. Sun, G. Annat, W. Neil and E. I. Izgorodina, Acc. Chem. Res., 2007, 40, 1165–1173.
4. M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629.
5. H. Olivier-Bourbigou, L. Magna and D. Morvan, Appl. Catal., A, 2010, 373, 1–56.
6. A. Brandt, J. Grasvik, J. P. Hallett and T. Welton, Green Chem., 2013, 15, 550–583.
7. G. Cevasco and C. Chiappe, Green Chem., 2014, 16, 2375–2385.
8. S. T. Keaveney, R. S. Haines and J. B. Harper, in Encyclopedia of Physical Organic Chemistry, ed. U. Wille, Wiley, in press.
9. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576.
10. K. R. Seddon, Kinet. Catal. Engl. Transl., 1996, 37, 693–697.
11. C. L. Hussey, Pure Appl. Chem., 1988, 60, 1763–1772.
12. M. J. Earle, J. M. S. S. Esperanca, M. A. Gilea, J. N. Canongia Lopes, L. P. N. Rebelo, J. W. Magee, K. R. Seddon and J. A. Widegren, Nature, 2006, 439, 831–834.
13. B. Wu, W. Liu, Y. Zhang and H. Wang, Chem. – Eur. J., 2009, 15, 1804–1810.
14. S. T. Keaveney, J. B. Harper and A. K. Croft, RSC Adv., 2015, 5, 35709–35729.
15. C. D. Hubbard, P. Illner and R. van Eldik, Chem. Soc. Rev., 2011, 40, 272–290.
16. C. Chiappe and C. S. Pomelli, Phys. Chem. Chem. Phys., 2013, 15, 412–423.
17. S. Zahn, M. Brehm, M. Brüssel, O. Hollóczki, M. Kohagen, S. Lehmann, F. Malberg, A. S. Pensado, M. Schöppke, H. Weber and B. Kirchner, J. Mol. Liq., 2014, 192, 71–76.
18. B. Kirchner, O. Hollóczki, J. N. Canongia Lopes and A. A. H. Pádua, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 202–214.
19. N. L. Lancaster, T. Welton and G. B. Young, J. Chem. Soc., Perkin Trans. 2, 2001, 2267–2270.
20. N. L. Lancaster, P. A. Salter, T. Welton and G. B. Young, J. Org. Chem., 2002, 67, 8855–8861.
21. N. L. Lancaster and T. Welton, J. Org. Chem., 2004, 69, 5986–5992.
22. L. Crowhurst, R. Falcone, N. L. Lancaster, V. Llopis-Mestre and T. Welton, J. Org. Chem., 2006, 71, 8847–8853.
23. G. Ranieri, J. P. Hallett and T. Welton, Ind. Eng. Chem. Res., 2008, 47, 638–644.
24. H. M. Yau, A. G. Howe, J. M. Hook, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2009, 7, 3572–3575.
25. H. M. Yau, A. K. Croft and J. B. Harper, Faraday Discuss., 2012, 154, 365–371.
26. E. E. L. Tanner, H. M. Yau, R. R. Hawker, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 6170–6175.
27. S. T. Keaveney, D. V. Francis, W. Cao, R. S. Haines and J. B. Harper, Aust. J. Chem., 2015, 68, 31–35.
28. A. Skrzypczak and P. Neta, Int. J. Chem. Kinet., 2004, 36, 253–258.
29. R. Bini, C. Chiappe, C. S. Pomelli and B. Parisi, J. Org. Chem., 2009, 74, 8522–8530.
30. S. T. Keaveney, K. S. Schaffarczyk McHale, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2014, 12, 7092–7099.
31. S. T. Keaveney, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2015, 13, 3771–3780.
32. J. Clayden, N. Greeves, S. Warren and P. Wothers, Organic Chemistry, 1st edn, Oxford University Press, 2001.
33. N. S. Isaacs, Physical Organic Chemistry, Addison Wesley Longman Limited, Harlow, 1998.
34. B. Y. W. Man, J. M. Hook and J. B. Harper, Tetrahedron Lett., 2005, 46, 7641–7645.
35. H. M. Yau, S. A. Barnes, J. M. Hook, T. G. A. Youngs, A. K. Croft and J. B. Harper, Chem. Commun., 2008, 3576–3578.
36. X. Creary, E. D. Willis and M. Gagnon, J. Am. Chem. Soc., 2005, 127, 18114–18120.
37. L.-y. Liu, B. Wang, H.-m. Yang, W.-x. Chang and J. Li, Tetrahedron Lett., 2011, 52, 5636–5639.
38. S. T. Keaveney and J. B. Harper, RSC Adv., 2013, 3, 15698–15704.
39. F. A. Carroll, Structure and Mechanism in Organic Chemistry, Brooks/Cole Publishing Company, Pacific Grove, CA, 1998.
40. H. M. Yau, S. T. Keaveney, B. J. Butler, E. E. L. Tanner, M. S. Guerry, S. R. D. George, M. H. Dunn, A. K. Croft and J. B. Harper, Pure Appl. Chem., 2013, 85, 1979–1990.
41. H. Srour, H. Rouault, C. C. Santini and Y. Chauvin, Green Chem., 2013, 15, 1341–1347.
42. S. Steines, P. Wasserscheid and B. Drießen-Hölscher, J. Prakt. Chem., 2000, 342, 348–354.
43. H. Eyring, J. Chem. Phys., 1935, 3, 107–115.
44. S. T. Keaveney, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2015, 13, 8925–8936.
45. J. B. Harper and R. M. Lynden-Bell, Mol. Phys., 2004, 102, 85–94.
46. C. G. Hanke, A. Johansson, J. B. Harper and R. M. Lynden-Bell, Chem. Phys. Lett., 2003, 374, 85–90.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of the preparations of the ionic liquid 1 and bromodiphenylmethane 5; discussion on identifying a suitable reaction to analyse for this study; experimental details of the kinetics analyses and the processing of the obtained ¹H NMR data; the exact compositions of all the stock solutions prepared; nucleophile dependent rate constant data, including the data on which Fig. 1 and 3 are based; mole fraction dependent rate constant data on which Fig. 2 and 5 are based; temperature dependent kinetic data (shown in Fig. 4 and 6) from which the activation parameters shown in Tables 1 and 2 are derived. See DOI: 10.1039/c5ob02598b

‡ It should be noted that the introduction of π systems may also introduce interactions between components of the ionic liquid and the starting material; this has been shown previously.^45,46 This would be expected to result in stabilisation of, and ordering about, the bromide 5 and hence might be expected to result in an increase in both the activation enthalpy and activation entropy. Whilst this may account in some part for the differences observed between the benzylic 5 and aliphatic 2 cases, the effect of charge localisation is considered more significant.

§ The concentration of the nucleophile 6a could be set to any value and the trend in the plot would be qualitatively the same. In this case, a value of the concentration of the pyridine of 0.1268 mol L⁻¹ was chosen so that in acetonitrile the ratio of the species reacting through unimolecular and bimolecular pathways was 1, allowing the trend to be clearly seen.

---