Multi-conformer molecules in solutions: an NMR-based DFT/MP2 conformational study of two glucopyranosides of a vitamin E model compound

Abstract

Overall conformations of both anomeric per-O-acetylated glucosyl derivatives of 2,2,5,7,8-pentamethylchroman-6-ol were studied in the context of their high flexibility, on the basis of NMR spectra in CDCl₃ solution and related DFT calculation results. A few computational protocols were used, including diverse density functional/basis set combinations with a special emphasis on accounting (at various steps of the study) for the impact of intramolecular London-dispersion (LD) effects on geometries and relative Gibbs free energies (ΔGs) of different conformers coexisting in solution. The solvent effect was simulated by an IEF-PCM approach with the UFF radii; its other variants, including the use of the recently introduced IDSCRF radii, were employed for a few compact B3LYP-GD3BJ optimized structures showing one small imaginary vibrational frequency. The advantage of using IDSCRF radii for such purposes was shown. Of the four tested DFT methods, only the application of the B3LYP/6-31+G(d,p) approximation afforded ensembles of 7–8 single forms for which population-average values of computed NMR parameters (δ_H, δ_C and some ⁿJ_HH data) were in close agreement with those measured experimentally; binuclear (δ_H,C 1 : 1) correlations, r_H,C² = 0.9998. The associated individual ΔG values, corrected for LD interactions by applying Grimme's DFT-D3 terms, afforded relative contents of different contributors to the analyzed conformational families in much better agreement with pertinent DFT/NMR-derived populations (i.e., both data sets were found to be practically equal within the limits of estimated errors) than those calculated from dispersion uncorrected ΔGs. All these main findings were confirmed by additional results obtained at the MP2 level of theory. Various other aspects of the study such as the crystal vs. solution structure, gg/gt rotamer ratio, diagnostic (de)shielding effects, dihydrogen C–H⋯H–C contacts, and doubtful applicability of some specialized DFT functionals (M06-2X, ωB97X-D and B3LYP-GD3BJ) for the description of highly flexible molecules are also discussed in detail.

---

Introduction

High-resolution nuclear magnetic resonance (NMR) spectroscopy is undoubtedly the most valuable experimental technique for the determination of the structure and dynamics of small- to medium-sized organic molecules, especially carbo- and heterocyclic ones, when elucidating a relative configuration and/or assessing the overall multi-conformer (composite) geometries¹ of such species in solution. Among various isotropic NMR parameters, chemical shifts, δ_Ks, and indirect spin–spin coupling constants (hereafter termed J_KL couplings) are the most informative observables employed for such purposes. Nowadays, these possibilities have become considerably enhanced for common spin-1/2 magnetic active nuclei by two methods of the NMR-oriented density functional theory (DFT) calculations, i.e., gauge-including atomic orbital (GIAO)² predictions of absolute shieldings σ_Ks (and thus interrelated δ_K data), and computations of J_KL values.³ The use of such approaches is crucial for structurally flexible systems affording only population-weighted averaged NMR spectra in solution. Indeed, reliable calculations of the above (not accessible in another way) NMR parameters for the major contributors to their conformational ensembles are usually necessary in all cases of this kind.¹

2,2,5,7,8-Pentamethylchroman-6-ol (PMC) – the parent system of title compounds – is a potent phenolic free radical scavenger related to α-tocopherol (vitamin E),⁴ in which a long lipophilic phytyl side chain is replaced by a methyl (Me) substituent. It is the potent hydrophilic α-tocopherol derivative,⁵ but its biological activity is not always shared by its parent α-tocopherol (e.g., it acts as a potent anti-inflammatory agent).^5b PMC shows over 5–10 times stronger dose-dependent inhibition of the agonist-induced platelet aggregation in human platelet-rich plasma, as compared to α-tocopherol.⁶ Among various α-tocopherol analogues, it is the most potent inhibitor of nuclear factor-kappa B (NF-κB) activity.⁷ Moreover, PMC has shown anti-androgen activity in prostate carcinoma cells and is considered a potent chemopreventive agent of androgen-dependent diseases, such as prostate cancer⁸ and other human cancers.⁹ Nevertheless, the potential therapeutic application of PMC is limited due to its relatively low water solubility. One of the most promising solutions is to convert PMC into its amphiphilic glycoconjugates.¹⁰ These derivatives as prodrugs would gain a favorable solubility in physiological fluids and a proper permeability through membranes and natural biological barriers e.g. blood to brain barriers. New data indicate that PMC can be helpful in designing such new potential medicinal compounds with a better clinical effectiveness.¹¹ Some glycosides of vitamin E and its short-chain analogues were described earlier.^10b,12 Also different structural aspects of this type and related model molecules, such as PMC and Trolox, were studied extensively in our laboratory by means of ¹³C NMR in solution¹³ and in the solid state (CP/MAS technique)¹⁴ as well as by ECD spectroscopy.¹⁵ It is obvious that for a complete understanding of the behavior of every system having potential biomedical activity, a good knowledge of its conformational properties (both structure and dynamics) is crucial. Therefore, a comprehensive ¹H and ¹³C NMR data-based DFT conformational investigation of the two peracetylated glucosyl derivatives of PMC, i.e., compounds 1α and 1β (see Fig. 1), was undertaken.

Fig. 1 Structures of the studied compounds with the atom numbering and five relevant torsion angles concerning their mobile molecular units, where Ar means the chroman system.¹⁶

In view of the foregoing, the title highly structurally flexible 2,3,4,6-tetra-O-acetyl-D-glycopyranosides seemed to be particularly suitable entities for testing of a few calculational DFT-level protocols currently available for the analysis of composite shapes¹ of small- to medium-sized multi-conformer systems. Indeed, such a mobility concerns even the aglycone (non-sugar) moiety of 1α in the solid state, as its 3,4-dihydro-2H-pyranyl (DHP) ring adopting two alternative half-chair (HC)-like forms was found disordered in the crystal structure at 100 K, along with related gem-dimethyl groups.¹⁸ Hence, ¹H and ¹³C NMR spectra of both anomers of 1 in CDCl₃ were fully interpreted and additionally analyzed in the light of σ_H and σ_C values GIAO-predicted for their preselected energetically reasonable forms. Some diagnostic J_HH and J_CH couplings were also calculated. The integral equation formalism (IEF)¹⁹ of an implicit solvation and UFF-radii cavities were mainly used within the polarizable continuum model (PCM)²⁰ approach. Its other variants were also employed for some structures with one small imaginary harmonic vibrational (IHV) frequency, showing an advantage of using the recently introduced²¹ and applied²² IDSCRF radii in such cases. Moreover, an empirical post factum correction of the computed Gibbs free energy, G, data^1c,23 for a proper account of long-range London dispersion (LD) forces of the van der Waals (vdW) type, which are neglected in conventional DFT approaches (with underestimation of LD),^24,25 was inter alia tested with the use of pairwise DFT-D3 corrections of Grimme.^25c

Thus, four inseparable points were especially addressed in this work: (i) a good representation of the overall solution shapes¹ of glucopyranosides 1α and 1β, considered to be highly flexible molecules, (ii) testing of a few DFT model chemistries (functional and basis set) accessible today for the most reliable prediction of the structure and molecular, e.g. NMR spectroscopy, properties of the individual forms of 1 coexisting in real solutions at equilibrium, and, particularly, (iii) explicitly accounting for the impact of weak intramolecular LD attractions^24,25 on separate geometries and/or (iv) post factum accounting for the influence of such interactions on their relative conformational energies (ΔG°). To the best of our knowledge, this kind of widespread NMR data- and dispersion-oriented DFT study of the multi-conformer systems, positively verified by additional results emerging from the much more expensive MP2 calculations, has not yet been published.

Results and discussion

NMR spectra of 1 and other related systems

The title O-glucopyranosides were synthesized from PMC²⁶ according to a literature-reported procedure^10b based on the Helferich glycosylation method,²⁷ using peracetylated β-glucose as a donor and a mild Lewis acid (ZnCl₂) as a glycosyl promoter, followed by deacetylation.²⁸ The resulting deprotected α/β-anomers were separated chromatographically and then subjected to acetylation (Experimental‡). The isolated products 1α and 1β gave spectral data fully consistent with the literature.^10b The molar α/β ratio of 36 : 64 (by ¹H NMR) was established when pure 1β was melted with ZnCl₂ (1.2 equiv.) at 390 ± 5 K under diminished pressure (30 Torr), whereas 1α was decomposed with the liberation of PMC under the same conditions.

Analysis of various types of NMR spectra recorded for 1α and 1β in a CDCl₃ solution at a 14.1 T magnetic field strength (for 1D spectra, see Fig. S1–S6‡) was performed as previously for the other multi-conformer systems.^1,29 Thus, the δ_H, δ_C and ³J_H,H values associated with their anomeric centers were found to be in agreement with those for D-glucopyranoses.³⁰ Also all cross peaks due to expected C–H connectivities within both molecules were localized in 2D spectra, including correlations across the glucosidic linkage in ¹H,¹³C HMBC plots. Moreover, diagnostic ¹J_C1′,H1′ couplings (of 172.1 and 163.4 Hz for 1α and 1β, respectively) fully compatible with the literature data (ca. 170–175 and 160–165 Hz for α- and β-forms, respectively)^30b were derived from HMBC spectra. Only assignments of the two slightly differentiated NMR lines coming from protons/carbons in 2a/2b-gem-dimethyl groups and two ¹³C lines of the C3′/C6′ acetate methyl groups were not provided by an NMR experiment; however all these signals were unambiguously assigned in further calculations (vide infra). An observed chemical shift non-equivalence of these former Me groups indicated that the C6–O6 rotation is not (nearly) a free-energy process, because sharp ¹H/¹³C resonance lines of the 2a/2b geminal groups are observed for PMC and its derivatives.^13a,26b On the other hand, cross peaks of the four H1′/H5a (where H1′ ≡ C1′–H, etc.), H1′/H7a, H5′/H5a and H5′/H7a pairs and the first two ones were found in ROESY spectra of 1α and 1β, respectively, as arising from related inter-residual H–H contacts. These nuclear Overhauser effect (NOE) data, well corroborated by broadening of a vast majority of the ¹H signals of aglycone moieties of both anomers (Fig. S1 and S4‡), confirmed a high degree of rotameric flexibility around their C1′–O6 and/or neighboring C6–O6 bonds. In turn, conformational mobility of the constituent semi-unsaturated DHP rings is additionally indicated by motional averaging of the ²J_H3,H4 values (Experimental‡).

Interestingly, two long-range couplings, ⁴J_H1′,H3′ = 0.4₀ and ⁴J_H1′,H5′ = 0.5₂ Hz, were revealed for a sugar residue of 1α in ¹H NMR spectra processed with resolution enhancement.³¹ Similar interactions (⁴J_H1,H5 = 0.5₄ and ⁴J_H1,H3 = 0.3₆ Hz) were also determined for methyl 2,3,4,6-tetra-O-acetyl-α-D-glucopyranoside 2α as the simplest aliphatic analogue of 1α (Fig. 2). The latter results are in good agreement with the corresponding heteronuclear couplings J_C,Hs found for 2α in C₆D₆ (³J_H1,C5 = 6.9 and ³J_H1,C3 = 5.6 Hz).³² Moreover small couplings, ⁴J_HH ∼ 0.4₅ Hz, between protons of the gem-dimethyl groups were found in both title systems. To the best of our knowledge, all these ⁴J_HH couplings, whose existence was confirmed by our calculations (vide infra), were not reported before and were possibly unobserved.³³ So, the sharp well-resolved multiplet consisting of 16 lines (dddd) due to an axial H5′ appeared in CDCl₃ at 4.528 and 3.986 ppm for 1α and 2α, respectively (Fig. S2 and S8‡). Additionally, clear NOE interactions H4′/H6′R were observed in the ROESY spectra of both these α-anomers, confirming the configuration at C6′.³² Among other issues, the origin of a 0.54 ppm variation in the above ¹H chemical shifts and especially a pronounced 1.00 ppm difference Δ_H5′ = δ_H5′α − δ_H5′β found for compounds 1 was a particularly intriguing question. Such large Δ_H5′ values were also determined for anomeric pairs of other O-glycosides of chroman-6-ol (3–8) possessing inter alia the mannoside, galactoside or 2-deoxyglucose residue; for details see Tables S1–S3.‡ Furthermore, it was found that Δ_H5 diminished with the change of bulkiness of the aglycone moiety, but the impact of the pyranose ring structure is also evident – compare the Δ_H5 values (1.00 vs. 0.70 ppm) for 1 and 8, respectively (Table S3‡). Nonetheless, one can conclude that Δ_H5 is a much better determinant of stereochemistry at C1 than the usually considered difference Δ_C1 = δ_C1α − δ_C1β, at least for glycopyranosides 1–8 (Table S2‡).

Fig. 2 Structures of two anomeric methyl glucosides.

Conformational study

Owing to the complexity and great flexibility of both glucosides 1, their conformational analysis was done on the basis of structural information available from the NMR data, which was supplemented with computational results. Thus, a few standard approaches were applied in two inseparable steps of the study. An extensive HF/DFT modeling of the series of low-energy candidate conformational states of both anomers 1 was performed at beginning, by starting with huge amounts of their molecular-mechanics (MM) models found initially. This step was followed by predictions of relevant NMR spectral parameters (J_KL and mainly δ_K values) of such DFT-optimized structures, carried out using different combinations of density functionals and basis sets (Calculational). Moreover, due to a fortunate lack of strong specific solvent–solute interactions, their solvation was simulated within the framework of an implicit solvation model, by using mainly an IEF-PCM^19,20 method as implemented in the Gaussian 09 package of programs.³⁴ Based on the G_{DFT 390} values computed in the standard way, it was found that 1β is more thermochemically stable than 1α, but the agreement with the equilibration experiment mentioned above was only qualitative (see however below).

In order to determine the fully relaxed overall shapes¹ of molecules 1α and 1β in the most general manner, a linear regression analysis of the measured δ_H and δ_C data vs. those values obtained from the σ_H/σ_C data GIAO predicted at the IEF-PCM(UFF,CHCl₃)/mPW1PW91/6-311+G(2d,p)³⁵//IEF-PCM(UFF,CHCl₃)B3LYP/6-31+G(d,p)³⁶ level was performed for some promising forms found at the beginning. The double-ζ (DZ) valence quality of the employed atomic basis sets was forced by the relatively large size of the molecules under study. Thus, the calculated data were plotted as usual^1,23b,37 against experimental ones, but using the binuclear δ^calcd_H,C(DFT) vs. δ^obsd_H,C correlation;^1a,37,38 see Computational details. The thus obtained individual NMR data-derived populations p_i were next confronted with pertinent results on energetics of different single forms of 1α (or 1β) coexisting in solution at equilibrium, i.e., relative total electronic-nuclear energies (0 K, ΔE_tots) or relative standard Gibbs free energies (298.15 K, ΔG°s), computed for local minima on conformational energy hypersurfaces of the analyzed solutes immersed in a polarizable continuum, the relative permittivity of which matches that of CHCl₃.

The above preliminary calculational vs. experimental data sets were subsequently analyzed in light of our previous results on the other non-rigid (flexible) molecules.^1,23b In particular, the reliability of a standard approach concerning energy-weighted fractional populations³⁹ and the reproduction of weak long-range attractive intramolecular LD forces of the vdW type,^24,25 operative in two relative large systems 1, were considered. Thus, all available data were analyzed in terms of Boltzmann populations of potential contributors to the overall composite shapes of both of these molecules, based on the G values computed for their individual conformers in simulated solutions. The structure of glycosides is usually described⁴⁰ by two torsion angles around the glycosidic linkage, i.e., φ (O5′–C1′–O6–C6) and ψ (C1′–O6–C6–C5), and the ω angle (O5′–C5′–C6′–O6′) within the exocyclic acetoxymethyl group (Fig. 1 and 3). Hence, great rotameric flexibility is generally possible, but only some of the above rotamers of 1α and 1β really exist in solution. In other words, their conformational freedom was found to be restricted to only a few (nearly) freely rotating bonds, as described later.

Fig. 3 Newman projections outlining the nomenclature used throughout for the discussed C5′–C6′ rotamers.

Fortunately, the first of the angles mentioned above was found at the same magnitude (φ = 127° and ca. −73° for 1α and 1β, respectively) in all our initial B3LYP-optimized structures, i.e., 8 forms of 1α and 7 forms of 1β, derived from the respective starting MMX geometries (Computational details). The D-glucopyranose ring of both systems was consistently computed to be a unit adopting the relatively rigid ⁴C₁ chair conformation.⁴¹ Also the three consecutive equatorial acetoxy groups in positions 2′, 3′ and 4′ were always found situated in the planes approximately perpendicular to an average sugar plane, in line with such arrangements determined in the crystals of 1α¹⁸ and 1β.⁴² Moreover, one of the three rotamers (each separated by ∼120° dihedral rotation) around the exocyclic C5′–C6′ bond in a pyranose ring, i.e., the tg form⁴³ with ω ≈ 180°, was not found within the used 25.1 kJ mol⁻¹ MMX energy cutoff. This finding was in agreement with the assumption that little or no contribution would be expected from the tg rotamer of 1, because of unfavorable steric interactions between the acetoxy groups borne by C4′ and C6′.^32,43a Indeed, its participation for anomers 2α and 2β having an identical glucose residue was suggested^32,43c to be only 4–11 and 1–8%, respectively, and so practically within an estimated uncertainty of 5–10% in the NMR data-based conformer population.^43c Thus, the other three staggered rotamers [namely gg (ω ≈ −60°),⁴³gt (ω ≈ 60°, χ ≈ ±180°)⁴³ and an unusual ‘bent’ form denoted hereafter as gt₉₀ (ω ≈ 60°, χ ≈ 90°), all shown schematically in Fig. 3 and characterized by the angles ω and χ (≡ C5′–C6′–O6′–C_C=O) given in parentheses], four O6–C6 rotamers [referred to as Rα⁻ (ψ ≈ −62°) and Rα⁺ (ψ ≈ 123°) for 1α as well as Rβ⁻ (ψ ≈ −80.5°) and Rβ ⁺ (ψ ≈ 104.5°) for 1β, with the ψ values stated above] and two half-chairs arising from the ring-puckering deformation of a DHP moiety,¹⁸i.e., HC⁻ (θ = −58.5°) and an opposite form HC⁺ (θ ≈ 58.5°) with the angle θ = C1–C2–C3–C4, were analyzed in detail. Hence, the twelve most promising candidate structures with all possible combinations of the local atom arrangements (geometric motifs) mentioned above, which were originally found by applying the GMMX random subroutine of PCMODEL⁴⁴ (above 15 forms), constructed from incomplete geometries of two crystallographically independent molecules coexisting in the crystal structure of 1α (2 forms)¹⁸ and additionally built with the MM+ force field⁴⁵ of Hyperchem⁴⁶ by adequate modification of the geometry of other forms in our hands (7 remaining forms),⁴⁷ were taken into account in all further studies for every two molecules (for full details, see Tables S4 and S5‡). In both structures found in the crystal of 1α, the CH₂OAc unit adopts the gt₉₀ form. As far as we know, the presence of such ‘bent’ rotamers in solution was not considered before.

However, the rather highly incoherent conformational landscape was found in a general manner outlined above. Indeed, several trial structures of 1α and 1β proposed as privileged on the basis of standard ΔG data (and for which all GIAO-based δ_H and δ_C values were a priori predicted) were ‘not visible’ in the measured NMR spectra. More precisely, simulated ¹H and ¹³C chemical shifts, obtained as Boltzmann-population-weighted sums of such NMR parameters computed for these individual forms of 1α and 1β, did not match the related values found experimentally. An occasional failure of such a common approach³⁹ for flexible molecules is poorly documented in the literature dealing with NMR^1,49 and infrared vibrational circular dichroism (VCD)⁵⁰ spectroscopy studies in solutions. The usage of a ‘solution-phase environment (spectroscopic) match criterion’ instead of an ‘energetic criterion’ was suggested in some cases.¹ These discrepancies most likely originate from known imperfections of the used theoretical approaches, e.g., not adequately mimicking the influence of surrounding media^1c,49,50 and/or accounting for LD effects^1c for multi-conformer systems, i.e., geometries, relative energies (ΔGs) and spectral responses of single contributors to their conformational families in solution. But we must also keep in mind that in certain physico-chemical and biophysical events, wide energy basins associated with ensembles of many structurally similar, highly flexible conformers (‘flat’ local minima) may be preferred over narrow energy wells of comparable depth and representing individual rigid forms (global minima), owing to the entropy factor.⁵¹

In view of the foregoing, the B3LYP-GD3BJ^25c,e,34 flavor of DFT corrected for dispersion energy was applied in additional geometry reoptimizations carried out ‘in CHCl₃’ starting with the 24 most promising B3LYP structures discussed earlier. However, all of these computational efforts, performed again using the standard IEF-PCM approach with UFF radii-cavities, led to very disappointing results. Indeed, much worse agreement between the values of predicted and observed NMR parameters was generally found for the structures of 1α and 1β optimized in this way (data not given). Analogous effects were also obtained with two other specialized DFT functionals, namely, M06-2X⁵² and ωB97X-D.⁵³ Thus, the M06-2X structures were similar to extended B3LYP geometries, while more compact shapes predicted with ωB97X-D were close to those B3LYP-GD3BJ optimized (for views of selected forms, see Fig. 4, S12 and S13‡). These new geometries of 1α and 1β, described in terms of five torsion angles (Fig. 1), are collected in Tables S4 and S5‡ together with those of initial B3LYP structures. Also pertinent Gibbs free energies are given there, with the exception of such values for some B3LYP-GD3BJ optimized geometries having one small IHV frequency (up to 10i cm⁻¹). For the latter structures some uncertainties in their G° values are expected, because the constituent zero-point vibrational energy (ZPVE) term is calculated only from non-imaginary frequencies.⁵⁴

Fig. 4 Chemcraft 3D drawings of two types of non-physical structures found at the IEF-PCM(UFF,CHCl₃)/B3LYP-GD3BJ/6-31+G(d,p) level: 14599_comp (top) and 12272_comp (bottom), see the text for details.

The main modifications of the geometry of 1α and 1β concern the angle φ, which increases from ca. 125° to 156° for 1α, and χ, which decreases from ca. −180° to −123° or even −107° for 1α and 1β, respectively. Particularly large rotational freedom, manifested by a relatively wide low-energy valley, exists for the C1′–O6 rotation in 1α (Tables S4 and S5‡). The greatest changes are observed on going from B3LYP to compact structures ωB97X-D and especially B3LYP-GD3BJ (cf. Fig. S10 and S11 vs. S12 and S13‡). Thus, a large movement of the aromatic part of aglycone to the C2′ acetoxy groups primarily takes place for most forms of 1α (arrangement of the type I, changes in φ), while the C6′ acetoxy units in all their gg rotamers move strongly towards the C4′ acetoxy groups with unexpected formation of tg forms via a C5′–C6′ rotation (type II, χ → ca. −123°); the latter displacement is less pronounced for M06-2X (χ → ca. −148°). In turn, Me groups of C6′ acetoxy units in gt rotamers of 1β move strongly towards the 2a-Me group in a DHP ring of aglycone with the formation of stabilizing C–H⋯H–C attractions⁵⁵ (type III, χ → ca. −108°); this change is marginal for M06-2X (χ → ca. −167°). Two B3LYP-GD3BJ-optimized non-physical geometries of the structures 14599_comp and 12272_comp⁵⁶ with LD effects of the type I/II and III (the latter exemplified in 12272_comp by two short dihydrogen CH⋯HC contacts of 2.327 and 2.753 Å), respectively, are shown in Fig. 4. The displacements of type I are a little similar to stabilizing intramolecular attractions originating from LD forces between aromatic rings and π-electron containing groups recognized in high-level correlated ab initio calculations concerning some oligopeptides and isolated small proteins in the gas-phase.^25a,b,57

The aforementioned atom displacements and especially the presence of tg forms instead of gg ones in analyzed solution mixtures (contrary to the observation vide supra) were perhaps the reason for the lack of consistency between the computed and measured NMR data. Hence, one can suppose that use of these specialized DFT functionals (ωB97X-D and B3LYP-GD3BJ, in particular) is rather unsuitable for modeling the ground-state geometry of the title and most likely also other floppy molecules with small barriers to conformational changes owing to an overestimation of LD attractions. Some recent examples of transition-state structures optimized by these or other similar methods – and for which also too strong intramolecular LD effects (and so not wholly reliable ΔGs) were computed – were reported for B3LYP-D3⁵⁸ and M06-2X and ωB97X-D.⁵⁹ Problems with the description of LD interactions in biologically relevant conformers (including sugars) by such a class of DFT methods were also identified by Goerigk.^25j Therefore, it was obvious that only B3LYP optimized geometries of glucopyranosides 1 should be further considered. Our choice was in line with the conclusion of Roy et al.^25h that the density functionals specifically designed to address dispersion behave rather erratically for some systems (but with a tendency to overestimate the strength of LD effects), while B3LYP can describe these interactions as well as or better than some specialized functionals.

As to small IHV frequencies found analytically for eight B3LYP-GD3BJ geometries of 1α and 1β, we decided to check whether the use of a standard IEF-PCM model of solvation was the most probable cause of such findings (as was suggested by one reviewer). Indeed, the IHV modes resulting from too short vdW radii of the lithium atom were found in the DFT study on some Li-containing species.⁶⁰ Accordingly, all eight ‘wrong’ B3LYP-GD3BJ structures were recalculated using the three other vdW atomic radii, namely, UA0 and Bondi (both available in Gaussian 09) and IDSCRF.⁶¹ The latter, isodensity-based SCRF radii were recently evaluated⁶¹ and applied by the Fang group in mechanistic considerations,^59,62 as a correction of the default IEF-PCM approach implemented within Gaussian 09. The new results thus obtained are collected in Table S6,‡ together with those concerning the precursor UFF radii-based structures. Inspection of this table revealed that the gradual change from UFF to IDSCRF via UA0 and Bondi radii gave good results in the majority of cases. Indeed, four positive or two slightly negative ω_e values were computed using the IDSCRF radii but a lack of improvement is also found (2 forms). Especially erratic results were obtained for the structure 13787 including an outstanding ω_e value of 12.5i cm⁻¹ found by the use of the radii of Bondi. It should be noted that a high-quality integration grid and a convergence threshold were applied in all calculations;^60,63 see Computational details. In conclusion, our results strongly suggest an imperfection of the IEF-PCM/B3LYP-GD3BJ approach. Indeed, all of these ‘wrong’ geometries are undoubtedly genuine energy minima because they are very similar to their ωB97X-D counterparts (or B3LYP-GD3BJ structures obtained with other vdW radii) showing real vibrational frequencies.⁶⁴ Moreover, only the use of the B3LYP-GD3BJ functional provides such wrong results for various radii. Hence, all of the above-discussed IHV frequencies, being well within the range of accepted computational accuracies [∼±20 (ref. 65) or even ∼±50 (ref. 60) cm⁻¹] arising from errors of the numerical integration procedures used in DFT calculations,^63c are considered to be artificial. Our findings indicate, on the other hand, that further improvement of the existing implicit solvation models is possible.

To circumvent the whole problem concerning the title compounds 1, a non-classical ‘method of gradual exclusion’ had to be used to make the analysis tractable. Thus, it was realized that (i) an unusual gt₉₀ rotamer, which was originally only found for two forms of 1α in our extensive MM search, can be safely discarded as a critical determinant of related δ_H data. Indeed, the δ_H values predicted for two anisochronous methylene protons at C6′ in the CHCH₂OAc molecular unit, adopting such ‘bent’ gt₉₀ forms, strongly deviate from the observed values by ca. −0.7 and +0.7 ppm for the prochiral H6′R and H6′S protons, respectively. In turn, two vicinal time-averaged J couplings within these units, measured for glucopyranosides 1α and 1β as ³J_H5′,H6′S = 2.5 ± 0.2 Hz and ³J_H5′,H6′R = 4.7 Hz,⁶⁶ indicated, in view of the above assumption and our predicted J_HH data given below in parentheses, that (ii) the contribution of gg forms (³J_H5′,H6′S ≈ 2.3 Hz, ³J_H5′,H6′R ≈ 2.2 Hz) to equilibrated mixtures must be approximately twice that of related gt forms (³J_H5′,H6′S ≈ 1.4 Hz, ³J_H5′,H6′R ≈ 9.1 Hz), because the measured ³J_HHs are mainly due to motional averaging of such rotamers in solution. This finding was qualitatively consistent with the gg/gt/tg ratio of 53 : 38 : 9 and 49 : 47 : 4 proposed, respectively, for 2α and 2β having an identical sugar part, on the basis of ³J_C5,H6s measured in C₆D₆ solution.³² Moreover, (iii) the participation of the puckers HC⁺ and HC⁻ of a flexible DHP ring is most likely comparable, as very similar values of δ_H and δ_C were found for the 2a/2bgem-dimethyl groups. An analogous conclusion can also be drawn from the X-ray analysis of 1α showing the coexistence of two different half-chair forms in the crystal state.¹⁸ It should be also noted that all the above guidelines (i)–(iii) were fully in line with considerations of the effect of magnetic anisotropy of the 6′-O-acetyl carbonyl group^43a and an aromatic core of the aglycone (diamagnetic ring current), respectively.

As a result, only eight structures of every anomer of 1 optimized by the IEF-PCM(UFF,CHCl₃)/B3LYP//6-31+G(d,p) method and denoted as forms 1αA to 1βH were further studied; their geometries and atomic coordinates are listed in Tables S4, S5, S15 and S16.‡ At this stage, Grimme's D3 scheme^25c was post factum applied to account for the impact of weak intramolecular LD effects on related energetic data. More precisely, the total standard Gibbs free energy 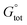of every single form was approximated by a dispersion-corrected value considered as including a harmonic DFT contribution, , plus a (negative) pairwise interatomic LD correction term E_disp,

where E_disp is Grimme's semi-empirical B3LYP(G) specific DFT-D3 correction. Such an approach was successfully used in our previous studies.^1c,23 Pertinent corrected (), atomic pairwise vdW dispersion terms (DFT-D V3 data),⁶⁷ corrected data and contributions p2_i (where i = A, B, C…H) of the forms 1αA–1βH to their equilibrium mixtures in simulated CHCl₃ solutions are collected in Tables S7 and S9‡ together with the p1_i values calculated, according to the Boltzmann distribution law, from the uncorrected (‘Boltzmann 1’ data). For completeness, the initial code names of all 16 finally selected conformers of 1 are also included. Because of the inherent limited accuracy of conventional DFT approaches, the differences in energies (E_tots or G°s) being less than the ‘chemical accuracy’ of 4 kJ mol⁻¹ means comparable thermochemical stability of the predicted structures.^38c,49b This opinion is consistent with our findings on relative stability of both anomers of 1. Indeed, the difference in values of G_{DFT 390} and G_{DFT-D3 390} estimated ‘in CHCl₃’ for their lowest-energy forms 1αA and 1βB amounts to 9.11 and 2.41 kJ mol⁻¹, respectively, whereas ΔG₃₉₀ = 1.87 kJ mol⁻¹ follows from an experimental α/β ratio of 36 : 64 (vide supra). These results strongly indicate the need for the usage of dispersion corrections and suggest that the discrepancy in our G_DFT-D3s is only 0.5 kJ mol⁻¹. Consequently, energetic ordering gathered in Tables S7 and S9‡ that resulted from similar thermodynamic data were considered relatively good indicators.

In the final stage of this research, the GIAO/DFT-based values of δ_H,Cs and a few J couplings predicted for the individual forms A–H of 1α and 1β were confronted with respective parameters of NMR spectra measured in solution by using a linear regression analysis (Computational details). Relative populations p3_i of these conformers, roughly known from the foregoing discussion rooted in an NMR experiment, were used as our supplementary and complementary guidelines. The analysis of all of the structural information indicated that a simultaneous fitting of chemical-shift values and some diagnostic ⁿJ_HH data regarding, respectively, the gem-dimethyl and CHCH₂OAc units in both glucosides 1 was of crucial importance. The findings from such a combined experimental–theoretical approach supported by the statistical treatment are shown graphically in Fig. 5 and summarized in Table 1. All three relevant statistical indicators (r², CRMSE, and CMAE; see Computational details) are given in the plots as estimates of the reliability of the results.

Fig. 5 Scatter plots of DFT computed vs. experimental (1 : 1) δ_H,C data sets for the overall multi-component solution conformation of 1α (left) and 1β (right); for additional information see the text, Table 1 and Computational details.

Table 1 Relative abundances of the forms A–H of glucosides 1α and 1β according to three different ‘theory vs. experiment’ considerations of the energetic (ΔG) and NMR (δ_H,C/J_HH) data^a

i	A	B	C	D	E	F	G	H
a The greatest divergence in the pi populations is shown in bold type. b Corresponding HC pairs of DHP rings (with the ± sign of θ) for the same gg or gt form. c For full details, see Tables S7–S10. d Without the dispersion correction. e With the dispersion correction. f Without the correction for ZPVEDFT. g With the correction for ZPVEDFT. h For cut-off subsets of the σH,C data (see text).
α-Anomer (1α)
C5–C6 rotamer	gg	gt	gt	gg	gg	gt	gt	gg
HC pair^b	I−	II+	III−	IV−	I+	II−	III+	IV+
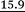
p1i × 100, Boltzmann 1, %^c^,^d	18.8		14.85	13.8	13.7	9.1	7.9
p2i × 100, Boltzmann 2, %^c^,^e	24.6 5		11.1	17.2	17.7 5	4.7 5	6.4
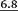
p3i × 100, Boltzmann 3, %^c^,^f	21.9		4.6	22.2	17.2	4.85	3.0
p4i × 100, Boltzmann 4, %^c^,^g	21.4		4.5	21.3	19.85	5.0	3.3
p5i × 100, DFT/NMR data, %	19	10	4	15	19	8	10	15
p6i × 100, MP2/NMR data, %^h	19.5	10	5	15	18	7	10	15.5
β-Anomer (1β)
C5–C6 rotamer	gt	gg	gg	gg	gt	gt	gt	gg
HC pair^b	I−	II−	II+	III+	I+	IV−	IV+	III−
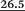
p1i × 100, Boltzmann 1, %^c^,^d		21.0	12.8	10.45	9.7	7.5	6.5
p2i × 100, Boltzmann 2, %^c^,^e		27.0	15.6	13.6 5	7.6	5.6	4.6
p3i × 100, Boltzmann 3, %^c^,^f		18.3	15.6	22.3	4.6	5.2	5.6
p4i × 100, Boltzmann 4, %^c^,^g		20.15	16.7	21.7	5.4	5.6	5.6
p5i × 100, DFT/NMR data, %	14	14.5	10.5	20	16	0	5	20
p6i × 100, MP2/NMR data, %^h	14	14.5	10.5	20	16	0	5	20

---

Inspection of Table 1 (and Tables S11 and S12,‡ with the p1 and p2-based values of selected NMR data, respectively) reveals that the use of dispersion corrected G°s really led to much better agreement between populations of single species accessed from the energy vs. DFT/NMR data, at least for the forms 1αA–1αF and 1βA–1βD; see italicized figures relating to p2 and p5 data. This result for the studied seven/eight-conformer objects is in full accord with a similar conclusion drawn from our previous study limited to the three-component systems.^1c The 3D shapes of the most privileged gg forms, i.e., 1αA and 1αE (p3 = 0.19) as well as 1βD and 1βH (p3 = 0.20), are depicted in Fig. 6. This finding seems to indicate that the aglycone part of both anomers adopts mainly the same orientation with respect to their glycone moieties (the Me group at C5 close to O5′). All conformers of 1 with percentage populations are shown in Fig. S10 and S11.‡ It should be noted that the magnitude of r² was not decisive in the analysis, because only very small changes in the magnitude of this correlation indicator were found for 1αA-1βH on going from the p1 (or p2) to p5 data (Tables 2, S11, and S12‡). In sharp contrast, a great change (from ∼1.0 to ∼1.8) in the gg/gt rotamer ratio was observed on coming from the p1 to p2 results, strongly suggesting that structures with the CHCH₂OAc unit in the gg conformation are favored by LD forces.

Fig. 6 Chemcraft 3D drawings of the four gg forms of glucopyranoside 1 favored in solution according to the DFT/NMR results: 1αA (19%, top, left), 1αE (19%, top, right), 1βD (20%, bottom, left) and 1βH (20%, bottom, right). Two different ring-flipped forms of a DHP moiety are visible for every anomer. For clarity, all hydrogen atoms have been omitted.

Table 2 Selected ¹H/¹³C chemical shifts [ppm] and J_HH couplings [Hz] relating to the 2a/2bgem-dimethyl and CHCH₂OAc units of forms A–H, respectively, found for the GIAO NMR based p3 (δ_Ks and J_H,Hs) and p6 (only δ_Ks) data

	α-Anomer (1α)				β-Anomer (1β)
Nucleus j	Exp.	Calcd^a	Scaled^b	−(δ^scaled − δ^obsd)	Exp.	Calcd^a	Scaled^b	−(δ^scaled − δ^obsd)
H2a	1.298	1.231^c	1.231	0.067	1.293	1.227^c	1.303	−0.010
H2b	1.268	1.199	1.201	0.067	1.281	1.215	1.292	−0.011
C2a	27.04	26.85	25.45	1.59	26.92	26.69	25.33	1.59
C2b	26.48	26.25	24.88	1.60	26.70	26.46	25.12	1.58
H2a	1.298	1.342^d	1.056	0.242	1.293	1.343^d	1.004	0.289
H2b	1.268	1.312	1.029	0.239	1.281	1.332	0.994	0.287
C2a	27.04	29.34	27.02	0.02	26.92	29.20	26.93	−0.01
C2b	26.48	28.77	26.49	−0.01	26.70	28.95	26.69	0.01

---

Coupling H,H	Exp.	Calcd^e	—	−(δ^scaled − δ^obsd)	Exp.	Calcd^e	—	−(δ^scaled − δ^obsd)
a δ ^calcdK,j = σK,TMS − (p3A·σK,A,j + p3B·σK,B,j + ⋯ + p3H·σK,H,j), K = H or C. b δ ^scaledK,j = (δ^calcdK,j − b)/a, for the least squares linear fitting values of the slope a and intercept b, see below and Fig. 5. c GIAO/DFT data-based results. d GIAO/MP2 data-based results. e J HH = p3A·JA,HH + p3B·JB,HH + ⋯ + p3H·JH,HH (found at both theory levels for the DFT-level J-data); see Computational details. f A binuclear (δH,C 1 : 1) regression analysis was applied, see also Computational details.
^3 J H5′,H6′S	2.34	2.06	—	0.28	2.74	1.98	—	0.76
^3 J H5′,H6′R	4.68	4.46	—	0.22	4.72	4.59	—	0.13
^2 J H6′R,H6′S	(−)12.37	−12.63	—	0.26	(−)12.18	−12.51	—	0.33
DFT/NMR^f	r C/H ^2 = 0.99983, gg/gt = 2.13, CRMSE = 0.75, CMAE = 0.51, δ^calcd = 1.0579 · δ^obsd − 0.0707				r C/H ^2 = 0.99977, gg/gt = 1.86, CRMSE = 0.87, CMAE = 0.61, δ^calcd = 1.0566 · δ^obsd − 0.0765
MP2/NMR^f	r C/H ^2 = 0.99930, gg/gt = 2.13, CRMSE = 0.73, CMAE = 0.58, δ^calcd = 1.0784 · δ^obsd + 0.2031				r C/H ^2 = 0.99922, gg/gt = 1.86, CRMSE = 0.79, CMAE = 0.67, δ^calcd = 1.0746 · δ^obsd + 0.2641

---

Overall, only a slightly weaker correlation between the predicted and experimental δ_H,C sets was found for 1β. Indeed, the greatest discrepancy in p2s/p5s (∼8%) was obtained for 1βE (Table 1). Nevertheless, only for these NMR-based populations very small differences in the simultaneously analyzed data of δ_H, δ_C and ⁿJ_HH were found in a laborious but critical step in achieving very good reproduction of the observed values of chemical shifts of 2a/2bgem-dimethyl groups and J_HHs in the CHCH₂OAc unit. Additionally, population-averaged values of the other computed J data discussed in the text, i.e., ²J_H3,H4 = 6.60, ⁴J_H1′,H3′ = −0.45, ⁴J_H1′,H5′ = −0.72, ⁴J_H2a,H2b = 0.46 and ¹J_C1′,H1′ = 168.79 Hz for 1α as well as ²J_H3,H4 = 6.59, ⁴J_H2a,H2b = 0.47 and ¹J_C1′,H1′ = 161.87 Hz for 1β, were obtained in good agreement with those found experimentally; for a scatter plot of selected relationships J^{calcd av}_HHvs. J^obsd_HH (r² = 0.99900) see Fig. S14.‡

Moreover, the structure 1βA, observed as its enantiomeric form in the crystal of 1β,⁴² was relatively strongly privileged in CHCl₃ solution (p5 = 0.14), in sharp contrast to the case of the α-anomer. Indeed, close inspection of the crystal structure of 1α¹⁸ suggests that the coexistence of the four species with a ‘bent’ gt₉₀ rotamer of the CHCH₂OAc segment (different from those located in our MM search) in the unit cell is due to crystal packing effects largely dominated by intermolecular LD contacts of the CH⋯HC type,⁵⁵ involving inter alia the Me group of this unit interacting with 2a/2b-gem-dimethyl groups of a neighboring molecule (see also above). A great similarity between angles φ, ψ and χ in both these main gt₉₀ conformers and their related non-physical solution M06-2X structures optimized with allowance for LD forces supports this conception (Table S4,‡ the forms 14229 and 14913). As a result, ‘extended’ gt and especially gg rotamers of this molecular unit in both glucosides 1 under study are favored in the solution state.

On the other hand, a definitive and unambiguous assignment of the ¹H/¹³C NMR signals of 2a/2bgem-dimethyl groups was simultaneously acquired in our analysis. Pertinent chemical-shift values are only slightly more differentiated for 1α, but a downward Me substituent labeled 2a was always found to resonate downfield of its upward counterpart 2b (Fig. 1 and Table 2); the spatial relationship between these groups adopted throughout this paper is the same as that used before.^13a Therefore, one cannot speak about an equatorial and axial position of the 2a and 2b methyl group, respectively, as was considered previously.^13a In this case each of these two Me groups occupies both such orientations during low-energy interconversions (rapid in the NMR timescale) between two different half-chair forms of a DHP ring.^13a,68 Interestingly, an experimental Δδ_C/Δδ_H ratio amounts to 18.5 ± 0.2 for both anomers and also the average values of δ are very similar, δ_H = 1.285 ± 0.002 ppm and δ_C = 26.78₅ ± 0.02₅ ppm. All the above facts indicate that the structural features and dynamics of the DHP part of both anomeric glucosides 1 in solution are comparable.

It should also be noted that the gg/gt rotamer ratio determined for 1α is slightly greater than that found for 1β [the α/β ratio (of both gg/gt ratios) ∼1.1₅], see Table 2, similarly to that estimated³² for the pair 2α and 2β having the same sugar moiety (α/β ∼ 1.3). In light of these results, more recent literature data^43c suggesting the gg/gt ratio of 0.61 and 0.52 for 2α and 2β, respectively, are questionable, but the associated α/β ratio ∼1.2 is correct.

The inherent uncertainty of the finest GIAO/DFT-based p5_i values is difficult to estimate, due to possible summation and/or cancellation of errors in two subsequent computations of geometries and chemical shifts (or ). The differences between the p2_i and p5_i results found for 1 (Table 1) suggest that such an uncertainty is of the order of 4–7%, under the assumption of perfect correctness of p2_i data. But one should remember a modest accuracy of typical ΔGs and so the relatively large errors in calculations of p1_is and perhaps also, to some extent, p2_is. Thus, it seems that the uncertainty in question is comparable with that reported previously for the best example of three-component systems studied analogously (most likely <5%).^1c So it was concluded that the values of p2_is and p5_is are consistent with each other within their errors; however, very good agreement with the NMR experimental observations was found for the latter data set only. Hence, one can invoke again the concept of superiority of the ‘solution match criterion’ over the ‘thermodynamic criterion’, stressing simultaneously that accounting for weak LD forces in calculations of ΔGs and thus Boltzmann distributions is mandatory in all such cases. A very similar conclusion was drawn earlier.^1c

The foregoing results based on the DFT data were finally compared with those arising from the total electronic-nuclear energies, E_tots, and GIAO predictions of σ_Ks obtained for solutions of 1αA–1βH at the MP2⁶⁹/6-311+G(2d,p) and MP2/6-311G(d,p) levels, respectively. As to energy data and thus conformer populations p3 and p4 found from relative energies ΔE_tot and ΔE₀ (Tables 1, S8 and S10‡),⁷⁰ the new results are generally consistent with DFT findings, with the exception of cases of 1αB, 1αH, 1βA, and 1βH (Table 1, numbers underlined). But also in these instances, the MP2 data-derived results are in agreement with the trends observed on going from p1s to p2s within the limits of inherent errors of both theoretical models.^71,72 Also ‘mean’ populations found for related p2/p4 pairs, namely 8.1, 13.3₅, 12.0 and 13.4%, are in line with the p5 DFT/NMR data. As previously stated, the greatest discrepancy between p4 and p6 values is found for 1βE. Therefore, one can then consider, based on such new data (Table 1, p3s and p4s), that the results of MP2 calculations are qualitatively consistent with the DFT-D3-type intramolecular LD attractions in the systems 1α and 1β estimated here. Moreover, according to the aforementioned data, it seems that the inclusion of DFT-level ZPVE terms in calculations of ΔE₀s and so p6 values was fully justified, despite some warnings on this topic concerning systems with the relatively flat potential energy hypersurfaces.⁷³

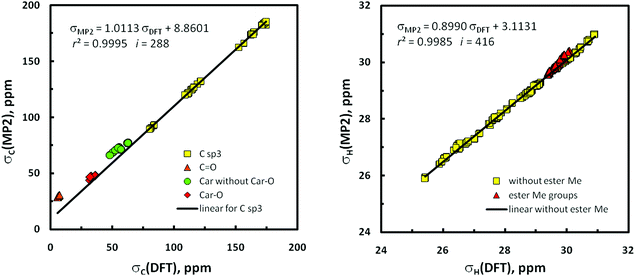
The situation with the results of GIAO/MP2 calculations⁷⁴ is more complicated. Generally, these data seem to be by far less exact than related DFT-level findings concerning the same geometries and being in good agreement with the empirical observations. Instead of very good correlation between σ_Cs computed at the MP2 vs. DFT level, awaited in light of the pioneering results of Wiberg (r²_C = 0.9994),⁷⁵ only a good relationship was found for all ¹³C nuclei in the 16 conformers under study (r²_C = 0.9977 for i = 16 × 28 unique nuclei);⁷⁶ the correlation between all σ_Hs is still weaker (r²_H = 0.9946, i = 16 × 38). Evidently, both models of chemistry provided different GIAO predictions for ¹³C nuclei involved in π-systems (especially in the ester C=O bonds). Indeed, exclusion of all sp² hybridized carbons in the σ_C set gives r²_C = 0.99953 (Fig. 7, right); four different clusters of data points due to sp² carbons are worth mentioning. The same is also true to some degree with σ_Hs, and omission of all protons of the methyl ester groups experiencing an anisotropic effect of neighboring C=O groups leads to r²_H = 0.99845 (Fig. 7, left). Therefore, only the use of two such cut-off subsets of the σ values in subsequent binuclear δ^calcd_H,C(MP2) vs. δ^obsd_H,C correlations important for this investigation was fully legitimate (for related plots, see Fig. S15‡). But the MP2/NMR populations thus obtained (p6_i values, Table 1) are slightly less reliable owing to a lack of some data points – as previously stated, the best reproduction of ‘diagnostic’ patterns of δ_Ks concerning the gem-dimethyl groups at C2 and ⁿJ_HHs around C6′ was of crucial importance. Slightly changed p6_is were thus obtained for 1α, but all attempts to correct the p5_i data used as tentative starting values for 1β were unsuccessful.

Fig. 7 Regression plots of the relationships between the IEF-PCM(UFF,CHCl₃)/GIAO/MP2 and DFT-mPW1PW91 calculated isotropic shieldings concerning the same geometries of the forms 1αA–1βH: (left) ¹³C nuclei and (right) ¹H nuclei; for additional information see the text and Computational details.

On the whole, satisfying agreement with the earlier DFT/NMR results was found (Table 1). The discrepancies between the DFT and MP2-derived values of Δδ (= δ^scaled − δ^obsd) concerning the 2a/2b Me groups arise mainly from different slopes of related best-fit lines (Table 2; cf.Fig. 5 and S15‡). Such Δδ data obtained for p3 and p4 abundances (Tables 2, S13 and S14‡) are less consistent, but those found for the p4s are better. Also the gg/gt ratios improve on going from p3 to p4 values (1α 5.0 → 4.7, 1β 4.1 → 3.7). However, what must be emphasized here is that all these data are incompatible with the NMR spectroscopic observations (gg/gt ∼ 2, vide supra). Interestingly, the reverse trend in gg/gt is observed on coming from p1 to p2 data evaluated from the DFT results (1α 1.1 → 2.0, 1β 1.0 → 1.7; Tables S11 and S12‡). Thus, is it possible that dispersive attractions (?) between H5′ and the two H6′ atoms in gg rotamers of the CHCH₂OAc fragment of systems 1 (see Fig. 3) are favored too much in MP2 and underestimated in B3LYP treatments? In summary, one can consider that the results emerging from MP2 calculations confirm the earlier DFT results, though certain disagreements between them (and with the experiment) were also identified. Particularly interesting are the foregoing discrepancies in σ_Cs predicted at both levels of theory.

For some other findings, it was recognized that the large differences Δ_H5 = δ_H5α − δ_H5β, observed for anomeric pairs of several O-glycosides of PMC (vide supra, see also Table S2‡), must arise from an aromatic ring-current effect of the constituent chroman system. Indeed, inspection of molecular representations of all forms A–H of 1α (Fig. S10‡) revealed that their hydrogen atoms at C5′ are situated within the deshielding cone produced by circulating π-electrons. By contrast, a relatively small shielding of both H6′ protons (in relation to those occurring in 1α) is suggested on the basis of 3D drawings of all forms of 1β (Fig. S11‡), in full agreement with the experiment.

Conclusions

In this combined theoretical/experimental study, two highly flexible glucoside derivatives of PMC (a model compound of α-tocopherol) were used to test several current calculational protocols accessible for predicting the overall shapes of multi-conformer systems and population-weighted averages of their NMR parameters based on high-quality spectroscopic data. A special emphasis was given to accounting for the impact of intramolecular LD effects on the geometries and relative Gibbs free energies (ΔGs) of various forms coexisting in solution. Detection of a few small ⁴J_HH coupling constants in both molecules is also worth mentioning.

Of the many possible single conformers of glucopyranosides 1α and 1β localized in initial Monte Carlo MM searches, only twelve of them were finally recognized in quantum-chemical calculations to contribute significantly (≥10%) to related conformational mixtures in solution, where solvent effects on geometries and NMR spectral properties of the analyzed solutes were mainly simulated with an IEF-PCM(UFF,CHCl₃) approach of implicit solvation. Simultaneous matching of computed vs. observed NMR chemical-shift sets by applying the binuclear (δ_H,C 1 : 1) linear regression analysis was considered the best procedure for disentangling the conformational preferences of these systems. The presence of their 2a/2b-gem-dimethyl and CHCH₂OAc structural units, as sensitive intrinsic magnetic probes for detecting time-averaged spatial arrangements of the atom arrays in their nearest electronic environments (local solute geometries), was recognized to be of crucial importance for achieving good reproduction of solution NMR spectra of both anomers.

Regarding the molecular structure of 1α and 1β, the four DFT functionals including three with a priori corrections for attractive LD forces (M06-2X, ωB97X-D and B3LYP-GD3BJ) gave different geometries. The best results were found with B3LYP, while the two last specialized DFT methods afforded tg rotamers of the CHCH₂OAc fragment instead of related gg forms in contradiction with the experiment. The advantage of the application of IDSCRF over default UFF radii in the IEF-PCM simulations of solvation was simultaneously shown for several B3LYP-GD3BJ optimized structures having one small imaginary vibrational frequency. All these findings strongly suggest that functional ωB97X-D and especially B3LYP-GD3BJ are rather not suitable for modeling the ground-state geometry of highly flexible molecules. Moreover, some serious problems with the IEF-PCM/B3LYP-GD3BJ approach were found.

The Gibbs free energies of individual forms of 1α and 1β optimized by the B3LYP/6-31+G(d,p) method were subjected to vdW (DFT-D3) corrections for LD effects to give the respective G_DFT-D3s. The latter values gave (via Boltzmann statistics) estimated populations of single forms in the solution mixtures (p2_is) being in much better agreement with NMR data-based populations (p5_is) than those calculated for uncorrected G_DFTs (p1_is). Related p2 and p5 values were found to be practically equivalent within their error limits, but only the latter values showed very good agreement with the observation. Very similar conformer populations were also derived from the MP2/NMR data (p6_is). These findings confirm the need to post factum perform LD corrections in DFT studies of this kind.

A gg/gt rotamer ratio of ∼2.0 was established for the CHCH₂OAc fragment of both glucosides on the basis of DFT data (the MP2 energetic results give a considerably overestimated value of ∼4.2). Also such a ratio, estimated from the G_DFT-D3 data, was much better than that found from the initial G_DFTs (∼1.8 vs. ∼1.0). The more compact gt₉₀ rotamer of this unit was not recognized in solution and so its presence in the crystal structure of 1α originates evidently from packing effects. In contrast, its gt rotamer identified in the crystal of 1β was found to be one of the five predominant forms in solution. It was also established that the differences Δ_H5 = δ_H5α − δ_H5β, observed for anomeric pairs of some O-glycopyranosides of PMC, are due to the aromatic ring-current effect of a chroman skeleton. Hence, this parameter is proposed as a determinant of stereochemistry at anomeric centers in molecules of this kind.

All the main findings of this work were confirmed by additional calculations performed at the MP2 level. Simultaneously, some interesting discrepancies in the values of σ_Cs predicted at both theory levels were recognized. One can suppose that with the applied (or equivalent)⁷⁷ MM/DFT methodology and a careful analysis of the results, it is possible to find all, or at least the huge majority, of the low-energy conformers of various other small- to medium-sized flexible molecules. Hence, we believe that our results prove useful for guiding similar joint NMR spectroscopic/DFT computational studies on further multi-conformer systems in solution, especially those having the sugar moiety as a structural motif.

Computational details

Geometry optimization, vibrational frequency and energy calculations

A stochastic conformational search for minima on the potential energy hypersurfaces of the objects 1α and β was performed with the Global-MMX (GMMX) subroutine built into the PCMODEL 8.5 package.^44,78 Specifically, a mixed MM protocol,⁷⁹ based on Monte-Carlo (MC) procedures used originally in the BAKMDL program,⁸⁰ was employed in which randomly selected atoms of the semi- and saturated (hetero)cyclic rings and all of the seven rotatable bonds were randomly moved in the Cartesian^70,81 and dihedral angle⁸² space and energies of such formed species were subsequently minimized within the MMX (1986) force field.⁸³ About 40 cycles of GMMX calculations, each embracing 5000 MC searching steps, were performed for every molecule with the bulk relative permittivity (dielectric constant, ε) of 4.71 (ref. 34) used for a rough simulation of the CHCl₃ environment. A search was continued until ∼180 unique energetically lowest energy lying structures of each anomer were generated within an arbitrarily chosen 25.1 kJ mol⁻¹ energy window. The thus-obtained MMX models were then subjected to a gradient geometry optimization, initially at HF/3-21G⁸⁴ and then (after sorting and removing duplicates) at HF/6-31G(d) levels, by using the Gaussian 09 suite of electronic structure programs.³⁴ All types of geometric motifs of various occurring rotameric forms were recognized in this way. Initial MMX structures of the seven not originally located conformers were built without any changes in atom numbering through adequate modifications of the partially (or fully) optimized geometries of the relevant closely related forms,⁴⁷ by using Hyperchem⁴⁶ (MM+ force field);⁴⁵ for full details see footnotes to Tables S4 and S5.‡ The MM+ calculations were followed by MMX optimizations in these additional cases. It should be noted that very large differences in energetic ordering of the input MM models of 1α and β (established via their MMX energies) and pertinent HF/3-21G optimized structures (via the ΔE_tot data) were generally found; a similar situation was observed previously.^23b

Final geometry refinement of the ‘best’ structures was carried out at the double-ζ (DZ) valence quality level of theory using the hybrid B3LYP^36a–c exchange–correlation functional, as implemented in the Gaussian code,^2c,36d in conjunction with the 6-31+G(d,p) basis set recommended for DFT calculations of energy data,^36f especially for the systems with lone electron pairs on heteroatoms.⁸⁵ For the sake of accuracy, the ‘Tight’ SCF and Opt convergence criteria were used in all computations.^1c,60,63 Moreover, a fine-pruned (150,590)⁸⁶ numerical integration grid having 150 radial shells and 590 angular points per shell was always selected applying the Int(Grid=150590) keyword,^63d–f because of soft modes coming from dynamic phenomena of methyl group rotations.³⁴ Simultaneously, an attempt to evaluate solvent influences on the solute structures and properties was made within an equilibrium solvation protocol^20b of an integral equation formalism-polarizable continuum model (IEF-PCM)^19,20 of solvation, by employing the UFF atomic radii when constructing the solvent cavity and other default parameters. Analogous optimizations in the implicit CHCl₃ solvent were also carried out with the use of a 6-31+G(d,p) basis set and three specialized DFT functionals a priori corrected for the contributions of LD effects, namely, B3LYP-GD3BJ [i.e., B3LYP with the addition of the D3 version of Grimme's dispersion^25c with Becke–Johnson damping^25e (Gaussian keyword: B3LYP/base EmpiricalDispersion=GD3BJ)],³⁴ M06-2X,⁵² and ωB97X-D.⁵³ Some additional structures were also optimized with IEF-PCM/B3LYP-GD3BJ applying three other atomic radii, i.e., UA0 and Bondi (both available in Gaussian 09) and IDSCRF⁶¹ (see also text). Fully-relaxed geometries of 16 finally considered forms of 1 found at the IEF-PCM(UFF,CHCl₃)/B3LYP/6-31+G(d,p) level are given in Tables S15 and S16,‡ while their 3D shapes are depicted in Fig. S10 and S11,‡ using graphical representations created with the ChemCraft program.⁸⁷

Moreover, vibrational wavenumbers ω_e were always evaluated in the rigid rotor-harmonic oscillator-ideal gas approximation of vibrational modes that was used in the frame of the same DFT method, to verify whether the located stationary points represented true minima (N_imag = 0) on the Born–Oppenheimer ground-state energy hypersurfaces of analyzed structures and to determine their unscaled ZPVE corrections and Gibbs free energies, 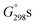, at standard ambient temperature and pressure (298.15 K, p = 1 atm), i.e., close to the NMR recording temperature of 302 ± 2 K. Finally, all of these data were corrected for vdW dispersion effects (LD forces)^1c,24,25 as was explained in the text, by using respective B3LYP(G) specific D3 Grimme's DFT-D V3 correcting terms^25c computed with the ORCA package.⁶⁷

In addition, individual total energies, E_tots, of all the forms 1αA–1βH were single-point calculated⁷⁴ by the second-order Møller–Plesset (MP2) perturbation method⁶⁹ with the 6-311+G(2d,p) basis set of triple-ζ (TZ) valence quality.⁷⁰ These computations were additional jobs in the MP2 runs carried out as is described below in the section on NMR spectra predictions.

For assessing relative abundances of individual forms in the conformational equilibria in solution, the fractional Boltzmann population (mole fraction, p_i) of each entity was found using the Boltzmann distribution function, , where j is the number of species in thermal equilibrium, R is the ideal gas constant, T is the system absolute temperature set at 298.15 K, and ΔG_i° is the ΔG value of the ith form relative to the energy of the most stable conformer. For the MP2-level results, ΔE₀s were used instead of ΔG values in the calculation of p3 and p4 data.⁷⁰

Prediction of NMR spectra

Single-point GIAO² formalism-based computations of isotropic NMR chemical shielding constants, σ_Ks, were carried out at the IEF-PCM(UFF,CHCl₃)/mPW1PW91/6-311+G(2d,p)³⁵ level on the IEF-PCM(UFF,CHCl₃)/B3LYP/6-31+G(d,p) computed structures, by using Gaussian 09. Our approach⁸⁸ was similar to that used by the Tantillo research group;^3c,35b,c however, these authors applied another solvent continuum model and used the gas-phase instead of (probably much better)⁸⁹ the solution-phase optimized solute structures used here. According to the classical tetramethylsilane (TMS) based protocol, the relative chemical shift, δ_K, of a given nucleus K in each molecular entity is defined as δ^calcd_K [ppm] = σ^ref_K − σ^calcd_K. For the thus predicted ¹H and ¹³C NMR spectra, σ^ref_K is equal to 31.7023 and 186.9100 ppm, respectively, as was computed in simulated CHCl₃ solution – analogously to that mentioned above – for the exact T_d symmetry⁹⁰ molecule of TMS as a dual-reference δ_K standard. Several other combinations of functional [B3LYP-GD3BJ,^25c,e,34 M06-2X⁵² or ωB97X-D⁵³ (first step) and mPW1PW91^35a (second step)] and basis set [6-31+G(d,p) (first step) or 6-311+G(2d,p) (second step)] were used in additional GIAO NMR predictions. All of these solution-state calculations were performed on the corresponding structures fully pre-optimized at the DZ quality level, see also text. Moreover, supplementary⁷⁴ time-consuming GIAO predictions of σ_Ks were performed at the IEF-PCM(UFF,CHCl₃)/MP2/6-311G(d,p)//IEF-PCM(UFF,CHCl₃)/B3LYP/6-31+G(d,p) level for all 16 forms 1αA–1βH in order to verify the correctness and internal consistency of the GIAO/mPW1PW91 results mentioned above, see text and also Fig. 7 and S15.‡ These MP2 runs were computationally very demanding tasks. After several initial tests, we were able to perform a single GIAO NMR calculation in 8–9 days, by using 24 processors (2.50 GHz), 128 GB of memory, and at least 7.2 TB of scratch disk space for temporary storage of data. The σ^calcd_Ks obtained in all of these cases were, as above, referred to TMS applying σ^ref_K terms evaluated at the same computational level: σ^ref_K (MP2) of 31.8587 and 198.8873 ppm, respectively.

In addition, some indirect couplings, ⁿJ_KL, were single-point computed for CDCl₃ solutions of 1 at the IEF-PCM(UFF,CHCl₃)/B3LYP/IGLO-II level^1c,91 with Gaussian 09. An extended NMR property-oriented IGLO-II basis set of Huzinaga modified next by Kutzelnigg and coworkers (also known as the HII or BII set)⁹² and widely used in predicting J_KL data^91,93 was downloaded from the EMSL Basis Set Library.⁹⁴ The five so-called pure d basis functions were employed for non-hydrogen atoms in all the NMR calculations mentioned above.

The GIAO computed σ_Hs of each of the three mutually exchanging hydrogen atoms in the Me groups were arithmetically averaged to produce a single σ_H (or δ_H) value for each Me group as a whole; the same concerns also the two methylene groups of the highly flexible DHP rings. A linear regression analysis of the relationships between the predicted and observed NMR parameters (δ_Ks, in particular) was achieved by a least-squares method; see also footnote b to Table 2. More precisely, the calculated data were plotted as usual^1,23b,37 against experimental ones; however binuclear^1a,37,38 1 : 1 correlations, δ^calcd_H,Cvs. δ^obsd_H,C, were applied instead of two separate classical mononuclear relationships. Such an associated H,C approach was strongly suggested by the analysis of the problems entailed inter alia in our previous study dealing with multiple (>2) conformers,^1c in which the application of δ_Cs for assessing populations of the single forms in solution was unsuccessful. The case of the superiority of structural results coming from the GIAO-derived δ_Hs over those from related δ_C data was reported by Koskowich et al.⁹⁵

The three relevant statistical metrics, i.e., a square of the Pearson correlation coefficient (r²), the corrected root-mean-square error [CRMSE equal to RMSE^49b,95,96 with the value^scaled data applied instead of the value^calcd ones] and the corrected mean absolute error [CMAE,⁹⁷ defined as (Σ_i|value^scaled − value^obsd|)/number of comparisons (i)], were used throughout the paper as estimates of uncertainties of the results. The greater value of r² (also called coefficient of determination and showing correlation significance) was considered as an indication of better adjustment of correlated data sets. All of the statistical analysis was performed using an MS Excel 2010 spreadsheet.

Acknowledgements

R. B. N. is grateful to Prof. Laurence A. Nafie (Syracuse University, USA) for the stimulating exchange of letters regarding the VCD spectra. He also thanks Prof. De-Cai Fang (Beijing Normal University, China) for providing the SCRF-RADII program and Dr Piotr Matczak (University of Łódź) for help in installing this software. This work was supported by the computer facilities and the Gaussian 09 software in the Academic Computer Centre CYFRONET (AGH – University of Science and Technology, Kraków) through computational grant No. MNiSW/SGI3700/UŁódzki/057/2010 and MNiSW/Zeus_lokalnie/UŁódzki/016/2013 (to R. B. N.). R. B. N. is also indebted to the staff of CYFRONET for their assistance in conducting MP2 calculations on the Prometheus supercomputer (within PL-Grid). The authors also thank two anonymous reviewers for their criticism, valuable comments and suggestion of some additional calculations, which helped us to improve the paper.

Notes and references

1. (a) E. Michalik and R. B. Nazarski, Tetrahedron, 2004, 60, 9213–9222; (b) R. B. Nazarski, J. Phys. Org. Chem., 2009, 22, 834–844; (c) R. B. Nazarski, B. Pasternak and S. Leśniak, Tetrahedron, 2011, 67, 6901–6916.
2. (a) R. Ditchfield, Mol. Phys., 1974, 27, 789–807 and references cited therein; ; (b) K. Wolinski, J. F. Hilton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260; (c) J. R. Cheeseman, G. W. Trucks, T. A. Keith and M. J. Frisch, J. Chem. Phys., 1996, 104, 5497–5509.
3. (a) T. Helgaker, M. Jaszuński and K. Ruud, Chem. Rev., 1999, 99, 293–352; (b) See also some chapters in Calculation of NMR and EPR Parameters. Theory and Applications, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2004 (c) M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, J. Chem. Rev., 2012, 112, 1839–1862.
4. G. W. Burton and K. U. Ingold, Acc. Chem. Res., 1986, 19, 194–201.
5. (a) P. B. Nielsen, A. Müllertz, T. Norling and H. G. Kristensen, Int. J. Pharm., 2001, 222, 217–224; (b) C.-C. Chang, J.-J. Lee, C.-W. Chiang, T. Jayakumar, G. Hsiao, C.-Y. Hsieh and J.-R. Sheu, Pharm. Biol., 2010, 48, 938–946.
6. (a) J. R. Sheu, C. R. Lee, G. Hsiao, W. C. Hung, Y. M. Lee, Y. C. Chen and M. H. Yen, Life Sci., 1999, 65, 197–206; (b) J. R. Sheu, C. R. Lee, C. C. Lin, Y. C. Kan, C. H. Lin, W. C. Hung, Y. M. Lee and M. H. Yen, Br. J. Pharmacol., 1999, 127, 1206–1212.
7. Y. J. Suzuki and L. Packer, Biochem. Biophys. Res. Commun., 1993, 193, 277–283.
8. T. A. Thompson and G. Wilding, Mol. Cancer Ther., 2003, 2, 797–803.
9. D. Liang, J. Lin, H. B. Grossman, J. Ma, B. Wei, C. P. Dinney and X. Wu, Cancer, Causes Control, Pap. Symp., 2008, 19, 981–992.
10. (a) S. Witkowski and P. Wałejko, Z. Naturforsch., B: Chem. Sci., 2001, 56, 411–415; (b) S. Witkowski and P. Wałejko, Z. Naturforsch., B: Chem. Sci., 2002, 57, 571–578; (c) A. Hryniewicka, P. Wałejko, J. Morzycki and S. Witkowski, Pol. J. Chem., 2009, 83, 78–80.
11. T. Parman, D. I. Bunin, H. H. Ng, J. E. McDunn, J. E. Wulff, A. Wang, R. Swezey, L. Rasay, D. G. Fairchild, I. M. Kapetanovic and C. E. Green, Toxicol. Sci., 2011, 124, 487–501.
12. (a) K. Shimoda, Y. Kondo, K. Abe, H. Hamada and H. Hamada, Tetrahedron Lett., 2006, 47, 2695–2698; (b) R. K. Uhrig, M. A. Picard, K. Beyreuther and M. Wiessler, Carbohydr. Res., 2000, 325, 72–80; (c) T. Satoh, H. Miyataka, K. Yamamoto and T. Hirano, Chem. Pharm. Bull., 2001, 49, 948–953.
13. (a) S. Witkowski, D. Maciejewska and I. Wawer, J. Chem. Soc., Perkin Trans. 2, 2000, 1471–1476 and references cited therein; ; (b) S. Witkowski and I. Wawer, J. Chem. Soc., Perkin Trans. 2, 2002, 433–436.
14. (a) I. Wawer and S. Witkowski, Curr. Org. Chem., 2001, 5, 987–999; (b) S. Witkowski, K. Paradowska and I. Wawer, Magn. Reson. Chem., 2004, 42, 863–869; (c) D. K. Stępień, M. K. Cyrański, Ł. Dobrzycki, P. Wałejko, A. Baj, S. Witkowski, K. Paradowska and I. Wawer, J. Mol. Struct., 2014, 1076, 512–517.
15. M. Górecki, A. Suszczyńska, M. Woźnica, A. Baj, M. Wolniak, M. K. Cyrański, S. Witkowski and J. Frelek, Org. Biomol. Chem., 2014, 12, 2235–2254.
16. The numbering of carbon atoms and the Nomenclature of Tocopherol and Related Compounds as proposed by the IUPAC-IUB Joint Commission on Biochemical Nomenclature (Recommendations 1981)¹⁷ was used. In the sugar part of both the examined molecules, the numbering with primes (1′, 2′, 3′ etc.) was applied throughout this work.
17. See, e.g., P. Karlson, H. B. F. Dixon, C. Liébecq, K. L. Loening, G. P. Moss, J. Reedijk, S. F. Velick and J. F. G. Vliegenthar, Pure Appl. Chem., 1982, 54, 1507–1510.
18. K. Brzezinski, P. Wałejko, A. Baj, S. Witkowski and Z. Dauter, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2011, 67, o718–o718.
19. J. Tomasi, B. Mennucci and E. Cancès, J. Mol. Struct. (THEOCHEM), 1999, 464, 211–226 and references cited therein.
20. (a) J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094; (b) G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110.
21. (a) J.-Y. Tao, W.-H. Mu, G. A. Chass, T.-H. Tang and D.-C. Fang, Int. J. Quantum Chem., 2013, 113, 975–984; (b) D.-C. Fang, IDSCRF-RADII, Beijing Normal University, Beijing, China.
22. For some very recent papers, see: (a) Y.-M. Xing, L. Zhang and D.-C. Fang, Organometallics, 2015, 34, 770–777; (b) L. Zhao and D.-C. Fang, Eur. J. Org. Chem., 2015, 4772–4781; (c) L. Zhang and D.-C. Fang, Org. Biomol. Chem., 2015, 13, 7950–7960; (d) W.-H. Mu, S.-Y. Xia, Y. Li, D.-C. Fang, G. Wei and G. A. Chass, J. Org. Chem., 2015, 80, 9108–9117.
23. (a) E. A. Skorupska, R. B. Nazarski, M. Ciechańska, A. Jóźwiak and A. Kłys, Tetrahedron, 2013, 69, 8147–8154; (b) R. B. Nazarski, J. Inclusion Phenom. Macrocyclic Chem., 2014, 78, 299–310.
24. See ref. 45a–k cited in ref. 1c.
25. See, e.g., (a) J. Vondrášek, L. Bendová, V. Klusák and P. Hobza, J. Am. Chem. Soc., 2005, 127, 2615–2619; (b) T. van Mourik, J. Chem. Theory Comput., 2008, 4, 1610–1619; (c) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104; (d) S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228; (e) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465; (f) N. Marom, A. Tkatchenko, M. Rossi, V. V. Gobre, O. Hod, M. Scheffler and L. Kronik, J. Chem. Theory Comput., 2011, 7, 3944–3951; (g) J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901; (h) D. Roy, M. Marianski, N. T. Maitra and J. J. Dannenberg, J. Chem. Phys., 2012, 137, 134109; (i) S. Grimme and M. Steinmetz, Phys. Chem. Chem. Phys., 2013, 15, 16031–16042; (j) L. Goerigk, J. Chem. Theory Comput., 2014, 10, 968–980.
26. (a) L. I. Smith, H. E. Ungnade, H. H. Hoehn and S. Wawzonek, J. Org. Chem., 1939, 4, 311–317; (b) Y. Yamamoto and K. Itonaga, Org. Lett., 2009, 11, 717–720.
27. B. Helferich and E. Schmitz-Hillebrecht, Berichte, 1933, 66, 378–383.
28. J. Herzig, A. Nudelman, H. E. Gottlieb and B. Fischer, J. Org. Chem., 1986, 51, 727–730.
29. R. B. Nazarski, Magn. Reson. Chem., 2003, 41, 70–74.
30. (a) J. F. Stoddart, Stereochemistry of Carbohydrates, Wiley-Interscience, New York, 1971, pp. 129–145; (b) D. R. Bundle and R. U. Lemieux, Methods Carbohydr. Chem., 1976, 7, 79–86.
31. See, e.g., (a) J. C. Lindon and A. G. Ferrige, Prog. Nucl. Magn. Reson. Spectrosc., 1980, 14, 27–66; (b) T. Kupka and J. O. Dzięgielewski, Magn. Reson. Chem., 1988, 26, 353–357; (c) F. A. Anet and D. J. O'Leary, Tetrahedron Lett., 1989, 30, 2755–2758; (d) L. Griffiths, Magn. Reson. Chem., 2001, 39, 194–202.
32. C. Morat, F. R. Taravel and M. R. Vignon, Magn. Reson. Chem., 1988, 26, 264–270.
33. See, e.g., papers with the 400 MHz NMR spectra of pure 2α: (a) R. M. van Well, K. P. Ravindranathan Kartha and R. A. Field, J. Carbohydr. Chem., 2005, 24, 463–474; (b) L. Shi, G. Zhang and F. Pan, Tetrahedron, 2008, 64, 2572–2575; (c) A. Kumar, Y. Geng and R. R. Schmidt, Eur. J. Org. Chem., 2012, 6846–6851; (d) D. Chatterjee, A. Paul, R. Yadav and S. Yadav, RSC Adv., 2015, 5, 29669–29674.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT 06492, USA, 2013.
35. (a) C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675; (b) M. W. Lodewyk and D. J. Tantillo, J. Nat. Prod., 2011, 74, 1339–1343; (c) M. W. Lodewyk, C. Soldi, P. B. Jones, M. M. Olmstead, J. Rita, J. T. Shaw and D. J. Tantillo, J. Am. Chem. Soc., 2012, 134, 18550–18553.
36. (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789; (b) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (d) P. J. Stephenes, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627; (e) M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269; (f) B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 1384–1388; (g) G. I. Csonka, A. D. French, G. P. Johnson and C. A. Stortz, J. Chem. Theory Comput., 2009, 5, 679–692.
37. R. B. Nazarski, J. Phys. Org. Chem., 2007, 20, 422–430.
38. (a) I. Alkorta and J. Elguero, New J. Chem., 1998, 22, 381–385; (b) A. Perczel and A. G. Császár, Eur. Phys. J. D, 2002, 20, 513–530 and their previous papers; ; (c) A. Buczek, M. Makowski, M. Jewgiński, R. Latajka, T. Kupka and M. A. Broda, Biopolymers, 2014, 101, 28–40; (d) R. Wałęsa, T. Ptak, D. Siodłak, T. Kupka and M. A. Broda, Magn. Reson. Chem., 2014, 52, 298–305; (e) R. Wałęsa, T. Kupka and M. A. Broda, Struct. Chem., 2015, 26, 1083–1093.
39. See, e.g., ref. 2b, 4e–h, j, 12, 15e, 18d, e and 34c cited in ref. 1c.
40. Symbols for Specifying the Conformation of Polysaccharide Chains [The IUPAC-IUB Joint Commission on Biochemical Nomenclature (Recommendations 1981)] – P. Karlson, H. B. F. Dixon, A. Cornish-Bowden, C. Liébecq, K. L. Loening, G. P. Moss, J. Reedijk, S. F. Velick and J. F. G. Vliegenthar, Pure Appl. Chem., 1983, 55, 1269–1272.
41. Nomenclature of Carbohydrates [The IUPAC-IUB Joint Commission on Biochemical Nomenclature (Recommendations 1996)] prepared for publication by A. D. McNaught, Pure Appl. Chem., 1996, 68, 1919–2008.
42. P. Wałejko and M. K. Cyrański, in preparation.
43. (a) V. S. Rao and A. S. Perlin, Can. J. Chem., 1983, 61, 2688–2694; (b) H. Ohrui, Y. Nishida, H. Itoh and H. Meguro, J. Org. Chem., 1991, 56, 1726–1731; (c) I. Tvaroška and J. Gajdoš, Carbohydr. Res., 1995, 271, 151–162; (d) G. D. Rockwell, T. B. Grindley and J.-P. Lepoittevin, J. Carbohydr. Chem., 1999, 18, 51–56; (e) M. Appell, G. Strati, J. L. Willett and F. A. Momany, Carbohydr. Res., 2004, 339, 537–551.
44. (a) PCMODEL V 8.5, Molecular Modeling Software for Windows Operating System, Apple Macintosh OS, Linux and Unix, Serena Software, Bloomington, IN 47402-3076, USA, 2003.
45. A. Hocquet and M. Langgård, J. Mol. Model., 1998, 4, 94–112.
46. HyperChem–Molecular Modeling System, Release 8.0.10 for Windows, Hypercube, Inc., 1115 NW, 4th Street, Gainesville, FL 32601, USA, 2011.
47. It was taking a shortcut to reduce the number of steps of an available GMMX searching protocol needed to find all the energy minima, because ‘the number of the conformations found is proportional to the time spent conducting the search’.⁴⁸.
48. W. Schepens, PhD thesis, Ghent University, Belgium, 2000 (as was cited in L. Piela, Ideas of Quantum Chemistry, Elsevier, Amsterdam, 2007, p. 292).
49. (a) A. F. C. Alcântara, D. Piló-Veloso, W. B. De Almeida, C. R. A. Maltha and L. C. A. Barbosa, J. Mol. Struct., 2006, 791, 180–185; (b) A. M. Belostotskii, J. Org. Chem., 2008, 73, 5723–5731; (c) G. P. Souza, C. Konzen, T. R. G. Simões, B. L. Rodrigues, A. F. C. Alcântara and H. O. Stumpf, J. Mol. Struct., 2012, 1016, 13–21.
50. (a) L. A. Nafie and T. B. Feedman, Biological and Pharmaceutical Applications of Vibrational Optical Activity, in Infrared and Raman Spectroscopy of Biological Materials, ed. H.-U. Gremlich and B. Yan, Marcel Dekker, Inc., New York, 2001, pp. 15–54; (b) Y. He, B. Wang, R. K. Dukor and L. A. Nafie, Appl. Spectrosc., 2011, 65, 699–723; (c) L. A. Nafie , personal communication (August 14, 2015).
51. (a) L. Piela, J. Kostrowicki and H. A. Scheraga, J. Phys. Chem., 1989, 93, 3339–3346; (b) J. Kostrowicki, L. Piela, B. J. Cherayil and H. A. Scheraga, J. Phys. Chem., 1991, 95, 4113–4119; (c) S. I. Sukharev, W. J. Sigurdson, C. Kung and F. Sachs, J. Gen. Physiol., 1999, 113, 525–539; (d) Z. Xiang, C. S. Soto and B. Honig, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 7432–7437.
52. (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241; (b) Y. Zhao and D. G. Truhlar, J. Phys. Chem. C, 2008, 112, 4061–4067.
53. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
54. J. W. Ochterski, Thermochemistry in Gaussian; http://www.gaussian.com/g_whitepap/thermo/thermo.pdf; accessed August 10, 2015.
55. (a) J. Echeverría, G. Aullón, D. Danovich, S. Shaik and S. Alvarez, Nat. Chem., 2011, 3, 323–330; (b) D. Danovich, S. Shaik, F. Neese, J. Echeverría, G. Aullón and S. Alvarez, J. Chem. Theory Comput., 2013, 9, 1977–1991; (c) W. C. McKee and P. v. R. Schleyer, J. Am. Chem. Soc., 2013, 135, 13008–13014 and references cited therein.
56. Initial code names xxxxxx of all of the structures of 1α and 1β originate from the MMX energies (xx.xxx in kcal mol⁻¹) of their simple MMX models, after omission of the decimal point.
57. (a) D. Ŕeha, H. Valdés, J. Vondrášek, P. Hobza, A. Abu-Riziq, B. Crews and M. S. de Vries, Chem. – Eur. J., 2005, 11, 6803–6817; (b) L. F. Holroyd and T. van Mourik, Chem. Phys. Lett., 2007, 442, 42–46; (c) H. Valdes, K. Pluháčková, M. Pitonák, J. Řezáč and P. Hobza, Phys. Chem. Chem. Phys., 2008, 10, 2747–2757; (d) H. Valdes, V. Spivok, J. Řezáč, D. Reha, A. Abu-Riziq, M. S. de Vries and P. Hobza, Chem. – Eur. J., 2008, 14, 4886–4898.
58. L. Ding, N. Ishida, M. Murakami and K. Morokuma, J. Am. Chem. Soc., 2014, 136, 169–178.
59. Y. Li and D.-C. Fang, Phys. Chem. Chem. Phys., 2014, 16, 15224–15230.
60. W.-H. Mu, G. A. Chass and D.-C. Fang, Int. J. Quantum Chem., 2008, 108, 1422–1434 and references cited therein.
61. (a) J.-Y. Tao, W.-H. Mu, G. A. Chass, T.-H. Tang and D.-C. Fang, Int. J. Quantum Chem., 2013, 113, 975–984; (b) D.-C. Fang, IDSCRF-RADII, Beijing Normal University, Beijing, China.
62. For some very recent papers, see: (a) Y.-M. Xing, L. Zhang and D.-C. Fang, Organometallics, 2015, 34, 770–777; (b) L. Zhao and D.-C. Fang, Eur. J. Org. Chem., 2015, 4772–4781; (c) L. Zhang and D.-C. Fang, Org. Biomol. Chem., 2015, 13, 7950–7960; (d) W.-H. Mu, S.-Y. Xia, Y. Li, D.-C. Fang, G. Wei and G. A. Chass, J. Org. Chem., 2015, 80, 9108–9117.
63. (a) P. Tähtinen, A. Bagno, K. D. Klika and K. Pihlaja, J. Am. Chem. Soc., 2003, 125, 4609–4618; (b) J. N. Woodford and G. S. Harbison, J. Chem. Theory Comput., 2006, 2, 1464–1475; (c) Z. Zhang, Q.-s. Li, Y. Xie, R. B. King and H. F. Schaefer III, New J. Chem., 2010, 34, 92–102; (d) A. Buczek, T. Kupka and M. A. Broda, J. Mol. Model., 2011, 17, 2029–2040; (e) M. A. Broda, A. Buczek and T. Kupka, Vib. Spectrosc., 2012, 63, 432–439; (f) T. Kupka, M. Stachów, E. Chełmecka, K. Pasterny, M. Stobińska, L. Stobiński and J. Kaminský, J. Chem. Theor. Comput., 2013, 9, 4275–4286.
64. A very similar approach was presented in ref. 63c.
65. D. C. Young, Computational Chemistry: A Practical Guide for Applying Techniques to Real-World Problems, John Wiley & Sons, New York, 2001, p. 94.
66. These are very similar to those reported^43a for methyl 2,3,4,6-tetra-O-acetyl-D-glucopyranoside in CDCl₃ (2α: ³J_H5,H6S = 2.4 and ³J_H5,H6R = 4.6 Hz, 2β: ³J_H5,H6S = 2.5 and ³J_H5,H6R = 4.6 Hz).
67. (a) F. Neese, ORCA – An ab initio, DFT and semiempirical SCF-MO package. Version 2.8.0.1, University of Bonn, Bonn, Germany, 2010; http://www.thch.uni-bonn.de/tc/orca; (b) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
68. S. Sofue, T. Yamasaki, H. Morita and Y. Kitahama, Polym. J., 1998, 30, 891–896.
69. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
70. Individual zero-point corrected total electronic-nuclear energies, E_0,is, were approximated here as E_0,i ≅ E_tot,i + ZPVE_DFT,_i where ZPVE_DFT,_i is an unscaled DFT-level zero-point vibrational energy correction (see Computational details). Undoubtedly, the use of ΔE₀s (0 K) instead of ΔGs (288.15 K) introduced additional errors in Boltzmann populations.
71. The problem of MP2 calculations is the inaccurate description (overestimation in most cases) of long-range LD forces when an extended basis set is used. Reliable energies are thus frequently obtained with the medium size basis sets. However, this is evidently due to a compensation of errors.^57c.
72. For the limitations of MP2 methods in the description of conformational energies, see also: (a) M. Goldey, A. Dutoi and M. Head-Gordon, Phys. Chem. Chem. Phys., 2013, 15, 15869–15875; (b) Y. K. Kang and H. S. Park, Chem. Phys. Lett., 2014, 600, 112–117.
73. P. Schreiner, P. v. R. Schleyer and H. F. Schaefer III, J. Org. Chem., 1997, 62, 4216–4228.
74. Such calculations were suggested by one of the referees.
75. K. B. Wiberg, J. Comput. Chem., 1999, 20, 1299–1303.
76. It should be noted that the MP2/6-311+G(d,p) optimized geometries were used in ref. 75 and that the GIAO predictions (MP2 vs. DFT-mPW1PW91) of σ_Cs were performed applying the 6-311+G(2d,p) basis set. Moreover, the GIAO/MP2 procedure was not as successful; mPW1PW91 gave smaller errors.⁷⁵ The lack of diffuse functions was most likely critical for our GIAO/MP2 results, but their use was computationally prohibitively expensive.
77. It is obvious that adequate scripting and data-management techniques used as a screening tool in the initial step of this study and similar studies (as suggested by one reviewer) would make such endeavors manageable for many other multi-conformer systems.
78. See also: (a) E. Kolehmainen, K. Laihia, M. Heinänen, K. Rissanen, R. Fröhlich, J. Korvola, P. Mänttäri and R. Kauppinen, J. Chem. Soc., Perkin Trans. 2, 1993, 641–648; (b) Ref. 22 cited in M. H. Chisholm, N. W. Eilerts, J. C. Huffman, S. S. Iyer, M. Pacold and K. Phomphrai, J. Am. Chem. Soc., 2000, 122, 11845–11854.
79. See, e.g., (a) M. Saunders, J. Am. Chem. Soc., 1987, 109, 3150–3152; (b) M. Saunders, J. Comput. Chem., 1989, 10, 203–208; (c) M. Saunders, K. N. Houk, Y.-D. Wu, W. C. Still, M. Lipton, G. Chang and W. C. Guida, J. Am. Chem. Soc., 1990, 112, 1419–1427.
80. (a) K. S. Steliou, BAKMDL, based on the original program by W. C. Still, 1989; (b) Y. Murakami, J.-i. Kikuchi, T. Ohno, T. Hirayama, Y. Hisaeda, H. Nishimura, J. P. Snyder and K. Steliou, J. Am. Chem. Soc., 1991, 113, 8229–8242 and references therein; ; (c) M. M. Midland, G. Asirwatham, J. C. Cheng, J. A. Miller and L. A. Morell, J. Org. Chem., 1994, 59, 4438–4442 and references cited therein.
81. D. M. Ferguson and D. J. Raber, J. Am. Chem. Soc., 1989, 111, 4379–4386.
82. (a) S. R. Wilson, W. Cui, J. W. Moskowitz and K. E. Schmidt, Tetrahedron Lett., 1988, 29, 4373–4376; (b) G. Chang, W. C. Guida and W. C. Still, J. Am. Chem. Soc., 1989, 111, 4371–4378.
83. J. J. Gajewski, K. E. Gillbert and J. McKelvey, MMX: An enhanced version of MM2 in Advances in Molecular Modeling, ed. D. Liotta, JAI Press, Inc., London, 1990, vol. 2, pp. 65–92.
84. D. Jiao, M. Barfield and V. J. Hruby, J. Am. Chem. Soc., 1993, 115, 10883–10887.
85. W. Migda and B. Rys, Magn. Reson. Chem., 2004, 42, 459–466 and ref. 10–15 cited therein.
86. J. Gräfenstein and D. Cremer, J. Chem. Phys., 2007, 127, 164113.
87. ChemCraft, Version 1.7 (built 375); http://www.chemcraftprog.com.
88. (a) R. B. Nazarski, unpublished results, 2013; ; (b) A. Marciniak, Master's Thesis, University of Łódź, Faculty of Chemistry, Łódź, 2014; (c) R. B. Nazarski and P. Wałejko, VIII Symposium on: Nuclear Magnetic Resonance in Chemistry, Physics and Biological Sciences, Warsaw, 24–26 September, 2014, poster; Programme & Book of Abstracts, page P-21.
89. See, e.g., (a) K. W. Wiitala, T. R. Hoye and C. J. Cramer, J. Chem. Theory Comput., 2006, 2, 1085–1092; (b) K. Dybiec and A. Gryff-Keller, Magn. Reson. Chem., 2009, 47, 63–66; (c) R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562.
90. (a) J. B. Foresman and Æ. Frisch, Exploring Chemistry with Electronic Structure Methods, Gaussian, Inc., Pittsburgh, PA 15106, USA, 2nd edn, 1996, ch. 4 + Errata; ; (b) R. Jain, T. Bally and P. R. Rablen, J. Org. Chem., 2009, 74, 4017–4023.
91. See, e.g., (a) H. Dodziuk, M. Jaszuński and W. Schilf, Magn. Reson. Chem., 2005, 43, 639–646; (b) S. Leśniak, A. Chrostowska, D. Kuc, M. Maciejczyk, S. Khayar, R. B. Nazarski and Ł. Urbaniak, Tetrahedron, 2009, 65, 10581–10589; (c) R. B. Nazarski and W. Makulski, Phys. Chem. Chem. Phys., 2014, 16, 15699–15708.
92. (a) S. Huzinaga, J. Chem. Phys., 1965, 42, 1293–1302; (b) S. Huzinaga, Approximate Atomic Functions. Technical Report, University of Alberta, Edmonton, Canada, 1971; (c) M. Schindler and W. Kutzelnigg, J. Chem. Phys., 1982, 76, 1919–1933; (d) W. Kutzelnigg, U. Fleischer and M. Schindler, The IGLO-Method: Ab initio Calculation and Interpretation of NMR Chemical Shifts and Magnetic Susceptibilities in NMR – Basic Principles and Progress (Deuterium and Shift Calculation), ed. P. Diehl, E. Fluck, H. Günther, R. Kosfeld and J. Seelig, Springer-Verlag, Berlin, 1991, vol. 23, pp. 165–262.
93. See ref. 38–43 cited in ref. 91c.
94. (a) EMSL Basis Set Library; https://bse.pnl.gov/bse/portal; ; (b) D. Feller, J. Comput. Chem., 1996, 17, 1571–1586; (c) K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
95. S. M. Koskowich, W. C. Johnson, R. S. Paley and P. R. Rablen, J. Org. Chem., 2008, 73, 3492–3496.
96. T. Chai and R. R. Draxler, Geosci. Model Dev., 2014, 7, 1247–1250.
97. S. G. Smith and J. M. Goodman, J. Org. Chem., 2009, 74, 4597–4607.

---

Footnotes

† Physical image vs. molecular structure relation, Part 19. For Part 18, see ref. 91c.

‡ Electronic supplementary information (ESI) available: Experimental – general information, synthesis and spectroscopic data, NMR spectra of 1α, 1β and 2α, Δ_H5 values for selected glucosides; calculation results for 1α and 1β – structural parameters, energetics and populations, molecular representations, scatter plots of J^cald_HHs vs. J^obsd_HHs and δ^calcd_H,C(MP2) vs. δ^obsd_H,C relationships, and Cartesian coordinates of DFT structures. See DOI: 10.1039/c5ob01865j

---