Open Access Article
Open Access ArticleMolecular fluorescence enhancement in plasmonic environments: exploring the role of nonlocal effects†
Christos
Tserkezis
 *a,
Nikolaos
Stefanou
b,
Martijn
Wubs
*a,
Nikolaos
Stefanou
b,
Martijn
Wubs
 ac and
N. Asger
Mortensen
ac and
N. Asger
Mortensen
 *ac
*ac
aDepartment of Photonics Engineering, Technical University of Denmark, Ørsteds Plads 343, DK-2800 Kgs. Lyngby, Denmark. E-mail: ctse@fotonik.dtu.dk
bDepartment of Solid State Physics, National and Kapodistrian University of Athens, University Campus, GR-15784 Athens, Greece
cCenter for Nanostructured Graphene, Technical University of Denmark, Ørsteds Plads 343, DK-2800 Kgs. Lyngby, Denmark. E-mail: asger@mail.aps.org
First published on 2nd September 2016
Abstract
Molecular spontaneous emission and fluorescence depend strongly on the emitter local environment. Plasmonic nanoparticles provide excellent templates for tailoring fluorophore emission, as they exhibit potential for both fluorescence enhancement and quenching, depending on emitter positioning in the nanoparticle vicinity. Here we explore the influence of hitherto disregarded nonclassical effects on the description of emitter–plasmon hybrids, focusing on the roles of the metal nonlocal response and especially size-dependent plasmon damping. Through extensive modelling of metallic nanospheres and nanoshells coupled to dipole emitters, we show that within a purely classical description a remarkable fluorescence enhancement can be achieved. However, once departing from the local-response approximation, and particularly by implementing the recent generalised nonlocal optical response theory, which provides a more complete physical description combining electron convection and diffusion, we show that not only are fluorescence rates dramatically reduced compared to the predictions of the local description and the common hydrodynamic Drude model, but the optimum emitter–nanoparticle distance is also strongly affected. In this respect, experimental measurements of fluorescence, the theoretical description of which requires a precise concurrent evaluation of far- and near-field properties of the system, constitute a novel, more sensitive probe for assessing the validity of state-of-the-art nonclassical theories.
1. Introduction
Strategies for enhancing molecular fluorescence are widely explored in modern nanotechnology, due to its great importance to a large variety of applications, from single-molecule sensing and imaging to biochemistry, diagnostics and medicine, or for loss compensation and the design of novel optical antennas in nanophotonics.1–7 Among the techniques exploited to improve fluorophore signals, metal-enhanced fluorescence has been attracting considerable interest, ever since Drexhage8 and Chance et al.9 conducted and successfully interpreted groundbreaking experiments on molecules in the vicinity of planar metal surfaces. Metallic nanoparticles (NPs) sustaining localised surface plasmons (LSPs), coherent electron oscillations that produce strongly enhanced electromagnetic fields confined in subwavelength volumes,10 were soon considered as efficient alternatives to metal films for fluorescence enhancement,11,12 but further development was hindered at the time by experimental limitations. Recent advances in nanofabrication and nanotechnology have enabled the preparation and precise control of such NPs, thus opening new possibilities for the design of efficient templates for molecule–plasmon interactions.13 In a seminal paper, Anger et al.14 studied the coupling of a single molecule to laboriously positioned adjacent gold nanospheres, resolving a controversy over both fluorescence enhancement15 and quenching16 being observed in plasmonic environments. Molecular fluorescence is now understood as a two-step process, depending not only on the modification of spontaneous emission rates due to changes in the emitter environment (Purcell effect),17 but also on the – equally sensitive to such changes – excitation rate of the molecule. While the first mechanism requires reduction of absorptive losses related to Joule heating, and therefore placing the molecule at a distance from the metal is preferred, the electric field decreases exponentially from the NP and molecules are more efficiently excited in its immediate vicinity. The interplay between these two competing mechanisms leads to an optimum emitter–NP distance, for which the fluorescence signal is more pronounced.14Considerable effort has been devoted to tailoring molecular fluorescence with plasmonic nanostructures. Almost simultaneously with Anger et al., Kühn et al.18 performed a similar experiment to report a 20-fold enhancement near a gold nanosphere. Several theoretical and experimental studies have addressed understanding and optimising molecular emission in the vicinity of metallic NPs of different shapes19–35 and aggregates thereof.36–43 Moreover, it is now possible to place fluorophores in the proximity of metallic NPs with unprecedented control over the emitter orientation and distance from the NP, exploiting for instance, DNA origami techniques44–48 or appropriate hosting molecules.49 Nevertheless, despite the plethora of complex architectures available, one of the most attractive plasmonic units remains the metallic nanoshell, owing to its simple spherical geometry, tunability and stability.50 Nanoshells are dielectric-metal core–shell nanospheres, in which hybridisation between the LSPs sustained on either side of the shell51 provides large flexibility in tuning the optical response and shifting the modes to match the fluorophore excitation or emission wavelength.52 At the same time, encapsulating a potentially harmful to living organisms emitter inside a noble-metal shell can be beneficial for biomedical applications, to increase biocompatibility.53,54 Optimised emission rates can be achieved either by modifying NP dimensions for molecules placed inside55 or outside56 the nanoshell, or by adding metal/dielectric layers in a nanomatryoshka geometry.57 Due to the increased sensitivity of fluorescence on small geometry modifications, a careful theoretical analysis is essential prior to the realisation of experiments. However, in most cases the description of dipole emitter–plasmonic NP hybrids is restricted within the framework of classical electrodynamics, and nonclassical effects, expected to be pronounced for small NPs, thin shells or small emitter–NP distances,58 have been widely disregarded.
One of the first, larger-scale corrections to classical plasmonics, important for characteristic lengths decreasing below 10–20 nm, is to take the nonlocal response of the metal into account.59,60 In the usual local-response approximation (LRA), the displacement field at each position inside the metal is assumed to depend only on the applied electric field at the same position; its spatial variation is very small compared to the entire material. This is immediately translated into a metal dielectric function which depends on the angular frequency, ω, but not on the wavevector, k. The situation changes however when the NP dimensions decrease to become comparable to a characteristic nonlocal length,59 requiring a k-dependent dielectric function. One of the most popular models to incorporate such effects is the hydrodynamic Drude model (HDM), which assimilates the conduction-band electrons of the metal to a fluid following the laws of hydrodynamics, with a pressure term for the induced current density which allows the excitation of a – classically absent – propagating longitudinal electric field component. This approach was first introduced in the 1970s (ref. 61) to describe the optical response of small metallic spheres beyond standard Mie theory,62 but it has recently returned to the forefront of nanophotonics due to its success in interpreting sensitive experiments.63–65 Several groups have developed analytical and numerical tools to treat a large variety of plasmonic architectures with HDM,66–71 including metallic core–shell nanowires,72 and nanoshells either in the quasistatic regime58,73 or with a fully-electrodynamic approach.74–77 Despite its popularity, HDM constitutes only a first-order correction to classical electrodynamics, and it fails to account for a series of phenomena: not only are quantum-mechanical effects such as electron spill-out and tunnelling60,78 disregarded, but also the well-known, experimentally observed size-dependent plasmon damping due to reduction of the electron mean free path79 and surface scattering80 is not included. The latter issue has been recently tackled by an extension of HDM, the generalised nonlocal optical response (GNOR) theory,81 in which size-dependent plasmon damping appears naturally via an additional constituent of the hydrodynamic description of induced charges in the metal, namely electron diffusion. Nevertheless, despite the continued development of nonclassical models for plasmonics,60 with the exception of few studies focusing on spontaneous emission58,74,82–84 or related physics associated with surface-enhanced Raman scattering85,86 and quantum-dot decay dynamics,87 a systematic study and optimisation of fluorescence sensitivity in the vicinity of nonlocal metallic NPs is widely missing, especially within the GNOR theory which has already been successful in predicting the electron energy-loss spectra of few-nm NPs with unprecedented precision.65
The effect of nonlocality and plasmon damping on the fluorescence of classical emitters near spherical noble-metal NPs, either homogeneous spheres or metallic nanoshells, is theoretically explored here. In contrast to earlier studies,82 a fully-electrodynamic description is adopted, in analogy to previous evaluation of radiative and nonradiative decay rates.58,74 NP dimensions and emitter distances are first optimised within LRA to obtain the maximal classically predicted enhancement rates. In this procedure, we also resolve the controversy of maximum fluorescence obtained at wavelengths either redshifted88 or in perfect agreement52 with the LSP modes. Subsequently, we gradually increase the complexity of our description to compare LRA results with calculations based on the HDM and GNOR models. We show that, while in most occasions HDM produces results that are qualitatively and quantitatively close to those of LRA, the impressive fluorescence enhancement factors predicted by these models are significantly reduced in GNOR, as a result of a combination of nonlocal plasmon blueshifts65 and drastic reduction of the field exciting the emitter. Our work is therefore useful in a twofold way: on the one hand, we provide new insight into the design of emitter–plasmon hybrid architectures for optical, biological and medical applications. On the other hand, by identifying an example of an observable for which the popular HDM produces distinctly different results from the more complete GNOR theory, we propose a new, more rigid test for nonclassical models. Since fluorescence calculations require knowledge of both near- and far-field properties of plasmonic systems, they are more sensitive to nonclassical corrections. Carefully designed and conducted experiments based on fluorescence measurements are therefore expected to provide better understanding of the efficacy and applicability of novel theoretical descriptions that go beyond classical electrodynamics.
2. Theoretical methods
Throughout this paper we consider spherical NPs containing a metallic component described by a dielectric function εm. The metal can be either gold or silver, noble metals for which the LSP resonances lie in the visible region. For an accurate account of the material properties, we rely on the experimental dielectric function εexp(≡ εm) of Johnson and Christy.89 The particles are either homogeneous metallic nanospheres, of radius R, or layered NPs consisting of a dielectric core of radius R1 covered by a concentric metallic shell of thickness W, so that the total NP radius is R = R1 + W, as shown schematically in Fig. 1. We restrict our analysis to spherical NPs, because their symmetry allows the derivation of analytical solutions, as we describe below. For the dielectric core we assume a dielectric constant εcore = 2.13, which is appropriate for silica, a commonly encountered nanoshell core material, while the embedding medium is air (εair = 1). The fluorescent molecule is modelled as an electric dipole of dipole moment pd, placed at a distance rd from the surface of the NP, with its dipole moment oscillating radially (along the emitter–NP axis, see Fig. 1). The dipole is excited by a total electric field E which is conceptually decomposed into an incoming plane wave of wavevector k and electric field E0, polarised along the emitter–NP axis, and the field scattered by the NP. We choose this combination of dipole orientation and incident light polarisation, as it is intuitively expected, and theoretically verified,90 that it will generate the highest fluorescence rate. Efficient experimental methods to achieve such sensitive positioning have been recently presented.14,47,49 The dependence of fluorescence enhancement on different emitter orientations is discussed in the ESI.†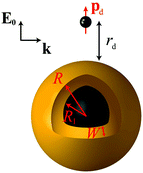 | ||
| Fig. 1 A classical emitter modelled as an electric point dipole of dipole moment pd, placed at a distance rd from the surface of a NP with a core–shell morphology. The NP consists of a dielectric core (εcore = 2.13) of radius R1 covered by a metallic shell of thickness W (described by a dielectric function εm obtained either from experimental data89 or from a Drude model), so that the total NP radius is R = R1 + W. A homogeneous metallic sphere can be viewed as the limiting case R1 = 0, R = W. The emitter–NP system is embedded in air (εair = 1), and illuminated in the excitation process by a plane wave of wavevector k, with its electric field E0 polarised along the emitter–NP axis. | ||
Extinction cross section (σext) spectra are calculated using62
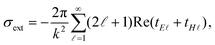 | (1) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) denotes the angular momentum, and tE
denotes the angular momentum, and tE![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and tH
and tH![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) are the Mie scattering coefficients, which are calculated analytically.62 For the Mie coefficients of a core–shell NP, recursive algorithms suitable for the description of nanomatryoshkas of any number of layers are usually employed.74,91 Here, however, we use an exact analytic expression, as we find that this approach provides more flexibility to tackle numerical instabilities that appear when nonlocal effects are included. Exact formulas for the Mie coefficients in all cases are provided in the ESI.† Within the nonlocal HDM and GNOR models, the excitation of longitudinal waves in the NPs is allowed, modifying the Mie solution. For the hard-wall NPs described here, where no electron spill out is permitted, one needs to impose the additional boundary conditions of a vanishing normal component of the induced current at the metal–dielectric interfaces.92 This can be rewritten in terms of the electric fields as ε∞Em·
are the Mie scattering coefficients, which are calculated analytically.62 For the Mie coefficients of a core–shell NP, recursive algorithms suitable for the description of nanomatryoshkas of any number of layers are usually employed.74,91 Here, however, we use an exact analytic expression, as we find that this approach provides more flexibility to tackle numerical instabilities that appear when nonlocal effects are included. Exact formulas for the Mie coefficients in all cases are provided in the ESI.† Within the nonlocal HDM and GNOR models, the excitation of longitudinal waves in the NPs is allowed, modifying the Mie solution. For the hard-wall NPs described here, where no electron spill out is permitted, one needs to impose the additional boundary conditions of a vanishing normal component of the induced current at the metal–dielectric interfaces.92 This can be rewritten in terms of the electric fields as ε∞Em·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) = εDED·
= εDED·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ,59 where
,59 where ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) is the unit vector normal to the interface, Em and ED are the electric fields in the metal and dielectric region respectively, εD is the permittivity of the dielectric region, and ε∞ the background contribution of core electrons and ions to the permittivity of the metal. The frequency- and wavevector-dependent longitudinal dielectric function of the metal is given by59,61
is the unit vector normal to the interface, Em and ED are the electric fields in the metal and dielectric region respectively, εD is the permittivity of the dielectric region, and ε∞ the background contribution of core electrons and ions to the permittivity of the metal. The frequency- and wavevector-dependent longitudinal dielectric function of the metal is given by59,61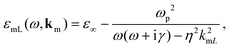 | (2) |
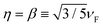 for HDM,61 where νF is the Fermi velocity of the metal, and
for HDM,61 where νF is the Fermi velocity of the metal, and 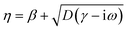 for GNOR, where D is the diffusion constant.81 We note that adding an imaginary part to η is an essential modification to the hydrodynamic parameter, which accounts for diffusion of the induced charges, a physical mechanism that is only captured by the GNOR model. To apply eqn (2) to the noble metals discussed throughout the paper, we obtain ε∞ from the experimental values, by subtracting the Drude part: ε∞ = εexp + ωp2/[ω(ω + iγ)]. We use ħωp = 9.02 eV, ħγ = 0.071 eV, νF = 1.39 × 106 m s−1, and D = 8.62 × 104 m2 s−1 for gold, and ħωp = 8.99 eV, ħγ = 0.025 eV, νF = 1.39 × 106 m s−1, and D = 9.62 × 104 m2 s−1 for silver.59
for GNOR, where D is the diffusion constant.81 We note that adding an imaginary part to η is an essential modification to the hydrodynamic parameter, which accounts for diffusion of the induced charges, a physical mechanism that is only captured by the GNOR model. To apply eqn (2) to the noble metals discussed throughout the paper, we obtain ε∞ from the experimental values, by subtracting the Drude part: ε∞ = εexp + ωp2/[ω(ω + iγ)]. We use ħωp = 9.02 eV, ħγ = 0.071 eV, νF = 1.39 × 106 m s−1, and D = 8.62 × 104 m2 s−1 for gold, and ħωp = 8.99 eV, ħγ = 0.025 eV, νF = 1.39 × 106 m s−1, and D = 9.62 × 104 m2 s−1 for silver.59
The fluorescence rate, γem, can be treated, to a good approximation, as the product of two independent processes, excitation of the emitter, expressed through an excitation rate γexc, and decay to its ground state accompanied by energy losses in radiative or nonradiative channels, expressed through the emitter quantum yield q. Then the fluorescence enhancement is given by14,88
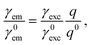 | (3) |
| γexc∝|pd·E(Rd)|2, | (4) |
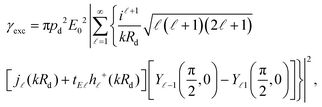 | (5) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (z) is the spherical Bessel function of complex argument z, h
(z) is the spherical Bessel function of complex argument z, h![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) +(z) is the corresponding spherical Hankel function of the first type, and Y
+(z) is the corresponding spherical Hankel function of the first type, and Y![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m(θ,ϕ) are the usual spherical harmonics. The excitation rate in free space can be obtained from eqn (5) by setting tE
m(θ,ϕ) are the usual spherical harmonics. The excitation rate in free space can be obtained from eqn (5) by setting tE![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 0, which describes the absence of a scattering object.
= 0, which describes the absence of a scattering object.
On the other hand, the quantum yield collectively describes the radiative and nonradiative decay rates of the molecule. In the absence of a structured environment, the internal quantum yield of the molecule, q0, is88
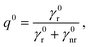 | (6) |
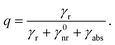 | (7) |
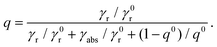 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88
88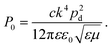 | (9) |
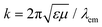 . For the radiated and absorbed power, we integrate the Poynting vector flux through the surface of a large sphere including both the emitter and the NP, and through the surface of the NP (where absorptive losses occur), respectively. Expanding the incoming and scattered fields into spherical waves, analytic expressions can be obtained, which for our specific geometry and dipole orientation are simplified to (see also the ESI†)93–95
. For the radiated and absorbed power, we integrate the Poynting vector flux through the surface of a large sphere including both the emitter and the NP, and through the surface of the NP (where absorptive losses occur), respectively. Expanding the incoming and scattered fields into spherical waves, analytic expressions can be obtained, which for our specific geometry and dipole orientation are simplified to (see also the ESI†)93–95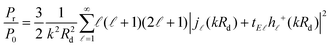 | (10) |
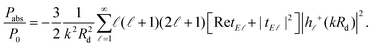 | (11) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 70 are required to accurately describe the emitter–NP interaction, depending on the specific geometry and model (in general, larger absorptive losses as in the case of GNOR ensure faster convergence). While quasistatic approximations are in good agreement with full-electrodynamic solutions for a relatively large rd,88 higher-order terms are crucial for an exact, converged calculation of the excitation field and the absorptive losses in the immediate proximity to the NP surface.14
= 70 are required to accurately describe the emitter–NP interaction, depending on the specific geometry and model (in general, larger absorptive losses as in the case of GNOR ensure faster convergence). While quasistatic approximations are in good agreement with full-electrodynamic solutions for a relatively large rd,88 higher-order terms are crucial for an exact, converged calculation of the excitation field and the absorptive losses in the immediate proximity to the NP surface.14
3. Results and discussion
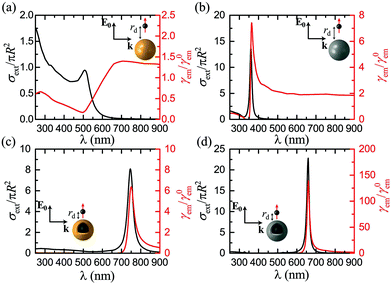
Before exploring the influence of the nonlocal and plasmon damping effects, and to facilitate the subsequent analysis, it is useful to tailor the NP geometry and emitter distance so as to produce sufficiently large fluorescence enhancement factors to make any corrections clearly visible. Motivated by previous studies,14,18,90 we first consider a gold nanosphere, and assume a radius R = 20 nm. This NP size is in fact a relatively poor choice for our purpose, as the ratio of radiative to absorptive losses is too small to produce the desired high quantum yield. Larger NPs have been used in the past to improve the radiation properties of the system.14,90 Nevertheless, here we deliberately aim to show that it is in fact possible to greatly increase fluorescence without resorting to extremely large NPs, exploiting the flexibility provided by the core–shell geometry of a nanoshell. The emitter distance is considered equal to rd = 15 nm, for which our simulations showed an optimum fluorescence enhancement. The extinction cross section spectrum (normalised to the geometrical cross section) of this nanosphere, which provides a good measure of the NP far-field response, is presented in Fig. 2a together with the corresponding fluorescence spectrum. The maximum fluorescence enhancement is obtained at wavelengths longer than the plasmon resonance, in agreement with the findings of Novotny et al.,14,88 but, for this particular NP size and emitter–NP distance, it is only a little larger than unity. Over a wide part of the visible spectrum, absorptive losses dominate the emitter–NP coupling, leading to strong fluorescence quenching, especially for wavelengths shorter than 500 nm where additional loss mechanisms prevail due to interband transitions.62Since the fingerprint of interband transitions in gold is strong, the far- and near-field optical properties of the emitter–NP hybrid are largely affected, and drawing conclusions about the plasmonic impact on fluorescence is not straightforward. It is therefore reasonable to explore different plasmonic materials to improve our understanding and possibly also to enhance fluorescence signals. In this regard, silver, which is a low-loss Drude-like metal over the entire visible range, and its interband transition-related absorption appears in the ultraviolet region, is a natural choice. Silver NPs are however often disregarded as potential emitter environments because, for a wide variety of fluorophores encountered in medical and biological applications, their LSP resonance is much blueshifted with respect to the molecule emission wavelength. It is somehow surprising, therefore, that a large fluorescence enhancement, more than twice the value achieved by the gold nanosphere shown in Fig. 2a, is calculated as shown in Fig. 2b for a silver NP with the same R and rd. Interestingly, this improved enhancement is obtained not only close to the silver nanosphere LSP resonance, but also over the entire visible spectrum. This happens because both the excitation rate and the quantum yield, the product of which defines fluorescence, are concurrently increased. Not only is the ratio of radiative to absorptive losses significantly enhanced, leading to a quantum yield close to unity over the entire visible spectrum, but also reducing losses significantly enhances the electromagnetic field at the position of the emitter, making its excitation more efficient. It is also worth noting that, in this case, the maximum fluorescence enhancement occurs (almost) at the LSP resonance, in contrast to the gold nanospheres explored earlier. Within a quasistatic description, the experimental redshifted maximum fluorescence44 has been justified by the difference in the resonance conditions for the radiative and nonradiative decay rates: γabs is expected to have its maximum at εm + 1 = 0, while for γr it occurs at εm + 2 = 0.88 However, as we show here, for low-loss plasmonic systems the enhancement of the excitation field (which has its maximum at the LSP resonance) can be large enough to limit the importance of the quantum yield.
Homogeneous metallic nanospheres are easier to synthesise, but they strongly lack in tunability, and metallic nanoshells provide a much larger flexibility to match the excitation or emission wavelength for a wide range of fluorophores. Interaction between the modes sustained at the inner and outer surfaces of the metal leads to the formation of hybrid plasmons,51 which can be engineered to cover the entire visible spectrum and part of the ultraviolet and near-infrared.75 We take advantage of this tunability as shown in Fig. 2c and d, where we substitute the homogeneous spheres for dielectric–metal core–shell NPs, similar to the ones considered recently for the strong coupling of quantum dots with LSPs.96 For a direct comparison with Fig. 2a and b we maintain the total NP radius at R = 20 nm, covering a silica sphere of radius R1 = 18 nm with a thin metal layer of W = 2 nm. This small shell thickness is essential to enhance plasmon hybridization and push the LSP resonances away from the regime of strong absorptive losses in gold. While it is still challenging to fabricate so thin nanoshells, successful steps towards this direction have been recently taken.97 With this NP choice, both for gold and silver nanoshells, the maximum fluorescence enhancement occurs at the LSP wavelength (here we focus on the dominant, bonding plasmonic mode), in agreement with experiments on large gold nanoshells.52 In addition to the shifting of the LSP modes, in the case of core–shell NP absorptive losses are also reduced to a great extent due to the involvement of a smaller quantity of metal. This loss reduction leads to a γem rate with its maximum much closer to the NP surface, at distances for which strong quenching is observed in the case of nanospheres. Bringing the emitter closer to the NP without most of the emitted energy being lost to Joule heating means that the electric field exciting the molecule can be significantly enhanced, leading to a stronger fluorescence signal. In the example of the thin silver nanoshell shown in Fig. 2d, an enhancement of more than 150 is achieved, larger than most values previously reported in the literature for such geometries.14,52,90
So far we have restricted our analysis to results obtained within classical electrodynamics. The main purpose of this paper, however, is to explore nonlocal effects, and how they influence the emitter–NP coupling. Unlike most earlier studies on nonlocal plasmonics, which were focused on the far-field response59,61,68 even when electric dipoles were used to excite the LSP modes,84 the combination of far- and near-field properties involved in fluorescence calculations amplifies the need for implementation of nonlocal theories. In Fig. 3 we present γem as a function of rd for the four examples presented in Fig. 2. In each case, we choose the wavelength λ (same for the excitation and emission process, see discussion in section 2) so as to obtain the maximum fluorescence signal according to Fig. 2, and compare the estimations of LRA with those of the HDM and GNOR nonlocal models. The main fingerprint of such hard-wall nonlocal models is a blueshift of the plasmon resonance, as compared to the results of LRA, which becomes larger as the NP size decreases.59 In the case of the relatively large solid spheres examined in Fig. 3a and b, nonlocal effects are known to have a nearly negligible effect on the far-field plasmon resonances.59,61,81 It is shown here that the small blueshifts predicted by HDM indeed affect the fluorescence rates only a little. In the specific examples shown in Fig. 3a and b, HDM produces a slightly larger fluorescence enhancement compared to LRA, although we have identified cases of small reduction as well. These usually minor differences depend on the exact position of the LSP modes: if the plasmon resonance calculated within LRA matches exactly the fluorophore emission wavelength, the small nonlocal blueshift will detune it to reduce γem. Due to the ultra-fine engineering requirements however, it is always possible that taking nonlocality into account will actually tune the NP resonance towards λem, leading to the small enhancement observed in Fig. 3a and b. The case is nevertheless much different within GNOR, which includes size-dependent plasmon damping79 as a natural constituent of the hydrodynamic description of the free-electron gas accounting for electron diffusion. Even though for the large NP sizes considered here its effect on the far-field spectra is still small, the combination of reducing the excitation field and detuning the LSP resonance produces a visible decrease in fluorescence enhancement, especially in the case of silver (Fig. 3b), thus highlighting the need for accurate calculations of the near field exciting the molecule.
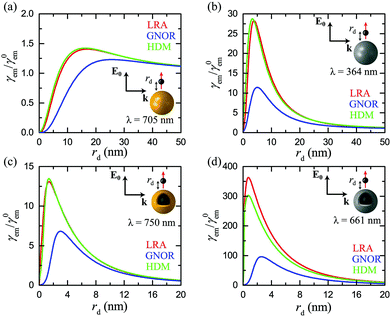 | ||
| Fig. 3 Normalised fluorescence γem as a function of the distance rd of a dipole emitter from the surface of the plasmonic nanospheres shown in the insets, at the optimum emission wavelength λ determined from Fig. 2. (a) A homogeneous gold nanosphere (R = 20 nm) at λ = 705 nm. (b) A homogeneous silver nanosphere (R = 20 nm) at λ = 364 nm. (c) A gold nanoshell (R = 20 nm, W = 2 nm) at λ = 750 nm. (d) A silver nanoshell (R = 20 nm, W = 2 nm) at λ = 661 nm. In all cases, red, blue, and green lines represent the predictions of the LRA, GNOR, and HDM models respectively. The emitter is modelled as a classical electric dipole oscillating radially, and the field exciting it is polarised along the emitter–NP axis. | ||
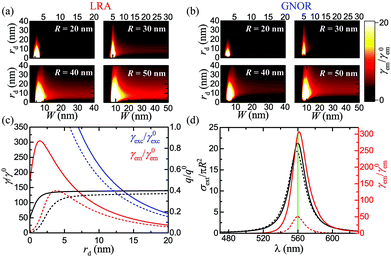
Although we have already identified a visible impact of nonlocality on homogeneous spheres, its effect is anticipated to be much stronger in metallic nanoshells. While the induced resonance shifts are expected to be much stronger in the case of the antibonding, cavity-like shell modes,75 nonlocality cannot be neglected in the case of bonding, particle-like modes either.58 The decrease in fluorescence enhancement and shift of the optimum emitter position observed in metallic nanospheres are indeed more pronounced in the case of nanoshells (Fig. 3c and d), especially for a silver nanoshell. In Fig. 3d both the small reduction of γem within HDM discussed earlier, and also an important four-fold decrease within GNOR compared to the results of LRA, can be observed. It is immediately clear from Fig. 3 that HDM, which is the most frequently adopted nonlocal model, produces only minor differences in the local results, suggesting the (premature) conclusion that nonlocality plays a limited role in fluorescence measurements, similarly to other sensing procedures.72 However, the dramatic reduction observed within GNOR unambiguously displays how a more complete nonlocal description of the free-electron fluid, including both induced-charge convection and diffusion, can be crucial for a more accurate description of the emitter–NP hybrid. Fortunately, even with these corrections taken into account, it is evident that silver nanoshells can still produce a significant fluorescence enhancement of the order of 100, while maintaining high enhancement values (>20) for a large range of emitter distances. We will therefore focus our remaining analysis to such silver nanoshells, comparing the results obtained within the LRA and GNOR models and disregarding HDM.
The example from Fig. 3d was chosen for consistency with the rest of the cases in the figure, as far as geometry is concerned, but it does not correspond to an optimised design or to a specific molecule. A more systematic study of nanoshell geometries should therefore provide further insight into the underlying physics. In Fig. 4 we fully explore the role of the nanoshell size and thickness, for a characteristic excitation and emission wavelength λ = 560 nm, close to λem of a commonly encountered fluorophore, Rhodamine-6G.88,90 We should note that for a more strict description, the excitation wavelength should be slightly shorter, and a value λexc = 532 nm is often used in the literature.36,90 However, this choice would render analysing the results of our subsequent parametric study, in which already the three geometrical parameters R, D, and rd are free, even more complicated. In any case, using λexc ≠ λem is straightforward, but adds only few quantitative changes to our analysis, as we verified by detailed simulations. As shown in Fig. 4a, changing the total size of the nanoshell can provide large engineering possibilities. For small NPs, there exists a narrow shell thickness range for which the LSP resonance is exactly tuned at λ, leading to very strong fluorescence signals, approaching γem = 150 for the smallest, R = 20 nm NP, with W = 3 nm. This enhancement becomes however about three times smaller once the intrinsic corrections of the GNOR model are applied (Fig. 4b). As the NP size increases, the maximum enhancement obtained within both LRA and GNOR models decreases, but a much wider region of shell thicknesses and emitter distances characterised by large (>10–15) fluorescence enhancements is obtained. Interestingly, these wide parameter ranges are preserved within GNOR, as can be seen especially for the R = 50 nm case. This broad enhancement plateau provides large fabrication advantages, as it shows that it is not required to achieve a very specific emitter distance or shell thickness – fabrication errors are largely tolerated.
To further illustrate the significant impact of nonclassical theories, we plot in Fig. 4c the excitation and fluorescence rates, together with the quantum yield, for a finely tailored, optimised nanoshell geometry (R = 29.5 nm, W = 4.5 nm), as obtained within LRA and GNOR. It is evident that, even though the quantum yield is also modified by the additional damping due to electron diffusion in GNOR, the large decrease in γem is mainly due to the strong reduction of the excitation rate, as can be seen by the large difference between the solid and dashed blue lines for LRA and GNOR, respectively. The effect of quantum yield modification manifests itself more clearly through the shifting of the optimum emitter position further away from the NP surface, where radiative transfer can eventually dominate the now stronger absorptive losses. The corresponding extinction and fluorescence spectra for the same nanoshell are presented in Fig. 4d, for an emitter placed at the optimum (according to detailed simulations) position of rd = 1.5 nm. It is again unambiguously verified that the best strategy for optimising fluorescence signals is to match the emitter characteristic wavelengths with the LSP resonance of the NP, as long as the emitter transitions occur away from additional loss mechanisms like interband transitions, and regardless of the theoretical model applied.
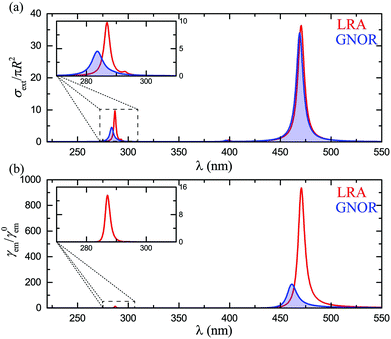
Finally, for a complete theoretical description, it is important to explore the case of cavity-like nanoshell modes and how they couple with classical emitters. As mentioned earlier, nonlocality induces larger frequency shifts for these modes, particularly for very thin shells.58,75 It is therefore anticipated that fluorescence signals, which are more sensitive to changes in the local environment, will be strongly affected. While, for consistency with the rest of the paper, these effects should also be explored in silver nanoshells, interband transitions in silver become now an important issue, as they almost completely conceal the cavity-like modes. To eliminate such absorptive losses and clearly observe the modes of interest, we assume a Drude model for the metallic material, εm = ε∞ − ωp2/[ω(ω + iγ)]. We consider ħω = 8.99 eV, ħγ = 0.05 eV, and ε∞ = 4, values which ensure good agreement with the optical response of silver NPs in the visible region, while the spectra are free of interband transition-related losses. The extinction spectra for such a nanoshell with R = 20 nm and W = 5 nm, calculated within LRA and GNOR, are shown in Fig. 5a. This shell is thin enough to ensure that the cavity-like mode is clearly discernible, but not shifted too far into the ultraviolet region. As discussed above, nonlocal effects induce a much larger blueshift for the cavity-like mode (better shown by the enlarged view of the inset), while size-dependent damping is also stronger. Drastic modifications of fluorescence signals are therefore expected. Indeed, in the fluorescence spectra shown in Fig. 5b, the clear peak obtained within LRA at 287 nm, matching the LSP resonance, vanishes completely within GNOR due to plasmon damping. This behaviour is in fact also observed (results not shown here) for higher-order particle-like (and, to a larger extent, cavity-like) modes, even for the large NP sizes (typically R > 50–60 nm) for which the extinction peak of the quadrupolar particle-like mode becomes more intense than the dipolar one. Only the particle-like dipole modes of metallic nanoshells are therefore good candidates for molecular fluorescence enhancement. Nevertheless, we have shown here that these modes can already be engineered over a wide spectral range, providing large flexibility to the design of single-molecule sensing architectures.
4. Conclusions
We have presented a detailed theoretical study of molecular fluorescence enhancement in the vicinity of metallic nanospheres and nanoshells. We have shown that large enhancement values, exceeding by an order of magnitude those obtained for nanospheres, can be achieved by appropriately tailoring the nanoshell geometry and fluorophore distance. These enhancement rates are however significantly reduced when a more complete description of the NP optical response, deviating from classical electrodynamics, is adopted. In particular, we have shown that within the recently developed GNOR theory, which concurrently accounts for nonlocal effects and size-dependent plasmon damping, both the maximum fluorescence enhancement rate and the optimum fluorophore position can be strongly modified, as a result of the combined action of nonlocal LSP shifting, increase of absorptive losses and reduction of the exciting field. Experimental verification of our GNOR predictions for fluorescence will highlight the importance of departing from HDM and adopting a more detailed description of the collective response of free electrons in the metal, especially when near-field optical properties are involved. Nevertheless, even after all these corrections are included, large fluorescence enhancement plateaus can still be obtained for a wide range of geometrical parameters, providing large flexibility to the experimental realisation of metal-enhanced fluorescence and single-molecule spectroscopy architectures. Our work combines the evaluation of far- and near-field properties through a sensitive, experimentally measurable quantity, and in this respect it provides a more rigid test for nonclassical electrodynamic theories, with the potential to trigger decisive experiments in the near future. Further theoretical work to describe effects such as statistical averaging of a large number of fluorophores with random positions and orientations, or coherent emission from several emitters, is also expected to expand our understanding of the coupling of fluorophores with nonlocal plasmonic NPs.Acknowledgements
C. T. was supported by funding from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme (FP7/2007–2013) under REA grant agreement number 609405 (COFUNDPostdocDTU). N. A. M. and M. W. acknowledge support from the Danish Council for Independent Research (FNU 1323-00087). M. W. acknowledges support from the Villum Foundation via the VKR Centre of Excellence NATEC-II.The Center for Nanostructured Graphene is sponsored by the Danish National Research Foundation, Project DNRF103.
Notes and references
- E. Fort and S. Grésillon, J. Phys. D: Appl. Phys., 2008, 41, 013001 CrossRef.
- Y. Fu and J. R. Lakowicz, Laser Photonics Rev., 2009, 3, 221–232 CrossRef CAS.
- P. Bharadwaj, B. Deutsch and L. Novotny, Adv. Opt. Photonics, 2009, 1, 438–483 CrossRef.
- V. Giannini, A. I. Fernández-Domínguez, S. C. Heck and S. A. Maier, Chem. Rev., 2011, 111, 3888–3912 CrossRef CAS PubMed.
- M. Agio, Nanoscale, 2012, 4, 692–706 RSC.
- W. Deng, F. Xie, H. T. M. C. M. Baltar and E. M. Goldys, Phys. Chem. Chem. Phys., 2013, 15, 15695–15708 RSC.
- D. Darvill, A. Centeno and F. Xie, Phys. Chem. Chem. Phys., 2013, 15, 15709–15726 RSC.
- K. H. Drexhage, J. Lumin., 1970, 1–2, 693–701 CrossRef.
- R. R. Chance, A. Prock and R. Silbey, Adv. Chem. Phys., 1978, 37, 1–65 CrossRef CAS.
- S. A. Maier, Plasmonics: Fundamentals and Applications, Springer, New York, 2007 Search PubMed.
- J. Gersten and A. Nitzan, J. Chem. Phys., 1981, 75, 1139–1152 CrossRef CAS.
- R. Ruppin, J. Chem. Phys., 1982, 76, 1681–1684 CrossRef CAS.
- D. Paria, K. Roy, H. J. Singh, S. Kumar, S. Raghavan, A. Ghosh and A. Ghosh, Adv. Mater., 2015, 27, 1751–1758 CrossRef CAS PubMed.
- P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002 CrossRef PubMed.
- K. T. Shimizu, W. K. Woo, B. R. Fisher, H. J. Eisler and M. G. Bawendi, Phys. Rev. Lett., 2002, 89, 117401 CrossRef CAS PubMed.
- E. Dulkeith, A. C. Morteani, T. Niedereichholz, T. A. Klar, J. Feldmann, S. A. Levi, F. C. J. M. van Veggel, D. N. Reinhoudt, M. Möller and D. I. Gittins, Phys. Rev. Lett., 2002, 89, 203002 CrossRef CAS PubMed.
- E. M. Purcell, Phys. Rev., 1946, 69, 681 CrossRef.
- S. Kühn, U. Håkanson, L. Rogobete and V. Sandoghdar, Phys. Rev. Lett., 2006, 97, 017402 CrossRef PubMed.
- P. C. Das and A. Puri, Phys. Rev. B: Condens. Matter, 2002, 65, 155416 CrossRef.
- L. A. Blanco and F. J. García de Abajo, Phys. Rev. B: Condens. Matter, 2004, 69, 205414 CrossRef.
- H. Mertens, A. F. Koenderink and A. Polman, Phys. Rev. B: Condens. Matter, 2007, 76, 115123 CrossRef.
- T. H. Taminiau, F. D. Stefani, F. B. Segerink and N. F. Van Hulst, Nat. Photonics, 2008, 2, 234–237 CrossRef CAS.
- G. Colas des Francs, A. Bouhelier, E. Finot, J. C. Weeber, A. Dereux, C. Girard and E. Dujardin, Opt. Express, 2008, 16, 17654–17666 CrossRef CAS PubMed.
- V. Giannini, J. A. Sánchez-Gil, O. L. Muskens and J. Gómez Rivas, J. Opt. Soc. Am. B, 2009, 26, 1569–1577 CrossRef CAS.
- X. Ma, H. Tan, T. Kipp and A. Mews, Nano Lett., 2010, 10, 4166–4174 CrossRef CAS PubMed.
- R. Esteban, T. V. Teperik and J. J. Greffet, Phys. Rev. Lett., 2010, 104, 026802 CrossRef CAS PubMed.
- S. Bharill, C. Chen, B. Stevens, J. Kaur, Z. Smilansky, W. Mandecki, I. Gryczynski, Z. Gryczynski, B. S. Cooperman and Y. E. Goldman, ACS Nano, 2011, 5, 399–407 CrossRef CAS PubMed.
- X.-W. Chen, M. Agio and V. Sandoghdar, Phys. Rev. Lett., 2012, 108, 233001 CrossRef PubMed.
- A. M. Kern, A. J. Meixner and O. J. F. Martin, ACS Nano, 2012, 6, 9828–9836 CrossRef CAS PubMed.
- G. Sun and J. B. Khurgin, Phys. Rev. A, 2012, 85, 063410 CrossRef.
- S. Derom, A. Berthelot, A. Pillonet, O. Benamara, A. M. Jurdyc, C. Girard and G. Colas des Francs, Nanotechnology, 2013, 24, 495704 CrossRef CAS PubMed.
- J. Chen, Y. Jin, N. Fahruddin and J. X. Zhao, Langmuir, 2013, 29, 1584–1591 CrossRef CAS PubMed.
- X. Meng, R. R. Grote, J. I. Dadap, N. C. Panoiu and R. M. Osgood Jr., Opt. Express, 2014, 22, 22018–22030 CrossRef PubMed.
- A. Rose, T. B. Hoang, F. McGuire, J. J. Mock, C. Ciracì, D. R. Smith and M. H. Mikkelsen, Nano Lett., 2014, 14, 4797–4802 CrossRef CAS PubMed.
- B. L. Darby, B. Auguié, M. Meyer, A. E. Pantoja and E. C. Le Ru, Nat. Photonics, 2016, 10, 40–45 CrossRef CAS.
- M. A. Noginov, G. Zhu, M. Bahoura, C. E. Small, C. Davison, J. Adegoke, V. P. Drachev, P. Nyga and V. M. Shalaev, Phys. Rev. B: Condens. Matter, 2006, 74, 184203 CrossRef.
- P. P. Pompa, L. Martiradonna, A. Della Torre, F. Della Sala, L. Manna, M. De Vittorio, F. Calabi, R. Cingolani and R. Rinaldi, Nat. Nanotechnol., 2006, 1, 126–130 CrossRef CAS PubMed.
- V. Yannopapas and N. V. Vitanov, J. Phys.: Condens. Matter, 2007, 19, 096210 CrossRef.
- A. Bek, R. Jansen, M. Ringler, S. Mayilo, T. A. Klar and J. Feldmann, Nano Lett., 2008, 8, 485–490 CrossRef CAS PubMed.
- M. Ringler, A. Schwemer, M. Wunderlich, A. Nichtl, K. Kürzinger, T. A. Klar and J. Feldmann, Phys. Rev. Lett., 2008, 100, 203002 CrossRef CAS PubMed.
- J.-W. Liaw, J.-H. Chen, C.-S. Chen and M.-K. Kuo, Opt. Express, 2009, 17, 13532–13540 CrossRef CAS PubMed.
- A. Kinkhabwala, Z. Yu, S. Fan, Y. Avlasevich, K. Müllen and W. E. Moerner, Nat. Photonics., 2009, 3, 654–657 CrossRef CAS.
- S. Evangelou, V. Yannopapas and E. Paspalakis, Phys. Rev. A, 2011, 83, 055805 CrossRef.
- Y. Chen, K. Munechika and D. S. Ginger, Nano Lett., 2007, 7, 690–696 CrossRef CAS PubMed.
- G. P. Acuna, M. Bucher, I. H. Stein, C. Steinhauer, A. Kuzyk, P. Holzmeister, R. Schreiber, A. Moroz, F. D. Stefani, T. Liedl, F. C. Simmel and P. Tinnefeld, ACS Nano, 2012, 6, 3189–3195 CrossRef CAS PubMed.
- C. Blum, N. Zijlstra, A. Lagendijk, M. Wubs, A. P. Mosk, V. Subramaniam and W. L. Vos, Phys. Rev. Lett., 2012, 109, 203601 CrossRef PubMed.
- P. Holzmeister, E. Pibiri, J. J. Schmied, T. Sen, G. P. Acuna and P. Tinnefeld, Nat. Commun., 2014, 5, 5356 CrossRef CAS PubMed.
- A. Puchkova, C. Vietz, E. Pibiri, B. Wünsch, M. Sanz Paz, G. P. Acuna and P. Tinnefeld, Nano Lett., 2015, 15, 8354–8359 CrossRef CAS PubMed.
- R. Chikkaraddy, B. de Nijs, F. Benz, S. J. Barrow, O. A. Scherman, R. Rosta, A. Demetriadou, P. Fox, O. Hess and J. J. Baumberg, Nature, 2016, 535, 117–120 CrossRef PubMed.
- C. Radloff and N. J. Halas, Appl. Phys. Lett., 2001, 79, 674–676 CrossRef CAS.
- E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, Science, 2003, 302, 419–422 CrossRef CAS PubMed.
- F. Tam, G. P. Goodrich, B. R. Johnson and N. J. Halas, Nano Lett., 2007, 7, 496–501 CrossRef CAS PubMed.
- Y. Jin and X. Gao, Nat. Nanotechnol., 2009, 4, 571–576 CrossRef CAS PubMed.
- B. Ji, E. Giovanelli, B. Habert, P. Spinicelli, M. Nasilowski, X. Xu, N. Lequeux, J.-P. Hugonin, F. Marquier, J.-J. Greffet and B. Dubertret, Nat. Nanotechnol., 2015, 10, 170–175 CrossRef CAS PubMed.
- J. Enderlein, Phys. Chem. Chem. Phys., 2002, 4, 2780–2786 RSC.
- T. Zhang, G. Lu, W. Li, J. Liu, L. Hou, P. Perriat, M. Martini, O. Tillement and Q. Gong, J. Phys. Chem. C, 2012, 116, 8804–8812 CAS.
- C. Ayala-Orozco, J. G. Liu, M. W. Knight, Y. Wang, J. K. Day, P. Nordlander and N. J. Halas, Nano Lett., 2014, 14, 2926–2933 CrossRef CAS PubMed.
- R. Chang and P. T. Leung, Phys. Rev. B: Condens. Matter, 2006, 73, 125438 CrossRef.
- S. Raza, S. I. Bozhevolnyi, M. Wubs and N. A. Mortensen, J. Phys.: Condens. Matter, 2015, 27, 183204 CrossRef PubMed.
- W. Zhu, R. Esteban, A. G. Borisov, J. J. Baumberg, P. Nordlander, H. J. Lezec, J. Aizpurua and K. B. Crozier, Nat. Commun., 2016, 7, 11495 CrossRef CAS PubMed.
- R. Ruppin, Phys. Rev. Lett., 1973, 31, 1434–1437 CrossRef.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, New York, 1983 Search PubMed.
- C. Ciracì, R. T. Hill, J. J. Mock, Y. Urzhumov, A. I. Fernández-Domínguez, S. A. Maier, J. B. Pendry, A. Chilkoti and D. R. Smith, Science, 2012, 337, 1072–1074 CrossRef PubMed.
- A. Wiener, A. I. Fernández-Domínguez, A. P. Horsfield, J. B. Pendry and S. A. Maier, Nano Lett., 2012, 12, 3308–3314 CrossRef CAS PubMed.
- S. Raza, S. Kadkhodazadeh, T. Christensen, M. Di Vece, M. Wubs, N. A. Mortensen and N. Stenger, Nat. Commun., 2015, 6, 8788 CrossRef CAS PubMed.
- R. Fuchs and F. Claro, Phys. Rev. B: Condens. Matter, 1987, 35, 3722–3727 CrossRef.
- A. Pack, M. Hietschold and R. Wannemacher, Opt. Commun., 2001, 194, 277–287 CrossRef CAS.
- J. M. McMahon, S. K. Gray and G. C. Schatz, Phys. Rev. Lett., 2009, 103, 097403 CrossRef PubMed.
- J. M. McMahon, S. K. Gray and G. C. Schatz, J. Phys. Chem. C, 2010, 114, 15903–15908 CAS.
- S. Raza, G. Toscano, A.-P. Jauho, M. Wubs and N. A. Mortensen, Phys. Rev. B: Condens. Matter, 2011, 84, 121412(R) CrossRef.
- C. Ciracì, Y. Urzhumov and D. R. Smith, J. Opt. Soc. Am. B, 2013, 30, 2731–2736 CrossRef.
- S. Raza, G. Toscano, A.-P. Jauho, N. A. Mortensen and M. Wubs, Plasmonics, 2013, 8, 193–199 CrossRef CAS.
- R. Rojas, F. Claro and R. Fuchs, Phys. Rev. B: Condens. Matter, 1988, 37, 6799–6807 CrossRef CAS.
- A. Moroz, Ann. Phys., 2005, 315, 352–418 CAS.
- C. Tserkezis, G. Gantzounis and N. Stefanou, J. Phys.: Condens. Matter, 2008, 20, 075232 CrossRef.
- C. David and F. J. García de Abajo, J. Phys. Chem. C, 2011, 115, 19470–19475 CAS.
- Y. Huang and L. Gao, J. Phys. Chem. C, 2014, 118, 30170–30178 CAS.
- T. V. Teperik, P. Nordlander, J. Aizpurua and A. G. Borisov, Phys. Rev. Lett., 2013, 110, 263901 CrossRef CAS PubMed.
- U. Kreibig and L. Genzel, Surf. Sci., 1985, 156, 678–700 CrossRef CAS.
- J. B. Khurgin and G. Sun, Opt. Express, 2015, 23, 30739–30748 CrossRef PubMed.
- N. A. Mortensen, S. Raza, M. Wubs, T. Søndergaard and S. I. Bozhevolnyi, Nat. Commun., 2014, 5, 3809 CAS.
- H. Y. Xie, H. Y. Chung, P. T. Leung and D. P. Tsai, Phys. Rev. B: Condens. Matter, 2009, 80, 155448 CrossRef.
- R. Filter, C. Bösel, G. Toscano, F. Lederer and C. Rockstuhl, Opt. Lett., 2014, 39, 6118–6121 CrossRef PubMed.
- T. Christensen, W. Yan, S. Raza, A.-P. Jauho, N. A. Mortensen and M. Wubs, ACS Nano, 2014, 8, 1745–1758 CrossRef CAS PubMed.
- G. Toscano, S. Raza, S. Xiao, M. Wubs, A.-P. Jauho, S. I. Bozhevolnyi and N. A. Mortensen, Opt. Lett., 2012, 37, 2538–2540 CrossRef CAS PubMed.
- Y. Zhao, X. Liu, D. Y. Lei and Y. Chai, Nanoscale, 2014, 6, 1311–1317 RSC.
- A. Vagov, I. A. Larkin, M. D. Croitoru and V. M. Axt, Phys. Rev. B: Condens. Matter, 2016, 93, 195414 CrossRef.
- P. Bharadwaj and L. Novotny, Opt. Express, 2007, 15, 14266–14274 CrossRef CAS PubMed.
- P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379 CrossRef CAS.
- T. Härtling, P. Reichenbach and L. M. Eng, Opt. Express, 2007, 15, 12806–12817 CrossRef.
- N. Stefanou, C. Tserkezis and G. Gantzounis, Proc. SPIE-Int. Soc. Opt. Eng., 2008, 6989, 698910 CrossRef.
- A. R. Melnyk and M. J. Harrison, Phys. Rev. B: Solid State, 1970, 2, 835–850 CrossRef.
- H. Chew, P. J. McNulty and M. Kerker, Phys. Rev. A, 1976, 13, 396–404 CrossRef.
- M. Kerker, D.-S. Wang and H. Chew, Appl. Opt., 1980, 19, 4159–4174 CrossRef CAS PubMed.
- H. Chew, J. Chem. Phys., 1987, 87, 1355–1360 CrossRef CAS.
- N. Zhou, M. Yuan, Y. Gao, D. Li and D. Yang, ACS Nano, 2016, 10, 4154–4163 CrossRef CAS PubMed.
- X. Zhang, L. Guo, J. Luo, X. Zhao, T. Wang, Y. Li and Y. Fu, ACS Appl. Mater. Interfaces, 2016, 8, 9889–9896 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Mie coefficients for local and nonlocal nanospheres and nanoshells, derivation of the equations for the dipole excitation rate, radiative and nonradiative losses, and fluorescence rates for different emitter orientations. See DOI: 10.1039/C6NR06393D |
| This journal is © The Royal Society of Chemistry 2016 |