Open Access Article
Open Access ArticleEpitaxial nucleation of CVD bilayer graphene on copper†
Yenan
Song
a,
Jianing
Zhuang
b,
Meng
Song
c,
Shaoqian
Yin
a,
Yu
Cheng
a,
Xuewei
Zhang
a,
Miao
Wang
c,
Rong
Xiang
d,
Yang
Xia
e,
Shigeo
Maruyama
d,
Pei
Zhao
*a,
Feng
Ding
*b and
Hongtao
Wang
*a
aInstitute of Applied Mechanics and Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province, Zhejiang University, Hangzhou 310012, P. R. China. E-mail: peizhao@zju.edu.cn; htw@zju.edu.cn
bInstitute of Textiles and Clothing, Hong Kong Polytechnic University, Kowloon, Hong Kong, China. E-mail: feng.ding@polyu.edu.hk
cDepartment of Physics, Zhejiang University, Hangzhou 310012, P. R. China
dDepartment of Mechanical Engineering, The University of Tokyo, Bunkyo-ku, Tokyo 113-8656, Japan
eInstitute of Microelectronics, Chinese Academy of Science, Beijing 100029, P. R. China
First published on 28th October 2016
Abstract
Bilayer graphene (BLG) has emerged as a promising candidate for next-generation electronic applications, especially when it exists in the Bernal-stacked form, but its large-scale production remains a challenge. Here we present an experimental and first-principles calculation study of the epitaxial chemical vapor deposition (CVD) nucleation process for Bernal-stacked BLG growth on Cu using ethanol as a precursor. Results show that a carefully adjusted flow rate of ethanol can yield a uniform BLG film with a surface coverage of nearly 90% and a Bernal-stacking ratio of nearly 100% on ordinary flat Cu substrates, and its epitaxial nucleation of the second layer is mainly due to the active CH3 radicals with the presence of a monolayer-graphene-covered Cu surface. We believe that this nucleation mechanism will help clarify the formation of BLG by the epitaxial CVD process, and lead to many new strategies for scalable synthesis of graphene with more controllable structures and numbers of layers.
Introduction
Bilayer graphene (BLG), a two-dimensional material consisting of two atomic layers of carbon honeycomb lattices, has emerged as a promising candidate for next-generation electronic applications, especially when it exists in the Bernal- (AB-) stacked form, due to the fact that a bandgap of ∼250 meV can be developed near its Dirac points by applying a vertical electric field across the two layers.1,2 However, by far the large-scale production of Bernal-stacked bilayer graphene remains a challenge. Although in the past few years there have been many exciting achievements in the synthesis of large-size and high-quality monolayer graphene (MLG) using the chemical vapor deposition (CVD) method on Cu substrates,3–5 developing a practical and scalable method to obtain Bernal-stacked BLG is still a hot pursuit for future applications.Previous reports have shown that the CVD synthesis of BLG on Cu is possible if more active carbon precursors or designed CVD processes are adopted,6–15 and the key point of these modifications to ordinary CVD is to overcome the self-limiting nature of MLG on Cu. Usually, the second layer of BLG grows underneath the first-grown layer with shared nucleation sites, especially when methane is used as the carbon precursor, as evidenced from the isotope-labeling results,10,11 therefore the growth of these second nuclei will be strongly restricted and stopped by the expansion of their covered first layer. Moreover, because the nucleation of graphene grains is a super-saturation process of carbon on the defective Cu surface, BLG growth from below also suggests a possible non-Bernal-stacking between the two graphene layers.11 On the other hand, several reports also demonstrated a layer-by-layer epitaxial growth of BLG by CVD,12–15 which has gradually become a topic of significant interest. Epitaxial CVD growth can yield relatively more uniform BLG with a high surface coverage and Bernal-stacking ratio, usually nearly 100%. During this growth, the second graphene layer grows on top of the first layer, and it is generally believed that the van der Waals (vdWs) force plays an important role in forming this high Bernal-stacking ratio.13–15 However, many crucial aspects of the epitaxial CVD growth of BLG are still not fully understood and require additional investigation, among which the most important and fundamental one is the nucleation process of the second graphene layer on the formed first layer, i.e., how the new graphene layer nucleates on top on the formed graphene in the absence of a direct contact with the catalytic Cu surface.
To this end, we present an experimental and first-principles calculation study of the epitaxial CVD nucleation process for Bernal-stacked BLG growth on Cu using ethanol as the precursor. Results show that a carefully adjusted flow rate of ethanol can yield a uniform BLG film with a surface coverage of nearly 90% and a Bernal-stacking ratio of nearly 100% on ordinary flat Cu substrates, and its epitaxial nucleation of the second layer is mainly due to the active CH3 radicals with the presence of a MLG-covered Cu surface. We believe that this nucleation mechanism will help clarify the formation of BLG by the epitaxial CVD process, and lead to many new strategies for scalable synthesis of graphene with more controllable structures and numbers of layers.
Results and discussion
Zhao et al. have previously reported that the growth of Bernal-stacked BLG is an equilibrium process using ethanol as the carbon precusor,15 but they used a folded Cu enclosure as the growth substrate, and uniform BLG was only obtained on the inside surface of the enclosure. This special substrate structure makes it difficult not only for the scaling-up synthesis, but also for the understanding of a more detailed growth mechanism. In our approach, we chose the ethanol-based CVD system to grow BLG but attempted to reproduce its results on flat Cu, which as we show later will largely help understand its nucleation mechanism. Moreover, a flat Cu foil significantly enlarges the size of a BLG film that can be grown in the CVD furnace when it is rolled up into a cylinder. As shown in the schematic image of the CVD system in Fig. S1 in the ESI,† we used the release valve of Ar gas to control its pressure to 0.5 atm. On the other hand, the ethanol tank was maintained at 19 °C, which resulted in a saturated vapor pressure of 0.53 kPa for ethanol. Therefore, the pressure ratio between Ar and ethanol was approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
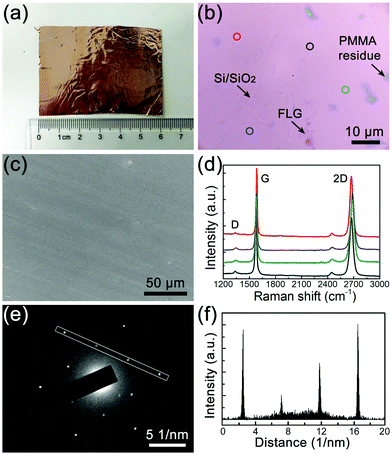
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and this ratio provided the detailed ethanol partial pressures that were used in the CVD experiments. Moreover, Ar also behaved as the carrying and diluting gas for ethanol in the experiments. The uniform and scalable BLG film was obtained on flat Cu foil under optimal conditions (20 sccm Ar/ethanol, 3 hour growth, partial pressure of ethanol is ∼3 Pa), as shown in Fig. 1a. Fig. 1b shows a typical optical microscopy (OM) image of the BLG film after being transferred onto a Si substrate with a 300 nm SiO2 layer, and the sample uniformity can be evaluated by its color contrast. No areas with different contrasts are apparent, indicating that the layer number is uniform. The scanning electron microscopy (SEM) image in Fig. 1c also demonstrates the uniformity of the as-grown graphene on the Cu foil. The layer number of the graphene film is confirmed by Raman spectroscopy, as shown by the representative Raman spectra in Fig. 1d, which all show features of Bernal-stacked BLG such as a 2D-band (∼2690 cm−1) to G-band (∼1582 cm−1) intensity ratio (I2D/IG) of ∼1, and an asymmetric 2D-band with a full width at half-maximum (FWHM) value of ∼45–60 cm−1.16Fig. 1e shows the select area electron diffraction (SAED) pattern of a BLG domain using transmission electron microcopy (TEM), and only a single set of 6-fold symmetric diffraction spots is observed. The corresponding spot intensities in Fig. 1f clearly demonstrate the Bernal-stacking structure of the BLG samples.15
1, and this ratio provided the detailed ethanol partial pressures that were used in the CVD experiments. Moreover, Ar also behaved as the carrying and diluting gas for ethanol in the experiments. The uniform and scalable BLG film was obtained on flat Cu foil under optimal conditions (20 sccm Ar/ethanol, 3 hour growth, partial pressure of ethanol is ∼3 Pa), as shown in Fig. 1a. Fig. 1b shows a typical optical microscopy (OM) image of the BLG film after being transferred onto a Si substrate with a 300 nm SiO2 layer, and the sample uniformity can be evaluated by its color contrast. No areas with different contrasts are apparent, indicating that the layer number is uniform. The scanning electron microscopy (SEM) image in Fig. 1c also demonstrates the uniformity of the as-grown graphene on the Cu foil. The layer number of the graphene film is confirmed by Raman spectroscopy, as shown by the representative Raman spectra in Fig. 1d, which all show features of Bernal-stacked BLG such as a 2D-band (∼2690 cm−1) to G-band (∼1582 cm−1) intensity ratio (I2D/IG) of ∼1, and an asymmetric 2D-band with a full width at half-maximum (FWHM) value of ∼45–60 cm−1.16Fig. 1e shows the select area electron diffraction (SAED) pattern of a BLG domain using transmission electron microcopy (TEM), and only a single set of 6-fold symmetric diffraction spots is observed. The corresponding spot intensities in Fig. 1f clearly demonstrate the Bernal-stacking structure of the BLG samples.15
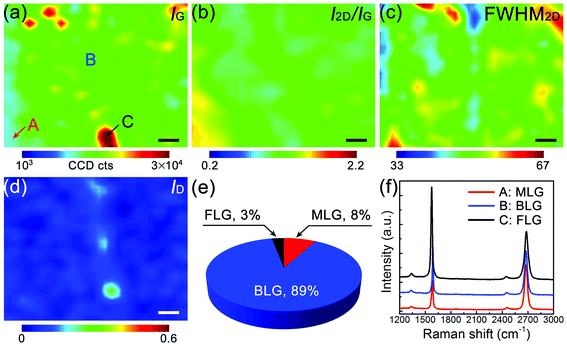
The uniformity of these BLG samples can be further evaluated by the Raman contour maps of their IG, I2D/IG, FWHM of the 2D-band, and the D-band to G-band intensity ratio (ID/IG), as shown in Fig. 2a–d, respectively. These Raman spectra were collected over a 4500 μm2 with 30 × 30 scanning points. We chose the range of Raman I2D/IG from 0.7 to 1.3 and the FWHM of the 2D-band from 45 to 60 cm−1 to evaluate Bernal-stacked BLG quality.15,17 The coverage of Bernal-stacked BLG, MLG and few-layer graphene (FLG) was determined to be ∼89%, ∼8% and ∼3%, respectively, and no Raman features from twisted BLG were observed.18Fig. 2f shows the Raman spectra that are representative of MLG, BLG and FLG in the BLG sample.
We interrupted the CVD process to obtain more information of the growth, by stopping the Ar/ethanol flow after different growth periods. The SEM images of these results are presented in Fig. 3a. The flow rate of Ar/ethanol is maintained at 20 sccm, and the corresponding partial pressure of ethanol is ∼3 Pa. After 3 min, many MLG islands are found to nucleate on the Cu surface, with typical sizes smaller than 5 μm. Most of these islands coalesce to achieve a coverage of ∼70% of the Cu surface. After 30 min, MLG is completely formed and no unfilled gaps between islands are observed. The self-limiting growth stage of this MLG is maintained for a short time and the nucleation of the second graphene layer starts soon. After 60 min, many new graphene islands appear and coalesce to form the second layer, with a total coverage of over 50% of the whole Cu/MLG surface. Moreover, it is visible that the graphene grain size of the secondly grown layer from ethanol is approximately 1 to 3 μm, significantly smaller than that from methane with equivalent pressure. The growth rate of the second layer is significantly reduced after 60 min and a continuous second layer is finally completed after 3 hours and achieves an equilibrium state (Fig. S2 in the ESI†).
Ethanol can affect the BLG growth on flat Cu in a more straightforward way, therefore it is necessary to investigate the relationship between the ethanol flow and the yield, as shown in Fig. 3b. Apparently, an appropriate partial pressure of ethanol is critical to obtain the best quality of BLG. When the partial pressure of ethanol is low, it yields MLG with unfilled gaps and randomly distributed BLG flakes, or a non-uniform graphene film with a discontinuous second layer. On the other hand, when the partial pressure of ethanol is high, graphene islands with more layers easily nucleate and expand, and finally yields a graphene film with more layers.
The previous BLG growth from ethanol has demonstrated that the growth follows a layer-by-layer epitaxy, in which the second layer grows atop the first one.15 Although it uses Cu enclosures instead of flat Cu foils, we believe that this difference will not change this epitaxial growth mode. In the typical “growth-from-below” model, after the first graphene layer is completed, the catalytically active Cu surface and the diffusion channels from the graphene grain edges to below the grains both disappear, making it prohibitive to expand the graphene layers that are below the first layer.3 The epitaxial growth mode of BLG in our experiments can also be confirmed by its time-dependent SEM images in Fig. 3, which clearly show that the grains of the second graphene layer start to form after the full coalescence of the first layer, and keep expanding with a prolonged CVD time.
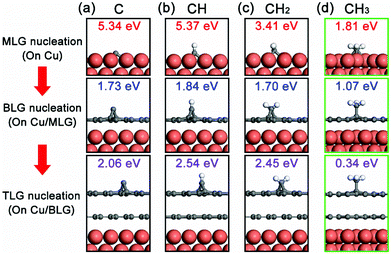
To reveal the nucleation mechanism of the epitaxial CVD growth of BLG on Cu, we performed a theoretical study using first-principles calculations. The calculations are based on the fact that the Cu surface can maintain its influence on graphene nucleation even after it is fully covered by a layer of graphene, evident from the experimental results that no second graphene layers can be grown on transferred MLG/SiO2/Si substrates in an equivalent CVD environment (Fig. S3 in the ESI†). We use the basic forms of carbon radicals CHi (i = 0, 1, 2, 3) as possible fundamental bricks for the nucleation of a new graphene layer, together with the Cu(111) surface and the formed graphene layer(s) as the studied system. More detailed geometries of these systems are shown in Fig. S4 in the ESI.† The relative binding strength of these CHi radicals on the Cu(111)/graphene surfaces can be presented in terms of their binding energy Eb
| Eb = Esub + ECHi − Esys | (1) |
This scenario of CH3-assisted nucleation is consistent with the reports of Wassei et al.12 and Yan et al.13 in which they both proposed that alkyl radicals are the main contributors to the epitaxial nucleation of a new graphene layer. This adsorption process of CH3 radicals on the first graphene layer can also be assisted by a trapping mediated process,20 in which a scattered CH3 radical can be trapped at the basal plane of the graphite surface for a short time at the environmental temperature much higher than its desorption temperature. This has been experimentally demonstrated by a Li-induced CH3Cl dissociative reaction with graphite.21 We believe that this nucleation mechanism can also be further extended to other epitaxial CVD growth systems for BLG.
The above discussion is based on the assumption that the metal substrate is dominated by the Cu(111) facet. Theoretically, the top layer atomic packing on a Cu(111) facet has a C6v symmetry,22 the same as graphene and therefore allows a highly orientated graphene synthesis. In the above BLG growth experiments, most graphene first layer domains are in the six-fold symmetry and therefore we believe that the substrate is dominated by Cu(111) facets. Moreover, because we are considering the growth of the second graphene layer on the top of the first one, the effect of the type of Cu facet must be minor. Therefore, we believe the main conclusion of this study can also be applied to other Cu facets.
Similar to ethanol, its thermal decomposition at high temperatures is not well understood yet. Ethanol may decompose via many energetically accessible product channels. Considering the bond energies of C–O and C–C, the following two reactions:
| C2H5OH → C2H4 + H2O | (2) |
| C2H5OH → CH3 + CH2OH | (3) |
For other alkanes that can also thermally decompose with CH3 radicals such as C2H6, Wassei et al. have shown that BLG with a coverage of up to 49% can be obtained. A previous report has shown that graphene layers can form on HOPG by CH3 radicals depending on the defects, and the largest sticking probability of 10−6 was observed when the HOPG surfaces are prestructured with nanometer-sized etch pits.29 Compared with C2H6, due to the decomposed products of H2, H2O, and/or other OH contained radicals, C2H5OH induces etching and regrowth sites in the firstly grown graphene layer,15 which may also simultaneously behave as more possible CH3 nucleation sites. This increases the nucleation probability of the new graphene layer, and results in a higher coverage of BLG. Moreover, besides generating CH3 nucleation sites, the OH radicals also play an important role in accelerating the growth by lowering the energy barrier of carbon adatoms.5
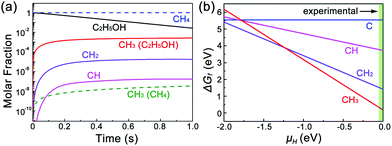
We further consider the stability of each CHi radical on a Cu/MLG surface. Fig. 5b shows the relative Gibbs free energies of species of each CHi radical on Cu(111)/MLG as a function of the chemical potential of H (μH). It is found that the stability of CHi highly depends on μH, and CH3 is the dominating species in the regime of μH > −1.24 eV. In our experiments, no H2 is used and μH mainly depends on the thermally decomposed H from ethanol. However, because the final decomposition products of ethanol usually react with H atoms,25–28 H atoms can hardly be generated in all ethanol decomposition channels and its chemical potential is close to 0, which prefers the nucleation of the second graphene layer by CH3 radicals.
Based on this, we propose the nucleation mechanism of ethanol-based epitaxial CVD growth for BLG on Cu in Fig. 6. For the MLG, ethanol behaves similarly as methane,30 and the C, CH, and CH2 radicals catalyzed from ethanol by Cu contribute the most to its nucleation and growth. After the MLG formation, the absence of a direct contact between ethanol and Cu makes it difficult to generate radicals of C, CH and CH2, whose binding energies do not match the nucleation of only BLG as well. On the other hand, CH3 radicals play a crucial role in nucleating the second graphene layer, not only because it is a product of thermally decomposed ethanol, but also because of its suitable binding energies on Cu/MLG and Cu/BLG.
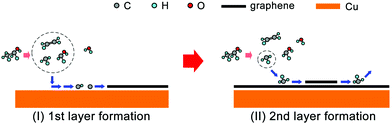 | ||
| Fig. 6 Schematic of the possible mechanism for epitaxial CVD growth of BLG on Cu using ethanol as the carbon precursor. | ||
Finally, it needs to be emphasized that after the grain nucleation of the second graphene layer by CH3 radicals, the following carbon deposition process remains unclear. Although the C–H dissociation energy is calculated to be 480 kJ mol−1,31 which makes it impossible for the direct dissociation of another C–H bond in the nucleated CH3 radical, the actual energy barrier for CH3 and H exchange is considerably lower and accessible at reaction temperatures.32 Moreover, the OH radicals may also play some role in lowering the activation energy of the edge dehydrogenation, similar to that in an oxygen-assisted CVD growth for the centimeter-scale graphene single crystals.5
Conclusion
In conclusion, we demonstrate an experimental and first-principles calculation study of the epitaxial CVD growth for Bernal-stacked BLG on Cu using ethanol. The surface coverage of BLG in the sample is nearly 90% and the Bernal-stacking ratio is nearly 100%. Under an equilibrium CVD environment, the BLG growth exhibits two self-limiting processes for the two graphene layers but with significantly different growth rates. First-principles calculation results show that the epitaxial nucleation of the second graphene layer is mainly due to the active CH3 radicals and the Cu substrate with a covered graphene layer. We believe that we have uncovered a new territory in the CVD nucleation mechanism of epitaxial graphene growth, and hope that this understanding will bring the advent of CVD graphene growth with more precise control of radicals in the future.Experimental section
BLG synthesis
BLG was synthesized by low-pressure CVD using bubbled ethanol. Commercially available Cu foil (25 μm thick, #46365, Alfa Aesar China Chemical Co., Ltd) was used as received. A flat Cu foil was placed in a hot-wall CVD quartz chamber (i.d. = 60 mm), and annealed at 1000 °C for 30 minutes with 100 sccm H2, followed by introducing a 20 sccm Ar/ethanol mixture gas. H2 was stopped at the growth step of graphene. After growth, the chamber was slowly cooled to room temperature at a rate of 10–20 °C min−1.Graphene transfer
BLG film on copper was firstly coated with polymethylmethacrylate (PMMA, 4 wt% in anisole) by the spin-coating method, and baked on a hotplate at 140 °C for 30 min. The graphene film on the other side of the Cu foil was treated by O2 plasma (100 W) for 30 s. The Cu substrate was then etched away in 1 M FeCl3 solution and the PMMA/graphene film was rinsed in DI water 3 times and transferred onto the Si/SiO2 substrate. Finally, the PMMA layer was removed by hot acetone.Characterization
Characterization of as-grown and transferred BLG was carried out by optical microscopy (Olympus BXFM-ILHS, Olympus Co., Ltd), scanning electron microscopy (SEM, 5 kV, S-3400, Hitachi Co., Ltd), confocal micro-Raman spectroscopy (LabRAM HR Evolution, Horiba Co., Ltd), and transmission electron microscopy (JEM-2100, JEOL Co., Ltd).First-principles calculations
The first-principles calculations are performed with the density-functional theory approach as implemented by the Vienna ab initio Simulation Package (VASP).33,34 The exchange–correlation energy is treated in the Perdew–Burke–Ernzerhof (PBE) version of the generalized-gradient approximation (GGA) functional.35,36 In order to accurately describe the vdWs between a CHi (i = 0, 1, 2, 3) radical and the Cu surface, the PBE functional with the vdWs correction (DFT-D3)37 has also been used. The energy cutoff of the plane-wave expansion is set at 400 eV. All structures are optimized by the conjugate gradient method until the forces acting on each atom are less than 0.01 eV Å−1. Cu(111) surfaces are modelled using slab geometry with four metal atomic layers in which the bottom-layer atoms are fixed at their respective bulk positions. For the geometry optimization, all atoms except for the fixed bottom-layer atoms are fully relaxed and then various CHi species are put on the metal substrate surface for further optimization.Ethanol decomposition simulation
Simulation of ethanol decomposition was performed using SENKIN,38,39 a computer program that predicts the time-dependent chemical-kinetic behaviour of a homogeneous gas mixture in a closed system. This has been incorporated into CHEMKIN-II,40 which is a package of computer codes for the analysis of gas-phase chemical kinetics. Constant-temperature and constant-pressure conditions were chosen for the calculations using temperatures and pressures that had been experimentally found to be optimum for BLG growth.Acknowledgements
The authors are grateful to Prof. Zhongfan Liu (Peking University, China) for his helpful discussions. Part of this work was financially supported by the National Science Foundation of China (11502231, 11321202, 11322219, 61471317), the National Program for Special Support of Top-Notch Young Professionals, Zhejiang Provincial Natural Science Foundation of China (LQ15A020001) and the National Key Scientific Instruments and Equipment Development Project of China (61427901).References
- Y. Zhang, T.-T. Tang, C. Girit, Z. Hao, M. C. Martin, A. Zettl, M. F. Crommie, Y. R. Shen and F. Wang, Nature, 2009, 459, 820–823 CrossRef CAS PubMed.
- K. F. Mak, C. H. Lui, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2009, 102, 256405 CrossRef PubMed.
- X. S. Li, W. W. Cai, J. H. An, S. Kim, J. Nah, D. X. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312–1314 CrossRef CAS PubMed.
- S. Bae, H. Kim, Y. Lee, X. Xu, J.-S. Park, Y. Zheng, J. Balakrishnan, T. Lei, H. Ri Kim, Y. I. Song, Y.-J. Kim, K. S. Kim, B. Ozyilmaz, J.-H. Ahn, B. H. Hong and S. Iijima, Nat. Nanotechnol., 2010, 5, 574–578 CrossRef CAS PubMed.
- Y. Hao, M. S. Bharathi, L. Wang, Y. Liu, H. Chen, S. Nie, X. Wang, H. Chou, C. Tan, B. Fallahazad, H. Ramanarayan, C. W. Magnuson, E. Tutuc, B. I. Yakobson, K. F. McCarty, Y.-W. Zhang, P. Kim, J. Hone, L. Colombo and R. S. Ruoff, Science, 2013, 342, 720–723 CrossRef CAS PubMed.
- S. Lee, K. Lee and Z. Zhong, Nano Lett., 2010, 10, 4702–4707 CrossRef CAS PubMed.
- Z. Sun, A.-R. O. Raji, Y. Zhu, C. Xiang, Z. Yan, C. Kittrell, E. L. G. Samuel and J. M. Tour, ACS Nano, 2012, 6, 9790–9796 CrossRef CAS PubMed.
- H. Zhou, W. J. Yu, L. Liu, R. Cheng, Y. Chen, X. Huang, Y. Liu, Y. Wang, Y. Huang and X. Duan, Nat. Commun., 2013, 4, 2096 Search PubMed.
- H.-B. Sun, J. Wu, Y. Han, J.-Y. Wang, F.-Q. Song and J.-G. Wan, J. Phys. Chem. C, 2014, 118, 14655–14661 CAS.
- Q. Li, H. Chou, J.-H. Zhong, J.-Y. Liu, A. Dolocan, J. Zhang, Y. Zhou, R. S. Ruoff, S. Chen and W. Cai, Nano Lett., 2013, 13, 486–490 CrossRef CAS PubMed.
- W. Fang, A. L. Hsu, R. Caudillo, Y. Song, A. G. Birdwell, E. Zakar, M. Kalbac, M. Dubey, T. Palacios, M. S. Dresselhaus, P. T. Araujo and J. Kong, Nano Lett., 2013, 13, 1541–1548 CAS.
- J. K. Wassei, M. Mecklenburg, J. A. Torres, J. D. Fowler, B. C. Regan, R. B. Kaner and B. H. Weiller, Small, 2012, 8, 1415–1422 CrossRef CAS PubMed.
- K. Yan, H. Peng, Y. Zhou, H. Li and Z. Liu, Nano Lett., 2011, 11, 1106–1110 CrossRef CAS PubMed.
- L. Liu, H. Zhou, R. Cheng, W. J. Yu, Y. Liu, Y. Chen, J. Shaw, X. Zhong, Y. Huang and X. Duan, ACS Nano, 2012, 6, 8241–8249 CrossRef CAS PubMed.
- P. Zhao, S. Kim, X. Chen, E. Einarsson, M. Wang, Y. Song, H. Wang, S. Chiashi, R. Xiang and S. Maruyama, ACS Nano, 2014, 8, 11631–11638 CrossRef CAS PubMed.
- L. M. Malard, M. A. Pimenta, G. Dresselhaus and M. S. Dresselhaus, Phys. Rep., 2009, 473, 51–87 CrossRef CAS.
- Z. Peng, Z. Yan, Z. Sun and J. M. Tour, ACS Nano, 2011, 5, 8241–8247 CrossRef CAS PubMed.
- Z. H. Ni, Y. Y. Wang, T. Yu, Y. M. You and Z. X. Shen, Phys. Rev. B: Condens. Matter, 2008, 77, 235403 CrossRef.
- H. Shu, X.-M. Tao and F. Ding, Nanoscale, 2015, 7, 1627–1634 RSC.
- C. T. Rettner, E. K. Schweizer and H. Stein, J. Chem. Phys., 1990, 93, 14442 CrossRef.
- L. Mandeltort, P. Choudhury, J. K. Johnson and J. T. Yates, J. Phys. Chem. Lett., 2012, 3, 1680–1683 CrossRef CAS PubMed.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- B. Hou, R. Xiang, T. Inoue, E. Einarsson, S. Chiashi, J. Shiomi, A. Miyoshi and S. Maruyama, Jpn. J. Appl. Phys., 2011, 50, 065101 CrossRef.
- R. Xiang, B. Hou, E. Einarsson, P. Zhao, S. Harish, K. Morimoto, Y. Miyauchi, S. Chiashi, Z. Tang and S. Maruyama, ACS Nano, 2013, 7, 3095–3103 CrossRef CAS PubMed.
- J. Park, R. S. Zhu and M. C. Lin, J. Chem. Phys., 2002, 117, 3224–3231 CrossRef CAS.
- J. Li, A. Kazakov and F. L. Dryer, J. Phys. Chem. A, 2004, 108, 7671–7680 CrossRef CAS.
- R. Sivaramakrishnan, M. C. Su, J. V. Michael, S. J. Klippenstein, L. B. Harding and B. Ruscic, J. Phys. Chem. A, 2010, 114, 9425–9439 CrossRef CAS PubMed.
- Z. F. Xu, K. Xu and M. C. Lin, J. Phys. Chem. A, 2011, 115, 3509–3522 CrossRef CAS PubMed.
- R. Wellmann, A. Böttcher, M. Kappes, U. Kohl and H. Niehus, Surf. Sci., 2003, 542, 81–93 CrossRef CAS.
- P. Zhao, A. Kumamoto, S. Kim, X. Chen, B. Hou, S. Chiashi, E. Einarsson, Y. Ikuhara and S. Maruyama, J. Phys. Chem. C, 2013, 117, 10755–10763 CAS.
- K. May, S. Dapprich, F. Furche, B. V. Unterreiner and R. Ahlrichs, Phys. Chem. Chem. Phys., 2000, 2, 5084 RSC.
- L. K. Rutz, H. Bockhorn and J. W. Bozzelli, Abstr. Pap. Am. Chem. Soc., 2004, 227, U1100–U1101 Search PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. Varykhalov, J. Sanchez-Barriga, A. M. Shikin, C. Biswas, E. Vescovo, A. Rybkin, D. Marchenko and O. Rader, Phys. Rev. Lett., 2008, 101, 157601 CrossRef CAS PubMed.
- Y. Murata, V. Petrova, B. B. Kappes, A. Ebnonnasir, I. Petrov, Y. H. Xie, C. V. Ciobanu and S. Kodambaka, ACS Nano, 2010, 4, 6509–6514 CrossRef CAS PubMed.
- R. Q. Zhao, Y. F. Zhang, T. Gao, Y. B. Gao, N. Liu, L. Fu and Z. F. Liu, Nano Res., 2011, 4, 712–721 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary figures. See DOI: 10.1039/c6nr04557j |
| This journal is © The Royal Society of Chemistry 2016 |