Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The persistence length of adsorbed dendronized polymers†
Lucie
Grebikova‡
a,
Svilen
Kozhuharov
a,
Plinio
Maroni
a,
Andrey
Mikhaylov
b,
Giovanni
Dietler
b,
A. Dieter
Schlüter
c,
Magnus
Ullner
d and
Michal
Borkovec
*a
aDepartment of Inorganic and Analytical Chemistry, University of Geneva, Sciences II, 30 Quai Ernest-Ansermet, 1205 Geneva, Switzerland. E-mail: michal.borkovec@unige.ch
bLaboratoire de Physique de la Matière Vivante, Ecole Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
cDepartment of Materials, ETH Zurich, Vladimir Prelog Weg 5, HCI J 541, Zurich, Switzerland
dTheoretical Chemistry, Center for Chemistry and Chemical Engineering, Lund University, P.O. Box 124, 221 00 Lund, Sweden
First published on 13th June 2016
Abstract
The persistence length of cationic dendronized polymers adsorbed onto oppositely charged substrates was studied by atomic force microscopy (AFM) and quantitative image analysis. One can find that a decrease in the ionic strength leads to an increase of the persistence length, but the nature of the substrate and of the generation of the side dendrons influence the persistence length substantially. The strongest effects as the ionic strength is being changed are observed for the fourth generation polymer adsorbed on mica, which is a hydrophilic and highly charged substrate. However, the observed dependence on the ionic strength is much weaker than the one predicted by the Odijk, Skolnik, and Fixman (OSF) theory for semi-flexible chains. Low-generation polymers show a variation with the ionic strength that resembles the one observed for simple and flexible polyelectrolytes in solution. For high-generation polymers, this dependence is weaker. Similar dependencies are found for silica and gold substrates. The observed behavior is probably caused by different extents of screening of the charged groups, which is modified by the polymer generation, and to a lesser extent, the nature of the substrate. For highly ordered pyrolytic graphite (HOPG), which is a hydrophobic and weakly charged substrate, the electrostatic contribution to the persistence length is much smaller. In the latter case, we suspect that specific interactions between the polymer and the substrate also play an important role.
Introduction
Odijk, Skolnik, and Fixman (OSF) have shown that the electrostatic part of the persistence length of a semi-flexible polyelectrolyte should decrease strongly with the salt level, and scale as I−1 where I denotes the ionic strength.1,2 For flexible chains, experiments, simulations, and variational calculations have mostly reported a much weaker dependence on the salt level, often obeying I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1/2. The variational calculations do not include the excluded volume effects, but the experiments and simulations do, which has been suggested as a reason for the deviation from the OSF result.3–8 Computer simulations of very long chains suggest a cross-over from the OSF behavior at very low salt concentrations to the I
−1/2. The variational calculations do not include the excluded volume effects, but the experiments and simulations do, which has been suggested as a reason for the deviation from the OSF result.3–8 Computer simulations of very long chains suggest a cross-over from the OSF behavior at very low salt concentrations to the I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1/2 dependence at higher salt levels.7–9
−1/2 dependence at higher salt levels.7–9
DNA is probably the most studied polymer with respect to the persistence length, and many different experimental tools have been used to address this question, including light scattering, fluorescence, and tweezer techniques.10–17 Persistence lengths obtained with flow dichroism, magnetic birefringence, and the force response measured with optical tweezers were found to be in agreement with the OSF prediction.10–12 A more recent fluorescence microscopy study, which covers a wide range of salt levels, however, suggests rather the I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1/2 dependence.13 These findings were in qualitative agreement with the quantitative analysis of the images of adsorbed DNA obtained by atomic force microscopy (AFM).14–17
−1/2 dependence.13 These findings were in qualitative agreement with the quantitative analysis of the images of adsorbed DNA obtained by atomic force microscopy (AFM).14–17
Persistence lengths of synthetic polyelectrolytes were equally studied with light, X-ray and neutron scattering, viscosity measurements, and birefringence studies.18–24 The persistence length for substituted polyglycines was suggested to follow the OSF model,18 while charged polyacrylates and polysulfonates rather agree with the I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1/2 dependence.19,20,22 While several authors studied the persistence length of polysaccharides, the quantitative results for its salt dependence do not seem to be available.25–28
−1/2 dependence.19,20,22 While several authors studied the persistence length of polysaccharides, the quantitative results for its salt dependence do not seem to be available.25–28
Dendronized polymers represent a new and promising class of polymers, and they are most suitable to investigate various model predictions over a wider parameter range than accessible with regular polymers.29–33 In particular, they offer the possibility to systematically vary their diameter through the generation of the side-dendrons, and thereby keep the chemical nature of the polymer the same.30 When the dendrons carry ionizable groups, variation of the generation also permits the variation of the charge density systematically. The present study makes use of this possibility, and investigates the persistence length of the adsorbed amino-functionalized dendronized polymers of different generations with AFM. Indeed, our results show that the line charge density and the polymer diameter have a major influence on the persistence length, which for higher generations differs from the expected behavior of flexible or semi-flexible polyelectrolytes in solution.
Experimental
Dendronized polymers
Amino-functionalized polymethacrylate-based dendronized polymers (DPs) were synthesized for different dendron generations (PGn, n = 1–4) by means of the attach-to route (Fig. 1). Their molecular mass was in the range of (0.3–5.8) × 106 g mol−1 depending on the generation of DPs. The polydispersity index of the side dendrons was about 1.01. These polymers were characterized by gel permeation chromatography and scattering techniques. Further details of the synthetic procedure and characterization are given elsewhere.30,31 The polymers were dissolved in electrolyte solutions adjusted with HCl to pH 4.0 and then, depending on the experimental conditions used, diluted to a final concentration of 5 mg L−1 either with 0.1 mM HCl or 1, 10, or 100 mM KCl solution adjusted to pH 4.0. Under these conditions, the amine groups are positively charged.Surfaces
Four types of substrates were used for the experiments, namely, mica, silica, gold, and highly ordered pyrolytic graphite (HOPG). High grade mica was obtained from Plano (Wetzlar, Germany) and cleaved with adhesive tape in air prior to use. Native oxidized silicon wafer surfaces (Silchem, Germany) were used as silica surfaces. These substrates were cleaned for 20 min with hot piranha solution, which is a mixture of H2SO4 98% and H2O2 30% in a volumetric ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, rinsed with pure water, dried in a stream of nitrogen, and kept in water prior to use. Gold Au(111) surfaces grown on mica were obtained from Phasis (Geneva, Switzerland). The gold surfaces were rinsed with 2% sodium dodecyl sulfate solution, washed with pure water, and dried in a stream of nitrogen. Finally, they were cleaned with an UV-ozone cleaner (PSD Pro, Novascan, Ames, USA) under an oxygen enriched atmosphere for 20 min. The entire cleaning procedure was repeated three times to ensure the cleanness of the gold surfaces. HOPG was obtained from Plano GmbH (Wetzlar, Germany) and cleaved with adhesive tape in air prior to use. Contact angles were measured with a video setup assembled in-house and they were obtained from the digital photographs of the sessile drops of pure water.
1, rinsed with pure water, dried in a stream of nitrogen, and kept in water prior to use. Gold Au(111) surfaces grown on mica were obtained from Phasis (Geneva, Switzerland). The gold surfaces were rinsed with 2% sodium dodecyl sulfate solution, washed with pure water, and dried in a stream of nitrogen. Finally, they were cleaned with an UV-ozone cleaner (PSD Pro, Novascan, Ames, USA) under an oxygen enriched atmosphere for 20 min. The entire cleaning procedure was repeated three times to ensure the cleanness of the gold surfaces. HOPG was obtained from Plano GmbH (Wetzlar, Germany) and cleaved with adhesive tape in air prior to use. Contact angles were measured with a video setup assembled in-house and they were obtained from the digital photographs of the sessile drops of pure water.
After cleaning, the surfaces were immersed in the polymer solution, and rinsed with the corresponding polymer-free electrolyte solution. The same solution was used for imaging. Mica and silica substrates were incubated in the polymer solution for 40 s, gold for 3 min, and HOPG for 10 min. These times were chosen to obtain a sufficiently high density of isolated adsorbed chains, while avoiding a too frequent inter-chain overlap.
Imaging
The adsorbed polymers were imaged in the respective electrolyte solutions with a Cypher AFM (Asylum Research, Santa Barbara, USA) in amplitude-modulation (AC) mode with an environmental scanner. Biolever mini cantilevers (BL-AC40TS, Olympus, Japan) with a nominal tip radius smaller than 9 nm and a resonance frequency of 25–35 kHz in water were used. The spring constants were in the range of 0.06–0.1 N m−1 as determined by monitoring the thermal fluctuations in air. Cantilevers were ozone cleaned with an UV-ozone cleaner (PSD Pro, Novascan, Ames, USA) under an oxygen enriched atmosphere for 20 minutes prior to use. The images were acquired in AC-mode in the respective electrolyte solutions. The imaging protocol used a scan rate of 4.88 Hz, a scan size of 500 nm × 500 nm, a free oscillation amplitude (FOA) of about 20 nm, and a set point corresponding to around 70% of the FOA. The experiments were carried out at the room temperature of 23 ± 2 °C.The persistence length of the adsorbed polymers was determined with an image analysis software.34 For each situation, the backbones of adsorbed 100–150 polymers were traced and the lateral coordinates of the backbone were recorded. Only the molecules that were entirely contained in the image frame where included in the analysis. From these lateral coordinates, the molecular length and other statistical averages were calculated.
In order to obtain the mass of adsorbed polymers from AFM images, the tip convolution effect must be considered. The tip shape profile was determined by imaging spherical nanoparticles that were adsorbed onto mica functionalized with poly(ethylene imine) of a molecular mass of 25 kg mol−1 (Polysciences, Eppenheim, Germany). To obtain the relevant shape profile, one must use particles whose sizes are comparable to the height of the polymers in question. In the case of PG1, gold nanoparticles (Sigma Aldrich) with a diameter of about 5 nm were used, while polystyrene particles (Nanosphere Size Standard, Thermo Scientific, USA) with an average diameter of around 30 nm were more suitable for higher generation polymers. The tip shape profile was calculated by means of an erosion algorithm, which assumes that the particles are spherical with a diameter equal to their height.35 Given the known tip profile, the AFM images were deconvoluted, and the volumes of the polymers were calculated from the recorded length and the respective height profiles with Gwyddion, which is freely available at http://gwyddion.net/. The density of 1.3 g cm−3 was used to convert the volume of an individual molecule to mass.36 The different masses of the individual molecules were averaged to obtain the number averaged molecular mass of the polymer sample. The cross-sectional diameter increases with the generation from about 3 nm for PG1 to about 10 nm for PG4. Such estimates of the molecular mass are also in reasonable agreement with gel permeation chromatography.37
The average molecular mass of the polymers could also be calculated from the length of the molecule. From the molecular geometry one can determine the length of one monomer to be 0.25 nm, and thus one can calculate the number of monomers in each molecule. Since the molecular mass of the monomer with the side-dendron is known from its molecular structure, the molecular mass can again be calculated. The two estimates of the molecular mass are in good agreement (Fig. S1†). Therefore, we are confident that individual molecules are being imaged.
The surface roughness was measured by acquiring four images of 1 μm × 1 μm in solution at pH 4.0 and an ionic strength of 0.1 mM for each surface. The root mean square (RMS) roughness was calculated for each image, and averaged.
Results
We address the persistence length of cationic dendronized polymers adsorbed onto different solid substrates in simple electrolyte solutions. A scheme of these polymers is given in Fig. 1 and additional properties of these polymers are presented in Table 1. The properties of the substrates used are given in Table 2. The persistence length will be shown to sensitively depend on the electrolyte concentration, generation of the dendrons, and to some extent, on the type of substrate. We will first discuss these effects qualitatively based on a gallery of AFM images, and subsequently quantify the variations in the persistence length with image analysis. All the experiments were carried out at pH 4.0, where the polymers are highly positively charged.| Polymer | Polymer radius (nm) | Maximum line charge density (nm−1) | Bare persistence length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 (nm) 0 (nm) |
Constant A | Exponent b |
|---|---|---|---|---|---|
| PG1 | 0.2 | 7.5 | 5.5 | 0.089 | 0.50 |
| PG2 | 0.5 | 15 | 5.5 | 0.10 | 0.50 |
| PG3 | 1.1 | 30 | 6.3 | 1.3 | 0.38 |
| PG4 | 2.0 | 60 | 7.1 | 3.5 | 0.33 |
| Substrate | RMS roughness (nm) | Contact angle (°) | Bare persistence length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 (nm) 0 (nm) |
Constant A | Exponent b |
|---|---|---|---|---|---|
| Mica | 0.07 | 0 | 7.1 | 3.5 | 0.33 |
| Silica | 0.21 | 38 | 7.1 | 2.5 | 0.33 |
| Gold | 0.19 | 42 | 7.1 | 2.0 | 0.33 |
| HOPG | 0.23 | 75 | 7.1 | 0.92 | 0.33 |
AFM gallery
Let us first illustrate the influence of various parameters visually. The ionic strength is known to strongly influence the conformation of charged polymers. This effect is illustrated in Fig. 2, which shows PG4 adsorbed on mica. The rows correspond to different ionic strengths, while the columns show three different images of the same substrate. The effect of the ionic strength is substantial. At the lowest ionic strengths of 0.1 mM, the chains are extended, almost rod-like. With increasing ionic strengths, the chains become more coiled. At the highest ionic strength of 100 mM, the polymers are highly coiled and collapsed. The extended conformations at low ionic strengths can be rationalized as originating from the electrostatic repulsion between the charged groups on the polymer. The progressive coiling with the increasing ionic strength is caused by the increasing screening of the electrostatic interactions by the ions present in solution.Fig. 2 shows the same PG4 polymers in all the images, in spite of the differences in the apparent width of the polymer chain. These differences reflect tip-convolution artifacts. Different images were recorded with different AFM-tips, and each of them had a different tip radius. The larger this radius is, the larger the apparent width of the polymer in the images. However, the height of the adsorbed polymers is 6.1 ± 0.1 nm, and remains the same across all the images. One can further observe an increase in the average length of the adsorbed polymers with decreasing ionic strengths (see also Table S1†). We suspect that this fractionation results from the inherent polydispersity in the chain length and the balance between the electrostatic interactions and diffusion. At high ionic strengths, the approach to the surface is largely governed by diffusion, which is faster for short polymers, while at low ionic strengths, the stronger and more long-range electrostatic interactions promote the adsorption of longer polymers.
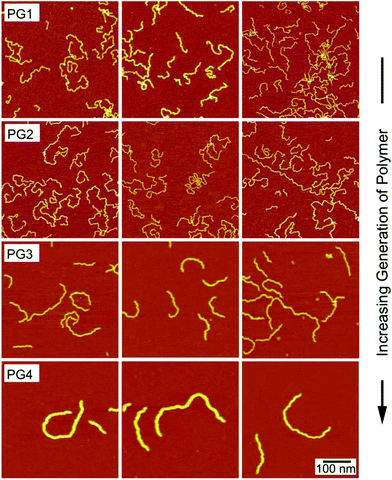
Fig. 3 shows the images of different polymer generations adsorbed on mica at an ionic strength of 0.1 mM. The rows now correspond to the different generations, while the columns again provide three different images of the same substrate. The polymers of low generation are highly coiled. When the generation is increased, the polymers become more stretched out. PG4 is extended and the backbone appears quite rigid. This stiffening effect is not surprising, since one expects that the dendrons decrease the chain flexibility with increasing generation due to packing constraints. Moreover, the line charge density of the polymers strongly increases with increasing generation, which could equally lead to a larger stiffness of the higher generation polymers. The increase in the thickness of the polymer chains with generation reflects the increase of the cross-sectional area with increasing generation, even though tip-convolution artifacts are equally present, especially for the lower generation polymers.
Fig. 4 shows the effect of substrate on the adsorption of PG4 in an electrolyte solution of an ionic strength of 0.1 mM. The rows of the figure correspond to different substrates, while the columns provide three different images of the same substrate. The conformations appear similar for the more hydrophilic substrates, namely mica, silica, and gold. The hydrophobicity of the substrates increases in this sequence, as can be inferred from the contact angles given in Table 2. When adsorbed on HOPG, the polymers are more collapsed. HOPG is the most hydrophobic substrate, which suggests that hydrophobic interactions are likely to be important as well. We further suspect that the polymers interact with HOPG specifically, since some 120° kinks in the polymer backbone can be observed (Fig. S3†). Similar kinks were reported for DNA adsorbed on HOPG.38–40 The apparent widths of the polymers sometimes differ in different images, and these differences are again due to tip-convolution artifacts.
Persistence length
Quantitative image analysis was used to determine the persistence length of the adsorbed polymers in two different ways. By assuming a worm-like chain (WLC) model, the persistence length![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) P can be calculated through the bond–bond correlation function or the internal end-to-end distance.14,17 The bond–bond correlation function decays exponentially, and the respective expression in two spatial dimensions reads:
P can be calculated through the bond–bond correlation function or the internal end-to-end distance.14,17 The bond–bond correlation function decays exponentially, and the respective expression in two spatial dimensions reads: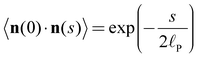 | (1) |
 | (2) |
This relation applies to the ideal chain, as suggested by the scaling 〈ξ2(s)〉 ∝ s for s ≫ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) P. When self-avoiding chains are considered, one can obtain 〈ξ2(s)〉 ∝ s1.5 as the scaling law.14
P. When self-avoiding chains are considered, one can obtain 〈ξ2(s)〉 ∝ s1.5 as the scaling law.14
Eqn (1) and (2) imply that the polymer equilibrates on the surface during the adsorption process. While the adsorbed polymers do not move laterally (Fig. S3†), they are likely to equilibrate to a certain extent close to the surface during the adsorption event. When the surface structures would correspond to the projections of three-dimensional solution structures, crossing of the polymer chains would be more frequent.17 The underlying adsorption process is probably similar to the irreversible adsorption of colloidal particles or dendrimers on surfaces.41
The correlation function and the mean-square end-to-end distance were calculated from the averages at different contour lengths. The representative results for PG2 and PG4 adsorbed on mica are shown for different ionic strengths in Fig. 5. The shortest contour length of about 1 nm was limited by the lateral resolution of the AFM images. We cannot entirely exclude the presence of additional directional fluctuations of the polymer backbone at shorter length scales. Such fluctuations would induce an additional decay of the correlation function at short distances as reported in computer simulation results.7,42,43 We have addressed the possible presence of such fluctuations by comparing two different estimates of the volume of the dendronized polymers. The first estimate was obtained from the volume of the adsorbed polymer, whereby the deconvolution of the AFM image and the tip was carried out. The second estimate was obtained from the molecular mass of a dendron, the length of a monomeric unit, and the length measured with AFM. The importance of such fluctuations would be signaled by the fact that the first estimate would exceed the second. The relatively good agreement between these two estimates (Fig. S2†) suggests that such short distance fluctuations are relatively unimportant. Nevertheless, such fluctuations could cause a minor short-ranged decay of the correlation function, which cannot be excluded. The presence of such short distance fluctuations was also suggested for DNA,24 but this conclusion was questioned more recently.44
The correlation functions are estimated to be accurate up to contour lengths of about 20–30 nm, while larger distances were subject to substantial sampling errors. The mean-square end-to-end distance could be reliably calculated to contour lengths of about 200–300 nm, while the overall length of the molecules limits the accuracy at larger distances. The respective contour lengths given in Table S1† are too small to make the effects of chain self-avoidance very important, and therefore eqn (2) remains a good approximation for the present purpose. The persistence length was obtained from the fits with the WLC model, namely eqn (1) and (2). The solid lines shown in Fig. 5 are the best fits. The resulting persistence lengths obtained from the two different quantities are compared in Fig. 6. The data are plotted versus the ionic strength for different generations and they indicate that the two methods yield entirely consistent results. These estimates of the persistence length are reliable in spite of the polydispersity in contour lengths, since the measurements are made at shorter length scales, and the polymers are highly uniform in all other respects as the side dendrons are close to monodisperse.
 | ||
| Fig. 6 Ionic strength dependence of the persistence length of charged dendronized polymers adsorbed on mica. The experimental data obtained from the directional correlation function (filled symbols) and the mean-square of the internal end-to-end distance (open symbols) are compared with a model given in eqn (3) that features a power-law dependence with the parameters given in Table 1. | ||
Fig. 6 and 7 show that the persistence length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) P decreases with increasing ionic strength I. This trend is in qualitative agreement with the OSF model. The persistence length of charged polymers in solution was suggested to contain two additive contributions, namely:1,2,13,22
P decreases with increasing ionic strength I. This trend is in qualitative agreement with the OSF model. The persistence length of charged polymers in solution was suggested to contain two additive contributions, namely:1,2,13,22
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) P = P = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 + AI−b 0 + AI−b | (3) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is the intrinsic persistence length of the neutral polymer chain, and A and b are constants. The second term in eqn (3) is the electrostatic contribution, whereby the OSF model predicts b = 1 while subsequently developed models for flexible chains point towards a weaker dependence with b = 1/2. Fig. 6 shows the ionic strength dependence of the persistence length of the dendronized polymers of different generations adsorbed on mica. The solid lines are the best fits with eqn (3). The data for the lower generations, namely PG1 and PG2, can be interpreted with b = 1/2. The higher generations lead to smaller exponents, namely for PG3 one can find that b = 0.38 and for PG4 b = 0.33. The intrinsic persistence length
0 is the intrinsic persistence length of the neutral polymer chain, and A and b are constants. The second term in eqn (3) is the electrostatic contribution, whereby the OSF model predicts b = 1 while subsequently developed models for flexible chains point towards a weaker dependence with b = 1/2. Fig. 6 shows the ionic strength dependence of the persistence length of the dendronized polymers of different generations adsorbed on mica. The solid lines are the best fits with eqn (3). The data for the lower generations, namely PG1 and PG2, can be interpreted with b = 1/2. The higher generations lead to smaller exponents, namely for PG3 one can find that b = 0.38 and for PG4 b = 0.33. The intrinsic persistence length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and the pre-factor A also depend on the generation (Table 1), although there is no significant difference between PG1 and PG2. These findings clearly demonstrate that the persistence length of the adsorbed polymers decreases with increasing ionic strength and that it further increases with the generation. This dependence on the generation is further illustrated in Fig. S4.†
0 and the pre-factor A also depend on the generation (Table 1), although there is no significant difference between PG1 and PG2. These findings clearly demonstrate that the persistence length of the adsorbed polymers decreases with increasing ionic strength and that it further increases with the generation. This dependence on the generation is further illustrated in Fig. S4.†
Fig. 7 shows the influence of the substrate on PG4 at an ionic strength of 0.1 mM. The solid lines are again the best fits with eqn (3). A good fit can be obtained with a common intrinsic persistence length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = 7.1 nm, but a smaller exponent, namely b = 0.33 (Table 2). The data obtained for the three more hydrophilic substrates, namely mica, silica, and gold, are all compatible with the same exponent and have similar pre-factors A. This generic behavior suggests that it could reflect the ionic strength dependence of the persistence length for the isolated chains in solution. While the data for the hydrophobic HOPG are consistent with the same exponent, the pre-factor is substantially lower, and the fit is of poorer quality. This behavior again supports the hypothesis that the adsorption mechanism of this substrate is different. While the hydrophobic interactions with the substrate could be relevant, a graph of the dependence of the persistence length on the contact angle shows that the first two generations are insensitive to the substrate and that all the generations have similar persistence lengths at 0.1 mM on HOPG (Fig. S5†). The differences between the generations become clearly apparent only for more hydrophilic substrates.
0 = 7.1 nm, but a smaller exponent, namely b = 0.33 (Table 2). The data obtained for the three more hydrophilic substrates, namely mica, silica, and gold, are all compatible with the same exponent and have similar pre-factors A. This generic behavior suggests that it could reflect the ionic strength dependence of the persistence length for the isolated chains in solution. While the data for the hydrophobic HOPG are consistent with the same exponent, the pre-factor is substantially lower, and the fit is of poorer quality. This behavior again supports the hypothesis that the adsorption mechanism of this substrate is different. While the hydrophobic interactions with the substrate could be relevant, a graph of the dependence of the persistence length on the contact angle shows that the first two generations are insensitive to the substrate and that all the generations have similar persistence lengths at 0.1 mM on HOPG (Fig. S5†). The differences between the generations become clearly apparent only for more hydrophilic substrates.
 | ||
| Fig. 7 Ionic strength dependence of the persistence length of charged dendronized polymers of generation 4 adsorbed on different substrates at pH 4.0. The experimental data obtained from the directional correlation function (filled symbols) and the mean-square of the internal end-to-end distance (open symbols) are compared with a model given in eqn (3) that features a power-law dependence with the parameters given in Table 2. | ||
Discussion
For high-generation polymers, we observe the same ionic strength dependence for all the substrates. Therefore, we suspect that this dependence is intrinsic to the polymer, and reflects the behavior of an individual chain in solution. The present data for lower generation polymers are consistent with b = 1/2, in agreement with the behavior reported for simple polyelectrolytes.17,18,20 The weaker ionic strength dependence observed for higher generation polymers is probably related to the different arrangements of the charged groups around the backbone. In the polymers of low generation, the charged groups are located close to the backbone, which allows the counterions to approach these groups from all radial directions, leading to effective screening. This configuration resembles other types of simple polyelectrolytes. With increasing generation of the side dendrons, however, the charged groups will have the tendency to accumulate at the outside of the cylindrical polymer tube, although some of these groups may also remain in the interior. However, the counterions will be able to approach the outside of the cylinder only. This situation leads to less effective screening, which induces a weaker ionic strength dependence of the persistence length.The weaker ionic strength dependence of the high-generation polymers could also be related to a variation of the line charge density with the ionic strength. While the solution pH was kept constant, the decrease in the ionic strength could lead to a decrease of the degree of dissociation due to an exchange between protons and cations originating from the salt. At first sight, one might suspect this effect to be minor, since the solution pH of 4.0 is substantially smaller than the acidity constant of the dendron-terminating primary amine groups (pKa ≃ 10).45 However, the line charge density of the dendronised polymers is very high (up to 60 nm−1, Table 1), and the strong electrostatic interactions between the ionized amine groups will hamper the ionization process.46 Therefore, even at pH 4.0, only a fraction of the amine groups may be ionized, especially for the higher generations. Under these conditions, the charge density of the polymer could thus vary significantly with the ionic strength due to ion exchange.
This variation in the charge density due to ionization cannot be easily separated from the condensation of other counterions (e.g., chloride). Manning has suggested that the effective line charge density should not exceed the inverse Bjerrum length, namely 1.4 nm−1.47 Later studies have shown that this threshold is modified by the ionic strength and polymer tube diameter.48,49 Given the relatively small diameters of the dendronized polymers (Table 1) and not too high ionic strengths used, we expect that these modifications will be relatively modest. The resulting variations in the line charge density will influence the electrostatic interactions between the backbone segments only weakly and do not explain the difference in ionic strength dependence compared to other polyelectrolytes.
Moreover, the nature of the substrate also plays a significant role. While the data obtained for all the substrates show the same ionic strength dependence characterized by the exponent b = 0.33, the pre-factor A varies with the substrate (Table 2). This pre-factor is large for more hydrophilic substrates, and decreases in the sequence, mica, silica, and gold. The lowest pre-factor is observed for the most hydrophobic HOPG substrate. As argued above, only a fraction of the amine groups are probably ionized in solution for the high-generation polymers. When such a polymer adsorbs on the highly negatively charged mica,50 these negative charges lead to dissociation of the amine groups, and to an increase of the line charge density of the polymer. The segments of such a highly charged polymer repel strongly at low ionic strengths, which leads to stiffening of the polymer chain and an increase of the persistence length. A similar mechanism should apply to the more weakly charged gold or silica substrate.51 However, when adsorbing onto HOPG, the ionization state of the molecule would remain approximately the same as in solution. The segments of such weakly charged polymers will repel only weakly, and thus the polymer remains more coiled even at low ionic strengths. We suspect that this effect could be the reason for the decrease of the pre-factor A given in eqn (3). This point of view is supported by the fact that in OSF theory, which is based on the Debye–Hückel approximation, the pre-factor A is proportional to the square of the line charge density of the polymer. The different behavior of HOPG is probably also influenced by specific interactions with the substrate. Furthermore, hydrophobic interactions could also play a role, not only for HOPG, but also for the other substrates.
Effective persistence (or Kuhn) lengths were also determined earlier from force–extension curves obtained from single molecule pulling experiments.52 While the trends with the generation were relatively similar, the striking difference to the present measurements is that the effective Kuhn lengths obtained from the force–extension curves are much smaller, typically in the range of 0.1–0.5 nm. This difference can be rationalized by the fact that the force profiles are probed at large extensions, where conformational fluctuations are limited and reflect local variations, which means that the effective Kuhn length is reduced to the bond length.53,54 Moreover, the dependence of the effective Kuhn length on the ionic strength obtained from the pulling experiments is reversed to the one observed here for the persistence length.
Conclusion
The dependence of the persistence length of cationic dendronized polymers adsorbed onto oppositely charged substrates was studied under different conditions, such as the solution ionic strength, generation of the side dendrons, and the nature of the substrate. A decrease in the ionic strength leads to an increase of the persistence length due to weaker screening of electrostatic interactions. The same ionic strength dependence is observed for all the substrates, suggesting that the observed behavior is inherent to the chain, and thus also reflects the properties of the polymers in solution. For high-generation polymers, the persistence length decreases approximately as I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1/3 with the ionic strength I. Low-generation polymers are consistent with an I
−1/3 with the ionic strength I. Low-generation polymers are consistent with an I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1/2 dependence, in agreement with the behavior of simple polyelectrolytes in solution.17,18,20 The unusually weak dependence of the persistence length on the ionic strength observed for the high-generation polymers is probably caused by the larger diameter of the polymer tube. For these polymers, the charged groups are probably screened less effectively by the electrolyte solution.
−1/2 dependence, in agreement with the behavior of simple polyelectrolytes in solution.17,18,20 The unusually weak dependence of the persistence length on the ionic strength observed for the high-generation polymers is probably caused by the larger diameter of the polymer tube. For these polymers, the charged groups are probably screened less effectively by the electrolyte solution.
Acknowledgements
Support of this research was provided by the National Research Program “Smart Materials” (NRP 62), the National Competence Center in Research (NCCR) for Bio-Inspired Materials, the Swiss National Science Foundation, ETH Zürich, EPFL Lausanne, and the University of Geneva. We acknowledge useful discussions with Avi Halperin and Martin Kröger.References
- T. Odijk, J. Polym. Sci., Part B: Polym. Phys., 1977, 15, 477–483 CAS.
- J. Skolnick and M. Fixman, Macromolecules, 1977, 10, 944–948 CrossRef CAS.
- A. R. Khokhlov and K. A. Khachaturian, Polymer, 1982, 23, 1742–1750 CrossRef CAS.
- T. Odijk and A. C. Houwaart, J. Polym. Sci., Part B: Polym. Phys., 1978, 16, 627–639 CAS.
- C. E. Reed and W. F. Reed, J. Chem. Phys., 1991, 94, 8479–8486 CrossRef CAS.
- R. R. Netz and H. Orland, Eur. Phys. J. B, 1999, 8, 81–98 CrossRef CAS.
- M. Ullner, J. Phys. Chem. B, 2003, 107, 8097–8110 CrossRef CAS.
- R. Everaers, A. Milchev and V. Yamakov, Eur. Phys. J. E, 2002, 8, 3–14 CrossRef CAS PubMed.
- T. T. Nguyen and B. I. Shklovskii, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2002, 66, 021801 CrossRef CAS PubMed.
- G. Maret and G. Weill, Biopolymers, 1983, 22, 2727–2744 CrossRef CAS PubMed.
- V. Rizzo and J. Schellman, Biopolymers, 1981, 20, 2143–2163 CrossRef CAS PubMed.
- C. G. Baumann, S. B. Smith, V. A. Bloomfield and C. Bustamante, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 6185–6190 CrossRef CAS.
- N. Makita, M. Ullner and K. Yoshikawa, Macromolecules, 2006, 39, 6200–6206 CrossRef CAS.
- K. Rechendorff, G. Witz, J. Adamcik and G. Dietler, J. Chem. Phys., 2009, 131, 095103 CrossRef PubMed.
- S. Mantelli, P. Muller, S. Harlepp and M. Maaloum, Soft Matter, 2011, 7, 3412–3416 RSC.
- J. Moukhtar, C. Faivre-Moskalenko, P. Milani, B. Audit, C. Valliant, E. Fontaine, F. Mongelard, G. Lavorel, P. St-Jean, P. Bouvet, F. Argoul and A. Arneodo, J. Phys. Chem. B, 2010, 114, 5125–5143 CrossRef CAS PubMed.
- C. Rivetti, M. Guthold and C. Bustamante, J. Mol. Biol., 1996, 264, 919–932 CrossRef CAS PubMed.
- H. K. Murnen, A. M. Rosales, A. V. Dobrynin, R. N. Zuckermann and R. A. Segalman, Soft Matter, 2013, 9, 90–98 RSC.
- M. Tricot, Macromolecules, 1984, 17, 1698–1704 CrossRef CAS.
- W. F. Reed, S. Ghosh, G. Medjahdi and J. Francois, Macromolecules, 1991, 24, 6189–6198 CrossRef CAS.
- V. Degiorgio, F. Mantegazza and R. Piazza, Europhys. Lett., 1991, 15, 75–80 CrossRef CAS.
- M. N. Spiteri, F. Boue, A. Lapp and J. P. Cotton, Phys. Rev. Lett., 1996, 77, 5218–5220 CrossRef CAS PubMed.
- T. J. Taylor and S. S. Stivala, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 1263–1272 CrossRef CAS.
- P. A. Wiggins, T. Van der Heijden, F. Moreno-Herrero, A. Spakowitz, R. Phillips, J. Widom, C. Dekker and P. C. Nelson, Nat. Nanotechnol., 2006, 1, 137–141 CrossRef CAS PubMed.
- J. Adamcik, J. M. Jung, J. Flakowski, P. De Los Rios, G. Dietler and R. Mezzenga, Nat. Nanotechnol., 2010, 5, 423–428 CrossRef CAS PubMed.
- S. Jordens, J. Adamcik, I. Amar-Yuli and R. Mezzenga, Biomacromolecules, 2011, 12, 187–193 CrossRef CAS PubMed.
- H. H. Lovelady, S. Shashidhara and W. G. Matthews, Biopolymers, 2014, 101, 329–335 CrossRef CAS PubMed.
- N. I. Abu-Lail and T. A. Camesano, J. Microsc., 2003, 212, 217–238 CrossRef CAS PubMed.
- A. D. Schlüter and J. P. Rabe, Angew. Chem., Int. Ed., 2000, 39, 864–883 CrossRef.
- Y. Guo, J. van Beek, B. Zhang, M. Colussi, P. Walde, A. Zhang, M. Kröger, A. Halperin and A. D. Schlüter, J. Am. Chem. Soc., 2009, 131, 11841–11854 CrossRef CAS PubMed.
- B. Zhang, R. Wepf, K. Fischer, M. Schmidt, S. Besse, P. Lindner, B. T. King, R. Sigel, P. Schurtenberger, Y. Talmon, Y. Ding, M. Kröger, A. Halperin and A. D. Schlüter, Angew. Chem., Int. Ed., 2011, 50, 737–740 CrossRef CAS PubMed.
- B. M. Rosen, C. J. Wilson, D. A. Wilson, M. Peterca, M. R. Imam and V. Percec, Chem. Rev., 2009, 109, 6275–6540 CrossRef CAS PubMed.
- D. Kurzbach, D. R. Kattnig, B. Z. Zhang, A. D. Schlüter and D. Hinderberger, J. Phys. Chem. Lett., 2011, 2, 1583–1587 CrossRef CAS.
- A. Mikhaylov, S. Sekatskii and G. Dietler, J. Adv. Microsc. Res., 2013, 8, 241–245 CrossRef CAS.
- J. S. Villarrubia, J. Res. Natl. Inst. Stand. Technol., 1997, 102, 425–454 CrossRef CAS PubMed.
- B. Zhang, R. Wepf, M. Kröger, A. Halperin and A. D. Schlüter, Macromolecules, 2011, 44, 6785–6792 CrossRef CAS.
- L. Grebikova, P. Maroni, L. Muresan, B. Z. Zhang, A. D. Schlüter and M. Borkovec, Macromolecules, 2013, 46, 3603–3610 CrossRef CAS.
- E. V. Dubrovin, S. Speller and I. V. Yaminsky, Langmuir, 2014, 30, 15423–15432 CrossRef CAS PubMed.
- J. Adamcik, S. Tobenas, G. Di Santo, D. Klinov and G. Dietler, Langmuir, 2009, 25, 3159–3162 CrossRef CAS PubMed.
- H. B. Wang, H. J. An, F. Zhang, Z. X. Zhang, M. Ye, P. Xiu, Y. Zhang and J. Hu, J. Vac. Sci. Technol., B, 2008, 26, L41–L44 Search PubMed.
- R. Pericet-Camara, B. P. Cahill, G. Papastavrou and M. Borkovec, Chem. Commun., 2007, 266–268 RSC.
- J. M. Y. Carrillo and A. V. Dobrynin, Macromolecules, 2011, 44, 5798–5816 CrossRef CAS.
- M. Manghi and R. R. Netz, Eur. Phys. J. E, 2004, 14, 67–77 CrossRef CAS PubMed.
- A. K. Mazur and M. Maaloum, Phys. Rev. Lett., 2014, 112 Search PubMed.
- A. E. Martell and R. M. Smith, Critical Stability Constants, Plenum Press, New York, 1982 Search PubMed.
- G. J. M. Koper and M. Borkovec, Polymer, 2010, 51, 5649–5662 CrossRef CAS.
- G. S. Manning, J. Chem. Phys., 1969, 51, 924–933 CrossRef CAS.
- E. Trizac and G. Tellez, Phys. Rev. Lett., 2006, 96, 038302 CrossRef PubMed.
- L. Bocquet, E. Trizac and M. Aubouy, J. Chem. Phys., 2002, 117, 8138–8152 CrossRef CAS.
- P. G. Hartley, I. Larson and P. J. Scales, Langmuir, 1997, 13, 2207–2214 CrossRef CAS.
- M. Giesbers, J. M. Kleijn and M. A. Cohen Stuart, J. Colloid Interface Sci., 2002, 248, 88–95 CrossRef CAS PubMed.
- L. Grebikova, P. Maroni, B. Z. Zhang, A. D. Schlüter and M. Borkovec, ACS Nano, 2014, 8, 2237–2245 CrossRef CAS PubMed.
- R. R. Netz, Macromolecules, 2001, 34, 7522–7529 CrossRef CAS.
- N. M. Toan and D. Thirumalai, Macromolecules, 2010, 43, 4394–4400 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional table and figures. See DOI: 10.1039/c6nr02665f |
| ‡ Present address: MESA+ Institute for Nanotechnology, P.O. Box 217, 7500 AE Enschede, The Netherlands. |
| This journal is © The Royal Society of Chemistry 2016 |