Influence of lipid bilayer properties on nanodisc formation mediated by styrene/maleic acid copolymers

Abstract

Copolymers of styrene and maleic acid (SMA) have gained great attention as alternatives to conventional detergents, as they offer decisive advantages for studying membrane proteins and lipids in vitro. These polymers self-insert into artificial and biological membranes and, at sufficiently high concentrations, solubilise them into disc-shaped nanostructures containing a lipid bilayer core surrounded by a polymer belt. We have used ³¹P nuclear magnetic resonance spectroscopy and dynamic light scattering to systematically study the solubilisation of vesicles composed of saturated or unsaturated phospholipids by an SMA copolymer with a 3 : 1 styrene/maleic acid molar ratio at different temperatures. Solubilisation was thermodynamically rationalised in terms of a three-stage model that treats various lipid/polymer aggregates as pseudophases. The solubilising capacity of SMA(3 : 1) towards a saturated lipid is higher in the gel than in the liquid–crystalline state of the membrane even though solubilisation is slower. Although the solubilisation of mixed fluid membranes is non-selective, the presence of a non-bilayer phospholipid lowers the threshold at which the membrane becomes saturated with SMA(3 : 1) but raises the polymer concentration required for complete solubilisation. Both of these trends can be explained by considering the vesicle-to-nanodisc transfer free energies of the lipid and the polymer. On the basis of the phase diagrams thus obtained, re-association of polymer-solubilised lipids with vesicles is possible under mild conditions, which has implications for the reconstitution of proteins and lipids from nanodiscs into vesicular membranes. Finally, the phase diagrams provide evidence for the absence of free SMA(3 : 1) in vesicular lipid suspensions.

---

Introduction

A recent development in the study of membrane proteins and lipid bilayers is the use of amphiphilic copolymers composed of styrene and maleic acid (SMA) units. SMA copolymers of different lengths and styrene/maleic acid ratios are able to directly solubilise phospholipids and membrane proteins from artificial^1,2 and natural bilayers^3–5 to form discoidal SMA/lipid particles (SMALPs). These nanodiscs contain a lipid bilayer core surrounded by a polymer belt^2,6 and have diameters of 10–30 nm,^2,6–8 which renders them suitable for optical spectroscopy,^{1,2,4,5,9–12} nuclear magnetic resonance (NMR) spectroscopy,^2,7,13 and other techniques requiring relatively small particles with a unimodal size distribution such as protein chromatography.^8,14–17

We have recently shown⁷ that solubilisation of large unilamellar vesicles (LUVs) formed from the unsaturated zwitterionic phospholipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) by an SMA copolymer having a styrene/maleic acid molar ratio of 3 : 1 (SMA(3 : 1)) can be conceptualised with the aid of a three-stage equilibrium model. This model, which originally was developed to explain the solubilisation of lipid bilayers by surfactants such as typical head-and-tail detergents,¹⁸ treats the different supramolecular aggregates formed during solubilisation as distinct pseudophases dispersed in an aqueous solution.^7,19,20 Accordingly, titration of a lipid (L) membrane with surfactant (S) initially results in the accommodation of surfactant molecules in the bilayer (b), thereby inducing increasingly positive curvature stress. At a critical surfactant/lipid molar ratio denoted R^b,SAT_S (cf. eqn (1) in ESI†), the bilayer becomes saturated (SAT) with surfactant. Addition of more surfactant initiates solubilisation, that is, extraction of phospholipids from the membrane in the form of mixed lipid/surfactant micelles (m). According to Gibbs’ phase rule, this leads to surfactant-saturated bilayer vesicles coexisting with lipid-saturated micelles until a second critical surfactant/lipid molar ratio R^m,SOL_S (eqn (2)†) is reached, where solubilisation (SOL) is complete. By determining the surfactant concentrations at the onset and completion of solubilisation at several lipid concentrations, it is possible to construct the corresponding pseudophase diagram, with the coexistence range separating the purely vesicular range from the purely micellar range. The slopes of the phase boundaries yield R^b,SAT_S and R^m,SOL_S and, through some simple relationships (eqn (3)–(8)†), the Gibbs free energies of lipid and surfactant transfer from vesicular bilayers into micelles, ΔG^b→m,o_L and ΔG^b→m,o_S, respectively. These values provide a quantitative, thermodynamic basis for rationalising the surfactant's detergency as reflected in its solubilising power towards the lipid membrane system under study.^7,18–20

It has been shown²¹ that membrane solubilisation by SMA copolymers is faster (i) for short-chain phospholipids, (ii) at elevated temperatures and, particularly, above the main phase transition temperature (T_m), and (iii) at higher ionic strengths. However, it remains unclear if and to what extent the kinetics of solubilisation reflects the solubilising power of SMA from a thermodynamic perspective, that is, if faster solubilisation correlates with lower R^b,SAT_S and R^m,SOL_S boundaries and less endergonic or more exergonic values of ΔG^b→m,o_L and ΔG^b→m,o_S, respectively. Here, we address this question by following the SMA(3 : 1)-mediated solubilisation of LUVs composed of the zwitterionic saturated phospholipid 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) both above and below its T_m to quantify the polymer's solubilising capacity towards membranes in the liquid–crystalline (i.e., fluid) and gel phases, respectively. Importantly, thermodynamic efficiency was found not to correlate with kinetic efficiency, as slow solubilisation of gel-phase membranes requires less SMA(3 : 1) than does faster solubilisation of fluid-phase membranes. On the basis of the phase diagrams thus obtained, we could demonstrate re-association of polymer-solubilised lipid with vesicular bilayer membranes both above and below T_m. Finally, we used mixed LUVs composed of the singly unsaturated phospholipids POPC and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE) to examine the influence of membrane composition on the thermodynamics of solubilisation. While the biophysical properties of the membrane such as lipid packing and phospholipid order were found to play an important role in determining the solubilising capacity of SMA(3 : 1), different lipid species residing in the same membrane were extracted non-preferentially throughout all stages of solubilisation.

Results

Solubilisation of fluid-phase DMPC vesicles

We first examined the SMA(3 : 1)-driven solubilisation of unilamellar vesicles composed of the saturated phospholipid DMPC at 30 °C, that is, 6 °C above its T_m. For this purpose, we used ³¹P NMR spectroscopy^22–24 to quantify the amount of lipid solubilised in SMALPs.⁷ In the absence of polymer and at SMA(3 : 1) concentrations below the SAT boundary, the signal arising from vesicular phospholipids was broadened beyond detection (Fig. 1a). At SMA(3 : 1) concentrations greater than SAT, an isotropic, Lorentzian-shaped peak appeared at −0.3 ppm, whose area increased linearly upon further addition of polymer until plateauing at the SOL boundary, where all lipid was solubilised into SMALPs (Fig. 1b). While the peak area remained constant beyond SOL, there was a slight downfield shift of the peak centre with increasing SMA(3 : 1) concentration. Such a shift reflects a change in the average chemical environment of the ³¹P nuclei, which we attribute to a rise in the fraction of phospholipid molecules found close to the nanodisc rim, that is, in the vicinity of the polymer. Plotting the SMA(3 : 1) concentrations at SAT and SOL for different DMPC concentrations yielded a phase diagram (Fig. 1c). From the slopes of the phase boundaries, we derived saturating and solubilising SMA(3 : 1)/DMPC molar ratios of R^b,SAT_S = 0.078 ± 0.008 and R^m,SOL_S = 0.144 ± 0.014, respectively. These values translate into vesicle-to-SMALP transfer free energies of ΔG^b→m,o_L = (0.15 ± 0.05) kJ mol⁻¹ and ΔG^b→m,o_S = −(1.36 ± 0.45) kJ mol⁻¹ for DMPC and SMA(3 : 1), respectively (Table S1†). Both the SAT and the SOL boundaries in the phase diagram (Fig. 1c) revealed a negligible ordinate intercept, confirming the absence of “free” SMA(3 : 1) in solution throughout the vesicular and coexistence ranges.⁷

Fig. 1 Solubilisation of fluid-phase DMPC vesicles by SMA(3 : 1) at 30 °C as monitored by ³¹P NMR. (a) NMR spectra of 10 mM DMPC initially present in the form of LUVs upon exposure to increasing concentrations of SMA(3 : 1). (b) Peak areas, A, at four DMPC concentrations as functions of SMA(3 : 1) concentration. Experimental data (circles) derived from titrations such as that in (a) and linear fits (lines) according to eqn (9)–(11).† (c) Phase diagram of DMPC/SMA(3 : 1) at 30 °C. Pairs of c^b,SAT_S and c^m,SOL_S (circles) obtained from breakpoints derived from local fits in (b) and global fits (solid lines) according to eqn (9), (10), and (12)† indicating the onset (SAT; red) and completion (SOL; blue) of solubilisation, respectively. Error bars are 95% confidence intervals of local fits based on eqn (9)–(11).† (d) NMR spectra of 2.5 mM DMPC and 0.4 mM SMA(3 : 1) initially present in the form of SMALPs upon addition of DMPC LUVs. Inset: Phase diagram of DMPC/SMA(3 : 1) at 30 °C indicating the SAT (red) and SOL (blue) boundaries from (c) and the DMPC concentrations tested in the reconstitution assay (triangles).

We also tested for reversibility of the solubilisation process, that is, whether lipids residing in preformed SMALPs are able to interact with and become re-associated with lipid vesicles, which might suggest a novel route for reconstituting SMALP-solubilised lipids and proteins into artificial vesicles. Guided by the phase diagram (Fig. 1c), we first solubilised 2.5 mM vesicular DMPC by adding 0.4 mM SMA(3 : 1) to form SMALPs. As expected, these preformed SMALPs produced a sharp NMR signal (Fig. 1d). Upon titration with increasing concentrations of DMPC in the form of LUVs, the signal intensity decreased as the SMA(3 : 1) concentration dropped below the SOL boundary and was broadened beyond detection when the SAT threshold was reached (Fig. 1d). Thus, re-association of phospholipids residing in SMALPs with vesicles can be triggered by addition of excess lipid, implying that the formation of freely diffusing nanodiscs is a dynamic and reversible process.

In the absence of SMA(3 : 1), dynamic light scattering (DLS) yielded a monoexponential autocorrelation function for DMPC LUVs (Fig. 2a), from which we derived a unimodal vesicle size distribution with a z-average size and peak width of (121 ± 12) nm (Fig. 2b and c). Complete solubilisation with SMA(3 : 1) gave rise to autocorrelation functions typical of small particles undergoing rapid Brownian motion (Fig. 2a–c). Importantly, however, the size of the SMALPs considerably decreased with increasing SMA(3 : 1) concentration. Irrespective of the lipid concentration tested, the nanodiscs displayed a z-average size and peak width of (29 ± 13) nm at an SMA(3 : 1)/DMPC ratio of 0.17, that is, slightly above R^m,SOL_S, but addition of excess SMA(3 : 1) further reduced the particle size to (13 ± 6) nm at an SMA(3 : 1)/DMPC ratio of 0.5 (Fig. 2d). The latter value is in good agreement with SMALP sizes reported for various combinations of phospholipids with excess SMA.^1,6,11,21 Our findings demonstrate that the average size of SMALPs can be tuned by controlling the polymer/lipid molar ratio. DLS also showed that subsolubilising SMA(3 : 1) concentrations led to the formation of larger particles in suspension (Fig. 2b and c), which have been speculated⁷ to represent vesicle aggregates or agglomerates cross-linked by polymer chains.

Fig. 2 Solubilisation of fluid-phase DMPC LUVs by SMA(3 : 1) at 30 °C as monitored by DLS. (a) Normalised autocorrelation functions, C(τ), versus delay time, τ, as determined for 4 mM DMPC LUVs (red) and after complete solubilisation with 2 mM SMA(3 : 1) (black). Note that the low ordinate intercept of the LUV autocorrelation function is due to excessive scattering resulting from the large number of vesicles initially present in the sample. Virtually identical size distribution functions and z-average values were obtained from diluted LUV suspensions (data not shown). (b) Intensity-weighted particle size distribution functions, f(d), versus hydrodynamic diameter, d, obtained upon exposure of 4 mM DMPC LUVs to increasing concentrations of SMA(3 : 1). (c) Total light scattering intensity at 90°, I, and z-average particle diameter, z, upon solubilisation of 4 mM DMPC LUVs with SMA(3 : 1). Also indicated are the SAT and SOL boundaries (dashed lines) derived from ³¹P NMR experiments (Fig. 1). Vertical bars denote peak widths as given by the corresponding PDI values. (d) z-Average particle diameters, z, at four DMPC concentrations as functions of the SMA(3 : 1)/DMPC molar ratio, R_SMA(3:1). Vertical bars denote peak widths as given by the corresponding PDI values.

Solubilisation of gel-phase DMPC vesicles

Similarly, we followed the solubilisation of DMPC LUVs at 10 °C, that is, 14 °C below T_m. Challenging LUVs with increasing SMA(3 : 1) concentrations resulted in the appearance of a sharp, isotropic ³¹P NMR peak (Fig. 3a). With saturating and solubilising SMA(3 : 1)/DMPC molar ratios of R^b,SAT_S = 0.039 ± 0.010 and R^m,SOL_S = 0.095 ± 0.011, respectively (Fig. 3b and c), the onset and completion of gel-phase DMPC solubilisation were found to occur at even lower SMA(3 : 1) concentrations as compared with fluid-phase DMPC (Fig. 1b and c). This was reflected in vesicle-to-SMALP transfer free energies of ΔG^b→m,o_L = (0.12 ± 0.05) kJ mol⁻¹ and ΔG^b→m,o_S = −(1.94 ± 0.79) kJ mol⁻¹ at 10 °C. These values were, respectively, less endergonic for the lipid and more exergonic for the polymer than the corresponding free energies at 30 °C (Table S1†). Thus, although solubilisation of DMPC vesicles is slower at temperatures below than above T_m,²¹ less polymer is required to initiate and complete the extraction of DMPC molecules from vesicles at 10 °C than at 30 °C. Re-association of SMALP-solubilised lipids with vesicles was possible also below T_m (Fig. S1d†).

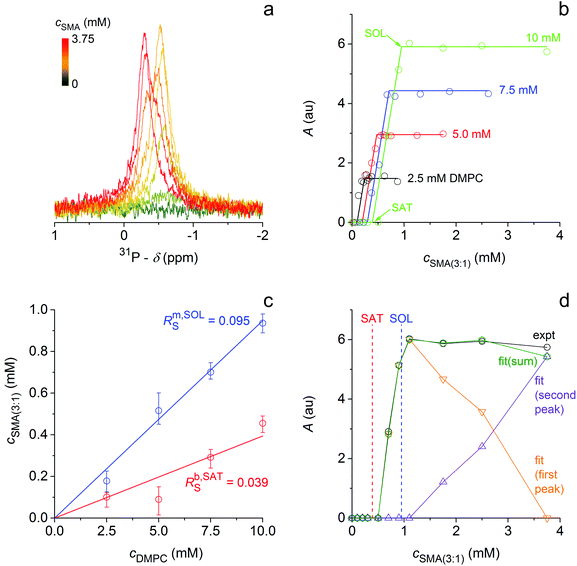Fig. 3 Solubilisation of gel-phase DMPC vesicles by SMA(3 : 1) at 10 °C as monitored by ³¹P NMR. (a) NMR spectra of 10 mM DMPC initially present in the form of LUVs upon exposure to increasing concentrations of SMA(3 : 1). (b) Peak areas, A, at four DMPC concentrations as functions of SMA(3 : 1) concentration. Experimental data (circles) derived from titrations such as that in (a) and linear fits (lines) according to eqn (9)–(11).† (c) Phase diagram of DMPC/SMA(3 : 1) at 10 °C. Pairs of c^b,SAT_S and c^m,SOL_S (circles) obtained from breakpoints of fits in (b) and global fits (solid lines) according to eqn (9), (10), and (12)† indicating the onset (SAT; red) and completion (SOL; blue) of solubilisation, respectively. Error bars are 95% confidence intervals of fits based on eqn (9)–(11).† (d) Peak areas, A, at 10 mM DMPC as functions of SMA(3 : 1) concentration. Experimental data (black) obtained from numerical peak integration and fitted values derived from a double-Lorentzian fit according to eqn (13)† for the first, upfield peak (orange), the second, downfield peak (purple), and the sum of both (green). Also indicated are the SAT and SOL boundaries (dashed lines) obtained from (c).

A conspicuous difference between the experiments above and those below T_m was the shape of the ³¹P NMR peak. Throughout the coexistence range at 10 °C, a single Lorentzian-shaped peak (Fig. 3a) was observed at −0.6 ppm, that is, −0.3 ppm upfield of the corresponding peak at 30 °C (Fig. 1a). At 10 °C, addition of SMA(3 : 1) beyond R^m,SOL_S caused a gradual reduction in the area of the original peak and a concomitant rise of a second Lorentzian-shaped peak at −0.3 ppm. The position of the latter peak was comparable to that of the single peak found at 30 °C, which changed only slightly in the course of the titration with SMA(3 : 1). This suggests that, at 10 °C, the two peaks at −0.6 ppm and −0.3 ppm represent gel-phase and fluid-phase DMPC, respectively. Thus, by fitting a double-Lorentzian function (eqn (13)†) to the NMR spectra, we found that the fraction of lipid tentatively assigned to the fluid phase increased linearly with the concentration of SMA(3 : 1) once solubilisation was complete (Fig. 3d). Another interesting difference with respect to solubilisation experiments performed at 30 °C was that the gel-phase nanodiscs existing at R^m,SOL_S were already very small, with a z-average diameter of (11 ± 4) nm, which decreased only marginally upon further addition of SMA(3 : 1) (Fig. S1a and b†).

Solubilisation of mixed POPC/POPE vesicles

Finally, we probed the solubilising activity of SMA(3 : 1) towards mixed membranes composed of POPC and POPE, the latter of which does not form bilayers on its own. To this end, we systematically increased the mole fraction of POPE in a POPC matrix from 0 mol mol⁻¹ (POPC/POPE(1 : 0)) to 0.75 mol mol⁻¹ (POPC/POPE(1 : 3)). As exemplified by a representative ³¹P NMR spectrum of a POPC/POPE(1 : 1) mixture (Fig. 4a), solubilisation with SMA(3 : 1) led to the appearance of two peaks centred at −0.16 ppm and 0.27 ppm corresponding to the signals arising from POPC and POPE, respectively.²⁵ The contribution of each phospholipid was quantified with the aid of a double-Lorentzian fit (eqn (13)†). For an equimolar lipid composition, the peak areas of the signals arising from POPC and POPE were identical across the entire range of SMA(3 : 1) concentrations (Fig. 4b), demonstrating that the polymer extracted both phospholipids non-preferentially from the vesicular bilayer not only upon complete solubilisation in the presence of excess SMA(3 : 1)^3,12,21,26 but throughout all solubilisation stages.

Fig. 4 Solubilisation of an equimolar POPC/POPE mixture by SMA(3 : 1) at 30 °C as monitored by ³¹P NMR. (a) NMR spectrum of 5 mM POPC/POPE(1 : 1) completely solubilised into SMALPs with 3 mM SMA(3 : 1) (black solid line). Lorentzian fits to signals arising from POPE (green dashed line) and POPC (orange dashed line) and the sum of both (red dashed line) according to eqn (13).† (b) Peak areas, A, at 5 mM POPC/POPE(1 : 1) derived from spectra such as that in (a) as functions of SMA(3 : 1) concentration. Experimental data (black) obtained from numerical peak integration and fitted values derived from a double-Lorentzian fit according to eqn (13)† for POPE (green), POPC (orange), and the sum of both (red). Also indicated are the SAT and SOL boundaries (dashed lines) obtained from (c). (c) Phase diagram of POPC/POPE(1 : 1) and SMA(3 : 1) mixtures. Pairs of c^b,SAT_S and c^m,SOL_S (circles) obtained from breakpoints of linear fits at individual lipid concentrations according to eqn (9)–(11)† and global fits (solid lines) according to eqn (9), (10), and (12)† indicating the onset (SAT; red) and completion (SOL; blue) of solubilisation, respectively. Error bars are 95% confidence intervals of fits based on eqn (9)–(11).†

The phase diagram obtained for POPC/POPE(1 : 1) is characterised by saturating and solubilising polymer/lipid ratios of R^b,SAT_S = 0.057 ± 0.009 and R^m,SOL_S = 0.211 ± 0.008, respectively (Fig. 4c), yielding transfer free energies of ΔG^b→m,o_L = (0.34 ± 0.04) kJ mol⁻¹ and ΔG^b→m,o_S = −(2.95 ± 0.45) kJ mol⁻¹ (Table S1†). In general, raising the fraction of POPE in the bilayer resulted in decreasing R^b,SAT_S but increasing R^m,SOL_S values (Fig. 5a), indicating that the membrane became saturated at lower SMA(3 : 1) contents but required more polymer for complete solubilisation. As a consequence, the disparate POPE dependencies of the two critical ratios resulted in a broadening of the coexistence range (Fig. 5a). In terms of Gibbs free-energy changes, this means that the transfer from vesicles into SMALPs became increasingly unfavourable for the lipid but even more favourable for the polymer, as reflected in increasing magnitudes of both ΔG^b→m,o_L and ΔG^b→m,o_S, respectively (Fig. 5b, Table S1†). Mixed POPC/POPE SMALPs exhibited a z-average diameter of (29 ± 12) nm just beyond R^m,SOL_S and further decreased in size, approaching (12 ± 5) nm in the presence of excess SMA(3 : 1) (Fig. S2a–c†). Notwithstanding the differences in the thermodynamics of solubilisation, these particle sizes were essentially identical for all POPC/POPE mixtures tested (Fig. S2c†) and were comparable to those determined for fluid-phase DMPC SMALPs (Fig. 2).

Fig. 5 Solubilisation thermodynamics of POPC/POPE LUVs by SMA(3 : 1) at 30 °C. (a) Saturating and solubilising molar ratios, R^b,SAT_S and R^m,SOL_S, respectively, as functions of the mole fraction of POPE, X_POPE, in the membrane. Data were derived from solubilisation experiments monitored by ³¹P NMR spectroscopy such as those in Fig. 4. Error bars represent 95% confidence intervals of fits based on eqn (9), (10), and (12).† (b) Vesicle-to-SMALP transfer free energies, ΔG^b→m,o_L and ΔG^b→m,o_S, for lipids and SMA(3 : 1), respectively, derived from values in (a) with the aid of eqn (3)–(8).†

Discussion

The ability to directly solubilise lipids and proteins from membranes into discoidal nanoparticles while retaining a bilayer architecture sets SMA copolymers apart not only from conventional head-and-tail detergents but also from other disc-forming amphiphiles such as bicelle-forming surfactant mixtures²⁷ and protein-bounded nanodiscs.²⁸ In the following, we discuss the most salient conclusions derived from the above experiments, namely, (i) the polymer-mediated solubilisation of gel-phase bilayers, (ii) the influence of acyl-chain packing on solubilisation, (iii) the re-association of lipids from nanodiscs with vesicular bilayers, (iv) the non-selectivity of mixed-membrane solubilisation, (v) the absence of “free” polymer, and (vi) discrepancies between the present thermodynamic observations and previous structural studies⁶ regarding the polymer/lipid ratio in SMALPs.

Solubilisation of gel-phase membranes

Although polymer-induced vesicle dissolution proceeds more slowly below than above T_m,²¹ we found that, from a thermodynamic viewpoint, solubilisation of gel-phase DMPC (Fig. 3b and c) is more efficient than when the same lipid is present in its liquid–crystalline state (Fig. 1b and c). Moreover, the SMALPs thus formed appear to contain a gel-phase bilayer core near R^m,SOL_S but experience acyl-chain melting as the concentration of SMA(3 : 1) is further increased (Fig. 3a and d). Similar observations have previously been made with conventional head-and-tail surfactants^29–32 and have been ascribed to the lower tolerance of tightly packed gel-phase membranes against perturbations caused by surfactant insertion into the lipid bilayer.¹⁹ Addition of surfactant to gel-phase membranes induces packing defects, and accumulation of high local surfactant concentrations in these defects induces strong positive curvature, which leads to the fracture of the vesicular bilayer at relatively low surfactant contents to give rise to gel-phase, surfactant-depleted lamellar sheets or discs surrounded by a surfactant-rich rim.^19,33–35 Further addition of surfactant causes both the overall size of these nanostructures and, accordingly, the size of their gel-phase core to decrease until there is no gel phase left in what can then be regarded as fluid, surfactant-rich micelles.^19,35 It seems very plausible that the superior solubilising power of SMA(3 : 1) below T_m is due to a similar mechanism: the polymer's phenyl groups can self-insert into the gel-phase bilayer only by creating packing defects, leading to the formation of gel-phase nanodiscs at R^b,SAT_S and throughout the coexistence range. Once solubilisation is complete at R^m,SOL_S, titration with more polymer gradually raises the proportion of fluid-phase lipid in the polymer-rich rim at the expense of gel-phase lipid in the nanodisc centre.

Influence of acyl-chain packing

POPC is a bilayer-forming lipid naturally occurring in eukaryotic cell and organelle membranes and is widely used for in vitro studies of membranes and membrane-interacting compounds.³⁶ By contrast, POPE does not form bilayers on its own; phospholipids with phosphoethanolamine headgroups are abundant in prokaryotes, accounting, for instance, for up to 70% of the lipids in the inner membrane and the inner leaflet of the outer membrane of Escherichia coli,³⁷ a Gram-negative bacterium extensively used for heterologous protein production.³⁸ Lacking the three N-methyl groups present in phosphocholine, the smaller phosphoethanolamine moiety reduces the lateral pressure in the headgroup regions of POPE-containing mixed lipid bilayers, which is compensated for by increased pressure in the acyl-chain core.^39–41 Since these changes in the lateral pressure profile have been shown²¹ to correlate with slower polymer-induced membrane solubilisation, we tested the influence of increasing POPE contents on the thermodynamics of SMALP formation. Although SMA(3 : 1) was able to completely solubilise mixed LUVs containing up to 75 mol% POPE (Fig. 4), increasing the lateral pressure in the bilayer core exerted a pronounced influence on the thermodynamics of solubilisation, namely, a decrease in R^b,SAT_S and a concomitant increase in R^m,SOL_S (Fig. 5a) or, equivalently, an increase in the positive value of ΔG^b→m,o_L and a concomitant decrease in the negative value of ΔG^b→m,o_S (Fig. 5b). The opposing trends in R^b,SAT_S and R^m,SOL_S can both be explained by considering the effect of POPE on the lateral pressure profile of the membrane. On the one hand, before solubilisation sets in, accommodation of SMA(3 : 1) chains in a membrane having an elevated POPE content may be hampered by high lateral pressure in the bilayer core, so that the membrane becomes saturated with polymer at lower SMA(3 : 1) concentrations than would be the case with a pure POPC bilayer. On the other hand, upon solubilisation, the SMA(3 : 1) chains surrounding a bilayer patch rich in POPE will experience increased lateral pressure from the acyl-chain region, which might hamper the insertion of the polymer's phenyl pendant groups and require more polymer molecules per unit length of SMALP edge to hold the nanodisc together.

From this and the preceding sections, it is apparent that both the physical state and the chemical composition of the lipid bilayer to be solubilised exert a pronounced influence on the vesicle-to-SMALP transfer free energies and, consequently, on the slopes of the saturation and solubilisation boundaries in the phase diagram. Nevertheless, in all cases investigated so far, the extraction of phospholipids from vesicles to form SMALPs incurs a much lower free-energy penalty than solubilisation by synthetic head-and-tail detergents and even by mild detergents such as bile salts and their derivatives (Fig. 6). Hence, these free-energy values reflect, from a thermodynamic viewpoint of lipid transfer, the native-likeness of nanodiscs formed upon solubilisation of membranes made from various phospholipids by SMA(3 : 1), which goes hand in hand with their structure- and activity-preserving properties towards membrane proteins.^{2,4,5,10,15,42}

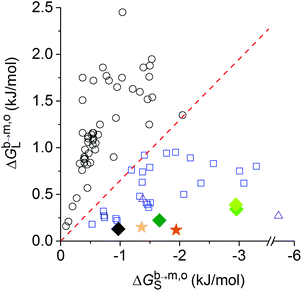Fig. 6 Thermodynamic classification of surfactants based on the bilayer-to-micelle transfer free energies of surfactants and lipids, ΔG^b→m,o_S and ΔG^b→m,o_L, respectively.⁷ Synthetic head-and-tail detergents (open black circles) on the one hand and bile salts and their derivatives (open blue squares), the lipopeptides P2A2 and surfactin (open purple triangles), as well as SMA(3 : 1) (full symbols) on the other hand are separated by a threshold (red dashed line) defined by ΔG^b→m,o_L = −0.65 × ΔG^b→m,o_S. Data for SMA(3 : 1) solubilisation refer to DMPC at 10 °C or 30 °C (dark and light orange star, respectively) as well as POPC/POPE (1 : 0)–POPC/POPE(1 : 3) (dark to light green diamonds); all other data are taken from ref. 7.

Lipid re-association with vesicles

It has been shown⁵ that SMALPs can deliver individual copies of the homotetrameric K⁺ channel KcsA into planar bilayers composed of E. coli polar lipid extract for electrophysiological measurements. However, quantitative reconstitution of membrane proteins and lipids from nanodiscs into other membrane systems such as vesicles remains to be demonstrated.⁴³ With the aid of the respective phase diagrams (Fig. 1c and 3c), we accomplished complete re-association of SMA(3 : 1)-solubilised DMPC with vesicles at temperatures both above and below T_m, as evidenced by a loss of the ³¹P NMR signal arising from small, fast-tumbling particles (Fig. 1d and S1d,† respectively). This observation could formally be explained by polymer-mediated tethering or adsorption of SMALPs to vesicles. In the light of the close agreement of these reconstitution titrations with the phase diagrams obtained from solubilisation experiments (insets in Fig. 1d and S1d†), however, it seems more likely that phospholipid molecules can indeed be reincorporated from SMALPs into vesicular bilayer membranes by addition of excess lipid in order to shift the equilibrium back into the purely vesicular range of the phase diagram. This, in turn, implies that high-yield reconstitution of nanodisc-embedded membrane proteins might also become feasible by simple addition of lipid vesicles to protein-containing SMALPs, without requiring harsher procedures such as polymer precipitation with divalent cations.⁴³ Such a mild yet quantitative reconstitution protocol would facilitate the scrutiny of membrane proteins with vectorial functions, such as channels and transporters, in a membrane-mimetic system with two distinct aqueous compartments.

Non-selective lipid solubilisation

From the two distinct ³¹P NMR signals obtained during the solubilisation of mixed POPC/POPE LUVs (Fig. 4a), we conclude that SMA(3 : 1) solubilises these two lipids in a non-preferential manner. This is in agreement with a number of studies showing that various SMA copolymers, when present in excess, extract lipids from native^3,12,26 and mixed artificial²¹ membranes in a non-selective fashion. In contrast with these earlier reports, the present results show that non-selectivity applies not only to the final solubilisation product at polymer concentrations much higher than R^m,SOL_S but throughout all stages of a solubilisation titration. This might be surprising in view of the stark influence of lipid composition on both the kinetics²¹ and the thermodynamics (Fig. 5) of solubilisation. It therefore becomes apparent that it is the bulk physical state of the bilayer membrane rather than the properties of individual lipid constituents that governs the solubilisation equilibrium without, however, biasing the lipid composition of the solubilised bilayer.

Absence of free polymer

An important conclusion emerging from all pseudophase diagrams thus far established for various lipid/SMA(3 : 1) mixtures (ref. 7 as well as Fig. 1c, 3c, and 4c) is that SMA(3 : 1) does not exist in a “free” form in the presence of lipid vesicles. That is, the polymer's affinity for lipids appears to be so high that, within the vesicular and coexistence ranges, it is always associated with lipids irrespective of the polymer/lipid ratio, albeit in different morphologies, such as vesicular membranes or nanodiscs. Population of a significant pool of free SMA(3 : 1) in the aqueous solution would manifest in a nonzero ordinate intercept in the phase diagrams, as observed for detergents with high critical micellar concentrations.^37,44,45 Note, however, that this does not formally rule out the existence of free polymer chains at polymer/lipid ratios higher than R^m,SOL_S or in protein-containing samples, as it is conceivable that membrane proteins retain lipid molecules in bilayer patches and, thus, render them unavailable for interaction with the polymer.⁴⁶ Then, addition of “excess” polymer could, in principle, result in the build-up of a pool of free polymer that coexists with polymer-bounded, protein-containing nanodiscs. Moreover, in view of the bivariate distribution of the length and the styrene/maleic acid ratio of SMA copolymers,⁴³ it is possible that there exists a fraction of relatively short polymer chains rich in maleic acid residues that are too hydrophilic to participate in the solubilisation of lipid membranes and the formation of SMALPs, irrespective of the polymer and lipid concentrations and the resulting aggregate morphologies in the sample. Such a polymer population would neither contribute to any of the phenomena investigated here nor manifest in the present approach based on phase diagrams but might possibly be responsible for some of the adverse effects tentatively ascribed to “free” polymer chains in membrane-protein studies.⁴³

Polymer/lipid ratio in SMALPs

Provided that there is no free polymer in solution, the polymer/lipid ratio in SMALPs must be identical to the overall ratio in the sample. This means that, with R^m,SOL_S = 0.144 in the exemplary case of DMPC at 30 °C (Fig. 1c), the polymer/lipid mass ratio in SMALPs is at least 0.85, corresponding to 46% of the total nanodisc mass being due to SMA(3 : 1). For a more typical molar ratio of 0.5 (e.g., Fig. 2d), the mass ratio and percentage are as high as 2.9 and 75%, respectively. Using the approximation that the densities of polymer and lipid are similar, we thus arrive at equally high volume fractions of SMA(3 : 1) in nanodiscs. This appears to be at odds with findings of an earlier study,⁶ where the dimensions of the lipid core and polymer belt of SMALPs formed from DMPC and the more hydrophilic polymer SMA(2 : 1) were characterised by small-angle neutron scattering (SANS). The disc dimensions estimated in that study would result in a volume contribution of the polymer belt of no more than 25%.

In trying to reconcile these seemingly contradictory results, we have to be aware of two major simplifications inherent to the structural model used for analysing and interpreting the SANS data.⁶ On the one hand, this model assumes SMALPs to consist of a pure lipid core bounded by a strictly separated, pure polymer belt. Obviously, this is, at best, a zeroth-order approximation, since the same⁶ and other studies² report spectroscopic evidence indicating intercalation of the polymer's phenyl groups into the acyl-chain region of the lipid bilayer core, thus reducing the “effective” volume of the polymer ascribed to the belt. On the other hand, a considerable amount of the polymer resides in the lipid bilayer or at the lipid/water interface of the SMALP core, as evidenced by the finite R^b,SAT_S values found here and previously.⁷ For example, with R^b,SAT_S = 0.078 for DMPC at 30 °C (Fig. 1c), the polymer/lipid mass ratio in the vesicular membrane at the onset of solubilisation and, thus, in the bilayer core of the SMALPs then formed amounts to 0.46, meaning that SMA(3 : 1) accounts for 32% of the total mass in the SMALP core. Conversely, the belt need not consist exclusively of polymer but might accommodate a substantial fraction of lipid. Both of the above factors, that is, the blurry boundary between the core and belt regions of SMALPs as well as the finite mutual solubilities of the lipid and the polymer, are not accounted for in the simple geometric model,⁶ calling for a more detailed structural scrutiny of SMALPs.

Conclusions

Styrene/maleic acid copolymers exhibit decisive advantages over conventional detergents by combining a strong solubilising capacity with a discoidal nanoparticle morphology harbouring a native-like lipid bilayer. Herein, we have shown that

• the kinetics of vesicle dissolution is a poor indicator of the three-stage solubilisation equilibrium, as gel-phase membranes are more susceptible than fluid-phase membranes to SMALP formation;

• the addition of more polymer than minimally required for complete solubilisation results in gradual size reduction of the SMALPs above T_m and seems to gradually abolish the gel phase below T_m;

• the bulk physical properties of the bilayer affect the vesicle-to-SMALP transfer free energies of both the lipid and the polymer and, hence, the saturating and solubilising polymer/lipid ratios defining the degree of detergency or solubilising power;

• polymer-solubilised lipids re-associate with vesicular bilayer membranes upon addition of excess lipid so as to shift the equilibrium back into the vesicular range of the phase diagram;

• polymer-mediated lipid solubilisation is non-preferential throughout the range of polymer/lipid ratios across which SMALP formation proceeds;

• there is no detectable population of free “solubilisation-competent” polymer chains in vesicular suspensions containing phospholipids and styrene/maleic acid copolymers, irrespective of temperature or lipid composition.

Experimental

Materials

DMPC, POPC, and POPE were obtained from Lipoid (Ludwigshafen, Germany). SMA(3 : 1) copolymer solution (trade name Xiran SL25010 S25) was kindly provided by Polyscope (Geleen, Netherlands). Chloroform was purchased from Fisher Scientific UK (Leics, UK), D₂O from Deutero (Kastellaun, Germany), 85% H₃PO₄ in D₂O from Sigma–Aldrich (Steinheim, Germany), NaCl from VWR (Darmstadt, Germany), and tris(hydroxymethyl)aminomethane (Tris) from Carl Roth (Karlsruhe, Germany). All chemicals were obtained in the highest available purity.

Vesicle preparation

LUVs composed of either DMPC or POPC were prepared by suspension of dry lipid powder in Tris buffer (50 mM Tris, 200 mM NaCl, pH 7.4) to a final lipid concentration of 40 mM followed by 35-fold extrusion at 30 °C through two stacked 100 nm polycarbonate filters with a block-heated Mini-Extruder (Avanti, Alabama, USA). Mixed LUVs composed of POPC and POPE were prepared by suspending dry lipid powders in chloroform at 40 mM lipid concentration and mixing at 3 : 1, 1 : 1, or 1 : 3 POPC/POPE molar ratios. Mixed lipid solutions were dried in a rotary evaporator at 60 °C and 20 kPa for 2 h and incubated in a desiccator at room temperature and 5 Pa for 16 h to remove traces of chloroform. Dry lipid films were suspended in Tris buffer at a final concentration of 40 mM total lipid and extruded as described above.

Preparation of SMA(3 : 1) stock solution

The random copolymer used in this study had a styrene/maleic acid molar ratio of 3 : 1, a mass-average molar mass of M_w = 10 kg mol⁻¹, and a number-average molar mass of M_n = 4 kg mol⁻¹. To prepare SMA(3 : 1) stock solutions, 3 mL of a Xiran SL25010 S25 solution was dialysed against Tris buffer using a 5 mL QuixSep dialyser (Membrane Filtration Products, Seguin, USA) and a Spectra/Por 3 dialysis membrane (Spectrum Laboratories, Rancho Dominguez, USA) with a molar-mass cutoff of 3.5 kg mol⁻¹. Dialysis was performed for 24 h under gentle stirring with membrane and buffer exchange after 16 h. Dialysed SMA(3 : 1) was filtered through a 0.22 μm poly(vinylidene fluoride) (PVDF) filter (Carl Roth, Karlsruhe, Germany), and the final SMA(3 : 1) concentration was determined by refractometry on an Abbemat 500 (Anton Paar, Graz, Austria) using a molar refractive index increment of dn/dc = 1.1178 M⁻¹.⁷ Note that the same refractive index value was derived using a series of SMA(3 : 1) solutions prepared from polymer powder obtained through hydrolysis of a commercial styrene/maleic anhydride product from the same supplier (Xiran SZ25010). Molar concentrations were calculated from mass concentrations on the basis of the above number-average molar mass. Samples were aliquoted, stored at −20 °C, and thawed prior to use.

³¹P NMR spectroscopy

For solubilisation experiments, 40 mM lipid in the form of LUVs and 17.5 mM SMA(3 : 1) in Tris buffer were used to prepare samples containing 2.5, 5.0, 7.5, or 10.0 mM lipid and 0–7 mM SMA(3 : 1). For reconstitution experiments, a mixture containing 2.5 mM DMPC and 0.28–0.40 mM SMA(3 : 1) in the form of SMALPs was incubated with 1.9–7.5 mM DMPC in the form of LUVs. All samples contained 10% D₂O for locking and were incubated for at least 16 h at 10 °C or 30 °C before measurements were performed at 10 °C or 30 °C on an Avance 400 spectrometer (Bruker Biospin, Rheinstetten, Germany) operating at a ³¹P resonance frequency of 162 MHz. We used a 5 mm broadband inverse probe to acquire 256 scans with an inverse-gated ¹H decoupling sequence, an acquisition time of 1.6 s, a sweep width of 9746 Hz, and a relaxation delay of 6 s. Data were multiplied by an exponential function with a line-broadening factor of 1.0 Hz before Fourier transformation. Chemical shifts were referenced to 85% H₃PO₄ in D₂O as external standard at 0 ppm. Total peak areas were calculated by numerical integration in TopSpin 3.2, while peak positions and individual peak areas in lipid mixtures were obtained by fitting the corresponding data to a Lorentzian-shaped curve (eqn (13)†) by nonlinear least-squares analysis.⁴⁷ Dependencies of ³¹P NMR peak areas on SMA(3 : 1)/lipid ratios were analysed in terms of a three-stage model (eqn (9)–(12)†) by nonlinear least-squares analysis.⁴⁷

Dynamic light scattering

DLS measurements were performed on a Zetasizer Nano S90 (Malvern Instruments, Worcestershire, UK) equipped with a 633 nm He–Ne laser and a photodetector mounted at an angle of 90°. Samples containing lipid and SMA(3 : 1) were incubated for 16 h at 30 °C or 10 °C for DMPC experiments above or below T_m, respectively, or at 30 °C for POPC/POPE mixtures. Measurements were carried out in a 45 μL quartz glass cuvette with a 3 mm × 3 mm cross-section (Hellma Analytics, Müllheim, Germany) at 30 °C or 10 °C. Each sample was measured twice, once with the attenuator position automatically optimised for determination of size distributions and a second time with maximum open attenuator position to ensure comparability of total scattering intensities. Data analysis was performed by fitting the experimentally determined autocorrelation function with a non-negatively constrained least-squares function⁴⁸ to obtain the intensity-weighted particle size distribution and by cumulant analysis⁴⁹ to yield the z-average particle size and the width of the size distribution as derived from the associated polydispersity index (PDI). Assuming Gaussian distributions of both the decay rate and the particle size, the standard deviation of the z-average particle size is .⁵⁰

Author contribution

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Acknowledgements

Dr. Harald Kelm (University of Kaiserslautern) is gratefully acknowledged for invaluable help with ³¹P NMR experiments. We thank Dr. Jana Broecker (University of Toronto), Jonas Dörr (Utrecht University, Netherlands), Abraham Olusegun Oluwole, Anne Grethen, Erik Frotscher, and Bartholomäus Danielczak (all University of Kaiserslautern) for helpful discussions. This work was supported by the Deutsche Forschungsgemeinschaft (DFG) through International Research Training Group (IRTG) 1830, by the Carl Zeiss Foundation with a scholarship to R. C. A., and by the Deutsche Akademische Austauschdienst (DAAD) with grant no. 56041134 to S. K.

References

1. T. J. Knowles, R. Finka, C. Smith, Y. Lin, T. Dafforn and M. Overduin, J. Am. Chem. Soc., 2009, 131, 7484.
2. M. C. Orwick, P. J. Judge, J. Procek, L. Lindholm, A. Graziadei, A. Engel, G. Gröbner and A. Watts, Angew. Chem., Int. Ed., 2012, 51, 4653.
3. A. R. Long, C. C. O'Brien, K. Malhotra, C. T. Schwall, A. D. Albert, A. Watts and N. N. Alder, BMC Biotechnol., 2013, 13, 41.
4. M. Jamshad, J. Charlton, Y. Lin, S. J. Routledge, Z. Bawa, T. J. Knowles, M. Overduin, N. Dekker, T. R. Dafforn, R. M. Bill, D. R. Poyner and M. Wheatley, Biosci. Rep., 2015, 35, 1.
5. J. M. Dörr, M. C. Koorengevel, M. Schäfer, A. V. Prokofyev, S. Scheidelaar, W. van der Cruijsen, T. R. Dafforn, M. Baldus and J. A. Killian, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18607.
6. M. Jamshad, V. Grimard, I. Idini, T. J. Knowles, M. R. Dowle, N. Schofield, P. Sridhar, Y. Lin, R. Finka, M. Wheatley, O. R. T. Thomas, R. E. Palmer, M. Overduin, C. Govaerts, J. Ruysschaert, K. J. Edler and T. R. Dafforn, Nano Res., 2015, 8, 774.
7. C. Vargas, R. Cuevas Arenas, E. Frotscher and S. Keller, Nanoscale, 2015, 7, 20685.
8. R. Zhang, I. D. Sahu, L. Liu, A. Osatuke, R. G. Comer, C. Dabney-Smith and G. A. Lorigan, Biochim. Biophys. Acta, 2014, 1848, 329.
9. C. Logez, M. Damian, C. Legros, C. Dupré, M. Guéry, S. Mary, R. Wagner, C. M'Kadmi, O. Nosjean, B. Fould, J. Marie, J. Fehrentz, J. Martinez, G. Ferry, J. A. Boutin and J. L. Banères, Biochemistry, 2016, 55, 38.
10. S. Gulati, M. Jamshad, T. J. Knowles, K. A. Morrison, R. Downing, N. Cant, R. Collins, J. B. Koendrick, R. C. Ford, M. Overduin, I. Kerr, T. R. Dafforn and A. J. Rothnie, Biochem. J., 2014, 461, 269.
11. M. Orwick-Rydmark, J. E. Lovett, A. Graziadei, L. Lindholm, M. R. Hicks and A. Watts, Nano Lett., 2012, 12, 4687.
12. D. J. K. Swainsbury, S. Scheidelaar, R. van Grondelle, J. A. Killian and M. R. Jones, Angew. Chem., Int. Ed., 2014, 53, 11803.
13. D. Li, J. Li, Y. Zhuang, L. Zhang, Y. Xiong, P. Shi and C. Tian, Protein Cell, 2015, 6, 229.
14. S. J. Routledge, L. Mikaliunaite, A. Patel, M. Clare, S. P. Cartwright, Z. Bawa, M. D. B. Wilks, F. Low, D. Hardy, A. J. Rothnie and R. M. Bill, Methods, 2016, 95, 26.
15. S. Paulin, M. Jamshad, T. R. Dafforn, J. Garcia-Lara, S. J. Foster, N. F. Galley, D. I. Roper, H. Rosado and P. W. Taylor, Nanotechnology, 2014, 25, 285101.
16. V. Postis, S. Rawson, J. K. Mitchell, S. C. Lee, R. A. Parslow, T. R. Dafforn, S. A. Baldwin and S. P. Muench, Biochim. Biophys. Acta, 2015, 1848, 496.
17. A. Periasamy, N. Shadiac, A. Amalraj, S. Garajová, Y. Nagarajan, S. Waters, H. D. T. Mertens and M. Hrmova, Biochim. Biophys. Acta, 2013, 1828, 743.
18. D. Lichtenberg, Biochim. Biophys. Acta, 1985, 821, 470.
19. H. Heerklotz, Q. Rev. Biophys., 2008, 41, 205.
20. D. Lichtenberg, H. Ahyayauch and F. M. Goñi, Biophys. J., 2013, 105, 289.
21. S. Scheidelaar, M. C. Koorengevel, J. D. Pardo, J. D. Meeldijk, E. Breukink and J. A. Killian, Biophys. J., 2015, 108, 279.
22. M. Roux and P. Champeil, FEBS Lett., 1984, 171, 169.
23. M. T. Paternostre, M. Roux and J. L. Rigaud, Biochemistry, 1988, 27, 2668.
24. D. Levy, A. Gulik, M. Seigneuret and J. L. Rigaud, Biochemistry, 1990, 29, 9480.
25. J. Schiller, M. Müller, B. Fuchs, K. Arnold and D. Huster, Curr. Anal. Chem., 2007, 3, 283.
26. I. Prabudiansyah, I. Kusters, A. Caforio and A. J. M. Driessen, Biochim. Biophys. Acta, 2015, 1848, 2050.
27. U. H. N. Dürr, R. Soong and A. Ramamoorthy, Prog. Nucl. Magn. Reson. Spectrosc., 2013, 69, 1.
28. A. Nath, W. M. Atkins and S. G. Sligar, Biochemistry, 2007, 46, 2059.
29. S. K. Patra, A. Alonso and F. M. Goñi, Biochim. Biophys. Acta, 1998, 1373, 112.
30. S. K. Patra, A. Alonso, J. L. R. Arrondo and F. M. Goñi, J. Liposome Res., 1999, 9, 247.
31. T. Nyholm and J. P. Slotte, Langmuir, 2001, 17, 4724.
32. B. Carion-Taravella, S. Lesieur, J. Chopineau, P. Lesieur and M. Ollivon, Langmuir, 2002, 18, 325.
33. S. Funari, B. Nuscher, G. Rapp and K. Beyer, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 8938.
34. F. Ollila and J. P. Slotte, Biochim. Biophys. Acta, 2002, 1564, 281.
35. H. Heerklotz, Biophys. J., 2002, 83, 2693.
36. D. E. Warschawski, A. A. Arnold, M. Beaugrand, A. Gravel, É. Chartrand and I. Marcotte, Biochim. Biophys. Acta, 2011, 1808, 1957.
37. H. Goldfine, J. Lipid Res., 1984, 25, 1501.
38. K. Duquesne and J. N. Sturgis, Methods Mol. Biol., 2010, 601, 205.
39. R. S. Cantor, J. Phys. Chem. B, 1997, 101, 1723.
40. R. S. Cantor, Biochemistry, 1997, 36, 2339.
41. E. Strandberg and A. S. Ulrich, Biochim. Biophys. Acta, 2015, 1848, 1944.
42. A. J. Bell, L. K. Frankel and T. M. Bricker, J. Biol. Chem., 2015, 290, 18429.
43. J. M. Dörr, S. Scheidelaar, M. C. Koorengevel, J. J. Dominguez, M. Schäfer, C. van Walree and J. A. Killian, Eur. Biophys. J., 2016, 45, 3.
44. O. O. Krylova, N. Jahnke and S. Keller, Biophys. Chem., 2010, 150, 105.
45. S. Keller, H. Heerklotz, N. Jahnke and A. Blume, Biophys. J., 2006, 90, 4509.
46. N. Jahnke, O. O. Krylova, T. Hoomann, C. Vargas, S. Fiedler, P. Pohl and S. Keller, Anal. Chem., 2014, 86, 920.
47. G. Kemmer and S. Keller, Nat. Protocols, 2010, 5, 267.
48. P. Hassan, S. Rana and G. Verma, Langmuir, 2015, 31, 3.
49. D. E. Koppel, J. Chem. Phys., 1972, 57, 4814.
50. M. Holzer, S. Barnert, J. Momm and R. Schubert, J. Chromatogr. A, 2009, 1216, 5838.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nr02089e

---