Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural evolution and metallicity of lead clusters†
Daniel A.
Götz
*a,
Armin
Shayeghi
a,
Roy L.
Johnston
b,
Peter
Schwerdtfeger
c and
Rolf
Schäfer
a
aEduard-Zintl-Institut, Technische Universität Darmstadt, Alarich-Weiss-Straße 8, 64287 Darmstadt, Germany. E-mail: goetz@cluster.pc.chemie.tu-darmstadt.de; Fax: +49 6151 1623841; Tel: +49 6151 1623845
bSchool of Chemistry, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
cCentre for Theoretical Chemistry and Physics, The New Zealand Institute for Advanced Study, Massey University (Albany), Bob Tindall Bldg., 0745 Auckland, New Zealand
First published on 16th May 2016
Abstract
The evolution of the metallic state in lead clusters and its structural implications are subject to ongoing discussions. Here we present molecular beam electric deflection studies of neutral PbN (N = 19–25, 31, 36, 54) clusters. Many of them exhibit dipole moments or anomalies of the polarizability indicating a non-metallic state. In order to resolve their structures, the configurational space is searched using the Pool Birmingham Cluster Genetic algorithm based on density functional theory. Spin–orbit effects on the geometries and dipole moments are taken into account by further relaxing them with two-component density functional theory. Geometries and dielectric properties from quantum chemical calculations are then used to simulate beam deflection profiles. Structures are assigned by the comparison of measured and simulated beam profiles. Energy gaps are calculated using time-dependent density functional theory. They are compared to Kubo gaps, which are an indicator of the metallicity in finite particles. Both, experimental and theoretical data suggest that lead clusters are not metallic up to at least 36 atoms.
1. Introduction
As clusters grow towards the bulk, their geometric and electronic structures undergo fundamental transitions. In particular, the evolution of the metallic state in metal atom clusters has drawn attention. The discussion of metallicity on the nanoscale is hampered by the fact that it is well defined only for the bulk, i.e. by a non-zero electronic density of states at the Fermi energy. Generally, clusters have a gap at EF because of their finite size and so they are never metallic in a strict sense. Issendorff and Cheshnovsky circumvented this issue by considering a cluster as metallic if its energy level spacing Egap at the Fermi energy drops below the Kubo gap.1 The Kubo gap represents the average energy level spacing in a metallic particle of finite size, if a statistical level distribution is assumed.2 However, the electronic structure of simple metal clusters like sodium is well described within the shell model where electrons are treated as free particles in a spherical box. This implicates highly degenerate energy levels and in contrast to the Kubo criteria substantial gaps for certain cluster sizes arise. Considering the Kubo criteria solely is therefore not sufficient to assess the metallic character of a cluster. This point has been discussed for zinc clusters thoroughly.3 Besides the electronic shell structure and the Kubo gap also the electronic screening and the bonding nature have to be taken into account. Although the concept of metallicity has to be used cautiously, we term a cluster metallic in the following if the mentioned criteria are sufficiently fulfilled.Experimental values for Egap can be derived from photoelectron spectroscopy (PES). The difference of the first two vertical photodetachement energies is the gap of the corresponding neutral cluster in the geometry of the anion. This gap is a reasonable approximation to the gap of the neutral cluster, if the ground state geometries of the anion and the neutral cluster do not differ substantially. Characteristic metal to insulator transitions (MIT) have been detected by PES for several cluster species. In HgN− clusters for example, the gap steadily decreases with the cluster size and closes at about N = 400.4 The gaps of SnN− clusters on the other hand close at around N = 40.5 In the same size regime the geometries of SnN+ clusters become spherical whereas prolate structures are preferred for smaller species as ion mobility measurements have shown.6 Although the charge state certainly influences the geometric structure of a cluster the relation between geometric structure and metallicity becomes evident here. The structure and properties of the next heavier homolog Pb are strongly influenced by spin–orbit (SO) effects.7 It is still not clear how the metallic state evolves in Pb clusters, i.e. if the MIT occurs at a certain critical size or by gradual gap closure. Early PES studies did not come to a clear conclusion.8,9 Later Senz et al. found reduced core–hole screening by PES as the cluster size drops below 20 atoms, indicating a MIT in this size regime.10 Recently, Heinzelmann et al. presented a time-dependent PES study where relaxation life times denote a non-metallic electronic structure for Pb28−.11 Despite the comprehensive experimental work on PbN− clusters it remains unclear where the MIT occurs.
In the present article we study neutral PbN clusters, which is straightforward since any influence of the excess charge is avoided. Several theoretical studies are dedicated to neutral Pb cluster.12–14 Wang et al. calculated gaps between highest occupied (HOMO) and lowest unoccupied molecular orbitals (LUMO) as well as densities of states up to Pb22 using density functional theory (DFT).15 They observed gaps around 1 eV for their largest cluster investigated and a considerable dependence on the geometric structure. However, the reliability of HOMO–LUMO gaps from DFT calculations has been questioned16 and they should be treated with caution.
In this study we employ the electric molecular beam deflection (MBD) method in order to shed light on the MIT in Pb clusters and its structural manifestation. The MBD probes dipole moments and polarizabilities of a given neutral cluster. Since a classical metallic particle cannot have a permanent dipole moment, i.e. the electronic screening should be almost perfect, it is a meaningful indicator for a non-metallic state. This was concisely pointed out by de Heer and co-workers for small sodium clusters.17 Beam profiles from MBD experiments are also sensitive for the cluster geometry. Hence, a structural assignment is possible, as demonstrated for several group 14 clusters.18–21 Former molecular beam deflection experiments on neutral lead clusters at 50 K indicated dipole moments or anomalies in the polarizability for several PbN (N ≤ 40) without suggesting any structures for them.22 We have repeated these measurements at 30 K to ensure the rigidity of the clusters. The experimental data are supported by an extensive global minimum search. Structures are further relaxed employing two-component (2c) DFT in order to account for SO effects on the geometries and dipole moments. The metallic character of the clusters is further evaluated by gaps from 2c time-dependent DFT (2c-TDDFT) calculations.
2. Experimental and computational methods
The experimental23 and computational21 procedures have been described earlier and we only give a brief outline here. Lead clusters are generated in a pulsed laser vaporization source using helium as carrier gas.24 The cluster–helium mixture is cooled in a cryogenic nozzle (Tnozzle = 30 K) before a molecular beam is formed by supersonic expansion into a high vacuum chamber. Two collimators shape the molecular beam to a rectangular profile before it enters an electric two-wire field unit. The external field with a gradient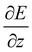 deflects a cluster in a quantum state i with mass m and velocity v by
deflects a cluster in a quantum state i with mass m and velocity v by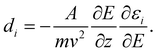 | (1) |
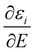 the Stark effect. The latter is a cluster specific quantity and determines its deflection behaviour. Downstream of the deflection unit the clusters arrive at a scanning slit plate, are photoionized by a F2 excimer laser (7.89 eV) and subsequently detected by a time-of-flight mass spectrometer. Photoionisation mass spectra are measured as a function of the slit position with and without applied electric field. The relative intensities of a cluster species in this mass spectra yield beam profiles as shown in Fig. 1a and 2a. The polarizability of a rigid, almost spherical rotor can be extracted from the beam profile by first order perturbation theory.22 Herein, experimental polarizabilities αexp are reported for PbN (N = 20–24), where no or a minor dipolar contribution to the beam shift due to a permanent dipole moment is observed.25
the Stark effect. The latter is a cluster specific quantity and determines its deflection behaviour. Downstream of the deflection unit the clusters arrive at a scanning slit plate, are photoionized by a F2 excimer laser (7.89 eV) and subsequently detected by a time-of-flight mass spectrometer. Photoionisation mass spectra are measured as a function of the slit position with and without applied electric field. The relative intensities of a cluster species in this mass spectra yield beam profiles as shown in Fig. 1a and 2a. The polarizability of a rigid, almost spherical rotor can be extracted from the beam profile by first order perturbation theory.22 Herein, experimental polarizabilities αexp are reported for PbN (N = 20–24), where no or a minor dipolar contribution to the beam shift due to a permanent dipole moment is observed.25
Promising lead cluster structures are obtained by a global optimization approach employing the Pool Birmingham Cluster Genetic Algorithm.26 Structures are relaxed using plane-wave DFT within in the Quantum Espresso program package.27 The Perdew–Burke–Ernzerhof28 (PBE) functional is used and 14 electrons for each lead atom are treated explicitly; the remaining core electrons are described by a pseudopotential29–31 with a suggested minimum cutoff of 40 Ry of the plane-wave basis. The following orbital based DFT calculations (PBE) are carried out using the Turbomole32 and NWChem33 program packages. Isomers within 0.5 eV of the global minimum (GM) are considered for further local optimizations at the scalar relativistic DFT level of theory with the def2-TZVP basis set34 and the Stuttgart energy consistent effective core potential (ECP).35 Vibrational analyses are performed to ensure all geometries correspond to true minima. These structures are used as starting geometries for 2c-DFT local optimizations (def2-TZVP-2c/Stuttgart SO-ECP).35–37 The results are shown in Fig. 1b and 2b (see the ESI† for the corresponding xyz coordinates).
Static isotropic polarizabilities αel are calculated for the 2c minimum structures at the scalar relativistic level of theory only. In order to estimate the gaps of the lead clusters 2c-TDDFT calculations have been carried out.38 Gaps from TDDFT calculations are expected to yield more accurate results than just taking HOMO–LUMO gaps from DFT calculations.16
The deflection of an ensemble of rigid rotors in an electric field can be simulated by a convolution of the undeflected profile with the dipole distribution function. The latter is readily obtained by a molecular dynamics simulation, where moments of inertia, dipole moments and polarizabilities from DFT calculations enter parametrically.19 The only free parameter in this simulation is the rotational temperature of the clusters. So, simulations are carried out for each isomer from Trot = 5–50 K. However, in accordance to previous studies Trot = 30 K is appropriate (see Fig. S1†).
3. Results and discussion
3.1. Structures and dielectric properties
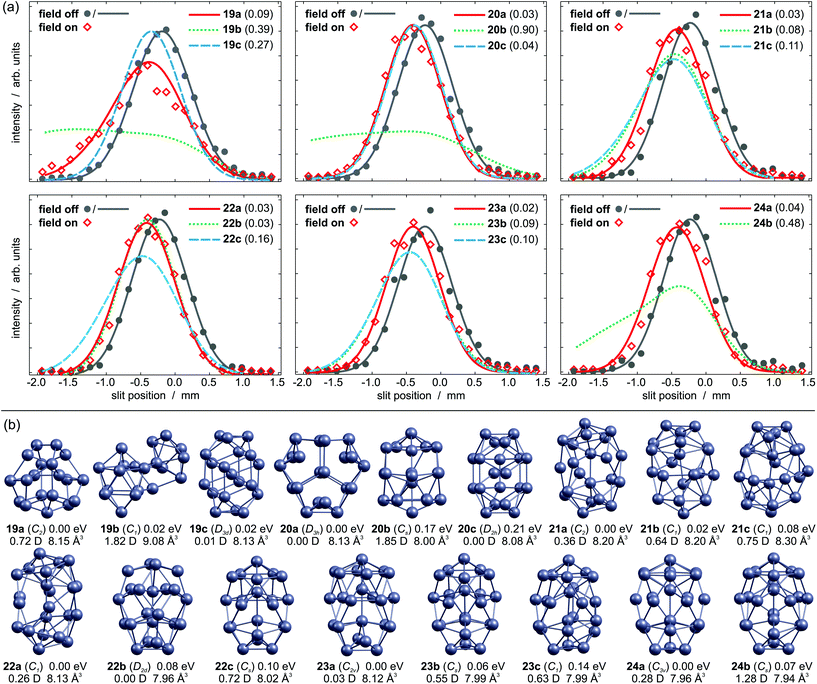
The experimental beam profiles of Pb19 are shown in Fig. 1a. A broadening is observed as the field is applied. This is characteristic for a cluster with permanent dipole moment. Fig. 1b displays the three lowest lying isomers identified by the GA run. The GM 19a is a C2 symmetric structure similar to the GM reported by Ho and coworkers.13 It has a moderate dipole moment of 0.72 D and its simulated beam profile well describes the experimental data. Isomer 19b is a peculiar structure consisting of Pb9 and Pb10 subunits only 0.02 eV above the GM; this geometry has a dipole moment of 1.82 D and the corresponding beam profile is significantly broadened. Therefore, it can be ruled out. Almost equal in energy is isomer 19c, an atom-centered prolate D3d structure with a vanishing dipole moment. This isomer does not fit the experimental data and so 19a is expected to be the dominant structure in the molecular beam.The three energetically lowest lying isomers of Pb20 are shown in Fig. 1b. The GM structure 20a is an oblate D3h symmetric cluster with a zero dipole moment. This is in very good agreement with the non-broadened experimental beam profile (Fig. 1a, αexp = 7.4 ± 1.4 Å3). Isomer 20b is 0.17 eV higher in energy and contains a hexagonal antiprism motif. It has a considerable dipole moment of 1.85 D, hence a substantial contribution to the experimental beam profile is excluded. Isomer 20c is a prolate structure with two central atoms and has previously been proposed as the GM.39 Although it nicely matches the experimental beam profile, it seems unlikely to be the dominating structure under our experimental conditions due to its high relative energy.
The beam profile of Pb21 in Fig. 1a is slightly broadened if the deflecting field is on, pointing towards a structure with small dipole moment (αexp = 7.2 ± 1.3 Å3). The C2 symmetric GM 21a is a prolate structure with two inner atoms and can be considered as two isolated pentagonal bipyramids (PBP) with seven glue atoms. It has a small dipole moment of 0.36 D and its simulated beam profile explains the experimental one very well. The higher lying isomers 21b and 21c can be both ruled out due to the increased beam broadening in the simulation. Hence, 21a appears to be the only relevant isomer in the experiment.
The GM of Pb22 is a C1 symmetric structure 22a, which is also shown in Fig. 1b. It resembles the motif of 21a with two individual PBP plus eight glue atoms and the simulated beam profile is in very good agreement with the experiment. However, isomer 22b has no permanent dipole moment due to its symmetry (D2d). No remarkable broadening is observed for the experimental beam profile (αexp = 6.9 ± 0.9 Å3), which is very well reproduced by the simulated beam profile. Both, 22a and 22b, sufficiently explain the experimental data and cannot be distinguished in our experiment, though the small αexp probably hints towards 22b. The higher lying isomer 22c can be ruled out based on its large dipole moment.
The experimental beam profile of Pb23 is shifted but not broadened, so a structure with a small or zero dipole moment is expected (αexp = 6.4 ± 0.9 Å3). This applies for the GM 23a, which contains a hexagonal antiprism motif. Its beam profile is in excellent agreement with the experiment. Isomer 23b has a very similar structure to 22c, but its dipole moment is too large to explain the experiment. Isomer 23c is a distorted version of 23b and cannot describe the experiment either.
No pronounced beam broadening is observed for Pb24 (αexp = 6.7 ± 1.1 Å3). Only two local minimum structures are found below 0.2 eV. The putative GM 24a is a prolate C3v symmetric structure, which is very similar to 23a with respect to the hexagonal antiprism motif. Its small dipole moment of 0.28 D causes a slightly broadened beam profile, which nicely explains the experiment. The structure of isomer 24b follows the pattern of 22c and 23b. Its considerable dipole moment of 1.28 D yields a significantly broadened beam profile in contrast to the experiment.
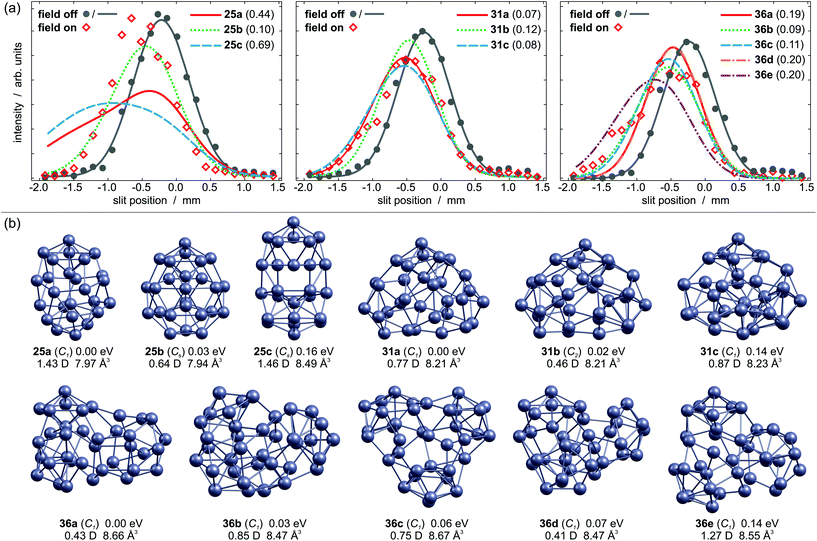
Fig. 2b displays energetically low lying local minimum structures and beam profiles of Pb31. The GM is the C1 symmetric structure 31a containing three PBP subunits. Its simulated beam profile is in reasonable agreement with the experimentally observed profile, which is substantially broadened. Isomer 31b is only 0.02 eV higher in energy. Its geometry is very similar to 31a, but it has a smaller dipole moment. This gives rise to a less broadened beam profile than the one observed experimentally. Isomer 31c has a similar dipole moment compared to 31a, so it is also able to explain the experimental findings. Nevertheless, a significant contribution to the experimental beam profile seems unlikely due to its high relative energy.
The Pb36 cluster shows a distinctive beam broadening if the electric field is on (Fig. 2a). In Fig. 2b the five lowest lying local minimum structures are reported. Their geometries all have C1 symmetry and permanent dipole moments ranging from 0.41 to 1.27 D. The GM 36a (μ0 = 0.43 D) contains three independent PBP, but it can also considered as three Pb9 subunits with nine glue atoms. The Pb9 cluster on the other hand consists of two interpenetrating PBP.21 However, the dipole moment of 36a is too small to explain the experimental beam broadening. Isomer 36b is only 0.03 eV higher in energy than 36a and has a dipole moment of 0.85 D. Its simulated beam profile resembles the experimental data very well. The structure also contains three Pb9 subunits. This applies also for isomer 36c, though the different relative arrangement gives rise to a dipole moment of 0.75 D, which still yields a reasonable agreement with the experiment. Isomer 36d fits the experimental data in similar quality as 36a and can therefore be ruled out. The simulated beam profile of 36e is too broad to explain the experiment. Isomer 36b appears to be predominant in the molecular beam though 36c cannot be ruled out.
The beam profiles of PbN (N = 19–24, 31, 36) are well described by rigid rotor simulations employing the structures and properties of low lying local minima. As shown in Fig. 2a this procedure does not hold for Pb25. Its beam profile is strongly shifted indicating an elevated polarizability, but is not broadened at all. The three energetically lowest lying isomers exhibit dipole moments between 0.64–1.46 D. Although the permanent dipole moment of a rigid rotor contributes to the total shift, a considerable beam broadening would be expected as well.25 Hence, none of them fits the measured beam profile within the rigid rotor simulation. The observed beam shift comes up to an effective polarizability of 10.90 ± 1.16 Å3, whereas DFT predicts values of 7.9–8.5 Å3. Since the polarizability of a cluster usually does not depend strongly on the geometry, it seems very unlikely that an isomer without permanent dipole moment and an increased polarizability has been missed out by the global optimization. In fact, more than 20 local minimum structures up to 0.5 eV have been found, but none of them provides a good fit to the experiment.
The dipole moment of a rigid cluster is fixed with respect to its geometry and the projection of the dipole moment on the field axis only depends on the rotational motion. In a thermally excited cluster, vibrational motions can couple to the rotation and induce or alter the dipole moment components. If these processes are not correlated to the rotational motion of the cluster, the beam broadening completely vanishes and only the beam shift is enhanced by a contribution of the permanent dipole moment μ0. The resulting effective polarizability αeff is described in a Langevin–Debye-type model
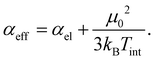 | (2) |
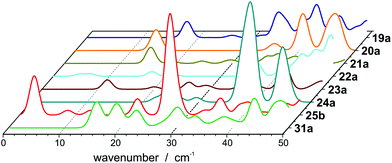
The internal temperature Tint is assumed to be equal to the nozzle temperature (30 K). Taking a dipole moment of μ0 = 1.43 D into account results in an effective polarizability of 14.55 Å3 for isomer 25a. Isomer 25b, which is only 0.03 eV higher in energy, has a dipole moment of 0.64 D, giving rise to an effective polarizability of 10.20 Å3. This value is in good agreement with the experiment, whereas αeff of isomer 25c is too large (15.35 Å3). The Langevin–Debye-type behaviour has been described for the Rh10 cluster at 49 K (ref. 40) and for silicon clusters at room temperature.41 At room temperature multiple vibrational modes are excited and isomerization processes become possible. This is certainly not the case for Pb25 at 30 K so the question persists why no beam broadening is observed for this cluster. It has been shown for organic molecules that the beam broadening can be quenched if certain vibrational modes are excited, which couple strongly to the rotational motion.42Fig. 3 displays harmonic frequency analyses of the relevant cluster species up to 50 cm−1. While all clusters show at least one weak IR active normal mode below 30 cm−1, only 25b has three intense modes in this range. Two are very close in energy at about 26.7 (A′′) and 26.9 cm−1 (A′), respectively. The third mode is very soft (2.6 cm−1) and corresponds to a hindered rotation of the central dimer relative to the cage (A′′). The excitations of these modes suffice to fully quench the beam broadening. Since all other clusters also have vibrational modes below 30 cm−1 we cannot exclude that the beam broadening is partially quenched for them, i.e. the experimental beam profile is less broadened than expected for a rigid cluster.
The results of the MBD experiments reveal that several PbN clusters (N = 19, 25, 31, 36) have significant dipole moments. Since an excellent electronic shielding, i.e. a vanishing dipole moment is expected for a metallic cluster, this strongly suggests that they are not metallic. The clusters PbN (N = 20–24) do not show a significant beam broadening or increased beam shift, what actually also applies for N = 26–30, 32–34, which have been omitted in this study due to the excessive computational cost of the global optimization. Since a vanishing permanent dipole moment is not a sufficient condition of metallicity their character cannot be assessed based on the MBD experiments only. However, the elucidated geometries give further insight. Li et al. proposed that the electron delocalization is obstructed by individual, strong covalently bound PBP Pb7 subunits.39 The occurance of such structural subunits in Pb clusters would further support that they are not metallic. Apart from 19a and 20a all experimentally identified isomers contain several PBP. In particular, PbN (N = 21–25) can be considered as two PBP with a growing number of glue atoms. Isomer 31a contains three PBP, though four are found in 31c. Despite the fact that the PBP is the dominant structural subunit, their number is not necessarily maximised in the GM. The situation is consistent for Pb36, though Pb9 subunits appear, which are basically two interpenetrating PBP. We note that the occurrence of subunits with localised electron density is of course related to the appearence of permanent dipole moments, i.e. due to the relative arrangement of the subunits in a certain cluster. However, for some cluster species the permanent dipole moment (almost) vanishes for symmetry reasons although they contain PBP subunits.
3.2. TDDFT gaps
The experimentally observed dipole moments and the assigned structures show that lead clusters up to 36 atoms do not fulfill typical criteria of metallicity. Further evidence for their metallic character comes from the size of the energy gap Egap compared to the Kubo gap EKubo, which is larger than Egap in a metallic particle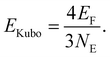 | (3) |
Gaps are calculated by 2c-TDDFT for PbN using experimentally proven geometries from section 1 and the literature.21Fig. 4 displays the results together with the Kubo gaps, taking four valence electrons per lead atom (NE) into account (EF(Pb) = 9.37 eV). The gaps vary with the cluster size and decrease from 0.75 eV for Pb7 to 0.26 eV for Pb36 with relative maxima for Pb9, Pb13, Pb19. In the jellium model maximum gaps are expected for PbN (N = 9, 10, 17, 20, …) due to shell closures. This is certainly not reflected by the data in Fig. 4. The gaps do not drop below the Kubo gap for any cluster size, which decreases from 0.45 for Pb7 to 0.09 eV for Pb36. The Pb23 has the smallest gap of all clusters considered (0.20 eV), which is only slightly larger than the corresponding Kubo gap (0.14 eV). Accordingly, the sizes of the gaps further corroborate the experimental results and show that also clusters can be considered as non-metallic, which do not have a significant permanent dipole moment. The correlation between the gaps and the dipole moments does not follow a clear trend. For the icosahedron Pb13 a zero dipole moment and the largest gap (0.92 eV) is observed, while other cluster like Pb12 (μ0 = 0.59 D) and Pb19 have large gaps and significant dipole moments. Nevertheless, we mention, that the trend of gaps and dipole moments is qualitatively similar for PbN (N = 19–25), i.e. clusters with small dipole moments have also small gaps (e.g. Pb23) and vice versa. This is interesting insofar as dipole moments and gaps vanish in the bulk limit.
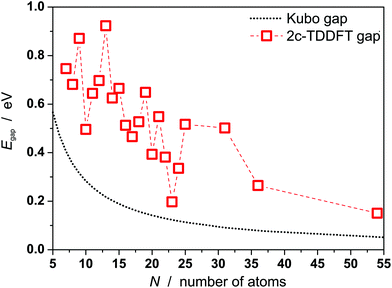 | ||
| Fig. 4 Kubo gaps for PbN (N = 7–25, 31, 36, 54) and gaps from 2c-TDDFT calculations. Apart from Pb54 the experimentally found geometries are used, which correspond to the GM or the GM + 1 for Pb16, Pb18 and Pb25, respectively. Structures of Pb7–Pb18 are taken from the literature.21 For Pb54 a cuboctahedral geometry is assumed.37 | ||
In order to estimate the evolution of the gaps for even larger sizes, the gap of Pb54 has been calculated. A global optimization as outlined in section 2 was not feasible here, but Pb54 is assumed to be an cuboctahedron.37 The dielectric properties of the local optimized geometry are μ0 = 0.00 D and αel = 8.42 Å3 (αexp = 7.6 ± 0.7 Å3, see Fig. S2†). It has a gap of 0.15 eV, what demonstrates that 2c-TDDFT gaps further decrease with increasing cluster size. Further, it is already very close to the Kubo gap (0.06 eV) indicating the onset of metallicity in this size regime.
4. Conclusions and outlook
We reported beam profiles from electric molecular beam deflection at 30 K for several medium sized lead clusters. Cluster structures are assigned to the observed beam profiles by the comparison of experimental with simulated beam profiles. For Pb19 and Pb20 we find an asymmetric and an oblate structure, respectively as GM. The trend towards atom centered structures starting with Pb13 is interrupted for Pb19 and Pb20. Prolate structures with two central atoms are identified for PbN (N = 21–25). The Pb25 cluster is a special case here, since it is not deflected like a rigid rotor, i.e. the beam broadening is completely quenched. This Langevin–Debye-type deflection suggests that Pb25 is fluxional already at 30 K. The vibrational analysis shows that Pb25 has a prominent IR active mode below 30 cm−1. Its excitation is obviously sufficient to suppress any beam broadening. This makes Pb25 an interesting starting point for further investigations of the deflection behaviour and the dynamics of flexible clusters.The metallicity of lead clusters has been evaluated in terms of their electron screening, their gaps and their structures. The observed dipole moments indicate an electronic screening which is typical for non-metallic systems. Gaps from TDDFT calculations show that they are considerably larger than the Kubo gaps. We have identified Pb7 PBP as predominating structural subunits, which have earlier been related to strong electron localization.39 With respect to their experimentally observed electronic screening behaviour and their gaps in comparison to the Kubo gap we conclude that lead clusters are not metallic up to at least Pb36. The non-metallicity of lead clusters is structurally not manifested in prolate geometries as in tin clusters but in the cumulation of Pb7 or Pb9 subunits. As quantum chemistry suggests the gaps further decrease for larger cluster sizes (Pb54). Finally we notice that spin–orbit coupling leads to a separation of 0.97 eV between the state with total angular momentum quantum number J = 0 (p21/2) and J = 1 (p11/2p13/2) in the 3P ground state of atomic lead.43 This renders Pb effectively as a closed-shell atom undergoing rather weak bonding in clusters and perhaps explains their increased fluxionality. This spin–orbit gap could substantially delay the onset of metallicity in lead clusters.
Acknowledgements
We acknowledge financial support by the DFG (grant SCHA 885/7-3 and SCHA 885/10-2). D. A. G. is grateful for a scholarship of the Cusanuswerk. The calculations reported here are performed on the following HPC facilities: The University of Birmingham BlueBEAR facility; the MidPlus Regional Centre of Excellence for Computational Science, Engineering and Mathematics, funded under EPSRC grant EP/K000128/1; and via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202). This work made use of the facilities of ARCHER, the UK's national high-performance computing service, which is funded by the Office of Science and Technology through EPSRC's High End Computing Programme; and Simurg, the High-Performance Supercomputer of Massey University.References
- B. von Issendorff and O. Cheshnovsky, Annu. Rev. Phys. Chem., 2005, 56, 549–580 CrossRef CAS PubMed.
- R. Kubo, J. Phys. Soc. Jpn., 1962, 17, 975–986 CrossRef CAS.
- A. Aguado, A. Vega, A. Lebon and B. von Issendorff, Angew. Chem., Int. Ed., 2015, 54, 2111–2115 CrossRef CAS PubMed.
- R. Busani, M. Folkers and O. Cheshnovsky, Phys. Rev. Lett., 1998, 81, 3836–3839 CrossRef CAS.
- L.-F. Cui, L.-M. Wang and L.-S. Wang, J. Chem. Phys., 2007, 126, 064505 CrossRef PubMed.
- A. A. Shvartsburg and M. F. Jarrold, Phys. Rev. A, 1999, 60, 1235–1239 CrossRef CAS.
- A. Hermann, J. Furthmüller, H. W. Gäggeler and P. Schwerdtfeger, Phys. Rev. B: Condens. Matter, 2010, 82, 155116 CrossRef.
- G. Ganteför, M. Gausa, K.-H. Meiwes-Broer and H. O. Lutz, Z. Phys. D: At., Mol. Clusters, 1989, 12, 405–409 CrossRef.
- C. Lüder and K.-H. Meiwes-Broer, Chem. Phys. Lett., 1998, 294, 391–396 CrossRef.
- V. Senz, T. Fischer, P. Oelßner, J. Tiggesbäumker, J. Stanzel, C. Bostedt, H. Thomas, M. Schöffler, L. Foucar, M. Martins, J. Neville, M. Neeb, T. Möller, W. Wurth, E. Rühl, R. Dörner, H. Schmidt-Böcking, W. Eberhardt, G. Ganteför, R. Treusch, P. Radcliffe and K.-H. Meiwes-Broer, Phys. Rev. Lett., 2009, 102, 138303 CrossRef CAS PubMed.
- J. Heinzelmann, P. Kruppa, S. Proch, Y. D. Kim and G. Ganteför, Chem. Phys. Lett., 2014, 603, 1–6 CrossRef CAS.
- J. P. K. Doye and S. C. Hendy, Eur. Phys. J. D, 2003, 22, 99–107 CrossRef CAS.
- X.-P. Li, W.-C. Lu, Q.-J. Zang, G.-J. Chen, C. Z. Wang and K. M. Ho, J. Phys. Chem. A, 2009, 113, 6217–6221 CrossRef CAS PubMed.
- X.-P. Li, W.-C. Lu, C. Z. Wang and K. M. Ho, J. Phys.: Condens. Matter, 2010, 22, 465501 CrossRef PubMed.
- B. Wang, J. Zhao, X. Chen, D. Shi and G. Wang, Phys. Rev. A, 2005, 71, 033201 CrossRef.
- G. Zhang and C. B. Musgrave, J. Phys. Chem. A, 2007, 111, 1554–1561 CrossRef CAS PubMed.
- J. Bowlan, A. Liang and W. A. de Heer, Phys. Rev. Lett., 2011, 106, 043401 CrossRef CAS PubMed.
- S. Schäfer, B. Assadollahzadeh, M. Mehring, P. Schwerdtfeger and R. Schäfer, J. Phys. Chem. A, 2008, 112, 12312–12319 CrossRef PubMed.
- S. Heiles, S. Schäfer and R. Schäfer, J. Chem. Phys., 2011, 135, 034303 CrossRef CAS PubMed.
- D. A. Götz, S. Heiles, R. L. Johnston and R. Schäfer, J. Chem. Phys., 2012, 136, 186101 CrossRef PubMed.
- D. A. Götz, A. Shayeghi, R. L. Johnston, P. Schwerdtfeger and R. Schäfer, J. Chem. Phys., 2014, 140, 164313 CrossRef PubMed.
- S. Schäfer, S. Heiles, J. A. Becker and R. Schäfer, J. Chem. Phys., 2008, 129, 044304 CrossRef PubMed.
- S. Schäfer, M. Mehring, R. Schäfer and P. Schwerdtfeger, Phys. Rev. A, 2007, 76, 052515 CrossRef.
- T. Bachels and R. Schäfer, Rev. Sci. Instrum., 1998, 69, 3794–3797 CrossRef CAS.
- M. Schnell, C. Herwig and J. A. Becker, Z. Phys. Chem., 2003, 217, 1003 CrossRef CAS.
- A. Shayeghi, D. Götz, J. B. A. Davis, R. Schäfer and R. L. Johnston, Phys. Chem. Chem. Phys., 2015, 17, 2104–2112 RSC.
- P. Giannozzi, S. Baroni, M. C. N. Bonini, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter, 1985, 32, 8412–8415 CrossRef CAS.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter, 1990, 41, 1227–1230 CrossRef.
- P. Schwerdtfeger, ChemPhysChem, 2011, 12, 3143–3155 CrossRef CAS PubMed.
- TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569 CrossRef CAS.
- M. K. Armbruster, W. Klopper and F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 4862–4865 RSC.
- M. K. Armbruster, F. Weigend, C. van Wuellen and W. Klopper, Phys. Chem. Chem. Phys., 2008, 10, 1748–1756 RSC.
- M. Kühn and F. Weigend, J. Chem. Theory Comput., 2013, 9, 5341–5348 CrossRef PubMed.
- H. Li, Y. Ji, F. Wang, S. F. Li, Q. Sun and Y. Jia, Phys. Rev. B: Condens. Matter, 2011, 83, 075429 CrossRef.
- M. K. Beyer and M. B. Knickelbein, J. Chem. Phys., 2007, 126, 104301 CrossRef PubMed.
- D. A. Götz, S. Heiles and R. Schäfer, Eur. Phys. J. D, 2012, 66, 293 CrossRef.
- R. Antoine, M. Abd El Rahim, M. Broyer, D. Rayane and P. Dugourd, J. Phys. Chem. A, 2006, 110, 10006–10011 CrossRef CAS PubMed.
- C. E. Moore, Atomic Energy Levels, Natl. Bur. Stand. Ref. Data Ser., Nat. Bur. Stand. (US) Circ. No. NSRDS-NBS 35 technical report, 1971.
Footnote |
| † Electronic supplementary information (ESI) available: Beam profile simulations for rotational temperatures Trot = 5–50 K, the beam profile of Pb54 and cluster coordinates in Å. See DOI: 10.1039/C6NR02080A |
| This journal is © The Royal Society of Chemistry 2016 |