Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Studying the effect of Zn-substitution on the magnetic and hyperthermic properties of cobalt ferrite nanoparticles†
V.
Mameli
ab,
A.
Musinu
ab,
A.
Ardu
abc,
G.
Ennas
ab,
D.
Peddis
d,
D.
Niznansky
e,
C.
Sangregorio
bf,
C.
Innocenti
bg,
Nguyen T. K.
Thanh
*hi and
C.
Cannas
*abc
aDepartment of Chemical and Geological Sciences, University of Cagliari, Monserrato, CA, Italy. E-mail: ccannas@unica.it
bConsorzio Interuniversitario Nazionale per la Scienza e Tecnologia dei Materiali (INSTM), Italy
cConsorzio AUSI, CREATE, Palazzo Bellavista Monteponi, Iglesias, CI, Italy
dIstituto di Struttura della Materia, Consiglio Nazionale delle Ricerche (ISM-CNR), Italy
eDepartment of Inorganic Chemistry, Charles University of Prague, Czech Republic
fIstituto di Chimica dei Composti OrganoMetallici, Consiglio Nazionale delle Ricerche (ICCOM-CNR), Sesto Fiorentino, FI, Italy
gLAboratorio di Magnetismo Molecolare (LA.M.M), Department of Chemistry, University of Florence, Sesto Fiorentino, FI, Italy
hBiophysics Group, Department of Physics and Astronomy, University College London, Gower Street, London, WC1E 6BT, UK
iUCL Healthcare Biomagnetic and Nanomaterials Laboratory, 21 Albemarle Street, London, W1S 4BS, UK. E-mail: ntk.thanh@ucl.ac.uk
First published on 8th April 2016
Abstract
The possibility to finely control nanostructured cubic ferrites (MIIFe2O4) paves the way to design materials with the desired magnetic properties for specific applications. However, the strict and complex interrelation among the chemical composition, size, polydispersity, shape and surface coating renders their correlation with the magnetic properties not trivial to predict. In this context, this work aims to discuss the magnetic properties and the heating abilities of Zn-substituted cobalt ferrite nanoparticles with different zinc contents (ZnxCo1−xFe2O4 with 0 < x < 0.6), specifically prepared with similar particle sizes (∼7 nm) and size distributions having the crystallite size (∼6 nm) and capping agent amount of 15%. All samples have high saturation magnetisation (Ms) values at 5 K (>100 emu g−1). The increase in the zinc content up to x = 0.46 in the structure has resulted in an increase of the saturation magnetisation (Ms) at 5 K. High Ms values have also been revealed at room temperature (∼90 emu g−1) for both CoFe2O4 and Zn0.30Co0.70Fe2O4 samples and their heating ability has been tested. Despite a similar saturation magnetisation, the specific absorption rate value for the cobalt ferrite is three times higher than the Zn-substituted one. DC magnetometry results were not sufficient to justify these data, the experimental conditions of SAR and static measurements being quite different. The synergic combination of DC with AC magnetometry and 57Fe Mössbauer spectroscopy represents a powerful tool to get new insights into the design of suitable heat mediators for magnetic fluid hyperthermia.
Introduction
Nanostructured metal oxides of the formula MIIFe2O4 (MII = Fe2+, Co2+, Mn2+, Ni2+, etc.), commonly referred to as cubic ferrites, are one of the most important materials for their ferrimagnetic properties closely related to their spinel structure. In the spinel structure, oxygen ions are close-packed in a cubic arrangement (ccp) in which metallic cations occupy one out of the eight tetrahedral interstices (indicated as round brackets) and half of the octahedral ones (squared brackets). Tetrahedral sites are filled by divalent cations in a direct or normal spinel (MII)[MIII]2O4, whereas trivalent cations replaced them in an inverse spinel (MIII)[MII;MIII]2O4.1Actually, real systems crystallise in a partially inverse structure with the following general formula:
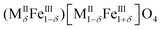 | (1) |
Spinel ferrites, being one of the most versatile systems, have found applications in a wide variety of fields that include data storage, catalysis, energy, environment, and in particular, biomedicine. Indeed, the use of magnetic nanoparticles for biomedical purposes has been proposed to a large extent in recent years.12,13 Early diagnosis and targeted therapies are key challenges in the field of biomedicine. The development of new technologies designed to answer to these issues has been a strong driving force in this research field. Different biomedical applications of magnetic nanoparticles have been developed: magnetic separation, magnetic resonance imaging (MRI),14 drug delivery15 and magnetic fluid hyperthermia (MFH).13,16 In particular, MFH is based on the ability of magnetic nanoparticles, when an alternate external magnetic field is applied, to convert the electromagnetic energy into heat. Different heat release mechanisms are involved depending on the magnetic behaviour: superparamagnetic or ferromagnetic. Néel and Brownian relaxation mechanisms are responsible for the heat delivery of superparamagnetic nanoparticles, both of them involving the reversal of the magnetisation vector inside the nanoparticle (Néel) or through the physical rotation of the particles themselves (Brownian). Therefore, the efficiency of magnetic nanoparticles as heat mediators is strictly related to their magnetic properties (saturation magnetisation and reversal energy barrier), besides the hydrodynamic ones depending on the environmental medium (viscosity, temperature). The most studied materials for biomedical applications are superparamagnetic iron oxides (SPIOs), i.e. maghemite (γ-Fe2O3) and magnetite (Fe3O4), nanoparticles, due to their biocompatibility (approved by U.S. Food and Drug Administration) and their low-cost. Nevertheless, much of the research on this topic is still devoted to the optimisation of the magnetic properties aimed to increase the heating ability and to reduce the nanoparticle dose to be injected into the human body. In particular, much effort points towards an increase of the saturation magnetisation17 investigating as alternative metal-based systems,18–21 and substituted-ferrite nanoparticles.22,23 Other strategies based on the coupling of ferrimagnetic spinels by building appropriate core–shell heterostructures have been proposed.24
Among cubic ferrites, CoFe2O4 is the material with the highest magnetocrystalline anisotropy and reasonably high magnetisation. Moreover, it shows excellent chemical and thermal stabilities, good mechanical properties1 and is also easily synthesised with different approaches.25–29 Despite its potential toxicity, cobalt-containing materials have been proposed as promising heat mediators due to their high anisotropy.23,30–37 The partial substitution of Co2+ with less toxic divalent ions such as Zn2+ (ZnxCo1−xFe2O4) has been proposed in order to increase the saturation magnetisation and to lower the toxicity.38,39 Moreover, the presence of zinc should induce the decrease of the Curie temperature opening the possibility to build auto-tuning systems.5,33,39 The magnetic properties of ZnxCo1−xFe2O4 (0 < x < 1) nanoparticles have been investigated over the last ten years.5,33,40–50 However, because of the strict interrelation among the different properties of the materials (size and size distribution, shape, chemical composition, capping agent), adjusting the magnetic properties exclusively on the basis of one parameter is quite rare. In particular, the systematic study of the effect of the composition on ferrite nanoparticles, leaving other parameters unchanged, is still lacking, to the best of our knowledge. Furthermore, only a few studies are devoted to the study of their heating ability.38,39
In this framework, an ad hoc set of Zn-substituted cobalt ferrite nanoparticles with different zinc amounts but with the same particle size, particle size distribution, crystallite size and capping agent amount has been selected and studied in order to shed light on the complex magnetic properties’ dependence on the properties of the material. The similarities among the samples are ideal to focus the investigation exclusively on the effect of the chemical composition on the magnetic structure (i.e., cationic distribution and spin canting), while the crystallite and particle size, polydispersity, and type and amount of capping agents remain constant. Room temperature properties have been studied and correlated to SAR values by means of a multi-technique approach that combines DC/AC magnetometry and 57Fe Mössbauer spectroscopy, characterised by different experimental time windows (10–100 s DC magnetometry; 0.001–1 s AC susceptibility; 10−9–10−7 s Mössbauer spectroscopy).51 To the best of our knowledge, a systematic and fundamental study of the effect on the magnetic properties and heat release based on the composition (ZnxCo1−xFe2O4) and cation distribution while leaving morphological and structural parameters almost unchanged is still lacking.
Experimental
Chemicals
Fe(III) acetylacetonate (97%), 1,2-hexadecanediol (90%), oleic acid (90%), dibenzylether (98%), and absolute ethanol have been purchased from Sigma Aldrich. Co(II) acetylacetonate (99%), Zn(II) acetylacetonate (99%), and oleylamine (80–90%) have been purchased from Acros Organics.Synthesis
The samples were synthesised by a surfactant-assisted thermal decomposition method previously described by Sun et al.52 Iron(III) acetylacetonate, cobalt(II) acetylacetonate, zinc(II) acetylacetonate, 1,2-hexadecanediol (10 mmol), oleic acid (6 mmol), oleylamine (6 mmol), and dibenzylether (20 mL) were added in a 250 mL three-neck round bottom flask. The system was heated to 200 °C for 2 h and to 280 °C for 1 h, under magnetic stirring and a blanket of nitrogen. The system was left to cool to room temperature. Then, 40 mL of absolute ethanol were added to precipitate the nanoparticles from the supernatant overnight. The as-obtained nanoparticles were separated from the supernatant by centrifugation at 4500 rpm (for 15 min), washed with ethanol and collected by centrifugation at 4500 rpm (for 15 min). The washing procedure was repeated several times and, finally, the nanoparticles were dispersed in hexane. Specific attention was paid to the control of the temperature during the synthesis in order to make it highly repeatable. To ensure it, an autotuning proportional–integral–derivative (PID) controller was used.Characterization
Four samples of ZnxCo1−xFe2O4 nanoparticles were synthesised as described above. The samples’ chemical composition was studied by means of inductively coupled plasma-atomic emission spectrometry (ICP-AES). The analyses have been repeated two times on different portions of the samples. The samples have been labelled on the basis of the actual composition as CoFe_Znx for a Zn content (x) equal to 0, 0.30, 0.46, and 0.53, respectively.X-Ray diffraction (XRD) patterns were collected by using two different instrument setups. The first one is a θ–θ Bragg–Brentano focalizing geometry Seifert X 3000 diffraction system equipped with a Cu Kα source (λ = 1.54056 Å), a graphite monochromator on the diffracted beam and a scintillation counter. Crystalline phases were identified by means of Analyze software. The second one is a PANalytical X'Pert PRO powder X-ray diffraction system equipped with a Co Kα source (λ = 1.78901 Å) and an X'Celerator detector. Phase identification was carried out by means of the X'Pert accompanying software program PANalytical High Score Plus. The mean crystallite size, <DXRD>, was obtained by Scherrer's equation:53
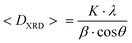 | (2) |
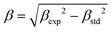 , where βexp is the experimental width of the peak and βstd is the instrumental one estimated by means of the pattern of a standard obtained under the same experimental conditions.
, where βexp is the experimental width of the peak and βstd is the instrumental one estimated by means of the pattern of a standard obtained under the same experimental conditions.
<DXRD> was calculated as a mean value by fitting, through Origin software, the most intense X-ray peaks (220), (311), (400), (422), (511) and (440) with the PseudoVoigt function, by using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Gaussian
1 Gaussian![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lorentzian ratio (mu = 0.5):
Lorentzian ratio (mu = 0.5):
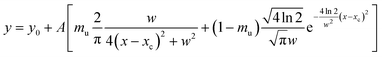 | (3) |
Refinement of the structural parameters was performed by the Rietveld method using the MAUD software54 adopting recommended fitting procedures.55 Structural models of the identified phases were obtained by an inorganic crystal structure database (ICSD, Karlsruhe, Germany).
The samples were analysed by transmission electron microscopy (TEM). The hexane colloidal dispersion was sonicated in an ultrasonic bath. Then, an aliquot was sampled and diluted with hexane. The diluted dispersion was then dropped on a carbon-coated copper grid and left to dry for TEM observations. The nanoparticles were observed in electron micrographs obtained with two different instruments. The first one is a TEM (JEOL JEM-1200 EX II) operating at 120 kV. The second microscope is a JEM 2010 UHR equipped with a Gatan imaging filter (GIF) with a 15 eV window and a 794 slow scan CCD camera. The mean particle size, <DTEM>, was obtained by measuring the average diameter of 350 particles using images collected in different parts of the grid. The polydispersity index, σTEM (%), has been evaluated as the ratio between the standard deviation and the average particle size. The images were analysed by PEBBLES software56 in a semi-automatic mode combined with a manual mode (in order to add, to the population, those particles not directly recognised by the software) and by adopting an ellipsoidal shape. The nanoparticle size distributions were fitted through Origin software using the log-normal function:
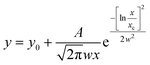 | (4) |
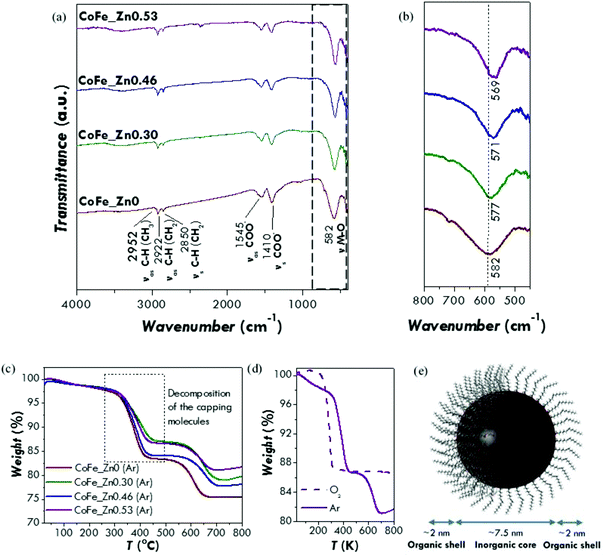
Fourier transform-infrared spectroscopy (FT-IR) and thermogravimetric (TGA) analyses were carried out in order to study the capping agent and to estimate the organic phase content. FT-IR spectra were recorded in the region from 400 to 4000 cm−1 by using a Bruker Equinox 55 spectrophotometer on KBr-dispersed sample pellets. TGA curves were obtained on powders by using a Mettler-Toledo TGA/SDTA 851 in the 25–1000 °C range, with a heating rate of 10 °C min−1 under 50 mL min−1 argon flow.
Magnetic properties were studied by means of a Quantum Design MPMS SQUID VSM (Hmax = 70 kOe). Different kinds of magnetic measurements were carried out. Magnetisation vs. magnetic field curves were measured at 300 K and 5 K between −70 kOe and +70 kOe. The saturation magnetisation (Ms) was estimated by using the equation
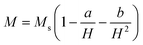 | (5) |
Field dependence of the remnant magnetisation was investigated through the DC demagnetisation (DCD) remanence protocol. The sample was saturated at −50 kOe and the DCD curve obtained by measuring the remanence MDCD(H) after applying reverse fields up to 50 kOe.
Calorimetric measurements of SAR were performed by means of a non-adiabatic experimental set-up built at the LAboratorio di Magnetismo Molecolare (LA.M.M) by means of a power supply CELESs MP6/400 (FIVES CELES), a water-cooled heating station connected to the power supply and an induction coil. Heating curves were recorded under a magnetic field of 17 kA m−1 and 183 kHz for 300 s on water colloidal dispersions of the magnetic nanoparticles. Indeed, the hydrophobic nanoparticles have been converted to hydrophilic ones by the intercalation process with cetyltrimethylammonium bromide (CTAB, (C16H33)N(CH3)3Br). The concentration of the colloidal dispersion was 3.5–4.0 mg ml−1 for all the samples. The temperature of the sample was monitored by an optical fiber probe (OPTOCON-FOTEMP) dipped into the solution. Samples were surrounded by polystyrene and hosted in a glass Dewar, equipped with an ethylene glycol thermostat, to ensure proper thermal isolation. The SAR values have been estimated by a linear curve fitting in the first 20 s of the heating curves (initial slope method).
57Fe Mössbauer spectra were measured in the transmission mode with 57Co diffuse into a Rh matrix as the source moving with constant acceleration. The spectrometer (Wissel) was calibrated by means of a standard α-Fe foil and the isomer shift was expressed with respect to this standard at 293 K. The samples were measured at 293 K and at 4 K under zero magnetic field. In order to get information on the distribution of the iron ions between the tetrahedral and octahedral sites of the spinel structure, field-spectra have been recorded at 4 K under 6 T in the perpendicular arrangement of the magnetic field vector with respect to the γ-beam. The fitting of the spectra was performed with the help of the NORMOS program using Lorentzian profiles.
AC susceptibility measurements were performed on the water colloidal dispersion of the nanoparticles by a Quantum Design MPMS SQUID dedicated insert, at 5 log-spaced exciting frequencies (1–1000 Hz) and in the temperature range 10–300 K, in the absence of a static magnetic field.
Dynamic light scattering measurements
Dynamic light scattering (DLS) measurements were performed on water colloidal dispersions at the same concentration used for the calorimetric measurements by means of a Malvern Instrument Zeta Zetasizer Ver 7.03 equipped with a He–Ne laser (λ = 633 nm, max 5 mW) and operated at a scattering angle of 173°. All measurements were performed using a refraction index value of 2.42 for the material and of 1.330 for the dispersant. In all analyses, 1 mL of particle suspensions was placed in a 12 mm × 12 mm polystyrene cuvette.Results and discussion
Composition, microstructure and morphology
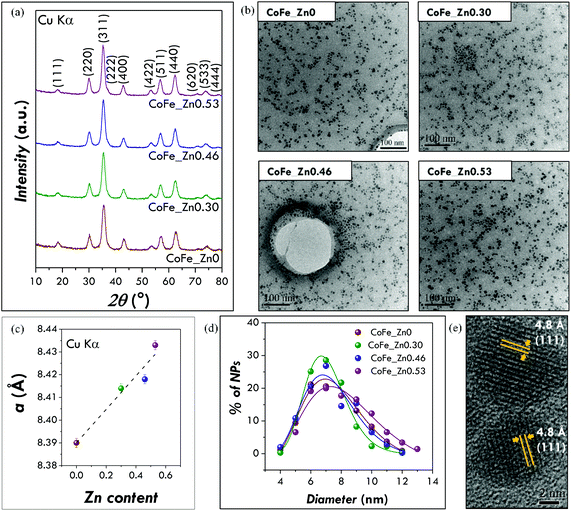
XRD patterns of four samples of ZnxCo1−xFe2O4, with the actual zinc content (x) obtained by ICP-AES equal to 0, 0.30, 0.46, and 0.53 suggest the presence of a unique spinel cubic phase (CoFe2O4, PDF card # 221086) (see Fig. 1a and ICP-AES analysis section in the ESI† for the experimental details). All the samples have a mean crystallite size of 6.2 ± 0.4 nm obtained with the X-ray copper source (Fig. 1a and Table 1). These results have been confirmed by the use of a cobalt source-equipped X-ray diffractometer (6.1 ± 0.4 nm) (Table 1 and Fig. S1†). The refinement of the structural parameters by the Rietveld method indicates that the lattice parameter linearly increases with increasing Zn content (Fig. 1c) in agreement with the Vegard rule58 suggesting the insertion of the zinc in the spinel structure. Indeed, the lattice parameters of mixed ferrites are often a linear interpolation of the lattice constants of the extreme phases, i.e. CoFe2O4 (8.38 Å) and ZnFe2O4 (8.44 Å). In particular, we can better explain this trend by considering the ionic radii of the metal ions and the general preferences of the cations for a specific coordination. Co2+ and Zn2+ have the same ionic radius (0.82 Å2, 0.74 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59) whereas Fe3+ is smaller (0.67 Å2, 0.65 Å
59) whereas Fe3+ is smaller (0.67 Å2, 0.65 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59). Taking into account that tetrahedral sites are smaller than the octahedral ones, a higher occupancy of the tetrahedral sites by bigger metal cations will lead to an expansion of the structure and, consequently, to an increase of the lattice parameter. This may suggest the substitution of the ferric ions by zinc ones in tetrahedral sites for the zinc-substituted samples, which is in agreement with the preference of zinc ions for the tetrahedral coordination.2 A raw estimation of the distribution of the metallic cations in the tetrahedral and octahedral sites has been attempted (see Table S1†). The data suggest a tendency to partially inverse structures. Moreover, the intensity ratios I(220)/I(400), I(220)/I(440) and I(422)/I(400) (Fig. S2†) are considered to be sensitive to the cation occupancies.46,60–62 A curve fitting confirms that these ratios linearly increase with increasing zinc content suggesting that the zinc ions occupy preferentially tetrahedral sites.
59). Taking into account that tetrahedral sites are smaller than the octahedral ones, a higher occupancy of the tetrahedral sites by bigger metal cations will lead to an expansion of the structure and, consequently, to an increase of the lattice parameter. This may suggest the substitution of the ferric ions by zinc ones in tetrahedral sites for the zinc-substituted samples, which is in agreement with the preference of zinc ions for the tetrahedral coordination.2 A raw estimation of the distribution of the metallic cations in the tetrahedral and octahedral sites has been attempted (see Table S1†). The data suggest a tendency to partially inverse structures. Moreover, the intensity ratios I(220)/I(400), I(220)/I(440) and I(422)/I(400) (Fig. S2†) are considered to be sensitive to the cation occupancies.46,60–62 A curve fitting confirms that these ratios linearly increase with increasing zinc content suggesting that the zinc ions occupy preferentially tetrahedral sites.
| Sample | Chemical composition | % of organic phase | <DXRD1> (nm) | <DXRD2> (nm) | a (Å) | <DTEM1> (nm) | σ TEM1 (%) | <DTEM2> (nm) | σ TEM2 (%) |
|---|---|---|---|---|---|---|---|---|---|
| Instrument | ICP-AES | TGA | XRD Cu Kα | XRD Co Kα | XRD Cu Kα | JEM 2010 | JEM 200 EX II | ||
| XRD 1: Seifert X 3000 (Cu Kα). XRD 2: PANalytical X'Pert PRO powder (Co Kα). TEM1: JEM 2010 UHR (200 kV). TEM2: JEOL JEM-200 EX II (120 kV). | |||||||||
| CoFe_Zn0 | CoFe2O4 | 17 | 6.1(3) | 6.0(1) | 8.390(2) | 7.5 | 22 | 7.7 | 18 |
| CoFe_Zn0.30 | Zn0.30Co0.70Fe2.00O4 | 13 | 5.9(2) | 5.8(1) | 8.414(2) | 7.1 | 19 | 6.9 | 18 |
| CoFe_Zn0.46 | Zn0.46Co0.54Fe2.02O4 | 16 | 6.0(3) | 6.0(2) | 8.418(2) | 7.3 | 22 | 7.3 | 22 |
| CoFe_Zn0.53 | Zn0.53Co0.47Fe2.02O4 | 13 | 6.7(4) | 6.6(2) | 8.433(2) | 8.0 | 24 | 7.6 | 21 |
| Mean values | 15 ± 2 | 6.2 ± 0.4 | 6.1 ± 0.4 | — | 7.5 ± 0.4 | 7.4 ± 0.4 | |||
TEM images (Fig. 1b) show pseudo-spheroidal log-normal-distributed nanoparticles with a mean diameter of 7.5 ± 0.4 nm and a polydispersity index of 22 ± 2% (Fig. 1d and Table 1). These values have been confirmed, as in the case of the crystallite size, by independent analyses with another instrument in another laboratory (Fig. S3†). A mean diameter of 7.4 ± 0.4 nm and a polydispersity of 20 ± 2% (Table 1) have been obtained. The absence of aggregation suggests that the nanoparticles are well capped by organic molecules, as expected due to their dispersibility in organic solvents. The similar values obtained for crystallite (6 nm) and particle (7.5 nm) sizes indicate that the nanoparticles have high crystallinity. This is also confirmed by HR-TEM images showing continuous atomic lattice fringes across the particle and the absence of evidence for structural defects (Fig. 1e).
FT-IR analysis has been used mainly to verify the presence of organic molecules at the surface of the particles (capping agent) and to identify them. Indeed, the several washing steps used to purify the nanoparticles from the by-products could in principle completely remove the nanoparticle-bound organic molecules. All the spectra show as principal vibrational modes the ones typical for the hydrocarbon chain (asymmetric and symmetric CH stretching of CH2 and CH3 groups) and the carboxylate groups (asymmetric and symmetric COO− stretching) (Fig. 2a and b; for further details on the complete assignments see Fig. S4†) indicating that the nanoparticles are capped by oleate groups.28 FT-IR can be also useful to give some information on the inorganic phase, the Me–O (Me = Co, Fe, Zn) stretching modes of spinel ferrites falling in the fingerprint range. The metal–oxygen stretching mode of the octahedral and tetrahedral sites moves towards lower values with increasing zinc content, from 582 cm−1 for CoFe2O4 to 569 cm−1 for Zn0.53Co0.47Fe2.0O4. Taking into account the values reported in the literature for cobalt (575 cm−1) and zinc (555 cm−1) ferrites,63 this trend can be interpreted in the light of a gradual substitution of cobalt ions by zinc ones within the spinel structure.
TGA curves (Fig. 2c) under an inert atmosphere (50 ml min−1 of Ar) show for all the samples two weight losses occurring between 300 and 400 °C and between 550 and 650 °C. The first one can be associated with the decomposition of the capping molecules whereas the second one could be due to a reduction process of the inorganic core under an argon atmosphere, as suggested by other authors for oleic acid-capped zinc and cobalt ferrite nanoparticles.64,65 In order to confirm this interpretation, a TGA curve has been recorded under an oxidative atmosphere (50 ml min−1 of O2) on the CoFe_Zn0.53 sample (Fig. 2c). In this case, the decomposition of the capping agent shifts towards a lower temperature (between 200 and 300 °C) but produces the same weight loss as the first weight loss of the Ar-measurement. No other weight losses have been observed, as expected for an oxidative atmosphere. Therefore, from the first weight loss in the Ar-TGA curves, the percentage of the capping agent has been calculated. Similar values have been obtained for all the samples with a mean percentage of (15 ± 2)% (Table 1). It is easy to demonstrate that this amount of the capping agent corresponds to a monolayer of oleate molecules surrounding the surface of the nanoparticles (Fig. 2d and S5†). Therefore, the combined FT-IR and TGA data indicate that all the samples are composed by nanoparticles capped by a single layer of oleate molecules. Moreover, the first derivative of the thermogravimetric curve points out that the weight loss is made up by two steps in the case of the zinc-substituted samples (Fig. S5b†). This can be probably related to different interactions between the capping molecules and the inorganic cores that occur exclusively when the zinc is present in the structure. For instance, it can be related to different bond strengths between the oleate group and the different surface metal ions.
The similarities, highlighted by the careful and multi-technique characterisation, on the particle size, particle size distribution, crystallite size and capping agent amount, enable us to discuss the magnetic properties and the heating abilities exclusively as a function of the chemical composition effect caused by different zinc contents.
Magnetic properties and magnetic structure
M vs. H curves have been measured at 5 K (Fig. 3) and the values of the main magnetic quantities have been estimated (Table 2). All the curves show a hysteretic behaviour without any anomalous shape associated with mixtures of hard/soft spinel phases,66 consistently with the presence of a unique spinel cubic phase. | ||
| Fig. 3 Magnetisation versus magnetic field curves at 5 K of the CoFe_Znx (with x = 0, 0.30, 0.46, 0.53) samples. | ||
| Sample | H c (kOe) | H sat (kOe) | M 7T (emu g−1) | M s (emu g−1) | M r/Ms |
|---|---|---|---|---|---|
| CoFe_Zn0 | 12 ± 1 | 36 ± 4 | 104 ± 2 | 109 ± 3 | 0.58 ± 0.03 |
| CoFe_Zn0.30 | 4.6 ± 0.5 | 22 ± 2 | 134 ± 3 | 142 ± 3 | 0.45 ± 0.02 |
| CoFe_Zn0.46 | 3.7 ± 0.4 | 21 ± 4 | 141 ± 3 | 157 ± 3 | 0.42 ± 0.02 |
| CoFe_Zn0.53 | 4.4 ± 0.4 | 17 ± 2 | 120 ± 2 | 140 ± 3 | 0.41 ± 0.02 |
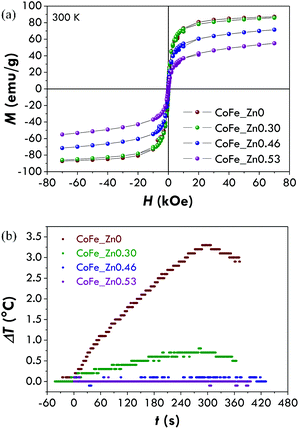
The hysteresis loop for the cobalt ferrite is characterised by a high coercive field, Hc, (12 ± 1 kOe) near the values previously reported for nanoparticles of a similar size.41,67–69 The coercive fields for the Zn-substituted samples were found to be equal to 4.6 ± 0.5 kOe (x = 0.30), 3.7 ± 0.4 kOe (x = 0.46) and 4.4 ± 0.4 kOe (x = 0.53). The reduced values of the coercive field for the Zn-containing samples with respect to the unsubstituted one is probably due to a decrease of the magnetocrystalline anisotropy occurring when Zn2+ replaces Co2+. It is interesting to note that an increase of x between 0.3 and 0.53 does not change the coercivity significantly. The same trend has been recorded for the saturation field (Hsat), which represents the field necessary to reverse the moment of the particles with the highest anisotropy energy. Hsat has been measured as the point in which the difference between the branches is under 3% of their maximum value. The saturation magnetisation (Ms) for the cobalt ferrite is about 110 emu g−1, higher than the value usually reported for bulk CoFe2O4 (80–90 emu g−1).1,2 This may suggest a partially inverse structure.70 As Zn2+ enters the structure, Ms increases up to about 160 emu g−1 for a Zn content of 0.46 and decreases for a higher Zn concentration (∼140 emu g−1). The Ms values are in agreement with the ones found for bulk Co–Zn ferrites4,71 and higher than those reported for nanoparticles with similar compositions.71
The differentiated remanence curve (Fig. 4), consisting of the derivative of MDCD with respect to Hreverse (χirr = dMDCD/dHreverse), represents the irreversible component of the susceptibility. This quantity can be considered as a measure of the energy barrier distribution which, in a nanoparticle system, is associated with a distribution of particle coercivities, and it is generally called the switching field distribution (SFD). It is worth underlining that the cobalt ferrite nanoparticles exhibit a SFD centred at a higher magnetic field (15.5 kOe) with respect to the zinc-substituted ones (between 5 and 6 kOe) in agreement with the trends observed in the M vs. H curves at 5 K for the coercive and saturation fields. In addition it should be underlined that the single peak in SFD clearly indicates the presence of a unique magnetic phase, confirming the morpho-structural characterization (i.e. XRD and TEM) and M vs. H measurements. It is worth noting that the presence of two magnetic phases, also exchange coupled, can be easily highlighted by DCD measurements.7
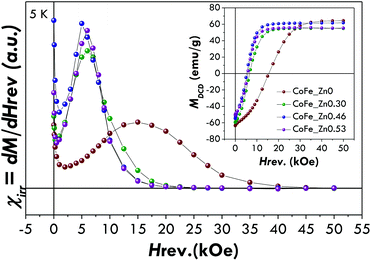 | ||
| Fig. 4 Irreversible susceptibility (χirr = dM/dHrev) derived by DCD curves of the CoFe_Znx (with x = 0, 0.30, 0.46, 0.53) samples. In the inset DCD curves are also shown. | ||
The reduced remnant magnetisation (Mr/Ms) has been found to be equal to 0.58 for the pure cobalt ferrite and lower than 0.5 for the Zn-doped samples. Although the value of 0.58 is far from that expected for the pure cubic anisotropy (the theoretical value is 0.8372), it suggests that CoFe2O4 nanoparticles have a mixed cubic/uniaxial anisotropy, whereas substitution by Zn2+ leads to uniaxial anisotropic nanoparticles.
These data indicate that the insertion of Zn2+ and the consequent decrease of Co2+ produce at 5 K both an increase of the saturation magnetisation and a decrease of the anisotropy with respect to the non-substituted sample.
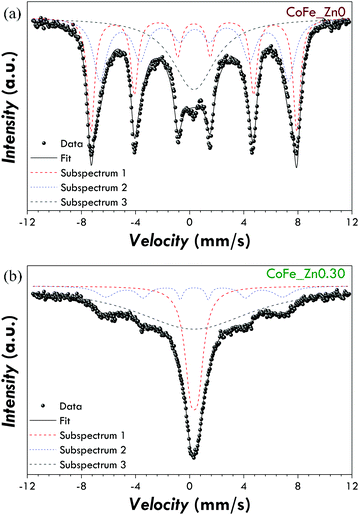
In order to interpret the magnetic behaviour, 57Fe Mössbauer spectroscopy measurements have been carried out at 4.2 K in the absence (Fig. S6 and Table S2†) and in the presence (Fig. 5 and Table 3) of an intense magnetic field (6 T) in order to obtain information on the cationic distribution and spin-canting phenomena. The distribution of iron ions in the octahedral and tetrahedral sites of the spinel structure can be obtained by means of the in-field measurements carried out at low temperature (Fig. 5 and Table 3). All the spectra can be fitted by two well separated sextets related to ferric ions located in the tetrahedral and octahedral sites of a spinel structure. The values of the isomer shift have been found to be higher than the values typical for ferric ions at room temperature (∼0.33 mm s−1). This is something expected as the isomer shift usually increases with decreasing temperature. The cationic distribution of the pure cobalt ferrite has been found to be (Co0.30Fe0.70)[Co0.70Fe1.30]O4 with an inversion degree of 0.70, in agreement with previous studies on CoFe2O4 nanoparticles synthesized by different methods.68,70,73 The substitution of cobalt ions with zinc ones leads to a spinel structure with a reduced inversion degree, which has been found to be equal to 0.50, 0.46, and 0.42 for the samples CoFe_Zn0.30, CoFe_Zn0.46 and CoFe_Zn0.53, respectively. This decrease in the inversion degree can be justified by taking into account the affinity of Zn2+ for tetrahedral sites,5,33,47,74 which forces the Fe3+ to occupy the octahedral ones. Moreover, the effective field values (Beff) are similar in all the samples for Td sites (about 59 T) whereas the Beff values for Oh sites are lower in the case of the zinc-substituted samples (47.7–48.1 T) with respect to the cobalt ferrite (49.4 T). Taking into account that the exchange interactions between octahedral and tetrahedral atoms (JAB) are stronger than the ones between two tetrahedral atoms (JAA) or two octahedral ones (JBB), the effective field of the octahedral sub-lattice will be more affected than the effective field of the tetrahedral sub-lattice when the diamagnetic Zn atoms will be in tetrahedral positions. The consequence is that with the increasing of Zn substitution, the Beff values of the octahedral sub-lattice decrease while the Beff values of the tetrahedral sub-lattice are almost constant. This phenomenon corresponds well with the hypothesis that zinc occupies preferentially 4-fold coordination sites in the spinel structure.
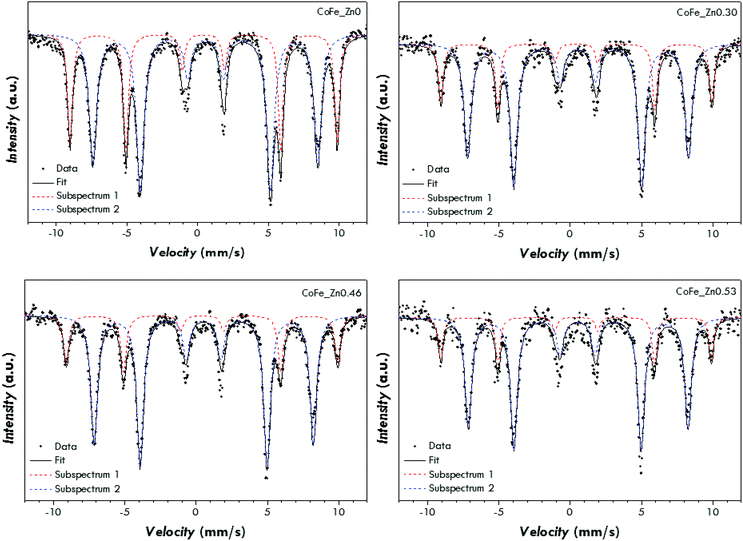 | ||
| Fig. 5 Mössbauer spectra of the CoFe_Znx (with x = 0, 0.30, 0.46, 0.53) samples at 4.2 K under an intense magnetic field (6 T). | ||
| Sample | Subsp. | δ (mm s−1) | ΔEQ (mm s−1) | B eff (T) | FWHM (mm s−1) | A (%) | Interpretation | Cationic distribution |
|---|---|---|---|---|---|---|---|---|
| CoFe_Zn0 | 1 | 0.42 | 0.02 | 58.7(1) | 0.41 | 35 | FeIII in tetrahedral sites of a spinel | (Co0.30(1)Fe0.70(1))[Co0.70(1)Fe1.30(3)]O4 |
| 2 | 0.56 | 0.00 | 49.4(1) | 0.63 | 65 | FeIII in octahedral sites of a spinel | ||
| CoFe_Zn0.30 | 1 | 0.43 | 0.00 | 59.1(1) | 0.41 | 25 | FeIII in tetrahedral sites of a spinel | (MII0.50(3)Fe0.50(2))[MII0.50(1)Fe1.50(3)]O4 |
| 2 | 0.54 | 0.01 | 48.1(1) | 0.61 | 75 | FeIII in octahedral sites of a spinel | ||
| CoFe_Zn0.46 | 1 | 0.42 | −0.01 | 59.1(1) | 0.46 | 23 | FeIII in tetrahedral sites of a spinel | (MII0.54(2)Fe0.46(2))[MII0.46(1)Fe1.54(3)]O4 |
| 2 | 0.54 | 0.01 | 47.7(1) | 0.57 | 77 | FeIII in octahedral sites of a spinel | ||
| CoFe_Zn0.53 | 1 | 0.42 | 0.00 | 58.9(1) | 0.40 | 21 | FeIII in tetrahedral sites of a spinel | (MII0.58(5)Fe0.42(3))[MII0.42(1)Fe1.58(5)]O4 |
| 2 | 0.54 | 0.05 | 47.8(1) | 0.57 | 79 | FeIII in octahedral sites of a spinel |
The Mössbauer measurement on the CoFe2O4 provides the complete cationic distribution for this sample. The theoretical Ms value for this cationic distribution can be calculated on the basis of the Néel model, which accounts for the existence of two magnetic sub-lattices in the spinel structure. This value has been found to be equal to ∼100 emu g−1, which is similar to the experimental Ms value (∼110 emu g−1), in agreement with the absence of spin canting. Indeed, the canting angle has been found to be around zero for all the samples (see Table S3†). The Néel model can also be applied to calculate the theoretical Ms values for the zinc-substituted samples by considering the cationic distribution obtained by the Mössbauer data and assuming that the zinc ions occupy tetrahedral sites. The theoretical values are ∼140 emu g−1, ∼150 emu g−1 and ∼160 emu g−1 for a zinc content of 0.30, 0.46 and 0.53. The values are close to the experimental ones with the exception of the sample with the highest zinc content that probably has a part of the zinc in the octahedral sites, since no evident spin canting phenomena have been revealed by Mössbauer spectroscopy (see Table S3†). Other authors report similar results, both for bulk and nanostructured Zn–Co ferrites, hypothesising cation distributions with a fraction of zinc ions in octahedral sites,71 although this hypothesis is commonly excluded due to the strong preference of zinc ions for a tetrahedral coordination.4,75 Thanks to the multi-technique approach used to characterise the sample, it is possible to reconstruct the cationic distribution on the CoFe_Zn0.53 sample by means of the experimental Ms values obtained by DC magnetometry, the iron ion occupancies found by Mössbauer spectroscopy and the total content of cobalt measured by ICP-OES. The as-obtained cationic distribution is (Zn0.36Co0.22Fe0.42)[Zn0.17Co0.25Fe1.58]O4 and it indicates that ∼30% of zinc ions occupy octahedral sites.
Magnetic properties and heating abilities
Since the increase of Ms with zinc substitution (within a certain zinc content range) can be appealing for biomedical applications, we also studied the magnetic behaviour at 300 K. In this case, M vs. H curves (Fig. 6a) display a superparamagnetic behaviour (i.e. zero remnant magnetisation and zero coercivity) with high Ms values for all the samples. Values near the one reported in the literature for bulk CoFe2O4 (80–90 emu g−1)1,2 and higher than that reported for nanoparticles of similar sizes31,70,76 have been obtained for the cobalt ferrite (CoFe_Zn0) and the sample with the lowest zinc content (CoFe_Zn0.30) (Table 4). This confirms that the surface disorder phenomenon (i.e. spin-canting) is negligible in these samples in agreement with the Mössbauer results and as already observed in the literature.77,78 A higher content of zinc produces a decrease of the saturation magnetisation at room temperature. The observed Ms values for Zn-substituted cobalt ferrites are higher than the ones reported in the literature for nanoparticles71 with similar compositions and similar to the ones found for bulk Co–Zn ferrites.71,75| Sample | M 7T (emu g−1) | M s (emu g−1) | SAR (W gox−1) | SAR (W gMe−1) | ILPox (nH m2 kgox−1) | ILPMe (nH m2 kgMe−1) | τ N (s) | τ B (s) |
|---|---|---|---|---|---|---|---|---|
| CoFe_Zn0 | 87 ± 2 | 92 ± 2 | 19 ± 3 | 26 ± 4 | 0.36 ± 0.05 | 0.49 ± 0.07 | 3.8·10−6 | 8.5·10−6 |
| CoFe_Zn0.30 | 86 ± 2 | 94 ± 2 | 6 ± 2 | 8 ± 2 | 0.11 ± 0.03 | 0.15 ± 0.05 | 2.8·10−9 | 1.1·10−5 |
| CoFe_Zn0.46 | 72 ± 2 | 84 ± 2 | — | — | — | — | — | — |
| CoFe_Zn0.53 | 55 ± 1 | 70 ± 2 | — | — | — | — | — | — |
In the case of ordered magnetic systems, the thermal behaviour of the magnetization is related to the presence of low energy collective excitations (i.e. spin-waves or magnons),79 depending on the particle size and on the chemical composition of the materials.9,80 In the samples under investigation, the increasing of the diamagnetic ion content leads to a different temperature dependence of magnetization, justifying the different Msvs. zinc content at 300 K and 5 K.
Due to the high saturation magnetisation values, we tested the hyperthermal efficiency of all the samples by recording heating curves (Fig. 6b) under a magnetic field of 183 kHz and 17 kA m−1. Only the samples CoFe_Zn0 and CoFe_Zn0.30 characterised by the highest saturation magnetisation values are responsible for a heat release but not to the same extent. In order to quantify the amount of heat released, the SAR has been calculated by the initial slope method and values equal to 19 ± 3 and 6 ± 2 W gox−1, respectively, have been obtained (Table 4).
A comparison with the literature data is not trivial because of the different procedures adopted to measure the heating curves, as, for instance, different frequencies and amplitudes of the external magnetic field. In this regard, in order to compare heating abilities obtained by different frequencies and amplitudes, Pankhurst et al. proposed to use a parameter named Intrinsic Loss Power (ILP) expressed in [nH m2 kg−1], defined as follows:81
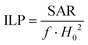 | (6) |
The ILP value calculated for the CoFe_Zn0 sample is 0.36 ± 0.05 nH m2 kg−1. This value is comparable with those obtained by other authors for cobalt ferrite of a similar particle size82 or similar crystallite size.23 Higher ILP values have been reported in the literature for bigger particles,36,82,83 for cobalt substituted iron oxide particles23,32 or for cobalt doped magnetosome chains.84
However, it is worth noting that the ILP is not a completely resolving tool for comparing with the literature data. Indeed, it can be applied only for superparamagnetic systems as it is based on linear response theory assumption. Furthermore, the difficulty in the comparison among the SAR values concerns other aspects that the ILP parameter does not deal with, such as differences in the experimental set-up adopted to measure the heating curve (adiabatic or non-adiabatic), in the solvents and in the analytical models adopted to determine the SAR values (initial slope method, Box–Lucas method, etc.). In addition, the comparison among literature data becomes even more difficult if we consider that often a complete chemical–physical characterisation of the systems in terms of the crystallite size, crystallinity degree, particle size and size distribution, type and amount of capping agent, etc. is lacking.
The difference in the efficiency between CoFe_Zn0 and CoFe_Zn0.30 is considerable despite the similarities in terms of the Ms, particle size, particle size distribution, crystallite size, and capping agent amount. It thus can be explained with the different anisotropies. Indeed, the magnetic measurements at 5 K have shown higher coercivity and saturation fields for the cobalt ferrite sample than the Zn-substituted one.
The results of DC magnetometry appear to be not sufficient to explain the different heating abilities of the samples. Indeed, we should consider that (i) the DC magnetometry is characterised by a time scale in the range 10–100 s; (ii) the relative extent of the measurement and relaxation time scales are critical to make the particles exhibit superparamagnetism rather than quasi-static properties. Therefore, 57Fe Mössbauer spectroscopy and AC magnetometry have been used to study the dynamic properties of the two samples and to understand the physical reasons for the different hyperthermal efficiencies in different samples.
In order to confirm this idea, Mössbauer spectra at room temperature have been recorded (Fig. 7 and S7† for the spectra of all the samples). Both the spectra can be fitted by means of a superposition of sextets and singlets. The isomer shift values suggest only the presence of Fe3+ (Table 5). The sextets account for the blocked spinel ferrite nanoparticles, the sharper singlet (e.g. subspectrum 1 in Fig. 7b) for superparamagnetic nanoparticles, whereas the broad singlet (subspectrum 3 in Fig. 7b) for the particles characterised by a relaxation time close to the measurement time scale. In agreement with the hypothesised scenario, the cobalt ferrite sample shows a higher area of the sextets than the Zn-substituted sample suggesting that it contains a higher percentage of blocked nanoparticles.
| Sample | Subsp. | δ (mm s−1) | ΔEQ (mm s−1) | B Hf (T) | FWHM [mm s−1] | State of iron |
|---|---|---|---|---|---|---|
| CoFe_Zn0 | 1 | 0.36 | −0.03 | 43.3 | 1.19 | Blocked |
| 2 | 0.32 | 0.00 | 47.2 | 0.64 | Blocked | |
| 3 | 0.32 | 0.00 | — | 3.84 | Unblocked | |
| CoFe_Zn0.30 | 1 | 0.34 | −0.56 | — | 1.05 | Unblocked |
| 2 | 0.34 | 0 | 40.6 | 0.23 | Blocked | |
| 3 | 0.33 | — | — | 10.61 | Unblocked | |
| CoFe_Zn0.46 | 1 | 0.34 | 0.52 | — | 0.66 | Unblocked |
| CoFe_Zn0.53 | 1 | 0.34 | 0.51 | — | 0.52 | Unblocked |
In this view, AC magnetometry has been used to measure the temperature dependence of the in-phase (χ′) and out-of-phase (χ′′) components of the magnetic susceptibility at different frequencies (1–1000 Hz) for both samples (Fig. 8). From these data, the Néel relaxation time, τN, has been estimated at 300 K for both the samples by using the Vogel–Fulcher model85 (for the fitting results see the Estimation of Néel relaxation time section in the ESI†):
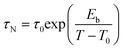 | (7) |
Besides the Néel relaxation, Brownian motion may also concur to the heat release of superparamagnetic nanoparticles. Therefore the Brownian relaxation time, τB, was estimated using the hydrodynamic diameter obtained by dynamic light scattering (DLS) analyses. Similar distributions of the hydrodynamic diameter, centred at 29.2 and 31.5 nm, were obtained for the samples CoFe_Zn0 and CoFe_Zn0.30, resulting in τB values of 8.5 × 10−6 s and 1.1 × 10−5 s, respectively. It arises that τN and τB for CoFe_Zn0 are of the same order of magnitude, suggesting that both the mechanisms contribute to the effective relaxation time. These estimates are nicely confirmed by the behaviour of the AC susceptibility at the melting point of the solutions (Fig. 8) where the Brownian mechanism begins. It should also be underlined that Hergt et al.86 indicated 7 nm as the critical diameter at which τN = τB for cobalt ferrite nanoparticles dispersed in water, indeed a size similar to that of the sample CoFe_Zn0 (∼7.5 nm). In contrast, in the case of CoFe_Zn0.30, τB is four orders of magnitude slower than τN, and thus its contribution is negligible. The maximum heating efficiency will be reached when the time of the faster relaxation process matches the characteristic time of the hyperthermic measurement, τSAR = 1/2πν = 8.7 × 10−7 s. Therefore, cobalt ferrite, with a τeff = (1/τN + 1/τB)−1 = 2.6 × 10−6 s, must be more efficient than the Zn-substituted sample (τeff = of ∼2.8 × 10−9 s).
Conclusions
Four Zn-substituted CoFe2O4 samples with different zinc contents, the same crystallite size, particle size and particle size distribution, and capping agent weight percentage have been ad hoc prepared. This ideal premise has allowed the study of the magnetic properties and the heating abilities exclusively on the basis of the different chemical compositions, the other material features being unchanged.High saturation magnetisation values from 109 emu g−1 to 157 emu g−1 have been obtained at 5 K by increasing the Zn content up to 0.46. A further increase of the Zn content has resulted in a decrease of the saturation magnetisation to a value of 140 emu g−1. The cationic distribution with the preferential 4-fold coordination of zinc ions has been found to justify the observed Msversus Zn content trend at 5 K. Two samples, CoFe2O4 and Zn0.30Co0.70Fe2O4, have also shown at room temperature high and similar saturation magnetisation values (∼90 emu g−1). Despite the similarities between the samples, CoFe2O4 has shown a triple SAR value of 19 W g−1. This different behaviour has been justified by studying on the one hand the relaxation dynamics by combining AC magnetometry and 57Fe Mössbauer spectroscopy and on the other hand by investigating the hydrodynamic properties of the samples. It has been found that the cobalt ferrite sample has both the Néel and Brownian relaxation times that match the characteristic time of the hyperthermic measurement whereas Zn0.30Co0.70Fe2O4 has a faster effective relaxation time. This in the light of the linear response theory gives rise to the higher efficiency of the cobalt ferrite samples.
The study here presented demonstrates the power of a multi-technique approach in the comprehension of both the magnetic properties and the heating abilities. Moreover, the fundamental condition for such an in-depth comprehension remains a systematic study of the effect produced by only one parameter at a time and keeping the other parameters unchanged (in this case the chemical composition). This must be reached by the synthesis of the ad hoc prepared samples. Finally, this kind of study is also needed for the proper design of the material based on a critical choice of the features to be tuned.
Acknowledgements
NTKT thanks The Royal Society for her University Research Fellowship, RAE, EPSRC and AOARD for funding. INPS (Istituto Nazionale di Previdenza Sociale) Gestione ex-INPDAP is acknowledged with thanks for the grant financing for Valentina Mameli. Consorzio AUSI (Consorzio per la promozione delle Attività Universitarie del Sulcis-Iglesiente) is gratefully acknowledged for the fellowship to A. Ardu. The use of the HRTEM facilities of C. G. S. (Centro Grandi Strumenti, University of Cagliari) is gratefully acknowledged. Thanks are due to Enrico Patrizi for the technical assistance in magnetization measurements.Notes and references
- B. D. Cullity and C. D. Graham, Introduction to Magnetic Materials, 2009 Search PubMed.
- J. Smit and H. P. J. Wijn, Ferrites, Philips’ Technical Library, 1959 Search PubMed.
- J. Mohapatra, A. Mitra, D. Bahadur and M. Aslam, CrystEngComm, 2013, 15, 524 RSC.
- G. A. Petitt and D. W. Forester, Phys. Rev. B: Solid State, 1971, 4, 3912–3923 CrossRef.
- I. Sharifi and H. Shokrollahi, J. Magn. Magn. Mater., 2012, 324, 2397–2403 CrossRef CAS.
- Z. Zi, Y. Sun, X. Zhu, Z. Yang, J. Dai and W. Song, J. Magn. Magn. Mater., 2009, 321, 1251–1255 CrossRef CAS.
- G. Muscas, N. Yaacoub, G. Concas, F. Sayed, R. Sayed Hassan, J. M. Greneche, C. Cannas, A. Musinu, V. Foglietti, S. Casciardi, C. Sangregorio and D. Peddis, Nanoscale, 2015, 7, 13576–13585 RSC.
- A. G. Roca, J. F. Marco, M. Del Puerto Morales and C. J. Serna, J. Phys. Chem. C, 2007, 111, 18577–18584 CAS.
- A. Demortière, P. Panissod, B. P. Pichon, G. Pourroy, D. Guillon, B. Donnio and S. Bégin-Colin, Nanoscale, 2011, 3, 225–232 RSC.
- M. V. Kovalenko, M. I. Bodnarchuk, R. T. Lechner, G. Hesser, F. Schäffler and W. Heiss, J. Am. Chem. Soc., 2007, 129, 6352–6353 CrossRef CAS PubMed.
- P. Guardia, A. Labarta and X. Batlle, J. Phys. Chem. C, 2011, 115, 390–396 CAS.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167–R181 CrossRef CAS.
- K. M. Krishnan, IEEE Trans. Magn., 2010, 46, 2523–2558 CrossRef CAS PubMed.
- R. Hachani, M. Lowdell, M. Birchall, A. Hervault, D. Mertz, S. Begin-Colin and N. T. K. Thanh, Nanoscale, 2016, 8, 3278–3287 RSC.
- Magnetic nanoparticles: from fabrication and clinical applications, ed. N. T. K. Thanh, CRC Press, 2012 Search PubMed.
- C. Blanco-Andujar, D. Ortega, P. Southern, S. A. Nesbitt, N. T. K. Thanh and Q. A. Pankhurst, Nanomedicine, 2016, 11, 121–136 CrossRef CAS PubMed.
- T. T. Thuy, S. Maenosono and N. T. K. Thanh, in Magnetic Nanoparticles: From Fabrication to Clinical Applications, 2012, pp. 99–126 Search PubMed.
- Y. Jing, H. Sohn, T. Kline, R. H. Victora and J.-P. Wang, J. Appl. Phys., 2009, 105, 07B305 Search PubMed.
- S. P. Sherlock, S. M. Tabakman, L. Xie and H. Dai, ACS Nano, 2011, 5, 1505–1512 CrossRef CAS PubMed.
- L. Lacroix, N. F. Huls, D. Ho, X. Sun, K. Cheng and S. Sun, Nano Lett., 2011, 11, 1641–1645 CrossRef CAS PubMed.
- J. Wu, W. Zhou, Q. Cheng and J. Yang, RSC Adv., 2015, 5, 22965–22971 RSC.
- J. Jang, H. Nah, J.-H. Lee, S. H. Moon, M. G. Kim and J. Cheon, Angew. Chem., Int. Ed., 2009, 48, 1234–1238 CrossRef CAS PubMed.
- E. Fantechi, C. Innocenti, M. Albino, E. Lottini and C. Sangregorio, J. Magn. Magn. Mater., 2015, 380, 365–371 CrossRef CAS.
- S.-H. Noh, W. Na, J.-T. Jang, J.-H. Lee, E. J. Lee, S. H. Moon, Y. Lim, J. Shin and J. Cheon, Nano Lett., 2012, 12, 3716–3721 CrossRef CAS PubMed.
- C. Cannas, A. Musinu, D. Peddis and G. Piccaluga, J. Nanopart. Res., 2004, 6, 223–232 CrossRef CAS.
- C. Cannas, A. Musinu, D. Peddis and G. Piccaluga, Chem. Mater., 2006, 18, 3835–3842 CrossRef CAS.
- C. Cannas, A. Ardu, A. Musinu, D. Peddis and G. Piccaluga, Chem. Mater., 2008, 20, 6364–6371 CrossRef CAS.
- C. Cannas, A. Musinu, A. Ardu, F. Orrú, D. Peddis, M. Casu, R. Sanna, F. Angius, G. Diaz and G. Piccaluga, Chem. Mater., 2010, 22, 3353–3361 CrossRef CAS.
- C. Cannas, A. Ardu, A. Musinu, L. Suber, G. Ciasca, H. Amenitsch and G. Campi, ACS Nano, 2015, 9, 7277–7286 CrossRef CAS PubMed.
- D.-H. Kim, D. E. Nikles, D. T. Johnson and C. S. Brazel, J. Magn. Magn. Mater., 2008, 320, 2390–2396 CrossRef CAS.
- H. M. Joshi, Y. P. Lin, M. Aslam, P. V. Prasad, E. A. Schultz-Sikma, R. Edelman, T. Meade and V. P. Dravid, J. Phys. Chem. C, 2009, 113, 17761–17767 CAS.
- E. Kita, S. Hashimoto, T. Kayano, M. Minagawa, H. Yanagihara, M. Kishimoto, K. Yamada, T. Oda, N. Ohkohchi, T. Takagi, T. Kanamori, Y. Ikehata and I. Nagano, J. Appl. Phys., 2010, 107, 09B321 CrossRef.
- M. Veverka, P. Veverka, Z. Jirák, O. Kaman, K. Knížek, M. Maryško, E. Pollert and K. Závěta, J. Magn. Magn. Mater., 2010, 322, 2386–2389 CrossRef CAS.
- E. Mazarío, P. Herrasti, M. P. Morales and N. Menéndez, Nanotechnology, 2012, 23, 355708 CrossRef PubMed.
- B. P. Pichon, O. Gerber, C. Lefevre, I. Florea, S. Fleutot, W. Baaziz, M. Pauly, M. Ohlmann, C. Ulhaq, O. Ersen, V. Pierron-Bohnes, P. Panissod, M. Drillon and S. Begin-Colin, Chem. Mater., 2011, 23, 2886–2900 CrossRef CAS.
- S. Nappini, E. Magnano, F. Bondino, I. Píš, A. Barla, E. Fantechi, F. Pineider, C. Sangregorio, L. Vaccari, L. Venturelli and P. Baglioni, J. Phys. Chem. C, 2015, 119, 25529–25541 CAS.
- L. T. Lu, N. T. Dung, L. D. Tung, C. T. Thanh, O. K. Quy, N. Van Chuc, S. Maenosono and N. T. K. Thanh, Nanoscale, 2015, 19596–19610 RSC.
- R. A. Bohara, N. D. Thorat, A. K. Chaurasia and S. H. Pawar, RSC Adv., 2015, 5, 47225–47234 RSC.
- D. S. Nikam, S. V. Jadhav, V. M. Khot, R. S. Ningthoujam, C. K. Hong, S. S. Mali and S. H. Pawar, RSC Adv., 2014, 4, 12662 RSC.
- R. Arulmurugan, G. Vaidyanathan, S. Sendhilnathan and B. Jeyadevan, J. Magn. Magn. Mater., 2006, 303, 131–137 CrossRef CAS.
- G. V. Duong, R. Sato Turtelli, N. Hanh, D. V. Linh, M. Reissner, H. Michor, J. Fidler, G. Wiesinger and R. Grössinger, J. Magn. Magn. Mater., 2006, 307, 313–317 CrossRef CAS.
- G. Vaidyanathan and S. Sendhilnathan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 403, 2157–2167 CrossRef CAS.
- Y. Köseoğlu, A. Baykal, F. Gözüak and H. Kavas, Polyhedron, 2009, 28, 2887–2892 CrossRef.
- S. S. Jadhav, S. E. Shirsath, S. M. Patange and K. M. Jadhav, J. Appl. Phys., 2010, 108, 093920 CrossRef.
- S. Singhal, T. Namgyal, S. Bansal and K. Chandra, J. Electromagn. Anal. Appl., 2010, 2, 376–381 CAS.
- D. Varshney, K. Verma and A. Kumar, J. Mol. Struct., 2011, 1006, 447–452 CrossRef CAS.
- R. Topkaya, A. Baykal and A. Demir, J. Nanopart. Res., 2012, 15, 1359 CrossRef.
- S. K. Dey, S. K. Dey, S. Majumder, A. Poddar, P. Dasgupta, S. Banerjee and S. Kumar, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 448, 247–252 CrossRef CAS.
- J. F. Hochepied and M. P. Pileni, J. Magn. Magn. Mater., 2001, 231, 45–52 CrossRef CAS.
- G. V. Duong, R. S. Turtelli, W. C. Nunes, E. Schafler, N. Hanh, R. Grössinger and M. Knobel, J. Non-Cryst. Solids, 2007, 353, 805–807 CrossRef CAS.
- Mössbauer Spectroscopy, ed. Y. Yoshida and G. Langouche, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013 Search PubMed.
- S. Sun, H. Zeng, D. B. Robinson, S. Raoux, P. M. Rice, S. X. Wang and G. Li, J. Am. Chem. Soc., 2004, 126, 273–279 CrossRef CAS PubMed.
- H. P. Klug and L. E. Alexander, X-ray Diffraction Procedures For Polycrystalline and Amorphous Materials, John Wiley & Sons, Inc., New York, 1954 Search PubMed.
- L. Lutterotti and P. Scardi, J. Appl. Crystallogr., 1990, 23, 246–252 CrossRef CAS.
- R. A. Young and D. B. Wiles, J. Appl. Crystallogr., 1982, 15, 430–438 CAS.
- S. Mondini, A. M. Ferretti, A. Puglisi and A. Ponti, Nanoscale, 2012, 4, 5356–5372 RSC.
- A. H. Morrish, The Physical Principles of Magnetism, 1965 Search PubMed.
- L. Vegard, Zeitschrift für Phys., 1921, 5, 17–26 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767 CrossRef.
- B. P. Ladgaonkar and A. S. Vaingankar, Mater. Chem. Phys., 1998, 56, 280–283 CrossRef CAS.
- E. Wolska, E. Riedel and W. Wolski, Phys. Status Solidi, 1992, 132, K51–K56 CrossRef CAS.
- S. E. Shirsath, M. L. Mane, Y. Yasukawa, X. Liu and A. Morisako, Phys. Chem. Chem. Phys., 2014, 16, 2347–2357 RSC.
- W. B. White and B. A. DeAngelis, Spectrochim. Acta, Part A, 1967, 23, 985–995 CrossRef CAS.
- S. Ayyappan, G. Paneerselvam, M. P. Antony and J. Philip, Mater. Chem. Phys., 2011, 128, 400–404 CrossRef CAS.
- S. Ayyappan, G. Panneerselvam, M. P. Antony and J. Philip, Mater. Chem. Phys., 2011, 130, 1300–1306 CrossRef CAS.
- Q. Song and Z. J. Zhang, J. Am. Chem. Soc., 2012, 134, 10182–10190 CrossRef CAS PubMed.
- Q. Song and Z. J. Zhang, J. Phys. Chem. B, 2006, 110, 11205–11209 CrossRef CAS PubMed.
- E. Fantechi, G. Campo, D. Carta, A. Corrias, C. de Julián Fernández, D. Gatteschi, C. Innocenti, F. Pineider, F. Rugi and C. Sangregorio, J. Phys. Chem. C, 2012, 116, 8261–8270 CAS.
- D. Peddis, C. Cannas, A. Musinu, A. Ardu, F. Orrù, D. Fiorani, S. Laureti, D. Rinaldi, G. Muscas, G. Concas and G. Piccaluga, Chem. Mater., 2013, 25, 2005–2013 CrossRef CAS.
- D. Peddis, N. Yaacoub, M. Ferretti, A. Martinelli, G. Piccaluga, A. Musinu, C. Cannas, G. Navarra, J. M. Greneche and D. Fiorani, J. Phys.: Condens. Matter, 2011, 23, 426004 CrossRef CAS PubMed.
- M. Veverka, Z. Jirák, O. Kaman, K. Knížek, M. Maryško, E. Pollert, K. Závěta, A. Lančok, M. Dlouhá and S. Vratislav, Nanotechnology, 2011, 22, 345701 CrossRef CAS PubMed.
- M. Walker, P. I. Mayo, K. O'Grady, S. W. Charles and R. W. Chantrell, J. Phys.: Condens. Matter, 1993, 5, 2779–2792 CrossRef.
- V. Blanco-Gutiérrez, J. A. Gallastegui, P. Bonville, M. J. Torralvo-Fernández and R. Sáez-Puche, J. Phys. Chem. C, 2012, 116, 24331–24339 Search PubMed.
- K. E. Sickafus, J. M. Wills and N. W. Grimes, J. Am. Ceram. Soc., 2004, 82, 3279–3292 CrossRef.
- P. B. Pandya, H. H. Joshi and R. G. Kulkarni, J. Mater. Sci., 1991, 26, 5509–5512 CrossRef CAS.
- Q. Song and Z. J. Zhang, J. Am. Chem. Soc., 2004, 126, 6164–6168 CrossRef CAS PubMed.
- X. Batlle, N. Pérez, P. Guardia, O. Iglesias, A. Labarta, F. Bartolomé, L. M. García, J. Bartolomé, A. G. Roca, M. P. Morales and C. J. Serna, J. Appl. Phys., 2011, 109, 07B524 CrossRef.
- A. G. Roca, D. Niznansky, J. Poltierova-Vejpravova, B. Bittova, M. A. Gonzalez-Fernandez, C. J. Serna and M. P. Morales, J. Appl. Phys., 2009, 105, 114307–114309 CrossRef.
- R. Hasegawa and R. Ray, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 211–214 CrossRef CAS.
- C. Vázquez-Vázquez, M. A. López-Quintela, M. C. Buján-Núñez and J. Rivas, J. Nanopart. Res., 2011, 13, 1663–1676 CrossRef.
- M. Kallumadil, M. Tada, T. Nakagawa, M. Abe, P. Southern and Q. A. Pankhurst, J. Magn. Magn. Mater., 2009, 321, 1509–1513 CrossRef CAS.
- J.-H. Lee, J.-T. Jang, J.-S. Choi, S. H. Moon, S.-H. Noh, J.-G. J.-W. Kim, I.-S. Kim, K. I. Park and J. Cheon, Nat. Nanotechnol., 2011, 6, 418–422 CrossRef CAS PubMed.
- E. Mazario, N. Menéndez, P. Herrasti, M. Cañete, V. Connord and J. Carrey, J. Phys. Chem. C, 2013, 117, 11405–11411 CAS.
- E. Alphandéry, S. Faure, O. Seksek, F. Guyot and I. Chebbi, ACS Nano, 2011, 5, 6279–6296 CrossRef PubMed.
- E. P. Shtrikman and S. Wohlfarth, Phys. Lett., 1981, 85, 467–470 CrossRef.
- R. Hergt, S. Dutz and M. Zeisberger, Nanotechnology, 2010, 21, 015706 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nr01303a |
| This journal is © The Royal Society of Chemistry 2016 |